Coda-derived source properties estimated using local earthquakes in the Sea of Marmara, Türkiye

Accurate estimates of the moment magnitude of earthquakes that physically measure the earthquake source energy are crucial for improving our understanding of seismic hazard in regions prone to tectonic activity. To address this demand, a method involving coda wave modelling was employed to estimate the moment magnitudes of earthquakes in the Sea of Marmara, northwestern Türkiye. This approach enabled us to model the source displacement spectrum of 303 local earthquakes efficiently recorded at 49 regional seismic stations between 2018 and 2020 in the region. The coda wave traces of individual events were inverted across 12 frequency ranges between 0.3 and 16 Hz. The resultant coda-derived moment magnitudes were found to be in good accordance with the conventional local magnitude estimates. However, the notable move-out between local magnitude and coda-derived moment magnitude estimates for smaller earthquakes less than a magnitude of 3.5 likely occurs due to potential biases arising from incorrect assumptions for anelastic attenuation and/or the finite sampling intervals of seismic recordings. Scaling relations between the total radiated energy and seismic moment imply a non-self-similar behaviour for the earthquakes in the Sea of Marmara. Our findings suggest that larger earthquakes in the study area exhibit distinct rupture dynamics compared to smaller ones, resulting in a more efficient release of seismic energy. Hence, we introduce an empirical relationship obtained from the scatter between local magnitude and coda-derived moment magnitude estimates.

1 Introduction

Having a strong and consistent understanding of source properties (e.g. moment magnitude M_L, released energy E_R, seismic moment M₀) is extremely important in tectonically active regions such as the Sea of Marmara located in the northwest of the North Anatolian Fault Zone (NAFZ) in NW Türkiye. This is essential for accurately assessing seismic hazard potential, as it primarily relies on creating dependable seismicity catalogues. Likewise, precise data on source parameters play a significant role in the development of regional attenuation properties.

Traditional magnitude scales, such as local, body wave, or surface wave magnitude scales (M_L, m_b, M_S) derived from direct wave analyses, may exhibit bias due to diverse factors, including source radiation pattern, directivity, and path heterogeneities. These effects can cause significant changes in direct wave amplitude measurements (e.g. Favreau and Archuleta, 2003). Over the past 4 decades since the pioneering study of Aki (1969), computational seismology has achieved remarkable progress, enabling the integration of scattered wave fields, i.e. coda waves, into studies of source parameters (e.g. Sato et al., 2012). These developments have expanded our understanding of seismic events and improved the accuracy of source parameter estimation. Aki and Chouet (1975) spotted that these scattered wave trains and their spectral content behave similarly at recordings of different stations for a given earthquake. They further noticed that coda duration is independent of azimuth or epicentral distance. More recently, studies analysing local and/or regional coda envelopes suggest that coda wave amplitudes are notably less variable, about 3 to 5 times, compared to direct wave amplitudes (e.g. Mayeda and Walter, 1996; Mayeda et al., 2003; Eken et al., 2004; Malagnini et al., 2004; Gök et al., 2016). It is widely recognized that local or regional coda waves mainly consist of scattered waves. These wave trains can be explained by Aki's single-scattering model (1969), which is significantly less sensitive to source radiation pattern effects compared to direct waves, owing to the volume-averaging property of coda waves that sample an entire focal sphere (e.g. Aki and Chouet, 1975; Rautian and Khalturin, 1978). For a more in-depth understanding of coda generation theory and advances in empirical observations and modelling efforts, see the analysis and summary of Sato et al. (2012).

Various methods depending on coda wave analysis have been utilized for earthquake source scaling. They are usually categorized into two groups. The first group of methods is known as the parametric approach and involves employing a coda normalization strategy. This requires applying corrections (including path effect, S-to-Coda transfer function, site effect, and any distance-dependent changes in coda envelope shape) to the measurements extracted from coda wave envelopes through empirically derived quality factors that account for seismic attenuation parameters (e.g. intrinsic and scattering factors) or site effect caused by near-surface geology conditions. To determine the final source properties, reference events with pre-estimated seismic moments based on waveform inversion techniques are used. Forward calculation of the synthetic coda envelopes is achieved by using either single-backscattering or more advanced multiple-backscattering approximations (Sato et al., 2012). Empirical coda envelope methods have successfully been applied in regions with complex tectonics, such as northern Italy (e.g. Morasca et al., 2008), Türkiye and the Middle East (e.g. Mayeda et al., 2003; Eken et al., 2004; Gök et al., 2016), and the Korean Peninsula (e.g. Yoo et al., 2011).

The approaches in the second group involve estimating source and structural properties using a joint inversion technique in which source-, path-, and site-specific factors are optimized simultaneously by comparing the observed coda envelope with its physically derived representative synthetic coda envelope within a selected time window, including both the observed coda and the direct S-wave parts. While the conventional coda normalization method corrects for undesired effects of source and site amplifications, it may not work well for small events with short coda lengths. This occurs mainly due to dominating random seismic noise that disrupts the requirement of a homogeneous coda wave energy distribution in space. To overcome this limitation, we incorporate source excitation and site amplification terms in the inversion process in which synthetic coda wave envelopes are analytically expressed via the radiative transfer theory (RTT). The RTT was originally implemented on coda waves by Sens-Schönfelder and Wegler (2006) and has successfully been tested on local and regional earthquakes ($\mathrm{4}\le M_{\mathrm{L}}\le \mathrm{6})$ detected by the German Regional Seismic Network. Moreover, it has been applied to investigate source- and frequency-dependent attenuation properties in various geological settings, including the Upper Rhine Graben and Molasse basin regions in Germany (Eulenfeld and Wegler, 2016), western Bohemia–Vogtland in Czechia (Gaebler et al., 2015a), the entire United States (Eulenfeld and Wegler, 2017), and the central and western NAFZ (Gaebler et al., 2019; Izgi et al., 2020). Previous studies (Gusev and Abubakirov, 1996) have further considered a more realistic Earth model with anisotropic scattering conditions, resulting in peak broadening effects of direct seismic wave arrivals. The propagation of P-wave elastic energy and the conversion between P- and S-wave energies with this approach has been used in Zeng et al. (1991), Przybilla and Korn (2008), and Gaebler et al. (2015b).

In this study, we generate source spectra for 303 local events with magnitudes $\mathrm{2.5}\le M_{\mathrm{L}}\le \mathrm{5.7}$ that occurred in the Sea of Marmara region as the product of a joint inversion of S-wave and coda wave components extracted. To estimate coda-derived source spectra and further moment magnitude and total radiated seismic energy of these selected earthquakes, we utilized an open-source Python-based software, Qopen (Eulenfeld, 2020), which employs the isotropic acoustic RTT to calculate synthetic coda envelopes. Gaebler et al. (2015a) noted that modelling outcomes from isotropic scattering were nearly equivalent to those inferred from more complex elastic RTT simulations with anisotropic scattering conditions. Adopting the joint inversion technique offers advantages, as it remains unaffected by potential biases that could arise from external information, such as source properties of a reference earthquake that are separately estimated and then used for calibration in coda normalization methods. The advantage of the approach exploited in this work stems from the analytical expression of a physical model incorporating source- and path-related parameters to describe the scattering process. Furthermore, the optimization process during the joint inversion enables source parameter estimates for relatively small events compared to those employed in coda normalization methods.

2 Regional settings and seismic hazard potential in the Sea of Marmara, NW Türkiye

Our study area is the Sea of Marmara, located in the northwest of the 1600 km-long right lateral strike-slip North Anatolian Fault Zone (NAFZ) that outlines a boundary between the Eurasian plate to the north and the Anatolian plate to the south (Taymaz et al., 1991, 2004, 2007, 2021). The NAFZ has experienced numerous devastating historical earthquakes that have ruptured throughout its the entire length with an overall westward migrating pattern (Stein et al., 1997). The first major earthquake of significant consequence within our specific area of interest occurred in 1912 along the Ganos segment situated in the westernmost part of the NAFZ. More recently, two destructive earthquakes, namely the Izmit earthquake (M_w 7.4, 17 August 1999) and the Düzce earthquake (M_w 7.2, 12 November 1999), affected the northwestern branch of the NAFZ. Barka et al. (2002), using the historical earthquake records published in Ambraseys and Jackson (2000), reported the region lying between the 1912 and 1999 ruptures represents a seismic gap in the Sea of Marmara. Following the 1999 M_w 7.4 Izmit earthquake, Coulomb stress change calculations performed by King et al. (2001) and Durand et al. (2013) demonstrate that new stress accumulation is focused on this western branch in the Sea of Marmara. In fact, precise locations of microseismicity indicated that the two 1999 earthquakes activated seismicity to the south of Istanbul along the northwestern branch of the NAFZ beneath the Sea of Marmara (e.g. Bohnhoff et al., 2013; Sato et al., 2004; Schmittbuhl et al., 2016). Martínez-Garzón et al. (2019, 2021) indicated a frequent interaction between seismic and aseismic slip based on their analyses on microseismicity recordings and borehole strainmeter data from the eastern Marmara. The seismic gap along the northern segment of the NAFZ within the Çınarcık Basin at the eastern shear zone of the Sea of Marmara is well identified by high-resolution observations of microseismicity (e.g. Sato et al., 2004; Bohnhoff et al., 2013) and geodetic locking depth estimates (Ergintav et al., 2014). The existing seismic gap of ∼ 150 km, the unruptured Main Marmara Fault segment (the combination of the northern boundary and the central Marmara segment) of the NAFZ beneath the Sea of Marmara, has been subject to several studies mainly involving spatiotemporal microseismicity characteristics (e.g. Sato et al., 2004; Bohnhoff et al., 2013; Schmittbuhl et al., 2016; Wollin et al., 2018; Irmak et al., 2021). This area is predicted to be the location of a potential major earthquake in the future, as postulated by Bohnhoff et al. (2013). Therefore, it is crucial to have accurate estimates of the physical measures of energy released during small to moderate earthquakes to improve seismic hazard assessments in this tectonically active region.

3 Data

In this study, we exploited digital waveforms of local earthquake recordings from 49 broadband seismic stations in the Sea of Marmara between 2018 and 2020 (Fig. 1). We benefited from revised earthquake catalogue information acquired from the Kandilli Observatory and Earthquake Research Institute (KOERI) to extract waveform data for a total of 375 examined events with station–event pair distance less than 200 km and focal depths less than 20 km. The majority of seismic activity related to the NAFZ in the Sea of Marmara. There are no further requirements, such as taking geographical distribution or azimuthal coverage into account, as coda waves provide a path-wide averaging effect (e.g. Mayeda et al., 2003).

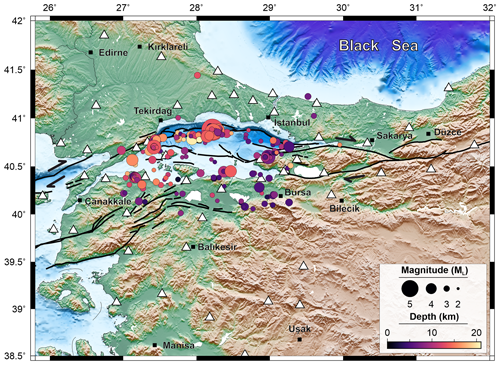
Figure 1 Spatial distribution of 303 local events ($\mathrm{2.5}\le M_{\mathrm{L}}\le \mathrm{5.7}$) that occurred between 2018 and 2020 displayed with circles colour-coded according to focal depths reported by the KOERI catalogue. White triangles indicate stations used in the present work.

Here, to start with, we first deconvolve the instrument response to better mimic the actual ground motion on seismograms. Our data pre-processing steps involved band-pass filtering of velocity seismograms using a Butterworth band-pass filter at several frequency bands with central frequencies of 0.3, 0.5, 0.7, 1, 1.4, 2.0, 2.8, 4.0, 6.0, 8.0, 12.0, and 16.0 Hz that varied depending on the spectral content of a specified event.

Later, we performed a Hilbert transform on the filtered waveform data between each frequency band to generate the total energy envelopes. To predict the P- and S-wave onsets on these envelopes, an average crustal velocity model was employed. Based on this information, several steps taken to ensure more accurate M₀, and thus coda-derived moment magnitude (M_w-coda), can be given as follows:

• i.

  The noise level before the P-wave onset must be disregarded.

• ii.

  The S-wave window must be defined, starting 8 s prior to and 10 s after the S-wave onset to include all direct S-wave energy effectively.

• iii.

  Following the S-wave window, a coda window must start 5 s before and end 150 s after the S-wave onset, or it must end if the signal-to-noise ratio (SNR) is 3.

Here, it is worth mentioning that the length of the coda windows might be shortened under two circumstances: when the SNR is less than 2.5 or when coda waves from two earthquakes (e.g. aftershock sequences) occur within the same analysis window, leading to an additional rise rather than a decrease in the envelope.

The earthquakes with a coda length of less than 10 s and the earthquakes with recordings from fewer than four stations were disregarded by our automated process. We further conducted a visual inspection of each waveform to ensure high-quality data. After applying these criteria, 6557 station–event pairs from 303 out of the 375 analysed earthquakes ($\mathrm{2.5}\le M_{\mathrm{L}}\le \mathrm{5.7}$ within a radius of 200 km) remained to undergo a further data modelling process.

4 Methods

4.1 M_w-coda estimation

We used an inversion scheme adopted by Eken (2019). The procedure was originally developed by Sens-Schönfelder and Wegler (2006), and Eulenfeld and Wegler (2016) later modified it to model intrinsic and scattering attenuation parameters.

The forward part dealing with the energy density computation for a particular frequency band, assuming a source that emits radiation uniformly in all directions (isotropic), is given by Sens-Schönfelder and Wegler (2006) as follows:

$$\begin{array}{}\text{(1)}& E_{\mathrm{mod}}\left(t,r\right)=WR\left(r\right)G\left(t,r,g\right)e^{-bt},\end{array}$$

where R and W indicate the energy site amplification factor and source term, respectively; b represents the intrinsic attenuation parameter; and $G\left(t,r,g\right)$ indicates the Green's function and considers both direct and scattered wave fields. Its analytical expression is given by Paasschens (1997) as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& G\left(t,r,g_{\mathrm{0}}\right)=\exp \left(-v_{\mathrm{0}}t{g}_{\mathrm{0}}\right)\left[{\displaystyle \frac{\mathit{\delta }\left(r-v_{\mathrm{0}}t\right)}{\mathrm{4}\mathit{\pi }{r}^{\mathrm{2}}}}+{\left({\displaystyle \frac{\mathrm{4}\mathit{\pi }{v}_{\mathrm{0}}}{\mathrm{3}{g}_{\mathrm{0}}}}\right)}^{-\frac{\mathrm{3}}{\mathrm{2}}}\right.\\ & t^{-\frac{\mathrm{3}}{\mathrm{2}}}{\left(\mathrm{1}-{\displaystyle \frac{r^{\mathrm{2}}}{v_{\mathrm{0}}^{\mathrm{2}}{t}^{\mathrm{2}}}}\right)}^{\frac{\mathrm{1}}{\mathrm{8}}}K\left(v_{\mathrm{0}}t{g}_{\mathrm{0}}{\left(\mathrm{1}-{\displaystyle \frac{r^{\mathrm{2}}}{v_{\mathrm{0}}^{\mathrm{2}}{t}^{\mathrm{2}}}}\right)}^{\frac{\mathrm{3}}{\mathrm{4}}}\right)\\ & H\left(v_{\mathrm{0}}t-r\right)\left.\right],\end{array}\end{array}$$

with $K\left(x\right)=e^x\sqrt{\mathrm{1}+\frac{\mathrm{2.026}}{x}}$,

where g₀ is the scattering coefficient and v₀ is the mean S-wave velocity. In Eq. (2), the term given within the Dirac delta function describes the direct wave, and the rest represents the scattered wave part of the Green's function.

Potential differences between predicted and observed energy densities for each earthquake recorded at each station using N_ij time samples in a specific frequency band can be minimized by

$$\begin{array}{}\text{(3)}& \mathit{ϵ}\left(g\right)={\sum }_{i,j,k}^{N_S,N_E,N_{ij}}{\left(\ln E_{ijk}^{\mathrm{obs}}-\ln E_{ijk}^{\mathrm{mod}}\left(g\right)\right)}^{\mathrm{2}},\end{array}$$

where N_S and N_E represent the number of stations (index i) and events (index j), respectively. Then, the scattering attenuation parameter (g) will be optimized following Eq. (4):

$$\begin{array}{}\text{(4)}& \ln E_{ijk}^{\mathrm{obs}}=\ln E_{ijk}^{\mathrm{mod}}\left(g\right).\end{array}$$

Substituting Eq. (1) into Eq. (4) will give Eq. (5):

$$\begin{array}{}\text{(5)}& \ln E_{ijk}^{\mathrm{obs}}=\ln G\left(t_{i,j,k},r_{ij},g\right)+\ln R_i+\ln W_j+b{t}_{ijk}.\end{array}$$

Equation (5) contains ${\sum }_{i,j}{N}_{ij}$ equations and $N_S+N_E+\mathrm{1}$ variables, as it indicates an overdetermined inversion problem by having b, R_i, and W_j unknown parameters. Thus Eq. (5) can be solved by using a least-squares approach. ϵ(g) can be defined by the sum over the squared residuals of the solution.

The three main steps followed in this inversion scheme to optimize unknown model parameters (g, b, R_i, and W_j) are given in Eulenfeld and Wegler (2016):

• i.

  Calculation of the Green's function for fixed scattering parameter g and minimizing Eq. (5) to solve for b, R_i, and W_j;

• ii.

  Calculation of ϵ(g) through Eq. (3);

• iii.

  Repeating steps (i) and (ii) by letting g vary to find the optimal b, R_i, and W_j until the error function ϵ(g) is minimized.

In Fig. 2, we present an example for this minimization process that was applied to the observed coda envelopes at 12 different frequency bands generated by using one selected earthquake recorded at 49 seismic stations of the study area.

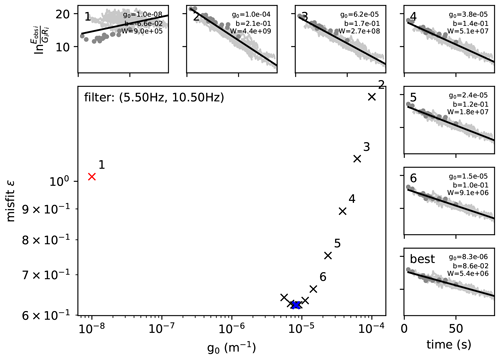
Figure 2 Optimization process for the event (30 November 2018 M_L=2.9 and M_w-coda=3.02) recorded at 23 diverse stations (frequency band 5.5–10.5 Hz). The large panel shows the plot of the ϵ as a function of g₀ for the given frequency band. The blue cross shows the least misfit. The small numbered panels display least-squares solutions for the different g₀ guesses and best fit for optimal g₀. Dark-grey dots represent the ratio $E_{\mathrm{obs}}/GR$, and grey lines represent the observed envelopes from different stations. The thick black line is the line fit to estimate b and W by using its slope.

The yield of the minimization of the error function ϵ(g) outlined above will be the spectral source energy term W_j, site response R_i, and attenuation parameters b and g that satisfy the optimal fitting between observed and predicted coda envelopes.

Using spectral source energy W in the frequency domain, the source displacement spectrum and thus M₀ and M_w can be obtained. Sato et al. (2012) describe the S-wave source displacement spectrum considering a double-couple source in the far field as

$$\begin{array}{}\text{(6)}& \mathit{\omega }M\left(f\right)=\sqrt{{\displaystyle \frac{\mathrm{5}{\mathit{\rho }}_{\mathrm{0}}{v}_{\mathrm{0}}^{\mathrm{5}}W}{\mathrm{2}\mathit{\pi }{f}^{\mathrm{2}}}}}.\end{array}$$

Here, W is the radiated S-wave energy at a centre frequency f, v₀ is the mean S-wave speed, and ρ₀ is the density of the medium.

Abercrombie (1995) elucidated the correlation between the obtained source displacement spectrum and the M₀ with

$$\begin{array}{}\text{(7)}& \mathit{\omega }M\left(f\right)=M_{\mathrm{0}}{\left(\mathrm{1}+{\left({\displaystyle \frac{f}{f_{\mathrm{c}}}}\right)}^{\mathit{\gamma }n}\right)}^{-\frac{\mathrm{1}}{\mathit{\gamma }}},\end{array}$$

where n and γ represent the high-frequency fall-off and the shape parameter, respectively. The latter determines the sharpness of the spectrum between the low-frequency constant level M₀ and the high-frequency fall-off with f⁻ⁿ. By taking the natural logarithm of Eq. (7), we then get

$$\begin{array}{}\text{(8)}& \ln \mathit{\omega }M\left(f\right)=\ln M_{\mathrm{0}}-{\displaystyle \frac{\mathrm{1}}{\mathit{\gamma }}}\ln \left(\mathrm{1}+{\left({\displaystyle \frac{f}{f_{\mathrm{c}}}}\right)}^{\mathit{\gamma }n}\right).\end{array}$$

The observed source displacement spectrum data ωM(f), can be used to determine the other parameters in an inversion, such as M₀, γ, n, and f_c. Lastly, one of the aims of the present work is to derive M_w-coda from the computed M₀ using the formula given by Hanks and Kanamori (1979).

In Eq. (8), an optimization problem is outlined, where the obtained data source displacement spectrum data (on the left) can be modelled to estimate four unknown parameters of the source (M₀, γ, n, and f_c). This is accomplished through a simultaneous least-squares inversion approach. Subsequently, M_w-coda can be computed using the modelled source parameters and M₀, employing a formula introduced by Hanks and Kanamori (1979):

$$\begin{array}{}\text{(9)}& M_{\text{w-coda}}={\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}{\log }_{\mathrm{10}}{M}_{\mathrm{0}}-\mathrm{6.07}.\end{array}$$

4.2 Total radiated seismic energy estimation

In order to estimate the E_R, we firstly integrate source displacement spectrum, ωM(f), following the theoretical formula given by Gök et al. (2009). To be able to exploit the considerable part of the energy associated to the lower frequency part, the observed spectrum is extrapolated to f=0  Hz.

Here, the S-wave radiated energy (E_β) can be calculated by taking the integral of the energy flux in a source sphere (Patton and Walter, 1993):

$$\begin{array}{}\text{(10)}& E_{\mathit{\beta }}={\displaystyle \frac{\mathrm{4}\mathit{\pi }}{\mathrm{4}\mathit{\rho }{\mathit{\beta }}^{\mathrm{5}}}}{\int }_{\mathrm{0}}^{\mathrm{\infty }}{\left|M\left(f\right)\right|}^{\mathrm{2}}\mathrm{d}f={\displaystyle \frac{{\mathit{\pi }}^{\mathrm{2}}{f}_{\mathrm{c}}^{\mathrm{3}}{M}_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{5}\mathit{\rho }{\mathit{\beta }}^{\mathrm{5}}}},\end{array}$$

where density ρ= 2700 kg m⁻³ and S-wave velocity β= 3.5 km s⁻¹. f_c and M₀ represent the corner frequency and seismic moment estimates obtained from the inversion procedure described in Eq. (8). Here, we assume that the contribution from the P-wave radiated energy (E_α) to the total radiated energy is about 7 % of S-wave (e.g. Boatwright and Fletcher, 1984; Mayeda and Walter, 1996). Finally, the sum of the P-wave and S-wave radiated energies yields the total seismic radiated energy (E_R).

5 Results and interpretations

5.1 Coda wave envelope fits

Our preferred acoustic RTT approach to perform forward calculation of the synthetic envelope modelling enabled the modelling of the S-wave energy propagation and thus the comparison between the synthetic and observed data, which is the portion of the seismograms directly between the S-wave arrival and the subsequent seismic coda. Previously, Ryzhik et al. (1996) and Gaebler et al. (2015b) proved the validity of this approach due to the dominance of S-wave energy throughout the seismic signal, encompassing both the initial S-wave arrival and the later portions of the seismic coda. In Fig. 3, envelope fit results are presented for a selected earthquake with M_L 2.9 at different frequency bands (with central frequencies of 3.0, 4.0, 6.0, 8.0, 12.0, and 16.0). The data window length of coda wave trains ranged from −10 to 100 s relative to the onset time for all events in the present study. For the optimization process, the bounds for g₀ and b were chosen to vary between ${\mathrm{10}}^{-\mathrm{8}}-{\mathrm{10}}^{-\mathrm{4}}$ and ${\mathrm{10}}^{-\mathrm{3}}-{\mathrm{10}}^{\mathrm{1}}$, respectively. Ultimately, unknown g₀, b, and W are determined by selecting the most suitable combination of model parameters enabling the lowest error value within each frequency band. Figure 2 shows a summary of the inversion process behind the envelope-fitting process. Accordingly, we can understand the range of the tested g₀ values and further associated estimations of b and W at each iteration. Overall coda envelope fittings clearly illustrate that the synthetic coda envelopes are effectively required by the observed data across diverse regions within the study area and for events with varying magnitudes. The decay of the seismic coda within time windows of up to −10–100 s is also precisely modelled, with a notably faster decay for higher frequencies. The quality of the envelope fits is comparable to those previously presented by Gaebler et al. (2015a), Eulenfeld and Wegler (2016), Gaebler et al. (2019), Eken (2019), and Izgi et al. (2020).

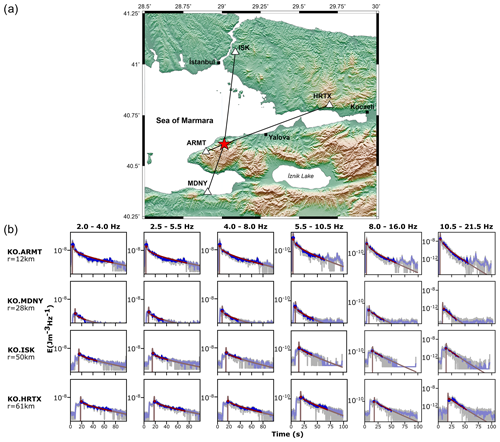
Figure 3 (a) Example event that occurred on 30 November 2018 with M_L=2.9 (shown with a red star) and station pairs (shown with white triangles). (b) Fits between observed and calculated energy densities for an example event. Grey and blue lines indicate the observed energy densities and its smoothed version, respectively. Red curves represent the computed synthetic envelopes calculated using the inversion process.

5.2 Coda wave source spectra

We present the observed values of 303 source spectra (Fig. 4) that were generated by implementing the estimated spectral source energy term W at each frequency into Eq. (7). Overall, the obtained spectra models (Fig. 4) appear to be consistent with a typically expected shape of a source displacement spectrum, featuring a flat region at around the low-frequency limit and a gradual decrease beyond a corner frequency. Earlier, Walter et al. (1995) and Mayeda et al. (2003) showed that the use of coda waves would be more advantageous in scaling up the earthquake size, as they are rather insensitive to differences in the source radiation pattern and path effect. This mainly stems from the influence of multiple scattering caused by small-scale heterogeneities lead to an averaging effect on coda waves. Eulenfeld and Wegler (2016) claimed the radiation pattern had a minor impact on the S-wave coda but that it could potentially disrupt attenuation models inferred from direct S-wave analyses if the station distribution concerning the earthquakes lacks comprehensive azimuthal coverage. The characteristics of a source displacement spectrum, for example, f_c, M₀, and n, may be misleading in traditional approaches (e.g. Abercrombie, 1995; Kwiatek et al., 2011), as they often underestimate potential complexities of the source and structure by considering a fixed frequency-independent attenuation effect described by a factor exponent ($-\mathit{\pi }ft{Q}^{-\mathrm{1}}$) over the spectrum and an omega-square model (Brune, 1970) with a constant high-frequency fall-off parameter, n=2. In the present work, however, we build the source spectra based on a source term decomposed from the effect of intrinsic and scattering attenuation. Separate estimation of source- and structure-related terms is achieved by a simultaneous inversion procedure in which the high-frequency fall-off parameter changes. In line with previous investigations (e.g. Ambeh and Fairhead, 1991; Eulenfeld and Wegler, 2016), we also noted that adopting a more realistic methodology, as opposed to the traditional approach using the omega-square model (where n>3), led to notable discrepancies. These deviations are significant to prompt a reassessment of the widely accepted use of this model for explaining minor earthquakes.

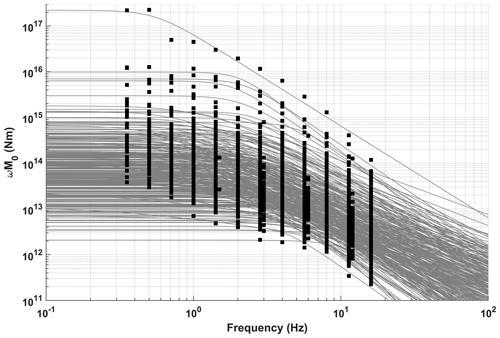
Figure 4 Black squares indicate observed source displacement spectra and grey curves represent predicted source displacement spectra for all 303 individual local earthquakes.

Earlier observations (e.g. Papageorgiou and Aki, 1983; Atkinson, 1990; Joyner, 1984) indicated that source spectra, especially for large earthquakes, could be better described by models involving two corner frequencies. More recently, Denolle and Shearer (2016) reported that the conventional single-corner-frequency spectral model failed to explain P-wave source spectra for large thrust earthquakes (M_w 5.5 and above). To overcome this, they proposed a double-corner-frequency model with a lower-corner frequency associated to source duration and an upper-corner frequency indicating a shorter timescale unrelated to source duration. This upper-corner frequency also exhibits its own scaling relationship. Uchide and Imanishi (2016) reported differences from the omega-square model for smaller earthquakes following the application of a spectral ratio technique to shallow earthquakes with magnitudes ranging between M_w 3.2–4.0 in Japan. They attributed these differences to fault heterogeneities, applied stress, and high-frequency fall-off exponent variations. We observed high-frequency fall-off parameters ranging from n=0.5 to n=3.5, as they were estimated between 2 and 2.5, aligned more closely with earthquakes with M_w-coda>3.5. The smaller magnitudes, on the other hand, exhibited a more scattered pattern in the variation of n (Fig. 5). Eulenfeld and Wegler (2016) argued that a more effective strategy for inverting station displacement spectra to estimate source parameters involves employing separate estimates of attenuation or accounting for path effects through empirically determined Green's functions. This is mostly required for smaller earthquakes (with n>2), given that an omega-square model can distort estimates of f_c and M₀, particularly in the regions of strong frequency-dependent quality factor (Q). Hence, we suggest that, when performing inversion for source parameters, it is essential to incorporate independent Q estimates or remove the path influence including the attenuation via empirically determined Green's functions (Eulenfeld and Wegler, 2016).

Figure 5 Scatter plot of M_w-coda as a function of M_L with high-frequency fall-off parameters n. The value of the n is colour-coded, with a legend on the right.

5.3 Coda-derived moment magnitude (M_w-coda)

A comparison between M_L-based catalogue magnitudes (the KOERI earthquake catalogues) and our M_w-coda indicates an overall good accordance between them, except for only a few outliers caused by small-magnitude earthquakes. This can be considered to be an effective usage of a straightforward model using first-order approximation for S-wave scattering with an isotropic acoustic radiative transfer approach in relating the amplitude and decay characteristics of coda wave envelopes to the M₀ of an earthquake at its source.

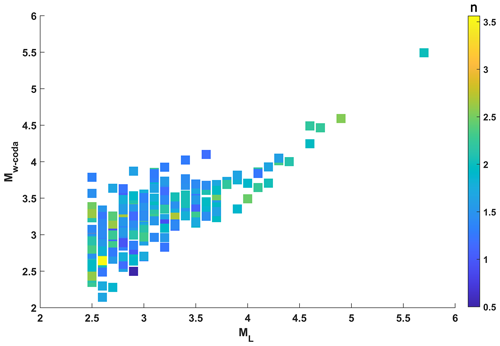
Here we introduce an empirical equation (Eq. 11) that is obtained based on a linear regression analysis between M_w-coda and M_L (Fig. 6). It can be used to convert M_L into M_w-coda for local earthquakes in this region and conduct a linear regression analysis between M_w-coda and M_L (Fig. 6).

$$\begin{array}{}\text{(11)}& M_{\text{w-coda}}=\left(\mathrm{0.6677}\mp \mathrm{0.0309}\right)M_{\mathrm{L}}+\mathrm{1.1914}\mp \mathrm{0.09345}\end{array}$$

In one of the earliest examples of this type of comparison, an empirical linear logarithmic relationship between M₀ and M_L for earthquakes near Oroville, California, was established by Bakun and Lindh (1977). Other studies have explored the optimal relation between M_w and M_L using linear and/or nonlinear curve-fitting techniques. Instead of using a single linear fit, Malagnini and Munafò (2018) proposed two separate linear fits for M_L–M_w data points from earthquakes in the central and northern Apennines, Italy, divided by a crossover at M_L=4.3. Various factors, i.e. source scaling, crustal attenuation and/or regional attenuation, focal depth, and rigidity of the source region, were considered in the regression analyses. Relatively complicated forms of empirical functions have been proposed in recent years, for instance, (1) a second-order polynomial form (e.g. Edwards and Rietbrock, 2009) associating local magnitude estimates from the Japan Meteorological Agency (JMA) with the M_w, a hybrid type of scaling relation (e.g. Goertz-Allmann et al., 2011) with a quadratic form in between ($\mathrm{2}\le M_{\mathrm{L}}\le \mathrm{4}$) and linear outside this range tested for Swiss earthquakes, or (2) a quadratic form of correlation between JMA magnitudes and M_w of the seismic activity in the Fukushima Hamadōri and northern Ibaraki prefecture areas of Japan (Uchide and Imanishi, 2018). The empirical curve derived in Uchide and Imanishi (2018) indicated a notable difference between these two magnitude scales. In their work, the graph's slope of $\mathrm{1}/\mathrm{2}$ for microearthquakes was attributed to potential biases stemming from anelastic attenuation and presumable limitations of recording through a finite sampling interval.

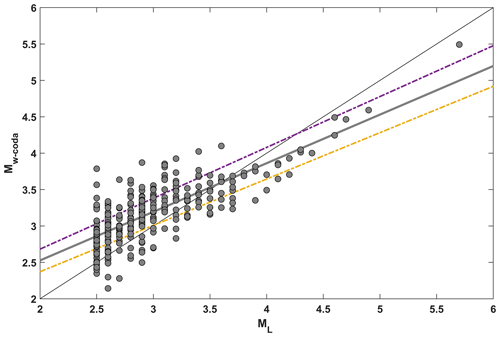
Figure 6 Scatter plot of M_w-coda as a function of M_L. The bold grey line represents the linear regression fit, and dashed lines are the standard deviation.

Our linear empirical relation between M_w-coda and M_L highlights an apparent move-out in Fig. 5 and Eq. (10) as being consistent with findings from early applications of the same type of coda wave modelling studies performed in different geological areas of Türkiye, including the central and western NAFZ (e.g. Gaebler et al., 2019; Izgi et al., 2020) and central Anatolia (Eken, 2019). This likely occurs due to the use of different magnitude scales for comparison. Traditional magnitude scales, such as M_L, based on phase amplitude measurements, are prone to being affected by attenuation and path variations (Pasyanos et al., 2016). In contrast, seismic-moment-based moment magnitude (M_w) directly measures the strength of an earthquake from fault slip. It is derived from a mostly flat portion of source spectra at lower frequencies, making it less affected by near-surface attenuation. The relatively good agreement between M_w-coda and M_L scales for the earthquakes with M_w-coda>3.5 demonstrates the efficacy of the non-empirical method in this tectonically complicated region. This is expected for larger earthquakes whose source displacement spectra will carry more energy at lower frequencies. A similar behaviour of such coherence was observed in this region in previous works, where source characteristics of local and regional earthquakes were examined using empirical coda methods assuming simple 1D radially symmetric path correction (e.g. Eken et al., 2004; Gök et al., 2016). Previous empirical coda envelope modelling studies (e.g. Mayeda et al., 2005a; Morasca et al., 2010) were able to estimate accurate coda-wave-derived source parameters using 2D path-corrected station techniques that account for amplitude–distance relationships. However, noticeable outliers in our estimates (Figs. 5 and 6) for the events with magnitudes less than M_w-coda 3.5 could be attributed to potential biases in M_L values extracted from the catalogue and to small biases in the intrinsic and scattering attenuation terms. Besides this, such discrepancies may reflect the effects of mode conversions between body and surface waves or surface-to-surface wave scattering, which extend beyond low frequencies (Sens-Schönfelder and Wegler, 2006).

5.4 Self-similarity

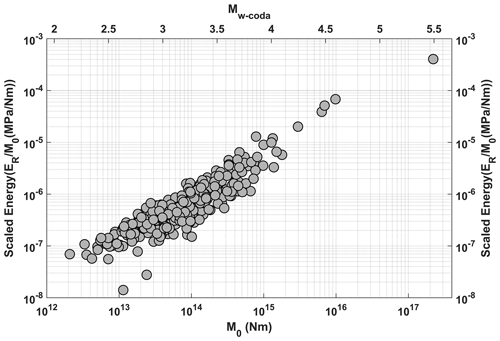
Accurate estimates of the M₀, overall radiated seismic energy of earthquakes, and associated scaled energy ($E_{\mathrm{R}}/M_{\mathrm{0}}$) are of great importance for clarifying dynamic modelling scenarios that are helpful to understand ground shaking for large, damaging earthquakes and the physics behind faulting process. This is mainly because of the issue of how big the earthquake ground motions are in proportion to radiated energy at the source (e.g. Brune, 1970). Whether earthquakes exhibit self-similar scaling or larger earthquakes differ in dynamics from smaller ones has been a subject of debate for a long time. Answering this question is essential for making both decent seismic hazard assessments and inferences on the fundamentals of rupture dynamics during an earthquake. Over many years, it has been widely accepted that the $E_{\mathrm{R}}/M_{\mathrm{0}}$ remains nearly constant for earthquakes of varying magnitudes from small to large (e.g. Aki, 1967; Kanamori and Anderson, 1975). However, several investigations within the last 2 decades have observed that this ratio would tend to increase proportionally with the M₀ (e.g. Abercrombie, 1995; Izutani and Kanamori, 2001; Kanamori et al., 1993; Mayeda and Walter, 1996; Mori et al., 2003; Prejean and Ellsworth, 2001; Richardson and Jordan, 2002). Conversely, there is almost an equal number of studies that advocate for a constant energy ratio (e.g. Choy and Boatwright, 1995; Ide et al., 2003; Ide and Beroza, 2001; McGarr, 1999; Prieto et al., 2004). Unfortunately, the substantial uncertainty surrounding seismic energy has led to a diversity of interpretations of this ratio, even among researchers analysing the same dataset.

Recent advancements in scaling the size of earthquake efforts that are based on distinctive approaches using local, regional, and teleseismic data with different frequency contents enable us to quantify scalar seismic moments, which usually exhibit small discrepancies (more than a factor of 2) for the same given event (Mayeda et al., 2005b). In contrast, the quantity of the released seismic energy of an earthquake is rather a dynamic phenomenon and thus remains a complex endeavour, often resulting in variations exceeding a factor of 2 among estimates obtained by various techniques (Pérez-Campos et al., 2003). It requires substantial corrections that consider path and site effects across a wide range of frequencies. Further corrections for the directivity and some other heterogeneities in source radiation pattern are equally important and must be considered. Thus, this ratio has been difficult and becomes the subject of recent debate among experts in the field of seismology. The uncertainty in seismic energy calculations causes different interpretations of the apparent stress associated to the fault rigidity, which may control the $\mathrm{energy}/\mathrm{moment}$ ratio or seismic energy density. To estimate M₀ and E_R, we benefit from the inherent averaging characteristic of coda waves that has been proved earlier to yield notably less variability in amplitude compared to any conventional direct phase methods (e.g. Eken et al., 2004; Mayeda et al., 2003; Shelly et al., 2022).

Figure 7 Scatter plot of scaled energy ($E_{\mathrm{R}}/M_{\mathrm{0}})$ as a function of both M₀ and M_w.

The relationship between M₀ and $E_{\mathrm{R}}/M_{\mathrm{0}}$ observed in this study (Fig. 7) indicates that $E_{\mathrm{R}}/M_{\mathrm{0}}$ values increase with the M₀ for crustal earthquakes with M_w-coda 2.5 and M_w-coda 5.7, implying these earthquakes are likely to follow non-self-similarity. Yoo et al. (2011) previously reported that the $E_{\mathrm{R}}/M_{\mathrm{0}}$ rapidly increases for smaller events in particular ($<M_{\mathrm{w}}\sim \mathrm{3.3})$. They attributed the size dependency of the scaled energy to the fact that the energy radiation efficiency through seismic waves greatly varies at lower magnitudes. On the other hand, we have not observed any distinct change in the trend of $E_{\mathrm{R}}/M_{\mathrm{0}}$ versus M₀ for events in our data. The similar sharp increase has been observed in some early studies of coda-based source modelling, where a different and fully empirical coda normalization method was used (Mayeda et al., 2007; Morasca et al., 2005; Yoo and Mayeda, 2013). Eulenfeld et al. (2021, 2023) used the same coda wave modelling approach as that used our study, where frequency-dependent source, site, and attenuation properties are inverted in a non-empirical stepwise approach based on a fully analytical RTT assumption in the forward calculation of synthetic coda envelopes. They also observed deviations from self-similar behaviour of the earthquake rupture. In the previous subsections of the Results and interpretations section, we already discussed that considering a constant attenuation ratio for events of different sizes, or simply the omega-square model, may lead to misleading estimates of source properties. As previously stated in Sect. 5.2, Eulenfeld and Wegler (2016) observed that modelling of source displacement spectra with n> 2 under the assumption of the omega-square model (n=2) would still result in a good fit due to the high trade-off between the attenuation and n. However, they observe that this causes a distortion of f_c and even M₀ estimates if the assumed frequency dependence of Q is not accurately considered. Consequently, they suggest the use of independently obtained estimates of Q when inverting station displacement spectra for source parameters. To reduce this risk, we therefore perform a stepwise inversion scheme where scattering and intrinsic attenuation are also modelled. This allows a realistic consideration of attenuation when estimating the source term at each frequency band. Shearer et al. (2019) claimed that assuming a fixed fall-off rate, which controls the spectral shape, may artificially result in non-self-similarity. To overcome this, we employed an inversion procedure for modelling source displacement spectra where the n term varied. The inversion for the source displacement spectra, in which independent and more realistic attenuation properties with varying n are considered, leads to a scaling of corner frequencies with M₀ that differs from the scaling associated with self-similarity. Under the assumption of the omega-square model, a constant $E_{\mathrm{R}}/M_{\mathrm{0}}$ independent of M₀ (or a constant stress drop independent of magnitude) implying self-similarity corresponds to a proportionality $M_{\mathrm{0}}\propto f_{\mathrm{c}}^{-\mathrm{3}}$. Eulenfeld et al. (2023) noticed that a breaking of self-similarity is not surprising when the exponent defining this trade-off between M₀ and f_c is smaller than −3. It is also equally important to note that the propagation of potential artefacts into the non-constant behaviour of the scaled-energy variation with M₀ can be attributed to the significant impact of the f_c compared to M₀. This is primarily due to the fact that M₀, which is estimated through the low-frequency plateau, is relatively insensitive to the selection of fitting parameters. In contrast, f_c is considerably more sensitive and variable. The most probable artefact, which may be related to the attenuation estimation or spectral fitting process, has the potential to the biased self-similarity analysis. This occurs due to a spurious masking effect associated with excess high-frequency attenuation, which causes the observed shift in f_c towards smaller frequencies for smaller events when direct waves are in use (Eulenfeld et al., 2023). The use of the Qopen approach, however, provides an advantage of allowing the attenuation to be determined independently from properties of the full waveform envelope instead of the short direct pulse, which diminishes possible bias in the estimation of f_c. The increasing variation in $E_{\mathrm{R}}/M_{\mathrm{0}}$ with M₀ resulting from source properties in the present study can be considered reliable, given that the Qopen algorithm is less sensitive to potential artefacts. This is due to the advantages of using coda waves and implementing a more realistic knowledge of frequency-dependent attenuation during modelling for source displacement spectra. Finally, our initial observation on the variation in scaled energy implies that different rupture dynamics work for large earthquakes than for small ones and that the seismic energy radiates more efficiently for relatively large earthquakes in the Sea of Marmara located in the northwestern part of the NAFZ.

6 Conclusion

This study provides the physical measure of the released seismic energy in M_w-coda for minor to moderate size local earthquakes ($\mathrm{2.5}\le M_{\mathrm{w}}\le \mathrm{5.7}$) that occurred between 2018 and 2020 in the Sea of Marmara region, NW Türkiye. This was accomplished by using digital waveform recordings taken from 49 three-component broadband seismic stations located within the study region. We used radiative transfer theory for the forward calculation of synthetic coda wave envelopes during an iterative inversion procedure employing a stepwise manner to model the source properties and the site and path effects simultaneously based on the smallest misfit between observed and synthetic envelopes. The good accordance between M_w-coda and M_L proves the competence of this non-empirical coda wave approach to obtain reliable estimates of source properties in this complex tectonic setting. The variability in the high-frequency fall-off parameter highlighted that, for smaller earthquakes (n >2), considering an omega-square model could distort estimates of f_c and M₀. This effect is particularly pronounced in regions where Q exhibits strong frequency dependency. A linear regression analysis further provided an empirical relation developed between M_w-coda and M_L, which can be a useful tool in the future to quickly convert catalogue magnitudes into M_w for local earthquakes in the study area. Finally, the scaled energy ($E_{\mathrm{R}}/M_{\mathrm{0}}$) exhibits an increasing pattern with reliable coda-wave-derived seismic moment estimates at almost all magnitude ranges, as this implies that small to moderate seismic activity in the region indicates a non-self-similar scaling at its source.