Uncertainty in regional estimates of capacity for carbon capture and storage

Carbon capture and storage (CCS) is a potentially important technology for the mitigation of industrial CO₂ emissions. However, the majority of the subsurface storage capacity is in saline aquifers, for which there is relatively little information. Published estimates of the potential storage capacity of such formations, based on limited data, often give no indication of the uncertainty, despite there being substantial uncertainty associated with the data used to calculate such estimates. Here, we test the hypothesis that the uncertainty in such estimates is a significant proportion of the estimated storage capacity, and should hence be evaluated as a part of any assessment. Using only publicly available data, a group of 13 experts independently estimated the storage capacity of seven regional saline aquifers. The experts produced a wide range of estimates for each aquifer due to a combination of using different published values for some variables and differences in their judgements of the aquifer properties such as area and thickness. The range of storage estimates produced by the experts shows that there is significant uncertainty in such estimates; in particular, the experts' range does not capture the highest possible capacity estimates. This means that by not accounting for uncertainty, such regional estimates may underestimate the true storage capacity. The result is applicable to single values of storage capacity of regional potential but not to detailed studies of a single storage site.

1 Introduction

Geological storage of carbon dioxide (CO₂) has been proposed as a potential technological solution to help reduce emissions of greenhouse gases, given the continued use of fossil fuels to meet much of the world's energy requirements. In carbon capture and storage (CCS), the CO₂ produced from industrial sources is captured and transported to a geological storage site and injected deep into the subsurface where it is stored indefinitely in the pore space of the rocks. Saline aquifers, rock formations where the pore space is filled with brines too saline for useful extraction, offer the largest storage capacity (Holloway, 1997). However, unlike hydrocarbon reservoirs, such formations often have limited legacy data. In order to identify potential storage sites that are worth the investment required for detailed assessment, attempts have been made to characterise regional saline aquifers using this legacy data on both a regional and national scale, e.g. the NATCARB Atlas for the USA (https://edx.netl.doe.gov/geocube/#natcarbviewer, last access: 1 October 2019) and the CO2 Stored database for the UK (http://www.co2stored.co.uk, last access: 1 October 2019). However, care must to taken to account for the substantial uncertainty associated with such regional assessments. The capacity of a geological formation to store CO₂ securely is a first-order concern in any storage assessment, and the basic methodology is well established (Bachu, 2000). Lack of capacity is one of the highest risks to carbon capture and storage projects (Polson et al., 2012) and uncertainty affects the design of transport and injection networks (Keating et al., 2011; Middleton et al., 2012a; Sanchez Fernandez et al., 2016).

Previous work on the subject includes the influence of estimated storage capacity due to uncertainty in thermophysical properties (pressure and temperature of the reservoir; Calvo et al., 2019). A rigorous Monte Carlo approach has been demonstrated using the CO₂-PENS tool (Keating et al., 2011), and it has been shown that uncertainty in reservoir parameters can impact reservoir cost and capacity estimates by as much as an order of magnitude (Middleton et al., 2012b). The approach allows for the integration of site-specific data over a large range of size scales (Middleton et al., 2012a). Integrated Monte Carlo simulations constructed using regional data have been used to assess CO₂ injectivity, the area of review, migration rate into confining rocks and the probability of detecting the injected CO₂ plume in monitoring wells (Dai et al., 2014). The state of the art is possibly the integrated assessment model developed by the US DOE-funded National Risk Assessment Partnership (Pawar et al., 2016). This approach has not yet been universally adopted and cannot be easily applied retrospectively to pre-existing studies.

Many published regional studies of CO₂ storage capacity quote single values for the capacity of individual formations, sometimes with ranges allowing for uncertainty in a single parameter such as the proportion of pore space that can be utilised for storage (“storage efficiency”), e.g. Medina et al. (2011). The reporting of individual studies varies but some provide storage estimates to six significant figures, implying a precision of greater than 0.001 %. However, this precision is clearly unachievable since the commonly used methodologies for capacity calculation of saline aquifers (e.g. Goodman et al., 2011) requires inputs which are inherently variable over the area of assessment, such as the thickness of the formation, net : gross ratio (the proportion of usable reservoir within the overall unit thickness) and porosity. When offshore locations are considered, data are usually available from only a small number of borehole penetrations, often with a spacing between boreholes of several kilometres. While there are published methods for dealing with such uncertainty (Burruss et al., 2009; Keating et al., 2011; Smith et al., 2011; Pawar et al., 2016), estimates of the variability in each input parameter must be made and suitable software employed for the calculation. Consequently the use of single-value storage estimates is both quicker and cheaper than full probabilistic assessments.

Furthermore, capacity assessments will largely depend on expert interpretation of geological data, and are therefore dependent on the prior knowledge and experience of individual experts (see Curtis, 2012, for summary). Studies have shown that geological experts are subject to a range of cognitive biases, as are all individuals (Kahneman et al., 1982), that combined with differences in prior experience can influence their interpretation of data leading to subjective results (e.g. Phillips, 1999; Polson and Curtis, 2010; Bond et al., 2012). As a result, an estimate of the uncertainty in single-value storage capacities is of practical use, not least with assessments already published but lacking an assessment of uncertainty. This is of particular practical importance where a storage estimate falls close to a cut-off value, below which, for example, a potential storage unit may be rejected as having a storage capacity that is too low to be economically viable. For example, a regional screening study (Wilkinson et al., 2010) rejected all units below an arbitrary 50 Mt of estimated CO₂ storage capacity. For an individual storage project the minimum acceptable storage capacity value is likely to be determined by the volume of CO₂ to be stored over the project lifetime.

Here, we test the hypothesis that the uncertainty in storage estimates is a significant proportion of the estimated storage capacity, and should hence be evaluated as a part of any assessment. For this study, an assessment of the precision of storage capacity estimates was conducted as part of a study of an area of the UK territorial waters, in the Inner Moray Firth area of the North Sea (Fig. 1). Subsurface geological data were available from boreholes drilled by the petroleum industry, both as individual well records released by the UK Government and summarised in scientific publications. The subsea strata are largely siliciclastics of Devonian to Jurassic age. They rest are unconformably on strata that were affected by the lower Palaeozoic Caledonian orogeny (Andrews et al., 1990), which are here considered to be basement (i.e. to have no storage potential). To the east of the area there is a variable-thickness cover of Cretaceous chalk, a fine-grained pelagic limestone, here not considered a potential store as it lacks an obvious seal. Questions concerning the presence of a suitable seal, trapping structures and potential leakage pathways were addressed in the wider study but are not reported here.

Figure 1 Location map of study area.

2 Materials and methods

A group of 13 graduate students, who had been trained in the methodology of storage capacity estimation and in at least basic geology relevant to CO₂ storage, assessed the capacity of the potential saline aquifers in the area. All the students were studying for a Masters of Science degree in Carbon Capture and Storage and can be considered to be expert in the subject, though their prior backgrounds are variable ranging from geosciences to engineering. The experts had to identify the potential reservoir formations (saline aquifers) within the area using the scientific literature, then collect the input information required to perform the basic storage capacity estimates (surface area, thickness, porosity, net : gross ratio). The product of these parameters is an estimate of the volume of porewater within the aquifer, which may be compressed or partly displaced allowing for the storage of CO₂.

$$\begin{array}{}\text{(1)}& M=Ah\mathrm{NG}\mathrm{\Phi }\mathit{\rho }E,\end{array}$$

where M is the mass of CO₂ that can be stored, A is the area that defines the region being assessed, h is the thickness of the saline aquifer, NG is the net : gross ratio, Φ is the porosity, ρ is the density of CO₂ and E is a storage efficiency factor.

For surface area, the experts were directed to maps within Cameron (1993) and Richards et al. (1993); each expert independently estimated the area. Uncertainty in this parameter is therefore due to the variable interpretation of the same data from expert to expert. For the other parameters, the experts were expected to locate suitable data, primarily using web-based search tools. The uncertainty in these parameters is therefore determined by the total number and range of published values, the ease with which experts could find relevant information, and the interpretation by the experts of the applicability and reliability of the data that they located.

For the purposes of this paper, the values for each variable provided by the experts were combined with constant values of CO₂ density (650 kg m⁻³) and storage efficiency (the proportion of pore space that can be utilised for storage, here taken to be 0.02), and the total storage capacities were recalculated for each expert using Eq. (1). This approach was undertaken to remove non-geological effects from the results, such as variation in estimated CO₂ density due to the use of different equations of state or pressure and temperature conditions of burial and also any calculation errors. These individual estimates are hereafter referred to as experts' estimates; however, they are not the estimates calculated by the individual experts but the estimates recalculated by the authors using the data collected by each expert. For each geological unit, the standard deviation of the storage estimates was calculated across the set of individual storage volume estimates. All experts gave express permission for their data to be used for this purpose.

In order to determine the full range of possible estimates from the expert-derived values, storage estimates were calculated for all possible combinations of the variables. The resulting distribution of the storage estimates, P(M), gives an indication of their uncertainty. However, as this method does not take into account the real uncertainty in each variable (which is unknown), P(M) is not the probability distribution of the storage capacity.

3 Results

There are seven geological units (which are either formations or members in formal nomenclature; Cameron et al., 1993; Richards et al., 1993) that are potential storage reservoirs in the area, henceforth called storage units. Figure 2 shows P(M) as a cumulative density function for each formation, and Table 1 shows the median and range of the individual expert estimates and the 5th, 95th and median of P(M). Both show a wide range of possible estimates for the storage capacity. The range of P(M) is typically between 2 and 6 times the median value, though in the case of the Orrin Formation the range is 13 times the median.

Table 1 Range of individual expert and distribution (P(M)) estimates of storage capacity. Numbers in brackets are values expressed as a percentage of the median. Raw data are available in the Supplement to this article. Raw data are available in the Supplement to this article.

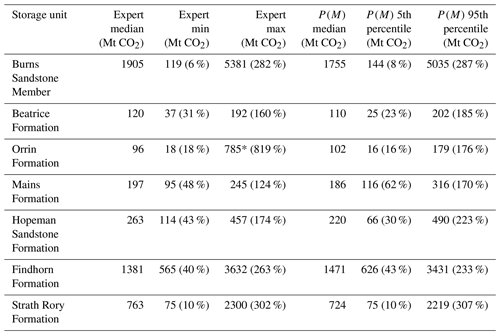
^* This is significantly higher than the 95th percentile due to one expert estimating the volume of the formation to be significantly higher than the other experts.

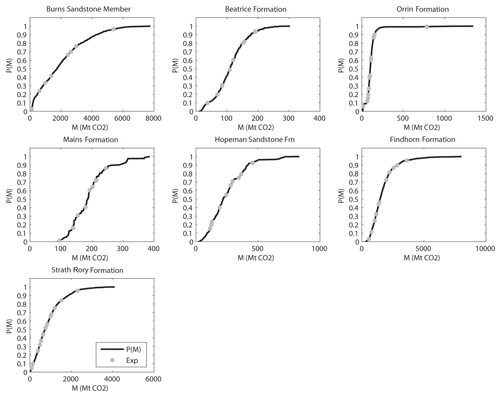
Figure 2 Range of storage capacity estimates using the different values for variables found by group of experts for seven saline aquifers. Range is shown as a cumulative density function but does not represent the true probability density function for each aquifer.

The median values of the expert estimates tend to be similar to the median of the distribution (within 10 %, except the Hopeman Sandstone Formation which is within 20 %). The individual expert estimates tend to cover the range from the 5th to 95th percentiles of P(M), though in three formations the minimum expert estimate exceeds the 5th percentile of P(M); in the case of the Hopeman Sandstone Formation, the lowest expert estimate is around the 15th percentile. For 2 formations, the maximum expert estimate is less than the 95th percentile of P(M) and for all formations the highest value of P(M) exceeds the maximum expert estimate by between 40 % and 120 %.

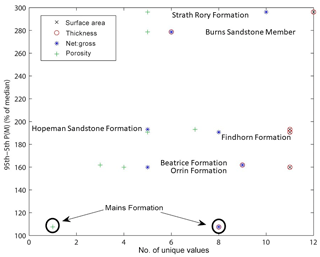
The 5th to 95th percentiles expressed as a percentage of the median value of P(M) can range from 8 % to 62 % for the 5th percentile and 170 %–307 % for the 95th percentile (the expert estimates show a similar range; Table 1). Figure 3 shows the range of P(M) against the number of unique values for the surface area, thickness, net : gross ratio and porosity. Surface area and thickness coincide because there are the same number of unique values for all formations.

Figure 3 The range of P(M) (5th–95th percentile) against number of unique values for the area, thickness, net : gross ratio and porosity.

4 Discussion

The storage capacity estimates of seven saline aquifers by a group of experts shows that any single estimate by one expert might be a gross under- or overestimation of the median storage capacity. Even using a cohort of experts to provide independent estimates of the storage capacity does not cover the full range of possible values using just the data that those same experts collected. In particular, the range of expert estimates underestimated the highest values of the storage capacity by at least 40 % (and up to 120 %). As there are no reasons to assume that any one combination of variables is more or less likely than any other, all possible combinations must be assumed to have the same probability. Hence the storage capacity calculated using all minimum or maximum values for all variables are equally likely as any other individual combination, though there are more combinations of variables that will produce storage capacities around the median value than the extremes, making an estimate around the median more likely overall.

The number of experts in the study was necessarily limited; however, using more experts would not alter the outcome of the study. More experts may increase the range of estimates produced but would certainly not decrease it. Having more experts might be predicted to decrease the standard deviation of the mean estimate; however, as above, there is no reason to consider that the mean estimate is a better estimate of the true (unknown) value of the storage capacity than any other value.

It is therefore evident that the uncertainty associated with a single estimate of CO₂ storage capacity for a saline aquifer is large compared to the precision with which at least some published values are presented. Given both the small database upon which estimates are typically based and the inherent variability in the geological parameters involved, the result is perhaps not surprising, and confirmed by more statistically rigorous studies, e.g. Keating et al. (2011). The exercise upon which the present paper is based was conducted using only publicly available data. The experts had access to a science library and to the Internet. It is apparent that the vast majority of the data were derived by searching the Web, including in most cases the data from the library which must obviously be located before it can be consulted. A source of uncertainty within the estimates is therefore the choice of search terms entered into Internet search tools, which could be crucial in either locating or missing key data sources. In this study, porosity tends to have fewer independent sources in the literature than the other parameters, leading to potential underestimation of the uncertainty in comparison to other parameters, and hence a smaller range of calculated storage capacity values for this parameter. The ability to calculate the uncertainty in a storage capacity estimate is therefore limited by data availability and uncertainty is likely to be underestimated if this is not taken into account. In the case of the Mains Formation, the range of calculated capacities is comparable to the median value (Fig. 3), as all the experts located a single published porosity value. In other words, the range of storage estimates is partly controlled by the number of published values and their accessibility or ease of location. In an extreme case as with the Mains Formation, the range of P(M) is likely to be underestimated.

A further potential source of variability in the storage estimates is the influence of the individual assessors. Both personal judgement and previous experience have been shown to influence geological interpretation (Polson and Curtis, 2010). In this case, personal judgement is exercised when faced with parameters for which several data values are available, with no indication of which are more representative of the regional mean, and with no objective method of ranking the precision or importance of the values. One approach under these circumstances is simply to average the available values; the resulting mean clearly depends on which data have been located by the individual expert.

Personal judgement is required when estimating net : gross ratio as the most common source of data are borehole logs with a summary lithology column showing whether the sediments within the reservoir interval are interpreted as sandstone, silty sandstone, siltstone or mudstone (there are no significant limestones in the study area). Clearly mudstone is a non-reservoir, and sandstone is a potential reservoir, but a more or less arbitrary boundary between the two must be drawn. A more experienced wireline log interpreter might choose to ignore the summary lithology column of the composite log, and choose a value of, for example, the gamma ray log as an arbitrary cut-off between reservoir and non-reservoir, or estimate porosity (see below) and use an arbitrary minimum value of ca. 10 % for reservoir.

The most important control on the quality of the estimate of reservoir thickness is probably the number of borehole logs used to estimate the mean value. The most commonly used sources of data in this study (Cameron, 1993; Richards et al., 1993) typically present three summary borehole logs of each storage unit. However, the experts had access to 28 other composite (summary) borehole logs from the region, released by the UK Government. Some experts chose to use the entire suite of logs provided, while others used only a subset. Even if all logs are used, it is possible to use a range of methods to calculate mean regional thickness. For example, one can simply calculate the mean of the storage unit thickness data; alternatively, one could construct a map and interpolate contours, then estimate mean thickness by some simple graphical method involving dividing the storage unit into zones of constant thickness interval and calculating an average thickness weighted to the areas of the zones. It is also possible to use commercial software to perform both the contouring and the reservoir volume calculation, in which case calculating the mean thickness is unnecessary. Each of these approaches will result in different estimates of the thickness of the reservoir (or final gross reservoir volume).

For porosity, literature values can be utilised if they exist but if a range is given then the mean must be estimated. Sometimes porosity data are only provided graphically (as a cross-plot of porosity versus log of permeability) and the mean value can only be estimated visually as the points are frequently too dense to be read individually from the graphs. Alternatively, porosity can be calculated from borehole logs using standard methods – using formation density compensated (FDC) and compensated neutron logs (CNLs) for example – either manually or by using petrophysical computer software if the wireline logs are available in digital form. Again, the choice of method will influence the result. Measured porosity data are most commonly from within hydrocarbon fields, where the spatial density of boreholes is greatest. Whether the porosity of oilfield reservoirs is representative of the associated aquifer, or is systematically higher and thus introduces a systematic error in the estimate of aquifer porosity, is a controversial issue (e.g. Wilkinson and Haszeldine, 2011) for which a judgement is necessary. In a commercial study, it is possible to purchase porosity data measured from borehole core; unsurprisingly, none of the experts chose this option in this study.

The study reported here could be considered to be typical of regional studies conducted with the aim of ascertaining which geological units in a region are worthy of further study, i.e. a scoping study. The data available to the experts will be only a fraction of the total data collected from the area, and the data must obviously be located before being utilised. In any hydrocarbon province, it is unlikely that all possible data can be used in a regional scoping study, due to the large (often very large) volumes of data that have been collected historically and due to the non-availability of some (or much) of the data due to commercial confidentiality. Unless there are previously published syntheses of data with calculated averages of parameters such as the thickness of storage units, some proportion of the total data will be selected and utilised, inherently introducing uncertainty into the result.

Furthermore, the experts in this study could not spend unlimited periods of time searching for data, or in processing it once obtained. Again, this restriction is likely to be encountered in a regional scoping study, where many potential stores must be assessed within a fixed budget. The North Sea is also typical of hydrocarbon provinces in that there are a large number of boreholes drilled into relatively small areas (i.e. producing hydrocarbon fields) and relatively small numbers of boreholes in the much larger intervening areas. The spacing of the boreholes (data density) is probably not atypical of other offshore hydrocarbon provinces, though onshore hydrocarbon provinces may have much higher borehole densities (i.e. boreholes per square kilometre). Borehole records in the UK are released by the UK Government, so the density of available data may be comparable to other areas of the world where borehole density is greater but where drilling results are not so readily available due to commercial confidentiality.

While the uncertainty in estimated storage capacities will vary from study to study, and can be reduced by costly data collection (or possibly purchase) for any given geological unit, the results here suggests that there is significant uncertainty in any storage capacity estimate that does not include a site-specific estimate of uncertainty. Note that this analysis does not take account of uncertainty in CO₂ density or storage efficiency. Storage efficiency, unless constrained on a unit-by-unit basis, can introduce an order-of-magnitude uncertainty to a storage estimate (e.g. Scottish Centre for Carbon Storage, 2009). The geological variability of a storage unit hence appears to impart less uncertainty into the storage estimate than the storage efficiency.

It is not possible to estimate the likely uncertainty of any single storage capacity estimate as there is no way to know whether it is at the lower, middle or upper range of P(M). However, these results show that the storage capacity could range from less than 10 % to over 300 % of any single value. This is considerably larger than uncertainty imparted by the inherent variability within a single well-constrained data set, where a study by Deng et al. (2012) found only a 4 % uncertainty at 95 % confidence. However, the same study found that incorporating uncertainty in the capacity estimate reduced the overall storage capacity by over 60 % compared to an earlier study using single values of input parameters. This supports the recommendation of Chadwick et al. (2008) that a (single) calculated storage capacity that is similar to the quantity of CO₂ to be stored should be regarded as a cautionary indicator for the suitability of a storage unit for a particular project.

Data for this study were limited to that in the public domain, which is probably realistic for a regional study where a potentially large number of candidate aquifers are assessed for first-order suitability for storage (e.g. Scottish Centre for Carbon Storage, 2009). It is probably not applicable to a detailed study of a single aquifer, where every effort is made to reduce key uncertainties and where confidential data may be available. For example, in the estimation of aquifer thickness, every borehole log that penetrates the storage unit could be utilised, removing the subjective element of choice associated with taking a subset of the available data. It is also likely that a more rigorous approach to uncertainty would be used in a single aquifer study, generating a reliable estimate of the likely range of capacity (e.g. Keating et al., 2011; Pawar et al., 2016). For this reason, the range of uncertainty for a detailed single-aquifer study should be substantially less than that derived here, and more comparable to the 4 % relative uncertainty at the 95 % confidence interval found in a detailed study by Deng et al. (2012).

5 Conclusions

The average standard deviation in CO₂ capacity for the storage units studied here is ±64 %. This is substantially greater than the implied precision of many published storage estimates. The geological uncertainty of a single storage capacity estimate for a storage unit with no other assessment of uncertainty might be in the range of 30 %–245 % of the estimated value or 6 % to 520 % more conservatively. For storage units where capacity is on the borderline of being economic or otherwise useable, this uncertainty may materially influence the decision of acceptance or rejection of the candidate unit. It should also be recognised that the analysis here does not exclude the possibility of the useable real-world storage capacity of a candidate storage unit being zero, due to, for example, an un-fixable leakage pathway or regulatory issues.

Uncertainty documented in this study is due to a mixture of spatial variability in the parameters combined with only limited availability of data, the number of independent (prior) estimates that are located for each parameter and the variation in interpretation of the same data by different experts. The range and standard deviation values in this study should be considered to be minimum values. The overall uncertainty is likely to be significantly larger as several sources of uncertainty are not accounted for in this study, in particular uncertainty due to storage efficiency could be larger than the geological uncertainty assessed here. Therefore a single assessment of a storage capacity of a geological unit, with no associated assessment of uncertainty, should be considered to have at least this degree of uncertainty in the absence of other information.