Improving subduction interface implementation in dynamic numerical models

Numerical subduction models often implement an entrained weak layer (WL) to facilitate decoupling of the slab and upper plate. This approach is attractive in its simplicity, and can provide stable, asymmetric subduction systems that persist for many tens of millions of years. In this study we undertake a methodological analysis of the WL approach, and use these insights to guide improvements to the implementation. The issue that primarily motivates the study is the emergence of significant spatial and temporal thickness variations within the WL. We show that these variations are mainly the response to volumetric flux gradients, caused by the change in boundary conditions as the WL material enters and exits the zone of decoupling. The time taken to reach a quasi-equilibrium thickness profile will depend on the total plate convergence, and is around 7 Myr for the models presented here. During the transient stage, width variations along the WL can exceed 4×, which may impact the effective strength of the interface, through physical effects if the rheology is linear, or simply if the interface becomes inadequately numerically resolved. The transient stage also induces strong sensitivity to model resolution. By prescribing a variable-thickness WL at the outset of the model, and by controlling the limits of the layer thickness during the model evolution, we find improved stability and resolution convergence of the models.

1 Introduction

The process of stable asymmetric subduction requires that the down-going plate is substantially decoupled from the overriding plate along the subduction interface (Gerya et al., 2008). Determining the combination of processes that allow plate-bounding faults to develop is a long-standing problem in geodynamics (Lenardic and Kaula, 1994; Trompert and Hansen, 1998; Moresi and Solomatov, 1998; Tackley, 2000; Bercovici, 2003; Bercovici and Ricard, 2014). Even when the subduction interface is assumed a priori, the implementation within a continuum modelling framework is not trivial. Accordingly, a range of modelling approaches have been developed. Different approaches may reflect the style of model (e.g. instantaneous vs. long term), the degree to which multiphysics are represented (e.g. hydrogeologic processes), the subduction driving forces (kinematic vs. dynamic), and numerical method (finite-difference vs. finite-element methods vs. boundary element methods). A common approach in long-term, dynamic models is to implement the subduction interface as a continuously entrained layer of weak material (WL). Figure 1a shows an example of this approach, implemented using Underworld2. This kind of approach is relatively simple to implement, and can provide stable, asymmetric subduction regimes that persist for many tens of millions of years, as shown in Fig. 1b. While the WL approach has been utilized in a broad range of studies, a detailed methodological analysis of this strategy is lacking (although valuable insights appear in Čıžková et al., 2002; Manea and Gurnis, 2007; Arcay, 2012, 2017; Androvičová et al., 2013). This study focuses on the behaviour of a constant-viscosity WL implementation, within a 2-D thermo-mechanical subduction setup. The results have relevance for the precision, efficiency, and reproducibility of dynamic subduction models.

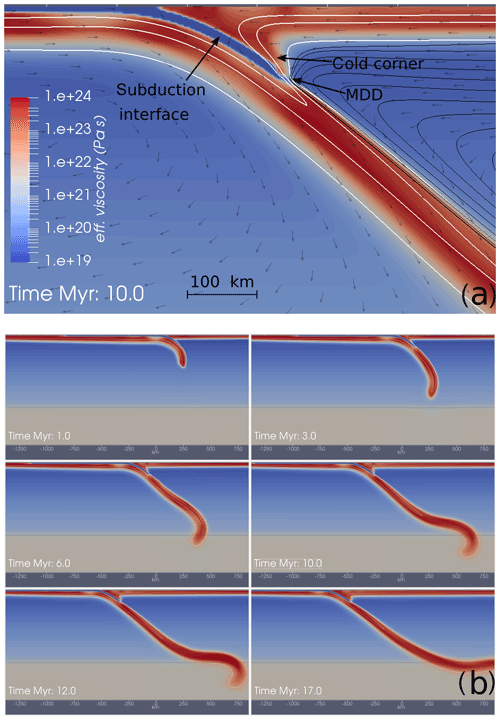
Figure 1 Example of dynamic subduction simulation. Colour map shows the effective viscosity on a logarithmic scale, and reveals the weak finite-width subduction interface which enables the decoupling of the slab and the upper plate. The implementation of the interface follows a modified WL approach, which we refer to as an embedded fault (EF). The subduction interface extends to 100 km depth, beyond which the slab and mantle become coupled (MDD). Above the MDD, part of the mantle wedge tends to become stagnant due to the strong temperature dependence of the rheology. This is often referred to as a cold corner. (a) Closeup of slab in the upper mantle. White contour lines show 400, 700, and 1200 ^∘C isotherms. Black lines are streamlines of the velocity in a fixed upper plate reference frame. Arrows show model velocity field. (b) Time evolution of the same model, showing slab rollback and interaction with the transition zone.

2 The subduction interface

The subduction interface refers to the plate boundary fault at Earth's convergent margins. Exhumed subduction interfaces are typified by melange zones, often hundreds of metres in width, with coherent blocks embedded within a sedimentary and/or serpentinized matrix (Shreve and Cloos, 1986; Vannucchi et al., 2008; Kimura et al., 2012; Bebout and Penniston-Dorland, 2016). The subduction interface zone is characterized by rheological and petrological complexity, low strength, and the abundance of water and the critical role of fluid pressure (Abers, 2005; Audet et al., 2009; Bachmann et al., 2009; Gao and Wang, 2014; Hardebeck, 2015; Duarte et al., 2015; Bebout and Penniston-Dorland, 2016). Subducted sediments can reach depths of up to 80 km (Bayet et al., 2018), similar to the inferred depth at which the slab and mantle become coupled, and can be traced in the composition of arc magmas (Plank and Langmuir, 1993). The proportion of subducted sediment may lead to large variations in the mechanical properties in the deep subduction interface (Behr and Becker, 2018). Entrainment of upper plate material in a process known as subduction erosion also occurs at a substantial number of convergent margins (Huene and Scholl, 1991). Subduction interfaces therefore incorporate material from the subducting plate, the accretionary prism, and the upper plate (Vannucchi et al., 2008). However, the degree to which variability in these influxes impacts long-term subduction dynamics is debated (Cloos and Shreve, 1988; Schellart and Rawlinson, 2013; Duarte et al., 2015; Behr and Becker, 2018).

Fluid pressure plays a key role in subduction zone interfaces as it determines the effective frictional strength, controls the seismic/aseismic character of slip (Audet and Schwartz, 2013), and dictates the extent of hydrous mineral formation along the subduction interface (Reynard, 2013). In the shallow megathrust, pore fluid water and clay minerals are thought to exert a major control on the rheology (Vrolijk, 1990). Seismic imaging demonstrates the presence of fluids along the plate boundary. In some cases pore pressures are inferred to be near lithostatic values (Audet et al., 2009). While many subduction zone megathrusts are capable of hosting great earthquakes, there is a spectrum of behaviour from locked to creeping. Ongoing debate surrounds the strength implications of this divergent behaviour (Gao and Wang, 2014; Hardebeck, 2015; Hardebeck and Loveless, 2018). The limit of the seismogenic zone can range from 5 to 50 km in depth (Tichelaar and Ruff, 1993). The topography of most forearcs is consistent with average shear stresses of 15 MPa over the long term (Lamb, 2006). Megathrust shear stresses in the range 1–100 MPa, with mean shear stresses also around 15 MPa, are consistent with results from heat flow studies (Peacock, 1996; Gao and Wang, 2014).

At greater depths, fluids are generated by devolatilization reactions (Bebout and Penniston-Dorland, 2016). The deeper part of the subduction interface where the slab is in contact with the serpentinized upper plate mantle is thought to be controlled primarily by weak hydrous minerals which allow effective slab–mantle decoupling but also inhibit unstable seismic slip (Hirauchi and Katayama, 2013; Reynard, 2013). It remains unclear whether the rheology of the deep subduction interface is dominated by viscous or (stable) plastic behaviour (Proctor and Hirth, 2016; Li and Ghosh, 2017). The thickness of subduction interfaces, particularly in the deeper aseismic zone, is not well constrained. Estimates range from between tens of metres to a few kilometres (Abers, 2005; Cloos and Shreve, 1988; Vannucchi et al., 2008, 2012). Behr and Becker (2018) used structural relationships in exhumed subduction interfaces to infer the relative strength of different lithologies. Metasediments and serpentinites which commonly form the matrix within the subduction melange appear to be the weakest components.

3 Past modelling approaches

In efforts to study subduction zone dynamics, a range of modelling approaches have been developed. The subduction interface is a necessary model component whenever both subducting and upper plates are included. One approach is to incorporate the interface directly as a kinematic constraint into the simulation, i.e. by specifying continuous normal and discontinuous tangential velocities in the model solution surrounding the fault (Billen et al., 2003; Christensen, 1996). This idea was developed into a dynamic framework with finite-element models that incorporate internal stress boundaries; the result is zero width faults within the continuum mechanical representation of the lithosphere (Zhong and Gurnis, 1992, 1995; Aagaard et al., 2017). Because moving mesh nodes are needed to capture proper fault advection, accurate tracking of large-scale deformation is challenging. A more common approach is to apply finite regions of weak constitutive behaviour within a static mesh. The velocity field naturally develops strain localization around the weak zone, although the “faults” are usually much broader than real plate boundaries. This approach was first applied as a spatially fixed low-viscosity zone that could decouple the plates but would not allow trench motion (e.g. Gurnis and Hager, 1988). This type of implementation was developed so that narrow low-strength weak zone “stencils” could also be advected to allow trench motion (Kincaid and Sacks, 1997; Billen and Hirth, 2007).

Over the past decade the use of an entrained weak layer (WL) has become an increasingly common strategy (e.g. Babeyko and Sobolev, 2008; Capitanio et al., 2010; Magni et al., 2012; Chertova et al., 2012; Čížková and Bina, 2013; Garel et al., 2014; Holt et al., 2015; Agrusta et al., 2017; Glerum et al., 2018; Arredondo and Billen, 2017). Rather than using a fixed weak zone, the subduction interface is typically implemented by imposing a material layer at the top of the subducting plate that is advected with the flow and continuously entrained into the decoupling region. The WL approach enables a mobile trench while also helping to accommodate plate bending, which is important in the absence of a free surface. Additionally, it isolates the extremely weak parts of the system (the plate boundary) from the plates, enabling long-term asymmetric subduction to occur. In this study, we focus on a simple constant-viscosity implementation of the WL using the Underworld2 code, as described in Sect. 2.

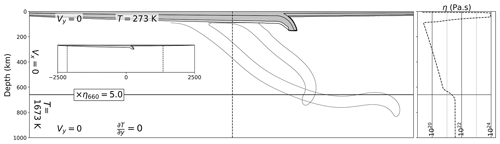
Figure 2 Initial conditions for 2-D thermo-mechanical subduction models. All models in this study have a 50 Myr initial slab age. Velocity boundary conditions are free slip on all walls of the domain (zero tangential stress). The dark grey region in the main panel shows parts of the model colder than 1100 ^∘C. The inset shows the full domain. Outlines show the slab position at 10 and 20 Myr. The right-hand panel shows the viscosity profile evaluated along the vertical dashed line in the main panel.

Although the WL is commonly implemented in numerical subduction models, there is some ambiguity as to whether this approach represents an attempt to explicitly model subduction interface dynamics, or should instead be conceived as an ad hoc solution to modelling the plate boundary. WL implementations do mimic several critical processes that are thought to contribute to the long-term weakness and stability of the subduction interface. One of these is the process of entrainment or “self-lubrication” (Lenardic and Kaula, 1994). The entrainment of both sediments and fluids along the slab interface likely plays a key role in maintaining subduction interface weakness. Additionally, the WL approach might be linked with deformation-localizing processes such as damage, grain size reduction, and fabric development. Indeed, WL models have been conceived as a limiting case in which comprehensive damage is assumed within the interface material and hence can be prescribed at the outset (Tagawa et al., 2007). Despite the fact that we can draw analogies to relevant physical processes, our view is that the WL approach constitutes an ad hoc solution to the sub-grid phenomena of plate boundary shear localization.

The behaviour of the WL is discussed is some detail in Arcay (2012, 2017). These studies highlight the tendency for the subduction interface to develop spontaneous thickness variation as the models evolve. Typically the interface widens near the trench, building a prism-like complex, and thins at depths beyond the brittle–ductile transition (>50 km). This pattern was also noted in the boundary element models of Gerardi and Ribe (2018), who attributed a downdip thickness variation to lubrication layer dynamics. The tendency for thinning will impact the level of mesh resolution required in a model (Arcay, 2017). Additionally, WL formulations are likely to evolve maximum subduction interface thickness around twice the imposed thickness, potentially impacting effective stress along the interface, as well as the accuracy of predicted thermal structure. Understanding and controlling these spontaneous width variations will be important in terms of using dynamic models to explore sensitive subduction zone processes, such as metamorphism and melting near the slab top.

4 Methods

4.1 Numerical model setup

The numerical subduction models developed in this study represent the time evolution of simplified conservation equations for mass, momentum, and energy within a 2-D Cartesian domain. Figure 2 provides an overview of the model domain, as well as initial and boundary conditions. The depth of the domain is 1000 km, and the aspect ratio is 5. Initial temperature conditions define two plates which meet at the centre of the domain, including a small asymmetric slab following a circular arc to a depth of 150 km. The subducting plate has an initial age of 50 Myr at the trench, while the upper plate age is 10 Myr. Both plates have a linear age profile with an initial age of zero at the sidewalls. This setup allows the model to evolve under the driving force of internal density anomalies (sometimes referred to as a fully dynamic model). Apart from the presence of a WL, there is no compositional difference between the subducting and upper plate, nor do we include any compositional differentiation within the oceanic lithosphere. The only aspects of the model setup that are varied are the details of subduction interface implementation (described in the following section) and the model resolution.

The mantle is treated as an incompressible, highly viscous fluid in which inertial forces and elastic stresses can be neglected. The mechanical behaviour of mantle (including the thermal lithosphere) is prescribed by a composite rheological model that includes a linear high-temperature creep law, as well as a scalar visco-plastic flow law, sufficient for capturing pseudo-brittle as well as distributed plastic deformation within the slab. Thermal buoyancy is the only source of density variation in the model. The thermal variations are coupled to the momentum equation through their effect on density, which follows the Boussinesq approximation. A detailed description of the governing equations, constitutive laws, and physical parameters is given in Appendix A.

Approximate solutions to the incompressible momentum and energy conservation equations are derived using the finite-element code Underworld2. Underworld2 is a Python API which provides functionality for the modelling of geodynamic processes. Underworld2 solves the discrete Stokes system through the standard mixed Galerkin finite-element formulation. The domain is partitioned into quadrilateral elements, with linear elements for velocity and constant elements for pressure (Q₁∕dP₀) (Arnold and Logg, 2014). Material properties are advected on Lagrangian tracer particles. Unless otherwise stated, models have a mesh resolution of 160 elements in the vertical direction, refined to provide an element width of ∼3 km at the surface, and a particle density of 30 tracers per element. Particles are added and removed to maintain density near this value. During quadrature, material properties are mapped to quadrature points using nearest-neighbour interpolation. The Lagrangian tracer particles are used to distinguish the subduction interface material from the rest of the system (lithosphere and mantle). Underworld2 solves the energy conservation equation using an explicit streamline upwind Petrov–Galerkin (SUPG) method (Brooks and Hughes, 1982). In this approach, a Petrov–Galerkin formulation is obtained by using a modified weighting function which affects upwinding-type behaviour. The Stokes system has free-slip conditions on all boundaries. The energy equation has constant (Dirichlet) and zero-flux (Neumann) on the top and bottom boundaries respectively. The left and right sidewalls have a constant temperature equal to the mantle potential temperature (1673 K). The surface temperature is 273 K.

4.2 Subduction interface implementation

The focus of our study is a common approach to modelling the subduction interface, sometimes referred to as a weak layer or weak crust. This approach has two intrinsic features: (1) the material that provides decoupling within the interplate zone is a distinct material type with rheology that contrasts with the plates/background material, and (2) the weak material layer is distributed along some or all of the subducting plate, so that the flow itself entrains new weak material into the decoupling region (Billen and Hirth, 2007; Garel et al., 2014; Čížková and Bina, 2013; Arredondo and Billen, 2017; Agrusta et al., 2017). In this study we use the abbreviation WL to refer to a typical implementation, namely one in which the distribution of weak material is fully self-evolving within the deforming subduction interface zone. We also demonstrate a modified version of this approach, which we refer to as an embedded fault (EF). The EF implementation differs from the WL in that the width of the interface is constrained in terms of its minimum and maximum thickness. While this manipulation of the interface material could be achieved in different ways, our implementation is based on a reference line of particles, which lie at the base of the weak interface and are advected along with the material swarm. At each time step we remap material types based on the relative position of the material particles with regard to the reference line.

The relationship between the EF reference line, the material swarm, and the mesh is shown in Fig. 3. In the EF approach, we also initialize the interface with a non-uniform thickness. For reasons discussed in the following sections, the thickness of the interface material within the decoupling zone should be close to double the thickness that is prescribed on the top of the subducting plate.

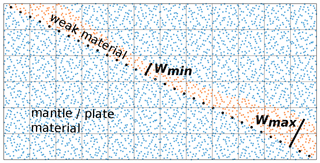
Figure 3 Schematic of the embedded fault (EF) implementation. The EF is a modification to the standard weak layer approach (WL). As with the WL, shear localizes due to a finite-width layer of weak material (represented by orange particles). A reference line of tracer particles (black points) is advected with the flow, at the base of the weak material layer. This line provides a reference to enforce width limits on the weak material, denoted by W_min and W_max. At each time step we remap material types based on the relative position of the material particles to the reference line. Note that the element size here is not shown to scale.

It is important to emphasize that differences between the WL and EF implementations relate only to the distribution of weak material within the model. All other aspects of the interface representation remain identical. In each case the interface has a constant viscosity. Weak material is continually prescribed along the uppermost part of the subducting plate as it moves away from the ridge, with a specified constant thickness (W_init=10 km). The upper plate does not contain any weak or interface material. For simplicity, there is no rheological variation between the shallow (frictional) megathrust and the deeper, viscous interface. To control the upper limit of the MDD, a depth-dependent cosine taper is used to transition the subduction interface rheology to the background mantle rheology. The taper for the transition (both WL and EF) begins at 100 km, and has a width of 30 km. Decoupling is strongly inhibited at depths greater than the taper onset. Hence the depth of the taper onset (100 km) effectively controls the upper limit of MDD. Likewise, at a distance of 800 km from the trench, along the subducting plate, the rheology of the interface material transitions to background mantle rheology. This avoids interaction of weak material with the spreading ridge.

5 Analysis of modelling approaches

5.1 The weak layer approach

Figure 4 shows the evolution of the subduction interface thickness over a 20 Myr period, based on the WL setup described in Sect. 4. This model reveals the spontaneous development of substantial WL thickness variations, not only near the trench (i.e. near the accretionary prism) but throughout the entirety of the decoupling zone. Previous studies have commented on the occurrence of similar thickness variations (Arcay, 2017; Gerardi and Ribe, 2018), although their origin has not been closely considered. We propose that such variations arise primarily from the way that the kinematics of the flow in the WL effect the downdip volumetric flux. In the following discussion we refer to a slab-based coordinate system in a fixed upper plate reference frame, where $\widehat{y}$ is the direction orthogonal to the slab midplane, $\widehat{s}$ is the direction parallel to the slab midplane, and the plate convergence velocity is equal to the subducting plate velocity (V_s). Before reaching the trench, the WL material travels with the subducting plate, with near-uniform velocity and negligible shear ($\frac{\partial V_{\mathrm{s}}}{\partial \widehat{y}}\approx \mathrm{0}$). In the subduction interface zone, however, the WL material decouples the slab and upper plate, and velocity gradients across the interface are finite. For a Newtonian rheology, the gradient is expected to be linear with $\frac{\partial V_{\mathrm{s}}}{\partial \widehat{y}}\approx \frac{V_{\mathrm{s}}}{W}$ (i.e. Couette flow). This change in velocity profile across the WL means that there is a smaller volumetric flux (per unit length normal to the interface) compared to the flux of material being delivered on the incoming subducting plate. To illustrate this point we consider a simple boundary-driven Stokes flow, as shown in Fig. 5, which provides a useful analogy to the flow in the WL. In this model, flow is driven by a constant tangential velocity on the lower boundary, while the upper boundary of the model has a patch of frictional (no slip) nodes, surrounded on both sides by a free-slip boundary condition. The step change in boundary conditions imposes volumetric flux gradients causing the weak layer (shown in blue) to thicken near the start of the no-slip region, and thin near the end. The width changes in the weak layer proceed until the overall volume flux reaches equilibrium.

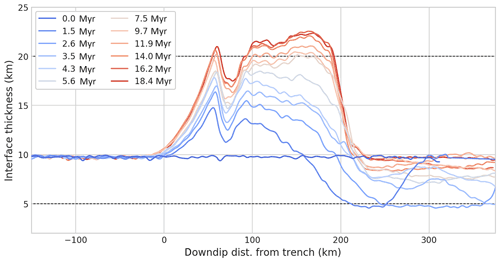
Figure 4 Interface thickness evolution in WL implementation. The initial layer thickness (W_init) is 10 km. Coloured lines show the evolving thickness plotted as a function of downdip distance from the trench. Dashed black lines show the expected maximum (equilibrium) and minimum (transient) thickness, based on a kinematic description of the flow evolving from a uniform thickness weak layer.

Returning to our subduction model results, the validity of our description can be tested by considering the thickness profile required for volume flux equilibrium. Assuming that the decoupling zone maintains a Couette profile, independent of the local thickness, flux equilibrium requires that the thickness of the WL in the decoupling zone be twice that imposed on the incoming plate. This prediction, based on a simplified kinematic description of flow in the interface, is broadly consistent with the long-term evolution observed in the WL models (e.g. Fig. 4).

While our discussion so far has mainly emphasized the transition of the WL from the oceanic part of the subducting plate into the decoupling zone, similar processes take place where the slab and the mantle become coupled (the MDD). When a constant interface width is prescribed, the interface thickness near the MDD initially decreases. Again, this is because the volumetric flux increases as Couette flow in the decoupling region transitions to the fully coupled flow. The location where the subduction interface thins provides a proxy for the MDD. Complexity arises due to the fact that the MDD in our model is not constant. Instead the MDD tends to become deeper as the corner of the mantle wedge cools and stagnates. This means that the effective boundary conditions on the flow within the interface are also time varying. This accounts for why the location of interface thinning migrates downdip as time progresses, as shown in Fig. 4.

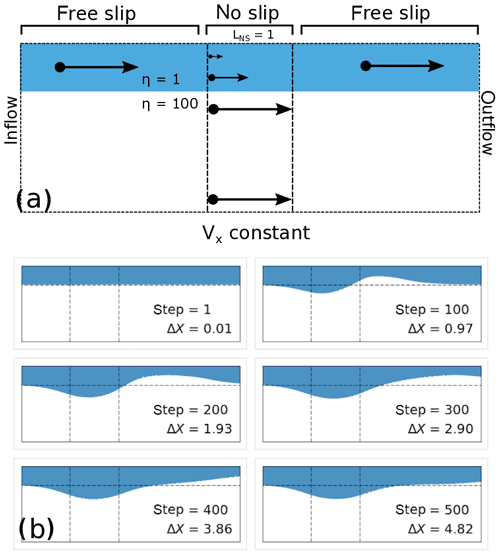
Figure 5 Analogue for WL thickness evolution. (a) Model setup for a boundary-driven flow where a weak layer (shown in blue) interacts with a stronger layer (white). The top surface of the model is free slip, except for a patch of no-slip nodes (V_x=0). The bottom surface has a constant horizontal velocity component. (b) Evolution of material in the boundary-driven model. ΔX represents the accumulated displacement along the bottom boundary, normalized by the width of the no-slip patch.

Based on analysis of the typical WL setup, we argue that the primary thickness variations reflect a simple response to changes in volumetric flux along the interface. In addition to these flux-controlled changes, Fig. 4 shows that the subduction interface also develops a persistent short-wavelength width perturbation just beneath the tip of the forearc at a downdip distance of ∼60–80 km. Here the interface thins by ∼3–4 km. This occurs in combination with strong, localized plastic deformation in the upper plate.

It seems likely that such short-wavelength anomalies may be affected by a range of factors, including the interface and lithosphere rheology, mesh resolution, and material advection scheme. If so, these features are likely to be somewhat model dependent, in contrast to the long-wavelength, flux-related thickness variations which reflect intrinsic kinematics of flow in the WL setup.

5.2 Improving the weak layer approach

The embedded fault (EF) implementation, described in Sect. 4, consists of two complementary strategies. Firstly, we may initiate the WL with a variable thickness. Secondly we can control the WL thickness throughout the simulation, by remapping WL material (particles) to background material, and vice versa. Given these controls, perhaps an obvious first issue to address is what happens if we simply enforce a constant width interface at all times. While this would in some ways be a desirable approach, doing so results in the development of a very spurious subduction morphology. Figure 6b shows results from such a case ($W_{\max }=W_{\min }=W_{\mathrm{init}}=\mathrm{10}$ km). After 15 million years of model evolution a very atypical subduction morphology has developed, with an extremely low-angle megathrust beneath a forearc region with a width of greater than 600 km. While geologically irrelevant, the example shown in Fig. 6b provides a useful insight into the way in which the flow in the interface can influence model dynamics. When the subduction interface is forced to remain at constant width, the interface is unable to evolve towards flux equilibrium. Persistent interface-normal velocity components result, and the compounding effect eventually distorts the morphology of the entire subduction hinge region.

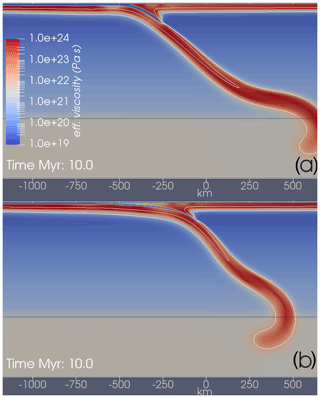
Figure 6 Effect of variable maximum W_max in EF models. The colour map shows the effective viscosity at a model time of 10 Myr. White lines show isotherms at 700 and 1200 ^∘C. Panel (a) shows the EF model with $W_{\max }=\mathrm{1.9}\times W_{\mathrm{init}}=\mathrm{19}$ km. Panel (b) shows the EF model with $W_{\max }=W_{\mathrm{init}}=\mathrm{10}$ km. In this case, due to the fact that the subduction interface cannot adjust its thickness, an extremely long, low-angle interface develops, with forearc distances of ∼500 km.

Figure 6a shows the slab morphology developed by instead using $W_{\max }=\mathrm{1.9}\times W_{\mathrm{init}}=\mathrm{19}$ km (we discuss the choice of 1.9 in the next section). The subduction morphology in this simulation is more realistic, and consistent with outcomes from a standard WL approach. The evolution of the interface thickness from the same simulation is shown in Fig. 8. In addition to controlling the width of the interface throughout the EF simulation, we have also prescribed the initial interface thickness in the decoupling zone (from the trench to a depth of 100 km) to have value equal to W_max (19 km). In this way, we have tried to preemptively impose a thickness profile closer to the flux equilibrium. Figure 8 shows that this strategy reduces, but does not fully eliminate, the transient stage of interface adjustment. It is difficult to fully eliminate the transient stage because the equilibrium interface thickness profile is partly determined by the MDD, which is not constant. The evolution of the MDD is a response to the cooling of the mantle wedge and the development of a stagnant “cold corner” (see Fig. 9). Prescribing initial temperature conditions that include the cold corner would be one way to further reduce the amount the transient adjustment of the interface. Figure 7 shows the state of the material swarm in the EF model, compared to the equivalent WL model. This reveals a typical distribution of interface material once a quasi-equilibrium thickness has been established.

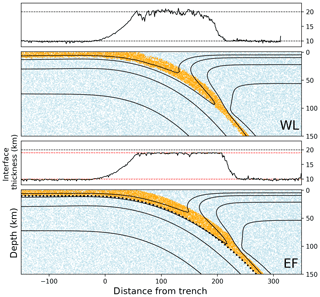
Figure 7 Distribution of subduction interface material. Results from a standard WL model are shown in the top panel. The EF model is shown in the bottom panel. Both models have a constant viscosity interface rheology. Model time is 12.5 Myr in both cases. In the lower panels, orange points are the subduction interface material, and blue points are the background material (mantle/lithosphere). Points in the material swarm and along the EF reference line have been down-sampled for clarity. Solid black lines over the material points are isotherms. Smaller panels show the measured interface thicknesses in each case; red horizontal lines show the thickness constraints W_min, W_max.

In addition to the thickness variations related to volumetric flux, the WL approach can develop short wavelength thickness variations, as seen in Fig. 4. In the EF implementation, we found that using a value of W_max slightly less than 2.0×W_init helps to suppress short wavelength thickness variations, without significantly effecting the overall model evolution. In other words, while we need to allow the interface to develop some amount of thickness variation, it may be advantageous to use a value slightly less than 2×W_init. Figure 10 shows results from a number of experiments where the value of W_max was changed. Qualitatively, we see that the models have very similar long-term evolution once W_max is greater that 1.75×W_init.

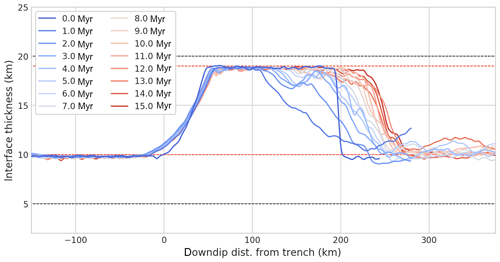
Figure 8 Interface thickness evolution, EF approach. In the EF implementation limits are imposed in the maximum and minimum thicknesses, as shown by the red dashed lines. Unlike the standard WL approach, the initial thickness of the interface is variable. The initial thickness of the interface within the decoupling region is equal to W_max. The black lines show the typical range in which a WL model will vary, assuming a constant initial thickness of 10 km (see also Fig. 4). The results shown here refer to the same model as shown in Figs. 1 and 6.

5.3 Stability and convergence

So far we have discussed results based on well-resolved models, with 160 elements across the 1000 km vertical domain. At this resolution, the vertically refined mesh provides 3.2 elements within the subduction interface (at W_init=10 km). Note that this increases to more than six elements in the decoupling zone, once the interface has thickened to ∼20 km. We now look at the convergence of models under variable resolution, based on a standard WL approach as well as the EF implementation. Figure 11 shows the slab temperature field at 10 Myr for a set of models with varying resolution: 72, 96, 128, 160, and 192 elements in the vertical dimension. The ratio of the initial interface width (W_init) to the element width has values of 1.4, 1.9, 2.6, 3.2, and 3.8 for the respective mesh resolutions. The dashed slab outline in Fig. 11 shows the morphology for a simulation with 192 elements in the vertical dimension; this is used as a reference model in the following analysis. Note that while we have varied the mesh resolution, all models have the same spatial particle density. Figure 11a shows results using a standard WL implementation. At the lowest resolution (72 elements) the simulation stalls and the slab undergoes runaway thermal decay. At 96 elements, the model is still strongly impacted by under-resolution of the subduction interface. Figure 11b shows equivalent results using the EF implementation. Qualitatively, we see that EF models are more stable at lower resolution. For instance, the EF model at the lowest resolution (72 elements) more closely reproduces the evolution of the reference model than does the WL model with 96 elements.

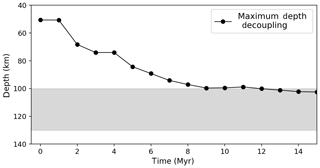
Figure 9 Evolution of the maximum depth of decoupling (MDD). As the mantle wedge cools, it progressively stagnates, driving deeper decoupling within the subduction interface. The grey region in the figure shows the depth interval over which the subduction interface transitions to the background mantle rheology as prescribed with a cosine taper (see Sect. 4). Results are from the same model as shown in Fig. 6a, i.e. an EF model with $W_{\max }=\mathrm{1.9}\times W_{\mathrm{init}}$.

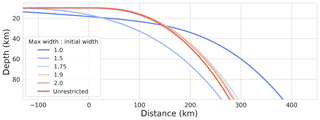
Figure 10 Embedded fault models (EF) with variable W_max. Lines show the morphology of the base of the subduction interface (the EF reference line) at 10 Myr for different models with varying W_max. When the interface thickness variation is strongly constrained, the evolution of the model is significantly effected. See also Fig. 6.

Figure 11 suggests that the EF models converge more closely with increasing resolution. We quantify this by tracking the relative error (L₂) of the temperature field in the lower-resolution models with respect to the reference model (192 elements). The relative error with respect to the reference model (T_ref) is

$$\begin{array}{}\text{(1)}& E={\left[{\displaystyle \frac{{\int }_{\mathrm{\Omega }}(T-T_{\mathrm{ref}})\cdot (T-T_{\mathrm{ref}})\mathrm{d}V}{{\int }_{\mathrm{\Omega }}{T}_{\mathrm{ref}}\cdot T_{\mathrm{ref}}\mathrm{d}V}}\right]}^{\mathrm{1}/\mathrm{2}}.\end{array}$$

Figure 13 shows relative error results for the same set of models shown in Fig. 11, confirming more rapid resolution convergence in the EF models relative to the standard WL approach. For most of the models shown in Fig. 13 the relative error accumulates rapidly in the first 7–10 million years of the simulation, while the error rate flattens after this. This is similar to the time taken for the WL interface to reach its equilibrium thickness (e.g. Fig. 4). This suggests that models are strongly resolution-sensitive during the transient phase of the interface adjustment. At low resolution (72, 96, 128 elements), errors in both WL or EF models express this sensitivity. Interestingly, at 160 elements, the EF case exhibits nearly constant error accumulation during the model evolution. This suggests that we have succeeded in reducing the sensitivity of the subduction interface implementation, relative to the overall error accumulation rate. The latter may be influenced by additional factors which we have not controlled for here, such as the time step size in the advection–diffusion implementation which is controlled by the mesh resolution.

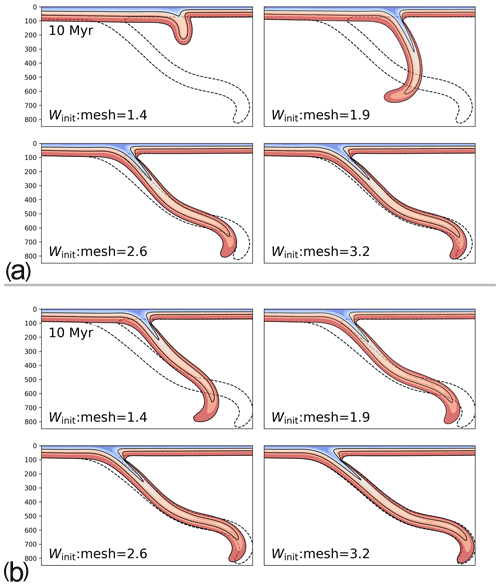
Figure 11 Implementation comparison with variable resolution. Colour map shows slab temperature field at 10 Myr, masked above 1250 ^∘C. Each figure shows a series of models run at different resolutions. The total number of elements in the vertical coordinate was 96, 127, 160, and 192. Corresponding subduction interface resolution is displayed in the figure, representing the initial fault thickness (W_init) divided by the local element size. (a) Models using standard WL implementation. (b) Models using the EF implementation.

Figure 12 shows the distribution of interface material in the lowest-resolution WL model (shown in the top left panel in Fig. 11a). In this case, under-resolution of the weak layer induces strong coupling between the slab and the upper plate at relatively shallow depths and begins to thin the WL, due to the development of strong flux gradients (as described in Sect. 5). This induces further coupling and yet more thinning. This proves to be catastrophic feedback process, causing the simulation to stall and enter runaway thermal decay. The EF approach provides stability in this context, by inhibiting the feedback cycle. While this behaviour is mainly relevant for models run at low resolution, the increased stability of the EF approach is a useful property, particularly from a model development perspective.

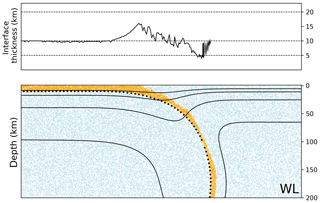
Figure 12 Interface thickness in under-resolved WL model. In the lower panel orange points show the subduction interface material, and blue points are the background material (mantle/lithosphere). The upper panel shows interface thickness. This figure shows the model state 10 Myr after model initiation. This model is also shown in the upper left panel of Fig. 11a.

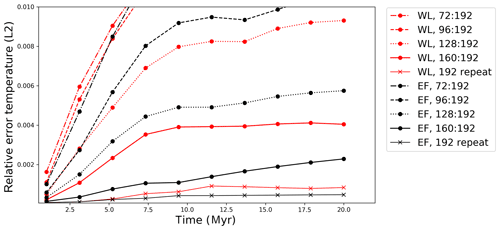
Figure 13 Convergence of models with varying resolution. Vertical axis shows the relative error (L₂) of the temperature field. We have truncated the vertical axis so as to focus on trends in the higher-resolution results. The error value is based on the error between the highest-resolution model (192 elements in the vertical axis) and each of the models with lower resolution, as labelled in the figure. Experiments were repeated at the highest resolution to provide a baseline for model reproducibility (labelled “repeat”).

6 Discussion and conclusions

The entrained weak layer (WL) is a common approach for implementing the subduction interface in long-term dynamic simulations. We have discussed aspects of WL implementation that can have an unintended impact on model evolution. The first involves the transient evolution of a uniform thickness interface to a variable thickness–uniform flux configuration. If not properly accounted for, thinning of the deeper part of the WL could lead to numerical under-resolution, as previously suggested (Arcay, 2017). If the WL has a viscous rheology, the thinning will lead to higher stresses. This can induce a positive feedback when higher stresses increase the amount of partial coupling, inducing further thinning. Even for seemingly well-resolved models, the transient behaviour of the subduction interface appears to be responsible for strong mesh sensitivity and poor resolution convergence. In general, models with plastic/frictional rheologies should be less sensitive to these transient adjustments, as the stress should not depend on the width of the interface.

Another tendency of the WL models is to develop persistent short-wavelength thickness variations. These may represent interface instabilities, as are observed in Couette flows past a deformable boundary (Shankar and Kumar, 2004). These tend to dominate on the shallow part of the boundary with the upper plate. While flux-related thickness variation will be expected for any model implementation of WL, boundary instabilities (short wavelength) are likely to be more variable across different codes. They may depend on additional details of implementation, such as the rheology of the plates, material advection, and interpolation schemes. Together, these issues are likely to hinder efforts to produce reproducible results between codes.

These unintended behaviours of the WL approach can be partly mitigated by controlling the thickness of the interface. We demonstrate a simple implementation of this concept, which utilizes a line of reference points at the base of the WL, allowing us to remap material types based on proximity to this line. We call this approach an embedded fault (EF). The ability to constrain the thickness of the interface improves the resolution convergence of numerical models, as well as the stability at lower resolutions. The EF does add complexity to models, in both the sense of implementation as well as the introduction of new parameters to control specific details (e.g. W_max). There are obviously other implementation strategies that could be developed in order to achieve similar outcomes. These should be explored in future studies. Overall, this study provides a better understanding of the behaviour of subduction models utilizing WL approaches. These insights offer a basis for achieving better outcomes in terms of model reproducibility and precision.

Appendix A: Governing equations, constitutive relationships, and physical parameters

A1 Continuity, momentum, and energy equations

On geological timescales the Earth's mantle behaves as a highly viscous, incompressible fluid, in which inertial forces can be neglected. The flow caused by internal buoyancy anomalies is described by the static force balance (momentum conservation) and continuity equations:

$$\begin{array}{}\text{(A1)}& {\displaystyle }{\mathit{\sigma }}_{ij,j}+\mathit{\rho }{g}_i=\mathrm{0},\text{(A2)}& {\displaystyle }{u}_{i,i}=\mathrm{0},\end{array}$$

where u_i is the ith component of the velocity. Repeated indices denote summation, and u_,i represents partial derivative with respect to the spatial coordinate x_i. The full stress tensor appearing in Eq. (A1) can be decomposed into deviatoric and mean components:

$$\begin{array}{}\text{(A3)}& {\mathit{\sigma }}_{ij}={\mathit{\tau }}_{ij}+p{\mathit{\delta }}_{ij}.\end{array}$$

It is noted that sign of the pressure (p) is opposite to the mean stress tensor, consistent with the convention that fluid flows from high to low pressure. The deviatoric stress tensor (τ) and the strain rate tensor (D_ij) are related according to the constitutive relationship:

$$\begin{array}{}\text{(A4)}& {\mathit{\tau }}_{ij}=\mathrm{2}\mathit{\eta }{D}_{ij}=\mathit{\eta }(u_{i,j}+u_{j,i}).\end{array}$$

Substituting Eqs. (A4) and (A3) into Eq. (A1) gives the Stokes equation, which involves two unknown variables: pressure and velocity. The Stokes and continuity equations are sufficient to solve for the two unknowns, together with appropriate boundary conditions. An approximate solution to these equations is derived using a Galerkin finite-element method, implemented in the Underworld2 code.

The thermal evolution of the system expresses the balance between heat transport by fluid motion, thermal diffusion, and internal heat generation by the first law of thermodynamics, assuming incompressibility:

$$\begin{array}{}\text{(A5)}& \mathit{\rho }{C}_{\mathrm{p}}{\displaystyle \frac{DT}{Dt}}=q_{i,i}+\mathit{\rho }Q,\end{array}$$

where T is the temperature and Q is the heat production rate (everywhere zero in this study). Diffusion rates are described by Fourier's law, which satisfies the second law for positive conductivity (k):

$$\begin{array}{}\text{(A6)}& q_i=-k{T}_{,i}.\end{array}$$

Inserting Eq. (A6) into Eq. (A5) and using the definition of the material derivative gives

$$\begin{array}{}\text{(A7)}& {\displaystyle \frac{\partial T}{\partial t}}+u_i{T}_{,i}=(\mathit{\kappa }{T}_{,i}{)}_{,i}+{\displaystyle \frac{Q}{C_{\mathrm{p}}}},\end{array}$$

where $\mathit{\kappa }=\frac{k}{\mathit{\rho }{C}_{\mathrm{p}}}$ is the thermal diffusivity.

The thermal variations are coupled to the momentum equation through their effect on density. At pressures in planetary interiors, silicate minerals are weakly compressible and this is generally considered to be a perturbation to an incompressible flow. The Boussinesq approximation accounts for the buoyancy forces while neglecting the associated volume change, allowing us to assume incompressibility (Eq. A2). In the case of density variations due to temperature, the equation of state is

$$\begin{array}{}\text{(A8)}& \mathit{\rho }={\mathit{\rho }}_{\mathrm{0}}(\mathrm{1}-\mathit{\alpha }(T-T_{\mathrm{p}}\left)\right),\end{array}$$

where ρ₀ is the density at a reference temperature (here the mantle potential temperature T_p). α is the coefficient of thermal expansion. It is generally much smaller than 1, making the Boussinesq approximation reasonable.

The equations and parameters that appear in the numerical models are based on equivalent dimensionless forms of the governing equations. We use the following characteristic scales (e.g Christensen, 1984):

$$\begin{array}{}\text{(A9)}& \begin{array}{rl}& \stackrel{\mathrm{‾}}{x_i}=x_i\left[{\displaystyle \frac{\mathrm{1}}{d}}\right],\stackrel{\mathrm{‾}}{u_i}=u_i\left[{\displaystyle \frac{d}{\mathit{\kappa }}}\right],\stackrel{\mathrm{‾}}{\mathit{\eta }}=\mathit{\eta }\left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\eta }}_{\mathrm{0}}}}\right],\stackrel{\mathrm{‾}}{\mathit{\tau }}=\mathit{\tau }\left[{\displaystyle \frac{d^{\mathrm{2}}}{\mathit{\kappa }{\mathit{\eta }}_{\mathrm{0}}}}\right],\\ & \stackrel{\mathrm{‾}}{t}=t\left[{\displaystyle \frac{\mathit{\kappa }}{d^{\mathrm{2}}}}\right],\stackrel{\mathrm{‾}}{T}=T\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }T}}\right],\end{array}\end{array}$$

where d is the mantle depth, t is time, η₀ is the reference viscosity, and $\mathrm{\Delta }T=(T_{\mathrm{s}}-T_{\mathrm{p}})$ is the superadiabatic temperature difference across the fluid layer. Substituting dimensional terms for scaled dimensionless values (e.g $x\to \stackrel{\mathrm{‾}}{x}d$) and rearranging allows us to write the Stokes equation as

$$\begin{array}{}\text{(A10)}& \mathrm{2}\stackrel{\mathrm{‾}}{\mathit{\eta }}{\stackrel{\mathrm{‾}}{D}}_{ij,j}+{\stackrel{\mathrm{‾}}{p}}_{,i}=Ra(\mathrm{1}-\stackrel{\mathrm{‾}}{T})(-{\mathit{\delta }}_{iz}).\end{array}$$

Overbars in Eq. (A10) represent dimensionless quantities, and all dimensional parameters are contained in the dimensionless ratio Ra, the Rayleigh number which can be interpreted as a ratio of advection and diffusion timescales:

$$\begin{array}{}\text{(A11)}& Ra={\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}g\mathit{\alpha }\mathrm{\Delta }T{D}^{\mathrm{3}}}{{\mathit{\eta }}_{\mathrm{0}}\mathit{\kappa }}}.\end{array}$$

The dimensionless viscosity, which has a functional dependence on the total pressure, the temperature, and the second invariant of the stress tensor, is described below.

The dimensionless form of the heat conservation equation is

$$\begin{array}{}\text{(A12)}& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{T}}{\partial \stackrel{\mathrm{‾}}{t}}}+{\stackrel{\mathrm{‾}}{u}}_i{\stackrel{\mathrm{‾}}{T}}_{,i}=({\stackrel{\mathrm{‾}}{T}}_{,i}{)}_{,i}+\stackrel{\mathrm{‾}}{Q},\end{array}$$

where the dimensionless internal heating is given by

$$\begin{array}{}\text{(A13)}& \stackrel{\mathrm{‾}}{Q}=Q\left[{\displaystyle \frac{d^{\mathrm{2}}}{\mathit{\kappa }{C}_{\mathrm{p}}\mathrm{\Delta }T}}\right].\end{array}$$

A2 Rheology

Mantle silicates deform through a range of mechanisms. The most important high-temperature creep mechanisms are diffusion creep (low stress), which results in a linear relationship between stress and strain that is strongly dependent on grain size, and dislocation creep (high stress), which leads to a power law relationship between stress and strain that is independent of grain size. In addition to high-temperature creep, some form of stress-limiting behaviour is expected to occur at low temperature, and high stress. Glide-controlled dislocation creep (or Peierls creep), which includes a stress dependence of the activation energy, is likely to play a role, particularly in the cold part of subducted slabs (Karato, 2012). Nevertheless, it remains unclear whether Peierls creep allows sufficient weakening, as geophysical constraints on slabs would imply (e.g. Jain et al., 2017; Krien and Fleitout, 2008; Alisic et al., 2010). In geodynamic calculations, the effect of the Peierls mechanism is similar to that of plastic, temperature-independent plasticity models (Agrusta et al., 2017; Garel et al., 2014; Čížková and Bina, 2013).

To keep the models as simple as possible we include two deformation mechanisms: grain-size-independent diffusion creep and a plastic yielding based on a truncated Drucker–Prager plasticity model. The plastic strain rates are capable of representing brittle failure at low pressure (near the surface) and low-temperature plasticity at high pressure (deep within the slab). The value of the yield stress limit is chosen on the basis of previous studies, and is consistent with several lines of evidence suggesting that slabs do not support more than a few hundred megapascals (Richards et al., 2001; Tackley, 2000; Watts and Zhong, 2000; Krien and Fleitout, 2008; Alisic et al., 2010). The viscosity associated with each deformation mechanism is combined using a harmonic average, denoted by η_c. The entire computational domain, except for the subduction interface, is governed by the same composite rheology: there is no compositional distinction between the mantle and plates.

Ductile flow laws for silicates often have an Arrhenius temperature and pressure dependence, controlled by the activation energy E, and activation volume V (Hirth and Kohlstedt, 2004). Additional dependencies, such as grain size and melt fraction, are neglected in this study, resulting in the following diffusion viscosity:

$$\begin{array}{}\text{(A14)}& {\mathit{\eta }}_{\mathrm{d}}=A\exp \left({\displaystyle \frac{E+p_{\mathrm{l}}V}{R{T}_a}}\right),\end{array}$$

where p_l indicates the lithostatic component of the pressure, and A is a constant. A linearized adiabatic term is added to the dimensionless temperature field, whenever it appears in an Arrhenius law.

$$\begin{array}{rl}{T}_a& =T+z\times T_{,z}\\ T_{,z}& ={\displaystyle \frac{-\mathit{\alpha }g{T}_{\mathrm{p}}}{C_{\mathrm{p}}}}\end{array}$$

The dimensionless form of the creep law applied in the models uses the following scalings:

$$\begin{array}{}\text{(A15)}& \stackrel{\mathrm{‾}}{E}=E\left[{\displaystyle \frac{\mathrm{1}}{R\mathrm{\Delta }T}}\right],\stackrel{\mathrm{‾}}{W}=V\left[{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}gd}{R\mathrm{\Delta }T}}\right],\stackrel{\mathrm{‾}}{A}=A\left[{\displaystyle \frac{\mathrm{1}}{{\mathit{\eta }}_{\mathrm{0}}}}\right].\end{array}$$

Note that $V\to \stackrel{\mathrm{‾}}{W}$ includes a change from pressure dependence (dimensional) to depth dependence (dimensionless): the dimensionless diffusion creep viscosity can be written

$$\begin{array}{}\text{(A16)}& {\stackrel{\mathrm{‾}}{\mathit{\eta }}}_d=\stackrel{\mathrm{‾}}{A}\exp \left({\displaystyle \frac{\stackrel{\mathrm{‾}}{E}+\stackrel{\mathrm{‾}}{z}\stackrel{\mathrm{‾}}{W}}{\stackrel{\mathrm{‾}}{T_{\mathrm{s}}}+{\stackrel{\mathrm{‾}}{T}}_a}}\right),\end{array}$$

where $\stackrel{\mathrm{‾}}{z}$ is the dimensionless depth and $\stackrel{\mathrm{‾}}{T_{\mathrm{s}}}$ is the dimensionless surface temperature. The dimensionless linearized adiabatic component is incorporated as follows.

$$\begin{array}{r}{\stackrel{\mathrm{‾}}{T}}_a=\stackrel{\mathrm{‾}}{T}+\stackrel{\mathrm{‾}}{z}\times {\stackrel{\mathrm{‾}}{T}}_{,\stackrel{\mathrm{‾}}{z}}\\ {\stackrel{\mathrm{‾}}{T^{\prime }}}_{,\stackrel{\mathrm{‾}}{z}}=T_{,z}\left[{\displaystyle \frac{d}{\mathrm{\Delta }T}}\right]\end{array}$$

The parameters chosen for the diffusion creep law are consistent with those derived from experimental data on dry olivine (Karato and Wu, 1993), providing an average upper mantle viscosity close to 1×10²⁰ Pa s. The relatively high value of the activation volume produces relatively low viscosity asthenosphere $\sim \mathrm{0.3}\times {\mathrm{10}}^{\mathrm{20}}$, relative to the transition zone $\sim \mathrm{5}\times {\mathrm{10}}^{\mathrm{20}}$. Additionally, a viscosity increase (×η₆₆₀) is applied at the 660 km discontinuity, consistent with inferences based on the geoid (Hager and O'Connell, 1981). For ($\times {\mathit{\eta }}_{\mathrm{660}}=\mathrm{10}$), the lower mantle just beneath 660 km is 50 times more viscous than the mean viscosity of the upper mantle. The parameters chosen produce radial viscosity profiles that are slightly higher than the “Haskell constraint” (${\mathit{\eta }}_{\mathrm{mean}}=\mathrm{1}\times {\mathrm{10}}^{\mathrm{21}}$) over the upper 1400 km of the mantle (e.g. Becker, 2017).

A range of pseudo-brittle and plastic deformation mechanisms can be approximated in the fluid constitutive model by allowing non-linearity in the viscosity ($\mathit{\eta }=\mathit{\eta }(T,p,J_{\mathrm{I}},\mathrm{\dots })$). The rheological model itself should be defined independently of the coordinate system, so it is necessary to define the constitutive model in terms of stress invariants (J_I). The standard viscoplastic approach (Spiegelman et al., 2016) defines an effective plastic viscosity η_p such that the deviatoric stress tensor is bounded by a yield stress τ_y:

$$\begin{array}{}\text{(A17)}& {\mathit{\tau }}_{\mathrm{y}}=\mathrm{2}{\mathit{\eta }}_{\mathrm{p}}{D}_{ij}.\end{array}$$

Assuming that η_p is isotropic and scalar (i.e. eigenvectors of the strain-rate tensor and deviatoric stress are identical), one can use the magnitude of both sides to define the scalar effective plastic viscosity as

$$\begin{array}{}\text{(A18)}& {\mathit{\eta }}_{\mathrm{p}}={\displaystyle \frac{{\mathit{\tau }}_{y\left(\mathrm{II}\right)}}{\mathrm{2}{\mathit{ϵ}}_{\mathrm{II}}}},\end{array}$$

where the subscript II denotes the square root of the tensor second invariant.

The yield stress function in the computational models is a truncated Drucker–Prager criterion:

$$\begin{array}{}\text{(A19)}& {\mathit{\tau }}_{\mathrm{y}}=\min ({\mathit{\tau }}_{\max },\mathit{\mu }p+C),\end{array}$$

where μ is the friction coefficient, and C is the cohesion. The Drucker–Prager yield surface is defined by the full pressure p. Because the pressure that appears in the dimensionless Stokes equation (Eq. A10) is a dynamic pressure ($\stackrel{\mathrm{‾}}{p}$), due to density variations only, the lithostatic pressure (a function of vertical coordinate) needs to be accounted for. The dimensionless form of the yield stress is given by

$$\begin{array}{}\text{(A20)}& {\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{\mathrm{y}}=\min ({\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{\max },\stackrel{\mathrm{‾}}{\mathit{\mu }}(\stackrel{\mathrm{‾}}{p}+\stackrel{\mathrm{‾}}{p_l}\stackrel{\mathrm{‾}}{z})+\stackrel{\mathrm{‾}}{C}),\end{array}$$

where

$$\begin{array}{}\text{(A21)}& \begin{array}{r}\stackrel{\mathrm{‾}}{\mathit{\mu }}=\mathit{\mu },\\ \stackrel{\mathrm{‾}}{C}=C\left[{\displaystyle \frac{d^{\mathrm{2}}}{\mathit{\kappa }{\mathit{\eta }}_{\mathrm{0}}}}\right],\\ {\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{\max }={\mathit{\tau }}_{\max }\left[{\displaystyle \frac{d^{\mathrm{2}}}{\mathit{\kappa }{\mathit{\eta }}_{\mathrm{0}}}}\right],\\ \stackrel{\mathrm{‾}}{P_l}=\stackrel{\mathrm{‾}}{z}\left[{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{0}}g{d}^{\mathrm{3}}}{\mathit{\kappa }{\mathit{\eta }}_{\mathrm{0}}}}\right].\end{array}\end{array}$$

The effective plastic viscosity (dimensionless) is given by

$$\begin{array}{}\text{(A22)}& {\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{p}}={\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\tau }}}_{\mathrm{y}\left(\mathrm{II}\right)}}{\mathrm{2}{\dot{\mathit{ϵ}}}_{\mathrm{II}}}}.\end{array}$$

The final (composite) viscosity is the harmonic average of the viscosity associated with creep and plastic yielding

$$\begin{array}{}\text{(A23)}& {\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{c}}={\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{d}}{\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{p}}}{{\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{d}}+{\stackrel{\mathrm{‾}}{\mathit{\eta }}}_{\mathrm{p}}}}.\end{array}$$

A3 Model parameters and scaling values

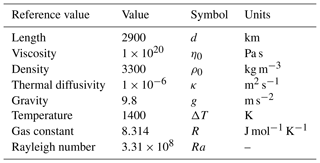
This section provides a record of model parameters and reference values that are used in the models. The dimensional parameters quoted here are non-dimensionalized using the scaling system described in Appendix A and reference values provided in Table A1. This scaling system is identical for all models used within the thesis.

Table A1 Reference values used to non-dimensionalize the Stokes and energy equations, as described in Appendix A.

Table A2 Typical model element resolution was 800×160. Sub. stands for subduction.

Dimensional model parameters: ^a Drucker–Prager. ^b Upper mantle. ^c Lower mantle.