Control of pre-existing fabric in fracture formation, reactivation and vein emplacement under variable fluid pressure conditions: an example from Archean greenstone belt, India

Most of the upper crustal fluid flows are strongly influenced by the pre-existing fractures/foliations in the rocks under a certain state of tectonic stress and fluid pressure condition. In the present study, we analyzed a wide range of crosscutting fractures that are filled with quartz veins of variable orientations and thicknesses, from the gold-bearing massive metabasalts (supracrustals) of the Chitradurga Schist Belt adjacent to the Chitradurga Shear Zone (CSZ), Western Dharwar Craton, southern India. The study involves the following steps: (1) analyzing the internal magnetic fabric, using anisotropy of magnetic susceptibility (AMS) studies, and determining strength of the host metabasalts, (2) quantifying the fluid pressure condition through lower hemisphere equal area projection of pole to veins by determining the driving pressure ratio (R^′), stress ratio (ϕ), and susceptibility to fracturing, and (3) deciphering the paleostress condition using fault-slip analysis. We interpret the NNW–SSE to NW–SE (mean 337/69^∘ NE) oriented magnetic fabric in the rocks of the region as having developed during regional D1/D2 deformation on account of NE–SW shortening. However, D3 deformation manifested by NW–SE to E–W shortening led to the sinistral movement along CSZ. As a consequence of this sinistral shearing, fractures with prominent orientations formed riedel shear components, with CSZ as the shear boundary. Subsequently, all the pre-existing fabrics along with the riedel shear components were reactivated and vein emplacement took place through episodic fluid pressure fluctuation from high to low P_f at shallow depth (∼ 2.4 km). However, NNW–SSE orientations were prone to reactivate under both high- and low-P_f conditions, thereby attaining maximum vein thickness along these orientations. The deduced paleostress from fault-slip analysis along with the kinematics of the fractures and veins are in good agreement with previously estimated regional tectonics. Thus, integrating multiple domains of studies helps in the logical interpretation of fluid flow conditions and vein emplacement mechanisms in the study area that has not been ventured before.

1 Introduction

The upper crust is replete with fractures/faults, which act as pathways for fluid flow and vein emplacement. Fracture formation and vein emplacement mechanisms are closely interrelated and require a detailed study to find out potential hydrothermal deposits. Fracture formation and reactivation involve a combination of regional stress field (far-field stress), stress ratio (Φ) and driving pressure ratio (R^′) that helps to determine the prevailing fluid pressure condition (Delaney et al., 1986; Jolly and Sanderson, 1997; McKeagney et al., 2004; Mazzarini and Isola, 2007; Martínez-Poza et al., 2014; Cucci et al., 2017). However, previous studies suggest that pre-existing anisotropy in host rocks plays a significant role in formation and propagation of fractures provided the anisotropy is favorably oriented to the far-field stresses (Ikari et al., 2015; Donath, 1961; Hoek, 1964; Attewell and Sandford, 1974). The presence of such favorably oriented anisotropy lowers the shear strength of the host rocks, enabling failure/slip along them at minimum compressive stress, prior to/during vein emplacement. Such conduits are reactivated at both high and low fluid pressures, forming pathways for fluid flow (Mondal and Mamtani 2013; Lahiri and Mamtani, 2016). Thus, the vein emplacement mechanism requires favorably oriented fractures that can be reactivated when fluid pressure gradually builds and exceeds the normal stresses acting on the fracture wall (Gudmundsson, 2011). This enables the fractures to open up under cyclic increase in fluid pressure along such pre-existing conduits, a mechanism known as fault-valve action (Sibson et al., 1988; Sibson, 1992, 1996, 2000; Boullier and Robert, 1992; Sibson and Scott, 1998; Petit et al., 1999; Cox et al., 2001, among others). Subsequently, fluid flows into the fractures, a phenomenon analogous to burping, triggering an immediate drop in fluid pressure. This sudden drop in fluid pressure is responsible for mineral deposition and vein formation (Cox et al., 1991, 2001; Cox, 1995). Vein materials thus deposited seal the fracture/fault planes, preparing the system for the next cycle of fluid pressure build-up, rupture, fluid flow and vein formation (Mondal and Mamtani, 2013; Lahiri and Mamtani, 2016; Marchesini et al., 2019). Thus, repeated cycles of elevated and depleted fluid pressure generate widespread networking of veins in host rocks. Studies conducted in the present approach help to understand the mechanism of fabric development and fracture formation vis-à-vis vein emplacement. This study also aims to provide detailed insight into the development of brittle structures and their role in understanding the tectonic evolution of Archean cratons.

The Chitradurga Schist Belt (Western Dharwar Craton, southern India) is a NW–SE trending Archean greenstone belt, known to harbor a widespread network of veins with potential epigenetic gold-bearing lodes (Gupta et al., 2014; Gopalakrishna et al., 2018). We have conducted this study in the meta-volcanic (metabasalts), hosting quartz veins of variable orientations and thicknesses, in and around the Chitradurga region. We emphasize understanding the mechanism of vein emplacement under a tectonic environment where propensity of fracture reactivation for vein emplacement is mutually dependent on both fluid pressure condition and the regional far-field stresses. The present paper is a comprehensive work which quantifies the fabric in the visually isotropic metabasalts of the Chitradurga Greenstone Belt and its role in fracture formation and in channelizing upper crustal fluids. We also found the potential reactivation ability of the fractures/faults at variable fluid pressure conditions to investigate the role of fractures/faults which are not favorably oriented to the pre-existing anisotropy and regional stress field and their contribution to vein emplacement in the study area.

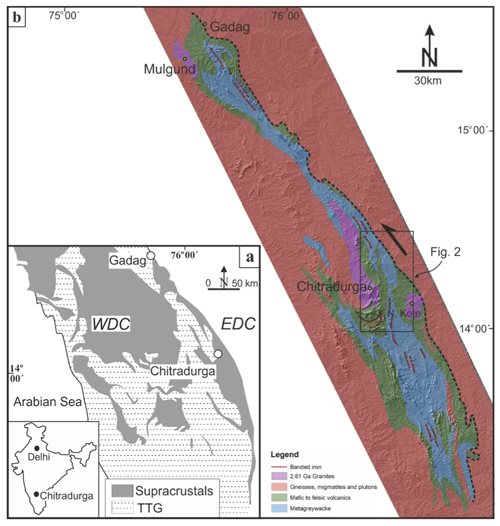
Figure 1 (a) Regional map of the Western Dharwar Craton, South Indian Shield (following Chadwick et al., 2003). Inset shows the map of India. EDC: Eastern Dharwar Craton; WDC: Western Dharwar Craton; TTG: tonalite–trondhjemite–granodiorite; supracrustals: volcano-sedimentary assemblages. (b) Regional geological map (DEM) of the Chitradurga Schist Belt (modified following Jayananda et al., 2013). Dotted line (in b) marks the eastern boundary of the Chitradurga Schist Belt, representing the Chitradurga Shear Zone (CSZ). Rectangular box near Chitradurga demarcates the study area.

2 Geology of the study area

The study was conducted in the Chitradurga Greenstone Belt of Dharwar Craton (southern India; Fig. 1a), which represents a complex geological history. Dharwar Craton exposes >3.0 Ga, Archean continental crusts, represented by the TTG (trondjemite–tonalite–granodiorite) gneiss also known as the peninsular gneiss (Jayananda et al., 2006). The craton stabilized during the accretion of the Eastern Dharwar Craton (EDC) and Western Dharwar Craton (WDC) at 2.75–2.51 Ga. The zone of accretion of the two tectonic blocks is marked by a shear zone, referred to as the Chitradurga Shear Zone (e.g., Naqvi and Rogers, 1987; Chadwick et al., 2003; Jayananda et al., 2006). The eastern part of the WDC marked by the Chitradurga Schist Belt (CSB) (Fig. 1b) is comprised of peninsular gneiss (3.4–3.0 Ga) and younger supracrustal rocks (Beckinsale et al., 1980; Sarma et al., 2011; Taylor et al., 1984). The latter comprises metavolcanics/metabasalts (greenstone belt; greenschist/lower amphibolite facies metamorphism), metamorphosed greywacke–argillite (interbanded with ferruginous chert and banded iron formation), polymict conglomerate, and ferruginous chert. The basaltic rocks of the schist belt have an island arc affinity (Chakrabarti et al., 2006). Regionally, the belt is surrounded by older peninsular gneisses and younger granitoids (Ramakrishnan and Vaidyanadhan, 2010). Previous geological investigations revealed the presence of various younger granites at ∼2.6 Ga (Jayananda et al., 2006; Chardon et al., 2002) which are associated with the schist belt, such as Chitradurga granite, J. N. Kote granite. The structural investigations of the adjacent metasedimentary rocks of the region show that the area has undergone three phases of deformation: D1, D2 and D3, respectively (Chadwick et al., 1989; Jayananda et al., 2006; Mondal and Mamtani, 2014). The D1/D2 deformations are coaxial with the NW–SE striking axial plane. D1 folds are tight to isoclinal and asymmetric, while the D2 folds are open to tight and upright. Earlier studies revealed that the folds (regional open; NE–SW striking vertical axial plane) related to early D3 deformation superposed the D1/D2 structures, thus resulting in dome-basin geometry in the metasedimentary rocks of that region (Chakrabarti et al., 2006; Mondal and Mamtani, 2014). However, a later phase of D3 deformation led to the formation of brittle structures in the younger granites of the CSB (Mondal and Mamtani, 2016). The NE–SW shortening during D1/D2 deformation was responsible for NW–SE oriented structural elements in the CSB (Chadwick et al., 2003), while NW–SE to E–W shortening direction prevailed during D3 deformation (Jayananda et al., 2006; Mondal, 2018; Mondal and Acharyya, 2018). A number of petrological and geochemical investigations have been carried out on the area in the past. These studies suggest the presence of actinolite, albite, chlorite, epidote, quartz and calcite in the basaltic rocks of the region (Chakrabarti et al., 2006). The CSB shows evidence of progressive metamorphism with a gradual increase in P–T conditions (approximately 3–4 Kb of pressure) from greenschist facies in the north to amphibolite facies in the south, suggesting the depth of deformation to be 10–12 km (during D1/D2). However, a recent study by Acharyya and Mondal (2019) shows that the brittle deformation during late D3 took place at a shallow depth of ∼2–4 km. The dashed rectangular area in Fig. 1b demarcates the study area. The present study focuses on the dark greyish to blackish, massive to fine grained, altered metabasalt hosting quartz veins of the region surrounded by metasedimentary sequences (Fig. 2). The metabasalts of the study area are devoid of any well-defined mesoscopic foliation. The foliation planes in the adjacent metasedimentary rocks of the region are found to be NW–SE oriented (mean strike/dip is 323/71^∘ NE). Since the metabasalts are devoid of mesoscopic field fabric, the anisotropy of magnetic susceptibility (AMS) study has been conducted in order to quantify their internal magnetic fabric.

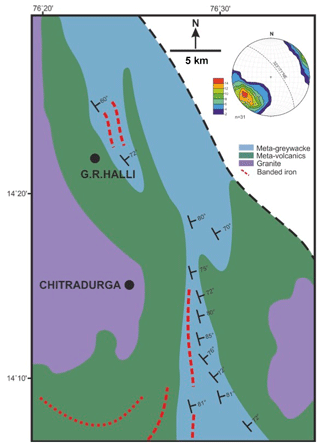
Figure 2 Geological map of the study area showing the foliation trends of the supracrustals. Lower hemisphere equal area projection shows the pole to foliation planes recorded from the region. Note that the mean foliation (dotted great circle) is 323/71^∘ NE, which is parallel to the CSZ (n: number of data). Color scheme of the legend indicates variation in the contour density.

3 Overview of brittle structures

Metabasalts of the study area are replete with fractures and faults of multiple orientations. Some of these fractures and faults are found to host quartz veins forming a crisscross pattern (Fig. 3a and c), and some of them are devoid of any vein material. Growth of vein materials (quartz crystals) is often found to be perpendicular to the vein wall, suggesting that dilation was significant in these veins (Fig. 3b). The maximum width and length of the quartz veins are ∼1.5 and ∼130 m, respectively. Some of the quartz veins are found to be displaced by other ones forming a crisscross network of veins in the study area (Fig. 3c). Wing cracks filled up with quartz veins are also observed (Fig. 3d). In a few places, the thicker quartz veins show series of successive fault planes with prominent slickenside lineations on them (Fig. 3e and inset). Those veins are often found to enclose angular metabasalt enclaves (host material, Fig. 3f), suggesting that fault-valve action was predominant in the region. Quartz veins are recorded with multiple median lines as evidence of a crack-seal mechanism due to cyclic fluid ingression (Fig. 3g). Some of the fault planes recorded in the study area have shallow plunging slickenside lineations, while others have moderate to high plunging lineations. Both left lateral faults (LLFs) and right lateral faults (RLFs) are recorded based on the movement of the hanging wall with respect to the footwall. Presence of congruous steps helps in the discrete identification of the normal faults (Fig. 3h). Although quartz veins of variable orientations and thicknesses are found, most of the veins are predominantly NNW–SSE trending (Fig. 4a). Most of the fractures and faults show a NNW–SSE trend (maxima), whereas some others form a WNW–ESE to NE–SW sub-maximum, respectively (Fig. 4b, c). Some WNW–ESE trending Mode-I (tensional) cracks with prominent tips are also recorded from the study area and are often filled up with quartz veins. It may be noted that the veins with maximum thicknesses are oriented along the NNW–SSE direction (Fig. 4d). In this study, 992 fracture data (strike/dip), 378 vein data (strike, dip and thickness) and 73 fault data (strike, dip and slip) have been measured from the metabasalt exposures at about 13 locations in the entire study area. All 73 fault planes with shallow to moderately plunging slickenside lineations are used to decipher the paleostress condition. Thus, the strict spatial and temporal relationships between brittle structures and veins provided by field observations help to quantify the fluid pressure conditions that prevailed during fracture reactivation and vein emplacement. They also provide information for reconstructing the tectonic stress conditions of the craton.

Figure 3 Field photographs from the study area. (a) Crisscross orientation of quartz veins in metabasalt. (b) Close-up of a quartz vein in metabasalt showing crystal growth direction perpendicular to the vein wall. (c) Cross-cutting nature in quartz veins showing dextral displacement (marked by yellow half-arrows). (d) Wing cracks filled up with quartz veins associated with sinistral shearing (marked by yellow arrow). (e) NE-dipping quartz vein showing slickenside lineations (maximum width recorded: 120 cm); inset showing a close-up of the fault plane found in (e). Marker pen placed along the orientation of the slickenside lineations. (f) Angular chunks of metabasalt (enclaves) enclosed within the faulted quartz vein. Dotted red line demarcates the enclave boundaries. Black arrow marks the slickenside lineation on the fault plane. (g) Field photograph of the quartz vein (close view) showing multiple median lines (marked with red arrows) as evidence of the crack-seal mechanism. This clearly indicates cyclic fluid ingression and fault-valve action that led to the formation of veins in the metabasalts of the Chitradurga region. (h) Fault planes in metabasalt showing congruous steps (marked by yellow arrow). Blue arrows in the respective figures point towards N.

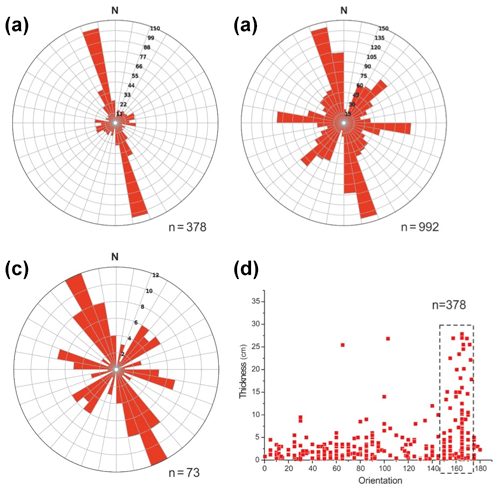
Figure 4 Rose diagrams and graphs of structural data recorded from the study area. (a–c) are the rose diagrams of the strike orientation of the quartz veins, fractures and fault planes, respectively. Note that the veins are mostly NNW–SSE striking, whereas the fractures and fault planes show variable orientations, with a NNW–SSE maximum and a WNW–ESE to NE–SW sub-maximum. (d) Graph of vein orientation vs. thickness, showing maximum vein thickness along NNW–SSE (marked with a black box). n: number of data.

4 Methods of analysis and results

The quartz veins have been emplaced in the massive metabasalts of the region that are devoid of any prominent mesoscopic foliation as mentioned above. In places, veins of one orientation are dissected and sometimes displaced by others that led to the formation of mesh-like structures (Fig. 3a, c). Sibson (1992) mentioned that such a mesh is formed when a rock contains fractures of variable orientations that may get reactivated due to a rise in fluid pressure. It is mentioned that in the Chitradurga region, veins of various orientations show mutually cross-cutting relationships, which implies repeated cycles of vein emplacement (see Sect. 3; Mondal and Mamtani, 2013; Sibson, 1992). Although veins have various orientations, NNW–SSE striking veins are the most common (Fig. 4a). It may be noted that the NW–SE to NNW–SSE direction, which defines the maximum strike orientation of quartz veins, fractures and faults, is also the orientation of the adjacent Chitradurga shear zone, the overall trend of the schist belt. This implies that there is a strong structural control on the formation of these quartz veins. It was shown earlier that the pre-existing anisotropy plays a critical role in propagating fractures and channelizing fluid in rocks (Sanderson and Zhang, 1999; Cox et al., 2001; Ikari et al., 2015). It is also known from rock mechanics investigations that the rock strength variation controls the strain partitioning and influences fluid flow (e.g., Tsidzi, 1990; Vishnu et al., 2018). Therefore, it is crucial to determine the orientation of anisotropy in host rocks and the state of stresses governing the upper crustal fluid flow vis-à-vis vein emplacement.

Three-dimensional Mohr circle analysis was performed by Jolly and Sanderson (1997) using dyke orientation data to examine the magma pressure condition that was responsible for the opening of pre-existing fractures during dyke emplacement. Further, the work has been extended to understand the fluid pressure condition and vein emplacement mechanism by McKeagney et al. (2004) (also see Yamaji et al., 2010). We present vein orientation data from the Chitradurga region (southern India), which is a province of epigenetic gold deposit (Gupta et al., 2014; Gopalakrishna et al., 2018).

We conduct an AMS study, followed by Brazilian tensile strength (BTS) determination, in order to quantify the internal magnetic fabric and tensile strength of the rocks within the study area. The 3-D Mohr circle construction using quartz vein orientation data helps to recognize the fluid pressure conditions under which they were emplaced. Further, these fluid pressure conditions were integrated with dilation tendency, slip tendency and fracture susceptibility in order to understand the mechanism of vein emplacement in the Chitradurga region. A combination of data obtained from these methods along with paleostress analysis using fault-slip data recorded from the study area provides a comprehensive evaluation of vein-forming conditions in the Chitradurga Greenstone Belt.

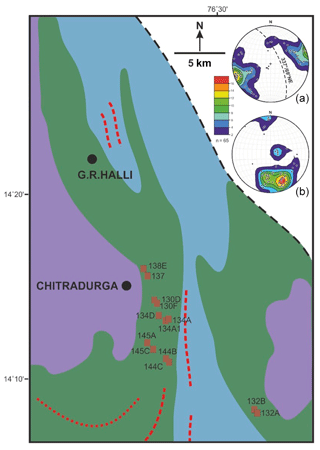
Figure 5 Map showing the location points (marked with brown boxes) from which oriented metabasalt samples for AMS analysis have been collected. (a) Lower hemisphere equal area projection of poles (K₃) to the magnetic foliation (K₁K₂) plane. Mean orientation of the K₁K₂ plane (dashed great circle) = 337/69^∘ NE. (b) Lower hemisphere equal area projection showing the distribution of magnetic lineation (K₁). Color scheme of the legend indicates variation in the contour density. n: number of data.

4.1 AMS

The quartz veins occur in massive metabasalt, which does not show any visible field foliation. However, such visibly massive rocks may preserve an internal fabric, which can be recognized through AMS studies (e.g., Tarling and Hrouda, 1993; Maffione et al., 2015; Mamtani and Greiling, 2005; Raposo et al., 2007; Loock et al., 2008; Mondal and Mamtani, 2014; Mondal, 2018). The study involves preparation of cylindrical core samples (25.4 mm diameter × 22 mm height) from oriented metabasalt blocks. These metabasalt block samples have been collected from 13 different locations (Fig. 5) in the study area. The prepared core samples are subjected to an external magnetic field and the induced magnetization for each core sample is measured in different directions. AMS is considered to be a symmetric second-rank tensor, represented by an ellipsoid with three mutually perpendicular principal axes, K₁, K₂ and K₃, respectively, where ($K_{\mathrm{1}}\ge K_{\mathrm{2}}\ge K_{\mathrm{3}}$). The orientation and magnitude of each of these principal axes are determined in this analysis, where K₁ represents the magnetic lineation and K₃ is the pole to the magnetic foliation (K₁K₂). Using the magnitudes of K₁, K₂ and K₃, several AMS parameters are calculated, such as magnetic susceptibility (K_m), magnitude of the magnetic foliation (F) and magnetic lineation (L), degree of magnetic anisotropy (P_j or P^′) and shape parameter (T). The formulae for the parameters are given below (following Tarling and Hrouda, 1993; Jelinek, 1981):

$$\begin{array}{}\text{(1)}& {\displaystyle }{K}_{\mathrm{m}}=(K_{\mathrm{1}}+K_{\mathrm{2}}+K_{\mathrm{3}})/\mathrm{3},\text{(2)}& {\displaystyle }F=(K_{\mathrm{2}}-K_{\mathrm{3}})/K_{\mathrm{m}},\text{(3)}& {\displaystyle }L=(K_{\mathrm{1}}-K_{\mathrm{2}})/K_{\mathrm{m}},\text{(4)}& {\displaystyle }{P}_j=\exp \sqrt{\mathit{\left\{}\mathrm{2}\right[({\mathit{\eta }}_{\mathrm{1}}-{\mathit{\eta }}_{\mathrm{m}}{)}^{\mathrm{2}}+({\mathit{\eta }}_{\mathrm{2}}-{\mathit{\eta }}_{\mathrm{m}}{)}^{\mathrm{2}}+({\mathit{\eta }}_{\mathrm{3}}-{\mathit{\eta }}_{\mathrm{m}}{)}^{\mathrm{2}}]\mathit{\}}},\text{(5)}& {\displaystyle }T=(\mathrm{2}{\mathit{\eta }}_{\mathrm{2}}-{\mathit{\eta }}_{\mathrm{1}}-{\mathit{\eta }}_{\mathrm{3}})/({\mathit{\eta }}_{\mathrm{1}}-{\mathit{\eta }}_{\mathrm{3}}).\end{array}$$

Here, η₁=ln K₁, η₂=ln K₂, η₃=ln K₃ and ${\mathit{\eta }}_{\mathrm{m}}=({\mathit{\eta }}_{\mathrm{1}}\cdot {\mathit{\eta }}_{\mathrm{2}}\cdot {\mathit{\eta }}_{\mathrm{3}}{)}^{\mathrm{1}/\mathrm{3}}$. In the above equations, P_j and T give the measure of the eccentricity and shape of the AMS ellipsoid, respectively. The value of T ranges between −1 and +1. Positive and negative values represent oblate and prolate shapes of the AMS ellipsoid (Tarling and Hrouda, 1993).

AMS measurements have been conducted in the spinner mode (field intensity of 300 A m⁻¹) using the KLY-4S Kappabridge (AGICO, Czech Republic); see Hrouda et al. (2006) for instrument details. The SUFAR program has been used to calculate the required AMS parameters described above for each sample. A total of 65 cores are prepared and analyzed. The mean value of the AMS parameters at each location is calculated using the Anisoft program (version 4.2, AGICO; Jelinek statistics, Jelinek, 1981). It is noted that the K_m varies between 37 and $\mathrm{1280}\times {\mathrm{10}}^{-\mathrm{6}}$ SI units, with most of the samples having K_m below $\mathrm{1000}\times {\mathrm{10}}^{-\mathrm{6}}$ SI units (see Supplement, sheet-1). This indicates that paramagnetic and ferromagnetic minerals contribute significantly to the AMS. Petrographic studies reveal the presence of actinolite, hornblende, chlorite, albite, epidote, and pyrite, which are inferred to contribute to the susceptibilities recorded in the samples. The P_j lies between 1.003 and 1.539, and the shape of the AMS ellipsoid is dominantly oblate (positive T values; see Supplement, sheet-1). It is noted that the magnetic foliation (K₁K₂ plane) is consistently NW–SE striking (mean orientation: 337/69^∘ towards NE; Fig. 5a). The magnetic lineations plunge variably from NNW through the sub-vertical to SSE (Fig. 5b).

Figure 6 Tensile strength determination of metabasalt samples. (a) Sample cores for Brazilian tensile strength (BTS) determination. $\text{Diameter}:\text{length}=\mathrm{2}:\mathrm{1}$. (b) Instruments used for measuring BTS. (c) Sample cores obtained after failure.

4.2 Tensile strength determination

It is known that the dilation occurs in a direction parallel to the minimum compressive principal stress (σ₃), when the fluid pressure (P_f) exceeds the normal stress acting on the fracture wall. Therefore, the fractures may occur at any depth when the effective stress (σ₃−P_f) is sufficient to counteract the tensile strength (T) of the rocks (Gudmundsson, 2011). We measure the tensile strength of the host metabasalts to quantify the mode of failure. The measurement of direct tensile strength requires machined specimens and also involves difficulty in applying tensile load to the cylindrical specimen during analysis. Therefore, tensile strength measurement of rocks using the Brazilian test has become imperative in rock mechanics. Compression-induced extensional fractures are generated in the test, which essentially involves line loading on a circular disk placed between two platens (Aydin and Basu, 2006; Basu et al., 2013; see Fig. 6). This tensile strength (T) is estimated from the elastic theory (ISRM, 1978; ASTM, 2001):

$$\begin{array}{}\text{(6)}& T={\displaystyle \frac{\mathrm{2}P}{\mathit{\pi }LD}}.\end{array}$$

Here, P is peak/failure load, and L and D are the length and diameter of the disk, respectively. For this analysis, 18 core samples were drilled from metabasalt blocks which were later resized to obtain the desirable cores for the analysis ($\text{length}:\text{diameter}=\mathrm{1}:\mathrm{2}$). The maximum tensile strength of each specimen at the instance of failure is recorded. The maximum tensile strength for 16 samples is averaged out to obtain the approximate tensile strength of metabasalts, which is ∼12 MPa. Since, in the geologic term, the tensile strength value must be negative, we consider this value to be about −12 MPa.

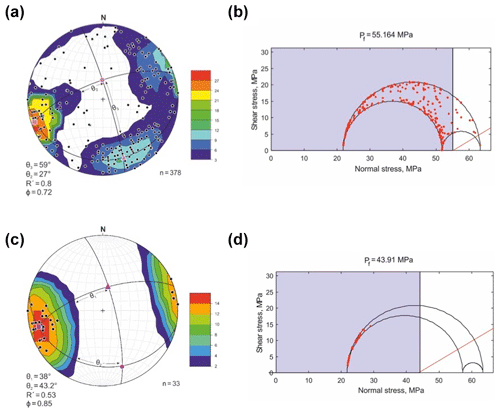
Figure 7 State of stresses and fluid pressure (P_f) conditions determined from vein orientation data in the study area. (a) Lower hemisphere equal area projection of pole to veins shows girdle distribution, implying P_f>σ₂ (following Jolly and Sanderson, 1997). The empty space devoid of any vein pole data helps to determine the position of σ₁ (using Bingham statistics of the Stereonet 9 software) and thereby defines the σ₁σ₂ and σ₁σ₃ planes. Angles θ₂ and θ₃ are measured, which are used to determine the stress ratio (ϕ) and driving pressure ratio (R^′), respectively. Color schemes of the legends indicate variation in the contour density. Pink circle (σ₁), pink triangle (σ₂) and pink square (σ₃), respectively. (b) 3-D Mohr circle diagram for high-P_f conditions. Red line in the Mohr circle represents the reactivation envelope for cohesionless fractures. Vein pole data lying within the blue zone, i.e., to the left of the P_f (black) line, represent fractures filled up with veins that are prone to reactivate (Fractend code available via Healy, 2017). (c) Lower hemisphere equal area projection of poles to vein data forming the WSW cluster in (a); this cluster distribution of vein pole data indicates P_f<σ₂. Cluster maxima define the σ₃ axis. Angles θ₁ and θ₂ are measured and, similarly, ϕ and R^′ are determined. (d) 3-D Mohr circle diagram for a low-P_f condition. Only a limited range of fractures filled up with veins are prone to reactivate. Red dots represent pole to vein data and the red line forms the reactivation envelope for cohesionless fractures. n: number of data.

4.3 Fluid pressure determination

Here, we have used the method proposed by Jolly and Sanderson (1997) to quantify the P_f conditions that led to the vein emplacement in metabasalts of the Chitradurga region (southern India). We have used the lower hemisphere equal area projection of the poles to quartz vein data. According to Jolly and Sanderson (1997), girdle distribution of vein pole data implies P_f>σ₂, described as a condition where a large number of fracture orientations are prone to reactivate, while P_f<σ₂ represents clustered distribution of vein pole data, where only a limited range of fracture orientations reactivates. Depending on the type of distribution (girdle/cluster), parameters such as stress ratio (ϕ) and driving pressure ratio (R^′) are calculated using ranges of fracture orientations (θ₁, θ₂ and θ₃) from the following equations provided by Jolly and Sanderson (1997) and Baer et al. (1994).

$$\begin{array}{}\text{(7)}& R^{\prime }={\displaystyle \frac{P_{\mathrm{f}}-{\mathit{\sigma }}_{\mathrm{3}}}{{\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}}}}={\displaystyle \frac{\mathrm{1}+\cos \mathrm{2}{\mathit{\theta }}_{\mathrm{2}}}{\mathrm{2}}}\end{array}$$

For P_f>σ₂,

$$\begin{array}{}\text{(8)}& \mathrm{\Phi }={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{2}}-{\mathit{\sigma }}_{\mathrm{3}}}{{\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}}}}=\mathrm{1}-{\displaystyle \frac{\mathrm{1}-\cos \mathrm{2}{\mathit{\theta }}_{\mathrm{2}}}{\mathrm{1}-\cos \mathrm{2}{\mathit{\theta }}_{\mathrm{3}}}}.\end{array}$$

For P_f<σ₂,

$$\begin{array}{}\text{(9)}& \mathrm{\Phi }={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{2}}-{\mathit{\sigma }}_{\mathrm{3}}}{{\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}}}}={\displaystyle \frac{\mathrm{1}+\cos \mathrm{2}{\mathit{\theta }}_{\mathrm{2}}}{\mathrm{1}+\cos \mathrm{2}{\mathit{\theta }}_{\mathrm{1}}}}.\end{array}$$

In Fig. 7a, the lower hemisphere equal area projection of pole to vein data shows a girdle distribution, implying a high fluid pressure condition (P_f>σ₂). From this distribution the orientations of the principal stress axes (σ₁, σ₂ and σ₃) are determined using the Bingham statistics of the Stereonet 9 software (http://www.geo.cornell.edu/geology/faculty/RWA/programs/stereonet.html, last access: February 2020). σ₁ is sub-vertical lying in the empty space devoid of any vein pole data. Subsequently, following Jolly and Sanderson (1997), the planes σ₁σ₂, σ₁σ₃ and σ₂σ₃ are constructed and the range of fracture orientations θ₂ and θ₃ is determined along the σ₁σ₃ and σ₁σ₂ planes, respectively. For this high-P_f condition, θ₂=27^∘, θ₃=59^∘, from which ϕ=0.72 and $R^{\prime }=\mathrm{0.8}$ are calculated. Thus, such a P_f condition enhances the chances of vein emplacement along various orientations. Although pole to vein data represent a girdle distribution pattern, the distribution of the data points shows three prominent clusters. The WSW cluster forms the highest-density cluster around the σ₃ axis, indicating a number of veins with similar orientations. The cluster primarily represents the NNW–SSE to NW–SE trending veins, attaining the maximum thickness. It should be noted that the majority of the veins are oriented along this direction (see Fig. 4a), which also suggests that the vein-forming fluid must have been channelized through a pre-existing anisotropy (trending NW–SE to NNW–SSE; see Sect. 4.1). These data are segregated and plotted separately in the lower hemisphere equal area projection, and thus the obtained contour defines the WSW cluster (Fig. 7c). We decided to extend the contour interval beyond the data points in order to incorporate the maximum range of vein orientations (θ) lying parallel/sub-parallel to the internal anisotropy (as evident from the anisotropy of magnetic susceptibility study) of the host rock. Also, the contour interval and significance level for each of the clusters were selected in such a way that the maximum number of data points are included, in order to obtain a statistically viable data cluster. Apart from the WSW cluster (with a high cluster density), the SE and the NE clusters (with higher data spreading) are also evaluated discretely (Fig. 8). The number of obtained clusters can also be analyzed through mixed Bingham analysis using K vs. BIC (i.e., the number of Bingham components of a mixed Bingham distribution vs. Bayesian information criterion; Yamaji and Sato, 2011). We have found that the lowest BIC values are obtained when K=3 (number of possible clusters for the given data set), thereby justifying the selection of the three clusters for the analysis. It is however difficult to quantify the lowest P_f value; we therefore intend to use the obtained P_f values from the respective clusters as examples of low-P_f conditions denoting P_f fluctuation rather than quantifying the lowest P_f condition of the study area. The orientations of the principal stress axes (σ₁, σ₂ and σ₃) are determined using the Bingham statistics of the Stereonet 9 software. Similarly, the σ₁σ₂, σ₁σ₃ and σ₂σ₃ planes are constructed and the range of fracture orientations θ₁ and θ₂ is calculated along the σ₂σ₃ and σ₁σ₃ planes. Again, for low-P_f conditions, θ₁=38^∘, θ₂=43.2^∘, ϕ=0.85 and $R^{\prime }=\mathrm{0.53}$ (WSW cluster, Fig. 7c); θ₁=32^∘, θ₂=35^∘, ϕ=0.93 and $R^{\prime }=\mathrm{0.67}$ (NE cluster, Fig. 8a); θ₁=30^∘, θ₂=44^∘, ϕ=0.69 and $R^{\prime }=\mathrm{0.52}$ (SE cluster, Fig. 8c). This implies that under a low fluid pressure condition (P_f<σ₂) only a limited range of fracture orientations is prone to reactivate. In each case, to determine the absolute P_f magnitude, pole to vein data are plotted in 3-D Mohr circles. Recent studies by Mondal and Acharyya (2018) documented the depth of faulting and fracturing in close proximity to the study area (Chitradurga granite) to be ∼2.4 km. A similar depth of fracturing has also been reported by Acharyya and Mondal (2019) from the elliptical clasts of the conglomerate bed within the Chitradurga Schist Belt. We have considered this depth to determine the magnitude of the maximum compressive stress (σ₁) during fracture formation, using σ₁=hρg, where h is the depth of fracturing in metabasalts (∼2.4 km), ρ is the approximate bulk density of the crust (2700 kg m⁻³), and g=9.8 m s⁻². Therefore, in a normal faulting regime, ${\mathit{\sigma }}_{\mathrm{v}}={\mathit{\sigma }}_{\mathrm{1}}\ge \mathrm{63.5}$ MPa, when depth of fracturing in metabasalt ∼2.4 km. The empirical approach by McGarr (1980) and Mazzarini et al. (2019) suggests that, at crustal depth <7 km, the differential stress (Δσ)=2τ_m, where τ_m is the shear stress at depth z (in km): ${\mathit{\tau }}_{\mathrm{m}}=\mathrm{5.0}+\mathrm{6.6}z$. Therefore, at ∼2.4 km depth the minimum compressive stress (σ₃) is found to be 21.82 MPa. In each case we consider the limiting values for both maximum and minimum compressive stresses. Magnitude for the intermediate compressive stress (σ₂) is determined using the respective stress ratios (ϕ) for both high- and low-P_f conditions, respectively. Following Jolly and Sanderson (1997), the 3-D Mohr circles are constructed using the above magnitudes of principal stresses and the angles determining the range of fracture orientations. Thus, well-defined P_f lines for both high-P_f (P_f=55.164 MPa; Fig. 7b) and low-P_f conditions (P_f=43.91 MPa; Fig. 7d, P_f=49.74, Fig. 8b and P_f=43.49, Fig. 8d) are obtained using the Fractend code (Healy, 2017).

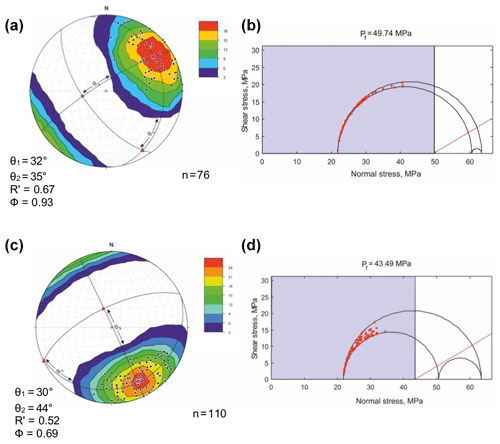
Figure 8 State of stress and fluid pressure (P_f) conditions determined from the vein orientation data in the study area. (a) Lower hemisphere equal area projection of poles to vein data forming the NE cluster. (b) 3-D Mohr circle diagram for the NE cluster. (c) Lower hemisphere equal area projection of poles to vein data forming the SE cluster. (d) 3-D Mohr circle diagram for the SE cluster. In the respective lower hemisphere equal area projections, cluster distribution of vein pole data indicates P_f<σ₂. Cluster maxima define the σ₃ axis. The ranges of fracture orientations (θ) are measured. Subsequently, ϕ and R^′ values are also determined similarly to Fig. 7. Pink circle (σ₁), pink triangle (σ₂) and pink square (σ₃), respectively. In the 3-D Mohr circle diagrams, only a limited range of fractures filled up with veins are prone to reactivate. Red dots represent pole to vein data and red line forms the reactivation envelope for cohesionless fractures. Vein pole data lying within the blue zone, i.e., to the left of the P_f (black) line, represent fractures filled up with veins that are prone to reactivate. n: number of data.

4.4 Dilation tendency, slip tendency and fracture susceptibility

Dilation tendency (T_d) and slip tendency (T_s) determine the propensity of any fracture orientation to reactivate through dilation or shearing, under a certain state of stress condition (Mazzarini et al., 2019). While a high dilation tendency ensures reactivation through dilation, a high slip tendency elevates chances of opening through shearing (Ferrill et al., 1999). According to Stephens et al. (2017), fracture planes suffer dilation when the difference between σ₁ and the normal stress acting on the plane is close enough to the magnitude of differential stress (${\mathit{\sigma }}_{\mathrm{D}}={\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}}$) and $T_{\mathrm{d}}=({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{n}})/{\mathit{\sigma }}_{\mathrm{D}}$. Slip tendency is denoted by the ratio of shear stress (σ_s) to normal stress (σ_n); ($T_{\mathrm{s}}={\mathit{\sigma }}_{\mathrm{s}}/{\mathit{\sigma }}_{\mathrm{n}}$) and also depends on the frictional characteristics of the rock (Morris et al., 1996), along with the fracture plane orientation. Under a particular state of stress condition, if the ratio of shear stress to normal stress is significantly large, then that particular fracture orientation is prone to reactivate. Fracture susceptibility (S_f) is defined as the variation of fluid pressure (ΔP_f) within a fracture plane that can lead to fluid-induced shear reactivation (Mildren et al., 2002; Stephens et al., 2017). Such reactivations depend on the shear and normal stresses acting on the fracture plane, along with the cohesion (=0 in this case) and the static coefficient of friction (μ_s); $S_{\mathrm{f}}={\mathit{\sigma }}_{\mathrm{n}}-({\mathit{\sigma }}_{\mathrm{s}}/{\mathit{\mu }}_{\mathrm{s}}$).

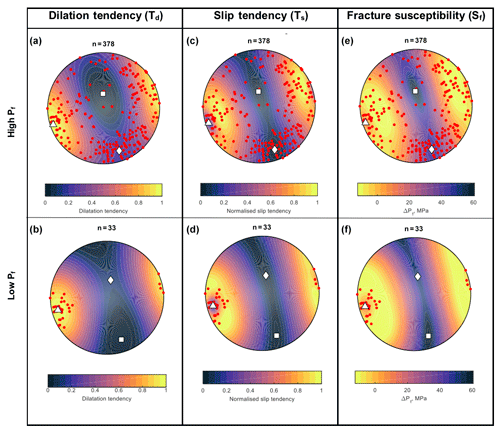
Figure 9 Lower hemisphere equal area projection for dilation tendency, slip tendency and fracture susceptibility in a given fluid pressure condition and for a specific stress state (Fractend code available via Healy, 2017). (a) and (b) represent dilation tendency for high and low P_f. (c) and (d) represent slip tendency for high and low P_f. (e) and (f) fracture susceptibility for high- and low-P_f conditions, respectively. Warm color zones in (a) and (b) represent vein orientations with a higher propensity for tensional opening. In (c) and (d) warm colors indicate vein attitudes that suffered shearing. In (e) and (f) the warm color zones stand for vein attitudes that are more prone to reactivate under low-P_f variation. “Thermal” color scheme from Thyng et al. (2016). White square (σ₁), white diamond (σ₂) and white triangle (σ₃). n: number of data.

Lower hemisphere equal area projections (see Fig. 9) of the pole to fracture (vein-filled) data help us to understand the variation in dilation tendency, slip tendency and susceptibility of fractures with respect to their orientations, under both high- and low-P_f conditions. The diagrams are prepared using the Fractend code (Healy, 2017). It is evident from Fig. 9a that the dilation tendency is high for the fracture orientations, which are at a high angle to the σ₃ axis; i.e., poles to these fractures form a well-defined cluster around σ₃. These fractures show a greater tendency towards dilational opening for both high- and low-P_f conditions (Fig. 9a and b). For fracture orientations with a higher slip tendency, i.e., susceptible to shear opening, poles to the fractures are at a low angle to the σ₃ axis. The fracture planes are therefore oriented at an angle to the maximum compressive stress axis σ₁, a condition favorable for shear reactivation for both high- and low-P_f conditions (Fig. 9c and d). Fracture susceptibility, which involves variation in fluid pressure (ΔP_f), is low for the fracture orientations with high dilation and slip tendencies, which indicates fluid-induced fracture reactivation in metabasalts (Fig. 9e and f) in the study area.

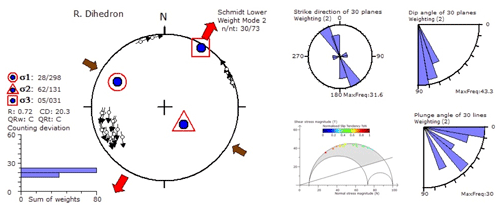
Figure 10 Paleostress analysis (using the right dihedron method) of faults recorded in the metabasalts of the study area for both left lateral and right lateral normal faults. Red arrow marks the extension direction (σ₃) and brown arrow marks the principal compression direction. The histogram shows the minimum values for counting deviation. n and nt are the number of data accepted for tensor calculation and total number of data, respectively. R (stress ratio) = $({\mathit{\sigma }}_{\mathrm{2}}-{\mathit{\sigma }}_{\mathrm{3}})/({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})$. Rose diagrams for fault plane strike, dip and plunge variations are also presented in the top right corner. Three-dimensional Mohr diagrams demonstrate possible areas of fault reactivation with variation in susceptibility; colored circles represent the pole to the fault planes. The failure envelope for Mohr's circle is based on a Byerlee (1978) initial friction angle of 16.7^∘. Note that the maximum extension is along the NNE–SSW direction.

4.5 Paleostress analysis

Normal faults of the study area with shallow to moderately plunging slickenside lineations and prominent slip directions are used to determine the stress regime under which these fractures and faults were formed and reactivated. Fault-slip data (orientations of fault planes and slip directions) recorded from the field were used for paleostress determination. Several methods are proposed for paleostress analyses using fault-slip data (e.g. Angelier, 1994; Dupin et al., 1993; Etchecopar et al., 1981; Gapais et al., 2000; Marrett and Allmendinger, 1990; Ramsay and Lisle, 2000; Twiss and Unruh, 1998; Yamaji, 2000; Žalohar and Vrabec, 2007, and the references therein). Since the fault-slip analysis methods are well established, here we prefer to represent only the salient aspects. The fault-slip analysis can be divided into two categories based on whether the fault-slip data are viewed as representing kinematic or dynamic information (Blenkinsop, 2006; Gapais et al., 2000; Twiss and Unruh, 1998) based on the following assumptions: (1) bulk state of stress is uniform and movements on the fault planes are independent of each other; (2) slip on the fault plane occurs along the direction of the maximum resolved shear stress under a given stress state (Wallace–Bott hypothesis); (3) faults are homogeneous and a part of the same tectonic event (Angelier, 1994; Gapais et al., 2000; Gephart and Forsyth, 1984; Twiss and Unruh, 1998). In this study, we have determined the paleostress direction, using fault-slip data measured from 73 shallow to moderately dipping normal faults (spatially distributed) in the metabasalt by the right dihedron method. Since some of the fault planes show variation in their strike orientations, the small amount of inhomogeneity in the data set is reduced in this process. Thus, the data sets are segregated methodically into homogeneous data subsets using the Win_Tensor software program (version 5.8.6; Delvaux and Sperner, 2003; Delvaux, 2011). In the present analysis all the collected data are represented in a single set and separation is done by using the right dihedron method without any sort of manual intervention. Following Delvaux and Sperner (2003), the data are filtered on the basis of stress ratio (R), orientation of the stress axes and symmetry of the measured sets. Out of 73 data, 30 data are accepted with a low value of counting deviation and nominal counting values of 0 and 100 for σ₁ and σ₃, respectively. Thus, the best-fitted reduced stress tensor is obtained for the accepted data subset (30 out of 73 fault data; see Fig. 10) at a “C” quality ranking. It also provides the relative orientations of the principal stress axes, stress ratio (R=0.72) and stress regime index ($R^{\prime }=\mathrm{1.25}$). The NNE–SSW directed extension direction obtained from this paleostress analysis (see Fig. 10) coincides well with the regional D3 extension direction. Data rejected in this process to obtain the best fit stress tensor when treated separately yield NNE–SSW oriented extension directions with small variations in the R and R^′ values. According to Delvaux and Sperner (2003), the obtained stress regime index indicates a transtensional to pure strike-slip domain, which is in good agreement with sinistral shearing along CSZ.

5 Discussions

5.1 Fabric development vs. regional tectonics

It was mentioned earlier that the metabasalts of the study area lack any distinct visible foliation. However, the AMS analysis suggests a prominent NNW–SSE to NW–SE oriented magnetic fabric in metabasalts. This magnetic fabric also matches well with the field foliation of the metasedimentary sequences surrounding the metabasalts and is also parallel to the regional trend of CSZ (see Fig. 2). This implies that the fabric in metabasalts of the study area must have been controlled by the regional D1/D2 deformation under ∼ NE–SW directed shortening that generated the field foliation in the metasedimentary sequences. Recently Mondal and Mamtani (2014) and Mondal (2018) interpreted the ∼ NW–SE oriented magnetic fabrics in the adjacent younger granites of the study area as being the result of co-axial (pure shear) deformation. Since these fabrics in metabasalts and adjacent younger granites are found to be parallel and manifested by the same NE–SW shortening, it is inferred that magnetic fabrics in the metabasalts of the study area are also a result of this co-axial deformation. The magnetic lineations in the metabasalts plunge due NNW through the sub-vertical to SSE (Fig. 5b). In the previous studies, these variations in the plunge of the magnetic lineations had been interpreted as a consequence of superposed deformation (e.g., Mamtani and Sengupta, 2010; Mondal and Mamtani, 2013). Field investigations also reveal the presence of a dome-basin structure in the metasedimentary rocks of the region (Mondal and Mamtani, 2013; Chakrabarti et al., 2006). Therefore, in the light of regional structural information and the above discussions, it is inferred that these variations in magnetic lineations of the metabasalts are the manifestations of dome-basin geometry that were produced due to the superposition of D3 over D1/D2 regional deformation. Recently, Mondal (2018) documented similar results from the vorticity analysis from the magnetic fabric data in adjacent Chitradurga granite. The studies by Bhatt et al. (2017) and Mondal and Acharyya (2018) suggest that the D1/D2 deformation lasted between 2614 and 2555 Ma, while the D3 deformation is approximated around ∼2537 Ma.

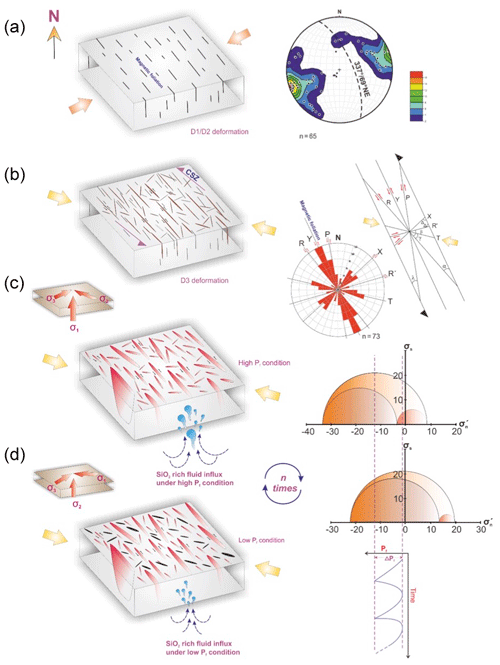
Figure 11 Schematic model showing formation and reactivation of fractures, along with vein emplacement in the metabasalt host rock. (a) Development of the NNW–SSE to NW–SE oriented magnetic fabrics in the rock unit under a NE–SW shortening related to D1/D2 deformation. Lower hemisphere equal area projection shows mean orientation of the magnetic fabric ∼337/69^∘ NE. n: number of data. (b) Formation of the Y, P, R, R^′, X and T shears related to the riedel shear system under a NW–SE to E–W shortening related to the late D3 deformation (half arrows representing the shear zone boundary). The angles (α, β, γ, λ and Δ) between the shear components are given following Logan et al. (1992). Φ=30^∘ (angle of internal friction) is measured from UCS studies of the samples from the study area. Corresponding riedel shear model, with CSZ as the shear boundary and a rose diagram showing orientations of the respective shear components. n: number of data. (c) and (d) showing vein emplacement under high-P_f and low-P_f conditions, respectively (states of stresses along the fracture planes are given in (c); σ₁ is vertical due to fluid overpressure). Corresponding 3-D Mohr circle diagrams quantifying the effective normal stresses (${\mathit{\sigma }}_{\mathrm{n}}^{\prime }={\mathit{\sigma }}_{\mathrm{n}}-P_{\mathrm{f}}$ are given in MPa) under both high- and low-P_f conditions, P_f variation (ΔP_f∼11.25 MPa), obtained from the dashed lines representing the mean stress in each case. A conceptual graph shows multiple cycles (n times) of high- and low-P_f conditions in the study area justifying fault-valve action that led to the emplacement of veins in the Chitradurga region.

5.2 Control of regional far-field stress on developing the brittle structures in the Chitradurga region

The above discussions suggest that (a) NNW–SSE to NW–SE oriented magnetic foliation developed during D1/D2 deformation under ∼ NE–SW directed shortening (Fig. 11a) and that (b) variation in plunge of magnetic lineation is a manifestation of dome-basin geometry on account of D3 deformation. It is argued that during D3 deformation under NW–SE to E–W directed shortening the CSZ evolved as a sinistral shear zone (Mondal and Acharyya, 2018). It may be noted that the angle between the mean orientation of the schist belt and the compression direction for D3 deformation is found to be ∼45^∘, which also supports the sinistral movement along the Chitradurga shear boundary.

It is mentioned in Sects. 2 and 3 that the study area is replete with a number of brittle structures such as fractures and faults. In places, these fractures are filled up with quartz veins. Therefore, it is now essential to evaluate whether and how these brittle structures and their kinematics can be fitted to the regional far-field stresses responsible for deformation in the Chitradurga region. The quartz vein orientation data from the northern part of the Chitradurga Schist Belt reveal that the vein emplacement took place during regional D3 deformation (Mondal and Mamtani, 2014). Recently, Mondal and Acharyya (2018) and Acharyya and Mondal (2019) suggested that the brittle structures (fractures/faults) in the Chitradurga granite (in close proximity to the study area) are related to the D3 deformation. Moreover, paleostress investigation using fault-slip data also reveals NNE–SSW directed extension was dominant during D3 deformation. Apart from this, evidence of any later deformation, i.e., post D3 deformation, has not been recorded from the study area (from previous studies and as per our field observations). Thus, based on the present studies and the above discussions, it is logically inferred that the formation of brittle structures (fractures/faults) as well as vein emplacement must be explained as a consequence of regional D3 deformation at a shallow depth. Mondal and Mamtani (2014) suggested that the Mulgund granite (2555±6 Ma; Sarma et al., 2011), which lies in close proximity to the metabasalts of the Chitradurga region, was emplaced syn-tectonically with CSZ. It is shown that the Mulgund granite underwent ductile deformation as it cooled and crystallized syn-tectonically with D3 deformation. The ductile deformation features in the granite were then superimposed by brittle structures during late D3, when the granite was fully solidified and had achieved a shallow depth (Mondal and Mamtani, 2016). Since both the lithologies (metabasalts and granites) have undergone the same deformation and the fractures in them developed syn-tectonically with adjacent CSZ, it is favorable to interpret the brittle structures, such as fractures and faults in metabasalts, as having developed on account of late D3 deformation under NW–SE to E–W directed compression at a shallow depth of about ∼2.4 km.

5.3 Regional tectonics and the mechanism of fracturing, faulting

We discussed earlier in Sect. 3 that the fractures and faults recorded in the metabasalts show a wide range of orientations with NNW–SSE maxima and WNW–ESE to NE–SW sub-maxima, respectively (Fig. 4b). Of these, fractures trending along WNW–ESE to E–W are sub-parallel to the D3 (late phase) shortening direction. As previously mentioned in Sect. 3, these WNW–ESE trending fractures have been regarded as tensional fractures. Similar orientations have also been recorded and interpreted as tensile fractures from the micro-granitoid enclaves in Chitradurga granite, as evident from the studies of Mondal and Acharyya (2018). However, it is essential to explain the predominance of fractures and faults along the NNW–SSE orientation (forming the maxima). In order to explain this, we refer to the pre-existing fabric in the metabasalts of the study area, i.e., the NNW–SSE to NW–SE oriented magnetic fabric developed during D1/D2 regional deformation (Fig. 5a). Earlier studies suggest that fractures are more likely to propagate along a pre-existing anisotropy, if and when the anisotropy is favorably oriented with respect to the regional stress field (Ikari et al., 2015). The CSZ, being a sinistral shear zone, exhibits a transtensional to pure strike slip stress regime, coeval with D3 deformation (NW–SE to E–W directed shortening).

In the later phase of D3 deformation, the favorably oriented NNW–SSE fabrics were reactivated under a compatible stress field, thereby causing reactivation of the pre-existing fabrics in the metabasalts. This however fails to justify the occurrence of the ∼ NW–SE and ∼ NE–SW oriented fractures within the metabasalts. From field investigations, the NE–SW oriented fractures show dextral movements, while the NNW–SSE and NW–SE oriented fractures are recorded with sinistral movements, respectively (see Fig. 3c and d). However, the fracture disposition and consistency in their respective orientations indicate that all of these fractures are coeval, related to the same deformational event, and have been reactivated under similar stress conditions. Moreover, any other brittle deformational event post D3 has not been recorded from the study area as mentioned earlier. Therefore, we need to explain the occurrence of such variably oriented fractures/faults within a single kinematic framework. The NNW–SSE and NW–SE orientations are most likely to be sinistral, whereas NE–SW orientations form the dextral shear components, respectively, considering CSZ to be the sinistral shear boundary (see Figs. 11b and 3c, d). Thus, the NNW–SSE to NW–SE (P, Y and R) and NE–SW to ENE–WSW (X and R^′) fractures coincide with the shear components of a riedel shear system considering the angle of internal friction (Φ) in metabasalts of the study area to be ∼30^∘. It may be noted that the value of Φ is approximated from the uniaxial compressive strength (UCS) studies of the metabasalt core samples following Sivakugan et al. (2014). These fracture planes (P, Y, R, X and R^′) acted as pathways for fluid flow and vein emplacement during the late D3 deformation.

5.4 Understanding the mechanism of fluid flow and vein emplacement in the Chitradurga region

In order to explain the vein emplacement mechanism along these weak zones, we need to consider the fluid pressure conditions that prevailed at the time of vein emplacement. In Sect. 4.3, we mentioned earlier that the lower hemisphere equal area projection of pole to vein data shows girdle distribution, indicating a high-P_f condition (∼55.164 MPa; >σ₂) in the study area. Under such high-P_f conditions, veins were emplaced along all possible orientations, including NNW–SSE, NW–SE, WNW–ESE, NE–SW and ENE–WSW trending fractures. The building fluid pressure surpassed the normal stresses acting on the fracture wall, and hence fluid burped into the weak planes, leading to fluid-induced reactivation of the fractures, promoting vein emplacement along them (Fig. 11c). However, the NNW–SSE trending veins show greater thickness and abundance with respect to other orientations (see Figs. 4d and 3e). We found that poles to these veins (NNW–SSE trending orientations) lie within the warm zones of the stereoplots obtained from the Fractend code (Healy, 2017), indicating higher dilation tendencies (see Fig. 9a and b). In Fig. 9a and b, it is perceived that poles to these orientations form a cluster around the σ₃ stress axis. Similarly, poles to the orientations trending NW–SE and NE–SW, respectively, have higher slip tendencies, indicating shear reactivation along them (Fig. 9c and d). Most of the poles to the NNW–SSE trending orientations lie within the overlapping warm zones, indicating high potential to reactivate in both shear and dilation modes (high slip and dilation tendencies). These orientations are susceptible to dilation as well as shear reactivation, depending on the predominance of fluid pressure and availability of fluid for inducing dilation or shear reactivation. Availability of fluid significantly reduces the effective normal stress (${\mathit{\sigma }}_{\mathrm{n}}^{\prime }={\mathit{\sigma }}_{\mathrm{n}}-P_{\mathrm{f}}$), where ${\mathit{\sigma }}_{\mathrm{n}}^{\prime }$ and σ_n are the effective normal stress and normal stress, respectively, acting on the fracture planes (see Fig. 11c and d). Under this condition, fluid burps into the fractures, leading to a significant drop in the fluid pressure. This sudden drop in the fluid pressure reduces the solubility of fluid materials, promoting deposition of veins followed by sealing of the pathways (Cox et al., 1991, 2001). Pathways thus remain sealed till the next cycle of fluid pressure build-up, fracture reactivation and vein deposition. However, in between two such cycles of high fluid pressure, intermediate low fluid pressure cycles persist, during which fluid pressure might not be substantially high to reactivate all the pre-existing pathways. Thus, a high fluid pressure cycle is followed by subsequent pulses of low fluid pressure causing selective reactivation of some of the pre-existing orientations. The orientations represented by the individual clusters (WSW, NE and SE) can be reactivated selectively depending on their respective orientation to the tectonic stress field and the fluid pressure magnitude. Hence, it is envisaged that these cycles of high- and low-P_f conditions might have been repeated multiple times (n times) until the fluid source was completely exhausted. In the present study, the low-P_f conditions are interpreted by discretely analyzing the clusters within the girdle distribution of pole to vein data in the lower hemisphere equal area projection (see Sect. 4.3). Such low P_f could not surpass the normal stresses of all the pre-existing pathways, and only the NNW–SSE oriented ones (related to the magnetic fabric of the metabasalts, considering the WSW cluster) with high dilation and slip tendencies were favorably oriented for reactivation and fluid flow. The above mechanism of fault-valve action is supported with field evidence showing occurrences of thick quartz veins enclosing angular chunks of metabasalt hosts with multiple sub-parallel fault planes (identified from the slickenside lineations); see Fig. 3e and f. Quartz veins with multiple median lines indicate predominance of a crack-seal mechanism due to cyclic fluid ingression (Fig. 3g). This suggests that the process of fracturing, fracture reactivation through faulting and vein emplacement (fault-valve action) prevailed throughout the D3 deformation. Thus, the processes of new fracture formation and reactivation were continuously persistent during the entire late D3 phase, with intermittent episodes of vein emplacement under both high- and low-P_f conditions. To evaluate the nature (mode) of failure/fracture formation in the metabasalts of the study area, we used tensile strength (T) from BTS studies. We estimated Δσ=41.68 MPa, which is less than 4T, suggesting that the modes of failure in the metabasalts are tensile (Sibson, 2000). Further, we also quantify the level of fluid pressure through the pore fluid factor (λ_v) for various P_f conditions in the study area. The λ_v is defined by the ratio of fluid pressure to the vertical stress (Sibson, 2000). It may be noted that the λ_v varies from 0.68 to 0.87, suggesting that the vein emplacement in the Chitradurga region took place under supra-hydrostatic fluid pressure conditions at a shallow crustal level.

6 Conclusions

In the present study, we commented on the vein emplacement mechanism of the Chitradurga Greenstone Belt (Dharwar Craton, southern India). We analyzed the magnetic fabric data recorded from AMS analysis of the metabasalt with the quartz veins. Three-dimensional Mohr circle and paleostress analysis was used to evaluate the vein emplacement vs. regional deformation. Following are the main findings and conclusions from the study.

1. The NW–SE oriented magnetic fabric recorded in the metabasalts (as evident from the AMS analysis) is a product of the D1/D2 regional deformation on account of NE–SW directed shortening. This fabric was also favorably oriented and, therefore, suitable for fracture propagation in relation to the prevailing stress field.

2. D3 deformation manifested by NW–SE to E–W directed shortening was coeval with the sinistral movement along CSZ. It is concluded that during late D3 deformation all pre-existing fabrics and the ones constituting the riedel shear system were reactivated, with CSZ acting as a shear boundary.

3. The variably oriented fractures and faults i.e., the NNW–SSE, NW–SE, WNW–ESE, NE–SW and ENE–WSW oriented ones, are identified as the P, Y, R, T, X and R^′ shear components of the riedel shear system. The NNW–SSE to NW–SE oriented shears (P, Y and R) are abundant owing to their favorable correspondence to the pre-existing AMS fabric.

4. Paleostress analysis using fault-slip data recorded from field studies reveals NNE–SSW directed extension, asserting reactivation under a WNW–ESE directed compression (related to D3 deformation).

5. Vein emplacement took place under both high- and low-P_f conditions. It is envisaged that multiple numbers of such alternating high- and low-P_f cycles prevailed in the process of fluid flow and vein emplacement in the region.

6. Vein emplacement took place along all possible orientations. Evidence of fault-valve behavior and fluid-induced fracture/fault reactivation has been recorded from field studies. However, the NNW–SSE trending orientations, having higher values of slip and dilation tendencies, channelized fluid during both high- and low-P_f conditions, thereby attaining maximum vein thickness.

7. The process of fracture formation, reactivation and faulting prevailed under a far-field compression related to late D3 deformation. However, intermittent episodes of fluid pressure build-up led to fluid-induced faulting, rupturing and vein emplacement in the region.