The relative contributions of scattering and viscoelasticity to the attenuation of S waves in Earth's mantle

The relative contributions of scattering and viscoelastic attenuation to the apparent attenuation of seismic body waves are estimated from synthetic and observed S waves multiply reflected from Earth's surface and the core–mantle boundary. The synthetic seismograms include the effects of viscoelasticity and scattering from small-scale heterogeneity predicted from both global tomography and from thermodynamic models of mantle heterogeneity that have been verified from amplitude coherence measurements of body waves observed at dense arrays. Assuming thermodynamic models provide an estimate of the maximum plausible power of heterogeneity measured by elastic velocity and density fluctuations, we predict a maximum scattering contribution of 43 % to the total measured attenuation of mantle S waves having a dominant frequency of 0.05 Hz. The contributions of scattering in the upper and lower mantle to the total apparent attenuation are estimated to be roughly equal. The relative strength of the coda surrounding observed ScSn waves from deep focus earthquakes is not consistent with a mantle having zero intrinsic attenuation.

1 Introduction

Seismic tomography reveals a laterally heterogeneous velocity structure in the mantle. Constraining the locations and dimensions of such elastic heterogeneities is critical to understanding the intricate details of the dynamic mixing process of the mantle, which is closely tied to the plate tectonic evolution of the Earth. Large-scale (∼1000 km) heterogeneities are likely caused by the buoyancy differences that drive thermal–chemical convection. The effects of thermal diffusion, however, limit small-scale (∼1 to 100 km) heterogeneities to chemical variations. Small-scale heterogeneities can scatter 0.1 to 1 Hz body waves, transferring energy from body wave pulses observed at a receiver to later time windows and receivers (Shearer, 2015). Mantle attenuation measured from P and S waves will hence always be a summation of a scattering and an intrinsic viscoelastic attenuation. The viscoelastic dispersion of dominantly intrinsic attenuation successfully explains the lower velocities of Earth models derived from low-frequency free oscillations observed in the millihertz band from those derived from 1 Hz body waves (Dziewonski and Anderson, 1981). Yet some extrapolations of the scale lengths and intensities of heterogeneity inferred from high-frequency body waves have suggested attenuation in the mantle may instead be dominated by scattering (Ricard et al., 2014; Sato, 2019).

The apparent attenuation of multiple ScS waves is an excellent observable to untangle the relative contributions of scattering and intrinsic attenuation. Many previous studies have used ScS and its reverberations within the mantle to obtain path-averaged values for the mantle attenuation. These attenuation measurements are usually represented in terms of a quality factor (Q or Q_ScS for ScS-based measurements). The estimates of these apparent attenuation measurements include both the intrinsic or viscoelastic attenuation of the wave amplitude and the attenuation caused by scattering effects. In this work, we will consider the apparent attenuation ($\frac{\mathrm{1}}{Q_{\mathrm{ScS}}}$) to be the addition of intrinsic attenuation ($\frac{\mathrm{1}}{Q_{\mathrm{intr}}}$) and scattering attenuation ($\frac{\mathrm{1}}{Q_{\mathrm{scat}}}$) for path-averaged observations of SH waves reflected from the free surface and core–mantle boundary. The intrinsic component accounts for the loss of energy due to friction and heat loss as the wave propagates through the mantle with different viscous properties caused by the motion of defects in the crystalline lattice structure of silicates or by the motion of melt at grain boundaries or in pores. Intrinsic attenuation manifests itself in body waves by amplitude decay, pulse broadening and velocity dispersion. The scattering attenuation accounts for the energy loss that is scattered into different directions as elastic heterogeneities are encountered along the path of a body wave. In addition to amplitude decay and pulse broadening of the main phase, scattering generates increased levels of coda energy comprised of redistributed energy arriving later than the main phase. Many past studies calculating the apparent attenuation of multiple ScS waves use spectral amplitude ratios (Kovach and Anderson, 1964; Yoshida and Tsujiura, 1975; Sipkin and Jordan, 1980; Lay and Wallace, 1983) and time domain amplitude ratios (Kanamori and Riviera, 2015) of adjacent ScS waveforms. An alternative analysis technique seeks the attenuation operator that converts an ScS_n−1 waveform into an ScS_n waveform (Jordan and Sipkin, 1977; Revenaugh and Jordan, 1989). Sipkin and Revenaugh (1994) concluded that a frequency domain approach works better for Q_ScS measurements, especially in continental regions that tend to have lower shear Q values compared to oceanic regions. Lee et al. (2003) compared observations and numerical simulations of coda envelope offsets before and after ScS synthesized with two-layer scattering models superimposed on a PREM (Dziewonski and Anderson, 1981) reference model to calculate the scattering contribution to total attenuation measurements. They concluded that scattering loss dominates intrinsic loss in the lower mantle.

Our effort employs an estimate for a ScSn attenuation operator to evaluate the relative percentages of scattering and intrinsic attenuation contributing to the apparent attenuation observed from simulated mantle heterogeneity models. Observations of scattered body waves together with geodynamic modeling have established that heterogeneities of scale lengths as small as 4 to 10 km with rms (root mean square) velocity perturbations of 1 % to 8 % can persist throughout the mantle, even in the presence of constant convective stirring (Hedlin et al., 1997; Shearer and Earle, 2008; Kaneshima and Helffrich, 2010). Our investigation considers the effects of similar dimensions and perturbation strengths for heterogeneity models. We also consider the effects of a model of mantle heterogeneity power obtained by applying stochastic tomography (Zheng and Wu, 2008) to invert for the heterogeneity spectrum of the upper 1000 km of the mantle from observations of amplitude and phase fluctuations of teleseismic P waves observed by the Earthscope USArray (Cormier et al., 2019). We assumed fluctuations of S velocity and density to be correlated with those of P velocity such that $\mathrm{\Delta }{V}_{\mathrm{S}}/V_{\mathrm{S}}=\mathrm{2}\mathrm{\Delta }{V}_{\mathrm{P}}/V_{\mathrm{P}}$ and $\mathrm{\Delta }\mathit{\rho }/\mathit{\rho }=\mathrm{0.8}\mathrm{\Delta }{V}_{\mathrm{P}}/V_{\mathrm{P}}$, taking the resultant depth-dependent power spectrum to be a maximum plausible model of mantle heterogeneity. With these assumptions, the power of the heterogeneity spectrum of S velocity closely matches that predicted by thermodynamically constrained estimates of mantle chemistry and phase. Such models (e.g., Stixrude and Lithgow-Bertelloni, 2007) predict significantly higher heterogeneity than the models of global tomography. Although the assumed chemistry and potential temperature of thermodynamic models have been shown to affect average mantle velocities, the depth position of predicted heterogeneity peaks and their maximum power, concentrated around mantle phase transitions, is relatively unaffected (Stixrude and Lithgow-Bertelloni, 2012).

2 Method

2.1 Models

Apparent attenuations are measured from ScSn waveforms observed in synthetic seismograms for four different models of mantle heterogeneity. All of these assume PREM as the one-dimensional background velocity and density model, with the PREM shear wave attenuations providing the purely intrinsic component of attenuation. MODEL 1 does not perturb PREM with any lateral heterogeneities. Therefore, the apparent attenuation measured for this case will be purely intrinsic. MODEL 2 (Fig. 1) applies a depth-dependent shear velocity perturbation to the PREM mantle similar to those determined from many seismic tomographic studies (Megnin and Romanowicz, 2000; Ritsema et al., 2004). MODEL 3 (Fig. 2) applies scaled shear velocity and density perturbations to the PREM mantle based on the stochastic P tomography model of Cormier et al. (2019) for the upper 1000 km of the mantle. MODEL 4 (Fig. 3) is the same as MODEL 3 in the upper 1000 km of the mantle but includes an additional peak in heterogeneity power in the lowermost mantle predicted by Stixrude and Lithgow-Bertelloni (2012) from the effect of the post-perovskite phase transition. In MODEL 5, the intrinsic attenuations are turned off while still applying the thermodynamic model of mantle heterogeneity to shear velocity perturbations. Hence, the synthetic seismograms for this model will exhibit purely scattering effects in any attenuation measurement. In all models, heterogeneities are represented as stochastic random media with an exponential autocorrelation having a corner scale equal to 10 km. In MODELS 2, 3, 4 and 5, we assume a relation between P velocity and density and shear velocity perturbations such that $\mathrm{\Delta }\mathit{\rho }/\mathit{\rho }=\mathrm{0.8}\mathrm{\Delta }{V}_{\mathrm{P}}/V_{\mathrm{P}}$ and $\mathrm{\Delta }{V}_{\mathrm{S}}/V_{\mathrm{S}}=\mathrm{2}\mathrm{\Delta }{V}_{\mathrm{P}}/V_{\mathrm{P}}$. The value for density perturbation in a mantle close to neutral buoyancy is relatively large but is commonly assumed in studies of crustal and upper mantle scattering based on Birch's law (Birch, 1952).

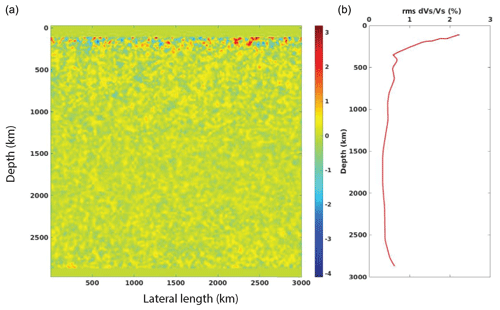
Figure 1 (b) Depth-dependent rms shear velocity perturbation profile applied in MODEL 2. This is extracted from S20RTS. (a) 2-D representation of the same depth-dependent profile. Heterogeneous media are for an exponential autocorrelation (corner scale a=10 km) function. Note the increase in heterogeneity power near the top and bottom of the mantle.

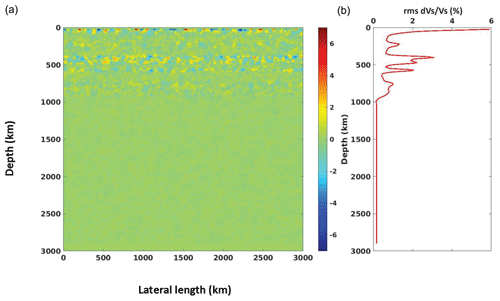
Figure 2 (b) Depth-dependent rms shear velocity perturbation profile applied in MODEL 3 vs. perturbation values from crust to 1000 km depth extracted from the stochastic tomography result of Cormier et al. (2019). (a) 2-D representation of the same depth-dependent profile. Compared to MODEL 2, note the additional peaks in heterogeneity power associated with phase transitions in the upper mantle.

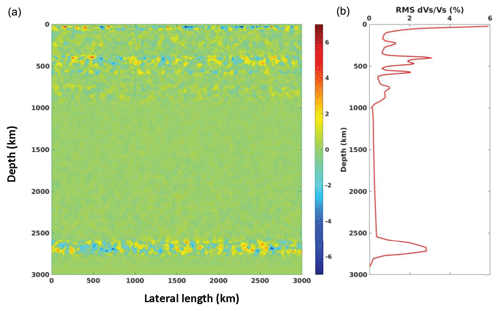
Figure 3 (b) Depth-dependent rms shear velocity perturbation profile applied in MODEL 4 vs. perturbation values from crust to 1000 km depth extracted from the stochastic tomography result of Cormier et al. (2019). Compared to MODEL 3, an additional peak is added near the core mantle boundary to incorporate the increased lower mantle associated with the post-perovskite phase change (Stixrude and Lithgow-Bertelloni, 2012). (a) 2-D representation of the same depth-dependent profile.

2.2 Apparent attenuation measurements

All simulations are performed by a numerical pseudospectral method in 2-D (Cormier, 2000), assuming an SH line source at 500 km depth with a Gaussian-shaped source–time function having a half-width of 1.2 s. Wave propagation uses a 2-D staggered grid with radial step size of 3.0 km and lateral step size of 5.427 km, with time sampling set to 0.025 s, ensuring stability and negligible grid dispersion. Intrinsic attenuation, taken to be approximately constant across a broad frequency band, is introduced by three memory functions using the methods described by Robertson et al. (1994). Waveforms are computed at a great circle distance of 18^∘ in order to avoid contamination of ScSn phases with depth phases or other nearby arrivals. These are corrected for 3-D geometric spreading, and a line-to-point source conversion is made. Although 2-D and 2.5-D simulations neglect the effects of out-of-plane scattering, a comparison of 2.5-D with 3-D scattering simulations by Wu and Irving (2017) suggests that errors due to the neglect of out-of-plane scattering on the coda of teleseismic body waves are small. For each of the five models, a two-parameter attenuation operator (Eq. 1) is determined that converts the ScS waveform into an ScSScS waveform. Each attenuation operator depends on Q_ScS and the high-frequency corner (1∕τ_m) of a relaxation spectrum, where attenuation is constant for 5 decades of frequency.

In the inversion procedure, the predicted ScSScS velocity waveform is generated by convolving the ScS waveform with an attenuation operator corresponding to a peak attenuation 1∕Q_ScS and a high-frequency corner 1∕τ_m. A least squares norm is calculated (Eq. 2) for the difference between observed and predicted ScSScS velocity waveforms, which are aligned by the arrival times of first maximum and normalized by the peak-to-trough amplitudes (Fig. 4). A search over the two attenuation parameters is then performed to minimize an L2 norm difference to maximize a Gaussian probability density constructed using the L2 norm difference (Cormier et al., 1998). Half-widths of the probability density functions are used to infer errors.

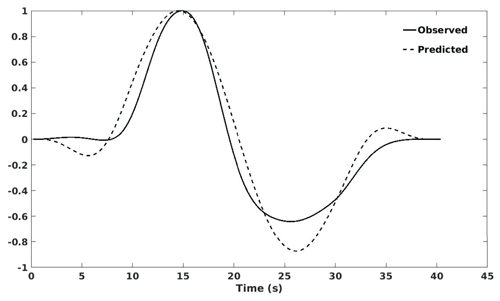
Figure 4 Observed and predicted ScSScS velocity waveform aligned by the arrival time of first extremum and normalized by the peak-to-trough amplitude. The least squares norm difference between these two waveforms is obtained using a summation of amplitude differences over time.

An operator to convert an ScS waveform into an ScSScS waveform is defined in the frequency domain by

$$\begin{array}{}\text{(1)}& O(\mathit{\omega },Q,\mathit{\tau })=\exp \left(-i\mathit{\omega }\left[\underset{\mathrm{ScSScS}}{\int }{\displaystyle \frac{\mathrm{d}s}{\widehat{V}\left(\mathit{\omega }\right)}}-\underset{\mathrm{ScS}}{\int }{\displaystyle \frac{\mathrm{d}s}{\widehat{V}\left(\mathit{\omega }\right)}}\right]\right),\end{array}$$

where

$$\begin{array}{}\text{(2)}& \widehat{V}(\mathit{\omega },Q,\mathit{\tau })={\displaystyle \frac{\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathit{\pi }{Q}_{\mathrm{ScS}}^{-\mathrm{1}}\ln \left(\frac{-i\mathit{\omega }+\mathrm{1}/{\mathit{\tau }}_{\mathrm{l}}}{-i\mathit{\omega }+\mathrm{1}/{\mathit{\tau }}_{\mathrm{m}}}\right)}}}{\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathit{\pi }{Q}_{\mathrm{ScS}}^{-\mathrm{1}}\ln \left(\frac{-i\mathrm{2}\mathit{\pi }+\mathrm{1}/{\mathit{\tau }}_{\mathrm{l}}}{-i\mathrm{2}\mathit{\pi }+\mathrm{1}/{\mathit{\tau }}_{\mathrm{m}}}\right)}}}},\end{array}$$

and where τ_l is the period of the low-frequency corner in the relaxation spectrum, and $\frac{{\mathit{\tau }}_{\mathrm{l}}}{{\mathit{\tau }}_{\mathrm{m}}}={\mathrm{10}}^{\mathrm{5}}$.

The least squares norm difference between observed and predicted waveforms is calculated from

$$\begin{array}{}\text{(3)}& \mathrm{L}\mathrm{2}\mathrm{N}(\mathrm{Obs},\mathrm{Pred})=\sqrt{\sum _t{\displaystyle \frac{\left({\mathrm{Amp}}_{\mathrm{obs}}\right(t)-{\mathrm{Amp}}_{\mathrm{pred}}(t){)}^{\mathrm{2}}}{{\mathit{\sigma }}^{\mathrm{2}}}}},\end{array}$$

where σ is a $\frac{\mathrm{noise}}{\mathrm{signal}}$ measurement from a 100 s time window preceding the ScSScS observation.

Our goal was to simply estimate an apparent attenuation parameter Q_ScS for the whole of the mantle when the effects of scattering are included rather than to seek a best fitting depth and frequency-dependent attenuation model. Accurate separation of depth from frequency dependence of attenuation benefits from observations of S and ScS over a range of source depths and distances as well as by an analysis of P waves to sample a broader frequency band. Nonetheless, our estimates for the high-frequency corner parameter 1∕τ_m were bounded by estimates for 1∕τ_m in the upper and lower mantle found by Choy and Cormier (1986).

3 Results

We found MODEL 1, which has pure intrinsic attenuation and no small-scale heterogeneity, to have an apparent attenuation value of 0.004167 corresponding to a Q_ScS=240. This estimated Q_ScS value differs by only 2.2 % from the theoretical estimate of the depth averaged Q_ScS obtained for PREM with the relation $Q_{\mathrm{ScS}}=({\int }_{x_{\mathrm{ScSScS}}}\mathrm{d}t-{\int }_{x_{\mathrm{ScS}}}\mathrm{d}t)/({\int }_{x_{\mathrm{ScSScS}}}\mathrm{d}t/Q_{\mathrm{S}}(x)-{\int }_{x_{\mathrm{ScS}}}\mathrm{d}t/Q_{\mathrm{S}}(x\left)\right)$. Here, x_ScSScS and x_ScS denote points along the path of ScSScS and ScS, respectively; Q_S(x) denotes the Q_S values at those points read from 1-D PREM. This result verifies the accuracy of the waveform L2 norm method for estimating Q_ScS.

Table 1 Apparent attenuation parameters and their errors estimated for the five simulated models using probability density functions shown in Fig. 5.

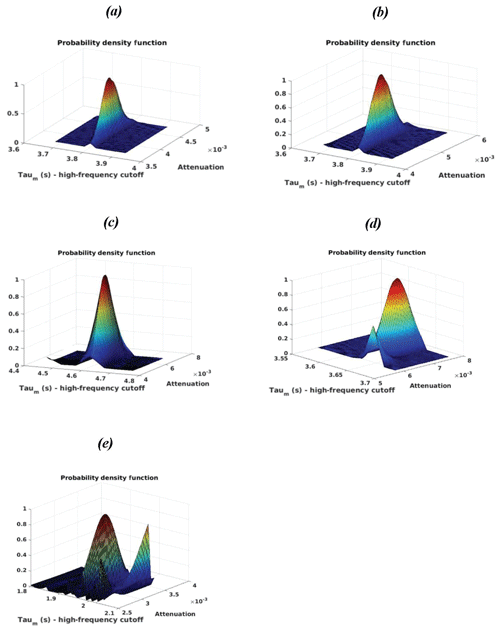
Figure 5 Gaussian probability density function constructed with the least squares norm difference between predictions and simulated observations for (a) MODEL 1, (b) MODEL 2, (c) MODEL 3, (d) MODEL 4 and (e) MODEL 5.

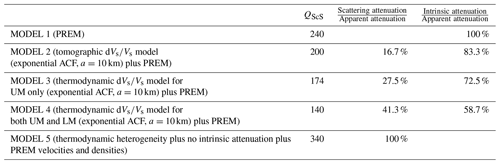
With MODEL 2, which has a conventional tomographic estimate of mantle heterogeneity, we find that the apparent attenuation is increased to 0.005 (Q_ScS decreased to 200). Together with the knowledge of the purely intrinsic contribution ($\frac{\mathrm{1}}{Q_{\mathrm{intr}}}$) calculated in MODEL 1, the scattering component of attenuation ($\frac{\mathrm{1}}{Q_{\mathrm{scat}}}$) in MODEL 2 is estimated to be 0.000833. Hence, the scattering caused by small-scale (∼10 km) heterogeneities with a dV_s∕V_s depth profile similar to S20RTS (Ritsema et al., 2004) would account for 16.7 % of the measured ScS apparent attenuation. MODEL 3, which has a higher amount of heterogeneity due to increased V_s perturbations associated with predicted lateral variations in phase changes in the upper mantle, results in a higher apparent attenuation of 0.005747 (Q_ScS=174). MODEL 4, which includes additional heterogeneity predicted for the effects of a post-perovskite phase transition results in an even higher apparent attenuation of 0.007100 (Q_ScS=140). We calculate that the scattering attenuation in the lower mantle (below 1000 km) and upper mantle (above 1000 km) of MODEL 4 to be 0.0014 and 0.0016 with their percent contributions to the total apparent attenuation being 19.6 % and 22.4 %, respectively. The overall scattering attenuation of MODEL 4 is 0.002933, with the scattering component accounting for 41.3 % of the measured ScS total apparent attenuation.

Finally, in MODEL 5, the intrinsic attenuation in the mantle is turned off while applying the mantle heterogeneity of MODEL 4. The apparent attenuation (now purely due to scattering) is measured to be 0.0029 (Q_ScS=340). This high Q value lies towards the upper bound of regional estimates (∼360) of Q_ScS (Nakanishi, 1979; Sipkin and Revenaugh, 1994; Gomer and Okal, 2003). It is also found that apparent attenuation measurements of MODEL 5 and MODEL 1 add up to be exactly equal to those of MODEL 4, validating the attenuation estimation method in conjunction with the assumption of $\frac{\mathrm{1}}{Q_{\mathrm{apparent}}}=\frac{\mathrm{1}}{Q_{(\mathrm{intr}+\mathrm{scat})}}=\frac{\mathrm{1}}{Q_{\mathrm{intr}}}-\frac{\mathrm{1}}{Q_{\mathrm{scat}}}$.

Figure 6 compares the levels of scattered coda energy arriving in the vicinity ($\sim \pm \mathrm{150}$ s) of the ScSScS main arrival generated by different models of mantle heterogeneity to the synthetic ScSScS predicted by MODEL 1 having no scattering. Observing the envelopes of squared velocity for MODEL 2 vs. MODEL 4, it is apparent that the levels of energy arriving in the coda and before the main phase significantly increase, and the ScSScS pulse width increases due to the presence of increased small-scale heterogeneity in the regions associated with mantle phase changes. It also is important to recognize that intrinsic attenuation can affect the ratio of coda energy to the main pulse. The results for MODEL 5, which omits intrinsic attenuation, demonstrate the importance of intrinsic attenuation for the coda as well as the direct phases. In this case, the coda, unaffected by intrinsic attenuation, approaches the amplitude of the direct ScSScS phase.

Figure 6 Upper–lower bounds of coda envelopes (shaded area) calculated from five random heterogeneity realizations of MODEL 2 (a), MODEL 4 (b) and MODEL 5 (c), compared to PREM (black line).

4 Discussion

4.1 Comparison with regional variations

To obtain recordings of clear ScS and ScSScS without interference by depth phases and other arrivals (S, SS, sS), we searched for waveforms of deep focus events in the 10 to 30^∘ distance with moment magnitude M_w>6. In Fig. S1 in the Supplement, we plot such events available in catalogues of the Incorporated Research Institutions for Seismology (IRIS) Data Management Center (DMC) from 1 January 1970 to 7 November 2019. The analysis of the waveforms and their codas in the full data set satisfying these conditions would be quite valuable to better constrain predictions regarding the real mantle. The main objective of this study, however, was to a describe a well-defined modeling method and to illustrate how this modeling may be used to constrain the mantle heterogeneity spectrum from ScS and ScSScS waveforms with several observations representative of the range of measured attenuations.

Table 2 Estimated relative contributions to apparent 1∕Q_ScS. ACF indicates an autocorrelation function.

Regional variations measured for Q_ScS generally fall in the range of 140–360 (Nakanishi, 1979; Sipkin and Revenaugh, 1994; Gomer and Okal, 2003). Variations on this order are confirmed when we apply our inversion method to two example multiple ScS observations observed from deep focus earthquakes (Fig. 7). We obtain Q_ScS=153 for an earthquake beneath the Papua New Guinea region observed at a station located at Charters Towers in Australia, and Q_ScS=200 for an earthquake beneath the eastern China–Russia border region observed at a station located in Yakutsk in eastern Siberia. In Fig. 8, we overlay synthetic seismograms computed from several of our models to determine how scattering in combination with intrinsic attenuation can affect the relative amplitudes of the direct ScSScS phase and its coda. The heterogeneity power of MODEL 2 inferred from global tomography is too weak to match the excitation of coda relative to ScSScS in both our data examples. Conventional tomographic models typically underestimate true perturbation intensities through the effects of regularization parameters that smooth over the effects of more intense and unresolvable small-scale heterogeneity (e.g., Ritsema et al., 2007). MODEL 4, having PREM attenuation and heterogeneity predicted for a thermodynamic model of the mantle, best matches the relative coda and direct phase excitations for both events. The match can be improved by either a small decrease in intrinsic attenuation or a small increase in heterogeneity power for the eastern China–Russia border region to Yakutsk. ScSn paths from both earthquakes traverse a region of the mantle on the back-arc side of dipping slabs, a southwest-dipping slab toward the Australian craton in the case of the New Guinea event (Tregoning and Gorbatov, 2004) and a western-dipping Kuril–Kamchatka slab (Koulakov et al., 2011) toward the Siberian craton in the case of the eastern China–Russia border event. The multiple ScSn paths for the eastern China–Russia border event are more slab parallel and distant from the descending slab and more strongly sample the cratonic upper mantle compared to the New Guinea event. Hence, it is likely that the intrinsic attenuation of PREM overestimates the effects of mantle attenuation on ScSn paths. Finally, a comparison of observations with the prediction of MODEL 5, having no intrinsic attenuation, overpredicts coda excitation relative to ScSScS for both events. This confirms that some intrinsic attenuation in the mantle is necessary to dampen the coda generated by the most extreme plausible suggestions of heterogeneity power.

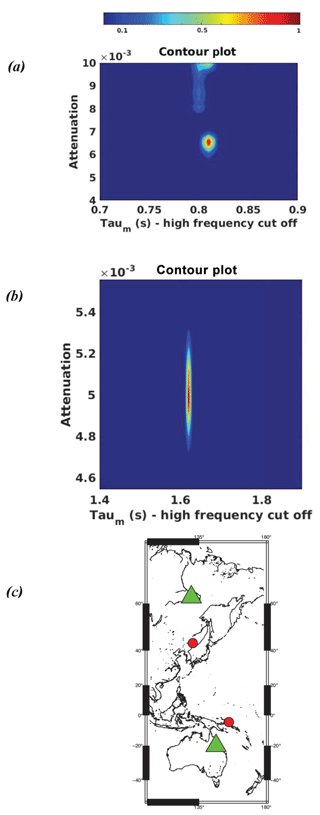
Figure 7 Contour plots of probability density functions obtained with multiple ScS observations in two regions. Event (circles) and station IU (triangles) locations for the two regions described below are shown in panel (c). (a) Mantle beneath Papua New Guinea region: observations are recorded by station CTAO (20.08^∘ S, 146.25^∘ E) for a 490 km deep, M_w 6.6 event (4.543^∘ S, 154.88^∘ E) which occurred on 2 May 1998, 13:34:28 UTC. Event–station distance is 17.6^∘. (b) Mantle beneath the eastern China–Russia border region: observations are recorded by station YAK (62.03^∘ N, 129.68^∘ E) for a 568 km deep, M_w 7.3 event (43.76^∘ N, 130.66^∘ E) which occurred on 28 June 2002, 17:19:30 UTC. Event–station distance is 18.3^∘.

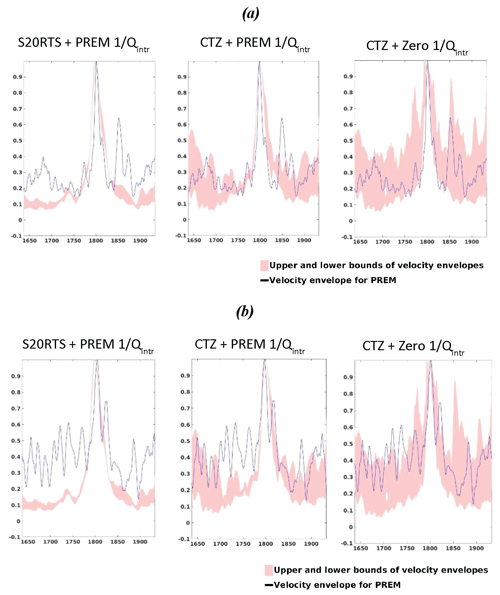
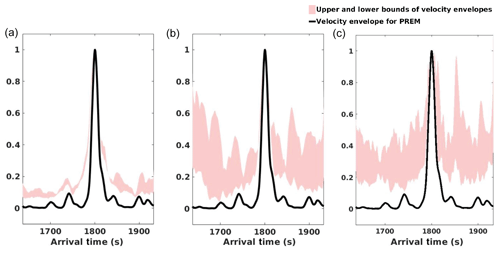
Figure 8 Upper–lower bounds of coda envelopes (shaded area) calculated from five random heterogeneity realizations of MODEL 2 (left), MODEL 4 (middle) and MODEL 5 (right), compared to the squared velocity envelopes of data traces (solid blue lines) from (a) Papua New Guinea data and (b) the eastern China–Russia border region.

4.2 Upper and lower mantle scattering and intrinsic attenuation

Strong depth dependence of mantle attenuation, both intrinsic and scattering, has long been documented. Intrinsic attenuation has been found to be relatively low in the middle and deep mantle compared to the upper mantle. Evidence of some scattering in the middle and deep mantle has been confirmed in studies of PKIKP precursors in the 120 to 140^∘ great circle range (e.g., Hedlin et al., 1997), including strong regional and depth variations that may be consistent with the effects of either remnant subducted oceanic crust or with a peak in heterogeneity power associated with a post-perovskite phase change. From a study of S and ScS coda, Lee et al. (2003) estimated that scattering attenuation dominates intrinsic attenuation in the lower mantle, reporting their results in terms of the scattering coefficients for a two-layered model of mantle heterogeneity. The scattering coefficients g are related to scattering attenuation by $g=\mathit{\omega }/\left(Q_{\mathrm{scat}}{V}_{\mathrm{s}}\right)$. Our results for MODEL 3 and MODEL 4 show that seismic albedo, the ratio of scattering loss to total attenuation, below 1000 km depth in the mantle is 30 %, while above 1000 km it is 27 %. This is assuming the PREM average intrinsic shear Q of 225 and 312 for the two depth regions. Hence, we do not observe scattering to dominate over intrinsic effects in either the lower or upper mantle, although regional exceptions can be expected. Additionally, considering the estimated scattering attenuations for MODEL 3 and MODEL 4, we can deduce the scattering coefficients to be $\mathrm{6.25}\times {\mathrm{10}}^{-\mathrm{5}}$ km⁻¹ for the mantle below 1000 km and $\mathrm{1.256}\times {\mathrm{10}}^{-\mathrm{4}}$ km⁻¹ for mantle above 1000 km in MODEL 4. These scattering coefficients, calculated for a dominant frequency of 0.05 Hz, are comparable to the low-frequency estimates of Lee et al. (2003). This result implies a relatively lower scattering coefficient (i.e., slightly lower scattering attenuation) in the lower mantle compared to the upper mantle in MODEL 4, which agrees with the Lee et al. (2003) estimates of scattering coefficients.

4.3 Origins of heterogeneity and scale length anisotropy

In suggesting that scattering attenuation may dominate intrinsic attenuation throughout the mantle, Ricard et al. (2014) considered the effects of heterogeneity distributed primarily in the form of horizontal layers based on geodynamic numerical experiments that predict folding and horizontal stretching of chemical heterogeneity (e.g., Manga, 1996), whose origin primarily originates from the convective cycling of oceanic crust. The attenuative effects of horizontally layered structure have been well known since the classic paper by O'Doherty and Anstey (1971) and are simply calculated. In this paper, we have instead considered the effects of scale lengths predicted by thermodynamic models in which variations in temperature and chemistry dictate the stability of silicate mineral phases. These variations in temperature and chemistry can also be connected to the convective cycling of oceanic crust but instead predict that peaks in heterogeneity power will be concentrated near phase transitions. Such models have not yet fully considered the effects of mechanical mixing on the anisotropy of scale lengths within these relatively narrow regions of depth. Nonetheless, thermodynamic models, when verified by observations of scattering effects that supplement tomographic imaging, may at least provide a more reliable estimate of the upper bound to velocity and density fluctuations in the mantle. Experiments similar to ours may be extended to include the effects of anisotropy of scale lengths. Our results indicate that some intrinsic attenuation will always be required to explain the attenuation of body waves, regardless of the state of isotropy of scale lengths.

5 Conclusions

An inversion algorithm for apparent mantle attenuation based on L2 norm differences between observed and predicted ScSScS velocity waveforms has been verified by inversion of synthetic seismograms and applied to estimate the relative contributions of intrinsic and scattering attenuation to the total apparent attenuation. Thermodynamic models of mantle heterogeneity predict significantly higher heterogeneity power than the predictions from global tomography and a correspondingly higher relative contribution to apparent attenuation measured from body waves. Taking the depth-dependent heterogeneity power of thermodynamic models of mantle heterogeneity as the maximum plausible heterogeneity, we estimate that scattering may explain up to 41.3 % of apparent mantle attenuation with up to 3 % rms shear velocity perturbations concentrated near mantle phase transitions and 1 % everywhere else. We estimate the scattering contribution to the apparent attenuation from heterogeneity in the upper and lower mantle to be roughly equal in global averages, but regional variations between upper and lower mantle scattering contributions are likely. These estimates agree well with the excitation of coda surrounding ScSn waves observed from deep focus earthquakes. These codas can only be matched by the existence of both intrinsic and scattering attenuation.