Asthenospheric anelasticity effects on ocean tide loading around the East China Sea observed with GPS

Anelasticity may decrease the shear modulus of the asthenosphere by 8 %–10 % at semidiurnal tidal periods compared with the reference 1 s period of seismological Earth models. We show that such anelastic effects are likely to be significant for ocean tide loading displacement at the M₂ tidal period around the East China Sea. By comparison with tide gauge observations, we establish that from nine selected ocean tide models (DTU10, EOT11a, FES2014b, GOT4.10c, HAMTIDE11a, NAO99b, NAO99Jb, OSU12, and TPXO9-Atlas), the regional model NAO99Jb is the most accurate in this region and that related errors in the predicted M₂ vertical ocean tide loading displacements will be 0.2–0.5 mm. In contrast, GPS observations on the Ryukyu Islands (Japan), with an uncertainty of 0.2–0.3 mm, show 90th-percentile discrepancies of 1.3 mm with respect to ocean tide loading displacements predicted using the purely elastic radial Preliminary Reference Earth Model (PREM). We show that the use of an anelastic PREM-based Earth model reduces these 90th-percentile discrepancies to 0.9 mm. Use of an anelastic radial Earth model consisting of a regional average of the laterally varying S362ANI model reduces the 90th-percentile to 0.7 mm, which is of the same order as the sum of the remaining errors due to uncertainties in the ocean tide model and the GPS observations.

1 Introduction

The periodic redistribution of ocean mass around the Earth's surface due to ocean tides deforms the solid Earth, a phenomenon known as ocean tide loading (OTL). The resulting OTL displacements can reach several centimetres in the vertical component and more than 1 cm in the horizontal components, with the Earth's response to the OTL depending strongly on the material properties within its interior (Farrell, 1972). In the past 2 decades, Global Positioning System (GPS) data analysis techniques have been developed to directly measure OTL displacements with millimetre accuracy and even submillimetre accuracy at some frequencies (e.g. Allinson et al., 2004; Thomas et al., 2007; Yuan et al., 2009; Penna et al., 2015). With parallel substantial advancements in the accuracy of global ocean tide models (Stammer et al., 2014; Ray et al., 2019), comparisons of GPS-observed and predicted (modelled) OTL displacements have several times revealed the deficiencies of using spherically symmetric, non-rotating, elastic, and isotropic (SNREI) Earth models. One of the reasons for these deficiencies is that these models have been derived from seismic data and represent the Earth's elastic properties at a reference period of 1 s but have typically been assumed to be directly applicable at tidal frequencies.

Ito et al. (2009) found the average amplitude ratios between GPS tidal displacement observations and an Earth tidal model (including OTL and Earth body tide) across Japan were greater than 1, indicating observational agreement with inelastic Earth models. Ito and Simons (2011) further attempted to invert GPS-observed displacements for one-dimensional profiles of the elastic moduli and density beneath the western United States, demonstrating the limitations of the Preliminary Reference Earth Model (PREM) (Dziewonski and Anderson, 1981). Also, Yuan and Chao (2012) and Yuan et al. (2013) reported continental-scale spatially coherent differences between GPS-observed and predicted OTL displacements at sites located more than 150 km inland from the coastline and attributed these differences to elastic and inelastic deficiencies in the a priori Earth body tide model. Subsequently, these GPS results were used by Lau et al. (2017) to look for lateral variations in body tide models of the lower mantle. For western Europe, Bos et al. (2015) showed that large discrepancies exist between GPS-observed and modelled OTL displacements, arising from disregarding anelastic dispersion in the asthenosphere that occurs when the elastic constants of the Earth model are modified to be applicable at tidal periods. Such an effect could bring about a reduction of around 8 %–10 % of the shear modulus in the asthenosphere at tidal frequencies. In addition, Martens et al. (2016) observed spatial coherence among residual M₂ OTL displacements across South America, postulating deficiencies in the a priori SNREI Earth models.

Bos et al. (2015) showed the feasibility of representing the behaviour of the asthenosphere across an absorption band from seismic to tidal frequencies by a constant quality factor Q, which provides a rough transformation to account for the anelastic dispersion effect. Hence, it can be postulated that the asthenosphere should always produce ∼8.5 % OTL displacement discrepancies with respect to a purely elastic PREM-based Earth model, not only in western Europe where Bos et al. (2015) demonstrated this effect but also all over the world. However, these discrepancies will not be equally observable in all localities, either because ocean tide amplitudes are too small within the 50–250 km distance range from the analysis point that samples asthenospheric behaviour or because regional uncertainties in ocean tide models are too large to be able to attribute any observed discrepancy to the Earth model. To identify regions where the findings of Bos et al. (2015) are testable, we have examined the global distribution of a “detectability ratio”. This is defined as the ratio between the elastic–anelastic OTL displacement discrepancy (taken to be the difference between OTL predicted using a purely elastic PREM Green's function, as described in Sect. 3, and that using Bos et al.'s (2015) anelastic S362ANI(M₂) Green's function) as the numerator and the combination of expected GPS observational and ocean tide model related errors as the denominator. For the latter, the ocean tide model related error is characterized as the standard deviation (SD) of the predicted elastic OTL displacements at each location, using each of the DTU10, EOT11a, FES2014b, GOT4.10c, HAMTIDE11a, NAO99b, OSU12, and TPXO9-Atlas numerical ocean tide models (see Table 1 for references). The GPS observational error is assigned a SD of 0.3 mm following Penna et al. (2015), which assumes that at least 2.5 years of continuous GPS data will be available.

Figure 1a shows a global 1∕8^∘ grid of detectability ratio for the M₂ vertical OTL displacement, which is unfavourable (less than 1) for most inland and deep ocean regions. Many of the areas where it exceeds 1, such as off the coasts of southern Greenland, eastern Africa, and western Central America, are poorly sampled with continuously operating GPS networks. However, the East China Sea (ECS) region exhibits a favourable combination of large OTL displacements and fairly consistent ocean tide models across much of it, so the detectability ratio here exceeds 3 across a wide area and contains a healthy distribution of long-running GPS sites (Fig. 1b shows the 102 GPS sites used). Accordingly, we have selected this as a suitable region for an independent test of Bos et al.'s (2015) conclusions. A further attraction of this region for the testing of Earth models is that its position overlying a subduction zone means that it represents a very different tectonic setting to the mature passive margin in western Europe studied by Bos et al. (2015).

Figure 1c shows the predicted M₂ vertical OTL displacements across the ECS region using the FES2014b ocean tide model (Carrère et al., 2016) and an elastic PREM Green's function. It can be seen that the M₂ vertical OTL displacement amplitudes are as large as 20–25 mm around the Ryukyu Islands and on the southeast coast of China, so the anelastic OTL displacement discrepancies would be expected to be about 2 mm and therefore detectable using GPS. Overall, the accuracy of recent ocean tide models is believed to be good, e.g. Stammer et al. (2014) show sub-centimetre M₂ root mean square (RMS) agreement between bottom pressure observations and seven recent models in the deep oceans globally and additionally, the FES2014b model has been suggested as providing a clear advancement in global ocean tide modelling (Ray et al., 2019). However, the fact that the tides in the ECS are large and complex owing to the irregular geometry of the basin (Lefèvre et al., 2000) implies that careful evaluation of the ocean tide models is still necessary in this region to ascertain the optimal model and thus minimize the effect of errors in ocean tide models on the OTL predictions.

In this paper, we first assess the accuracy of a selection of up-to-date ocean tide models in the ECS and quantify their contribution to the predicted OTL error budget. We then describe the kinematic GPS analysis approach for obtaining the observed OTL displacements. Finally, we examine the evidence of asthenospheric anelasticity effects in the ECS region based on the GPS-observed OTL displacements. We consider the M₂ constituent and the vertical component of OTL displacement, as these are dominant in the ECS region.

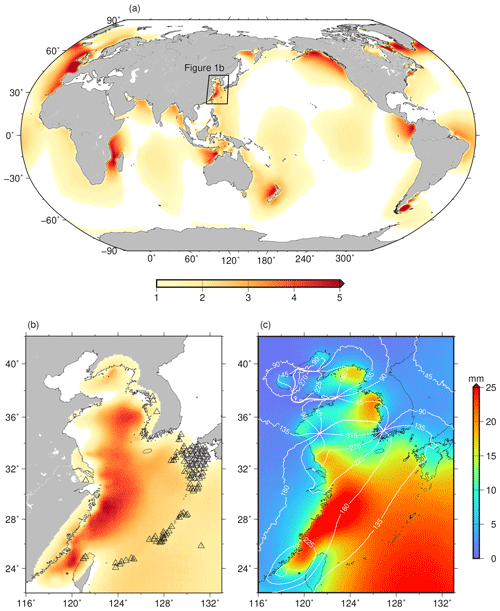
Figure 1 (a) Global distribution (1∕8^∘ grid) of M₂ “detectability ratio” of the difference between vertical OTL displacements predicted using purely elastic and anelastic Green's functions, to uncertainty in residual OTL displacements predicted using eight ocean tide models and the GPS observational error. (b) Detectability ratio in the East China Sea (ECS) region, showing the GPS sites used in this study as triangles. The colour scale is the same as in (a). (c) The M₂ vertical OTL displacement amplitudes and Greenwich phase lags for a 1∕8^∘ grid across the ECS region using the FES2014b ocean tide model and an elastic PREM Green's function.

2 Ocean tide model accuracy assessment using tide gauges

A prerequisite for using GPS measurements of OTL displacement for evaluating the Earth's interior material properties is that the impact of ocean tide model errors on the predicted OTL displacement is understood and found to be near negligible. Therefore, we first evaluate the quality of ocean tide models in the ECS region (considered throughout this paper as 116 to 133^∘ E in longitude and 23 to 42^∘ N in latitude) by assessing their consistency with each other and by comparing them with tide gauge observations.

To date, no single ocean tide model has been demonstrated as optimal in all regions of the world (Stammer et al., 2014; Ray et al., 2019), so we selected eight recent global models (DTU10, EOT11a, FES2014b, GOT4.10c, HAMTIDE11a, NAO99b, OSU12, TPXO9-Atlas) and one regional model (NAO99Jb) for the quality assessment. The key features of the models are listed in Table 1. All models, except for GOT4.10c, directly assimilate TOPEX/Poseidon (T/P) altimeter data plus, for some of the models, data from one or more of the ERS-1/2, Geosat Follow-On (GFO), Jason-1/2, Envisat, and ICESat altimetry satellites, as well as tide gauge data. FES2014b, HAMTIDE11a, NAO99b, and TPXO9 are barotropic data-assimilative models. DTU10 and EOT11a are both based on an empirical correction to the global hydrodynamic tide model FES2004 (Lyard et al., 2006), while the a priori model for GOT4.10c is a collection of global and regional models blended at mutual boundaries. OSU12 is a purely empirical model determined by an analysis of multi-mission satellite altimeter measurements. TPXO9-Atlas is obtained by combining the base global TPXO9 and local solutions for all coastal areas including around Antarctica and the Arctic Ocean. The regional model, NAO99Jb, covers the area from 110 to 165^∘ E in longitude and from 20 to 65^∘ N in latitude, including the whole area of our considered ECS region, and assimilates more local tide gauge data than do the other models.

Table 1 Summary of the selected ocean tide models.

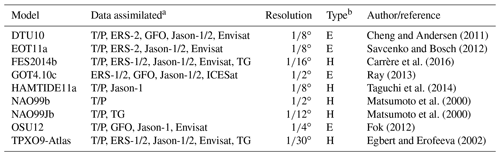
^a T/P, TOPEX/Poseidon; GFO, Geosat Follow-on; TG, tide gauge. ^b E, empirical adjustment to an adopted a priori model; H, assimilation into a barotropic hydrodynamic model.

To evaluate the consistency among the different ocean tide models for the dominant M₂ constituent, all models were bilinearly interpolated onto a common 1∕16^∘ grid across the ECS region, and the SDs of the phasor differences from the mean were computed per grid point using Eq. (2) of Stammer et al. (2014) and are shown in Fig. 2. It can be seen that away from the coastlines, all models are quite similar with the SDs no more than 1–2 cm, which likely arises because they have more or less assimilated the same altimeter data, albeit over different durations. However, closer to the coast large intermodel discrepancies arise, especially in the Seto Inland Sea and near the coast of eastern China and the western Korean Peninsula, where the SD exceeds 30 cm in places. To check if the large discrepancies are caused by the older models, we considered the three most recent models (FES2014b, GOT4.10c, and TPXO9-Atlas) and computed the differences per pair of FES2014b-GOT4.10c, FES2014b-(TPXO9-Atlas), and GOT4.10c-(TPXO9-Atlas). However, similar patterns and size of errors as in Fig. 2 were obtained with the modern model difference pairs. The only changes were that the intermodel differences for the more modern models tend to tail off slightly more rapidly on moving away from the coast of eastern China.

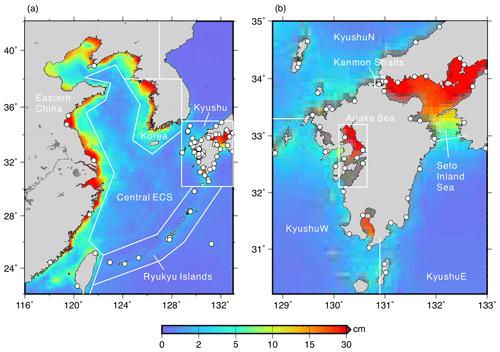
Figure 2 The M₂ standard deviations for nine ocean tide models (DTU10, EOT11a, FES2014b, GOT4.10c, HAMTIDE11a, NAO99Jb, NAO99b, OSU12, and TPXO9-Atlas). Panel (a) shows the whole East China Sea (ECS) region, while (b) is an enlargement of the Kyushu subarea of (a). The white labelled polygons define the subareas for which the quality of the ocean tide models has been evaluated, and the white dots represent the locations of coastal tide gauges.

To ascertain which models are the causes of the large SDs in some subareas and to assess their accuracy, we compared each model with observations from 75 coastal tide gauges (58 from the Japan Oceanographic Data Center and 17 from the University of Hawaii Sea Level Center) in the ECS region, as shown in Fig. 2. Unfortunately no tide gauge data are currently available within the Korea subarea. Using the UTide package (Codiga, 2011), the tidal constants observed at these locations were deduced from hourly sea level time series spanning 4 to 69 years, with a median time-series length of 26 years. For time series shorter than 18.6 years, we applied nodal corrections during the harmonic tidal analysis (Foreman et al., 2009). The observed tidal constants are listed in Table S1 in the Supplement.

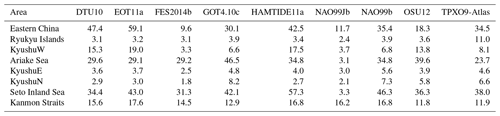
In order to investigate in detail the problematic coastal areas of eastern China, the western Korean Peninsula, and the Seto Inland Sea, the region is divided into the separate subareas shown in Fig. 2, basically in accordance with the zones of intermodel discrepancy. Moreover, for the sake of describing the ocean tide model errors as precisely as possible in the next section, the subarea denoted as Kyushu is further divided. The M₂ phasor difference between each model and each tide gauge was computed, and the RMS of these differences per model for all tide gauges in each subarea is listed in Table 2.

For eastern China, FES2014b and NAO99Jb perform quite well (RMS of 10–12 cm), whereas DTU10 and EOT11a are the worst models (RMS of 47–59 cm). This could be explained by the fact that the FES2004 model, on which DTU10 and EOT11a are both based, has several grossly incorrect tidal values in this area owing to the insufficient satellite altimetry data available at the time. Such problems with the earlier set of finite element solution (FES) ocean tide models were also seen from tidal gravity observations in Wuhan, China (Baker and Bos, 2003), near this subarea. RMS agreements of better than 4 cm between tide gauge observations and each of the models are obtained for the Ryukyu Islands subarea, except for TPXO9-Atlas. This is despite TPXO9-Atlas having the finest resolution among the models (1∕30^∘), whereas the coarser (1∕2^∘) GOT4.10c and NAO99b models have better than 4 cm RMS agreement. Around the island of Kyushu, the observations compare consistently well with FES2014b and NAO99Jb (RMS lower than 4 cm), while the comparisons are poor for DTU10, EOT11a, HAMTIDE11a, OSU12, and TPXO9-Atlas along the west coast of Kyushu and for GOT4.10c and NAO99b along the north coast of Kyushu. NAO99Jb exhibits the best agreement with the observations in the Ariake Sea and Seto Inland Sea, which is expected as it assimilates data from 219 local tide gauges (Matsumoto et al., 2000). This also results in NAO99Jb being more accurate than NAO99b in most parts of the ECS region. However, the agreement between NAO99Jb and the tide gauges is no better than the other models in the Kanmon Straits, because the tide gauges there were installed in 2011, after the release of NAO99Jb, and hence none of their data have been assimilated. Nonetheless, NAO99Jb is the most accurate ocean tide model in the ECS region as a whole.

Table 2 The root mean square (in centimetres) of the M₂ phasor differences between each of the nine ocean tide models and the tide gauge observations in each defined subarea of the East China Sea region.

3 Impact of ocean tide model errors on OTL displacement

In this section we assess the impact of ocean tide model errors on the predicted OTL displacements, which is needed to ensure the confident geophysical interpretation of the GPS-observed OTL displacement residuals considered thereafter. For a particular tidal constituent, the OTL displacement u at a point r on the Earth's surface may be computed (predicted) with the following convolution integral (Farrell, 1972):

$$\begin{array}{}\text{(1)}& u\left(\mathit{r}\right)=\underset{\mathrm{\Omega }}{\int }\mathit{\rho }G\left(\left|\mathit{r}-{\mathit{r}}^{\prime }\right|\right)Z\left({\mathit{r}}^{\prime }\right)\mathrm{d}\mathrm{\Omega },\end{array}$$

where Ω represents the global water areas, ρ is the density of seawater, G is a Green's function that describes the displacement at r from a unit point load, and Z is the tide height at r^′, written as a complex number to include both the amplitude and varying phase lag. Here, the convolution integral is determined by numerical integration and may be written as

$$\begin{array}{}\text{(2)}& u\left(\mathit{r}\right)=\sum _{\mathrm{\Omega }}\mathit{\rho }{Z}_i{G}_i,\end{array}$$

where G_i here is the integrated Green's function for the ith element of Ω, as per Agnew (1997), and the tidal heights Z_i are represented over Ω by inputting a global ocean tide model.

Bos et al. (2015) took the SD of predicted OTL displacements computed per point for a set of ocean tide models as the error contribution of the ocean tide models in western Europe, assuming that there were no systematic biases shared by the models. However, we have shown in Sect. 2 that for the ECS region, the SD among the models is not always a good indicator of their accuracy. To check this, M₂ vertical OTL displacements were computed for a 1∕8^∘ grid across the ECS region for each of the nine ocean tide models (NAO99Jb was augmented globally outside its boundary by FES2014b) using the SPOTL (NLOADF) software version 3.3.0.2 (Agnew, 1997). A Green's function computed based on the isotropic, purely elastic version of PREM was input (as for all elastic PREM-generated results in this paper) and is provided in Table S3 in the Supplement. As the GPS sites considered in this study are on land, the upper 3 km water layer in PREM was replaced with the density and elastic properties from the underlying rock layer. The OTL displacement SDs among the models per point are shown in Fig. 3a, and it can be seen that the distribution of the SDs is similar to those shown for the ocean tide models in Fig. 2, with large SDs of up to 2.5 mm arising around eastern China, the western Korean Peninsula, and the Seto Inland Sea. However, as shown in Sect. 2, these large SDs arise from large errors in some (but not all) of the nine ocean tide models, and NAO99Jb was shown to be the most accurate model across the ECS region. Therefore, it is unreasonable to use the intermodel SD as an indicator of OTL displacement accuracy for all of the ECS region. Instead, we now present an approach which allows us to quantify (to the first order) the resulting OTL displacement prediction error individually for a particular ocean tide model.

Assuming the ocean is divided into k specified water areas Ω_k (e.g as per Table 2) and that the ocean tide model error magnitude per area is δ_k, the corresponding OTL accuracy δu_k is

$$\begin{array}{}\text{(3)}& \mathit{\delta }{u}_k\left(\mathit{r}\right)=\sum _{{\mathrm{\Omega }}_k}\mathit{\rho }{\mathit{\delta }}_k{G}_i.\end{array}$$

Then, assuming no correlation between each of the k areas, the total OTL displacement prediction error may be computed as

$$\begin{array}{}\text{(4)}& \mathit{\delta }u\left(\mathit{r}\right)=\sqrt{\sum \mathit{\delta }{u}_k^{\mathrm{2}}\left(\mathit{r}\right)}.\end{array}$$

Note that in practice there are likely to be negative correlations between adjacent water areas, which will result in the error estimates from Eq. (4) being too large (conservative).

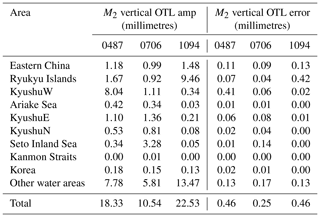
To evaluate the OTL error using Eq. (4) for NAO99Jb, the most accurate ocean tide model in the ECS region, we define the ocean tide model errors for the separate subareas (as per Fig. 2) as the RMS difference between NAO99Jb and the tide gauge observations within the subarea (Table 2). For the Korean subarea, although no tide gauge data source is available, the error of NAO99Jb for Korea can be estimated as the mean value of the RMS of the areas around Kyushu excluding the Kanmon Straits, considering the fact that NAO99Jb also assimilated the tide gauge data around the Korean Peninsula. The “other water areas” (comprising the central ECS subarea and all other global water areas not named in Fig. 2) are either open oceans or narrow coastal areas that are far from the ECS. To be conservative, a slightly larger value of 0.7 cm is chosen as the RMS error of NAO99Jb and its complement of FES2014b for these areas, in accordance with the largest RMS model differences of 0.66 cm for deep oceans inferred by Stammer et al. (2014).

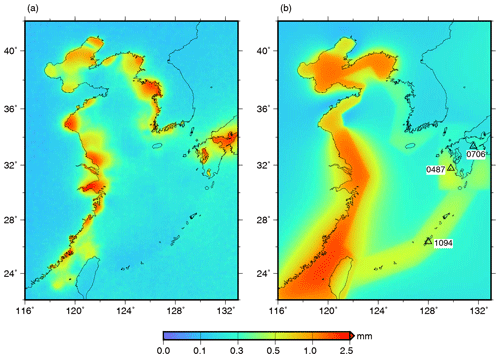
Figure 3 (a) The standard deviation of M₂ vertical OTL displacements, computed using the nine ocean tide models and an elastic PREM Green's function. (b) The M₂ vertical OTL errors per grid point according to Eq. (4), using the RMS errors in NAO99Jb based on comparisons with tide gauges and an elastic PREM Green's function. The triangles (and accompanying names) denote GPS sites which are considered for detailed OTL computation analysis.

Using Eq. (4) and inputting the NAO99Jb RMS errors per subarea, the M₂ vertical OTL displacement errors at each point of a 1∕8^∘ grid were computed and are shown in Fig. 3b. It can be seen that the largest errors of 1–2 mm are for the points falling within the eastern China subarea, but these can be explained by the NAO99Jb model having a fairly large assumed RMS error of 11.7 cm for this subarea, and this has the largest influence on the OTL displacement there. This is, however, likely very conservative and results in errors for much of the eastern China subarea that are too large, because it can be seen from Figs. 2 and 3 that it is only very close to the coast where large intermodel discrepancies arise. Away from the coast much of the intermodel ocean tide agreements for the eastern China subarea are about 2 cm. For the rest of the ECS region, notably where most of the GPS sites are located, the OTL errors arising from NAO99Jb model RMS errors are no more than ∼0.5 mm, even for sites on the east of Kyushu where the intermodel OTL SDs are large (∼2.5 mm).

To provide a more detailed indication of the influence on the OTL of the NAO99Jb ocean tide model errors from each of the defined subareas, three GPS sites (0487, 0706, and 1094) are considered, located on the east and west sides of Kyushu and on the Ryukyu Islands, respectively (Fig. 3b). The contribution of each subarea to both the OTL displacement and its accompanying error are shown in Table 3, which provides further clarification that the local ocean tides are the principal contributor to the OTL displacements, as well as the OTL errors. The large effect from the “other water areas” is mainly due to their vast area, although most of this is far from our study area and will have no impact on regional comparison of Earth models. The Kanmon Straits and eastern China, where NAO99Jb performs relatively poorly, have little effect on the OTL displacements at these sites, with contributions to the OTL amplitude and error of only 1.0–1.5 mm and less than 0.1 mm, respectively. Furthermore, the effect of the ocean tide model errors from these two subareas is no more than 0.13 mm for all three sites. These computations were repeated for all the GPS sites, and only three of the 102 GPS sites had a total OTL prediction error greater than 0.5 mm. It can therefore be concluded that the OTL displacements computed using the NAO99Jb ocean model are suitable for investigating possible anelasticity effects in the ECS region.

Table 3 The contribution of the defined water subareas in Fig. 2 to the M₂ vertical OTL displacement amplitudes and the resulting errors at GPS sites 0487, 0706, and 1094 according to Eq. (4), using the NAO99Jb model and its RMS errors.

4 Kinematic GPS estimation of OTL displacement

Using the NASA GNSS-Inferred Positioning System (GIPSY) software in kinematic precise point positioning (PPP) mode, Penna et al. (2015) showed for sites in western Europe with at least 2.5 years of GPS data (4 years recommended) that vertical OTL displacements may be estimated with a precision of about 0.2–0.4 mm. We apply the same approach for GPS sites in the ECS region. In order to assess the accuracy and precision of the OTL displacements, particularly to check that the tuned coordinate and tropospheric delay process noise values for western Europe are applicable for the ECS region, we insert an artificial harmonic displacement per GPS site. We then assess how well it is recovered from the kinematic PPP GPS processing, as per Penna et al. (2015) but in the coordinate time series used for the final OTL displacement estimation rather than as a preliminary investigation step.

4.1 GPS data source

All available continuous GPS data in the ECS region were collated for the window 2013.0–2017.0, with the distribution of the 102 sites used shown in Fig. 1. These comprised 96 sites from the GPS Earth Observation Network (GEONET), which all had at least 95 % data availability throughout the 4-year window considered and are located mainly on the Ryukyu Islands and Kyushu. We also collated data from six International GNSS Service (IGS) sites in China and South Korea, although two sites (SHAO and YONS) only had 2.5 years of data. On the Ryukyu Islands and along the coast of Kyushu, the sites exhibit detectability ratios of greater than 1, with the median value being 2.1, although close to the Seto Island Sea the ratio reduces to less than 1. The data spans of at least 2.5 and typically 4 years are sufficient to separate the different major tidal constituents robustly according to the Rayleigh criterion.

4.2 Data analysis strategy

Full details of the GPS data processing strategy used are provided in Penna et al. (2015); in summary it is as follows. Daily, 30 h, kinematic PPP GPS solutions were generated for each site using GIPSY version 6.4 software with Jet Propulsion Laboratory (JPL) reprocessed version 2.1 fiducial satellite orbits, Earth orientation parameters, and 30 s satellite clocks held fixed in the IGb08 reference frame. A priori hydrostatic and wet zenith tropospheric delays from the European Centre for Medium-Range Weather Forecasts reanalysis products were used, with residual zenith tropospheric delays estimated every 5 min (applying a process noise of 0.1 mm s${}^{-\mathrm{1}/\mathrm{2}}$), together with north–south and east–west tropospheric gradients. The VMF1 gridded mapping function was used with an elevation cut-off angle of 10^∘, and corrections were applied for solid Earth and pole tides according to the International Earth Rotation Service (IERS) Conventions 2010 (Petit and Luzum, 2010), along with IGS satellite and receiver antenna phase centre variation corrections. Ambiguities were fixed to integers according to the approach of Bertiger et al. (2010). Receiver coordinates were estimated every 5 min, with a coordinate process noise of 3.2 mm s${}^{-\mathrm{1}/\mathrm{2}}$ applied. OTL displacement was modelled using the IERS Conventions (2010) HARDISP.F routine, based on amplitudes and phase lags generated using the NLOADF software with the NAO99Jb model (augmented in the rest of the world with the FES2014b model) and a PREM elastic Green's function, computed in the centre of mass of the solid Earth and oceans (CM) frame to be compatible with the JPL orbits. In each daily solution, an artificial 13.96 h harmonic signal of 3.0 mm amplitude was introduced in each of the east, north, and vertical components, with the phase referenced to zero defined at the GPS timeframe epoch J2000, and hence the GPS harmonic estimation capability with the aforementioned GIPSY processing settings assessed. The value of 13.96 h was chosen as the period of this displacement following Penna et al. (2015), as it is approximately in the semidiurnal band but is distinct from the main tidal harmonics, so it will not be contaminated by geophysical signals.

The estimated coordinates at 5 min resolution within the central 24 h of the daily 30 h kinematic PPP GPS solutions (which ran from 21:00 UTC the previous day to 03:00 UTC the next day) were averaged in nonoverlapping, 30 min bins then concatenated to form coordinate time series. Harmonic analysis was then undertaken using UTide to estimate the residual M₂ vertical OTL displacement signal per site, and also a 13.96 h harmonic was estimated to assess how well the introduced 3.0 mm amplitude artificial signal could be recovered. The resulting UTide formal errors were 0.1–0.2 mm.

4.3 Results

The M₂ vertical OTL residual phasors extracted from the harmonic analysis are listed in Table S2 in the Supplement and shown in Fig. 4, along with the artificial 13.96 h harmonic signal residual phasors. It can be seen from Fig. 4 that on the Ryukyu Islands and in the west coastal area of Kyushu the M₂ vertical OTL GPS-observed minus model discrepancies (residuals) can reach over 1.5 mm, corresponding to about 7 % of the total loading signal. The typical magnitudes of phasor differences between the recovered and original artificial 13.96 h harmonic signals are 0.2–0.3 mm, providing an indication of the accuracy level of our GPS-observed M₂ vertical OTL displacements and indicating that the optimal process noise values found for western Europe by Penna et al. (2015) are also applicable to the ECS region. Since the ocean tide error of NAO99Jb maps to only an error of 0.2–0.5 mm for the predicted M₂ vertical OTL displacement values across the Ryukyu Islands and Kyushu (Fig. 3b), it can be concluded that the 1.5 mm discrepancies must be dominated by errors in the elastic PREM Green's function.

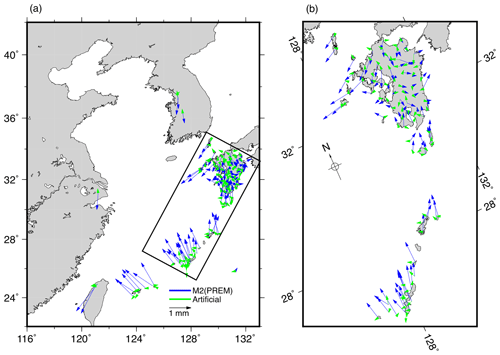
Figure 4 Phasor differences (in blue) between the GPS-observed M₂ vertical OTL displacements and the predictions computed using the NAO99Jb regional ocean tide model (augmented elsewhere globally with FES2014b) and an elastic PREM Green's function. Also shown (in green) are the phasor differences between the recovered and original artificial ∼13.96 h harmonic vertical displacement signal of 3.0 mm amplitude. (a) Shows the whole ECS region, while (b) is an enlargement of Kyushu and part of the Ryukyu Islands, from the boxed region in (a).

5 Optimal Green's function for the East China Sea region

As Green's functions essentially depend on the material properties of the adopted Earth models, an improvement of the agreement between GPS-observed and predicted OTL values (reduction in the observational residuals) could be expected by modifying the Earth models, and the representation of the asthenosphere has been demonstrated to be especially important (Bos et al., 2015). So far we have used Green's functions computed from isotropic, purely elastic PREM, and we first consider whether the more recent elastic S362ANI Earth model (Kustowski et al., 2008), which is a transversely isotropic seismic tomographic model for the mantle, results in a reduction in the residuals. This model provides horizontal and vertical shear velocities (transversely isotropic) on a regular longitude–latitude grid for various depths. For each depth layer between longitudes 122 and 133^∘ E and latitudes 23 and 35^∘ N, we computed averaged shear velocities, which were used to compute the load Love numbers following Bos and Scherneck (2013), together with the density and compressional velocities of the STW105 model that was also developed by Kustowski et al. (2008). It can be seen from Table 4 that using the elastic S362ANI Green's function reduces the overall RMS of the residuals by about 0.1 mm compared to the elastic PREM Green's function (and similarly for the maximum and 90th-percentile values), which could be explained by its use of the regional mean shear velocity.

We next considered whether using Green's functions with the anelastic dispersion effect in each of PREM and S362ANI results in reductions in the residuals. The elastic properties for these Earth models have been derived from seismic observations and are valid at the reference period of 1 s. To include the anelastic dispersion effect, the values of the shear modulus were converted from a period of 1 s to the period of the M₂ harmonic using the relation formula given by eq. (9.66) in Dahlen and Tromp (1998) with a constant absorption band, as described by Bos et al. (2015). The bulk modulus has a much higher-quality factor Q and is assumed not to be affected. After modifying the shear modulus, the load Love numbers were computed as described in Bos and Scherneck (2013), and the respective anelastic Green's functions will be hereafter referred to as PREM_M2 and S362ANI_M2 (these, together with all the Green's functions used in this section, are listed in Tables S3 and S4 in the Supplement). It can be seen from Table 4 that use of PREM_M2 and S362ANI_M2 reduces the overall RMS of the residuals from ∼0.5 to ∼0.4 mm. However, if only the GPS sites on the Ryukyu Islands are considered, the RMS residual is reduced from ∼0.7 mm with elastic PREM and elastic S362ANI, to ∼0.5 mm with PREM_M2 and to ∼0.4 mm with S362ANI_M2. The respective 90th-percentile residual values reduce from 1.3 mm with PREM to 0.9 mm with PREM_M2 and to ∼0.7 mm with S362ANI_M2. This reduction across the Ryukyu Islands when using S362ANI_M2 instead of PREM can be clearly seen in Fig. 5. However, one can observe that the residual phasors for S362ANI_M2 still show some correlations along the Ryukyu Islands, which might be due to the tectonic setting of the subduction zone.

Table 4 Statistics (in millimetres) of the phasor differences between the GPS-observed and predicted M₂ vertical OTL displacements using the NAO99Jb regional ocean tide model (augmented elsewhere globally with FES2014b) and various Green's functions. The label 90th denotes the percentile.

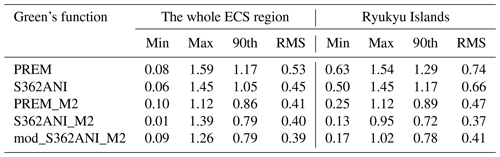
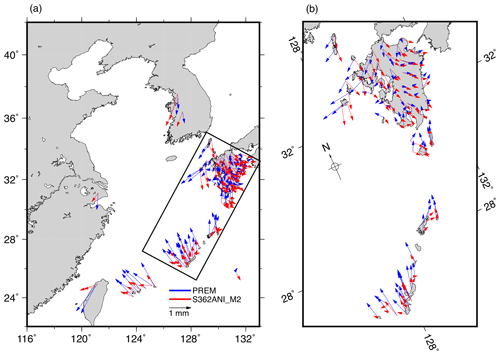
Figure 5 Phasor differences between our GPS-observed M₂ vertical OTL displacements and the predictions computed using the NAO99Jb regional ocean tide model (augmented elsewhere globally with FES2014b) and the elastic PREM (blue phasors) and S362ANI_M2 (red phasors) Green's functions. Panel (a) shows the whole ECS region, while (b) is an enlargement of Kyushu and part of the Ryukyu Islands, for the boxed region in (a).

As residuals at the ∼0.7 mm level remain after accounting for anelasticity effects with the regional S362ANI_M2 model, we also tested the optimality of the Green's function by computing a range of Green's functions based on different asthenosphere depths and values of Q. For the density and compressional velocity, S362ANI only provides global mean profiles. In our work, the asthenosphere is defined a priori to be between depths of 80 and 220 km with a Q of 70 as per Kustowski et al. (2008). Following a similar method to Bos et al. (2015), we vary the depths of the top (D1) and bottom (D2) of the asthenosphere of S362ANI and the amount of anelastic dispersion (Q) in this layer. For each combination of these three parameters, a new Green's function was computed via the load Love number formulation. While computing the load Love numbers, we transformed the shear modulus from the reference period (1 s) to M₂ as described above. The Q value in the other layers is at least twice that of the asthenosphere, so the frequency dependence will be smaller, but to be consistent the elastic properties were also transformed to the period of harmonic M₂. However, these Q values were not varied in our inversion. New Green's functions were then derived and used to predict the M₂ vertical OTL values using the NAO99Jb ocean tide model. This transformation produces complex-valued shear moduli and therefore complex-valued Green's functions, but the imaginary part is less than 5 % of the real part (Bos et al., 2015) and can be neglected. The optimal Green's function was considered to be that which minimized the sum of the squared misfits between the observed and predicted OTL phasor values using all the GPS sites. It was obtained when Q was 90 (corresponding to a reduction of the shear modulus of about 7.6 % at the M₂ period), and the estimated values of D1 and D2 were 40 and 220 km, respectively, implying an asthenosphere extending to shallower depths than its original definition for this region in S362ANI. It can be seen from Table 4 that the residuals statistics with this mod_S362ANI_M2 Green's function are practically identical to those using S362ANI_M2 (and although not shown, very similar patterns for the residuals arise as in Fig. 5), which confirms the large influence of the asthenosphere. In terms of practical usage for the region, S362ANI_M2 with its correction of S362ANI for anelastic dispersion provides a simple way to improve predicted OTL displacements instead of performing the complex numerical optimization scheme each time. As a further simple practical implementation for the region, the global PREM_M2 leads to almost comparable results as S362ANI_M2.

As a further check on the explanation of the observed and model discrepancies which we have attributed to asthenospheric anelasticity, we used the CARGA programme (Bos and Baker, 2005) to compute the effect of varying seawater density on the M₂ vertical OTL displacements for the 102 GPS sites. First we computed the OTL displacements using a constant global density of seawater of 1030 kg m⁻³. Then we recomputed the OTL displacements using the spatially varying (0.25^∘ × 0.25^∘) mean column seawater density from the World Ocean Atlas (Boyer et al., 2013) and found the mean change in M₂ vertical amplitude at our GPS sites was 0.03 mm (maximum difference of 0.16 mm). We then also corrected the mean seawater density per column for compressibility according to Ray (2013) and found that the mean change in M₂ vertical OTL displacement amplitude increased to 0.11 mm (maximum difference of 0.37 mm). Whilst such magnitude differences now have the potential to be detectable by geodetic observations, they are too small to explain our observed 1.5 mm discrepancies.

6 Conclusions

By introducing the detectability ratio for the asthenospheric anelasticity effects and considering the distribution of the available GPS sites, the ECS region was selected as a potential area to observe the anelastic dispersion in the asthenosphere. Using an intercomparison of eight recent global models (DTU10, EOT11a, FES2014b, GOT4.10c, HAMTIDE11a, NAO99b, OSU12, TPXO9-Atlas) and one regional (NAO99Jb) model and a validation with tide gauges, NAO99Jb has been demonstrated to be the most accurate tide model in the region. In the open sea areas NAO99Jb could be slightly worse than the other ocean tide models, due to the assimilation of more satellite altimetry data in the latter, but this does not outweigh the benefits of forcing the NAO99Jb model to fit a large number of tide gauge observations. We quantified the impact of the errors in NAO99Jb on the predicted OTL values, based on the RMS difference between NAO99Jb and the tide gauge observations. Compared to the approach of using the SD of predicted OTL displacements as the error contribution of the ocean tide models, this method can allow for systematic biases shared by the models, so the outputs are more conservative. For the GPS sites located in Japan, the errors in NAO99Jb result in M₂ vertical OTL displacement errors of 0.2–0.5 mm.

We then estimated the M₂ vertical OTL displacements for 102 sites around the ECS using GPS with typical accuracy of 0.2–0.3 mm. On the Ryukyu Islands and in the west coastal area of Kyushu, the discrepancies between GPS-observed and predicted values can reach over 1.5 mm (1.3 mm 90th percentile) when using the NAO99Jb tide model and the purely elastic PREM Green's function. The discrepancies cannot be explained by the sum of the remaining errors due to ocean tide models and the uncertainty in the GPS observations themselves or by the small change in elastic parameters that results from using a regional average of the elastic S362ANI model in place of PREM. However, modelling of the anelastic dispersion effect using the Q values, which lowers the shear modulus by about 8 % in the asthenosphere, reduces the 90th-percentile discrepancies to 0.9 and 0.7 mm for PREM and S362ANI, respectively. We estimated a regionally optimal Green's function by varying the depth and thickness of the asthenosphere of the S362ANI Earth model and its Q values, but this resulted in essentially no further reduction in the discrepancies.

This paper has confirmed the importance of considering the asthenospheric anelasticity effects observed by Bos et al. (2015). It is necessary to incorporate dissipative effects for the Green's functions based on seismic Earth models; use of elastic parameters at 1 s period is insufficient. The PREM_M2 Green's function is near-optimal for the ECS region and western Europe, and it represents a sensible compromise with global applicability, so it is therefore a pragmatic choice for OTL prediction in geodetic analysis. For sites in areas where the detectability ratio exceeds 1 as shown in Fig. 1a or where the highest accuracy is demanded, a regional anelastic Green's function calculated directly from a laterally varying Earth model such as S362ANI should be considered.