Introduction: Handling uncertainty in the geosciences: identification, mitigation and communication

In the geosciences, data are acquired, processed, analysed, modelled and interpreted in order to generate knowledge. Such a complex procedure is affected by uncertainties related to the objective (e.g. the data, technologies and techniques employed) as well as the subjective (knowledge, skills and biases of the geoscientist) aspects of the knowledge generation workflow. Unlike in other scientific disciplines, uncertainty and its impact on the validity of geoscientific outputs have often been overlooked or only discussed superficially. However, for geological outputs to provide meaningful insights, the uncertainties, errors and assumptions made throughout the data acquisition, processing, modelling and interpretation procedures need to be carefully considered. This special issue illustrates and brings attention to why and how uncertainty handling (i.e. analysis, mitigation and communication) is a critical aspect within the geosciences. In this introductory paper, we (1) outline the terminology and describe the relationships between a number of descriptors often used to characterise and classify uncertainty and error, (2) present the collection of research papers that together form the special issue, the idea for which stems from a 2018 European Geosciences Union's General Assembly session entitled “Understanding the unknowns: recognition, quantification, influence and minimisation of uncertainty in the geosciences”, and (3) discuss the limitations of the “traditional” treatment of uncertainty in the geosciences.

“The efforts of many researchers have already cast much darkness on the subject, and it is likely that, if they continue, we will soon know nothing about it at all.” – Mark Twain

1 Introduction to this special issue

Over the past 50 years, development of new acquisition, analytical and experimental techniques in the geosciences, alongside the associated rise in available data has led to major breakthroughs in our understanding of the Earth, such as the development of plate tectonic theory or the acknowledgement of anthropogenic global warming. With ever-more powerful information technology, many aspects of geoscience now rely on computer-assisted models and simulations. Computers are not only extremely powerful tools for the integration and analysis of big data, which otherwise would simply be unmanageable, but they are also instrumental in the testing of hypotheses and visualisation of processes acting over the full range of terrestrial spatial and temporal scales. However, for geological outputs to provide meaningful insights, the uncertainties, errors and assumptions made throughout the data acquisition, processing, analysis, modelling and interpretation procedures need to be carefully considered. Unlike in other scientific disciplines in which uncertainty analysis is a key component of research, geological outputs (maps, interpretations, models, simulations) are frequently presented unaccompanied by uncertainty estimates, perhaps due to the disciplinary expectation of a single (flawless) deterministic model or unequivocal interpretation and corresponding outputs. This is a bar to effective interdisciplinarity in the geosciences, because it maintains a situation in which there can be no explicit understanding of how differing datasets and modelling approaches conflict with and complement one another. Routine handling of uncertainty (analysis, mitigation and communication) is thus an urgently pending need in the geosciences.

With this concern in mind, a multidisciplinary session was organised during the 2018 European Geosciences Union (EGU)'s General Assembly, with the title “Understanding the unknowns: recognition, quantification, influence and minimisation of uncertainty in the geosciences”. The session was conceived as a forum in which geoscientists from different fields could share their different views and approaches on how to handle uncertainty. The session was well attended and included contributions from most of the classical geoscience fields, including sedimentology, palaeoclimate, structural geology, tectonics, geochemistry and geophysics.

This special issue on uncertainty encompasses 12 articles covering the quantification and management of uncertainty in a broad range of geological disciplines, including seismic interpretation (Alcalde et al., 2019; Schaaf and Bond, 2019), mantle dynamic models (Bodur and Rey, 2019; Mather and Fullea, 2019), field geology (Andrews et al., 2019; Bárbara et al., 2019; Pakyuz-Charrier et al., 2019; Stamm et al., 2019; Wilson et al., 2019), plate kinematic modelling (Causer et al., 2020) and subsurface resource evaluation (Miocic et al., 2019; Wilkinson and Polson, 2019). This collection of original research contributions, some of which were presented at the aforementioned EGU 2018 session, highlights the importance of understanding uncertainty, often neglected by interpreters, geomodellers and experimentalists.

2 Definitions of error and uncertainty

Although they are often used interchangeably when they do appear in geoscientific literature, “error” and “uncertainty” are not synonymous terms. Effectively quantifying and discussing these two concepts when presenting results (which in the geosciences may be statements, measurements, calculations or models) therefore starts by understanding the difference between them. The concept “error” describes the estimated difference between a single measured value and some assumed or known reference “true value”, usually comprises both systematic and random components. Errors are often dealt with and quantified in all fields of science, and their effects addressed purely with statistical approaches. However, when the “true value” is accepted to be practically or absolutely unknowable and/or unmeasurable, as is often the case in geosciences with its instances of deep burial and deep time, we must instead deal with “uncertainty”. Uncertainty can be described as a consequence of the mismatches between the quantity and quality of the knowledge available and those of the knowledge required for rational decision (model) making (Tannert et al., 2007) or, in other words, as “a function of our ignorance”. Describing uncertainty requires recognition that our knowledge is flawed and limited, identifying the “known unknowns” and acknowledging that there may also be “unknown unknowns” (things we do not even know we do not know). Quantifying uncertainties is thus the process of analysing how far away our ideas might stray from any “describable truth”. In this way, “error” is a difference, a measure of precision; “uncertainty” is a range, or estimate of accuracy. Figure 1 illustrates the differences between error and uncertainty, and the relationship of the former with other quality descriptors and performance characteristics commonly used in the geosciences (accuracy, precision, trueness and bias). In summary:

• Error is the quantified difference between a knowable parameter and a measured variable. It is quantifiable as a combination of both systematic error and random error.

Trueness, precision and accuracy relate to error and require some knowledge or expectation of a “true value” for comparison.

• Trueness is the closeness of agreement between the average value obtained from a large series of test results and the expected true value.  Trueness is largely affected by systematic error.

• Precision is the closeness of agreement between independent measurements. Precision is largely affected by random error.

• Accuracy is the agreement between a measurement and the expected true value. It is an expression of the relative size of error.

However, the following are also applicable:

• Uncertainty characterises the range of values within which a practically unmeasurable or unknowable parameter is estimated to lie at some level of confidence. Any repetition of the estimation process at the same confidence level should be expected to produce a result within the limits of the uncertainty range. The final uncertainty budget of an output may incorporate several “systematic uncertainties” that have to be quantified. For example, in geochronology, the decay constant of a given isotope system carries with it an uncertainty, which does not change, but which is an additional component that has to be propagated onto the final quoted uncertainty of an age.

In some geoscientific disciplines, for example, in the fields of geochemistry and geochronology, terms such as measurement uncertainty and error have fixed meanings, although misuse is still common. Potts (2012) provide a useful translation of the International Vocabulary of Metrology 2008 (VIM3, Bureau Internationale des Poids et Mesures) for analysts in geoscience. However, outside of these fields focused on chemical data, the terminology becomes looser, which is largely a reflection of the complex use of language.

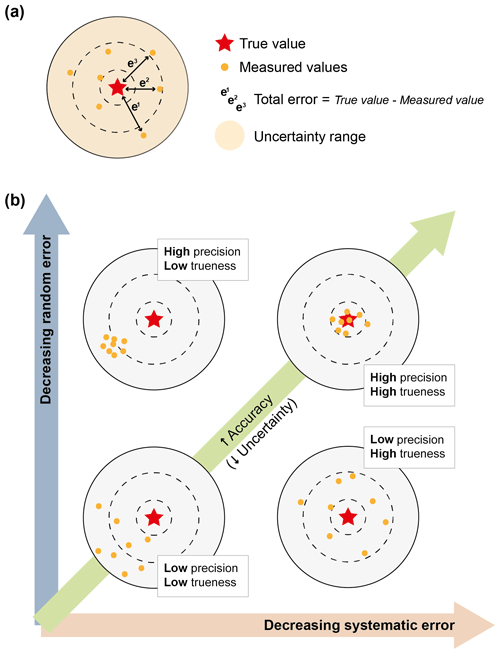
Figure 1 Visual representation of (a) the difference between error and uncertainty and (b) the relationships between commonly used quality descriptors and performance characteristics.

Enumerating all the types of uncertainty in the measurement and interpretation of geological objects, phenomena and processes is therefore not an easy task. A commonly used classification divides total uncertainty into two groups: “objective” and “subjective”. Objective uncertainty is, in principle, irreducible, whereas subjective uncertainty can be reduced with additional investigative efforts (Campos et al., 2007), although this is not necessarily a linear path (Wilson et al., 2019) and the focus of certainty may change with additional information (i.e. as we become aware of an unknown). For these reasons, it might be useful to think about uncertainties not on the basis of types but of their sources (Hora, 1996) by distinguishing between objective (source being the data and inputs) and subjective (source being a person) uncertainties (Fig. 2) (Tannert et al., 2007). Objective uncertainty (also called “stochastic” uncertainty) is associated with the data, i.e. with the acquisition, analysis or interpretation techniques and means used to handle it. For example, navigational errors in shipborne collected magnetic data, the limitations of current subsurface imaging techniques or geochemical composition variations measured upon repeated testing of a single sample, all result in objective uncertainties. On the other hand, subjective uncertainty corresponds to the variability that results from knowledge or skill deficiencies in the subject, which may be individual researchers, research groups or potentially whole research communities. Biases, flawed experimental procedures or the lack of scientific consensus over certain concepts all lead to subjective uncertainties.

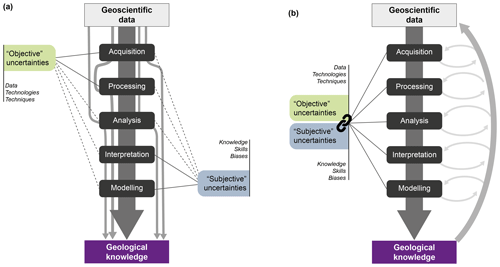
Figure 2 The process for generating geological knowledge requires the acquisition, processing, analysis and interpretation of geoscientific data. All of these stages are susceptible to objective (i.e. data-/technique-related) and subjective (i.e. person-related) uncertainty at different levels. (a) “Traditional” and (b) revised understanding of the sources of uncertainty within the process of knowledge generation, as discussed in the text.

This distinction between objective and subjective uncertainty, which originated in the fields of epistemology and psychology, has been adopted in a number of significant articles with the aim of understanding their role and impact in the geosciences (Bond, 2015; Frodeman, 1995). Both operate in the different stages of geological knowledge generation (Fig. 2a). Although both are recognised by geoscientists, subjective uncertainty in the form of interpretational uncertainty is largely ignored in practice. This is surprising given that Earth sciences, particularly geology, are distinctly interpretative disciplines (Frodeman, 1995), and as such recognising and describing how, where and why geological results and interpretations may be wrong should be a powerful tool for a geoscientist. The reason for the relative avoidance of subjective uncertainty in geosciences may be that it often cannot be easily assessed quantitatively with statistical analysis or probabilistic theory but instead requires qualitative approaches drawn from cognitive psychology (Wilson et al., 2019). Additionally, a false perception exists in Earth sciences that total uncertainty in most geological outputs is bound to decrease alongside the increase in input data quality and availability. This is exemplified in the experiment outlined by Wilson et al. (2019), who observed participant certainty decreasing along with an increase in available data. It also assumes that information-related limitations are the principal factor controlling diverging interpretations of a given dataset. However, this is often not the case in reality. For example, Eagles et al. (2015) illustrate this issue by showing how diverging interpretations of the location of continent–ocean boundaries worldwide are not a consequence of the challenges of interpreting data of varying ages and quality but instead result from diverging conceptual models that inform interpretation of the available data.

3 Dealing with uncertainty: quantification, mitigation and communication

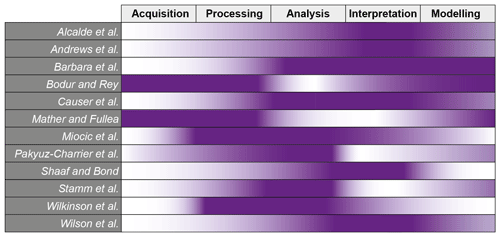
The papers compiled in this special issue describe different challenges related to the handling of uncertainty (chiefly quantifying and mitigating uncertainty). They cover different topic areas and focus on different elements in the process of geological knowledge generation (Table 1). Here, we briefly summarise the contributions to the special issue, grouping the contributions based on an assumed generic geological knowledge generation workflow. As described in Fig. 2, this workflow starts with data acquisition and proceeds via processing and analysis to the final stages of interpretation and modelling.

Table 1 Aspects of uncertainty discussed in each of the papers compiled in this special issue. Darker shading indicates stronger focus.

3.1 Acquisition – data availability, accessibility, resolution

Many geological parameters and concepts that are not directly observable or measurable can be interpreted from signals in potential field data. Two different examples of this are covered in this special issue. For example, crustal geothermal gradients can be computed from the temperature difference between the Earth's surface and the 580 ^∘C isotherm (or “Curie” depth), but it requires certain knowledge of the isotherm's depth. Therefore, although the Curie depth offers a valuable constraint to estimate geothermal heat flow, uncertainties in the former will directly impact estimates of the latter. Many previous studies constrain the location of Curie depth on the basis of spectral analyses of geomagnetic anomalies, involving subjective identification of facets in spectral power plots that leads to the under-representation of uncertainty. Aiming to avoid this, Mather and Fullea (2019) instead propose a Bayesian approach where Curie depths are expressed in probabilistic terms and accompanied by quantified uncertainties. Depths estimated in this way can then be confidently used as boundary conditions to compute crustal temperature distributions.

A further example is presented by Bodur and Rey (2019), who discuss the uncertainties in dynamic topography estimates made on the basis of mantle tomography observations. Viscous stresses transmitted vertically to the lithosphere from zones of contrasting buoyancy in the Earth's mantle are known to be responsible for long wavelength uplift or subsidence. Dynamic topography can be defined as the surface expressions of these mantle fluctuations. At the present day, dynamic topography can be estimated from the non-isostatically compensated component of Earth's topography. An alternative approach extracts dynamic topography on the basis of seismically mapped density anomalies in the mantle. This results in dynamic topography amplitudes that are generally larger than those obtained from residual topography calculations. The difference in estimates from the two approaches is an illustration of uncertainty resulting from our incomplete knowledge of the structure of the lithosphere and the viscosity structure in the Earth's interior. In their manuscript, Bodur and Rey (2019) hypothesise that these discrepancies in dynamic topography estimates may be related to an oversimplification of mantle rheology in numerical models of present-day mantle flow. They do this on the basis of the results of a series of coupled 3-D thermomechanical numerical experiments simulating the dynamic topography signal resulting from a sphere located at a certain depth in the mantle, whose density is greater than that of its surroundings and under a variety of different rheological assumptions.

3.2 Processing and analysis – assumptions and quantification of uncertainty

Several papers consider the assumptions made when processing and analysing data to make predictions and the uncertainties associated with them. Quantifying and/or qualifying these uncertainties often relies on stochastic approaches, which form the main focus of two contributions.

3.2.1 Assumptions and approaches

Globally, as we move towards a net-zero carbon economy, new energy transition technologies are of growing importance. Reflecting this importance, two papers in the special issue focus on the uncertainties in understanding aspects of subsurface carbon storage. In the first, Miocic et al. (2019) employ various models to estimate the sealing capacity of faults in the context of CO₂ capture and storage systems (CCSs). Since deployment of CCS technology is very immature in comparison to that of the petroleum industry, the available data on CO₂ storage are limited in comparison to the wealth of knowledge generated over many decades of hydrocarbon exploration and production. Thus, geoscientists need to use knowledge and techniques developed by the petroleum industry to inform and predict the behaviour of CO₂ in the subsurface. In their paper, Miocic et al. (2019) translate standard uncertainty modelling techniques from the oil and gas industry to calculate the maximum supported column heights of CO₂, given different fault sealing parameters. This is essential to be confident that a fault will not leak CO₂ after its injection into a reservoir. Miocic et al. (2019)'s models quantify the uncertainties associated with their different input parameters, including the CO₂–brine–fault rock system wettability and fault rock composition. Their results suggest that fault rocks that previously supported hydrocarbon columns might not support the same height of CO₂, and that therefore risk assessments must incorporate CO₂-specific models to produce accurate estimations.

Wilkinson and Polson (2019) also present a study based on CCSs in their case to quantify the uncertainty associated with the calculation of storage capacity in saline aquifers. In their elicitation experiment, 13 experts provided storage capacity estimations for seven storage units located in the Inner Moray Firth, offshore Scotland, based on published data. This experiment simulates real-world scoping studies, used to appraise storage units within a broader target area. The authors identify different sources of uncertainty stemming from the data and techniques used for the storage capacity calculations, as well as from the personal judgement of the experts, as reported in other similar elicitation experiments (e.g. Alcalde et al., 2017; Bond et al., 2012; Polson and Curtis, 2010). Wilkinson and Polson (2019) point out that the geological uncertainty reported in most published storage estimates is greater than the precision associated with these estimates. Interestingly, the authors indicate that incorporating more expert assessments (i.e. more estimated storage capacity values) to the dataset, whilst reducing the standard deviation of the mean estimate, might not move the mean estimate closer to the true value. Thus, adding more values to the assessment might reduce uncertainty without increasing accuracy.

Geological models often present one plausible scenario built from the best-estimate interpretation of data and therefore ignoring other potentially equally probable solutions that match the available constraints. Furthermore, models often fail to capture the key uncertainties relevant for their end users. These considerations are explored by Bárbara et al. (2019) using the Lubina and Montanazo mature oil fields (western Mediterranean) as a case study to investigate how structural uncertainty can affect the accuracy and reliability of static and dynamic reservoir models and, in turn, impact predictions of gross rock volume (GRV, or the volume of reservoir rock above the oil–water contact). They explore two approaches to capturing uncertainty in the interpretation of faults and horizons within the fields' small highly fractured reservoir which, in turn, is critical to obtain improved volume estimations. They conclude that manually interpreting the size and location of uncertainty envelopes around faults and horizons, although prone to human error and bias, results in more accurate predictions of the impact of uncertainty. Conversely, modelling structural uncertainty as constant-size envelopes leads to less accurate horizon prediction errors and more widely distributed GRV predictions. Their study also illustrates how, by considering a large number of the possible scenarios that satisfy the available data, an improved understanding of the real magnitude of structural uncertainty can be achieved.

3.2.2 Stochastic modelling

In an age of expansive digital data and increasing computer power, approaches to uncertainty utilising stochastic modelling to parameterise uncertainties are a growing field. Pakyuz-Charrier et al. (2019) propose a methodology for Monte Carlo simulation of uncertainty propagation (MCUP) in 3-D geological modelling. In the Monte Carlo process for 3-D geological modelling, each structural input (e.g. interface points, fold axes) is replaced by a probability distribution, and the set of distributions is then sampled with Monte Carlo methods to generate multiple statistically plausible datasets that are then converted into 3-D geological models and merged into probabilistic models characterised by uncertainty indices. However, important differences within these models are observed in terms of topology (i.e. in terms of their mathematical spatial properties) to investigate how the different surfaces in the models intersect. These differences (or model heterogeneity) are detrimental to the generation of uncertainty index models, that assumes homogeneity in surface intersections between the models and hence can affect the reliability of the 3-D geological model outputs. To address this issue, the authors use topological signatures to calculate clusters that help to classify topologically distinct models. This type of analysis can help to increase confidence in the uncertainty indices of the models, hence reducing the overall model uncertainty.

Also focusing on using stochastic structural modelling, Stamm et al. (2019) use probabilistic uncertainty quantification (Markov chain Monte Carlo simulations) to aid in the decision-making processes. The authors employ custom “loss functions”, instead of traditional approaches (such as the use of percentiles and median values), to extract as much information as possible from the probabilistic distributions that determine the target parameter, reinforcing the decision-making process. Stamm et al. (2019) test this approach by calculating a set of probabilistic distributions of maximum hydrocarbon volume from a synthetic 3-D structural model: a potential reservoir formed by an anticlinal fold that is cut by a normal fault. In their experiment, they introduce uncertainties in the different input parameters that result in variations in depth, thickness and shapes of the target reservoir layer, as well as the degree of fault offsets. Two secondary sets of information, layer thickness and shale smear factor likelihoods were added into the modelling using Bayesian inference to explore how the addition of information changes the decision uncertainty. Based on their results, the authors suggest that the loss functions could be successfully employed in decision-making processes in the hydrocarbon and other economically meaningful sectors, at least as a powerful preliminary decision recommendation tool.

3.3 Interpretation and data modelling – human biases and subjectivity

Five papers in the special issue address the challenge of quantifying subjective uncertainty. The first considers how information technology may be used to minimise subjective bias, whilst the remaining four quantify subjectivity in data collection and interpretation.

3.3.1 Common biases and technology-based approaches to minimise them

An overview of cognitive biases that result from the use of heuristics (i.e. rules of thumb) to make decisions marks the start of the paper by Wilson et al. (2019). The paper goes on to consider how optimal decisions are made and defines in detail three of the main cognitive biases that influence decision-making in Earth science: availability bias, framing bias and anchoring bias. Debiasing strategies are then discussed and the question raised as to whether better decision-making can be taught. The paper reviews examples in which choice architecture has been used effectively to aid decision-making in geoscience but acknowledges issues in effectively employing self-correcting debiasing strategies. Using theoretical plots of conclusion certainty vs. data, the authors illustrate the changing relationship between certainty and data, and the potential influence of debiasing nudges. The authors propose that advances in artificial intelligence and information technology can be used to employ “digital nudging” to positive effect in many geoscience workflows. In the final section of the paper, they consider two case studies: the first for optimising field data collection with unmanned aerial vehicles (UAVs) to minimise anchoring bias and the second to minimise availability bias when making fault interpretations in seismic image data. The paper concludes with a reflection on the potential pitfalls and gains of using digital nudges as a debiasing strategy in Earth science applications.

3.3.2 Quantification of subjectivity in data collection and interpretation

Four papers in the special issue address quantification of subjective uncertainty by gathering data from multiple participants to provide a range in data collection statistics or interpretation outputs. Andrews et al. (2019) focus on the collection of data to describe natural fractures using a range of field techniques and from field photographs in a laboratory exercise. The authors found differences between the field data and those collected from photographs of the same outcrops, as well as differences between individuals and groups. Rather than focusing on experience, differences between individuals were interpreted as being dominated by the “type” of participant (e.g. to what extent a participant is concerned with detail). The impact on calculated fracture attributes from the different sources was significant. The findings also have implications for determining the number of individual fractures required to be recorded for a statistically significant representation of the overall fracture attributes (i.e. how long a scan line is required or the circumference of a circular scan line). Finally, Andrews et al. (2019) consider what can be done to minimise bias in fracture data collection. Their recommendations can be amended to inform other types of geological data collection, particularly the collection of field data for quantitative analysis.

Two further papers, by Alcalde et al. (2019) and Schaaf and Bond (2019), consider interpretation of seismic image data. Alcalde et al. (2019) compared 161 alternative interpretations of a vertically exaggerated seismic image and showed that, whilst the extent of vertical exaggeration had minimal impact on the interpretation output, the initial conceptual model applied by the interpreters played a dominant role on the interpretation output. The interpretations of the seismic image can be divided into three overarching conceptual models. The authors argue that the conceptual model applied is dominated by choice in how to interpret the rightward and leftward dipping fabrics in the seismic image, as either horizons or faults. Alcalde et al. (2019) show that there is no evidence for reassessment of the initial conceptual model applied even when geological “rules” such as the expected range in normal or reverse fault dip are broken. This supports evidence described by various authors (e.g. Rankey and Mitchell, 2003; Bond et al., 2007, 2008) and also analysed in detail in Wilson et al. (2019) that anchoring to initial conceptual models can determine final outcome.

Schaaf and Bond (2019) present a statistical assessment of uncertainty in the interpretation of a 3-D seismic dataset. Using a total of 78 interpretations of the same seismic dataset, they discuss how interpretational uncertainty relates to seismic data quality. The 78 participants were tasked with interpreting three horizons as well as a fault network imaged in the supplied dataset. The range of interpretations encompassed 11 distinct fault network topologies, of which five were interpreted by five or more participants. The range of interpretations was compared to the root mean square seismic amplitude attribute (RMSA), as a proxy for seismic image data quality. The authors found a correlation between the range in seismic image quality (RMSA) and uncertainty in fault placement, concluding that seismic image quality determines the spatial statistical distribution of interpreted faults. Where the seismic image quality is good, the spatial distribution of fault interpretations is close to normal, whereas in areas of extensive poor seismic image quality the distribution of fault interpretations is almost uniform. In the discussion, the authors discuss their findings with reference to stochastic and deterministic modelling of fault properties and the potential for machine learning approaches.

Causer et al. (2020) also discuss the impact of interpretational uncertainty, this time within the framework of plate kinematic modelling. They do so by examining and illustrating the impact that differing interpretations of the same data have on plate kinematic reconstructions of the North Atlantic. Plate models, here and elsewhere in the world, often rely on the identification and mapping of so-called “break-up features” as markers for the location and age of first seafloor spreading. Causer et al. (2020) use new seismic data and existing interpretations across the extended continental margin of Newfoundland to show that some commonly used breakup markers in this part of the world are not indicative of oceanic lithosphere but instead are located within exhumed mantle domains and pre-date the growth of oceanic crust. Additionally, they illustrate how differing interpretations exist for the location of some of these features, evidencing the difficulty in identifying and mapping them precisely and highlighting the magnitude of interpretational uncertainty. They conclude that a different approach, not reliant on the interpretation of breakup features, is required to quantitatively constrain plate motions.

4 A broad view of uncertainty

The process of transforming geoscientific data into meaningful geological knowledge can, in most cases, be broken down into five interrelated stages, namely acquisition, processing, analysis, interpretation and modelling (Fig. 2). Each of these stages, when present, is affected by a certain degree of uncertainty. This uncertainty (objective/subjective or both), in turn, has a direct impact on the validity and value of the geological knowledge gained as a result. Conventionally, geoscientists tend to associate objective uncertainties to stages of a more technical/empirical nature such as acquisition or processing of data (e.g. measurement uncertainty due to limited resolution of a given technique). Conversely, subjective uncertainties are expected to be present in stages to which interpretation and reasoning are central (e.g. cognitive biases in data interpretation). However, both objective and subjective uncertainties are strongly interlinked and, in most cases, operate throughout the entire process of knowledge generation. Take, for example, the acquisition of fracture data from a given outcrop. Subconsciously, more effort might be taken to avoid objective uncertainty (e.g. purposely accounting for equipment limitations or the impact of using satellite imagery instead of in situ measurements). However, significant subjective uncertainties also exist within the acquisition stage (e.g. data collector understanding of the difference between fractures and bedding, spontaneous selection of fractures to be measured, changes in attention to detail and measurement process during a lengthy field campaign, or acquisition planning based on logistical concerns (e.g. the distance or the quality of the outcrops) but also on prior geological knowledge (e.g. location of outcrops expected to be relevant to the study at hand). As a result, data collection carries substantial “pre-programmed” uncertainties (both objective and subjective). Although we acknowledge that the explicit classification of uncertainty into two distinct categories (objective and subjective) can aid their identification (Walker et al., 2003), this separation can wrongly reinforce the idea that they are indeed independent components of uncertainty (Fig. 2a).

A further complication to the quantification of uncertainty in any given study comes from the fact that the knowledge generation workflow is rarely linear, despite often being perceived and represented as such. To better represent the challenges in dealing with “inherited” uncertainties, we illustrate a non-linear, almost fractal nature, model of the knowledge generation process in the geosciences (Fig. 2b). Although most papers in this special issue focus on either objective or subjective uncertainties, Alcalde et al. (2019) and Wilkinson and Polson (2019) partially investigate interrelationships between both uncertainty types. We propose that this line of research should be explored further to better understand the relationships and weight of each type of uncertainty in the decision-making and knowledge generation process.