Localized shear and distributed strain accumulation as competing shear accommodation mechanisms in crustal shear zones: constraining their dictating factors

Understanding the underlying mechanisms of strain localization in the Earth’s lithosphere is crucial for explaining the mechanics of tectonic plate boundaries and various failure-assisted geophysical phenomena, such as earthquakes. Geological field observations suggest that shear zones are the most important lithospheric structures demonstrating intense shear localization at plate boundaries, accommodating a major portion of tectonic deformations. Despite extensive studies over the past several decades, the factors governing how shear zones accommodate bulk shear, whether via distributed strain (i.e. the development of macroscopic S (schistosity) foliations normal to the principal shortening strain axis) or via localized shearing (i.e. the formation of shear-parallel C bands, where C refers to the French “cisaillement” (shear)), remain largely unexplored. This study aims to address this gap in knowledge by providing observational evidence of varying S and C development in crustal shear zones from two geological terrains in eastern India. These field observations are complemented by 2D viscoplastic numerical simulations within a strain-softening rheological framework to constrain the factors controlling two competing shear accommodation mechanisms: distributed strain accumulation and shear band formation. The model-based analysis recognizes the bulk shear rate $\left({\dot{\mathit{\gamma }}}_{\mathrm{b}}\right)$, initial viscosity (η_v), and initial cohesion (C_i) of a shear zone as the most critical factors determining the dominance of one mechanism over the other. For a given C_i value, low ${\dot{\mathit{\gamma }}}_{\mathrm{b}}$ and η_v values facilitate the formation of S foliation (uniformly distributed strain), which transitions to a C-dominated shear accommodation mechanism as η_v increases. However, increasing ${\dot{\mathit{\gamma }}}_{\mathrm{b}}$ facilitates shear accommodation through a combination of the two mechanisms, leading to S–C structures. The article finally discusses the conditions under which shear zones can significantly intensify rates of localized shear, producing rapid slip events, such as frictional melting and seismic activities.

1 Introduction

Shear zones are long, narrow regions of strain localization, relative to their surroundings, that accommodate large amounts of tectonic movement. They occur on various scales, ranging from grain-size scales (millimetres) to crustal scales (hundreds of kilometres), and at varying depths, covering the upper crust to the upper mantle (Adam et al., 2005; Vauchez et al., 2012; Fossen and Cavalcante, 2017). In the Earth’s lithospheric deformations, large-scale shear zones often play a critical role in triggering catastrophic phenomena, such as fault-driven earthquakes (Fagereng et al., 2014; French and Condit, 2019; Kotowski and Behr, 2019; Beall et al., 2021; Rodriguez Padilla et al., 2022), landslides (Korup et al., 2007; Hughes et al., 2020), and abrupt topographic modifications (Malik et al., 2006; Wang et al., 2020; Rodriguez Padilla, 2023). They also act as potential locations for the shear-induced partial melting of rocks, as widely documented in the examination of their association with pseudotachylytes (Sibson, 1975; Papa et al., 2023), which can dramatically augment fault-slip rates and associated strain accumulation processes, leading to mega-earthquake events (Di Toro et al., 2006; Rice, 2006; Menegon et al., 2021). Understanding their internal shear accommodation mechanisms has thus become a critical area of study in solid earth geophysics, especially with regard to rheological contributions to shear enhancement processes. Both field and experimental observations suggest that crustal shear zones generally accommodate strain by contrasting microscale deformation mechanisms in brittle and viscous regimes (Fossen and Cavalcante, 2017). In the brittle regime, grain-scale fracturing, grain rotation, and frictional sliding are the principal mechanisms (Sibson, 1977; Logan, 1979), whereas dislocation-assisted creep (crystal plastic), grain-boundary sliding, and syn-kinematic recrystallization are the dominant mechanisms in the viscous regime (Passchier and Trouw, 2005). However, shear zones typically evolve through strain partitioning along macroscopic shear bands, irrespective of their internal deformation mechanisms, the growth of which is generally controlled by various microscale deformation mechanisms, such as dynamic recrystallization, syn-kinematic recrystallization, grain-size reduction, and fluid-assisted mechanical weakening. The bands share a large fraction of the bulk shear in the shear zones.

The origin of shear bands in rocks and practical solid materials, such as metals and polymers, has remained a subject of challenging studies over several decades, particularly in the context of failure analysis (Bowden and Raha, 1970; Wang and Lade, 2001; Torki and Benzerga, 2018; Finch et al., 2020; del Castillo et al., 2021). Compression test experiments on homogeneous isotropic solids show shear band localization in conjugate sets, with dihedral angles varying in the range of 60 to 90°, depending on deformation conditions (such as strain rate) and certain mechanical properties, e.g. the coefficient of internal friction, the dilatancy factor, and the strain-hardening parameter (Bowden and Raha, 1970; Roscoe, 1970; Rudnicki and Rice, 1975; Vardoulakis et al., 1978; Anand and Spitzig, 1980, 1982; Wang and Lade, 2001; Kaus, 2010; Torki and Benzerga, 2018; Mukhopadhyay et al., 2023). Several theoretical models have predicted the angles of shear bands relative to the compression axis in isotropic materials as a function of the physical variables mentioned above (Hutchinson and Tvergaard, 1981; Anand and Su, 2005). Layered brittle–viscous composites also undergo failure in conjugate shear bands, although their modes of development switch from localized to distributed as the thickness and viscosity ratios of brittle–viscous layers increase (Schueller et al., 2010). A similar line of research in failure studies focuses on the mechanisms of shear localization in the simple shear deformation of granular rocks. These mechanisms suggest that shear bands develop in a more complex manner, forming multiple sets as opposed to the simple conjugate sets of band formation formed under compressional deformation. The multiple shear bands in granular materials, described as Y, B, P, and R bands, form at characteristic angles relative to the bulk shear direction (Logan, 1979; Logan et al., 1992). Here, Y and B bands are oriented parallel to the shear direction (with B bands localizing preferentially at the shear zone boundaries), and P bands occur at angles of 15–45°, with their vergence occurring in the shear direction. R (Riedel) bands constitute the most dominant two sets of antithetically vergent shear bands: one set at low angles (∼ 15–20°) and the other at high angles (60–70°) with the shear direction. These are conventionally symbolized as R₁ and R₂ bands, respectively (Roy et al., 2021). In shear deformations, these secondary shear bands generally occur as discrete planar zones, often marked by the localization of gouge materials with intense grain-size reduction (Volpe et al., 2022; Casas et al., 2023).

The mechanics of shear band formation in shear deformation is still a lively problem and has rejuvenated theoretical and experimental studies of shear failure in the last couple of decades (Fossen, 2010; Hall, 2013). Numerical shear experiments on granular materials suggest that shear bands localize shear not through any bifurcation of local mechanical states but via a long-range geometrical interaction between material particles (Ord et al., 2007). On the other hand, Mair and Abe (2008) have demonstrated through 3D numerical simulations a direct correlation between strain localization and grain-size reduction in fault gouge. Laboratory experiments have been conducted on quartz–feldspar-rich granular materials and carbonates (Logan, 1979; Marone and Scholz, 1989; Marone et al., 1990; Beeler et al., 1996). A direction of these experimental investigations suggests that the relative growth of multiple sets of bands depends significantly on phyllosilicate and water content in granular aggregates (Morgenstern and Tchalenko, 1967; Wijeyesekera and De Freitas, 1976; Maltman, 1977; Logan and Rauenzahn, 1987; Rutter et al., 1986; Logan et al., 1992; Saffer and Marone, 2003; Collettini et al., 2011; Haines et al., 2013; Giorgetti et al., 2015; Orellana et al., 2018; Okamoto et al., 2019; Ruggieri et al., 2021; Volpe et al., 2022). Shear deformation of viscous materials also produces secondary shear bands, as seen in brittle materials, and studies in this area have gained serious attention due to their implications for interpreting various geodynamic processes, such as lithospheric subduction, deformation-assisted fluid/melt migration, and earthquake generation in viscous regimes (Katz et al., 2006; Kirkpatrick et al., 2021; Beall et al., 2021; Tulley et al., 2022; Mancktelow et al., 2022). The mode of strain accommodation in viscous shear zones, however, largely differs from that discussed above for granular shear zones showing brittle behaviour. Although viscous materials typically accommodate shear through continuous deformations without any macroscopic fractures in shear zones (Rutter et al., 1986), many authors have reported brittle features (such as Riedel fractures, “V” pull-aparts in minerals, and strain-dependent transitions from brittle fractures to mylonitic shearing) in viscous shear zones (Paterson and Wong, 2005; Fusseis et al., 2006; Fusseis and Handy, 2008; Mukherjee and Koyi, 2010; Doglioni et al., 2011; Meyer et al., 2017). Experiments performed under conditions that mimic the brittle–viscous transition zone show the localization of shear in the form of bands, where both brittle and viscous features dominate as functions of temperature, strain rate, and microscale mechanisms of deformation (Schmocker et al., 2003; Pec et al., 2016; Marti et al., 2017, 2018, 2020). Previous studies have used various rheological models to investigate the processes of strain localization in the lithosphere and their controlling factors. Some of these studies have invoked a power-law viscous rheology to explain the mechanism of shear localization in terms of porosity bands in viscous regimes (Katz et al., 2006). A parallel line of study has combined a pressure-dependent yield criterion with viscous rheology to deal with the problem of shear band formation (Mancktelow, 2006; Moresi et al., 2007a, b; Lemiale et al., 2008). On the other hand, Bercovici and Karato (2002) have theoretically demonstrated strain localization in the lithosphere, taking into account thermal-, damage-, and grain-size-controlled feedback mechanisms.

Both extensive numerical and experimental modelling (Shimamoto, 1986, 1989; Burlini and Bruhn, 2005; Misra et al., 2009; Meyer et al., 2017; Finch et al., 2020), as well as field observations, have led to a common finding that viscous shear zones accommodate their bulk shear deformation via two principal mechanisms: uniformly distributed strain accumulation and localized shearing. Distributed strain accumulation imparts pervasive planar fabrics (called S (schistosity) foliation in the literature) that track the x–y plane of the finite-strain ellipsoid, often defined by flattened grain shapes and preferred orientations of phyllosilicates, e.g. muscovite, biotite, and chlorite. In contrast, localized shearing occurs in spaced zones, forming shear bands either parallel to or at low angles relative to the principal shear plane; these shear bands are commonly described as C and C^′ bands, respectively, where C refers to the French “cisaillement” (shear) (Berthé et al., 1979; Bos and Spiers, 2001; Niemeijer and Spiers, 2005, 2006; Tesei et al., 2012, 2014). These bands accommodate large shear strains compared to their surroundings, and they are characterized by extreme grain refinement. In some cases, shear bands (termed C^′′ bands) occur sporadically at high angles in the shear direction. Among these bands, C bands are the most dominant structures in natural shear zones, and they develop as closely spaced planar zones to form foliation, as widely reported in examinations of typical S–C mylonites in viscous shear zones, where S and C foliations interact with one another, producing an anastomosing network of structural characteristics in the sheared rocks. Some authors have also described these fabrics with respect to brittle shear zones (Lin, 1999).

It follows from the preceding discussion that shear deformation in crustal shear zones generally occurs through a combination of distributed viscous strain (homogeneous S-foliation development) and localized zones (shear band formation) of viscous strain (Lister and Snoke, 1984; Burlini and Bruhn, 2005; Mancktelow, 2006; Misra et al., 2009; Marques et al., 2011b). Nevertheless, the relative formation of these features is still a subject of debate. Some authors (Berthé et al., 1979) have proposed that S foliations and C bands form simultaneously. However, recent studies (Bukovská et al., 2013, 2016) have claimed a non-synchronous origin for the two shear zone features, suggesting a significant time gap (∼ 10 Myr) between the formation of S foliations and C bands. On the other hand, some shear zones develop distributed viscous strains to produce penetrative planar fabrics with little or no shear localization (Ramsay et al., 1983; Marques et al., 2013; Fossen and Cavalcante, 2017; Gomez-Rivas et al., 2017; Pennacchioni and Mancktelow, 2018), as often documented in shear zones with S mylonites. Conversely, another class of shear zones can accommodate shear mainly through shear bands, with little or no distributed strain in the inter-band regions, as evidenced by the absence of or minimal penetrative-foliation development, even at the grain scale (Lister and Snoke, 1984; Mukhopadhyay and Deb, 1995; Lloyd and Kendall, 2005). This type of shear zone is generally dominated by C mylonites. What controls these two modes of shear accommodation is, however, less explored. In a recent study, Tokle et al. (2023) addressed this problem using sheared quartzite, considering phyllosilicate content as a controlling factor, where phyllosilicates allow strains to localize preferentially in bands, leaving quartzite grains less deformed. Schueller et al. (2010) recognized the composite structure of alternate low- and high-viscosity layers and the viscosity ratio of these layers as factors that determine the occurrence of distributed versus localized fracturing in shear zones. Numerical simulations have shown that the growth of macroscopic shear bands or mesoscopic-scale slip planes can occur in granular materials, depending on the initial densities and the loading paths (Darve et al., 2021). Despite these studies, the problem of distributed viscous strain versus localized shear band formation, especially in terms of a generalized rheological scheme, needs further attention, which constitutes the central theme of this article.

To address this problem, the present study examines the modes of shear accommodation (distributed strain accumulation versus localized shearing) on macroscopic scales in crustal shear zones within the Chotanagpur Granite Gneissic Complex and the Singhbhum shear zone, located in the eastern Indian cratons. The shear zones show spectacular variations in their macroscopic structural features, based on which they are classified into three categories: (i) shear zones dominated by shear-parallel high-strain zones (C bands), separated by regions of weak or no distributed deformation (S foliations); (ii) shear zones dominated by S foliations, without any strong shear-parallel C-band localization; and (iii) shear zones with competing developments of both C bands and domains of distributed S foliations. We use viscoplastic models within a macroscopic rheological framework (i.e. a continuum mechanics approach), where the viscous component simulates macroscopically distributed continuous deformations, while yield behaviour (the plastic component) is introduced to couple the process of strain localization in the viscously deforming shear zones. This rheological model allows us to investigate the factors controlling these two competing mechanisms of deformation accommodation: distributed strain and localized shear band formation. The article presents a map showing the fields of their growth as functions of two fundamental kinematic and rheological parameters: bulk shear rate and the initial viscosity of shear zone rocks. This study also discusses possible shear rate enhancement processes and their implications for underpinning the origins of slip-induced catastrophic processes, such as frictional melting and earthquakes in viscous regimes.

2 Field observations

2.1 Study area

We studied crustal shear zones in two tectonic regions of a Precambrian craton: the Singhbhum shear zone (SSZ) and the Chotanagpur Granite Gneissic Complex (CGGC), located in eastern India (Fig. 1). A detailed description of their overall geological setting is presented in Sect. S1 in the Supplement. The SSZ is a spectacular arcuate thrust-type shear zone, about 200 km long and 2 km wide, situated at the interface between the Archean nucleus in the south and the North Singhbhum Mobile Belt (NSMB). Our field investigations conducted in the SSZ concentrated on the southeastern flank of the zone, specifically the village of Patharghara (22°32^′37.911^′′ N, 86°26^′31.223^′′ E), located near the old Surda copper mines and the town of Musabani (22°30^′59.3^′′ N, 86°26^′26.5^′′ E) in the district of Purbi Singhbhum, Jharkhand. The main rock types in this area are quartzite mylonites, mica and chlorite schists, and mylonitized granite. The CGGC lies north of the NSMB, mostly covered by a variety of granite gneisses, dotted with minor lithologies (e.g. mafic and ultramafic intrusives; Mahadevan, 1992). The host rocks are metamorphosed to amphibolite and granulite grades (Roy et al., 2021). We conducted our field investigations in the northern part of the district of Purulia – specifically in Bero Hills (23°31^′54.4^′′ N, 86°45^′35.5^′′ E) and Belamu Pahar, Anandanagar (23°27^′56.1^′′ N, 86°03^′26.6^′′ E) – where excellent outcrop-scale viscous shear zones are exposed in granite gneisses. These shear zones are typically a few centimetres to tens of metres long, with thicknesses varying from a fraction of a centimetre to several centimetres, often showing sharp deflections of steeply dipping foliations in the host rocks. The CGGC shear zones mostly developed under simple shear strain, with a kinematical vorticity number corresponding to $W_{\mathrm{k}}=\mathrm{0.8}-\mathrm{1}$ (Dasgupta et al., 2015).

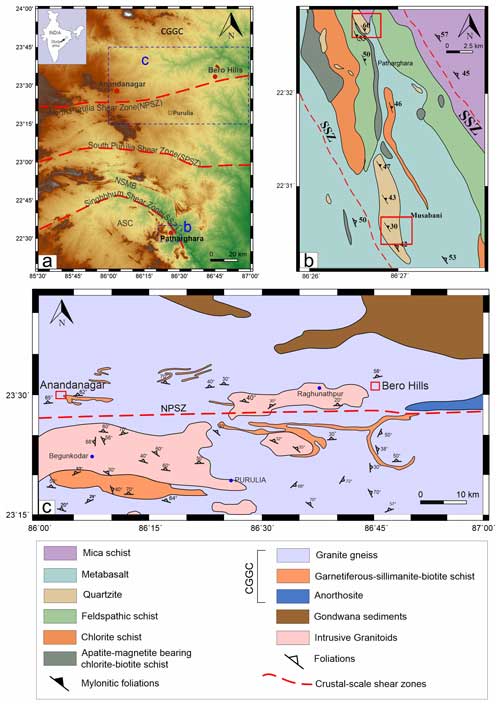
Figure 1 A simplified geological map of (a) an eastern Indian Precambrian craton, showing the disposition of the Singhbhum shear zone (SSZ) and the Chotanagpur Granite Gneissic Complex (CGGC) (modified after Mukhopadhyay and Deb, 1995; Mazumder et al., 2012; Roy et al., 2021, 2022). Detailed geological maps of the two major study areas: (b) the Patharghara and Musabani regions and (c) the Purulia region. ASC: Archean Singhbhum Craton. NSMB: North Singhbhum Mobile Belt. SPSZ: South Purulia Shear Zone. NPSZ: North Purulia Shear Zone. The red squares indicate the field areas.

2.2 Macrostructural characteristics of SSZ rocks

Sheared quartzites in Patharghara show closely spaced, macroscale, NE-dipping (20–60°) shear surfaces (C). Their exposed counterparts profusely contain slickenlines, indicating dominantly down-dip slip motion in the shear zones (Fig. 2a). At this location, the macroscopic shear structures are characterized by a single set of parallel bands (called C bands, analogous to C fabrics in mylonites), with some gentle local undulations. The C spacing varies over a wide range (from 2 mm to 7 cm). The sheared rocks are markedly devoid of S foliations on the macroscale, as reported for type-II S–C mylonites by Lister and Snoke (1984).

Figure 2 Field examples of C-dominated shear zones hosted in quartzites observed in the Patharghara and Musabani regions of the SSZ. Note the strongly developed sub-parallel to parallel C shear bands with varying spatial densities. (a) Slickenlines observed on the C surfaces, indicating slip along these planes. (b–d) Intense shear localization along C bands with varying spatial densities. The bands are characterized by marked grain-size reduction. SZ: shear zone.

Sheared quartzites in the Musabani area also show strongly developed C bands, marked by drastic grain-size reduction (Fig. 2c and d). The band structures always dip in the NE direction, however, with varying magnitudes, from gentle (∼ 20°) to steep (∼ 45°) dips. They are laterally quite persistent, with a single C band traceable over several metres in both the down-dip and strike directions. The C bands are heterogeneously developed in the sheared rock, resulting in a strong variation in their spatial density: ${\mathit{\lambda }}^{*}=$ (width of shear zone/inter-band distance) = 3.93 to 183.15 (Fig. 2b and c). Extremely closely spaced C bands in some places give rise to the appearance of a typical penetrative foliation, as widely reported for C mylonites (Fig. 2d). We measured the C spacing, normalized to the effective local shear zone thickness, as an indicator of rheology, which will be discussed later (Sect. 2.4). Macroscopic S foliations are characteristically absent in the sheared quartzites.

Microstructural studies under an optical microscope reveal that C-band domains are regions of extreme grain refinement due to dynamic recrystallization (Fig. S5). In some places, the bands localize isolated slip surfaces, often occupied by minerals such as biotite and various oxides. The matrix domains also show recrystallization microstructures, but they have grain sizes that are markedly greater than those observed in the shear bands. The recrystallized grains locally develop grain elongation in some areas, although they do not form any strong S fabrics. The microstructural characteristics of sheared quartzite are further detailed in Sect. S2.

2.3 Shear zones in the CGGC and their internal structures

Field investigations conducted in Bero Hills have revealed sub-vertical shear zones in granite gneiss at varied scales, with thicknesses ranging from a few centimetres to more than a metre and lengths extending up to tens of metres. Their internal structures consist of a combination of spaced C bands and penetrative foliations (called S foliations, analogous to S fabrics in mylonites, as described earlier), consistently forming angular relationships with one another (Fig. 3). Individual C bands show varying thicknesses (2.7 mm to 5.1 cm), and the inter-band spacing also varies over a wide range (9 cm to 1.8 m). The bands are typically characterized by grain-size reduction, which can be detected macroscopically in the field. In some places, they contain undeformed elongated pods of the host rock as remnant masses, with their long axes oriented along the bulk shear plane. The shear zones have extensively developed penetrative foliations that are oriented at angles to the shear zone boundary, often forming an anastomosing network with the C bands. This distributed S foliation forms the lowest angles with C bands close to the band structure, which increases away from the shear band. The average angle of foliation in the principal shear direction at this location varies from 15 to 30°. Some domains within a shear zone remain virtually undeformed, as reflected in the absence of C bands and distributed foliations. Microstructural studies of shear zone rocks show extreme recrystallization-assisted grain-size reduction and secondary mineralization preferentially along shear-parallel slip surfaces in the band domains. The inter-band regions, on the other hand, consist of much larger recrystallized quartz grains, forming well-developed shape fabrics (S) at angles relative to the shear direction (see Sects. S2 and S3 for further details). Shear band domains often contain large porphyroclasts with strong asymmetric drag structures, consistent with the overall shear sense (Fig. S7e). All these microstructural signatures indicate that the shear zones evolved through the localization of high-strain zones (domains of grain refinement with slip surfaces) in a viscous-deformation regime (discussed further in Sect. S2). We evaluated the area of macroscopic S-foliation development, calculated as the ratio between the domain consisting of homogeneous S foliation and the total area of the shear zone, as a measure of distributed deformations in the shear zones. The calculated values range from 0.22 to 0.83, implying that the shear accommodation mechanisms involving distributed strain accumulation vary spatially in viscous shear zones.

Figure 3 Outcrop-scale viscous shear zones containing penetrative S foliations in close association with widely spaced C bands (Bero Hills region of the CGGC). (a–c) Sigmoidal patterns of S foliations in the domains between C bands in the shear zone. In some places, fluid-assisted quartzo-feldspathic materials occur locally in C bands. The overall foliation trends occur persistently at an angle of 20° in the C-band direction. WR: wall rock. SZ: shear zone.

Most of the shear zones in the Anandanagar area are hosted in porphyritic granite gneisses (Fig. 4a–d), with lengths ranging from a few centimetres to more than 100 m and thicknesses varying from a fraction of a centimetre to tens of centimetres. Some of these zones are hosted in quartzo-feldspathic pegmatites. Their internal structures are dominated by distributed S foliations, showing few or no macroscopic shear-parallel bands. Under the microscope, these rocks are found to contain a persistent shape fabric, defined by the preferred orientations of the constituting mineral grains at an angle relative to the shear direction (Sect. S2; Fig. S8). The microscale shape fabrics correspond to the macroscopic S foliation observed in the field. The major constituting minerals, quartz and feldspar, have undergone extensive recrystallization, implying a dominant role of crystal plastic mechanisms in shear deformations (discussed further in Sects. S2 and S3). The shear zones are generally devoid of any drag zone at their interface with the host rocks, barring a few locations where they show foliation drag and offset across-shear-zone minor veins. The shear zones in pegmatites show obliquely orientated penetrative S foliations at varying angles to their boundaries (15 to 35°). Assuming simple shear kinematics, the S angles yield a finite shear strain of 1.6 in these shear zones. Shear zones in porphyritic granite similarly show obliquely oriented S foliations (Fig. 4d), leaving some protoliths of undeformed host rock within them. To summarize, shear zones in Anandanagar have accommodated shear predominantly through distributed strain (i.e. S foliation development), with minimal C-band-assisted deformation partitioning.

Figure 4 Field examples of S-dominated viscous shear zones from the Anandanagar region of the CGGC terrain. (a–d) Shear zones accommodating shear entirely through distributed strain accumulation, forming S foliations. Note the complete absence of shear bands within them. Insets show the histogram plots of S-foliation orientation (θ) with respect to the shear direction. WR: wall rock. SZ: shear zone.

2.4 A synthesis of the field observations

The relative development of distributed S foliation and localized C bands in the shear zones of our study areas (the SSZ and CGGC), as described in the preceding section, suggests two extreme shear accommodation mechanisms (summarized in Sect. S4). In the SSZ, these mechanisms accommodate a large amount of shear along localized C bands, leaving the inter-band regions as domains of relatively weak S-foliation development. In contrast, shear zones in the Anandanagar area are dominated by distributed viscous deformation, with little or no macroscale shear band formation. Some shear zones in the CGGC have evolved in a hybrid mode, where the two mechanisms – distributed viscous strain and localized C-band formation – operate equally. Based on the field data, we constructed a field diagram of shear zones with varying C versus S dominance using normalized C spacing and the areal percentage of S-foliation domains. C-dominated shear zones lie in the lower region of the field diagram, while S-dominated shear zones (characterized by a large areal percentage of S foliation) occupy the extreme-right regime of the field diagram. The shear zone field data cluster to form distinct regions in the diagram (Fig. 5).

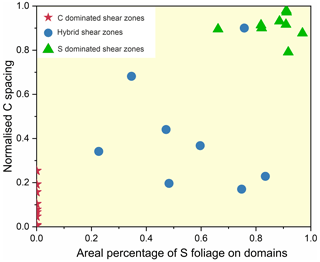
Figure 5 Graphical plots of C-band spacing versus the areal fraction of S-foliation domains. The plots delineate three distinct fields for S-dominated, C-dominated, and hybrid shear zones. The data are collected from shear zones in the CGGC and the SSZ. The C-band spacing is normalized to the shear zone thickness.

3 Numerical modelling

3.1 Basic premises

Several earlier authors have used mechanical models based on viscoplastic rheology, where viscous properties are coupled with a yield criterion and post-yield weakening mechanisms to establish the rheological framework (Regenauer-Lieb and Yuen, 2003; Mancktelow, 2006; Moresi et al., 2007a). We adopt a similar rheological approach to constrain the macroscopic-scale shear accommodation mechanisms in the shear zones described in the preceding section. Microstructural characteristics (details provided in Sects. S2 and S3) suggest that shear zone deformations have occurred predominantly through crystal plastic creep, resulting in grain-size reduction by means of dynamic recrystallization. This microstructural evidence supports our consideration of viscous rheology for shear zone modelling. Furthermore, the structural features described in the previous section reveal that shear deformations also have localized high-strain zones in the form of shear bands, which show extreme grain refinement through recrystallization, implying an abrupt increase in shear rates locally within the shear zone. These features are often associated with band-parallel isolated slip surfaces at the microscale. All these grain-scale features indicate that shear zones have undergone differential mechanical weakening, which we implement by combining a pressure-dependent yield criterion with viscous rheology. Within this rheological framework, the shear zones are modelled as narrow zones of viscous–plastic materials undergoing Stokes flow, applicable for incompressible, slow, and non-inertial viscous fluid flows (Gerya and Yuen, 2007; Jacquey and Cacace, 2020; Ranalli, 1997). The shear zone materials are assumed to yield plastically at threshold stresses. The model shear zones are approximated to crustal rheological regimes, setting their geometrical characteristics (e.g. length-to-thickness ratios) and kinematic conditions as applicable to the corresponding natural prototypes.

3.2 Mathematical formulation

In our shear zone modelling, the mathematical formulation considers a two-layer system that embodies naturally formed shear zones, where a mechanically weak zone is hosted within relatively stronger surrounding rock (the rock wall) (Mancktelow, 2006; Pennacchioni and Mancktelow, 2018; Cawood and Platt, 2021). This modelling approach is effective for developing numerical, time-evolving, and dynamically consistent shear zone models in 2D Cartesian domains within the theoretical framework of computational fluid dynamics (CFD). The CFD simulations, in this instance, assume an incompressible Boussinesq fluid flow, approximating the long-timescale (million-year) kinematic state of the Earth's lithospheric deformations. We employ the following continuity and momentum conservation equations in the CFD modelling:

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\nabla }.u_i=\mathrm{0},\text{(2)}& {\displaystyle }-\mathrm{\nabla }P+\mathrm{\nabla }\cdot {\mathit{\tau }}_{ij}+\mathit{\rho }{g}_i=\mathrm{0},\end{array}$$

where u denotes velocity, $P=\mathrm{0.5}({\mathit{\sigma }}_{xx}+{\mathit{\sigma }}_{yy})$ represents pressure, τ is the deviatoric stress tensor, and g denotes gravitational acceleration. In Eq. (2), the inertial forces are neglected, as applicable to long-term flows in the Earth's interior. The deviatoric stress tensor (τ_ij) is derived by subtracting the isotropic part from the total stress tensor (σ_ij). Assuming incompressible viscoplastic rheology, the deviatoric stress tensor (τ_ij) can be equated with the strain rate tensor as follows:

$$\begin{array}{}\text{(3)}& {\mathit{\tau }}_{ij}=\mathrm{2}{\mathit{\eta }}_{\text{eff}}{\dot{\mathit{\epsilon }}}_{ij}={\mathit{\eta }}_{\text{eff}}\left({\displaystyle \frac{\partial u_i}{\partial x_j}}+{\displaystyle \frac{\partial u_j}{\partial x_i}}\right),\end{array}$$

where ${\dot{\mathit{\epsilon }}}_{ij}$ is the strain rate tensor and η_eff is the effective viscosity, which includes the viscosities η_v (viscous creep) and η_p (plastic creep) in their reciprocal form (Sandiford and Moresi, 2019), given as

$$\begin{array}{}\text{(4)}& {\mathit{\eta }}_{\text{eff}}={\left({\displaystyle \frac{\mathrm{1}}{{\mathit{\eta }}_{\mathrm{v}}}}+{\displaystyle \frac{\mathrm{1}}{{\mathit{\eta }}_{\mathrm{p}}}}\right)}^{-\mathrm{1}}.\end{array}$$

The shear zone modelling is implemented in an incompressible viscoplastic rheological framework (Ranalli, 1995), conventionally represented by a series-connected frictional block–dashpot mechanical model. This consideration allows us to resolve the deviatoric-strain rate into two parts: viscous (${\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{v}}$) and plastic (${\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{p}}$), with the latter given in the form of

$$\begin{array}{}\text{(5)}& {\dot{\mathit{\epsilon }}}_{ij}={\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{v}}+{\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{p}},\end{array}$$

where

$$\begin{array}{}\text{(6)}& {\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{v}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\tau }}_{ij}}{{\mathit{\eta }}_{\mathrm{v}}}}\text{and}{\dot{\mathit{\epsilon }}}_{ij}^{\mathrm{p}}=\left\{\begin{array}{l}\mathrm{0}\text{if }{J}_{\mathrm{2}}<{\mathit{\sigma }}_{\mathrm{yield}}\\ \mathit{\chi }\frac{{\mathit{\tau }}_{ij}}{\mathrm{2}{J}_{\mathrm{2}}}\text{if }{J}_{\mathrm{2}}\ge {\mathit{\sigma }}_{\mathrm{yield}}.\end{array}\right.\end{array}$$

J₂ $=\mathrm{3}({\mathit{\sigma }}_{jj}{)}^{\mathrm{2}}-\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\sigma }}_{ij}{\mathit{\sigma }}_{ij}$ represents the second stress invariant, which determines the plastic creep at the yield point, and χ is a plastic multiplier.

Natural shear zones accommodate shear mostly via large, long-term permanent strains. Thus, the elastic (reversible) strain component is negligibly small (${\dot{\mathit{\epsilon }}}_{ij}^e\to \mathrm{0}$) compared to the permanent viscous and plastic strains. Therefore, we ignore its effects on the shear zone models. Post-yield viscous weakening of the material, where the modified viscosity decreases non-linearly with increasing plastic strain, is introduced to incorporate strain-softening rheology into the shear zone models. Plastic yielding is implemented by locally rescaling the effective viscosity in such a way that the stress does not exceed the yield stress, also known as the viscosity-rescaling method (Willett, 1992; Kachanov, 2004; Glerum et al., 2018). The effective viscosity is then given by

$$\begin{array}{}\text{(7)}& {\mathit{\eta }}_{\text{eff}}={\displaystyle \frac{{\mathit{\tau }}_{ij}}{\mathrm{2}\left|\dot{\mathit{\epsilon }}\right|}},\end{array}$$

where $\dot{\mathit{\epsilon }}$ represents the second invariant of ${\dot{\mathit{\epsilon }}}_{ij}$. Moreover, η_eff signifies the reduced viscosity once the yield limit is attained. It should be noted that the non-linearity introduced by the post-yield plastic rheology is solved iteratively using Eq. (7). This equation provides the necessary conditions for introducing weakening into the shear zones with parametrically imposed strain-rate-weakening laws, as implemented in many earlier viscoplastic models (Mancktelow, 2006; Glerum et al., 2018; Roy et al., 2021). In such yield-controlled rheology, the effective viscosity decreases non-linearly with increasing finite strain (Fig. S10). To model shear zones formed at middle–lower crustal depths (Duretz et al., 2014; Gueydan et al., 2014; Reber et al., 2015), as applicable to our field studies, we have considered a linear relation between yield stress (σ_yield) and pressure ($P=-\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\sigma }}_{jj}$) and have modelled the yield behaviour by employing a pressure-dependent plasticity (Drucker–Prager) criterion (Roy et al., 2021; Rast and Ruh, 2021). Based on this criterion, a yield function, F, can be defined in the following form:

$$\begin{array}{}\text{(8)}& F={\mathit{\sigma }}_{\mathrm{yield}}-\sqrt{\mathrm{3}}\sin \left(\mathit{\varphi }\right)P-\sqrt{\mathrm{3}}C\left({\mathit{\gamma }}_{\text{pl}}\right)\cos \left(\mathit{\varphi }\right),\end{array}$$

where C(γ_pl) is the material cohesion, expressed as a function of plastic strain (γ_pl), and ϕ is the angle of internal friction. The cohesion is assumed to weaken with increasing accumulated plastic strain as follows:

$$\begin{array}{}\text{(9)}& C=C_{\mathrm{i}}+(C_{\mathrm{f}}-C_{\mathrm{i}})min\left(\mathrm{1},{\displaystyle \frac{{\mathit{\gamma }}_{\text{pl}}}{{\mathit{\gamma }}_o}}\right),\end{array}$$

where C_i is the initial cohesion and C_f is the final cohesion of the shear zone material. Moreover, ${\mathit{\gamma }}_{\text{pl}}={\int }_{\mathrm{0}}^t{\dot{\mathit{\epsilon }}}_{\mathrm{p}}\mathrm{d}t$ indicates accumulated plastic strain in regions where the yield limit is reached, and γ_o=0.1 is taken as the reference strain. No syn-deformational healing of cohesion is implemented in the present models.

3.3 Model setup

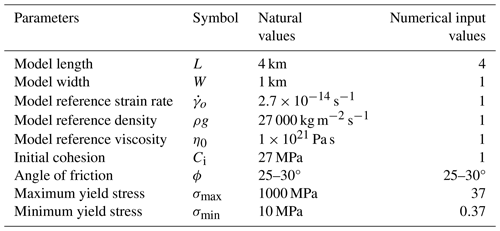
Based on the mathematical formulation described in the preceding section, we developed 2D shear zone models using the open-source code Underworld2 (http://www.underworldcode.org/, last access: 22 October 2024) to solve the mass and momentum conservation equations (Eqs. 1 and 2) under incompressible conditions, allowing us to obtain the pressure and velocity conditions within the shear zone domain. This code works within a continuum mechanics approximation and has been extensively used to deal with a range of geological and geophysical problems (Beall et al., 2019; Mansour et al., 2020; Roy et al., 2024). As explained in Moresi et al. (2007b) and Mansour et al. (2020), the code discretizes the geometrical domain into a standard Eulerian finite-element mesh, and the domain is coupled with the particle-in-cell approach (, ). To implement the particle-in-cell approach, the code discretizes the material domain into sets of Lagrangian material points, which allow us to find material properties that are history-dependent (in the present case, the plastic history of the material) and can be tracked over the entire simulation run. Physical properties of the shear zone materials, such as density and viscosity, are mapped using particle indexing. Our modelling excludes the effects of temperature diffusion and any inertia in the system. The shear zone models were developed in a 4L×L rectangular domain, where L represents the reference length scale. The model domain, occupied by incompressible viscoplastic materials, is discretized into a quadrilateral mesh comprising 584×324 elements. We considered a three-layer model architecture (Roy et al., 2022) to simulate viscous shear zones, consisting of an intensely sheared core flanked by drag zones on either side, hosted in unsheared rocks that structurally resemble those observed in the field (Figs. 2–4). The procedure for modelling the three-layer structure is discussed in detail in Sect. S6. We imposed the following velocity boundary conditions on the shear zone models: the side boundaries were subjected to a periodic boundary condition (Fig. 6), whereas the bottom and top boundaries were assigned a prescribed velocity in the horizontal direction, keeping the overall strain rate constant throughout the simulation. The boundary velocities produced a dextral simple shear movement, with the maximum tensile stress (σ₁) axis oriented at an angle of 45° in the bulk shear direction. Our model simulations were run by varying three major parameters: (1) initial viscosity (η_v), (2) initial cohesion (C_i), and (3) bulk shear rates (${\dot{\mathit{\gamma }}}_{\mathrm{b}}$) in the system, with the first two characterizing the rheology and the third representing the bulk kinematics of a shear zone. We varied η_v between 1η_o and 100η_o and, similarly, ${\dot{\mathit{\gamma }}}_{\mathrm{b}}$ between $\mathrm{1}{\dot{\mathit{\gamma }}}_o$ and $\mathrm{100}{\dot{\mathit{\gamma }}}_o$, where η_o and ${\dot{\mathit{\gamma }}}_o$ are the background viscosity and shear rate, respectively. All material parameters used in the simulations are summarized in Table 1.

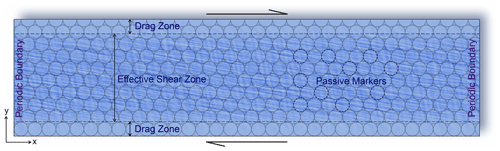
Figure 6 A representative initial shear zone model used for numerical-simulation experiments run with a viscoplastic rheological approximation. The model consists of a three-layer mechanical structure comprising a core flanked by drag zones, hosted between two undeformable boundaries, as commonly observed in geological settings. The model domain is imprinted with initially circular passive markers to determine the finite-strain distributions across the shear zone. Further details regarding the model boundary conditions are provided in the text.

Table 1 Numerical-model parameters and their values.

3.4 Model shear zone characteristics

The simulations presented in this study primarily aim to constrain the rheological and kinematic conditions determining the shear accommodation mechanisms that lead to the development of C, S, and S–C structures of crustal shear zones described in our field observations (Figs. 2–4). This section presents three sets of simulations to demonstrate the distinctive modes of strain evolution in model shear zones, designated as reference models (RMs).

In the first set of simulations for reference model 1 (RM1), run with values of η_v=1η₀, ${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{0.5}{\dot{\mathit{\gamma }}}_{\mathrm{0}}$, and C_i=2C₀, model shear zones accommodate the applied shear entirely through uniformly distributed continuous viscous deformations (Video S1), as revealed by the deformed elliptical shapes of initially circular passive markers in the model (Fig. 7a(ii)). The homogeneous strain continues to increase with progressive shear but does not show any tendency to localize discernible shear bands throughout the simulation run-time (Fig. 7a(iv)). Increasing finite bulk shear (γ_b) results in the flattening of passive ellipses, with decreasing inclinations of their major axes in the bulk shear direction, in agreement with the strain ellipses from the homogeneous simple shear equation (Fig. 8); this relationship is described as follows:

$$\begin{array}{}\text{(10)}& \tan \mathrm{2}\mathit{\theta }={\displaystyle \frac{\mathrm{2}}{{\mathit{\gamma }}_{\mathrm{b}}}}.\end{array}$$

This finding suggests that this type of model shear zone accommodates bulk shear entirely through homogeneous viscous strain, allowing no strain localization associated with pressure-dependent yield. This primarily occurs as the flow stress condition always lies below the yield point, which is evident from the clear absence of shear bands (Fig. 7a(iv)). The RM1 simulations consistently fail to produce shear band structures at any stage of the shear zone evolution. Consequently, distributed deformation emerges as the principal mechanism for accommodating shear.

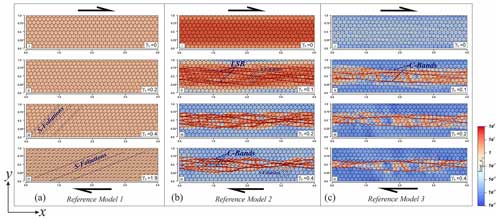
Figure 7 Evolution of the shear zones in the three reference models under dextral shear: (a) reference model 1 (η_v=η₀, ${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{0.5}{\dot{\mathit{\gamma }}}_o$, and C_i=2C₀), (b) reference model 2 (η_v=50η₀, ${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{10}{\dot{\mathit{\gamma }}}_o$, and C_i=1C₀), and (c) reference model 3 (η_v=100η₀ (where η₀ represents background viscosity), ${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{3}{\dot{\mathit{\gamma }}}_o$ (where ${\dot{\mathit{\gamma }}}_o$ represents the shear rate), and C_i=1C₀). The colour bar represents the logarithmic magnitude of the strain rate invariant. Note the transition of the shear accommodation mechanism from distributed strain accumulation to spaced shear band localization, as observed from RM1 to RM3. RM2 produces low-angle shear bands (LSBs) in the initial stage of shear deformation (γ_b<0.2), which are subsequently replaced by shear-parallel C bands with progressive shearing movement.

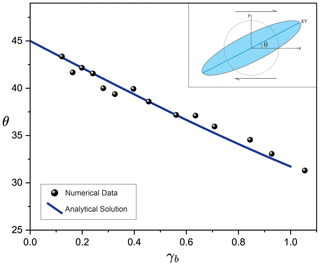
Figure 8 Inclination (θ) of the major axis of the finite-strain ellipse (shown in the inset) as a function of the finite shear (γ_b), obtained from RM1 numerical simulations (black dots). Passive circular markers were placed in the model domain to obtain the strain ellipses. It is noteworthy that the numerical data regression agrees well with the analytical solution (solid blue line; Eq. 10), implying that the model shear zone has accommodated shear through distributed strain accumulation.

The simulations for reference model 2 (RM2) were run at high bulk shear rates (${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{10}{\dot{\mathit{\gamma }}}_o$) and with high viscosity (η_v=50η_o) while maintaining C_i=1C₀. When γ_b=0.09, the RM2 simulation run developed finely spaced low-angle (θ≈13°) shear bands and a few sporadic high-angle (θ≈85°) shear bands (Video S2). The densely packed low-angle bands impart a low-angle foliation in the shear zone (Fig.7b(ii)). An increase in γ_b gives rise to penetrative distributed viscous strains, as revealed by the elliptical shapes of the initially circular passive markers in the model, and the distributed strain accumulates steadily (Fig. 7b(ii)) until γ_b reaches a threshold value (0.15), at which point the band structure undergoes a drastic transformation involving the appearance of shear-parallel C bands when γ_b>0.15 (Fig. 7b(iii)). The shear zone ultimately accommodates shear through a set of sub-parallel, widely spaced (${\mathit{\lambda }}^{*}=$ ∼ 0.263) C surfaces, forming a weak network, albeit doing so locally with the earlier-formed low-angle bands (Fig. 7b(iv)). P bands localize sporadically, with a tendency to network with the principal C bands. During the post-yield period, C-band-assisted shearing becomes the dominant shear accommodation mechanism, manifested in the disruption of the deformed passive markers (Fig. 7b(iv)). The model shear zones thus accommodate the bulk shear initially via uniformly distributed viscous strain, switching to localized C-band-assisted shear accommodation.

The simulation for reference model 3 (RM3) is assigned an extremely high initial viscosity (η_v=100η_o) and a moderate bulk shear rate (${\dot{\mathit{\gamma }}}_{\mathrm{b}}=\mathrm{3}{\dot{\mathit{\gamma }}}_o$), producing a band growth pattern remarkably different from that observed in the RM2 simulations (Video S3). When γ_b=0.08, the model first develops a set of low-angle shear bands at an angle of ∼ 15° in the shear direction, characterized by a narrow, long, and closely spaced (λ≈0.006) geometry, along with sporadically occurring thick, high-angle shear bands (λ≈0.19). With progressively increasing bulk shear (γ_b>0.1), shear band formation becomes the primary shear accommodation mechanism, leading to a complete structural transformation into thick, widely spaced (${\mathit{\lambda }}^{*}\approx \mathrm{0.26}$) shear-parallel C bands, with virtually no traces of low-angle shear bands (Fig. 7c(ii)). The RM3 simulations show shear-zone evolution with minimal or no distributed viscous deformations, as indicated by the undeformed shapes of the initially circular markers in the model (Fig. 7c(iii)). The post-yielding slip in the C bands results in intense local deformations along the trace of these bands (Fig. 7c(iv)). However, the low-angle shear bands that formed at low finite bulk shear (γ_b<0.1) had little effect on the deformation of passive markers, implying that their slip was negligible.

3.5 C-band localization versus distributed deformations: rheological constraints

Our simulation results reveal a functional relationship between the two distinct, competing shear accommodation mechanisms (distributed strain and localized shearing), the bulk shear rate (${\dot{\mathit{\gamma }}}_{\mathrm{b}}$), and the initial viscosity (η_v) of the shear zones. The plotted data illustrate this relationship in a log-scale representation of the ${\dot{\mathit{\gamma }}}^{*}$(=$\frac{{\dot{\mathit{\gamma }}}_{\mathrm{b}}}{{\dot{\mathit{\gamma }}}_{\mathrm{0}}}$) vs. η^*(=$\frac{{\mathit{\eta }}_{\mathrm{v}}}{{\mathit{\eta }}_{\mathrm{0}}}$) space for a given value of C_i=1C₀, where ${\dot{\mathit{\gamma }}}_{\mathrm{0}}$ and η₀ are the background shear rate and viscosity, respectively, representing the regional shear rate and wall rock viscosity (see Fig. 9). The field diagram indicates that low ${\dot{\mathit{\gamma }}}_{\mathrm{b}}$ and η_v values facilitate distributed strain accumulation throughout all the shear zones. However, this mechanism is completely replaced by shear localization in the form of C bands with increasing η_v. The field diagram also shows that increasing ${\dot{\mathit{\gamma }}}_{\mathrm{b}}$ initially results in homogeneous-strain-assisted shear accommodation, but once the yield point is surpassed, it switches to the C-band mechanism. It is noteworthy that the individual fields for each of these strain accumulation processes can change depending on the involvement of more complex grain-scale processes in shear deformations.

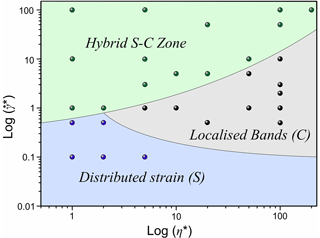
Figure 9 Field diagram of the three shear accommodation mechanisms in a space defined by the log-scale representation of γ^* ($\frac{{\dot{\mathit{\gamma }}}_{\mathrm{b}}}{{\dot{\mathit{\gamma }}}_{\mathrm{0}}}$) and η^* ($\frac{{\mathit{\eta }}_{\mathrm{v}}}{{\mathit{\eta }}_{\mathrm{0}}}$), constructed based on numerical simulations, where C_i=1C₀. Moreover, ${\dot{\mathit{\gamma }}}_{\mathrm{0}}$ and η₀ represent the background shear rate and viscosity in the regional setting. It is noteworthy that increasing the initial viscosity of crustal-shear-zone materials facilitates the C-band-assisted shear accommodation mechanism.

4 Discussion

4.1 Shear accommodation mechanisms and their crustal conditions

Field observations presented in Sect. 2 reveal contrasting structural characteristics in crustal shear zones within the SSZ and CGGC. For example, sheared rocks in the Anandanagar shear zones contain S foliations oblique to the shear zone boundaries, with minimal or no macroscopic C bands, whereas those in Patharghara and Musabani extensively display shear-parallel C bands but no macroscopic S foliations. On the other hand, shear zones in Bero Hills contain both of these structural features (summarized in Sect. S4). Modelling of viscous shear zones in the framework of incompressible viscous rheology, using a pressure-sensitive yield criterion, suggests that these varying internal structural characteristics originate from their contrasting shear accommodation mechanisms. S-dominated shear zones accommodate their bulk shear through spatially distributed viscous deformations across the entire shear zone, whereas those dominated by C bands accommodate shear through strain localization, forming spaced shear bands.

These two end-member mechanisms of crustal shear zones are also manifested in their internal structural architectures. Shear zones are architecturally more homogeneous, showing uniformly developed S foliation in the case of the first mechanism and geometrical continuity of across-shear-zone passive markers, e.g. quartz veins. In contrast, the second mechanism results in heterogeneous structural architectures, characterized by a close association of localized zones of intense shearing, resulting in grain refinement and fluid-assisted mineralization in these zones, while leaving adjoining regions relatively undeformed. Earlier authors (Mancktelow, 2006; Meyer et al., 2017) have shown that a transition from a distributed shear accommodation mechanism to its localizing counterpart can be explained by a drop in fluid pressure within the shear zones (pressure-dependent yield), along with an enhancement of viscous mechanisms caused by the additional effects of fluid-assisted mineralogical changes and grain-size reduction due to recrystallization. The microstructural analyses of shear zone rocks from our field area reveal that these rocks are characterized by dynamic recrystallization and grain refinement. There is also evidence of fluid migration and mineralization along local slip surfaces, which probably further enhances the weakening process to localize strain across these zones. Such softening processes can be equated with the strain-rate-dependent weakening factor implemented in our numerical models.

The numerical simulations indicate that the type of internal strain accommodation mechanism is sensitive to the bulk strain rate in the tectonic setting. Crustal deformations at low strain rates favour the development of internally homogeneous viscous shear zones via the first mechanism (Fig. 7a), as observed in a region within the CGGC terrain that records regional deformations. Such internally homogeneous shear zones have also been extensively reported from different geological terrains (e.g. Ramsay et al., 1983; Fossen and Cavalcante, 2017; Pennacchioni and Mancktelow, 2018). On the other hand, high-strain-rate kinematic conditions, which generally occur in specific crustal regimes, e.g. terrain boundaries and accretionary wedges in subduction zones, can give rise to internally heterogeneous shear zones, characterized by strong strain partitioning in numerical simulations (Fig. 7c). Our model interpretations are consistent with field observations from the Singhbhum shear zone (SSZ), obtained along the boundary between the Proterozoic NSMB and the Archean Singhbhum Craton, where strain rates are expected to be high (Ghosh and Sengupta, 1987). Several workers have provided evidence of slip and vein emplacement along shear surfaces in viscous shear zones from subduction margins (e.g. Platt et al., 2018; Ujiie et al., 2018; Tulley et al., 2022). These surfaces often contain undeformed lenses formed by the networking of anastomosing shear band structures (Carreras et al., 2010). These heterogeneities are generally attributed to fluid-mediated mineralogical transformations along subducting plates or inherent lithological heterogeneities within the plate boundaries. Based on our numerical simulations, we propose that shear zones in initially mechanically homogeneous systems under conditions of high strain rates can evolve to become structurally heterogeneous due to the domination of shear accommodation mechanisms induced by localized shearing, followed by various syn-shearing transformations, e.g. fluid-assisted mineral transformations.

Relative viscosity (η^*) and initial cohesion (C_i) of shear zone rocks also play a pivotal role in determining the internal architectural characteristics of our model shear zones. Low η^* values, as observed in high-temperature environments at deep-crustal levels, favour the homogeneous structural characteristics of our model shear zones (Fig. 7a), which become extremely heterogeneous as η^* increases to threshold values (${\mathit{\eta }}^{*}=\mathrm{2}$). In contrast, reducing cohesion, which may be assisted by syn-shearing microscale fracturing and fluid migration (Wu and Lavier, 2016; Menegon et al., 2021), can facilitate shear band formation, resulting in heterogeneous structures within the shear zones (Fig. 7b).

4.2 Mylonite characteristics: indicator of shear accommodation mechanisms

Mylonites are typical rocks representative of viscous shear zones, produced by intense shearing and grain-size reduction, accompanying the formation of characteristic structural fabrics. Among these, C and S are the most common planar fabrics in mylonites, as discussed in Sect. 1. However, field observations show wide variations in the relative development of these two structural manifestations at the macroscopic scale, ranging from S foliations to C-band-dominated structures in shear zones. This type of macroscopic variation can be compared with those corresponding to mylonites based on microscale fabrics, which are classified as type I (mylonites containing S and C fabrics) and type II (mylonites containing C fabrics) (Lister and Snoke, 1984). Although a broad spectrum of type-I and type-II S–C mylonites have been reported from natural viscous shear zones (Gates and Glover III, 1989; Mukhopadhyay and Deb, 1995; Cacciari et al., 2024), their origin deserves discussion, especially in the context of shear localization mechanics. When correlating the shear zone fabrics with the model strain fields, it appears that shear deformation preferentially localizes at significantly higher strain rates in narrow, discrete, shear-parallel planar zones, resulting in intense grain refinement through dynamic recrystallization, to form C fabrics. This process can similarly occur at the macroscopic scale to produce C bands, as obtained from our numerical models (Fig. 7c). On the other hand, distributed viscous strain throughout the shear zone can flatten primary mineral grains to reorient them along x–y planes of the finite-strain ellipsoid, forming S fabrics at an angle relative to the shear direction. This fabric development synchronously participates in dynamic recrystallization to produce a fraction of smaller grains. These mechanisms can give rise to macroscopic S foliation in the distributed viscous domains if the shear zone rocks were initially coarse-grained or rich in platy minerals, such as muscovite, biotite, and chlorite, as observed in the CGGC (Fig. 4). Our simulation results reveal that shear zones growing in high-viscosity rocks localize densely packed shear surfaces (Fig. 9) with little or no distributed strain. This mechanical condition can thus produce shear-parallel foliation without penetrative fabrics, as observed in ideal type-II mylonites. Lowering the initial viscosity transforms the shear accommodation mechanism, facilitating the setting of distributed strain accumulation (Fig. 9), a favourable condition for the development of selective S fabrics, i.e. type-I mylonites. To summarize, the shear accommodation mechanism induced by shear band formation under the conditions of high viscosity and/or high shear rates (Fig. 9) favours C-dominated mylonites (type II), whereas that induced by the development of distributed strain under conditions of low viscosity and high strain rates (Fig. 9) facilitates type-I S–C mylonites in crustal shear zones. It should be noted that mylonitic-fabric developments, as discussed above, can be much more complex due to various grain-scale factors, such as crystallographic orientations; polymineralic assemblage; and grain-boundary processes, e.g. grain-boundary migration (Finch et al., 2020, 2022). The fabric growth in such cases generally tracks the local strain fields developed under the influence of microscale heterogeneities (Mukhopadhyay et al., 2023).

A prolonged debate, which is still lively, centres on the synchronous versus sequential development of S and C foliations in the evolution of shear zones. From field evidence, Berthé et al. (1979) showed the coexistence of S and C foliations at shear zone boundaries, with both exhibiting increasing spatial density towards the shear zone core. Their observation is in favour of synchronous foliation development. However, this interpretation is not universally accepted and is confronted with an alternative proposition, claiming that S foliations precede C localization. This structural sequence can occur when shear zones first accommodate shear via distributed strain, followed by localized yielding that produces C surfaces. Lister and Snoke (1984) elaborated on and categorized mylonites into three types based on the temporal relationship between S and C fabrics. They showed that, in some cases, both S and C foliations form synchronously in the same shear event, whereas in other settings, e.g. an older metamorphic complex, they grow in two successive events, where S foliations formed in the earlier event are overprinted by C localization during the later deformation event. Their study finds a third possibility for a complex structural sequence, in which transient flow patterns present during ongoing shearing cause C foliations to align in the shortening field, leading to their folding and the formation of a new set of S fabrics. Numerical simulations conducted by Finch et al. (2020) and analogue experiments conducted by Dell'angelo and Tullis (1989) on quartzites provide additional insights. At low strain levels, the dominant foliations are primarily S foliations, with C^′ shear bands forming preferentially in the core regions of the shear zones; however, there is no distinct slip in highly strained samples. Studies have also shown that there can be a considerable time gap between the formation of S fabrics and that of C bands (Bukovská et al., 2013, 2016). On the other hand, experiments conducted on quartz–feldspar aggregates produce weak S–C foliations, implying that monomineralic rocks, such as quartzite, may not readily form S–C foliations. Burlini and Bruhn (2005) suggested that distributed viscous strain and shear localization are two competing processes. According to them, a brittle event occurs prior to the onset of yielding; otherwise, the shear zone develops distributed strain throughout the entire sample. Based on our numerical-model results, we propose the development of distributed viscous strain and localized shearing as two end-member shear accommodation mechanisms, which can occur synchronously, although one may dominate over the other depending on the rheological conditions of the shear zones. Consequently, a shear zone can continue to accommodate viscous strain even after C-band formation (or vice versa in progressive shear).

4.3 Rheological controls and their tectonic implications

Earlier field and experimental investigations, as well as numerical simulations, have dealt with the problem of strain partitioning in polymineralic rocks and have demonstrated the distinctive roles of distributed viscous strain and localized strain in shear zones (Mancktelow, 2006; Katz et al., 2006; Burlini and Bruhn, 2005; Misra et al., 2009; Finch et al., 2020; Tokle et al., 2023). The present study takes into account the pivotal effects of bulk rheology and kinematics on strain partitioning and shows that the interplay of bulk viscosity, shear rate, and cohesion of materials within shear zones is the primary determining factor of shear zone processes. Depending on these characteristics, as discussed in the preceding section, shear zones may undergo shearing entirely through viscous strains, with little or no internal shear localization that could produce porosity bands (Katz et al., 2006), to enhance permeability in shear zones. In such situations, they would hardly act as pathways for fluid or melt migration. In contrast, the same shear zones can profusely produce shear bands under favourable conditions pertaining to the aforementioned factors, providing effective permeability for fluid migration, as often recorded in the form of shear-parallel veins and pegmatites (Creus et al., 2023; Koizumi et al., 2023). The role of crustal shear zones in deep-earth fluid transport processes, as shown by many authors (Cox, 2002; Fusseis et al., 2009; Spruzeniece and Piazolo, 2015; Précigout et al., 2017), thus depends primarily on the mode of shear zone evolution controlled by the accommodation mechanisms of distributed strain versus localized shear.

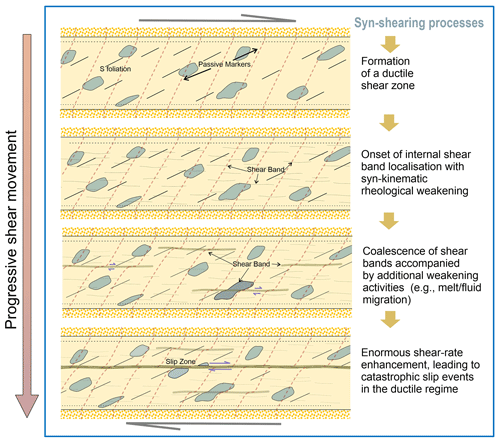
Figure 10 A visual representation illustrating various developmental phases of crustal-scale shear zones subjected to dextral shear motion. The gradual escalation of shear, coupled with diverse syn-kinematic strain-softening mechanisms, may culminate in catastrophic slip events within the viscous regime.

Several recent studies (Vissers et al., 2020; Allison and Dunham, 2021; Lavier et al., 2021; Mildon et al., 2022) have reported a number of phenomena, such as earthquake generation and frictional melting (pseudotachylites), from shear zones that indicate the occurrence of extremely high shear rates, which are difficult to explain with relatively slow shear kinematics. Evidently, there must be some weakening mechanisms in shear zone processes to amplify the shear rates by several orders, e.g. from 10⁻¹² to 10⁻³ s⁻¹ (Kelemen and Hirth, 2004). Understanding the process of such shear rate enhancement is critically important for interpreting many important deep-earth processes in viscous regimes, such as earthquakes within the subducting lithosphere, especially at depths ranging from 50 to 300 km. It is important to note that viscous mechanisms primarily govern deformation at high pressures and temperatures corresponding to such depths and thus cannot account for seismic-fault events (Platt et al., 2018; Gou et al., 2019). To address this problem, a range of explanations have been hypothesized for the mechanisms of intermediate-depth earthquakes, such as dehydration embrittlement and thermal runaway. Dehydration embrittlement, as proposed by Hacker et al. (2003) and Frohlich (2006), results from enhanced pore pressures caused by fluids released from metamorphic reactions. On the other hand, thermal runaway occurs due to the interplay between weakening triggered by various factors and temperature-dependent rock rheology (Kelemen and Hirth, 2007; Andersen et al., 2008; John et al., 2009; Braeck and Podladchikov, 2007; Thielmann and Kaus, 2012). Field evidence supporting thermal runaway includes the presence of pseudotachylites (e.g. Andersen et al., 2008); in fact, some evidence has been reported from viscous settings far below the brittle–viscous transition.

Our study provides an alternative explanation for strain localization and strain-induced slip within shear zones. Model results indicate that shear zones localize shear bands with significantly reduced effective viscosity. These strain-softening phenomena are generally attributed to factors such as grain-size reduction, mineral reactions, and the development of crystallographic-preferred orientation. The model shear bands locally enhance strain rates by an order of ∼ 2–3. The viscoplastic model employed in this study incorporates a pressure-dependent yield criterion, contributing to strain localization in zones of strain softening (Fig. 10). We ran a set of simulations by increasing the degree of strain softening in this criterion to test how much softening is required to attain higher-order strain rates. The simulation results suggest that exceptionally high shear rates can localize along shear bands in the viscous regime due to the effects of additional shear-softening processes, e.g. porosity-driven metamorphic fluids or melts. For example, theoretical calculations predict a dramatic reduction in effective viscosity by an order of ∼ 2–3 (Holtzman, 2016) with the addition of a small fraction (∼ 5 %) of melts or hydrothermal fluids. We thus propose that viscous shear zones can produce earthquakes (Fig. 10) if their evolution is modulated by shear-band-assisted strain rate enhancement during a yield event, accompanied by additional syn-shearing weakening factors (such as fluids and melts), to further enhance the strain rates. Under such high strain rates, the mechanical setting can undergo a viscous-to-brittle rheological transition, which triggers the sudden release of stored elastic-strain energy in the form of seismic waves (Schubnel et al., 2013; Prieto et al., 2017).

4.4 Model limitations

The rheological (viscoplastic) approach adopted in the present modelling explains the shear accommodation mechanisms in crustal shear zones at a macroscopic level. There is a limitation in this approach as it does not account for fabric developments under the influence of complex grain-scale phenomena, such as strain perturbations due to crystallographic or mineralogical heterogeneities. The numerical modelling also excludes the transient thermal effects of syn-shearing processes, such as shear heating. Such heating can play an additional role in facilitating mechanical weakening and the process of shear localization (Kelemen and Hirth, 2004). Considering that there are no large lithological variations in the present study area, the field diagram shows the modes of shear accommodation as a function of shear zone viscosity and strain rate with respect to constant initial cohesion (C_o). However, C_o can vary to a large extent in geological terrains due to various factors, such as lithology, and this variation can influence the field of each shear accommodation mechanism, as shown in the diagram (Fig. 9). In addition, the individual fields can vary depending on the rheological complexity, which is not explored in the present model. Despite these limitations, this study provides a first-hand insight into the mechanics of strain partitioning in crustal shear zones.

5 Conclusions

This study combined field observations and numerical simulations to show that shear-parallel strain localization and homogeneous viscous deformation act as two competing mechanisms of deformation accommodation in crustal shear zones. We can summarize the findings in the following points:

• Shear zones produce strongly varying internal structural characteristics, modulated by the two competing shear accommodation mechanisms. The mechanism of localized shear gives rise to shear-parallel band formation, whereas distributed strain accumulations result in the development of penetrative S foliation that tracks the x–y plane of the finite-strain ellipsoids.

• These two competing mechanisms are controlled by three factors: bulk strain rate, bulk viscosity, and initial cohesion. By increasing the bulk viscosity and strain rate, or reducing cohesive strength, the shear accommodation mechanisms shift from distributed strain accumulation to localized C-band formation.

• For a specific shear rate threshold (${\dot{\mathit{\gamma }}}^{*}=\mathrm{0.5}$) under given viscosity and cohesion conditions, viscous shear zones can produce both S foliations and C bands (e.g. S–C mylonites) through mechanisms of distributed strain accumulation and localized shear accommodation, respectively.

• The homogeneous versus heterogeneous internal architectural characteristics of shear zones hosted in initially homogeneous rocks depend largely on shear accommodation mechanisms. The mechanism of distributed strain accumulation gives rise to more uniform structural architectures in low-strain (${\dot{\mathit{\gamma }}}^{*}<\mathrm{0.5}$) crustal conditions, compared to the structural architectures produced by the mechanism of localized shear in high-strain (${\dot{\mathit{\gamma }}}^{*}>\mathrm{0.5}$) crustal environments.