On unifying carbonate rheology

We review the results from twenty four experimental works conducted on the rheology of carbonates from the last fifty years to revisit the long-noted discordance in the experimental results from a range of limestones and marbles. Such an exercise is needed to bring together the various datasets generated in the twenty three years since the last major review, as many of them observe relationships that run contrary to existing rheological models. By revisiting the large data set, we find that most low and high stress experimental measurements can be explained by the combined effect of grain size and the molar fraction of magnesium carbonate (XMgCO₃). Our results highlight that much of the calcite-dolomite series exists in a continuum of strength that changes with XMgCO₃. In contrast to previous findings, we establish that diffusion creep in calcite is sensitive to both grain size and magnesium content, showing that an increase in XMgCO₃ acts to weaken a rock. While in dislocation creep we confirm the observation that XMgCO₃ has a strengthening effect but extend it beyond synthetic Mg-calcite samples to natural starting materials. Most notably our results suggest that when the composition of a carbonate is factored in then grain size can be shown to have a weakening effect in high temperature creep for fine grained rocks. This is the opposite finding to the currently accepted flow law for high homologous temperature deformation of calcite rocks where a decrease in grain size strengthens a rock. We contextualise these new results by combining them with data from natural shear zones to show that carbonates are much weaker than would be expected from previous flow laws in a crustal section. Ultimately our review provides new pragmatic flow laws for carbonates in the calcite-dolomite series for diffusion and dislocation creep.

1 Introduction

During mountain building, marine sediments are incorporated into an orogeny and often become subsequently important tectonic horizons (e.g. Pfiffner, 1982; Burkhard, 1990; Bestmann et al., 2000; Herwegh and Pfiffner, 2005; Ebert et al., 2007; Nania et al., 2022). Many of these sediments are calcareous and they have a range of compositions, distributions of mineral phases and grain sizes inherited from their depositional environments. Importantly these chemical and micro-structural characteristics can change with time as the material experiences metamorphism and deformation (Ebert et al., 2007). Figure 1 shows this variety, both in composition, in this case equilibrated molar fraction of magnesium (XMgCO₃) and deformationally induced steady state grain size. Understanding the effect these changes have on rock rheology is of great importance for evaluating crustal deformation and is most readily established through laboratory deformation experiments.

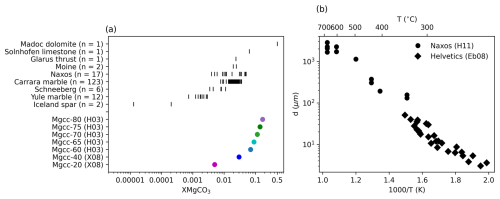
Figure 1 Compilation of measurements from natural and synthetic carbonates (see Tables 1 and 2 for references). Figure 1a shows the variation in the amount of magnesium, while Fig. 1b shows the how the steady state grain sizes of carbonate mylonites change with temperature. Abbreviations are H03: Herwegh et al. (2003), X08: Xu et al. (2008), Eb08: Ebert et al. (2008) and H11: Herwegh et al. (2011).

Over the years experiments on carbonates have explored the role of different lattice impurities (Herwegh et al., 2003; Freund et al., 2004; Xu et al., 2008; Davis et al., 2008; Holyoke et al., 2013), the distribution of minor secondary phases (Olgaard, 1978; Walker et al., 1990; Austin et al., 2014), the effect of incorporating proportions of a stronger phase (Bruhn et al., 1999; Rybacki et al., 2003; Renner et al., 2007; Delle Piane et al., 2009; Kushnir et al., 2015), water content (Rutter, 1972; Olgaard, 1978; de Bresser et al., 2005) and the role of other microstructural characteristics like grain-size (Schmid et al., 1977; Walker et al., 1990; Rutter, 1995; Pieri et al., 2001; Renner et al., 2002; Herwegh et al., 2003; Barnhoorn et al., 2004; Xu et al., 2008). All of these variables have been shown to have some effect on rock strength, which makes understanding the deformation behaviour of calcite rich rocks complex.

Here we revisit and review a range of data from deformation experiments preformed on several carbonates at high homologous temperatures with a focus on the role of grain size and magnesium content. Our motivation for doing so is that, since the last major review on calcite rheology (Renner and Evans, 2002), several new experiments have been conducted that further illuminated the role of these two important variables (e.g. Pieri et al., 2001; Herwegh et al., 2003; Barnhoorn et al., 2004; Xu et al., 2008). In particular we are interested in the fact that some of the more recent experiments may not conform to the constitutive relation that is currently used to unify dislocation creep in carbonates, the modified Peierls law (Renner et al., 2002; Renner and Evans, 2002). For example, Barnhoorn et al. (2004) found that during shear zone formation and grain size reduction through dynamic recrystallisation lead to material weakening and not strengthening as would be expected by the modified Peierls law. So far, these newer results and older data have not been compiled and comprehensively compared to one another. Making an up to date comparison is of particular interest for carbonates because of the long standing observation of a lack of conformity between the high stress rheologies of various calcite single crystals, limestones and marbles (cf. Renner et al., 2002; Renner and Evans, 2002).

In this contribution we collate data from a range of deformation experiments and make this needed comparison. Starting from a core set of deformation experiments that record both grain size and magnesium content, trends are revealed and then compared to a wide range of data spanning the whole magnesium carbonate series to ultimately provide a perspective and flow laws that unify observations from most carbonate deformation experiments to date.

2 Problems with the current model

A primary insight of Renner and Evans (2002) was that experiments gained strength with decreasing grain size (Fig. 2a). However that observation was made in the absence of chemistry. If experimental data which also had chemical characterisation reported are plotted to visualise the variation of magnesium (Fig. 2b), then a different trend emerges - material strength increases with increasing magnesium. This fits with the experimental observations of Xu et al. (2008) where synthetic carbonates in the dislocation creep field were shown to harden with the concentration of magnesium. Continuing to account for chemistry also reveals that high stress domains of experimental data associated with the dislocation creep field are in fact grain size weakening (Fig. 2c), and not hardening as predicted by the modified Peierls law used by both Renner et al. (2002) and Xu et al. (2008) to fit data. Lastly, it was noted by Holyoke et al. (2014) that comparisons of exponents and activation energies for calcite, dolomite and magnesite might reflect shared rate-controlling mechanisms in dislocation creep for calcite and magnesite and across all three materials in diffusion creep. All of these observations highlight that while both grain size and magnesium are clearly important for carbonate rheology, we have not fully understood their effects. The following methods, results and discussion attempt to better characterise the effect of grain size and magnesium across a range of nominally pure, magnesium bearing and second-phase rich carbonates.

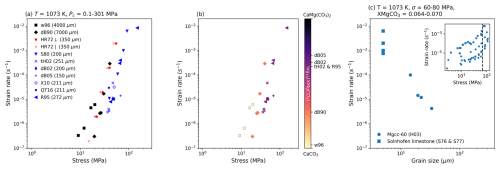
Figure 2 A starting point for evaluating carbonate rheology (see Table 3 for references and experiment abbreviations). (a) visualises the core observation for the current understanding of calcite rheology, rocks are stronger for smaller grain sizes (cf. Renner and Evans, 2002). Data is colour coded by material: black = Iceland spar; red = Yule marble; blue = Carrara marble. (b) shows an alternative trend where a rock strengthens with magnesium. (c) highlights a consequence of this observation, that grain size actually has a weakening effect if data are observed at a fixed magnesium content. The dashed line in the inset highlights the stress at which grain size is evaluated in the main plot of (c).

3 Methods

We revisit data from 24 publications that conducted carbonate deformation experiments as well as several studies that performed chemical and microstructural characterisations of naturally deformed carbonates. Data were collated from both reported values in tables and extracted from figures of publications (see supplemental material for a text file of all data). The rest of this section outlines how data were converted to the appropriate units for comparison.

Oden (1985)Schenk et al. (2005)Schenk et al. (2005)Covey-Crump and Rutter (1989)Walker et al. (1990)Renner et al. (2002)Xu et al. (2008)Herwegh et al. (2003)Wang et al. (1996)de Bresser and Spiers (1990)McGee (1999)Busenberg and Plummer (1983)Busenberg and Plummer (1989)Rutter (1995)Covey-Crump (1998)Pieri et al. (2001)Barnhoorn et al. (2005)Ter Heege et al. (2002)de Bresser (2002)de Bresser et al. (2005)Oesterling (2004)Barnhoorn et al. (2005)

Table 1 Reported and converted magnesium values of naturally deformed carbonates and experimental starting material.

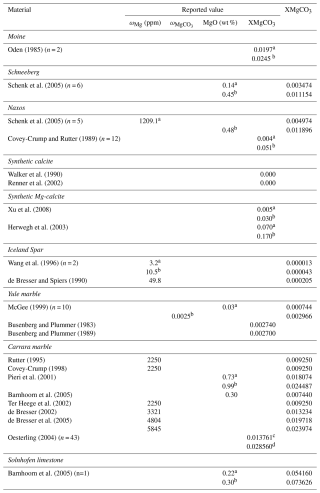
^a Minimum value, ^b maximum value, ^c minimum from range from Sample D2-W (2k-7), both inside and outside of shear zone, ^d maximum from range from Sample D2-W (2k-7), both inside and outside of shear zone.

Table 2 Naturally deformed carbonates from shear zones in the Helvetic Alps (Ebert et al., 2008) and Naxos (Herwegh et al., 2011).

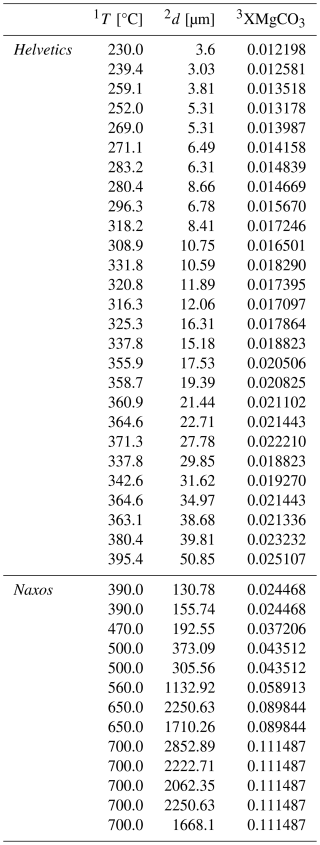
¹ T = deformation temperature, ² d = grain size, ³ XMgCO₃ = molar fraction of MgCO₃ converted from T.

Walker et al. (1990)Renner et al. (2002)Xu et al. (2008)Herwegh et al. (2003)Delle Piane et al. (2008)Davis et al. (2008)Wang et al. (1996)de Bresser and Spiers (1990)Heard and Raleigh (1972)Heard and Raleigh (1972)Schmid et al. (1980)Barnhoorn et al. (2004)Rutter (1995)Ter Heege et al. (2002)de Bresser (2002)de Bresser et al. (2005)Xu and Evans (2010)Quintanilla-Terminel and Evans (2016)Davis et al. (2008)Holyoke et al. (2013)Holyoke et al. (2014)Holyoke et al. (2014)Walker et al. (1990)Renner et al. (2007)Schmid (1976)Schmid et al. (1977)Schmid (1982)

Table 3 Experimentally deformed carbonates.

¹ Abb = experiment abbreviation, ² T = deformation temperature, ³ P_c = confining pressure, ⁴ $d/d_p$ = grain-size/second phase grain-size, ⁵ f_p = area/volume fraction of second phases, – not applicable/not reported, * value taken from Barnhoorn et al. (2005).

3.1 Converting reported Mg content into XMgCO₃

To compare data to one another we have chosen to convert all reported magnesium values to molar fractions of magnesium carbonate (XMgCO₃) in the following way. Firstly, if the carbonate data fall somewhere between pure calcite and dolomite, then the molecular weight of this Mg-carbonate (MW_Mgcc) can be defined as:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathrm{MW}}_{\mathrm{Mgcc}}& =\left(\left(\mathrm{1}-{\mathrm{XMgCO}}_{\mathrm{3}}\right)\cdot {\mathrm{MW}}_{{\mathrm{CaCO}}_{\mathrm{3}}}\right)\\ & +\left({\mathrm{XMgCO}}_{\mathrm{3}}\cdot {\mathrm{MW}}_{{\mathrm{MgCO}}_{\mathrm{3}}}\right)\end{array}\end{array}$$

If considering data reported as the mass fraction of magnesium (ω_Mg), it follows that:

$$\begin{array}{}\text{(2)}& {\mathit{\omega }}_{\mathrm{Mg}}={\displaystyle \frac{{\mathrm{MW}}_{\mathrm{Mg}}}{{\mathrm{MW}}_{\mathrm{Mgcc}}}}\cdot {\mathrm{XMgCO}}_{\mathrm{3}}\end{array}$$

Substituting in Eq. (1) gives:

$$\begin{array}{}\text{(3)}& {\mathit{\omega }}_{\mathrm{Mg}}={\displaystyle \frac{{\mathrm{MW}}_{\mathrm{Mg}}\cdot {\mathrm{XMgCO}}_{\mathrm{3}}}{\begin{array}{c}\left(\left(\mathrm{1}-{\mathrm{XMgCO}}_{\mathrm{3}}\right)\cdot {\mathrm{MW}}_{{\mathrm{CaCO}}_{\mathrm{3}}}\right)\\ +\left({\mathrm{XMgCO}}_{\mathrm{3}}\cdot {\mathrm{MW}}_{{\mathrm{MgCO}}_{\mathrm{3}}}\right)\end{array}}}\end{array}$$

Which can be rearranged to yield XMgCO₃:

$$\begin{array}{}\text{(4)}& {\mathrm{XMgCO}}_{\mathrm{3}}={\displaystyle \frac{{\mathrm{MW}}_{{\mathrm{CaCO}}_{\mathrm{3}}}}{{\mathrm{MW}}_{{\mathrm{CaCO}}_{\mathrm{3}}}-{\mathrm{MW}}_{{\mathrm{MgCO}}_{\mathrm{3}}}+\left(\frac{{\mathrm{MW}}_{\mathrm{Mg}}}{{\mathit{\omega }}_{\mathrm{Mg}}}\right)}}\end{array}$$

A python script is provided for converting data in the supplemental material.

3.2 Modelling XMgCO₃ from temperature data

The calcite-dolomite solvus as defined by Anovitz and Essene (1987) was used to convert between XMgCO₃ and temperature in datasets from natural carbonates. The relationship is only valid between 473 and 1173 K.

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathrm{0}& =T-A\left({\mathrm{XMgCO}}_{\mathrm{3}}\right)-B/{\left({\mathrm{XMgCO}}_{\mathrm{3}}\right)}^{\mathrm{2}}\\ & -C{\left({\mathrm{XMgCO}}_{\mathrm{3}}\right)}^{\mathrm{2}}-D{\left({\mathrm{XMgCO}}_{\mathrm{3}}\right)}^{\mathrm{0.5}}-E;\\ A& =-\mathrm{2360.0},B=-\mathrm{0.01345},C=\mathrm{2620.0},\\ D& =\mathrm{2608.0},E=\mathrm{334.0}\end{array}\end{array}$$

3.3 Converting mechanical data

When data from torsion experiments are compared to other data, the reported shear stress (τ) and shear strain rate ($\dot{\mathit{\gamma }}$) values are converted to equivalent stress (σ_eff) and equivalent strain rate (${\dot{\mathit{\epsilon }}}_{\mathrm{eff}}$) following the relationships outlined in Paterson and Olgaard (2000).

$${\dot{\mathit{\epsilon }}}_{\mathrm{eff}}={\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{3}}}}\dot{\mathit{\gamma }}\text{and}{\mathit{\sigma }}_{\mathrm{eff}}=\sqrt{\mathrm{3}}\mathit{\tau }$$

3.4 Normalisation of data

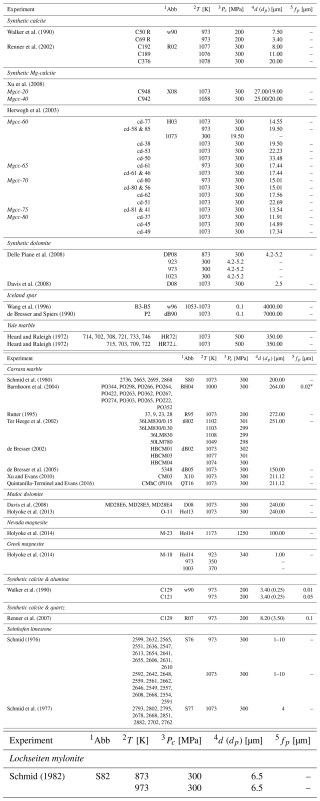
A normalisation exercise was used as the primary method of analysis. For this exercise, two data sets with known grain size and magnesium contents were used: synthetic Mg-calcite experiments from Herwegh et al. (2003) and a suite of natural samples (Wang et al., 1996; de Bresser and Spiers, 1990; Ter Heege et al., 2002; de Bresser et al., 2005; Rutter, 1995). For the normalisation exercise we focused on data from 1073 K because this temperature had the greatest range in grain size and magnesium across the literature (see Table 4).

If experimental data are governed by the same underlying constitutive relationship then the normalisation of data should collapse all data on to one line in the relevant parameter space. For example, if $A=f(B,C^{-n})$ then if one was to plot data as ACⁿ against B, data would all fall on one line. In this way, if the value of n is unknown then one can iteratively arrive at its value by systematically normalising data by different values of n until data fall on one line in ACⁿ vs. B space.

In this contribution such a procedure was used to establish if there are independent effects of grain size and magnesium on the strain rate in carbonates. We can only do this for data where the strain rate, stress, grain size, XMgCO₃ and temperature are all known. Such an analysis can obtain parameters that account separately for any sensitivities in variables that exist when combined with a constitutive relationship.

In this contribution we do not utilise any kind of iterative regression to establish when data lie on one curve, but rely on a qualitative assessment of when data most tightly follow one relationship. This means that we cannot provide an uncertainty on the exponents obtained. Moreover, we cannot provide any kind of meaningful uncertainty propagated from the other parameters because we use data from a large number of studies in which individual measurement uncertainties are not always reported.

To help the reader visualise what such a normalisation means for data manipulation we have included Fig. 3. In this figure we plot some of the data from Herwegh et al. (2003) that is shown in the results but with only the effect of grain size accounted for in the normalisation. It can be seen how for each fixed XMgCO₃ value data collapses on to one line, leaving only the effect of XMgCO₃.

To check the veracity of the exercise outlined above, we interrogated the results against both the data it was fit from and a wide range of other experimentally deformed carbonate with various temperatures, grain sizes, magnesium and second phase contents.

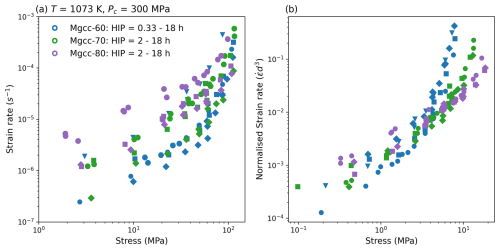
Figure 3 An example of normalising data. (a) shows a selection of synthetic Mg-calcite experiments from Herwegh et al. (2003) that then have each data points strain rate normalised by the sample grain size to the power of 3 in (b). The power of 3 is the reciprocal exponent to that expected for a constitutive relation governed by grain boundary diffusion.

Herwegh et al. (2003)Wang et al. (1996)de Bresser and Spiers (1990)Ter Heege et al. (2002)de Bresser et al. (2005)Rutter (1995)

Table 4 Experimental studies used in the normalisation. All experiments were run at 1073 K.

^* d = grain-size, – not used in normalisation.

4 Results

Treating synthetic and natural samples separately, strain rate and stress data from deformation experiments were manipulated through multiplication of grain size and XMgCO₃ values to various exponents (Fig. 4). The grain size (min = 14.55 µm, max = 7000.00 µm) and XMgCO₃ (min = 0.000013, max = 0.17) values used for each experimental data point were sourced from literature and are reported in Tables 1 and 3.

Starting from

$$\dot{\mathit{\epsilon }}=f\left(\mathit{\sigma }\right){\mid }_T$$

The normalisation is such that fine grained synthetic sample data are transformed to:

$$\dot{\mathit{\epsilon }}{d}^{\mathrm{3}}{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{1.5}}=\mathit{\sigma }{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.6}}$$

and results for coarse grained natural samples become:

$$\dot{\mathit{\epsilon }}{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{1.5}}=\mathit{\sigma }{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.3}}$$

For synthetic data both low and high stress domains are sensitive to grain size, while stress and strain rate require multiplication by XMgCO₃ to different exponents to collapse data on to one curve (Fig. 4a). Natural samples are not grain size sensitive and also require separate XMgCO₃ exponents (Fig. 4b). In both datasets the strain rate XMgCO₃ exponent is the same (−1.5) but is different for stress (−0.6 vs. −0.3).

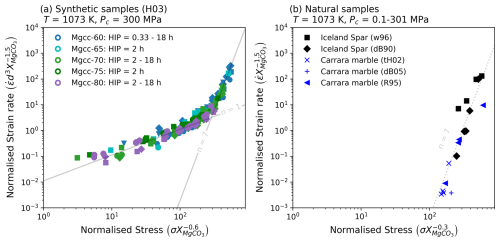
Figure 4 Normalisation of calcite data for data sets where grain size and magnesium contents were both known. See Table 4 for references of experiments and ranges of XMgCO₃ and grain size used.

These normalisation parameters can by used in conjunction with an assumed strain rate function to obtain useable flow law parameters. If the total strain rate is the sum of all rate accommodating micro mechanisms:

$$\sum _{n=i}^j{\dot{\mathit{\epsilon }}}_n={\dot{\mathit{\epsilon }}}_i+{\dot{\mathit{\epsilon }}}_{i+\mathrm{1}}+\mathrm{\dots }+{\dot{\mathit{\epsilon }}}_j,$$

and the normalised strain rate is a function of the normalised stress, we can substitute strain rate functions for the various deformation mechanism regimes that we think contribute to deformation and then invert the normalisation for flow law parameters. In our data there are two domains in which it appears that different deformation mechanisms are apparent: a low stress domain with where data have a slope of 1 in log-log space, and a high stress domain characterised by a slope of 7 in log-log space (Fig. 4). For simplicity we assumed these to represent diffusion creep (${\dot{\mathit{\epsilon }}}_{\mathrm{diff}}$) and dislocation creep (${\dot{\mathit{\epsilon }}}_{\mathrm{dis}}$) fields and with classical temperature dependant power-law flow laws.

Substituting power-law flow laws for diffusion and dislocation creep gives us the following grain size and XMgCO₃ sensitivities:

Fine grained synthetic samples (FG):

$$\begin{array}{rl}{\dot{\mathit{\epsilon }}}_{\mathrm{norm}}& =f\left({\mathit{\sigma }}_{\mathrm{norm}}\right)\\ & \Rightarrow \dot{\mathit{\epsilon }}{d}^{\mathrm{3}}{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{1.5}}=\\ & \left[A_{\mathrm{diff}}^{\mathrm{FG}}(\mathit{\sigma }{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.6}}{)}^{n_{\mathrm{diff}}^{\mathrm{FG}}}\exp \left(-{\displaystyle \frac{Q_{\mathrm{diff}}^{\mathrm{FG}}}{\mathrm{RT}}}\right)\right]\\ & +\left[A_{\mathrm{dis}}^{\mathrm{FG}}(\mathit{\sigma }{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.6}}{)}^{n_{\mathrm{dis}}^{\mathrm{FG}}}\exp \left(-{\displaystyle \frac{Q_{\mathrm{dis}}^{\mathrm{FG}}}{\mathrm{RT}}}\right)\right]\end{array}$$

Coarse grained natural samples (CG):

$$\begin{array}{rl}{\dot{\mathit{\epsilon }}}_{\mathrm{norm}}& =f\left({\mathit{\sigma }}_{\mathrm{norm}}\right)\\ & \Rightarrow \dot{\mathit{\epsilon }}{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{1.5}}=\left[A_{\mathrm{dis}}^{\mathrm{CG}}(\mathit{\sigma }{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.3}}{)}^{n_{\mathrm{dis}}^{\mathrm{CG}}}\exp \left(-{\displaystyle \frac{Q_{\mathrm{dis}}^{\mathrm{CG}}}{\mathrm{RT}}}\right)\right]\end{array}$$

Taking the observed stress exponents of n_diff = 1 and n_dis = 7, we can rearrange for the parameters:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\dot{\mathit{\epsilon }}}_{\mathrm{diff}}^{\mathrm{FG}}=A_{\mathrm{diff}}^{\mathrm{FG}}\left({\displaystyle \frac{d_{\mathrm{ref}}}{d^{\mathrm{3}}}}\right)X_{{\mathrm{MgCO}}_{\mathrm{3}}}^{\mathrm{0.8}}\left({\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{1}}}{{\mathit{\sigma }}^{\mathrm{ref}}}}\right)\exp \left(-{\displaystyle \frac{Q_{\mathrm{diff}}^{\mathrm{FG}}}{\mathrm{RT}}}\right)\text{(7)}& {\displaystyle }{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{FG}}=A_{\mathrm{dis}}^{\mathrm{FG}}\left({\displaystyle \frac{d_{\mathrm{ref}}}{d^{\mathrm{3}}}}\right)X_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{2.7}}\left({\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{7}}}{{\mathit{\sigma }}^{\mathrm{ref}}}}\right)\exp \left(-{\displaystyle \frac{Q_{\mathrm{dis}}^{\mathrm{FG}}}{\mathrm{RT}}}\right)\text{(8)}& {\displaystyle }{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{CG}}=A_{\mathrm{dis}}^{\mathrm{CG}}{X}_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{0.6}}\left({\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{7}}}{{\mathit{\sigma }}^{\mathrm{ref}}}}\right)\exp \left(-{\displaystyle \frac{Q_{\mathrm{dis}}^{\mathrm{CG}}}{\mathrm{RT}}}\right)\end{array}$$

in all cases a reference stress (1 MPa) and reference grain size (1 µm) are used to ensure that the frequency factor will have correct units for a first order rate equation (i.e. s⁻¹).

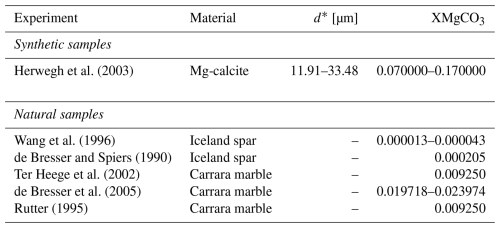
Three key results are established in Eqs. (6)–(8): (1) fine grained synthetic samples are grain size sensitive to the same exponent (d⁻³) across both mechanisms; (2) that XMgCO₃ has two opposing effects in diffusion (weakening) and dislocation creep (strengthening); and (3) the XMgCO₃ sensitivity of coarse grained natural samples is only half that of the compositional sensitivity of fine grained. Using data from experiments to invert for the frequency factor (A) and an assumed activation energy of 200 kJmol⁻¹ (cf. Herwegh et al., 2003; Renner and Evans, 2002) for both diffusion and dislocation creep (see Table 5), these last two points about XMgCO₃ sensitivity are illustrated in Fig. 5.

Table 5 Flow law fitting parameters.

¹ A = frequency factor, ² n = stress exponent, ³ m = grain size exponent, ⁴ u = XMgCO₃ exponent, ⁵ Q = activation energy, – not applicable.

Figure 5 Plotting the flow laws obtained from normalisation. Curves are plotted at 673 K and the corresponding stable XMgCO₃ solvus value for 673 K, 0.03, is marked on plots. Colour bars are presented with tick values that correspond to the discrete values of the modelled curves.

5 Discussion

The normalisation exercise revealed that the effects of grain size and magnesium can be separated in calcite rocks. That the effect of magnesium is different for deformation mechanism domains and different between natural and synthetic starting materials. It also showed that dislocation creep in fine grained synthetic samples is grain size sensitive but that coarse grained natural samples are grain size insensitive. Most interesting of all is that magnesium switches from having a weakening effect at low stress to a strengthening effect at high stress.

The following will discuss these points and evaluate how Eqs. (6)–(8) perform across a wide range of carbonate deformation experiments and what these new rheological laws mean for the strength of natural shear zones. In light of the apparent divide identified in the results between fine and coarse grained carbonates, we choose to evaluate the derived equations with data from experiments that are separated into these categories of fine and coarse grained samples in Sect. 5.2 and 5.3.

Despite Eqs. (6)–(8) being defined for calcite data we include in the following discussion comparisons to dolomite and magnesite data. This is done because, as first noted by Holyoke et al. (2014), there are similarities and possible systematic variations across the calcite, dolomite and magnesite rheological data. In particular because calcite and magnesite share essentially the same structure (the same symmetry but with magnesite having a contracted unit cell compared to calcite) they could conceivably behave similarly in dislocation creep. While this is less likely for dolomite where different cation ordering exists and for which different slip systems activate. Additionally, the conformity of diffusion creep rheological parameters across Mg-calcite, dolomite and magnesite strongly suggest a shared deformation mechanism. Our new XMgCO₃ sensitive equations may be able to pragmatically model rheological behaviour across the series and we use these end-member data sets to evaluate this.

In the following discussion please refer back to Table 3 for all experimental abbreviations.

5.1 XMgCO₃ sensitivity in calcite

Before comparing the results to other carbonates in the Ca-Mg series (e.g. dolomite and magnesite) it is important to discuss why XMgCO₃ may have an effect on different micromechanisms in calcite rocks.

5.1.1 Weakening in the diffusion creep field

The effect of magnesium on diffusion creep was first noted in the original work of Herwegh et al. (2003). However, they interpreted that magnesium indirectly affected strain rate through its control on grain growth kinetics, and by extension, grain size. Hence it was concluded that the constitutive relation for Mg-carbonate or calcite did not require an XMgCO₃ term. Contrary to this, our new analysis suggests that the effect of magnesium can be separated empirically from grain size. Therefore, while the two variables are inter-dependent, we claim that magnesium has a quantifiable and direct affect on the diffusion creep rheology of carbonates: an increase in XMgCO₃ weakens a carbonate experiencing diffusion creep by a power of $X_{{\mathrm{MgCO}}_{\mathrm{3}}}^{\mathrm{0.8}}$ (Fig. 5a).

Considering that Mg has a smaller ionic radius than Ca, it may be that the energy required to mobilise a Mg cation is lower and hence a carbonate with more Mg may deform at a faster rate for the equivalent work done. However, this is at odds with the observation of the same or broadly similar activation energies across Mg-carbonates (Herwegh et al., 2003), and more broadly across the whole Mg-Ca carbonate series (Holyoke et al., 2014). These observation suggests that mechanisms activated are thermodynamically equivalent, possibly the same mechanism for all chemistries. An alternative posit is that chemical diffusion of magnesium plays a larger role in driving cation exchange (Fisler and Cygan, 1999; Huang et al., 2008). In this case the local spatial gradients in chemistry would encourage exchange and inter-diffusion of species. This is expected to be faster than self diffusion but has a similar activation energy (231.7 kJ mol⁻¹, Huang et al., 2008) as reported for cation species self diffusion or diffusion creep of calcite (Herwegh et al., 2003; Renner and Evans, 2002). If this is the case, then one should expect that local spatial gradients are reduced as XMgCO₃ increases, and magnesium content should have less of an effect on the strain rate. This is what we observe. Figure 5a highlights that an increase in XMgCO₃ has an ever diminishing effect on diffusion creep curves.

5.1.2 Strengthening in the dislocation field

Magnesium was previously shown to strengthen Mg-carbonates in the dislocation field (Xu et al., 2008). Specifically it was demonstrated that, for a fixed strain rate, the strength of a Mg-carbonate could be described as a function of the molar percent of magnesium to the $\mathrm{1}/\mathrm{3}$ power. Our results agree with this and build on it (Fig. 5a and c). Indeed, our results suggest that this compositional effect on creep extends beyond synthetic Mg-carbonates to natural calcite samples. As discussed in the work of Xu et al. (2008), the strengthening by XMgCO₃ may be due to solute-drag in the glide plane or inhomogeneity in the cation structures producing obstacles to the progress of linear defects. This second possibility may be unlikely if chemical diffusion is substantial, as discussed earlier for diffusion creep, because any heterogeneity in the magnesium cation distribution would become dispersed and remove these potential obstacles (Fisler and Cygan, 1999). In either case, increasing the molar fraction of magnesium would have the effect of hardening the carbonate. This points to a continuum in strength in dislocation creep across much of the calcite-dolomite series, not necessarily including dolomite, but the exact sensitivity seems to change between fine and coarse grained samples at high stress.

5.2 The rheology of fine grained carbonates

5.2.1 Comparing to the data it was derived from

Equations (6)–(8) can be compared to the data they were derived from as a sense check on the results before comparing them to other data. Together Fig. 6a and b show that a composite of the fine grained flow laws (Eqs. 6 and 7) fit the data well and notably they perform much better than the published diffusion creep flow law of Herwegh et al. (2003). It also appears that the composite fine grained flow law performs adequately when compared to data acquired by Herwegh et al. (2003) at a lower temperature (Fig. 6c). As a last comparison, a composite of the fine grained diffusion creep and coarse grained dislocation creep was compared to data collected at 1073 K (Fig. 6d) to evaluate if the grain size sensitivity of dislocation creep identified in the normalisation could be modelled with the transition away from grain size sensitivity. It can be seen that a grain size intensive dislocation creep law fails to capture the behaviour of the experiments at higher stress. In total Fig. 6 provides confidence that Eqs. (6)–(8) do fit the data they were derived from, being robust enough to also fit data from the same series but acquired at a lower temperature.

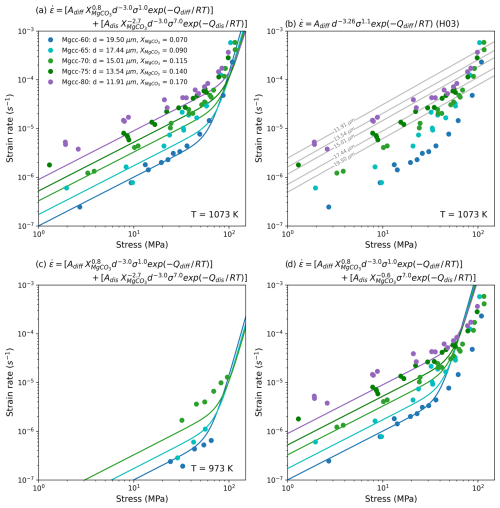
Figure 6 Plotting flow laws obtained from normalisation against data used in fit (a); to the fit of Herwegh et al. (2003) (b); to a lower temperature data set from Herwegh et al. (2003) not used in normalisation (c); and a pragmatic check to see if using the obtained coarse grained flow law can explain the fine grained high stress data (d).

5.2.2 Comparing to other experimental data

End-member performance: Pure calcite, dolomite and magnesite

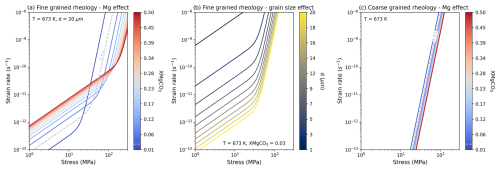
As a test of the limits of the normalisation results we can compare Eqs. (6)–(7) to pure synthetic calcite (Renner et al., 2002), very low XMgCO₃ synthetic Mg-calcite (Xu et al., 2008),synthetic dolomite experiments (Delle Piane et al., 2008; Davis et al., 2008) and Greek magnesite (Holyoke et al., 2014). A XMgCO₃ minimum of 0.001 is taken as a sensible limit because data used in the normalisation is restricted to this order of magnitude.

Figure 7a shows that data from pure and very low XMgCO₃ experiments can be fit. Considering the uncertainties associated with grain size measurements the data are fit well. For dolomite (Fig. 7b and c) lower temperature data are fit well but the relationship breaks down at higher temperature. However in the case of data from Delle Piane et al. (2008) Eqs. (6)–(7) perform better than the flow law defined by Delle Piane et al. (2008), with the exception of the highest temperature experiments. In contrast, our equations require larger grain sizes to fit the dolomite data of Davis et al. (2008) and the magnesite data of Holyoke et al. (2013). This may reflect the large, but broadly unquantified, uncertainty associated with grain size measurement (cf. Berger et al., 2011).

Unfortunately, we do not have any fine grained dolomite or magnesite data at high enough stress and temperature to be in the dislocation creep field and as such cannot evaluate if the high stress XMgCO₃ sensitivity is successful in modelling the data points. If the XMgCO₃ strengthening mechanisms discussed above, of solute drag or chemical diffusion driven by spatial gradients, are responsible for our observations then it is unlikely that dolomite can be modelled with our high stress rheology (n=7). This is because the crystallography of dolomite is much more ordered, with Ca²⁺ and Mg²⁺ becoming segregated into alternating layers, and different rate limiting mechanisms will apply. In contrast fine grained magnesite at higher stress and temperature might be modelled with our flow laws and this should be tested with new data.

Figure 7 Exploring how well the fine grained flow laws obtained fit calcite, dolomite and magnesite end member data. Please refer to Table 3 for experiment abbreviations.

Rheology of samples with different grain size controlling mechanisms

We identified three experiments with similar XMgCO₃ values that can be used to understand how well Eqs. (6)–(7) model the rheology of carbonates with contrasting grain size controls: statically grown grain size (Fig. 8a) (Xu et al., 2008), a dynamically recrystallised grain size (Fig. 8b) (Barnhoorn et al., 2004) and a second phase controlled grain size (Fig. 8c) (Schmid, 1982).

Figure 8a shows that, in line with results above, Eqs. (6)–(7) fit synthetic Mg-cc data well. Equations (6)–(7) also perform well when compared to an experiment where the grain size evolved to stable grain size during deformation (Fig. 8b). Reinforcing the framing of our discussion into fine and coarse grained samples, the rheology of the coarser grained starting material cannot be modelled with Eqs. (6)–(7). Lastly, it appears that the low stress rheology of a second phase controlled mylonite from the Glarus thrust can be modelled with the new laws, but the high stress behaviour deviates, possibly resulting from a very high second phase content (f_p≤0.3). Notably the newly defined XMgCO₃-sensitive diffusion creep law performs much better than the diffusion creep law of Herwegh et al. (2003).

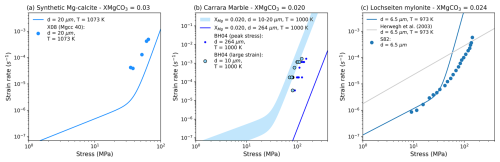
Figure 8 Exploring how well the fine grained flow laws fit data from experiments with stable microstructures generated with different processes that share the same magnesium content: statically annealed synthetic sample (a), before and after dynamic recrystallisation of a natural marble (b), and a natural second-phase rich ultramylonite from a large shear zone (c). Please refer to Table 3 for experiment abbreviations.

Second-phase rich carbonates

In nature, very few carbonate mylonites consist of nominally pure calcite aggregates. Despite the volumetric dominance of calcite as a matrix phase, the vast majority of these mylonites contain variable amounts of other minerals, so called second phases (e.g. Ebert et al., 2007; Herwegh and Jenni, 2001; Herwegh and Kunze, 2002; Herwegh and Pfiffner, 2005; Herwegh et al., 2008). It is therefore important to evaluate the effect of such second phases on calcite rheology of mylonites, this is reflected in the partial success of Eqs. (6)–(7) in modelling the Lochseiten mylonite data. It is important to ask how well the equations fit carbonates with other lower second phase contents.

Equations (6)–(7) were compared to experiments run on synthetic calcite samples with fine grained alumina added (Walker et al., 1990), Solnhofen limestone (Schmid, 1976; Schmid et al., 1977), synthetic mixtures of calcite and quartz (Renner et al., 2007) and Lochseiten mylonite data from various temperatures (Schmid, 1982). Figure 9 shows that for lower second phase contents (Fig. 9a and b) data appear to be fit well. In the case of diffusion creep of the Lochseiten mylonite, the data fit Eq. (6) at higher temperatures but not at lower temperatures (Fig. 9c). Figure 9d shows that, as the second phase content rises to 10 % and above, the observed rheologies depart from our model.

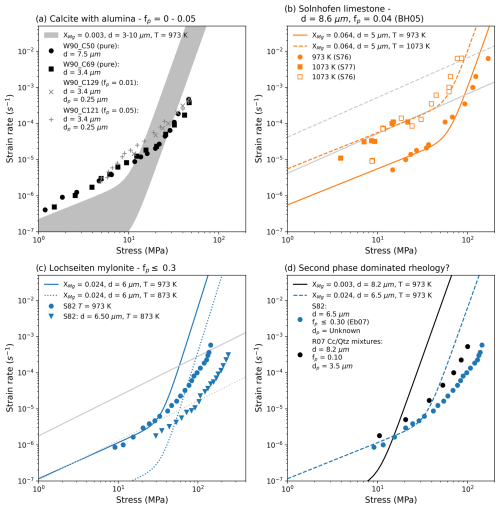
Figure 9 Exploring how well the fine grained flow laws can fit carbonates with a variety of second-phases contents: synthetic samples doped with alumina (a), Solnhofen limestone (b), a natural second-phase rich ultramylonite deformed at two different temperatures (c). (d) highlights the limits of the the flow laws to model the rheology of second-phases rich carbonates by comparing them to data from a synthetic calcite-quartz mixture with no magnesium to a natural ultramylonite with magnesium. (b) and (c) show the equivalent diffusion creep flow law of Herwegh et al. (2003) as grey lines. Please refer to Table 3 for experiment abbreviations.

5.3 The rheology of coarse grained carbonates

The normalisation of experimental results of coarse grained natural samples was limited to datasets where chemical and mechanical analyses were both run on the same samples. This restricted the data to two Iceland spar and three Carrara marble experiments (Wang et al., 1996; de Bresser and Spiers, 1990; Ter Heege et al., 2002; de Bresser et al., 2005; Rutter, 1995). Despite this, when compared to other coarse grained calcite experiments the data fit the model relatively well (Fig. 10a–c), but could not account for experiments run on dolomite or magnesite (Fig. 10d).

As discussed in Sect. 5.2, this is not surprising for dolomite, as its different crystallography likely promotes different accommodation mechanisms during deformation (cf. Davis et al., 2008), but is more surprising that magnensite cannot be fit with all of its similarities to calcite. Holyoke et al. (2014) found that that the activation barrier for dislocation glide in calcite and magnesite was not affected significantly by cation size or bonding, seen in similar activate energies, implying that to connect both materials with one equation an additional XMgCO₃ sensitivity would need to be placed, as we have done, in the constitutive law. The inability of Eq. (8) to replicate the magnesite data might simply reflect an issue with the XMgCO₃ exponent our work arrived at.

In all calcite experimental cases it is clear that the range of possible mechanical fits shown with coloured regions, which are given by the available XMgCO₃ data (see Table 1), are narrower than the spread of data points. For some outlying data there are easy explanations. For example, in Iceland spar experiments the concentration of Mn also influences rheology (cf. Wang et al., 1996) and for the highest stress data point of Rutter (1995) this can be explained by a marked increase in strain. However, the fit clearly overestimates the strength of Yule marble and does not capture the experimental data point of de Bresser et al. (2005) with in the range of Carrara marble experimental results. Regardless, it would appear that much of the characteristics of the rheology of coarse grained natural calcite samples is fit well with Eq. (8).

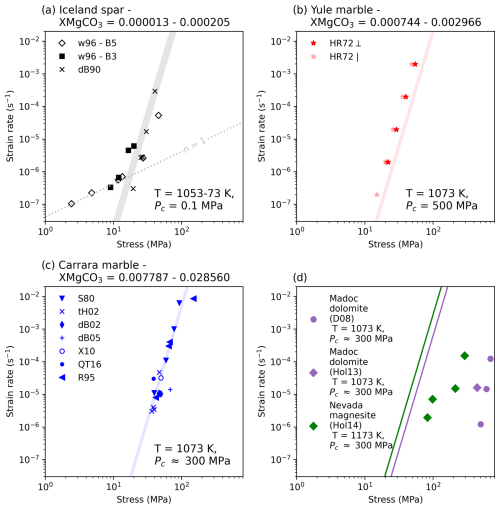
Figure 10 Exploring how well the coarse grained flow law fits both the data it was fit from and other data where Mg is known for the material but not the experiment itself. Shaded areas use the max and min XMgCO₃ values to bracket the possible rheology. Dolomite and Magnesite are modelled as XMgCO₃ = 0.5 and 1.0. Please refer to Table 3 for experiment abbreviations.

Figure 11 The effect of grain size on strain rate in the dislocation creep field at fixed XMgCO₃ values.

5.4 Grain size sensitive dislocation creep?

One puzzling result is that fine grained samples are grain size sensitive in the dislocation creep field. The various underlying mechanisms documented for dislocation creep in calcite are not grain size dependent in a way that weakens the rock (cf. Renner et al., 2002). This raises several questions: is this effect real or a result of differences in sample fabrication? Why would there be a difference between fine and coarse grained samples in dislocation creep?

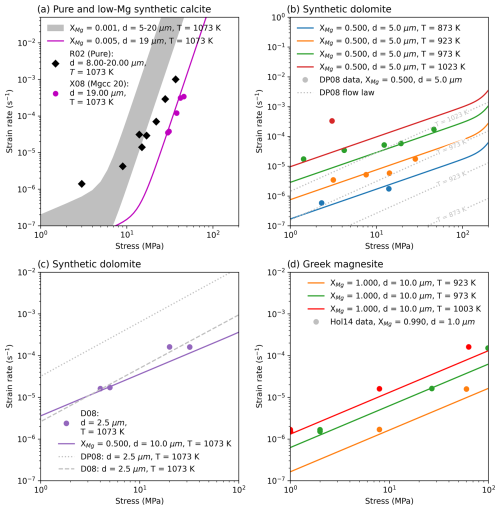
Figure 11 shows data from fine and coarse grained samples, that are both synthetic and natural, with XMgCO₃ values that are close together. Data plotted for XMgCO₃ ≈ 0.07 is made up from a fine grained synthetic starting material, Mgcc-60 (Herwegh et al., 2003), and a fine grained natural starting material, Solnhofen limestone (Schmid, 1976; Schmid et al., 1977). While data plotted for XMgCO₃ ≈ 0.03 is made up from a fine grained synthetic starting material, Mgcc-40 (Xu et al., 2008), and a coarse grained natural starting material, Carrara marble (Ter Heege et al., 2002). Together these data highlight that: (1) the grain size sensitivity of fine grained carbonates is not restricted to synthetic samples alone – it is not an artifact of Hot Isostatic Pressing (HIP) used in synthetic sample preparation; (2) there is a transition towards a grain size insensitive dislocation creep field. We conclude from this that grain size sensitive and grain size insensitive dislocation creep fields are real.

Grain size sensitive dislocation creep rheologies have been phenomenologically described in other experiments run on geological materials. For example in olivine (Hansen et al., 2011, 2019), quartz (Fukuda et al., 2017), ice (Qi and Goldsby, 2021) and calcite (Renner et al., 2002; Renner and Evans, 2002; Sly et al., 2019). These grain size sensitivities have been found to be both strengthening and weakening and have been explained in different ways. For olivine when grain size has a weakening effect (d^−0.7, Hansen et al., 2011) a rheological model of dislocation‐accommodated grain boundary sliding was proposed. In this case dislocations are thought to be generated at grain boundaries and triple junctions and as such a grain size dependence emerges. For quartz when grain size has a weakening effect (d^−0.51, Fukuda et al., 2017) it was suggested that experiments recorded a mixed signature of end member grain size sensitive and insensitive mechanisms. In ice, grain size weakening (d^−0.35, Qi and Goldsby, 2021) was also explained by a contribution of the dislocation‐accommodated grain boundary sliding mechanism when the grain size was larger than the equilibrium subgrain size. By contrast cases where a grain size hardening effect was observed, there a modified Hall-Petch relation has been proposed: the smaller the grain size the stronger the material (e.g. Renner et al., 2002; Hansen et al., 2019). Our results do not align with any of these models, we find that the strain rate in the dislocation field is sensitive to what one would expect from a diffusion creep deformation mechanism (d⁻³). Moreover, Fig. 11 implies that there is a transition as grain size increases towards a grain size insensitive rheology and any underlying model would need to explain this.

To explain the ever diminishing effect of grain size in the dislocation field we can turn to recent work by Breithaupt et al. (2023), who proposed a self-consistent model for deformation mediated by dislocations in which they were able to show how a material could transition from a grain size strengthening to weakening and ultimately grain size insensitive rheology as grain size increased. In this model the grain size sensitivity of a dislocation accommodated deformation changes because the effect of how dislocations are stored and recovered in crystals changes with grain size. Breithaupt et al. (2023) applied their model to olivine and found that it agreed with the grain size exponent measured by Hansen et al. (2011). If one extends the model of Breithaupt et al. (2023) to include diffusion creep then our phenomenological curves become more comparable (cf. Figs. 1c and 3.3 in Breithaupt et al., 2023; Breithaupt, 2022). Thus it might be that for the calcite experiments we revisit there is a mixed signal of diffusion creep and a grain size sensitive model for dislocations that relates not to grain boundaries as sources of dislocations, but to how dislocations are intrinsically stored and recovered in grains, and how the effects of this changes with the size of grains. The model of Breithaupt et al. (2023) also allows some explanation of the variation (hardening vs weakening) in the effect of grain size in different calcite experiments. The previous work of Renner et al. (2002) and Sly et al. (2019) that found a strengthening effect of finer grain sizes likely capture specific conditions where diffusion creep has not been activated and hence record a domain where the Hall-Petch effect dominates (cf. Figs. 7 and 9b in Renner et al., 2002). For Sly et al. (2019) this is likely because experiments were run at much lower temperatures. Alternatively, for Renner et al. (2002) the difference might be due to a much finer grain size than the experiments of Herwegh et al. (2003). While the grain sizes of Renner et al. (2002) and Herwegh et al. (2003) seem cover a similar range they use different grain size quantification methods (line intercept vs area-weighted) and if one was to convert the values of Renner et al. (2002) this might lead to as much as a halving of the value reported (cf. Table 5 in Berger et al., 2011).

Regardless of the underlying reasons, what is clear is that our fine grained calcite data cannot be modelled well with a grain size insensitive dislocation creep rheology and some component of grain size sensitivity is needed. Short of adapting the model of Breithaupt et al. (2023) to include the effect of XMgCO₃, one could be pragmatically guided by Fig. 11 to explicitly model different rheologies based on grain size domains.

For example using Eqs. (6)–(8),

$$\begin{array}{}\text{(9)}& {\displaystyle }\text{for}d<\mathrm{30}\mathrm{\mu }\mathrm{m},{\dot{\mathit{\epsilon }}}_{\mathrm{tot}}={\dot{\mathit{\epsilon }}}_{\mathrm{diff}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{FG}}\text{(10)}& {\displaystyle }\text{for}\mathrm{30}<d<\mathrm{200}\mathrm{\mu }\mathrm{m},{\dot{\mathit{\epsilon }}}_{\mathrm{tot}}={\dot{\mathit{\epsilon }}}_{\mathrm{diff}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{CG}}\text{(11)}& {\displaystyle }\text{for}d>\mathrm{200}\mathrm{\mu }\mathrm{m},{\dot{\mathit{\epsilon }}}_{\mathrm{tot}}={\dot{\mathit{\epsilon }}}_{\mathrm{diff}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{CG}}\end{array}$$

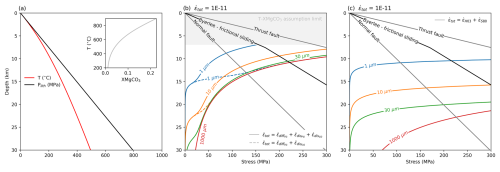
Figure 12 Modelling crustal strength for a given temperature-pressure-depth-XMgCO₃ profile (a). The reference stress state with depth is P_lith = ρgz. The geotherm is calculated following an assumed constant heat flow in a stable continental crust (cf. Stüwe, 2007, Eq. 3.70: h_r = 10×10³ m, S₀ = 3$\times {\mathrm{10}}^{-\mathrm{6}}$ Wm⁻³, z_c = 30×10³ m, q_m = 0.025 Wm⁻², C₂ = 300 K). The calcite-dolomite carbonate solvus of Anovitz and Essene (1987) is used to relate T and XMgCO−3. (b) shows the strength for various grain sizes using two combinations of the three flow laws obtained (Eqs. 6–8). (c) shows how strength changes using a composite flow law made up of previously published dislocation and diffusion creep rheologies (Schmid et al., 1980; Herwegh et al., 2003). Frictional strength envelops are given by Byerlee's law for frictional sliding (Byerlee, 1978) and Sibson (1974), assuming μ = 0.75 and λ = 0.5.

Using an assumed geotherm, pressure with depth relation and the calcite-dolomite solvus to relate temperature to XMgCO₃ (equation 23 in Anovitz and Essene, 1987), Fig. 12 illustrates this pragmatic approach (solid lines in Fig. 12b) and compares it to a case for fine grained dislocation creep rheology that shows no grain size effect (dashed lines in Fig. 12b), and the published flow laws for calcite (Schmid et al., 1980; Herwegh et al., 2003) (Fig. 12c). The first point of note is that, regardless of which composite rheology one chooses from our results, a XMgCO₃ sensitive flow law predicts much weaker carbonates with depth for a given grain size. This shows that the effect of XMgCO₃ must be included explicitly when modelling crustal strength. We know from natural shear zones that grain size also changes with temperature and so the effect shown in Fig. 12 will not fully capture the strength profile of carbonates.

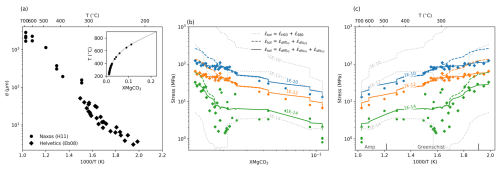
Figure 13 Modelling crustal strength using real grain size and temperature data (a). XMgCO₃ values are derived from temperature values (inset in a). (b) and (c) show the stress expected for a variation in XMgCO₃ and temperature using two combinations of the three flow laws obtained (Eqs. 6–8). For the purposes of visualisation figure moving average curves are shown for the various rheological models with data points only shown for ${\dot{\mathit{\epsilon }}}_{\mathrm{tot}}={\dot{\mathit{\epsilon }}}_{\mathrm{diff}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{FG}}+{\dot{\mathit{\epsilon }}}_{\mathrm{dis}}^{\mathrm{CG}}$. A composite flow law made up of previously published dislocation and diffusion creep rheologies is shown for comparison as dashed grey lines. Three strain rates are modelled and they are noted on the moving average curves.

5.5 Application to natural carbonate shear zones

Using temperature and grain size measurements from natural carbonate shear zone mylonites we can account for the combined effect of grain size and XMgCO₃ on strength. Figure 13 shows data from mylonites deformed at greenschist to amphibolite facies conditions from several thrusts of the Helvetic Nappes (Ebert et al., 2008) and from Naxos (Herwegh et al., 2011). As before, the calcite-dolomite solvus can be used to relate temperature measurements to inferred XMgCO₃ values. For the purposes of visualisation Fig. 13 shows moving average curves for the various rheological models but only shows data points for one rheology – the pragmatic composite rheology, e.g. Eqs. (6)–(8).

Most notably, for faster strain rates ($\mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{12}}$) at lower greenschist facies conditions the strength of carbonates flattens out with depth. This occurs because of the competing effects grain size and magnesium at these conditions (weakening – $\propto d^{-\mathrm{3}}$ and $X_{{\mathrm{MgCO}}_{\mathrm{3}}}^{-\mathrm{2.7}}$; strengthening – $\propto X_{{\mathrm{MgCO}}_{\mathrm{3}}}^{\mathrm{0.8}}$). Carbonate rheology in these shear zones seems to balance out the effects of moving from smaller to larger grain sizes and an increasing XMgCO₃ content. For higher temperatures it is expected that a shear zone will widen, and therefore strain rate will decrease, making it hard to compare data from the Helvetics and Naxos together. Field observations from the Helvetic nappes suggest that, when accounting for shear widths, strain rates are relatively constant and can be reasonably modelled with values of between $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{10}}$ and $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{11}}$ (Herwegh and Pfiffner, 2005). Following from this if we only use data from the Helvetics and assume a strain rate of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{11}}$ we can more carefully consider the strength of a crustal scale carbonate shear zone. Using the same data as previously, Fig. 14 presents only data from the Helvetics. The blue and orange diamond markers give upper and lower bounds on crustal strength for rheologies that are grain size and XMgCO₃ sensitive. If fine grained shear zones deform by a grain size sensitive dislocation creep flow law (blue diamonds) then the crustal strength becomes very close to constant for an interval of roughly 200 °C. This is comparable to estimates that come from accounting for grain size distributions (crosses in Fig. 14). If however, the rheology is considered to be a composite of a grain size and XMgCO₃ sensitive diffusion creep mechanism and a XMgCO₃ sensitive dislocation creep mechanism (orange diamonds) then a shear zone would show more strength evolution with increasing temperature but it would still be weaker than predicted by piezometric relations.

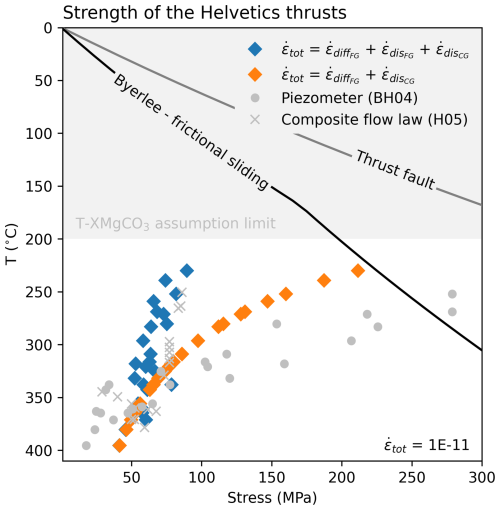
Figure 14 A crustal strength profile constructed with only the Helvetic thrust data set (Ebert et al., 2008). Strength estimates from a grain size paleopiezometer (Barnhoorn et al., 2004) and from naturally constrained rheological modelling that includes grain size distributions (Herwegh et al., 2005) are plotted for comparison. Frictional envelopes follow the same assuptions as Fig. 12.

6 Summary and outlook

We have brought together much of the existing literature of carbonate deformation experiments run at high homologous temperatures and found that most data can be explained well by the distinct effects of grain size and the molar fraction of magnesium carbonate. For a given grain size, the above results highlight that there is a quantifiable continuum in strength of carbonates with magnesium content and that the role of magnesium changes with deformation mechanism (Fig. 5a). Furthermore for a given molar fraction of magnesium, our review of the data show that at high stresses, at which dislocation mediated deformation will occur, finer grain sizes produce higher strain rates (Fig. 11). This is contrary to the current use of the modified Peierls law for calcite dislocation creep rheology at high homologous temperatures, where grain size has a hardening effect.

Together these new results suggest that the deformation of magnesium carbonates should be considered in a more unified fashion. For low stress, high temperature, diffusion creep behaviour it might be more pragmatic to view these carbonates as existing in a continuum of material strength and not as distinct materials. Data across the calcite-dolomite-magnesite XMgCO₃ data seem to mostly fit our fine grained diffusion creep flow law. This is not true for the dislocation creep field where dolomite, nor magnesite, seems to not conform to predictions of a continuous change in strength with magnesium. In cases of mixed grain/clast populations of calcite and dolomite one should still identify both the phase proportions and XMgCO₃ of equilibrated dolomite and calcite if one wishes to calculate a mixed rheology (e.g. Dimanov and Dresen, 2005; Renner et al., 2007).

The two biggest limitations of our contribution are that we can neither provide an underlying microphysical model nor uncertainty estimates for parameters. Regarding uncertainty, some of this limitation is unavoidable as not all experimental data we revisit can report errors or the kind of errors cannot be compared. The most complex parameter to compare between datasets is grain size and it is unclear if one would obtain a sensible error from propagating what is available in the literature. Beyond this future work may try and use a more sophisticated method to fit for exponents which could give fitting errors. Despite this, our first attempt seems to provide flow laws that can replicate a wide range of carbonate experiments. As for accounting for a microphysical model, this is particularly challenging because our data show that the underlying deformation mechanisms need to account for both the effect of magnesium and a grain size weakening dislocation creep. Across the 24 publications we revisit microstructures are not always provided and as such we cannot unequivocally establish if other processes like twinning are significantly impacting strength and grain size adjustments at high homologous temperatures in the data we revisit (cf. Rybacki et al., 2021). We assume that any mixed activity of processes that effect grain size and strength ultimately homogenise to give us our observed bulk grain size sensitivity in dislocation creep (d⁻³). In light of our above discussion, the best starting point would appear to be to build on the work of Breithaupt et al. (2023) and include a physically sensible magnesium dependence.

An important conclusion of this work is that even small differences in magnesium can have a large effect, especially when compounded by the role of grain size. Our discussion explored how crustal strength might significantly deviate from the current expectations, producing a very weak and almost uniform rheology with temperature and therefore depth (Fig. 14). If true, this calls into question the predictions of carbonate paleopiezometry for crustal strength. Integrating the effect of XMgCO₃ into carbonate rheology would appear to be supported by recent field evidence in calc-mylonites from extensional detachments where dolomitic mylonites were interpreted to be weaker than adjacent calcite mylonites (Coleman et al., 2025). The final strain localisation observed in the dolomitic mylonites preserved the activity of diffusion creep for which our results would predict that dolomite would have been an order of magnitude weaker than most calcite compositions (Fig. 5). Our results could also extend to the olivine system where it has also been shown that flow strength depends on iron concentration (Zhao et al., 2009, 2018). For olivine the relative activity of creep mechanisms and their sensitivity to chemistry will be different but the way in which the extra chemical parameter might impact strength estimates should be established. As such our work highlights the need to better integrate the effects of solid solutions into the rheology of important rock forming minerals.