Seismic attenuation and dispersion in poroelastic media with fractures of variable aperture distributions

Considering poroelastic media containing periodically distributed parallel fractures, we numerically quantify the effects that fractures with variable aperture distributions have on seismic wave attenuation and velocity dispersion due to fluid pressure diffusion (FPD). To achieve this, realistic models of fractures are generated with a stratified percolation algorithm which provides statistical control over geometrical fracture properties such as density and distribution of contact areas. The results are sensitive to both geometrical properties, showing that an increase in the density of contact areas as well as a decrease in their correlation length reduce the effective seismic attenuation and the corresponding velocity dispersion. Moreover, we demonstrate that if equivalent physical properties accounting for the effects of contact areas are employed, simple planar fractures can be used to emulate the seismic response of fractures with realistic aperture distributions. The excellent agreement between their seismic responses was verified for all wave incidence angles and wave modes.

1 Introduction

Fractures in rocks occur in a wide range of scales (from microscale to continental), and their identification and characterisation are important tasks for several areas such as oil and gas exploration and extraction, production of geothermal energy, nuclear waste disposal and civil engineering works, among others (Schoenberg and Sayers, 1995; Metz et al., 2005; Tester et al., 2007). Given that seismic waves are known to be significantly affected by the presence of fractures (e.g. anisotropy, attenuation, dispersion, scattering), seismic methods are a valuable tool for detecting and characterising fractures. An important cause of seismic attenuation and velocity dispersion occurs when a fluid-saturated heterogenous rock is deformed by a propagating wave. In such a case, the compressibility contrast between the heterogeneities creates fluid pressure gradients. Then, the fluid pressure returns to equilibrium through a fluid pressure diffusion (FPD) process during which energy is dissipated due to viscous friction (e.g. Pride and Berryman, 2003; Gurevich et al., 2009; Müller et al., 2010). In the case that the rock heterogeneity is a fracture, FPD is generated as a consequence of the compressibility contrast between the fracture and the embedding background. Furthermore, when a propagating wave deforms a medium having intersecting and fluid-saturated fractures, a pressure gradient can also arise between them, resulting in additional energy dissipation due to FPD but affecting higher wave frequencies than the previously mentioned phenomenon (Rubino et al., 2013; Quintal et al., 2014, 2016).

Several authors have studied fracture-related FPD effects on seismic attenuation and velocity dispersion (Chapman, 2003; Brajanovski et al., 2005; Carcione et al., 2013; Rubino et al., 2013; Quintal et al., 2014; Caspari et al., 2016, 2019), as well as on the effective anisotropy (Maultzsch et al., 2003; Masson and Pride, 2014; Tillotson et al., 2014; Amalokwu et al., 2015; Rubino et al., 2016, 2017) and scattering (Nakagawa and Schoenberg, 2007; Barbosa et al., 2016; Caspari et al., 2019), based on experimental or theoretical works. A common approach to study seismic attenuation and velocity dispersion in fluid-saturated fractured media consists of numerically solving Biot's (Biot, 1941, 1962) poroelasticity equations (Masson and Pride, 2007; Quintal et al., 2011, 2014; Rubino et al., 2013). In such studies, fractures are modelled as very compliant, highly porous and highly permeable heterogeneities embedded in a much stiffer, less porous and less permeable homogenous background (Pride et al., 2004).

Fractures can be conceptualised as two uneven surfaces in contact, which produce variable separation between their boundaries or walls (e.g. Montemagno and Pyrak-Nolte, 1999; Jaeger et al., 2007; Masson and Pride, 2015). In spite of this, fractures are often modelled as simple thin layers of constant thickness. The validity of such representation relies on assumptions such as incident wavelengths larger than the fracture microstructure, an appropriate selection of the properties of the material filling the fractures, among others. Furthermore, analytical solutions are based on simplifications such as assuming elastic materials, idealised geometries for the fracture microstructures and/or neglecting heterogeneities interactions. In this sense, Hudson and Liu (1999) obtained equivalent mechanical properties for a constant-thickness layer by representing a fracture as a plane distribution of circular dry or fluid-filled cracks (i.e. open regions of fractures). They found that the geometrical properties that dominate the mechanical behaviour of the fracture are cracks density and length. Still, their model assumes elastic media and crack or contact areas interactions are neglected. Also in an elastic framework, Zhao et al. (2016) have demonstrated the important role played by cracks' interaction on the stress field and, consequently, their effects on the overall rock stiffness. Hudson et al. (1996) proposed an analytical solution for obtaining the equivalent elastic properties of a constant-thickness layer by representing a fracture as an aligned distribution of circular cracks, accounting for their interaction and considering fluid or viscoelastic material filling the cracks. However, this model is limited to an elastic background and a single fracture. By considering 2-D models and following a poroelastic approach based on Biot's (Biot, 1941) equations, Rubino et al. (2014) numerically studied seismic attenuation and dispersion in fluid-saturated fractured media considering several distributions and densities of fracture contact areas. They found that contact areas have a strong effect on the level of seismic wave attenuation and dispersion caused by FPD between fracture and background, and also that the distribution of contact areas and material properties plays an important role on the effective seismic response. Nevertheless, they performed 2-D simulations which cannot account for realistic distributions of fracture aperture and contact areas. To our knowledge, the analysis of the impact of realistic aperture distribution of fractures on seismic attenuation and dispersion due to FPD remains largely unexplored.

Nolte and Pyrak-Nolte (1991) presented a stratified percolation workflow which can be used for generating fractures with realistic aperture distribution. The proposed methodology allows to define the structure of the fractures in terms of density and distribution of contact areas. Pyrak-Nolte and Morris (2000) studied the effects that such geometrical fracture properties have on the fracture stiffness and on the fluid flow through the fractures under normal stress changes. Moreover, they established a relation between the hydraulic and mechanical behaviours of fractures. However, FPD effects on the seismic response of fractures with realistic aperture distribution were not considered in their work.

In this work, we follow the workflow proposed by Nolte and Pyrak-Nolte (1991) to generate fracture models and use them to numerically quantify the effects that fractures with variable aperture distributions have on seismic wave attenuation and stiffness modulus dispersion for a medium containing a periodic distribution of fractures. For normally incident compressional waves, we perform a sensitivity analysis in terms of density and distribution of contact areas. Subsequently, we extend the results for all incidence angles and wave modes by computing the stiffness matrix coefficients. Finally, we numerically show that the same frequency-dependent seismic attenuation and velocity dispersion can be obtained for fractures with intricate aperture distributions and for fractures with constant aperture, provided that appropriate fracture properties are used in the latter case. These equivalent fracture properties must take into account not only the properties of the fracture-filling material but also the mechanical effects associated with the aperture distribution.

2 Numerical upscaling

To study attenuation and dispersion of seismic waves in a fluid-saturated rock with parallel and periodically distributed fractures, we model fractures as poroelastic media embedded in a homogenous poroelastic background. The aperture of the modelled fractures can be spatially variable. In the present work, we refer as open regions of the fracture to the zones where the fracture walls are not in contact (non-zero aperture) and are filled with a highly permeable and porous material. Contact areas (zero aperture), on the other hand, are represented by a porous material having the same properties as the background medium. We define the density of the contact areas as the ratio between the area of the fracture walls in contact and the area of the entire fracture. In this work, we use similar material properties to those employed by Rubino et al. (2014) but assuming a lower permeability for the background (Table 1). The material properties of the background are representative of sandstone (Bourbie et al., 1987).

Assuming that the prevailing wavelengths are much larger than the fracture aperture and spacing, we can obtain the effective seismic properties of the fractured medium by performing oscillatory relaxation tests on a representative elementary volume (REV) of the medium. We solve the quasi-static poroelastic equations given by Biot (1941) with a finite element scheme. The equations are written in the u-p (denoting solid displacement and fluid pressure, respectively) formulation, as proposed by Quintal et al. (2011), but in the space–frequency domain following the approach of Rubino et al. (2009). The effective stiffness moduli are obtained by applying homogeneous harmonic displacements normal to a boundary of the model in the case of P waves, or a shear displacement in the case of S waves. The numerical model, which consists of one horizontal fracture embedded in a homogenous background (Fig. 1a, left), is the REV of a medium containing parallel and periodically distributed fractures. On the right side of Fig. 1a, we provide a sketch of the described test for the case of normal incidence of a P wave, in which a vertical displacement is applied to the top boundary while no normal solid displacements are allowed at the lateral boundaries and at the bottom of the model. Additionally, the model is fully saturated with water and the test is performed at undrained conditions; that is, no fluid flow across the model boundaries is permitted.

Table 1 Material properties.

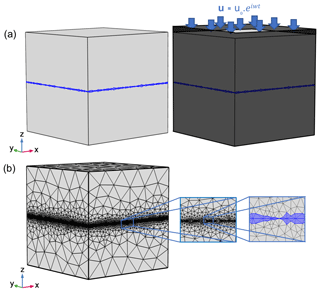
Figure 1 (a) REV (left) and oscillatory relaxation test, in which no normal solid displacements are allowed at the laterals and bottom of the numerical model and a vertical displacement is applied at the top of the model (right). (b) Tetrahedral meshing of the numerical model.

2.1 Equations of poroelasticity

Biot's (1941) equations in the space–frequency domain and in absence of external forces are

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathrm{\nabla }\cdot \mathit{\sigma }=\mathrm{0},\text{(2)}& {\displaystyle }i\mathit{\omega }\mathit{w}=-\left({\displaystyle \frac{\mathit{\kappa }}{\mathit{\eta }}}\right)\mathrm{\nabla }p,\end{array}$$

where σ is the total stress tensor, w is the relative fluid displacement vector, p is the fluid pressure, ω is the angular frequency, and i is the complex unity. The material properties κ and η are the permeability and the fluid viscosity, respectively. Equations (1) and (2), the total balance of forces and Darcy's law, respectively, are also known as consolidation equations. These equations are coupled through the constitutive equations of the porous medium (Biot, 1962):

$$\begin{array}{}\text{(3)}& {\displaystyle }\mathit{\sigma }=\mathrm{2}{\mathit{\mu }}_{\mathrm{m}}\mathit{ϵ}+\mathbf{I}\left({\mathit{\lambda }}_{\mathrm{m}}e-\mathit{\alpha }p\right),\text{(4)}& {\displaystyle }p=-M\mathit{\alpha }e-M\mathrm{\nabla }\cdot \mathit{w},\end{array}$$

where ϵ is the strain tensor, I denotes the identity tensor, and e is the cubical dilatation given by the trace of the strain tensor. The symbols λ_m and μ_m denote Lamé's parameters of the dry frame, and α and M are Biot's poroelastic parameters given by

$$\begin{array}{}\text{(5)}& {\displaystyle }\mathit{\alpha }=\mathrm{1}-{\displaystyle \frac{K_{\mathrm{m}}}{K_{\mathrm{s}}}},\text{(6)}& {\displaystyle }M={\left({\displaystyle \frac{\mathit{\alpha }-\mathit{\varphi }}{K_{\mathrm{s}}}}+{\displaystyle \frac{\mathit{\varphi }}{K_{\mathrm{f}}}}\right)}^{-\mathrm{1}},\end{array}$$

where K_m, K_s and K_f are the bulk modulus of the dry frame, the solid grains composing the rock frame and the fluid, respectively, and (ϕ) is the porosity. Combining Eqs. (2) and (4), the following expression can be obtained:

$$\begin{array}{}\text{(7)}& \mathrm{\nabla }\cdot \left(-{\displaystyle \frac{\mathit{\kappa }}{\mathit{\eta }}}\mathrm{\nabla }p\right)+\mathit{\alpha }i\mathit{\omega }\mathrm{\nabla }\cdot \mathit{u}+{\displaystyle \frac{i\mathit{\omega }p}{M}}=\mathrm{0},\end{array}$$

where u is the solid displacement vector. Finally, Eqs. (1) and (7), with the total stress tensor given by Eq. (3), can be used to express the consolidation equations in terms of the unknowns u and p. In 3-D, the solid displacement vector u has three directional components and the fluid pressure is a scalar.

2.2 Effective properties

We solve the system of Eqs. (1) and (7) employing Eq. (3) and using the finite element method. Considering auxiliary functions to represent the variables between nodes, the “weak” formulation is obtained by combining the differential equations (“strong” form) with natural (undrained) boundary conditions in an integral form, which allows for reducing the order of the spatial derivatives (Quintal et al., 2011). We input directly the weak formulation in the finite element software, COMSOL Multiphysics, where the boundary conditions corresponding to the described relaxation tests are imposed. The numerical model is discretised in tetrahedral elements (Fig. 1b), where quadratic interpolation is applied. The unknowns u and p are calculated for each considered frequency, from which the stress and strain fields are obtained in each element of the numerical model. For the case of a compressional wave propagating normal to the fractures (z direction), the complex effective P-wave modulus (H) and the P-wave attenuation, estimated as the inverse of the quality factor (O'Connell and Budiansky, 1978), are computed according to the following expressions:

$$\begin{array}{}\text{(8)}& {\displaystyle }H\left(\mathit{\omega }\right)={\displaystyle \frac{\langle {\mathit{\sigma }}_{zz}\left(\mathit{\omega }\right)\rangle }{\langle {\mathit{ϵ}}_{zz}\left(\mathit{\omega }\right)\rangle }},\text{(9)}& {\displaystyle }{Q}^{-\mathrm{1}}\left(\mathit{\omega }\right)={\displaystyle \frac{\langle \mathrm{Im}\left[H\right(\mathit{\omega }\left)\right]\rangle }{\langle \mathrm{Re}\left[H\right(\mathit{\omega }\left)\right]\rangle }},\end{array}$$

where 〈σ_zz(ω)〉 and 〈ϵ_zz(ω)〉 represent the volumetric averages of σ_zz and ϵ_zz over the whole numerical model for each frequency (e.g. Masson and Pride, 2007; Rubino et al., 2009; Jänicke et al., 2014), and Re and Im correspond to the real and imaginary parts of a complex number.

3 Results

In order to numerically analyse the general impact that fractures with variable aperture produce on seismic attenuation and velocity dispersion, we first consider fractures with simple geometries and distributions of contact areas. Then, we extend the investigation to fractures having realistic aperture distributions and perform a sensitivity analysis of the effective seismic response of the fractured medium in terms of density and correlation length of contact areas.

3.1 Fractures with simple aperture distributions

We first consider simple fracture models for illustrating general effects of contact areas distributions on the P-wave modulus normal to the fractures and the associated seismic attenuation. The numerical model is a cube of 4 cm sides having a horizontal fracture crossing its centre, that is, normal to the vertical (z) direction. This model is an REV of a medium containing a periodic distribution of parallel fractures with 4 cm separation between the central planes of two consecutive fractures. Figure 2 shows a representation of the central plane of a fracture with regular distribution of contact areas and another one with pseudo-random distribution. The aperture of the open regions of the fracture is constant and equal to 0.4 mm (blue regions), whereas the white square zones correspond to contact areas (i.e. aperture equal to zero). In both cases, the contact area density is 20 %.

The numerical results for the real part of the effective P-wave modulus and seismic attenuation normal to the fracture are presented in Fig. 3. When the P wave compresses the fractured medium, it creates a fluid pressure gradient between the fracture and the background due to their compressibility contrast. Consequently, a FPD process tends to equilibrate the pressures resulting in energy dissipation because of viscous friction in the pore fluid. Both models exhibit significant P-wave modulus dispersion and attenuation due to FPD between the fracture and the background. Although the responses presented in Fig. 3 are similar, the highest dispersion and attenuation is observed for the pseudo-random distribution of contact areas. The largest difference in their P-wave modulus responses occurs at the low-frequency limit. We compare these results with the analytical solution of White et al. (1975) for a fracture represented as a thin layer of constant thickness filled with the same soft material but without contact areas. Two models having fractures of constant thickness are considered, one of a thin layer having constant aperture of 0.4 mm and another one having equal total volume of open regions (that is, removing the volume occupied by the contact areas) as in the models shown in Fig. 2. We observe that the presence of contact areas reduces seismic attenuation as they increase the fracture stiffness. For a thin layer with the same volume as the open regions of fractures of Fig. 2 (i.e. a constant thickness of 0.32 mm), we observe minor changes in the seismic response with respect to the thin layer having 0.4 mm aperture. This means that the effects of contact areas on the mechanical behaviour of the fracture are more significant than the effects of reducing the volume of the open regions.

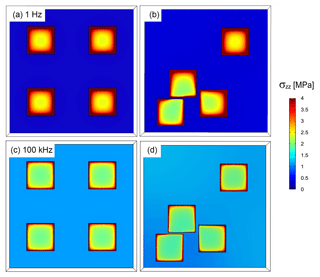
For better understanding the impact of contact area distributions on the seismic responses shown in Fig. 3, we plot the real part of the vertical component of the total stress field at the low- and high-frequency limits at the centre of the fracture (Fig. 4). The interaction between contact areas in the pseudo-random case results in a stress shielding, which means that the proximity of the contact areas caused a reduction of the stresses on them (Zhao et al., 2016). From Eq. (8), and given that the overall strain in the sample is the same in both cases, it follows that a reduction in the overall stress of the sample translates into a decrease of the effective P-wave modulus, in comparison with the regular distribution. At the low-frequency limit, as there is enough time for FPD between the fracture and the background, the stiffening effect of the fluid in the fractures is minimal. Therefore, given that the magnitude of the interaction effects depends on the compressibility contrast between contact areas and regions of open fracture, these are maximal at low frequencies. Further, Fig. 3 shows that the real part of the P-wave modulus for both models converges to a similar value at the high-frequency limit. This occurs because there is no time for fluid pressure exchange between the fracture and the background during a half-wave period, and therefore the stiffening effect of the fluid saturating the fracture is maximal. Hence, the effects of the interaction of the contact areas on the stress field are minimal, since the compressibility contrast between the background and the fracture is reduced (Fig. 4).

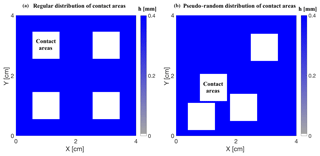
Figure 2 Fracture apertures with regular (a) and pseudo-random (b) distributions of contact areas. Blue zones represent open regions of the fracture with 0.4 mm aperture. Each contact area size is 0.9 × 0.9 cm, and the contact area density is 20 %.

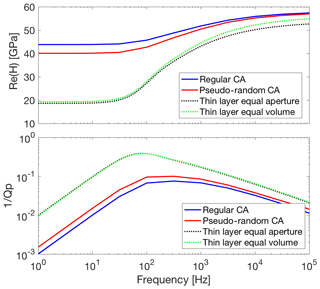
Figure 3 Real part of P-wave modulus (H) and attenuation as a function of frequency for wave propagation normal to the fracture models illustrated in Fig. 2. We also include White's solutions for two thin layer models having equal aperture and equal volume, respectively, of the open region of the fractures in Fig. 2.

Figure 4 Real part of the vertical (z) component of the total stress field at the centre of the fractures illustrated in Fig. 2 at 1 Hz (a, b) and at 100 kHz (c, d).

3.2 Fractures with realistic aperture distributions

In order to analyse the seismic response of realistic fractures, we perform numerical simulations considering fractures with variable aperture distributions generated following the stratified percolation approach of Nolte and Pyrak-Nolte (1991). Using this approach, a realistic spatial distribution of fracture contact areas can be generated with controlled statistical properties such as correlation length and density. Moreover, it allows us to produce variable aperture distributions of the open regions. A description of how the fracture models are generated is given in Appendix A. The consideration of such aperture distributions as realistic is based on their comparison with the imaging of the aperture distribution of a natural fracture network presented by Montemagno and Pyrak-Nolte (1999). The aperture of the fractures is given by the distance between the walls which are perfectly symmetrical with respect to the centre of the fracture (Fig. 1). After generation of fractures, the correlation length of contact areas is calculated following the approach of Blair et al. (1993), also used by Pyrak-Nolte and Morris (2000), which represents an approximation to their mean length. Consequently, for a given contact area density, as the correlation length decreases, the fracture exhibits more contact areas with smaller sizes and a narrower distribution of distances between them. Thus, increasing the correlation length of contact areas produces an increase in the mean distance between contact areas, that is, the mean length of the open regions. Using these kinds of fracture models, Pyrak-Nolte and Morris (2000) discussed the effects that contact area distributions produce on the mechanical properties of a fracture (i.e. specific stiffness), and they showed that uncorrelated distributions of contact areas produce stiffer fractures than correlated ones. This is in agreement with the results presented in Fig. 3, since a regular distribution of contact areas is analogous to an uncorrelated distribution considering that both have a narrow distribution of distances between contact areas.

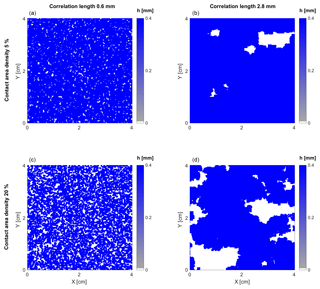
Figure 5 shows four fracture aperture distributions chosen for analysing the effects of density and correlation length of contact area on the seismic response of a fractured medium. To do so, we consider four REVs as the one presented in Fig. 1 with a different distribution of apertures for the horizontal fracture given by the models A, B, C and D of Fig. 5. The real part of the P-wave modulus and attenuation for a normally incident wave are shown in Fig. 6. We observe that a higher contact area density as well as a lower correlation length (model C) produce a stiffer fracture, as it can be seen from the relatively high and non-dispersive real part of the P-wave modulus. These observations can be understood by looking at Fig. 4 as, in this case, a regular distribution of contact areas is equivalent to an uncorrelated distribution. Moreover, these results are in agreement with analytical solutions, considering that an increase in the correlation length represents also an increase in the mean crack (or open region) length (Hudson and Liu, 1999; Zimmerman and Main, 2004). In such solutions, the excess compliance of a fracture increases with a larger crack length and decreases with a greater contact area density. Fracture B has the lowest density and the highest correlation length of contact areas. As expected, it is effectively the most compliant as can be seen in Fig. 6, given that it exhibits the lowest P-wave modulus and highest dispersion and attenuation. Interestingly, fractures A and D show comparable seismic responses despite their different aperture distributions. This is related to the fact that increasing the correlation length compensates for the increase in contact area density, resulting in fractures with similar effective compliances. Lastly, note that although the effect of the distribution of contact areas is maximal at the low-frequency limit, it also plays an important role for the effective compliance of the rock at the high-frequency limit (Fig. 6).

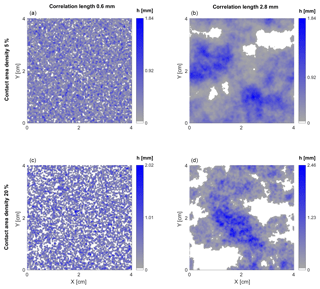
Figure 5 Fracture aperture distributions generated using a stratified percolation workflow (Nolte and Pyrak-Nolte, 1991). Upper models have 5 % of contact area density, while lower models have 20 %. Left models have a small correlation length and right models have a bigger correlation length. All models have a mean aperture of 0.4 mm and they are referred to in the text as models A to D (panels a–d, respectively).

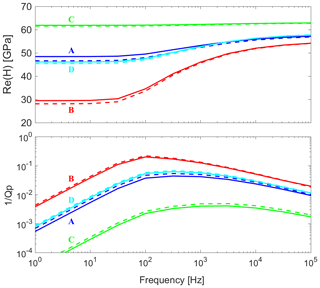
Figure 6 Real part of P-wave modulus (H) and attenuation for wave propagation normal to the fractures as a function of frequency. Solid lines correspond to fractures A, B, C and D with spatially variable aperture in the open regions (Fig. 5), while dashed lines correspond to fractures A, B, C and D with binary aperture (Fig. 7).

A common assumption in analytical models is that fracture compliance depends on the fracture volume and the distribution of the fracture microstructure, such as mean crack radius (e.g. Guo et al., 2017). For analysing the effect of the variable aperture in the open regions of the fractures, we consider simpler fracture models having the same contact area distributions of those shown in Fig. 5 but setting constant the aperture in the open fracture regions. The aperture is fixed to their mean value (i.e. 0.4 mm) (Fig. 7). We refer to this process as binarisation of the fractures, since it results in two values for the fracture aperture: zero in the contact areas and 0.4 mm in the open regions. During this process, the volume of the open regions, that is, the volume of the most compliant poroelastic material, remains unchanged. The seismic responses are also shown in Fig. 6, and we observe good agreement between results from fractures with binarised aperture (dashed lines) and those from the previous fractures with variable aperture in the open regions (solid lines). From this analysis of Fig. 6, the volume of the open regions of the fractures and the distribution of contact areas are the main characteristics controlling the fracture seismic response, which is in agreement with analytical models.

Figure 7 Fracture with binary aperture distributions derived from fracture models A to D in Fig. 5. The aperture in the open fracture regions is set equal to the mean value (0.4 mm) of the aperture distribution shown in Fig. 5.

In the analysis presented above, each fracture is one realisation of a pseudo-random generation process with given contact area density and correlation length. In order to analyse the variability of the results, we generated several fracture models with the same characteristics as model B (Fig. 5), which are referred to as realisations. We choose model B because it exhibits the highest attenuation (Fig. 6), and hence the variability of the results is expected to be higher than for uncorrelated distributions of contact areas (such as models A and C). For numerical convenience and supported by the comparison shown in Fig. 6, we consider binarised fracture models as in Fig. 7. The fracture models illustrated in Fig. 8a have equal contact area density (5 %) and correlation length (2.8 mm) to fracture B. In Fig. 8b, the corresponding real part of the P-wave modulus and attenuation are displayed as black circles for frequencies representative of the relaxed and unrelaxed limits (1 and 100 kHz, respectively) and at the attenuation peak frequency (∼100 Hz). The seismic response for model B of Fig. 5 is plotted as a solid red line for reference. The standard deviations of the real part of the P-wave modulus normal to the fractures are presented in Fig. 8c as a function of the number of realisations. We observe larger variability for low frequencies. As we previously illustrated in Fig. 4, this occurs because at the low-frequency limit, pore fluid pressure opposition to compression is minimal, and therefore the compressibility contrast between the background and the open regions of the fractures reaches the maximal value. As a consequence, the effects of the interaction between contact areas are more important and then a change in contact areas geometry, as the one taking place in each realisation, produces a slightly different fracture compliance. As frequency increases, there is less time for fluid pressure equilibration between fracture and background, the stiffening effect of the fluid saturating the fractures increases, and the effects of the interaction between contact areas are less significant, resulting in a smaller variability of the P-wave modulus. For the three analysed frequencies, the variability of the standard deviation became approximately stable after 15 realisations, and it is lower than 1 GPa. In other words, it is always lower than 2 % of the real-valued P-wave modulus.

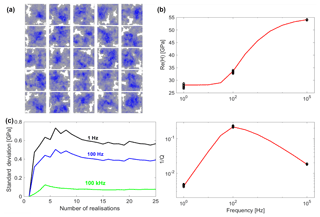
Figure 8 (a) Realisations generated with constrains of density and correlation length of contact areas equal to those of model B. The mean aperture value of all fractures is 0.4 mm. (b) Real part of the P-wave modulus and seismic attenuation normal to the fractures as a function of frequency. The solid red lines show seismic responses of fracture B and the black circles correspond to each realisation shown in panel (a) at considered frequencies after being binarised. (c) Standard deviation of the real part of the P-wave modulus as a function of total number of realisations.

3.3 Comparison between realistic and simplified equivalent fracture models

In studies on the effective seismic response of fractured media, a fracture is frequently represented as a thin compliant layer of constant thickness (e.g. Schoenberg, 1980; Gurevich, 2003; Brajanovski et al., 2006; Nakagawa and Schoenberg, 2007; Barbosa et al., 2016). To analyse the validity of such simple approaches, we estimate equivalent elastic properties of a fracture from the excess compliance computed for realistic fracture models (Fig. 5). We then compare the seismic response of simple fracture models, using the derived equivalent properties, with the numerical results for realistic fractures presented in Fig. 6.

For estimating the equivalent properties of the fractures, we follow the linear slip theory (Schoenberg and Douma, 1988), where the compliance of a dry rock can be split into the contributions from the background and from the presence of fractures, and compliance is defined as the inverse of the stiffness. In this case,

$$\begin{array}{}\text{(10)}& \mathbf{S}={\mathbf{S}}_{\mathrm{b}}+\mathbf{\Delta }\mathbf{S},\end{array}$$

where S is the total compliance matrix with coefficients S_ij and S_b is the compliance matrix of the dry background. The matrix ΔS is the excess compliance of the rock due to the presence of fractures which, in turn, is approximated as

$$\begin{array}{}\text{(11)}& \mathbf{\Delta }\mathbf{S}=\left(\begin{array}{cccccc}\mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& Z_N& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& Z_T& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& Z_T& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}\end{array}\right).\end{array}$$

Using Eqs. (10) and (11), and the fact that the effective stiffness matrix is the inverse of the compliance matrix, that is $\mathbf{C}={\mathbf{S}}^{-\mathrm{1}}$, the normal and shear excess compliances (Z_N and Z_T), respectively, can be obtained as

$$\begin{array}{}\text{(12)}& {\displaystyle }{Z}_N={\displaystyle \frac{L_{\mathrm{m}}-C_{\mathrm{33}}^{\mathrm{dry}}}{C_{\mathrm{33}}^{\mathrm{dry}}{L}_{\mathrm{m}}}},\text{(13)}& {\displaystyle }{Z}_T={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{m}}-C_{\mathrm{44}}^{\mathrm{dry}}}{C_{\mathrm{44}}^{\mathrm{dry}}{\mathit{\mu }}_{\mathrm{m}}}},\end{array}$$

where L_m and μ_m are the P-wave and shear moduli of the dry background based on properties given in Table 1. $C_{kk}^{\mathrm{dry}}$ values ($k=\mathrm{3},\mathrm{4}$) are numerically computed from applying corresponding compressional and shear oscillatory tests to the dry fractured models. Finally, we calculate the equivalent elastic properties from the excess compliances as (Brajanovski et al., 2005)

$$\begin{array}{}\text{(14)}& {\displaystyle }{\mathit{\mu }}_{\mathrm{fr}}^{\mathrm{eqv}}={\displaystyle \frac{f_{\mathrm{c}}}{Z_T}},\text{(15)}& {\displaystyle }{K}_{\mathrm{fr}}^{\mathrm{eqv}}={\displaystyle \frac{f_{\mathrm{c}}}{Z_N}}-{\displaystyle \frac{\mathrm{4}}{\mathrm{3}}}{\mathit{\mu }}_{\mathrm{fr}}^{\mathrm{eqv}},\end{array}$$

where ${\mathit{\mu }}_{\mathrm{fr}}^{\mathrm{eqv}}$ and $K_{\mathrm{fr}}^{\mathrm{eqv}}$ represent the dry shear and bulk moduli, respectively, of an equivalent fracture of constant thickness, and f_c is the fracture volume fraction of the models, given by the ratio between the fracture volume and the volume of the numerical volume. In this case, as the area in the plane xy of the numerical model is equal to that of the fracture (Fig. 1), f_c is given by the ratio between the fracture mean aperture and the height of the model (i.e. $f_{\mathrm{c}}=h_{\mathrm{mean}}/H$). In order to keep the pore volume of the fractures the same for the equivalent planar fractures, we also calculate the weighted average of the fractures porosities (i.e. fracture equivalent porosity ${\mathit{\varphi }}_{\mathrm{fr}}^{\mathrm{eqv}}$) for the models shown in Fig. 5 accounting for the effect of contact areas. That is,

$$\begin{array}{}\text{(16)}& {\mathit{\varphi }}_{\mathrm{fr}}^{\mathrm{eqv}}={\mathit{\varphi }}_{\mathrm{b}}{\mathit{\rho }}_{\mathrm{ca}}+{\mathit{\varphi }}_{\mathrm{fr}}(\mathrm{1}-{\mathit{\rho }}_{\mathrm{ca}}),\end{array}$$

where ϕ_b is the background porosity (which is the same as for the contact areas), ϕ_fr is the porosity of the open regions of the fracture, ρ_ca is the contact area density, with ρ_ca=0.05 for models A and B, and ρ_ca=0.2 for models C and D (Fig. 5). Also, ϕ_b=0.1 and ϕ_fr=0.9 as presented in Table 1. Values obtained from Eqs. (12)–(16) are shown in Table 2.

To support the consideration of our models as realistic, the fracture compliances presented in Table 2 are in reasonable agreement with estimated values observed in field and laboratory experiments for fractured rocks (Worthington and Lubbe, 2007; Hobday and Worthington, 2012; Barbosa et al., 2019). According to the linear trend proposed by Worthington and Lubbe (2007), our models are representative of fractures with lengths ranging from a few metres to tens of metres. Furthermore, fixing a similar value for both the normal and shear compliances is usually assumed (Liu et al., 2000; Sayers, 2002); that is $Z_N/Z_T\approx \mathrm{1}$. Lubbe et al. (2008) used rock samples with artificial fractures to calculate normal and shear compliances from laboratory measurements and they found fracture compliance ratios approaching 0.5. In agreement with their results, the fractures presented in this work exhibit compliance ratios between 0.5 and 1, but closer to 0.5 (Table 2).

Table 2 Fracture normal and shear excess compliances and equivalent properties of a fracture represented as a poroelastic thin layer.

3.3.1 P-wave modulus analysis

After computing the equivalent dry bulk and shear moduli and porosity for each fracture (Eqs. 12–16), as well as the mean aperture, we employ the analytical solution of White et al. (1975) to quantify the P-wave modulus normal to a periodic distribution of constant-thickness fractures having these equivalent fracture properties (${\mathit{\mu }}_{\mathrm{fr}}^{\mathrm{eqv}}$, $K_{\mathrm{fr}}^{\mathrm{eqv}}$, ${\mathit{\varphi }}_{\mathrm{fr}}^{\mathrm{eqv}}$ and h_mean). Figure 9 shows excellent agreement of the real part of the P-wave modulus and attenuation between fractures with variable aperture distributions (Fig. 5) and equivalent constant-thickness fractures. These results show that a very simple fracture geometry, such as a thin layer of constant thickness, can approximate much more complicated fracture geometries if appropriate equivalent properties (accounting for contact area distributions) are used.

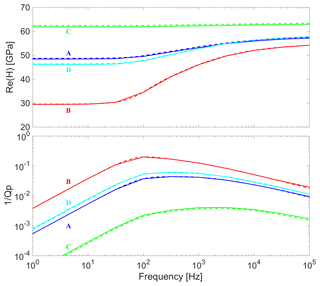
Figure 9 Real part of P-wave modulus (H) and attenuation for wave propagation normal to the fractures as functions of frequency. Solid lines correspond to fracture models A, B, C and D from Fig. 5 with variable aperture distributions. Dashed lines correspond to fracture models of constant thickness using equivalent fracture properties (Table 2).

3.3.2 Stiffness matrix generalisation

To further verify and generalise the validity of the equivalent fracture model of constant thickness, we extended the methodology presented by Rubino et al. (2016) to numerically compute the effective stiffness matrix from 3-D simulations for the realistic fracture models of Fig. 5. To do so, we numerically performed oscillatory relaxation tests following the methodology described in Sect. 2 but considering three normal relaxation tests (one for each direction: x, y and z) and three shear relaxation tests (shearing in the xy, xz and yz planes). We compare the results with those of the analytical solution for transverse isotropy (TI) media proposed by Krzikalla and Müller (2011). This analytical solution is based on the relaxed and unrelaxed poroelastic Backus averages of a layered porous medium consisting of a periodic distribution of a stiff background and a soft thin layer. Moreover, they showed that a single relaxation function can be used to link the relaxed and unrelaxed limits of all components of the stiffness matrix. The corresponding frequency dependence is derived from the P-wave modulus predicted by White et al. (1975). We use such soft layer to approximate a fracture of constant thickness having the equivalent properties (${\mathit{\mu }}_{\mathrm{fr}}^{\mathrm{eqv}}$, $K_{\mathrm{fr}}^{\mathrm{eqv}}$, ${\mathit{\varphi }}_{\mathrm{fr}}^{\mathrm{eqv}}$ and h_mean) obtained as described above.

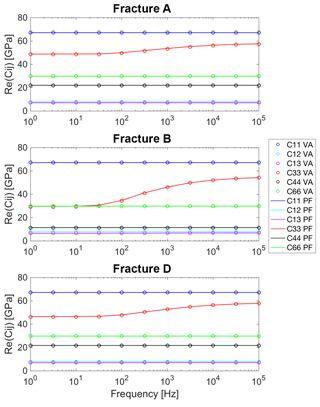
Figure 10 Real part of the components of the effective stiffness matrix as functions of frequency. Circles correspond to numerical simulation for fracture models A, B and D with variable aperture (VA) distributions shown in Fig. 5 (fracture model C was omitted due to its negligible P-wave modulus dispersion). Solid lines correspond to the analytical solution of Krzikalla and Müller (2011) for planar fracture (PF) models using equivalent fracture properties (Table 2).

Figure 10 illustrates the real part of the five independent coefficients C_ij for a medium with TI and C₆₆, given by $C_{\mathrm{66}}=\mathrm{0.5}(C_{\mathrm{11}}-C_{\mathrm{12}})$. The circles in the plots correspond to fractures with variable aperture distribution (Fig. 5), and the solid lines correspond to the analytical solution considering fractures of constant thickness with equivalent properties (Table 2). For brevity, fracture C was omitted due to its negligible P-wave modulus (C₃₃) dispersion. The stiffness matrix coefficients C₁₁ and C₃₃ dominate the stress in the medium as a response to a horizontal and vertical compression, respectively (x and z directions). C₄₄ and C₆₆, on the other hand, dominate the stress as a response to a vertical and a horizontal shear deformation, respectively (yz and xy directions). The coupling coefficients C₁₂ and C₁₃ are also shown. The effective anisotropy of all the models is vertical transverse isotropy (VTI), although models D and B, due to their high correlation lengths, present a subtle discrepancy between C₄₄ and C₅₅, which is below 0.7 GPa (omitted in the figure for brevity). Furthermore, all the stiffness coefficients of fracture models A and D are similar, which extends the conclusion about the counteracting effects of the correlation length and density of the contact areas observed for the normal P-wave modulus to the overall anisotropy of the models (Sect. 3.2). Finally, the excellent agreement between the results for models with realistic and simple geometries for all the stiffness matrix coefficients generalises our results of Sect. 3.3.1 to all incidence angles and wave modes.

4 Discussion

Obtaining information on the hydraulic and mechanical behaviours of fractures by means of their seismic responses is an ultimate goal in fracture characterisation. Pyrak-Nolte and Morris (2000) showed that in response to an increase in normal stress applied to a fracture, new contact areas would be created, affecting the fluid flow path through the fracture. In this work, we used similar fracture models to study the relationship between fracture microstructure and their corresponding seismic response. We showed that the effective seismic attenuation and velocity dispersion due to FPD between the fracture and the background are sensitive to changes in the correlation length and the density of contact areas. This suggests that the effects of FPD on the seismic response of fractures are potentially affected by normal stress variations and thus represent an opportunity for indirectly monitoring the associated fluid flow changes.

Milani et al. (2016) showed that in the case of aligned periodically distributed fractures having constant aperture, the models are essentially unidimensional, and no boundary effects would play a role given that the stress fields are constant within the sample as a consequence of Eq. (1). However, the distribution of the fracture apertures that we considered imply a departure from the unidimensional solution, suggesting that boundary effects may affect the results. To study these possible effects, we plotted the normalised vertical stress field in the case of the binarised model B (i) for a single repeating unit cell (RUC) and (ii) for four RUCs (not shown here). Since we found both normalised stress fields to be equal, this analysis supports the fact that no boundary effects or undesired interaction between fractures are affecting the results of the numerical relaxation tests. Moreover, this represents an extension of the results shown by Milani et al. (2016) for fractured media with 2-D geometries to 3-D.

We also showed that the density and correlation length of contact areas control the normal and shear fracture compliances (Fig. 6), and thus first-order analytical solutions based on these properties, such as the model proposed by Hudson and Liu (1999), could represent a good approximation to the mechanical behaviour of realistic fractures. However, as shown in Fig. 4, the effects of the mechanical interactions between contact areas must be considered for accurately obtaining the equivalent properties of the material filling the fractures. In this sense, we showed in Fig. 10 that a simple layer of constant thickness can successfully reproduce the seismic response of fractures with intricate aperture distributions provided that appropriate elastic moduli, porosity and aperture are used. In this work, such equivalent properties are calculated from the excess compliances of the realistic fractures, and therefore they account for the effects of distribution and interaction of contact areas. Furthermore, since the linear slip model can be interpreted as an approximation of the seismic response of a constant-thickness fracture (Schoenberg and Douma, 1988; Brajanovski et al., 2005; Guo et al., 2017), our results suggest that this model can also satisfactorily approximate the seismic response of the realistic fracture models considered in Fig. 5.

5 Conclusions

The aim of the present contribution was to analyse the effects of variable aperture distributions of 3-D fracture models on FPD between fractures and background. To do so, we numerically quantified the effective frequency-dependent stiffness matrix coefficients and seismic attenuation for realistic fracture models representing REVs of media containing periodically distributed parallel fractures. Our fracture models were characterised by aperture distributions generated using a stratified percolation algorithm and accounting for different densities and correlation lengths of contact areas. We showed that for a given density of contact areas, fractures with correlated distributions of contact areas (i.e. highest correlation length) exhibit higher P-wave modulus dispersion and seismic attenuation than those with a low correlation. Furthermore, lower P-wave modulus dispersion and seismic attenuation were observed when increasing contact area density for a given correlation length. This compensatory effect allows fractures with highly different aperture distributions to produce similar seismic responses. Moreover, although the effects of distribution of contact areas on the P-wave modulus are maximal at the low-frequency limit, these distributions also play an important role at the high-frequency limit. We also observed that, if the distribution of contact areas is fixed, fracture mean aperture (which controls fracture volume) dominates the seismic response due to FPD effects, while the variable aperture in the open regions of the fracture has a negligible influence.

Finally, we demonstrated that a simple fracture geometry such as thin layers with constant aperture and appropriate equivalent physical properties produces the same effective anisotropic seismic response of fractures with a much more intricate geometry. The equivalent elastic properties can be obtained from the excess fracture compliances, determined according to the linear slip theory, as long as the effects of contact areas are accounted for. Our results validate the use of simple models of fractures having constant thickness for numerically simulating the effects of fractures with realistic geometries which, in turn, can significantly reduce computational cost and overcome meshing limitations.

Appendix A: Realistic fracture model generation

To generate the fracture models shown in Fig. 5, we follow the stratified percolation approach described by Nolte and Pyrak-Nolte (1991). To do so, we define a matrix initialised with zeros in all its cells, which represents the initial aperture distribution (aperture equal to zero) of a square fracture. The first step consists of stochastically selecting a number (x) of matrix cells. Then, each of those x cells becomes the centre of a new stochastic distribution of x cells confined to a square area around them. The squares are defined by a certain number of cells of the matrix. This process is repeated n times, called tiers, by reducing the size of the squares from one tier to the next one. It means that, if a fix number of cells (x) are stochastically located inside each of the squares corresponding to the previous tier, this finally results in selecting xⁿ cells inside the matrix. In the last tier, which is number n (corresponding to the minimum square size), a value 1 is assigned to each of the xⁿ selected cells. Moreover, as there could be overlap between the areas of the squares in all the tiers, and this is a cumulative process, at each time a value 1 is added to a cell of the matrix, the aperture of the fracture at that cell is increased. After the values of the (x) cells of the last tier (n) have been added with a 1, the contact areas are given by the matrix cells remaining with the initial zeros as values. The correlation length of the contact areas is calculated after the generation process following the methodology proposed by (Blair et al., 1993). In general, a high number of tiers (n) with a low number of cells (x) creates a correlated distribution of contact areas. On the other hand, a low number of tiers (n) with a big number of cells (x) builds a non-correlated distribution of contact areas (Pyrak-Nolte and Morris, 2000). The workflow for building up our models consists of importing the matrix, generated using the above-described algorithm, into COMSOL Multiphysics by using an .stl format. The matrix, representing the aperture distribution of the fracture, is converted into a surface and a fracture volume is generated by symmetrically duplicating the fracture surface with respect to the horizontal middle plane. As a result of this process, we obtain a fracture volume with symmetrical walls. Finally, the obtained fracture volume is vertically scaled to yield the desired mean fracture aperture and embedded in a cubic model (Fig. 1a).