The Geodynamic World Builder: a solution for complex initial conditions in numerical modeling

The Geodynamic World Builder is an open-source code library intended to set up initial conditions for computational geodynamic models in both Cartesian and spherical geometries. The inputs for the JavaScript Object Notation (JSON)-style parameter file are not mathematical but rather a structured nested list describing tectonic features, e.g., a continental, an oceanic or a subducting plate. Each of these tectonic features can be assigned a specific temperature profile (e.g., plate model) or composition label (e.g., uniform). For each point in space, the Geodynamic World Builder can return the composition and/or temperature. It is written in C++ but can be used in almost any language through its C and Fortran wrappers. Various examples of 2-D and 3-D subduction settings are presented. The Geodynamic World Builder comes with an extensive online user manual.

1 Introduction

Geodynamic modeling has been used in the past four decades to help us better understand the physical processes of Earth's interior, including large-scale mantle convection and plate tectonics, or detailed processes of crustal deformation. Numerical modeling of geodynamic processes involves solving the pertinent partial differential equations (PDEs) of mass, momentum and energy conservation supplemented with rheological laws, material parameters and with an equation of thermodynamic state relating, e.g., density, temperature and pressure (e.g., Gerya, 2010; Schubert et al., 2001). In addition, these PDEs must be constrained by boundary conditions (e.g., velocity, pressure, temperature or heat-flux boundary conditions), which can be time dependent, and by initial conditions which describe the starting model for solving the geodynamic problem at hand. For example, 3-D initial models of a geometrically simplified nature are often constructed for modeling of generic subduction evolution using plate boundaries and lithosphere domains that are parallel to the sides of the (rectangular) model domain (e.g., Yamato et al., 2009; Stegman et al., 2010; Brune and Autin, 2013; Schellart and Moresi, 2013; Duretz et al., 2014; Holt et al., 2015; Leng and Gurnis, 2015; Naliboff and Buiter, 2015; Kiraly et al., 2016; Schellart, 2017). When numerically simulating (regions of) the Earth, geometrically more complex initial models are required, e.g., involving the starting plate tectonic layout, initial trench geometry and slab shape for use in either instantaneous dynamics modeling or as an initial model for modeling of subduction evolution (e.g., Alisic et al., 2012; Liu and Stegman, 2011; Jadamec and Billen, 2010, 2012; Chertova et al., 2014; Billen and Arredondo, 2018; Zhou et al., 2018). Such initial model setups cannot be easily created, adapted or shared with the community, nor easily transferred to another code. We present in this paper a solution to these problems in the form of an open-source code library, the Geodynamic World Builder (GWB), which has been designed to be user-friendly, extensible and portable across different platforms. We present the first stable version of the GWB which focuses on creating geometrically complex 3-D initial models (geometry, composition and temperature) consisting of first-order plate tectonic features such as continental and oceanic plates, oceanic ridges and transform faults and 3-D lithosphere subduction. These configured initial models are intended to help advance research into simulations instantaneous dynamic modeling and of plate tectonic evolution with a wide range of geometric complexity.

2 Geodynamic World Builder philosophy

2.1 User philosophy

In this section, we describe the philosophy of how tectonic features such as plates, ridges, faults and slabs can be parameterized by lines and areas that implicitly define volumes to which temperature and composition models can be assigned. A composition is a part of the model that is assigned a particular identifying label and in addition an indicator which is given a value between 0 and 1. This indicator can be used by codes using the GWB output to ascribe physical properties to different model regions.

To minimize user effort, the GWB utilizes a parametrization of 3-D structures by 2-D coordinate input, by defining their (projected) location on the surface. The GWB can be used to create initial models in Cartesian and spherical geometries.

User input files should be specified in JavaScript Object Notation (JSON) (http://json.org/, last access: 17 August 2019), which is an internationally standardized language (ISO/IEC 21778). We use a relaxed form of JSON which allows comments, NaNs and tailing commas to improve usability through RapidJSON (http://rapidjson.org/, last access: 17 August 2019). The user inputs coordinates and can assign particular properties to features such as “linear” for a temperature profile or “uniform” for the compositional makeup of the plate. Note that only a subset of the options is mentioned in this paper. We refer to the online Geodynamic World Builder manual (https://geodynamicworldbuilder.github.io, last access: 17 August 2019) for the complete listing.

The GWB uses a hierarchical overlay of features. This means that features defined first are spatially overlain by features defined later in places where both overlap. The GWB recognizes two types of features: area features and line features, which will be explained in the following sections. A possible third type of features, point features, will be discussed in Sect. 4.

2.1.1 Continental lithosphere plate

A continental plate is an “area feature” in the GWB and is defined by its surface perimeter and its thickness. The perimeter is specified as a list of points which enclose the continental area. Within the defined volume of the continental plate, the GWB offers various options for defining temperature values and compositions. For example, a continental plate can be assigned multiple layers of different compositions and a linear geotherm that matches a predefined adiabatic mantle temperature at the base of the lithosphere. We note that continental lithosphere with a variable thickness is a development for future releases of the GWB but can be mimicked in the present version by specifying contiguous continental areas with different thickness. Also, continental topography is currently not explicitly implemented, but it can be achieved through a sticky air approach, where air is a composition of varying thickness atop the model (Schmeling et al., 2008; Crameri et al., 2012).

2.1.2 Oceanic lithosphere plate

Like the continental plate, the oceanic plate is parameterized as an area feature with a flat surface. We have implemented the “plate model” (e.g., Fowler, 2005) for assigning an age-dependent temperature to oceanic lithosphere. In Sect. 3.1.2, we will show an example of a ridge–transform system with ridge jumps. The workaround for implementing oceanic bathymetry is the same as that for the continental lithosphere plate.

2.1.3 The mantle

The upper and lower mantles can also be parameterized as an area feature that starts below the lithosphere or at the surface and is overlain by lithosphere in a later building stage. This allows for defining a upper and lower mantle and to insert specific volumetric structures such as large low shear wave velocity provinces (LLSVPs) at the core-mantle boundary in the same way as, for example, an oceanic plate but at depth. In the present version, these mantle features can be assigned a radially uniform, linear or adiabatic temperature profile. Future versions may include laterally varying temperature or compositions, e.g., scaled from seismic tomography models (e.g., Steinberger et al., 2015).

2.1.4 A subducting plate

A subducting plate is a “line feature” in the GWB and is defined by the location of the trench and one or more depth segments each describing a part of the geometry of the subducting slab. They are defined by a length and by thicknesses and dip angles at the beginning and end of the slab segment. In sequence, these segments can make up a smoothly varying slab geometry which can, for example, flatten in the upper mantle transition zone, or may prescribe a slab entering the lower mantle. Every point in the trench coordinate list defines a vertical section of the subducting plate that may consist of one or several slab segments. Both sections and segments can vary in length, dip angle or thickness. The length of a subducting slab is always computed as the length along the top of the slab so that this can straightforwardly represent the amount of relative plate convergence during a certain period. The dip angle is defined as the angle between the surface and the local plunge of the slab. The dip angle is specified at the start and end points of each depth segment along the vertical section. Dip angles are linearly interpolated along a segment. The overall direction of slab dip can be to either side of the trench and is selected by specifying for each subducting plate an additional point at the surface, the “dip point”, at the slab dip side of the trench segment (see Fig. 8). Slab dip is linearly interpolated between subsequent vertical slab segments. This parametrization allows for constructing smoothly varying 3-D slab morphology (see, for example, Fig. 9). Note that it is also possible to give slabs a starting depth to configure detached slabs.

For each point at the surface of the slab, the depth and the distance to the trench, as measured along the surface, are available and can be used to assign slab temperatures, e.g., by using the McKenzie (1970) slab temperature model. Because the McKenzie (1970) slab temperature model will be used in all examples involving slabs, we will present the equations and implementation here shortly. The temperature in every point in the slab is given by

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& T(x_{\mathrm{s}},z_{\mathrm{s}})=\exp \left({\displaystyle \frac{\mathit{\alpha }g}{C_{\mathrm{p}}}}d\right)\left({\mathit{\theta }}_{\mathrm{1}}+\mathrm{2}\left({\mathit{\theta }}_{\mathrm{1}}-\mathrm{273.15}\right)\sum _{n=\mathrm{1}}^{\mathrm{\infty }}{\displaystyle \frac{(-\mathrm{1}{)}^n}{n\mathit{\pi }}}\right.\\ & \left.\exp \left(\left(R-{\left(R^{\mathrm{2}}+n^{\mathrm{2}}{\mathit{\pi }}^{\mathrm{2}}\right)}^{\frac{\mathrm{1}}{\mathrm{2}}}\right)x_{\mathrm{s}}\right)\sin \left(n\mathit{\pi }{z}_{\mathrm{s}}\right)\right),\end{array}\end{array}$$

where x_s is the dimensionless down dip distance $x_{\mathrm{s}}=\frac{x}{l}$, where x is the down dip distance, and l is the thickness of the subducting plate; z_s is the dimensionless distance from the bottom of the slab to the top: $z_{\mathrm{s}}=\frac{z}{l}$, where z is distance form the bottom of the slab, α is the thermal expansion coefficient, g is the norm of the gravity, C_p is the specific heat at constant pressure, d is the depth below the surface, θ₁ is the potential mantle temperature at the earths surface, and R is the thermal Reynolds number defined as

$$\begin{array}{}\text{(2)}& R={\displaystyle \frac{\mathit{\rho }{C}_{\mathrm{p}}vl}{\mathrm{2}\mathit{\kappa }}},\end{array}$$

where ρ is the density, v is the velocity down dip, l is the thickness of the slab, and κ is the thermal conductivity. This formulation is slightly different from the one presented in McKenzie (1970), with the difference that this formulation is not dependent on a constant angle for the slab but directly on the depth, which is what the angle is used for in the original paper.

2.1.5 A fault

To allow for complicated fault shapes (e.g., listric faults), faults are also parameterized as line features. An important difference between faults and subducting plates is that for subducting plates the trench defines the top of the plate at the plate boundary, while for faults the line feature defines the center of the fault with respect to which a fault thickness can be defined.

2.2 Code philosophy

The following design principles define the Geodynamic World Builder:

1. A single text-based input file centered around plate tectonic terminology (as explained in Sect. 2.1). The particular syntax is specified in the online manual and will be illustrated with examples below.

2. Code, language and platform independence: The GWB is designed to be integrated in the different geodynamic codes through a simple interface. The library is written in C++ and has official interfaces (wrappers) to C and Fortran, and it is possible to call the GWB from the command line. Note that the C wrapper enables calling the GWB from almost any other language like Python and MATLAB. The code is continuously tested with every change on the Linux, OS X and Windows operating systems.

3. Up-to-date user manual and code documentation. Manual and doxygen (http://doxygen.nl/, last access: 17 August 2019) code documentation are provided through https://geodynamicworldbuilder.github.io (last access: 17 August 2019).

4. Safe use in parallel codes: The GWB is split into two phases. The setup phase, encapsulated in the function create_world, is not thread-safe, but upon completion the generated “world object” is thread-safe and can be used to query temperature and compositions in parallel.

5. Readable and extensible code: Following ASPECT (Kronbichler et al., 2012; Heister et al., 2017), we use a plugin system for different parts of the code. Such plugins enable users to add functionalities such as plate tectonic features or coordinate systems without knowledge of the rest of the code.

6. Version numbering (using Semantic Versioning 2.0.0; https://semver.org/, last access: 17 August 2019). The input file should specify the major version number that must match the version number of the used GWB. Before the release of major version 1, backwards incompatible changes may be made in minor versions, because they will be beta releases. This implies that the input files for major version 0 also must contain the minor version number. All these features help to ensure reproducibility of results.

3 Using the World Builder

To exemplify input files and to show the capabilities of the Geodynamic World Builder, we show here three 2-D examples and two 3-D examples of the GWB visualized through the stand-alone visualization application. This application creates so-called vtu files which can be visualized by programs like ParaView (https://www.paraview.org/, last access: 17 August 2019). Furthermore, we show examples of GWB use with the SEPRAN (van den Berg et al., 2015), ELEFANT (Plunder et al., 2018) and ASPECT codes. These examples are intended to illustrate the ease of use in different codes instead of the physics details of the models shown. The annotated input files to create these models are presented in Appendices A to F and are part of the GWB repository.

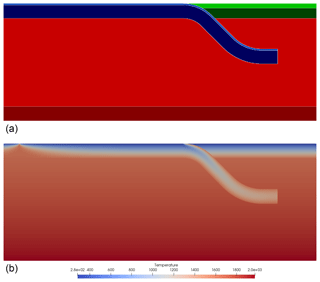
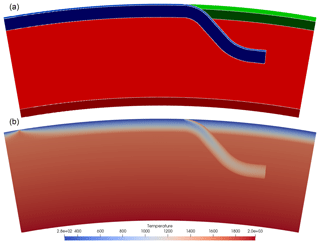
Figure 1 se-2019-24Panel (a) shows the distribution of different compositions through the model domain. The oceanic crust composition is light blue, the oceanic lithosphere is dark blue, the continental crust is light green, the continental lithosphere is dark green, the upper mantle is light red, and the lower mantle is dark red. Panel (b) shows the temperature distribution (in Kelvin) in the model.

3.1 Stand-alone examples

The GWB has an option to create a ParaView file of the GWB input file. This can be useful for model creation or visualization support of presenting geodynamic hypotheses, or for checking the user-designed model prior to using it in a next step, e.g., for creating an initial model for geodynamic modeling.

3.1.1 2-D subduction

Here, we show two subduction models, one in Cartesian coordinates (Fig. 1) and the same model in spherical (effectively cylindrical) coordinates (Fig. 2), which were created through the input files in Appendix A. These input files only differ in the selected coordinate system and whether the supplied coordinates are in meters or in degrees. The model has a 95 km thick oceanic plate, of which the top 10 km define the crust, and which turns into a 500 km long subducting slab in the center of the domain. The temperature in the oceanic plate follows the plate model (Fowler, 2005) with a bottom temperature of 1600 K. The slab temperature is computed using the McKenzie model for a particular slab history. The model also contains a 100 km thick continental plate of which the top 30 km is crust. Furthermore, the upper and lower mantles are given different compositions and follow a linear temperature profile in the upper mantle from 1600 K at 95 km depth to 1820 K at 660 km depth and in the lower mantle from 1820 at 660 km depth to 2000 at 1160 km depth.

This example is created by placing the features in a particular order in the input file. The features overlay, and in this case overwrite, an adiabatic background temperature and all compositions set to zero. This example consists of five features: an oceanic plate, a continental plate, an upper mantle, a lower mantle and a subducting plate. The first four do not overlap in their input definition, so the order of definition in the Geodynamic World Builder input file does not make a difference in the result. The subducting plate overwrites parts of the oceanic plate, continental plate and the upper mantle, which is effectuated by defining the slab after these three features. For each feature, temperature and composition models are selected.

Figure 2 The same as setup as in Fig. 1 but now in spherical geometry. Panel (a) shows the composition; panel (b) shows the temperature.

3.1.2 3-D ocean spreading

We show in Fig. 3 a 3-D rifting model with two rift systems next to each other. The temperature is defined by the plate model. The mantle is given an adiabatic geotherm defined by θ_Sexp (αgd∕C_p), where θ_S is the potential surface temperature of the mantle, α is the thermal expansion coefficient, g is the gravitational acceleration, C_p is the specific heat, and d is the depth. The input file of this example consists of the definition of the mantle domain followed by two oceanic plates, which form the two ridge–plate systems. The two oceanic plates are exactly the same, except for the shifted ridge location. The input file for this example can be found in Appendix B.

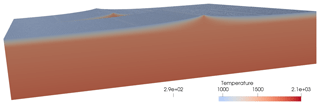
Figure 3 The temperature field of the 3-D two-rift system example. Material with a temperature below 950 K has been omitted in order to better show the rifts. Note the second rift system in the background.

Figure 4 The temperature field of the 3-D subduction example. Note the smooth transition between the upper and lower parts of the subduction system in the top figure and the curved geometry of the slab in panel (b). For visualization purposes, we have omitted the top 25 km of the model in panel (a).

3.1.3 3-D subduction

Figure 4 shows a 3-D example defining a subduction geometry similar to the one in Plunder et al. (2018). In this example, the trench consists of three connected straight lines. To create a smooth transition between these sections, the user can choose to use a monotone spline interpolation between the coordinates given by the user. This example includes a linear temperature upper and lower mantle as described in the 2-D subduction example. The 95 km thick oceanic plate and the 120 km thick continental plate features are both defined before the subducting plate feature, of which the trench is defined along the interface between the two. The slab itself is 95 km thick and consists of four segments: one 200 km long segment which goes from a dip angle of 0 to 45^∘ and one 400 km long segment which has an angle of 45^∘, one 200 km long segment which goes from 45 to 0^∘ and one 100 km long segment with a constant dip angle of 0^∘. The input file for this example can be found in Appendix C.

3.2 Using the GWB with SEPRAN

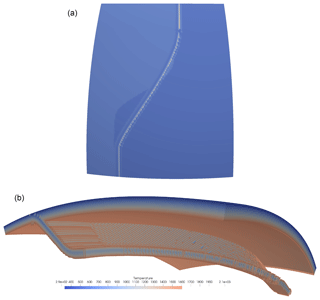
SEPRAN is a general purpose finite element toolkit applied in engineering problems as well as in development of 2-D and 3-D numerical models in geodynamics and planetary science (Chertova et al., 2012, 2014; Čížková et al., 2012; van den Berg et al., 2015, 2019; Zhao et al., 2019). The model contains a lithospheric slab subducting under an overriding plate as shown in Fig. 5. Subduction is driven in a self-consistent way by the ridge push resulting from the thickening of the oceanic plate and the negative buoyancy of the subducted slab. Free-slip impermeable boundary conditions are imposed on the flow. The top of the subducting lithosphere consists of a weak crustal layer, 10 km thick and with a uniform viscosity of 10²⁰ Pa ⋅ s. This weak crustal layer plays an essential role in preventing the locking of the subducting lithosphere with the overriding plate that would stop the subduction process (Androvičová et al., 2013). The mantle underlying the crust has a temperature- and pressure-dependent viscosity with an Arrhenius-type parametrization representative of diffusion creep in olivine under upper mantle pressure and temperature conditions. Viscosity is modeled as a material property for the crustal layer material and the mantle material. Material transport is implemented using particle tracers that are advected by the convective flow. The medium is described as a mechanical mixture of materials with contrasting properties.

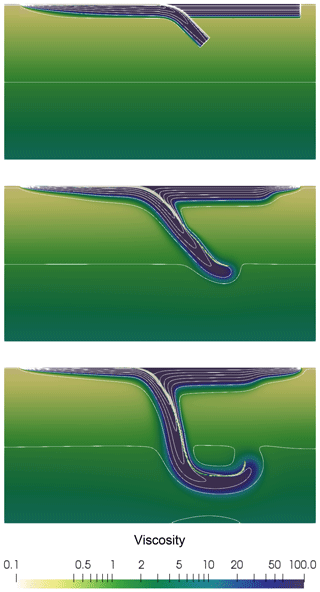
Figure 5 Dimensionless viscosity field in log scale superimposed with 10 (dimensionless) temperature (between 0 and 0.82) isocontours.

A 2-D rectangular domain of 1000 km depth and 2000 km width is used. The initial thermal and composition state is created using the Fortran wrapper of the GWB library. The GWB tool is called in a loop over all nodal points of the finite element method (FEM) mesh to define the initial temperature field for the subsequent convection calculations. In a similar way, the material distribution of the initial state is defined by calling the composition function of the GWB library in a program loop over particle tracers. The input file for this example can be found in Appendix D.

3.3 Using the GWB with ELEFANT

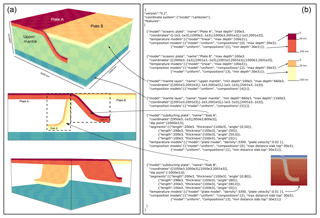
ELEFANT is a 2-D/3-D finite element code for geodynamic problems (Maffione et al., 2015; Lavecchia et al., 2017; Thieulot, 2017; Plunder et al., 2018) written in Fortran. It principally relies on bi-/trilinear velocity-constant pressure elements and uses the marker-in-cell technique to track materials. In order to demonstrate the GWB flexibility of use, a 3-D double subduction setup was created with the Fortran wrapper of the GWB (see Fig. 6): a composition between 1 and 6 was then easily assigned to all markers (two different oceanic crusts and oceanic lithospheres, one upper mantle and one lower mantle) and a temperature based on the McKenzie model (McKenzie, 1970) was prescribed onto the FE mesh, as shown in Fig. 7.

Figure 6 Example ELEFANT query routine using the GWB-supplied Fortran wrappers composition_3d() and temperature_3d(): (a) a loop runs over all markers and determines for each the composition at its location; (b) a loop runs over all grid points and the GWB returns its temperature as a function of their spatial coordinates.

Figure 7 (a) Markers for five compositions (the mantle markers have been left out for ease of visualization) with the resulting velocity field. (b) Temperature field.

The domain is a Cartesian box with dimensions $\mathrm{2000}\times \mathrm{2000}\times \mathrm{800}$ km and the finite element mesh counts $\mathrm{120}\times \mathrm{120}\times \mathrm{50}=\mathrm{720}\mathrm{000}$ elements. Each element contains 64 randomly distributed markers. Free-slip boundary conditions are imposed at the bottom (z=0), top (z=L_z) and sides (y=0 and y=L_y) of the domain. The other two sides, x=0 and x=L_x, are a mix of free-slip (for z<100 or z>690 km) and open boundary conditions (for $\mathrm{100}<z<\mathrm{690}$ km) (Chertova et al., 2012). The input file for this example can be found in Appendix E.

Since this example shows many interesting GWB features in action, while remaining relatively simple to explain, we provided Fig. 8, which visually links the statements in the GWB with the results.

Figure 8 Connection between the GWB input file (a) and the resulting marker fields (b). Small upper inserts in panel (b) show each plate layering, while the bottom insert shows the temperature field zoomed in on slab B.

3.4 Using the GWB with ASPECT

ASPECT is an open-source community FEM designed for geodynamic problems (Heister et al., 2017; Kronbichler et al., 2012). The model which was run with ASPECT is a 3-D Cartesian model of a curved subduction system similar to the plate tectonic setting of the Lesser Antilles subduction of the eastern Caribbean region. The lithosphere consists of a strong zero-velocity Caribbean upper plate, surrounded by an oceanic North American plate to the north and northeast and the oceanic–continental South American plate to the south and southeast. In the model, the North American and South American plates move west at a average rate over the past 5 Myr of 1.4 cm yr⁻¹ relative to the Caribbean plate (Boschman et al., 2014). The Lesser Antilles trench curves around the east and north of the Caribbean plate. To the south, the Caribbean plate is partially decoupled from the South American plate by a 50 km wide weak zone. To the northwest, a 250 km wide weak zone, from the western end of the trench to the western edge of the model, partially decouples the North American plate from the Caribbean plate. Below the lithosphere, the sidewalls are open (Chertova et al., 2012, 2014) allowing for horizontal in-/outflow of mantle material. From 660 km down, a denser and more viscous material has been prescribed to delay sinking of the slab into the lower mantle. The top boundary is a free surface (Rose et al., 2017) and the bottom boundary has a prescribed zero velocity. The result of about 2.5 million years of evolution is shown in Fig. 9.

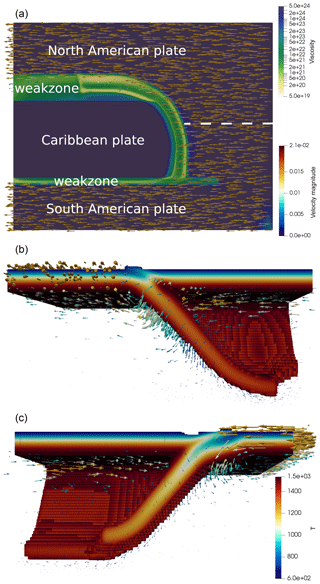
Figure 9 The 3-D ASPECT Caribbean example after 2.5 million years of evolution. The top image is a top view of the model where the top 50 km section is removed and where the viscosity field is shown with the velocity field indicated by the arrows. The bottom two figures are cutouts of the temperature field between 600 and 1535 K, showing in color the temperature (T), and with arrows the velocity fields, highlighting the velocity field in the slab and lithosphere.

The details of the setup are presented in Appendix F.

3.5 Performance

The finite element mesh used in the example of Sect. 3.4 is built in several steps by ASPECT: the code starts with a regular grid and allows adaptive mesh refinement to take place one level at the time. Each step of this process calls the GWB library. The first step generates a grid counting 28 000 elements and reports a total setup time for the initial conditions of 3.6 s on 480 MPI processes. The second step mesh counts 99 000 elements, while the setup of the initial conditions took (cumulatively) 10 s. The third step sees the number of element jump to about 560 000 elements, while its total (cumulative) time to setup the initial conditions remains low at about 36 s. This figure represents about 0.7 % of the total wall time of the first time step and a negligible portion of the total wall time of the 20 Myr long simulation.

4 Discussion

We presented the Geodynamic World Builder version 0.2.0 as a tool for constructing 2-D and 3-D initial models of geodynamic settings involving crust/lithosphere, plate boundaries and subduction. The interface of the GWB with a numerical modeling code is based on a query of the modeling code to supply temperature, density or other information at a particular position. The advantage of this is that it allows for fast and parallel use for filling, for example, the temperature field of a geodynamics model. A downside of this approach is that operations which require information of neighbors, like adding diffusion, would be more expensive to perform. We think that at least the case of adding diffusion is more suited to be performed in the geodynamic model “tha” in the GWB. This paper discusses version 0.2.0 of the Geodynamic World Builder, which is considered to be a beta version of the code. Input format and/or functionality may change between minor versions and this will be documented on the website. From version 1.0.0, we will use Semantic Versioning 2.0.0 (https://semver.org/spec/v2.0.0.html, last access: 17 August 2019), and backwards incompatible changes will only be made in every major version of the code. Future improvements may, for example, include extra temperature or composition modules, e.g., derived from tomographic models, new or improved features or even new output interfaces, e.g., velocity boundary conditions or initial topography. As an extension to area and line features, adding point features is another possible improvement to the Geodynamic World Builder. These can represent, for example, a spherical weak seed or a plume. Because of a simple query interface, it is in principle possible to use the GWB in connection with existing numerical modeling codes used by the geodynamic community. The use of the GWB can also just be restricted to creating 2-D or 3-D geodynamic models/cartoons for, e.g., teaching purposes or for illustrating a complex geodynamic setting.

Appendix A: 2-D subduction examples

A1 Cartesian input file

Listing A1 2-D Cartesian subduction example. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

A2 Spherical input file

Listing A2 2-D spherical subduction example. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

Appendix B: 3-D ocean spreading example input file

Listing B1 3-D ocean spreading example input file. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

Appendix C: 3-D subduction example input file

Listing C1 3-D subduction spreading example input file. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

Appendix D: SEPRAN 2-D subduction

Listing D1 2-D SEPRAN subduction example input file. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

Appendix E: ELEFANT 3-D Double subduction setup

Listing E1 3-D double subduction example input file. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.

Appendix F: ASPECT 3-D curved subduction

Listing F1 Input for the ASPECT example. The lines of green text (preceded by the double forward slashes) are comments and have no effect on the result.