the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Time-lapse gravity and levelling surveys reveal mass loss and ongoing subsidence in the urban subrosion-prone area of Bad Frankenhausen, Germany
Gerald Gabriel
Adelheid Weise
Detlef Vogel
We present results of sophisticated, high-precision time-lapse gravity monitoring that was conducted over 4 years in Bad Frankenhausen (Germany). To our knowledge, this is the first successful attempt to monitor subrosion-induced mass changes in urban areas with repeated gravimetry. The method provides an approach to estimate the mass of dissolved rocks in the subsurface.
Subrosion, i.e. leaching and transfer of soluble rocks, occurs worldwide. Mainly in urban areas, any resulting ground subsidence can cause severe damage, especially if catastrophic events, i.e. collapse sinkholes, occur. Monitoring strategies typically make use of established geodetic methods, such as levelling, and therefore focus on the associated deformation processes.
In this study, we combine levelling and highly precise time-lapse gravity observations. Our investigation area is the urban area of Bad Frankenhausen in central Germany, which is prone to subrosion, as many subsidence and sinkhole features on the surface reveal. The city and the surrounding areas are underlain by soluble Permian deposits, which are continuously dissolved by meteoric water and groundwater in a strongly fractured environment. Between 2014 and 2018, a total of 17 high-precision time-lapse gravimetry and 18 levelling campaigns were carried out in quarterly intervals within a local monitoring network. This network covers historical sinkhole areas but also areas that are considered to be stable. Our results reveal ongoing subsidence of up to 30.4 mm a−1 locally, with distinct spatiotemporal variations. Furthermore, we observe a significant time-variable gravity decrease on the order of 8 µGal over 4 years at several measurement points.
In the processing workflow, after the application of all required corrections and least squares adjustment to our gravity observations, a significant effect of varying soil water content on the adjusted gravity differences was figured out. Therefore, we place special focus on the correlation of these observations and the correction of the adjusted gravity differences for soil water variations using the Global Land Data Assimilation System (GLDAS) Noah model to separate these effects from subrosion-induced gravity changes.
Our investigations demonstrate the feasibility of high-precision time-lapse gravity monitoring in urban areas for sinkhole investigations. Although the observed rates of gravity decrease of 1–2 µGal a−1 are small, we suggest that it is significantly associated with subterranean mass loss due to subrosion processes. We discuss limitations and implications of our approach, as well as give a first quantitative estimation of mass transfer at different depths and for different densities of dissolved rocks.
- Article
(15757 KB) - Full-text XML
- BibTeX
- EndNote
Sinkholes or dolines are ground subsidence phenomena that occur worldwide due to both natural and anthropogenic causes (e.g. Caramanna et al., 2008; Parise and Lollino, 2011; Gutiérrez et al., 2014; Sahu and Lokhande, 2015). They are enclosed depressions with internal drainage that are characteristic features of terrains underlain by soluble rocks (Gutiérrez et al., 2008; Kaufmann, 2014) and may span less than a metre to several hundreds of metres in diameter and tens to hundreds of metres in depth (Williams, 2004; Messerklinger, 2014). Ford and Williams (2007) estimated that karst rocks such as limestone, dolomite, anhydrite, gypsum, and salt underlie about 20 % of the Earth's ice-free continental surface. Thus, the capability for solution and mass transfer by meteoric or groundwater exists. Two main categories of sinkholes have been distinguished: solution and subsidence sinkholes (e.g. Waltham and Fookes, 2003; Waltham et al., 2005; Beck, 2012; Gutiérrez, 2016). The first group results from differential dissolutional weakening of exposed or merely soil-covered karst rocks. The subsequent slow subsidence forms sagging or suffosion sinkholes and is considered to be less hazardous from an engineering point of view (Gutiérrez et al., 2014). The second group represents a wide spectrum of dolines generated by subsurface chemical dissolution or mechanical erosion, termed subrosion in the following. It is further classified by the affected material (cover, cap rock, or bedrock), the process of subsidence mechanism (collapse, suffosion, or sagging), and the dissolution rate (Cooper, 1986; Beck, 1988). Subrosion and the development of sinkholes may be influenced by numerous anthropogenic factors such as mining (Brady and Brown, 2006; Mesescu, 2011), tunnelling (Song et al., 2012), water abstraction (Bell, 1988; Aurit et al., 2013), water impoundment (Hunt et al., 2013), and other large-scale hydrological projects in karst regions, which enhance the natural process of dissolution (Milanovic, 2002; Gutiérrez and Lizaga, 2016). In karst environments, collapse sinkholes are often related to gravitational subsurface cavity collapse (Parise and Lollino, 2011; Waltham, 2016), where stress conditions exceed the material stability of the surrounding rocks, which may be related to sudden water-level changes (e.g. Lollino et al., 2013) or seismic activity (e.g. Kawashima et al., 2010).
If very fast suffosion takes place or sinkholes suddenly collapse in urban areas, they are a severe hazard for residents, economical and residential buildings, and infrastructure in general (e.g. Brinkmann et al., 2008; Lei et al., 2013; Gutiérrez, 2016; Wadas et al., 2017). Hence, ongoing urbanization and the growth of the world's population increase the requirement for detailed investigation of subrosion processes and sinkhole development for risk assessment.
Several geophysical and geodetic methods are applicable for the investigation of potentially unstable ground, subrosion processes, and the accompanied development of sinkholes. Surface deformation and sinkhole development can be monitored by airborne lidar (e.g. Filin et al., 2011; Miao et al., 2013), photogrammetry (e.g. Lee et al., 2016; Al-Halbouni et al., 2017), and interferometric synthetic aperture radar (InSAR) (e.g. Nof et al., 2013; Shviro et al., 2017), or ground-based geodetic methods such as high-precision levelling (e.g. Sevil et al., 2017; Desir et al., 2018), ground-based lidar (Benito-Calvo et al., 2018), Global Navigation Satellite System (GNSS) applications (e.g. Kent and Dunaway, 2013; Kersten et al., 2017; Weise et al., 2018), and ground-based InSAR (Intrieri et al., 2015), which are more suitable for small-scale studies and local investigations. Information on, e.g. morphology of cavities, sinkhole fills, or fissures can be investigated by ground-penetrating radar, electrical resistivity tomography, (micro)gravity surveys (e.g. Rybakov et al., 2001; Pivetta and Braitenberg, 2015; Braitenberg et al., 2016), or nuclear magnetic resonance (e.g. Gómez-Ortiz and Martín-Crespo, 2012; Miensopust et al., 2015), as well as magnetometry (e.g. Bosch and Müller, 2001; Rybakov et al., 2005). Due to electromagnetic noise and ferrous materials, electromagnetic methods and magnetometry are often not feasible in urban areas. Information about underground structures and physical rock parameters can be obtained by shear-wave seismic reflection profiles that are especially suitable to resolve shallow geological structures with high resolution (e.g. Krawczyk et al., 2012; Wadas et al., 2016, 2017; Polom et al., 2018). Furthermore, seismic reflection and seismic refraction give information about deeper layers (e.g. Higuera-Díaz et al., 2007; Sargent and Goulty, 2009). Another valuable tool for the understanding of the development and propagation of collapse sinkholes is numerical modelling (e.g. Augarde et al., 2003; Kaufmann et al., 2018; Al-Halbouni et al., 2018). The use of tiltmeters (Sandia National Laboratories, 2016), borehole strainmeters (Zini et al., 2015), or borehole measurements in general (Yechieli et al., 2003; Song et al., 2012) are sparse and not applicable in densely built-up urban areas due to high costs and strict approval procedures (Schmidt, 2005). Some multidisciplinary field studies include gravimetry (e.g. Patterson et al., 1995; Tuckwell et al., 2008; Dahm et al., 2010; Ezersky et al., 2013; Kaufmann, 2014; Pazzi et al., 2018) but focus structural interpretations of the Bouguer anomaly above and around assumed subrosion features. Hence, and with sparse exceptions (Lambrecht et al., 2005; Benito-Calvo et al., 2018), the majority of the mentioned ground-based methods are applied to localize sinkholes, image the actual state of sinkhole development, and concentrate on their spatial extent or physical parameters at a certain point of time.
In contrast, the time-lapse gravity method can deliver enhanced information about the variable local gravity field over time. It is non-invasive and directly sensitive to temporal mass movements on different spatial and temporal scales. Time-lapse gravity observations were successfully applied to monitor, e.g. subsurface water storage changes in general (Naujoks et al., 2008; Pfeffer et al., 2013) and in karst regions (Van Camp et al., 2006; Jacob et al., 2010; Champollion et al., 2018), CO2 storage changes (Nooner et al., 2007; Wilkinson et al., 2017), or withdrawal or intrusions beneath volcanic edifices (Jentzsch et al., 2004; Hautmann et al., 2014; Carbone et al., 2017).
We present a study that reveals potential subrosion-related mass transfer in the subsurface using spring gravity meters for a time-lapse survey over 4 years. A special focus is placed on the hydrological correction, which strongly means soil water content and changes in groundwater level. Both are challenging impacts on gravity variations (e.g. Bonatz, 1967; Mäkinen and Tattari, 1988), especially in urban areas and where no special hydrological monitoring sites exist. We introduce the survey area of Bad Frankenhausen, located in Thuringia in Germany (Sect. 2), and the monitoring concept, including data processing and a hydrological soil water correction approach (Sect. 3). The results show constant gravity decrease, as well as continuous subsidence at specific points inside of our measurement network (Sect. 4), which is assumed to be caused by underground mass redistribution. This is also discussed in Sect. 5, such as the feasibility of the time-lapse gravity method for sinkhole monitoring under urban conditions.
Sinkholes in Germany occur over the whole country due to the dissolution of various soluble rocks in the subsurface (Fig. 1a). These are mainly near-surface salt diapirs in northern Germany (Krawczyk et al., 2012; Kaufmann et al., 2018), and carbonates and sulfates in the central and southern parts of the country (Kaufmann, 2014; Wadas et al., 2017).
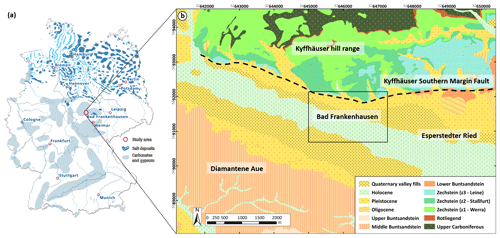
Figure 1Geological overview of the study area. (a) Distribution of soluble deposits in Germany and location of the study area Bad Frankenhausen in the transition zone between salt and carbonate deposits, after Krawczyk et al. (2015). (b) Geological map showing Permian, Triassic, and Cenozoic deposits of the study area and its surroundings (simplified after Schriel and Bülow, 1926a, b; CS: ETRS 1989 UTM Zone 32N).
Our study area is located in the centre of Bad Frankenhausen (BF), a small city in northern Thuringia in central Germany, which is located in the transition zone of soluble rock packages (Fig. 1a; Wadas et al., 2016). It is bounded by the Kyffhäuser hill range to the north (Fig. 1b) and the Thuringian Basin to the south (an extensive geological overview of Thuringia is given by Seidel, 2003). Geological units in the working area were deposited in the Permian and the Triassic, and are divided by the W–E-trending and northwards-dipping Kyffhäuser Southern Margin Fault (KSM Fault) (Wadas et al., 2016).
The sediments to the north of the KSM Fault are mainly Zechstein evaporites developed from seven evaporation-transgression cycles of the epicontinental Zechstein sea in the Upper Permian (258–250 Ma). These are alternating layers of conglomerates, carbonates, sulfates, and rock salt (Richter and Bernburg, 1953). The main occurrent marine formations in the research area are termed Werra, Staßfurt, and Leine (Fig. 1b). Extensive units of anhydrites, carbonates, copper shales, and conglomerates, mainly from the Werra and Staßfurt formations, can be found in the Kyffhäuser hill range. Scattered Leine Formation deposits consisting of salt clays, anhydrites, and carbonates cover the region to the northwest of BF (Schriel and Bülow, 1926a, b).
The sediments to the south of the KSM Fault are mainly sandstones, claystones, and shales that were deposited during the Triassic terrestrial sedimentation phase after the marine sedimentation phase of the Permian. Triassic Buntsandstein, Muschelkalk, and Keuper overlay the Permian evaporites (for thickness values of the rock units, see Schriel and Bülow, 1926a). Quaternary deposits are floodplain sediments, claystones, and siltstones, as well as glacial gravels and aeolian silt deposits.
The whole region is prone to subrosion, as proven by many features on the surface (Fig. 2). This is predominant along the KSM Fault (Fig. 2a) and part of an about 250 km long tourist trail – the “Karst Trail” – along the southern Harz hill range. Several studies show that the Upper Permian in this region is strongly fractured, and therefore the mechanical integrity of the subsurface is disturbed. Kaufmann (2014) used a combination of different geophysical methods and joint inversion to show that the fractured zones can serve as pathways for meteoric and groundwater, and hence accelerate the underground dissolution. Proven by salt springs and about 20 000 subrosion structures, which shape the landscape south of the Harz Mountains (Knolle et al., 2017), the Upper Permian provides the solvable material in the near-surface area (Kugler, 1958), especially along the KSM Fault, where the southward-draining groundwater from the Kyffhäuser hill range ascends (Reuter, unpublished data). The different types and ages of the subrosion features document the ongoing subrosion processes over time. Underground cave growth (Fig. 2b; a description of the Barbarossa Cave is given by Kupetz and Mucke, 1989) and weakening of the rock units lead and led to the development of collapse (Fig. 2c, d) and sagging sinkholes, which strongly affect urban constructions in and around BF. The most famous subrosion feature in the area is the leaning church tower of BF that currently has an inclination of 4.93∘ (Fig. 2e) and has been stabilized by a steel pylon construction. Since the last collapse of the Quellgrund sinkhole in 1908, the tower's inclination has been increasing rapidly due to disturbances within the drainage system beneath the building (Sven Schmidt, Thuringian State Institute for Environment and Geology (TLUG), personal communication, 2016). Several cavities and disrupted zones were investigated by three research core drillings (depth: 100–458 m) between 2013 and 2015 around the leaning church tower and mainly in the upper 100 m of the cap rock, which mainly consists of Zechstein anhydrites and gypsum (Sven Schmidt, TLUG, personal communication, 2016). Other investigations show similar results; e.g. the company SOCON Sonar Control found and surveyed a large cavity (volume: 95.5 m3, depth: 14.5–20.5 m, radius: 8 m) directly beneath the tower by using an ultrasonic sound method through an older drill hole beside the tower walls. In addition, the bigger part of infrastructure and buildings shows cracks and damage, which led, e.g. to the necessity to rebuild the leaking swimming pool in the city centre, several building renovations, and reconstruction work.
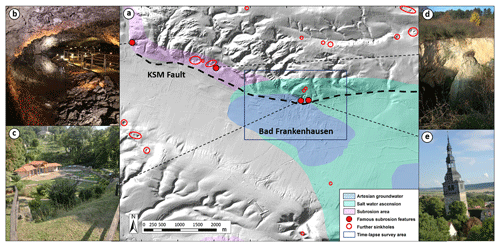
Figure 2Subrosion features in Bad Frankenhausen (BF) and its surroundings. (a) Digital elevation model and the colour-coded hydrogeological assessment of BF and its surroundings (provided by Thuringian State Institute of Environment and Geology, 2016; Sven Schmidt, personal communication, 2016; same map extent as in Fig. 1). Salt water ascension and artesian groundwater conditions affect the survey area (dark blue rectangle). Along the Kyffhäuser Southern Margin Fault (KSM Fault; bold dashed line), a potential fluid path, and thus a subrosion area, several sinkholes (red circles), as well as famous subrosion features occur (filled red circles; see panels b–e; sketch after Wadas et al., 2016). (b) Barbarossa Cave (detected in 1865) as part of an educational trail showing karst features along the subrosion area. (c) The oldest sinkhole, Quellgrund (first mentioned in 998 AD; collapsed for several times and for the last time in 1908; depth now is approximately 10 m), in the centre of the survey area comprises two natural brines with salinities of 4 % and 9.8 %. (d) One of the most recent sinkholes (collapsed in 2009), in a field beside the largest sinkhole of the region, the Äbtissingrube. (e) The leaning church tower of BF (inclination: 4.93∘) is a very famous subrosion feature and a magnet for tourists.
Sinkhole development and ongoing subsidence in urban regions such as BF represent severe hazard. Therefore, we aim to detect mass redistribution caused by subrosion by applying time-lapse gravity monitoring to improve the understanding of subrosion processes.
Our general approach is the high-precision monitoring of subrosion-induced time-variable gravity and height changes using regular repeated measurement campaigns. Including March 2014, when a 2-week long reference campaign was performed, a total of 17 time-lapse gravimetry (1 week of measurement time) and 18 levelling campaigns were carried out quarterly. The frequency of the campaigns has been reduced to half-yearly intervals since the beginning of 2018. The observed temporal components provide the possibility to derive evidence for ongoing subrosion and afford a quantification of the mass relocation in the subsurface. Therefore, the time-lapse measurements have to be close mesh and of high quality. Potential error sources have to be avoided as much as possible. Realistic error estimations are required when considering the results with respect to significance. All this must be taken into account during planning, measurement, and data analysis. The key requirements in this context are appropriate instrumentation, the local stability of the individual measurement locations, their long-term availability in variable infrastructural surroundings, and a method (measurement and data analysis), which must be robust against inner-city noise (pedestrians, cars, construction work) and systematic errors. In the following, we describe our implemented conception for the monitoring and the data analysis.
3.1 Measurement: monitoring network
A local combined geodetic–gravimetric measurement network was established in Bad Frankenhausen in March 2014 (Fig. 3), based on previous studies (gravimetry for structural investigations, levelling), site inspection, experiences from similar studies (Naujoks et al., 2008), and information about future construction work in the measurement area. The northern part of the city centre on the edge of the KSM Fault (Fig. 2a) is subject to subsidence of up to several millimetres per year (Fig. 3c) as determined by levelling surveys from 2000 to 2010 carried out by Scholte (Glückauf Vermessung Sondershausen, unpublished data). Furthermore, the Bouguer anomaly in this area, which is trend reduced by a second-order polynomial (Fig. 3b), correlates qualitatively with the sinkhole areas I–III (cf. Fig. 3c). The negative gravity anomalies are considered to be the first evidence for subsurface subrosion-induced density contrasts. Hence, our extensive measurement network (125 levelling points – 15 of them for time-lapse gravity monitoring) covers the northern city with the focus on known sinkhole areas and zones of gravimetric minima in the medieval centre. The connection to superior reference systems provides stability control of the whole network. Our levelling network is tied to the second-order trigonometric benchmark RP1 (RP: reference point, Fig. 3a, Fig. 4c) and to LRP (reference point for levelling) of third order at both ends of a 2.75 km long E–W-orientated profile (Fig. 3a). In combination with the levelling network, we defined 12 points as a gravimetric network in a close-mesh arrangement (Fig. 3, blue dots: G01–G12) and three points as gravity reference points (Fig. 3, red dots: RP1, RP2, RP3). Most of the measurement points were installed on infrastructure such as cobblestoned footpaths and marked by synthetic survey markers, which cover steel piles in 30 cm deep-drilled holes (Fig. 4a). Gravity points on meadows (G02, G11, G12) are self-made concrete pedestals of 80 cm depth to reduce noise and soil freezing effects. They are marked by brass survey markers (Fig. 4b).
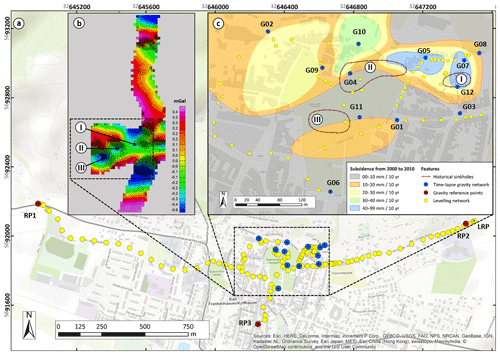
Figure 3Combined geodetic–gravimetric network for the time-lapse surveys in BF that started in March 2014 within the dark blue rectangle in Fig. 2a. (a) Conception of measurement points in BF with respect to the trend-corrected, residual Bouguer anomaly (b), results of levelling surveys (c), and famous subrosion features (Fig. 2c, e). Red and blue coloured points show the gravimetric network, which is complemented by the levelling network marked as yellow points. (b) Trend-corrected Bouguer anomaly within the medieval centre of BF from measurements of structural gravimetry in September 2013. (c) Results of levelling surveys over 10 years show approximated areas of equal subsidence rates, after Scholte (Glückauf Vermessung Sondershausen, unpublished data). Historical sinkholes in this sketch are (i) the leaning church tower of BF (Fig. 2e), (ii) Quellgrund (Fig. 2c), and (iii) a broken and rebuilt swimming pool caused by stress fractures related to subsidence. The locations of historical sinkhole areas coincide with areas of negative gravity anomalies.

Figure 4Installation of the monitoring network. (a) Drilling of levelling/gravity points that were stabilized by 30 cm long steel piles and marked by synthetic survey markers. (b) Pouring of an 80 cm deep concrete base with even surface and brass survey markers. (c) Example of benchmark RP1 operated by the Thuringian State Office for Surveying and Geoinformation (TLVermGEO, personal communication, 2013).
3.2 Measurement: devices and data acquisition
3.2.1 Instrumental array
Up to four different gravity meters of various manufacturers were used per campaign (Fig. 5). The gravimetrical setup consisted of astasized relative metal spring gravity meters of LaCoste & Romberg G-type with feedback (LCR-G, acc1: ≤10 µGal; 1 µGal = 10 nm s−2) and ZLS Burris (acc: ≤5 µGal), as well as non-astasized quartz spring Scintrex CG3 (acc: ≤8 µGal) and CG5 (acc: ≤5 µGal) gravity meters (detailed description of the instruments – LCR: Torge, 1989; Scintrex: Scintrex, 1995, 2006; ZLS Burris: Jentzsch et al., 2018). The mentioned accuracies are dependent on the noise level, the measurement conditions, and (especially concerning the Scintrex instruments) the age of the instrument itself. Instrument heights above point label were controlled for each observation. The gravity measurements were accompanied by levelling using a Leica DNA03 digital level (standard deviation per kilometre double run: 0.3 mm; see Leica Geosystems AG, 2006) with two Invar bars to provide height references for gravity height reductions and to conduct subsidence monitoring. Additional equipment consisted of tripods, parasol to avoid effects of sunshine and rain, and sensors for air pressure.
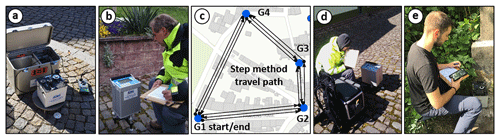
Figure 5Overview of the gravity meters and the method that was used in this study. The accuracies (acc) were obtained from least squares adjustments per campaign and are valid for the single measurement of a gravity difference. (a) LaCoste & Romberg G-Type (acc: ≤10 µGal). (b) Scintrex CG5 (acc: ≤5 µGal). (c) Travel path for the application of the step method – four points in a polygon mean 13 measurements. (d) Scintrex CG3 (acc: ≤8 µGal). (e) ZLS Burris Gravity Meter (acc: ≤5 µGal).
3.2.2 Calibration setup for gravity meters
In preparation for the single measurement campaigns, instrumental error sources were reduced by determination of instrument-specific calibration factors and their stability control to 10−4. This means that the inaccuracies due to calibration are, within the effective gravity range of 6 mGal, on the order of 0.6 µGal. The gravity meters were calibrated using the calibration line in the university tower building in Hanover, Germany (Kanngieser et al., 1983) and the Harz mountain calibration line (Torge, 1989). The estimated accuracies of their gravity differences are in the range of 1 µGal for Hanover and 2 µGal for Harz (Timmen, 2010; Timmen et al., 2018). Frequent calibrations have shown stable calibration factors for all used instruments. Besides, regular laboratory tests with respect to dependencies on instrumental air pressure effects, drift behaviour, and tilt were performed for accurate instrument modulation.
3.2.3 Time-lapse gravity monitoring
Evidence of mass loss due to underground leaching requires a measurement concept, which focuses on both accuracy and efficiency. The most convenient procedure is the measurement of gravity differences between the points in a network applying the step method for optimal drift control (Torge, 1989). Therefore, the gravimetric measurement network (Fig. 3) was subdivided into polygons consisting of four to six points each. In a four-point polygon, this resulted in a total amount of 13 measurements; i.e. four differences were each measured three times (Fig. 5c). The advantage of this method is an optimal drift determination and the possibility of statistical validation of each measured gravity difference. At a measurement point, and for statistical and accuracy reasons, different settings were used depending on the type of gravity meter: Scintrex – 10 measurements in cycles of 60 s (45 s registration, 15 s break); LCR-G – three measurements at three spindle positions (±0.1 scale units) using feedback; ZLS Burris – five measurements at a fixed spindle position using only feedback (range: ±25 mGal).
3.3 Data analysis: processing steps
Measured height changes obtained by levelling campaigns are processed using Nigra, a special software for the analysis of levelling (TrukkSoft, 2018). Here, the height differences are not adjusted, but discrepancies are distributed along a profile or in loops after the averaging of all double-observed height differences.
Gravimetric time series contain numerous effects that superimpose the signal of interest. Therefore, and to compare the observed gravity differences between network points for different campaigns, as well as to identify a potential subrosion signal due to mass redistribution, several processing steps had to be applied (Table 1). Highly sensitive gravity meters are affected by shocks and tilt, e.g. by passing cars or pedestrians, which can produce errors like jumps or spikes in the datasets. Especially, Scintrex gravity meters are sensitive to transportation effects, i.e. to long-lasting run-in periods due to the relaxation of accumulated tension in the sensor (Reudink et al., 2014; Klees et al., 2017). These effects mainly occur after tilting a Scintrex instrument by ≥8∘ for several minutes during transportation. Additionally, random and systematic errors occur. Hence, preprocessing was applied to correct the data per point for outliers, jumps, spikes, and running-in behaviour, and finally, to average them.
The pre-corrected mean gravity records contain different instrumental and environmental signal content (explained in detail, e.g. by Torge, 1989 or Timmen, 2010), which varies continuously with time or occurs irregularly, and superimposes the potential subrosion signal. Thus, the observations of each single gravity meter and all gravity meters combined were analysed by a least squares adjustment (Wolf, 1975) using the Fortran-based programme package GNLSA 1.01 (Wenzel, 1985, unpublished data). It executes the correction of data for Earth tides and ocean loading tides, gravitative and instrumental air pressure effects, height reduction of the gravity meter mass suspension relating to the point label by using the vertical standard gravity gradient on Earth's surface of −0.3086 mGal m−1, as well as the application of all calibration factors as described in Sect. 3.2. It also includes the adjustment of linear drifts. If drift effects appeared as highly non-linear on some days, we divided these days and introduced “additional” gravity meters instead. Another important requirement was the weighting of gravity meters during the least squares adjustment according to their precision level. The results of running GNLSA are adjusted gravity differences plus SD for every possible difference in the network and adjusted linear drift parameters for each campaign. Furthermore, gravity values plus SD for each single measurement point are calculated from the adjusted gravity differences based on given absolute levels of reference points.
Subsequently, a post-processing takes places. Firstly, temporal height variations of gravity points as derived from the levelling campaigns were taken into account using the vertical standard gravity gradient on Earth's surface. Secondly, the gravity differences show seasonal effects (Sect. 4.2, Figs. 8, 9), which correlate well with temporal variations in the soil water content. These were considered within data post-processing as described in the following section.
3.4 Data analysis: hydrological effects
So far, the gravimetric potentially subrosion-induced signal of interest is still superimposed by hydrological effects like changes in groundwater table and soil water content (Bonatz, 1967; Mäkinen and Tattari, 1988). These are characterized by spatial point-to-point and temporal campaign-to-campaign variations. Hydrological effects are also dependent on the topography around a measurement point (Naujoks et al., 2008; Deville et al., 2013). Unfortunately, no recordings of groundwater level and soil water content are available in or near the measurement area.
Soil water content can vary in two ways: irregularly and seasonally. To compute its effect on gravity data, several models on different scales and resolution are available (e.g. Meng and Quiring, 2008; Ford and Quiring, 2013). In this study, the Global Land Data Assimilation System (GLDAS – model type: Noah) from NASA was chosen (Rodell et al., 2004), because no local soil water models are available for our measurement area in that quality. It includes extensive regional climate data (temperature, air pressure, humidity, long-wave radiation) on a grid over Europe and provides monthly soil water content that covers the upper 2 m of depth. GLDAS Noah is available online and open source (Beaudoing and Rodell, 2016). The computed varying soil water content has the dimension of “mm water column” and was interpolated for the first day of each measurement campaign. The correction of gravity differences is based on the determination of respectively associated regression coefficients in the dimension of µGal mm−1. Here, a regression coefficient symbolizes the differences in the time-variable soil water content between two points of a gravity difference and further discrepancies in point conditions such as topography, porosity, or sealing. We multiplied a single coefficient with the soil water content and reduced the result from the associated time-variable gravity difference. The remaining signal in the gravity differences contains mainly long-periodic subrosion-related gravity variations, in case subrosion is taking place, plus short-periodic noise, and location-dependent non-computable groundwater effects.
(Wenzel, 1985)(Rodell et al., 2004)With regard to groundwater variations, it is known from some drillings that the depth of groundwater in Bad Frankenhausen varies between 2.5 m in the southern and up to 10–20 m in the northern part of our monitoring network. However, no specific evidence of the local groundwater level depth is available. A few gauges of groundwater level exist at a distance of 5–10 km. The groundwater level only partially correlates with the soil water content from the GLDAS model in a seasonal range. As a first proxy, and under the assumption that these groundwater variations are roughly valid for the measurement area as well, the previously determined regression coefficient for soil water content could partly include the effect of groundwater changes. Also it has to be considered that the groundwater signal has a phase shift relative to the soil water content. If local groundwater data were available, a second regression coefficient for groundwater correlation could be calculated.
4.1 Levelling
The results over 4 years of levelling are shown in Fig. 6 as an overview. Achieved accuracies over all campaigns are in the range of ±1.5 mm for the 2.75 km long E–W-orientated profile and ±1.0 mm for the loops in the northern city centre (Fig. 6b). The reference points for levelling (RP1, LRP; see Fig. 3) were stable over the past 4 years. In Fig. 6, the measurement network is overlain by colour-coded points showing the height changes in April 2018 relative to March 2014. Most of the points do not change significantly in height (green colour), mainly on the E–W profile and outside of the mentioned sinkhole areas. Here, the height variations are in the range of ±2.5 mm a−1.
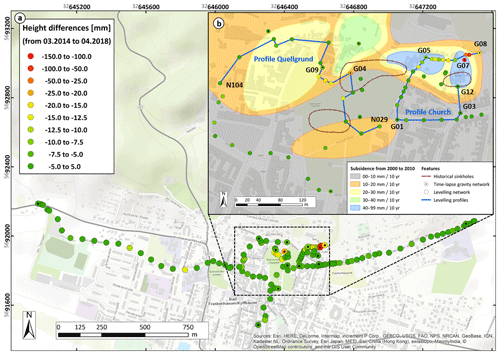
Figure 6Levelling results over 4 years. (a) Measurement network in BF showing colour-coded height changes between April 2018 and the reference measurement in March 2014. Additional black points mark the gravimetric network. (b) Height variations over 4 years in the medieval centre of BF, with up to −121.7 mm at point G07. They are compared to the location of historical sinkholes (brown polygons) and the levelling results obtained by Scholte (Glückauf Vermessung Sondershausen, unpublished data). The blue lines mark the current levelling profiles that show the time-variable development of subsidence in Fig. 7.
Within the medieval centre of BF, two areas of continuous height changes are remarkable (yellow–orange–red dots in Fig. 6b). The first of these is located around gravity points G04 and G09 and covers the western–southwestern slope area of the ancient Quellgrund sinkhole. Subsidence rates are 3.5–5.4 mm a−1 with the local maximum of 21.7 mm in total over 4 years at point G04. The second area includes gravity points G05, G07, and G08 and is located northwest–northeast of the leaning church tower. Subsidence rates are 3.0–30.4 mm a−1 with the local maximum of 121.7 mm in total over 4 years at point G07.
Within these areas, two profiles covering the local sinkhole territory were defined to show the time-variable development of the subsidence (blue lines in Fig. 6b, profiles shown in Fig. 7). Curves are smoothed by a weighted moving average of width three values (weighting factors: , wn=0.8, ). Additionally, levelling observations were affected by seasonal variations, e.g. due to ground frost or drying. We reduced these seasonal and area-wide effects by using a constant offset based on seasonally constant levelling points to emphasize the evolving subrosion patterns within instable zones. Figure 7 displays yearly variations relative to March 2014 and, additionally, the last measurement campaign in April 2018. The church profile (gravity point G07 is not included) reveals irregular subsidence from northwest to northeast of the leaning church tower, i.e. between points G05 and G08, which correlates qualitatively with the results of Scholte (Glückauf Vermessung Sondershausen, unpublished data). Subsidence rates from 2014 to 2016 were 2–6 mm a−1 and have decreased since 2017 to 1–4 mm a−1 with the exception of, e.g. point G08. To the south and west of the leaning church tower, no significant height changes can be detected. The Quellgrund profile shows a similar pattern. The subsidence rates from 2014 to 2016 were 0–4 mm a−1 and decreased abruptly between 2017 and 2018 to 0–0.5 mm a−1.
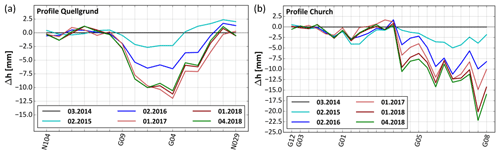
Figure 7Levelling results along two selected profiles in the network (cf. Fig. 6) showing ongoing but irregular subsidence in yearly time intervals (curves are smoothed by a weighted moving average of width three and offset due to, e.g. effects of ground frost, to emphasize the evolving subrosion patterns). (a) Profile alongside and across the historical Quellgrund sinkhole shows subsidence of up to 12 mm in the sinkhole and on its western–southwestern margin. (b) Profile around the leaning church tower shows subsidence of up to 22 mm along the northern part of the church tower.
All height changes at gravity points were used to correct time-lapse gravity results for subsidence and to refer them to the reference campaign in March 2014.
4.2 Time-lapse gravity
4.2.1 Reference points
Gravity reference points provide stability control of the whole network and the possibility to calculate gravity values plus SD for each single measurement point from the adjusted gravity differences (Δg). After least squares adjustment (LSA), the Δg between predefined reference points RP1 and RP2 (cf. Fig. 3) for time-lapse gravity observation shows small but significant gravity changes, and therefore RP1 and RP2 were not used as reference points. Reference point RP3 was defined later, in June 2015, and is located at the town hall site in BF. Close by, in the cellar of the town hall, three absolute gravity campaigns were carried out in June 2015, August 2016, and August 2018. The results show that the town hall site is stable within standard deviations of ±2 µGal (c=981 171 700 µGal; 2015: c+47.3 µGal; 2016: c+45.2 µGal; 2018: c+44.4 µGal; Ludger Timmen, Leibniz University Hanover, personal communication, 4 December 2018). In the next step, we considered the temporal variations of all Δg between our network points and RP3 before correcting the hydrological effect of soil water content, to define new stable reference points for further data analysis. Figure 8a shows the variations of the Δg between RP3 and gravity points G01, G03, and G05, which scatter around zero (including seasonal effects of ±2–3 µGal), and thus they were chosen as new reference points within our measurement network. The algebraic sign of a Δg is dependent on the order of the sequence of calculation (). Based on the results, we assume that the new reference points were stable before August 2015 as well.
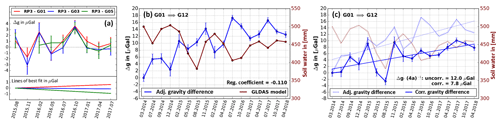
Figure 8Results of time-lapse gravity monitoring shown by the adjusted gravity differences (Δg) between the stable reference point RP3 and points G01, G03, and G05, as well as, exemplarily shown, by the adjusted gravity difference between points G01 and G12 (). (a) Δg scatter around zero and reveal that gravity points G01, G03, and G05 are stable. In addition, the best linear fit shows an insignificant trend of <1 µGal over 2 years for the three shown Δg. The Δg values are based on the absolute gravity measurements at point RP3, carried out by Leibniz University Hanover (LUH), which prove that RP3 is stable (Ludger Timmen, LUH, personal communication, 4 December 2018). (b) Δg (blue) compared to the soil water content from GLDAS (brown) and the calculated regression coefficient between both in the dimension of µGal mm−1. (c) Δg (solid blue) corrected for soil water using the regression coefficient. Dotted lines show the previous state. Regression lines show the Δg over 4 years before and after the hydrological correction, as well as the decrease of the trend.
4.2.2 Gravity differences
In the following, all shown and discussed results are related to our reference campaign in March 2014. Gravity differences (Δg) were determined in the LSA for each possible Δg between the 12 measurement points in the northern city centre (66 overall; see Fig. 3c). Some of them could not be measured in a few campaigns (column 3 in Table 2) caused by, e.g. construction work. The SDs of adjusted Δg vary between 1.1 and 3.6 µGal depending on the season, the combination of used gravity meters, and the number of adjusted Δg per campaign (Table 2). From the beginning of the study until now, the accuracy of the results of the LSA could be successively increased, i.a. due to the purchase of the high-precision gravity meters (Scintrex CG5 and ZLS Burris). These instruments perform their own correction of the gravity observations for tilt and temperature effects.
Table 2Abstract of time-lapse gravimetric field campaigns. Shown are the dates of the campaigns, unusable gravity points, the gravity meters used for the observations per campaign (instruments are LaCoste & Romberg G-Type: LCR-G, Scintrex: CG3 and CG5, ZLS Burris: ZLS), and their number (no.). Furthermore shown are the standard deviations of adjusted gravity differences (SD of Δg), the standard deviations of gravity values on measurement points (SD per point), and the total number of adjusted gravity differences (no. of Δg) per campaign.
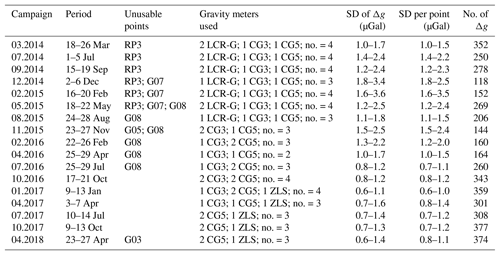
The results of the LSA are presented as an example with the temporal variations over 4 years of the Δg and their SD between the stable point G01 (Fig. 8a) and point G12, which shows the highest gravity decrease in our measurement network (Fig. 8b, c; values of G12 subtracted from the values of G01). In addition, the seasonal content is obviously significant. The SDs are shown as error bars that get smaller from campaign to campaign, mostly because the LCR gravity meters of lower precision are no longer part of the instrumental setup. Assuming that point G01 is stable, the variations define a trend in Δg of 3.0 µGal a−1 (dotted line in Fig. 8c), which has displayed an overall gravity decrease at G12 of 12.0 µGal since March 2014. The temporal variations of Δg in Fig. 8b show seasonal signals of 2–6 µGal oscillating between minima mainly in the winter months, e.g. December 2014 and February 2016, and maxima mainly in the summer months, e.g. July 2016 and July 2017. These Δg variations are compared to the varying soil water content obtained from the global hydrological model GLDAS (Sect. 3.4).
The Δg G01–G12 correlates very well with the hydrological model (brown curve in Fig. 8b), except for the time span between February 2015 and November 2015, which is not clearly understood. Here, the variations in soil water content show a maximum. These peaks can also be affected by other gravitational mass changes, e.g. groundwater variations, which cannot be considered here (Sect. 3.4). For this example of Δg variations, a regression coefficient of −0.110 µGal mm−1 was determined between Δg and the soil water content, and used to correct Δg for the soil water variations (Fig. 8c, solid blue curve). The hydrological correction smoothes the curve for seasonal variations in soil water content mainly in the second period of our observation, starting from February 2016, and decreases the 4-year trend in gravity by 4.2 µGal. Between February and November 2015, the hydrological correction seems to produce an increase in the seasonal signal, which could also be induced by a minimum or phase shift of groundwater level, that is not corrected here. However, the remaining signal reveals a significant trend of gravity decrease over 4 years at point G12.
A hydrological correction applying an individual regression coefficient is done for each Δg in our network. A selection of Δg variations arranged in a rectangle between four measurement points is shown in Fig. 9. In Fig. 9d, the above discussed Δg G01–G12 is displayed like in Fig. 8b. Firstly, the correction of seasonal variations in the other gravity differences shows the same quality in the displayed graphics as described for Δg G01–G12. Furthermore, the remaining gravity decrease of 7.8 µGal over 4 years in the Δg G01–G12 is related to a gravity decrease at G12. Following the variations of Δg anticlockwise results in a gravity decrease at G10 by 4.2 µGal over 4 years, which is the difference of the gravity decrease of 7.8 µGal at G12 and the remaining gravity variation of −3.6 µGal over 4 years of the Δg G12–G10 (Fig. 9b). The same procedure reveals a gravity decrease of 0.8 µGal over 4 years at point G09, which is insignificant, and thus G09 and its difference to G01 are stable within the SD as well (Fig. 9c). The remaining trends over 4 years of the four gravity differences in Fig. 9 add up to 0.1 µGal over 4 years, which may result from rounding during data processing and trend fitting. However, the results show the feasibility of the applied hydrological correction using individual regression coefficients for each Δg without producing any loop errors and thus the possibility of identification of stable or instable gravity differences in the network.
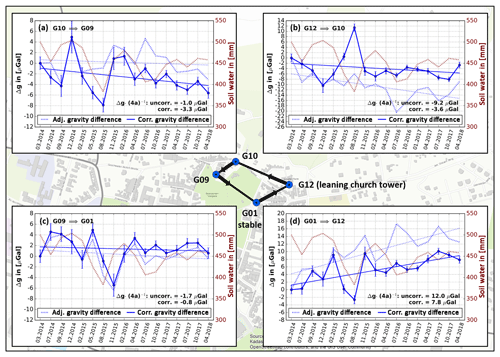
Figure 9Selected adjusted gravity differences (Δg, ) in the measurement network arranged in a rectangle consisting of gravity points G01, G12, G10, and G09, and corrected for soil water variations. (a) Δg G10–G09 reveals gravity decrease at G10, because G09 is stable within the SD. (b) Δg G12–G10 reveals faster gravity decrease at G12 than at G10, relative to each other. (c) Δg G09–G01 shows insignificant variations and reveals that also G09 is stable within the SD. (d) Δg G01–G12 shows a significant gravity decrease at G12 relative to G01, which is located next to the leaning church tower, because G01 is stable within the SD (cf. Fig. 8a).
4.2.3 Gravity values
For gravity investigations, it is not mandatory that gravity values on installed benchmarks are stable over time (Weise et al., 2018). The careful selection of the benchmark locations prior to the installation of the monitoring network is based upon the expectation of favourable noise and environmental conditions at these points. However, during the operation time of the network, these assumptions can turn out to be wrong or not sustainable, e.g. due to unknown/changing hydrological conditions of soil or groundwater, or construction work. Hence, the possibility of temporal gravity changes at these benchmarks must be properly considered during interpretation and discussion of results. Under the assumption that G01, G03, and G05 are stable relative to the stable point RP3 (Fig. 8a) and relative to each other in all LSA, the absolute gravity values were set fixed for the two points G01 and G03, according to the adjusted Δg G01–G03 of the reference campaign. Then, we derived gravity values for each point in our measurement network from the LSA. Now, instead of Δg between measurement points, the time-variable changes of gravity on individual gravity points are considered. Mean gravity values, each over 1 year of observation starting from the first campaign in March 2014, are displayed in Fig. 10 as bar charts per point. They are corrected for hydrology using the changes in the gravity trends obtained from the hydrological correction in Sect. 3.4 for each gravity difference related to the stable point G01. The results reveal areas of gravitational stability and of significant gravity decrease over 4 years (Fig. 10). Two patterns are discernible: (i) invariable points (G01, G03, G05, G06, G08, G09) within the SD; (ii) continuous gravity decrease, which is obvious for points G07, G11, and G12. Points G02, G04, and G10 show a gravity increase that appears relative to the reference date (March 2014) in the first year (brown bar) and then also ongoing gravity decrease – this could be an effect of discrepancy between the mean of the first year and the reference value from the first campaign, respectively. It is conspicuous that a gravity decrease mainly is taking place within or very close to the known historical sinkhole areas (see Fig. 3). Furthermore, it is apparent that the gravity decrease on a single point (G) and the time-variable Δg between stable point G01 and G show similar results, which is a matter of course.
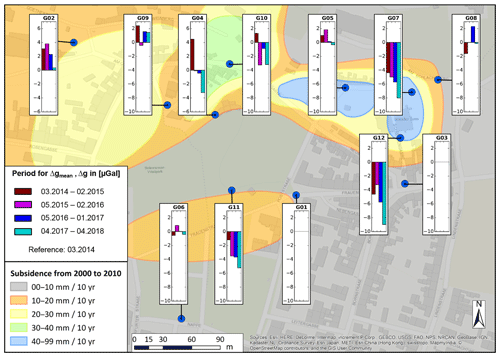
Figure 10Temporal variations of mean gravity Δgmean over each year of data, referenced to March 2014, on the points of the gravimetric network (blue dots). The gravity values for each survey point are derived from least squares adjustments assuming that G01 and G03 are stable over time. The adjusted gravity differences are hydrologically corrected for soil water content by applying an individual regression coefficient for each gravity difference.
The approach presented here combines repeated levelling and time-lapse gravimetric surveys in a local measurement network in BF, Thuringia, central Germany. The aim is to identify surface deformation and mass transfer in the subsurface, in an area that is prone to subrosion, as several features on the surface reveal. After 4 years (17 gravimetry and 18 levelling campaigns) of regular quarterly measurements, we have obtained convincing and meaningful results, implications, and limits. Plausible surface deformation (subsidence) and gravity changes (gravity decrease) were detected in subrosion-prone areas of BF, which means mass transport in the subsurface. Although the temporal changes are small, i.e. a few µGal in gravity over 4 years, the surveys and later data analysis were realized at high effort to gain gravity observations with high precision. This includes a suitable measurement concept and data analysis (LSA), error estimation and propagation, and finally, a new, simple, but effective, method applied for hydrological correction of gravity differences (Sect. 3). The results discussed below were achieved in spite of challenging urban area conditions.
Levelling. Vertical deformation of several mm a−1 was found around the historical sinkhole areas in the measurement network. The deformation rates vary with time and strongly decrease for the campaigns in 2017, which was a rainy year. The origin of non-linear surface deformation in BF is not well understood and requires continuous observation, further research, and comparison with other data. The seasonal height variations due to ground frost would be reduced by installing holes drilled below the depth of frost and filled with longer steel piles than we did to mark levelling points (Sect. 3.1).
The sources of subsidence in BF can be a combination of geogenic and anthropogenic origin. Evidence of leaching of soluble rocks is the occurrence of two natural brine sources inside of Quellgrund, which extract approximately 250 t of salt per day from the subsurface (Sven Schmidt, TLUG, personal communication, 2017). Thus, subrosion processes and the corresponding subsidence could be affected by human activities due to water extraction. As another example, we found extensive subsidence of 7.5–30.5 mm a−1 at three points northwards of the leaning church tower of BF, including gravity point G07 (Fig. 6b). These subsidence rates are significantly higher than those displayed by the levelling profiles in Fig. 7. In the church area, several cavities were found at depths up to 100 m through several research core drillings (one of these was surveyed using borehole-based ultrasonic sonar; see Sect. 2), which also reveals evidence for underground leaching. Partially, the high subsidence rates could be affected by compaction loading due to intensive construction and recultivation work, which were carried out northwards of the leaning church tower between 2014 and 2016. The load of the northeastward sagging tower itself has an effect on the subsidence rates in this area as well. However, the ongoing subsidence seems to show slightly lower rates after the reconstruction work ended.
Time-lapse gravity. Besides stable gravity differences in obviously stable areas, several gravity differences and certain points in the network have been detected to show significant gravity decrease of up to about 2 µGal a−1 with SD of 1–2 µGal over the whole period of 4 years. This is an indication of local mass redistribution and has been observed mainly in and close to known historical sinkhole areas, which could be evidence for ongoing subrosion processes in the subsurface. The order of gravity decrease of 1–2 µGal a−1 is small compared to the results of other studies that have investigated underground mass transfer, e.g. greater two-digit µGal range observed by Hautmann et al. (2014) in a volcanic environment. However, the significance of the results is given by the high precision level of our gravity results (SD ≈1 µGal) after LSA and error propagation in our local network, as shown in Sect. 4.2 and Table 2, and by rather continuous rates of found gravity decrease. This has been proven to be due to the use of a highly accurate instrumentation and its appropriate use at measurement site conditions with a sophisticated concept of network configuration and high number of observations, as well as the regular control of their calibration stability. The SD level of the adjusted gravity differences was improved by an extensive preprocessing for data quality improvement and the high sophisticated application of LSA (e.g. drift control, required corrections, and weighting of gravity meters; see Sect. 3.3). Here, the accuracies of the gravity meters indeed have an effect as the used combinations of instruments show (Sect. 3.2 and Table 2). Hence, the data quality was further increased by using exclusively the newer Scintrex CG5 and ZLS Burris gravity meters, which achieve SD in the range of 3–4 µGal for one observed gravity difference.
We were able to emphasize and interpret subrosion-induced signals for several gravity differences on several survey points by applying a first attempt of correction for seasonal hydrological variations. We have used the global GLDAS Noah model to estimate the effect of a varying soil water content to each single gravity difference in our monitoring network. A regression coefficient for each gravity difference was determined and used to correct it for local soil water content. The regression coefficient represents temporal and spatial deviations in hydrology between two different measurement points, dependent on their geological, topographical, and infrastructural conditions. Although this correction works successfully, the remaining seasonal signals suggest that groundwater has to be considered additionally and the global soil water model may not be completely compatible for local studies. For future and similar studies, we propose to test repeated in situ measurements of the soil water content using ground-penetrating radar or nuclear magnetic resonance, which is especially appropriate to determine local soil water content within the vadose zone (de Pasquale and Mohnke, 2014). Both methods provide spatial information for soil water distribution. In this context, time-domain reflectometry in drill holes for point-specific 1-D profiles of water content can only be a first approximation because of the heterogeneity of soils, and furthermore drill holes are needed. Additionally, the remaining signal contains groundwater changes. In particular, in 2015, where soil water had an extreme minimum, the signals suggest further “mass loss” (Fig. 9). Here, the gravity minimum also can hint at very low groundwater levels and hydrological mass deficits in the aquifer layers. Unfortunately, groundwater gauges are not available in the measurement area; i.e. due to the lack of information about groundwater mechanisms, it is currently not possible to make any assumption about the effect of groundwater on the time-lapse gravity records and thus on the subrosion processes. Therefore, groundwater recordings at high precision level or hydrological models at best should be taken into account for future and similar studies.
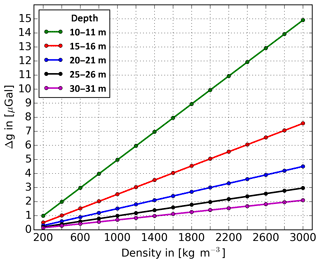
Figure 11Expected changes in gravity against density for a 1 m thick dissolved layer located beneath a survey point and at different depths, with a spatial dimension of dx=10 m, dy=10 m, and dz=1 m.
An idea, in which way our results could be explained by underground mass transfer, is given in Fig. 11 as a simple approximation. The gravity effect of a 1 m thick layer of different densities with horizontal dimensions of 10 m in both the x and y directions, which is located and centred beneath a single surface point, is displayed. For example, a cavity similar to the one surveyed beneath the leaning church tower (Sect. 2) would have to propagate for 1 m towards Earth's surface, with a density of disappearing rocks of 2600 kg m−3 (density measured by LIAG Hanover using drill cores from the 458 m deep research drilling at the leaning church tower of BF), to explain a gravity decrease of 6.5 µGal (red curve). This could fit to the found gravity decrease at gravity points G07 and G12 (Fig. 9), which are located very close to the leaning church tower, after about 3–4 years. Erosion rates known from literature can vary from 0.1 mm a−1 for limestone (Waltham et al., 2005; Gabrovšek and Stepišnik, 2011) to 0.5–1.0 m a−1 for gypsum under favourable subrosion conditions (Waltham et al., 2005). The erosion rates determined by the approximation of our simple model are on the order of about 0.25 m a−1. This fits to favourable geological subrosion conditions in our measurement area, in which the caprock mostly consists of anhydrite and gypsum. The erosion itself is proven by several small cavities (Sect. 2). Also, it can be discussed if the mass loss is only according to dissolution processes or if, e.g. a roof collapse of a cavity, i.e. breccia, can result in larger rate of mass loss. However, such estimations are indeed subject to the principle of ambiguity in gravity investigations, which has to be considered during interpretation. For an extensive modelling of subrosion processes based on gravity data, very long gravity time series as well as a detailed geological model of the study area are required, which is subject to future work. In addition, and for similar studies, we propose to dense up the measurement network for areas that are demonstrably not gravitationally stable (in our case, around the leaning church tower) and thus to give up few points in stable areas due to high measurement effort. Especially in local studies, which investigate shallow structures, it is required to derive detailed information about the spatial dimension of areas that are prone to gravity decrease due to underground mass redistribution.
In this study, we show the feasibility and the success of an approach that combines levelling and time-lapse gravimetric surveys in the urban area of Bad Frankenhausen in Germany, which is intensely prone to subrosion. We used ground-based time-lapse gravimetry, which is a non-invasive and powerful geophysical tool to monitor mass movements in the subsurface, and precise levelling to investigate the accompanied subsidence. A total of 17 time-lapse gravimetry and 18 levelling campaigns were carried out over 4 years in a local combined network. Despite challenging measurement conditions and the lack of permanent monitoring sites for environmental or hydrological parameters, we identified subrosion-related signal content in our measurements. To our knowledge, the presented field study is the first long-term, high-resolution time-lapse gravity study in a subrosion-prone area. Furthermore, it is the first attempt to quantify mass movements related to underground leaching, as well as to correct time-lapse gravity records for varying soil water content using a regression coefficient. The main results and modifications for future work based on the findings can be summarized as follows:
-
Subsidence in Bad Frankenhausen, on the order of millimetres up to several centimetres per year, is an ongoing process with possible non-linear periods, which is evidence of ongoing leaching.
-
A significant gravity decrease of 1–2 µGal a−1 has been observed on several points, which is additional evidence of subsurface mass relocation.
-
Survey points should be stable with respect to seasonal elevation effects (ground frost) and inner-city noise. Well suited are poured concrete pedestals for time-lapse gravimetric surveys and drilled holes filled by steel piles for levelling, both below frost depth.
-
Survey points should be connected to a superior reference system for stability control of the whole network and significant results.
-
Correction of gravity observations for varying soil water content using the global GLDAS Noah model is an effective approach to reduce the seasonal signal but requires further investigation. We propose in situ measurements using ground-penetrating radar (GPR) or nuclear magnetic resonance (NMR). Additionally, we recommend monitoring of the groundwater level.
-
If time-lapse gravity monitoring is conducted in areas of large subsidence, a more precise determination of the vertical gravity gradient should be considered to improve the correction of height changes in the time-lapse gravity records. Even more, the vertical gravity gradient can be considered as a separate parameter to be monitored. The second or even third derivative of the gravity potential is more sensitive to near-surface density variations, i.e. subrosion-induced mass changes (e.g. Eppelbaum, 2009). However, a precise determination of the gradient requires much effort and is of course also sensitive to near-surface hydrological mass variations.
-
For similar studies, we recommend to exclusively use highly precise gravity meters (Scintrex CG5 or CG6, ZLS Burris) and observe gravity differences at least three times each with three to four instruments in order to improve the quality and validity of gravity differences significantly.
-
After 4 years of observation, it becomes possible to model or quantify the amount of weakening of soluble layers by leaching or subsurface cavity growth. However, longer time series, i.e. additional data acquisition, are required to increase the resilience of the approach presented and to detect non-linearities in gravity variations.
-
In support of point 8, due to ambiguity in gravimetry, determination of the spatial extent of local areas, in which gravity is changing, requires local densification of the measurement network.
Besides ongoing data acquisition, the next step is to create a geological model of the study area based on close-mesh Bouguer anomalies, physical rock parameters derived from other studies in this area (e.g. Wadas et al., 2016), and borehole measurements. On the basis of this model, we aim to identify depth and thickness of potential sinkhole areas in BF and to investigate additional structures which are not being resolved by our time-lapse observations yet. The time-variable subrosion-induced mass transports will be then investigated related to their depth and extent by adapting the geological model for each survey period.
In the future and for similar studies, it is recommendable to focus on the investigation of the role of hydrology and its parameters (e.g. flow intensity, flow path, flow direction) for sinkhole development.
Geodetic–gravimetric data are property of LIAG Hanover and will be used for further investigations and publications by the authors. The data are available from the authors upon request. Please contact the first author for details. The specific soil water GLDAS Noah model used here is provided by Beaudoing and Rodell (2016).
MK analysed the gravity data, developed software (pre-processing, hydrological correction), produced figures, and wrote the paper. GG developed the overall scientific concept of the project and established the monitoring network. AW and MK developed the new hydrological correction concept. DV performed the processing and validation of levelling data. All authors contributed to the fieldwork, the scientific discussion and interpretation, and reviewing and editing the paper.
The authors declare that they have no conflict of interest.
Sincere thanks are given to the technical staff of LIAG Hanover for extensive measurement work despite difficult weather circumstances: Jan Bergmann-Barrocas, Jan Bayerle, Dieter Eppig, Eckhardt Großmann, Norman Krause, Sven Wedig, and Erwin Wagner. Furthermore, we thank Ludger Timmen and the University of Hanover, Germany, for the frequent loan of a Scintrex CG3 gravity meter. We appreciate David Tanner for his advice and help with improving the manuscript as well as the English grammar and spelling. We acknowledge the valuable reviews of the reviewers, Carla Braitenberg and Lev Eppelbaum, that have contributed to the improvement of this article.
The work is part of the project SIMULTAN, funded by the Federal Ministry for Education and Research (BMBF, grant no. 03G0843A), which is gratefully acknowledged.
This paper was edited by Ulrike Werban and reviewed by Carla Braitenberg and Lev Eppelbaum.
Al-Halbouni, D., Holohan, E. P., Saberi, L., Alrshdan, H., Sawarieh, A., Closson, D., Walter, T. R., and Dahm, T.: Sinkholes, subsidence and subrosion on the eastern shore of the Dead Sea as revealed by a close-range photogrammetric survey, Geomorphology, 285, 305–324, https://doi.org/10.1016/j.geomorph.2017.02.006, 2017. a
Al-Halbouni, D., Holohan, E. P., Taheri, A., Schöpfer, M. P. J., Emam, S., and Dahm, T.: Geomechanical modelling of sinkhole development using distinct elements: model verification for a single void space and application to the Dead Sea area, Solid Earth, 9, 1341–1373, https://doi.org/10.5194/se-9-1341-2018, 2018. a
Augarde, C. E., Lyamin, A. V., and Sloan, S. W.: Prediction of Undrained Sinkhole Collapse, J. Geotech. Geoenviron., 129, 197–205, https://doi.org/10.1061/(ASCE)1090-0241(2003)129:3(197), 2003. a
Aurit, M. D., Peterson, R. O., and Blanford, J. I.: A GIS Analysis of the Relationship between Sinkholes, Dry-Well Complaints and Groundwater Pumping for Frost-Freeze Protection of Winter Strawberry Production in Florida, PLoS ONE, 8, e53832, https://doi.org/10.1371/journal.pone.0053832, 2013. a
Beaudoing, H. and Rodell, M.: GLDAS Noah Land Surface Model L4 monthly 0.25 x 0.25 degree V2.1, Greenbelt, Maryland, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), NASA/GSFC/HSL, https://doi.org/10.5067/SXAVCZFAQLNO, 2016. a, b
Beck, B. F.: Environmental and engineering effects of Sinkholes – the processes behind the problems, Environ. Geol., 12, 71–78, https://doi.org/10.1007/BF02574791, 1988. a
Beck, B. F.: Soil piping and sinkhole failures, in: Encyclopedia of Caves, 2nd Edn., Elsevier, 718–723, 2012. a
Bell, F. G.: Subsidence associated with the abstraction of fluids, Geol. Soc. Eng. Geol. Sp., 5, 363–376, https://doi.org/10.1144/GSL.ENG.1988.005.01.40, 1988. a
Benito-Calvo, A., Gutiérrez, F., Martínez-Fernández, A., Carbonel, D., Karampaglidis, T., Desir, G., Sevil, J., Guerrero, J., Fabregat, I., and García-Arnay, A.: 4D Monitoring of Active Sinkholes with a Terrestrial Laser Scanner (TLS): A Case Study in the Evaporite Karst of the Ebro Valley, NE Spain, Remote Sensing, 10, 571–589, https://doi.org/10.3390/rs10040571, 2018. a, b
Bonatz, M.: Der Gravitationseinfluss der Bodenfeuchtigkeit, Zeitrschrift für Vermessungswesen, 92, 135–139, 1967. a, b
Bosch, F. P. and Müller, I.: Continuous gradient VLF measurements: a new possibility for high resolution mapping of karst structure, First Break, 19, 343–350, https://doi.org/10.1046/j.1365-2397.2001.00173.x, 2001. a
Brady, B. H. G. and Brown, E. T.: Rock Mechanics – For underground mining, Springer Science, Berlin, Germany, 3rd Edn., https://doi.org/10.1007/978-1-4020-2116-9, 2006. a
Braitenberg, C., Sampietro, D., Pivetta, T., Zuliani, D., Barbagallo, A., Fabris, P., Rossi, L., Fabbri, L., and Mansi, A. H.: Gravity for Detecting Caves: Airborne and Terrestrial Simulations Based on a Comprehensive Karstic Cave Benchmark, Pure Appl. Geophys., 173, 1243–1264, https://doi.org/10.1007/s00024-015-1182-y, 2016. a
Brinkmann, R., Parise, M., and Dye, D.: Sinkhole distribution in a rapidly developing urban environment: Hillsborough County, Tampa Bay area, Florida, Eng. Geol., 99, 169–184, https://doi.org/10.1016/j.enggeo.2007.11.020, 2008. a
Caramanna, G., Ciotoli, G., and Nisio, S.: A review of natural sinkhole phenomena in Italian plain areas, Nat. Hazards, 45, 145–172, https://doi.org/10.1007/s11069-007-9165-7, 2008. a
Carbone, D., Poland, M. P., Diament, M., and Greco, F.: The added value of time-variable microgravimetry to the understanding of how volcanoes work, Earth-Sci. Rev., 169, 146–179, https://doi.org/10.1016/j.earscirev.2017.04.014, 2017. a
Champollion, C., Deville, S., Chéry, J., Doerflinger, E., Le Moigne, N., Bayer, R., Vernant, P., and Mazzilli, N.: Estimating epikarst water storage by time-lapse surface-to-depth gravity measurements, Hydrol. Earth Syst. Sci., 22, 3825–3839, https://doi.org/10.5194/hess-22-3825-2018, 2018. a
Cooper, A. H.: Subsidence and foundering of strata caused by the dissolution of Permian gypsum in the Ripon and Bedale areas, North Yorkshire, Geol. Soc. Spec. Publ., 22, 127–139, https://doi.org/10.1144/GSL.SP.1986.022.01.11, 1986. a
Dahm, T., Kühn, D., Ohrnberger, M., Kröger, J., Wiederhold, H., Reuther, C. D., Dehghani, A., and Scherbaum, F.: Combining geophysical data sets to study the dynamics of shallow evaporites in urban environments: Application to Hamburg, Germany, Geophys. J. Int., 181, 154–172, https://doi.org/10.1111/j.1365-246X.2010.04521.x, 2010. a
de Pasquale, G. and Mohnke, O.: Numerical Study of Prepolarized Surface Nuclear Magnetic Resonance in the Vadose Zone, Vadose Zone J., 13, 1–9, https://doi.org/10.2136/vzj2014.060069, 2014. a
Desir, G., Gutiérrez, F., Merino, J., Carbonel, D., Benito-Calvo, A., Guerrero, J., and Fabregat, I.: Rapid subsidence in damaging sinkholes: Measurement by high-precision leveling and the role of salt dissolution, Geomorphology, 303, 393–409, https://doi.org/10.1016/j.geomorph.2017.12.004, 2018. a
Deville, S., Jacob, T., Chéry, J., and Champollion, C.: On the impact of topography and building mask on time varying gravity due to local hydrology, Geophys. J. Int., 192, 82–93, https://doi.org/10.1093/gji/ggs007, 2013. a
Eppelbaum, L. V.: Application of Microgravity at Archaeological Sites in Irael: Some Estimation Derived from 3-D Modeling and Quantitative Analysis of Gravity Field, in: Proceedings of the 22nd Symposium on the Application of Geophysics to Engineering and Environmental Problems 2009 (SAGEEP), 434–446, 2009. a
Ezersky, M. G., Eppelbaum, L. V., Al-Zoubi, A., Keydar, S., Abueladas, A., Akkawi, E., and Medvedev, B.: Geophysical prediction and following development sinkholes in two Dead Sea areas, Israel and Jordan, Environ. Earth Sci., 70, 1463–1478, https://doi.org/10.1007/s12665-013-2233-2, 2013. a
Filin, S., Baruch, A., Avni, Y., and Marco, S.: Sinkhole characterization in the Dead Sea area using airborne laser scanning, Nat. Hazards, 58, 1135–1154, https://doi.org/10.1007/s11069-011-9718-7, 2011. a
Ford, D. and Williams, P. D.: Karst Hydrogeology and Geomorphology, Wiley, Chichester, https://doi.org/10.1002/9781118684986, 2007. a
Ford, T. W. and Quiring, S. M.: Comparison and application of multiple methods for temporal interpolation of daily soil moisture, Int. J. Climatol., 34, 2604–2621, https://doi.org/10.1002/joc.3862, 2013. a
Gabrovšek, F. and Stepišnik, U.: On the formation of collapse dolines: A modelling perspective, Geomorphology, 134, 23–31, https://doi.org/10.1016/j.geomorph.2011.06.007, 2011. a
Gómez-Ortiz, D. and Martín-Crespo, T.: Assessing the risk of subsidence of a sinkhole collapse using ground penetrating radar and electrical resistivity tomography, Eng. Geol., 149-150, 1–12, https://doi.org/10.1016/j.enggeo.2012.07.022, 2012. a
Gutiérrez, F.: Sinkhole Hazards, Oxf. Res. Encyclop. Nat. Haz. Sci., 1–85, https://doi.org/10.1093/acrefore/9780199389407.013.40, 2016. a, b
Gutiérrez, F. and Lizaga, I.: Sinkholes, collapse structures and large landslides in an active salt dome submerged by a reservoir: The unique case of the Ambal ridge in the Karun River, Zagros Mountains, Iran, Geomorphology, 254, 88–103, https://doi.org/10.1016/j.geomorph.2015.11.020, 2016. a
Gutiérrez, F., Guerrero, J., and Lucha, P.: A genetic classification of sinkholes illustrated from evaporite paleokarst exposures in Spain, Environ. Geol., 53, 993–1006, https://doi.org/10.1007/s00254-007-0727-5, 2008. a
Gutiérrez, F., Parise, M., De Waele, J., and Jourde, H.: A review on natural and human-induced geohazards and impacts in karst, Earth-Sci. Rev., 138, 61–88, https://doi.org/10.1016/j.earscirev.2014.08.002, 2014. a, b
Hautmann, S., Gottsmann, J., Camacho, A. G., Van Camp, M., and Fournier, N.: Continuous and campaign-style gravimetric investigations on Montserrat 2006 to 2009, Geol. Soc. Mem., 39, 241–251, https://doi.org/10.1144/M39.14, 2014. a, b
Higuera-Díaz, I. C., Carpenter, P. J., and Thompson, M. D.: Identification of buried sinkholes using refraction tomography at Ft. Campbell Army Airfield, Kentucky, Environ. Geol., 53, 805–812, https://doi.org/10.1007/s00254-007-0693-y, 2007. a
Hunt, B. B., Smith, B. A., Adams, M. T., Hiers, S. E., and Brown, N.: Cover-Collapse Sinkhole Development in the Cretaceous Edwards Limestone, Central Texas, in: Proceedings of the 13th Multidisciplinary Conference on Sinkholes and the Engineering amd Environmetal Impacts of Karst. Carlsbad, New Mexico, edited by: Land, L., Doctor, D. H., and Stephenson, J. B., 89–102, 2013. a
Intrieri, E., Gigli, G., Nocentini, M., Lombardi, L., Mugnai, F., Fidolini, F., and Casagli, N.: Sinkhole monitoring and early warning: An experimental and successful GB-InSAR application, Geomorphology, 241, 304–314, https://doi.org/10.1016/j.geomorph.2015.04.018, 2015. a
Jacob, T., Bayer, R., Chery, J., and Le Moigne, N.: Time-lapse microgravity surveys reveal water storage heterogeneity of a karst aquifer, J. Geophys. Res.-Sol. Ea., 115, B06402, https://doi.org/10.1029/2009JB006616, 2010. a
Jentzsch, G., Weise, A., Rey, C., and Gerstenecker, C.: Gravity Changes and Internal Processes: Some Results Obtained from Observations at Three Volcanoes, Pure Appl. Geophys., 161, 1415–1431, https://doi.org/10.1007/s00024-004-2512-7, 2004. a
Jentzsch, G., Schulz, R., and Weise, A.: Automated Burris gravity meter for single and continuous observation, Geodesy and Geodynamics, 9, 204–209, https://doi.org/10.1016/j.geog.2017.09.007, 2018. a
Kanngieser, E., Kummer, K., Torge, W., and Wenzel, H.-G.: Das Gravimeter-Eichsystem Hannover, 120, Wissenschaftliche Arbeiten der Fachrichtung Vermessungswesen der Universität Hannover, 1983. a
Kaufmann, G.: Geophysical mapping of solution and collapse sinkholes, J. Appl. Geophys., 111, 271–288, https://doi.org/10.1016/j.jappgeo.2014.10.011, 2014. a, b, c, d
Kaufmann, G., Romanov, D., Tippelt, T., Vienken, T., Werban, U., Dietrich, P., Mai, F., and Börner, F.: Mapping and modelling of collapse sinkholes in soluble rock: The Münsterdorf site, northern Germany, J. Appl. Geophys., 154, 64–80, https://doi.org/10.1016/j.jappgeo.2018.04.021, 2018. a, b
Kawashima, K., Aydan, O., Aoki, T., Kishimoto, I., Konagai, K., Matsui, T., Sakuta, J., Takahashi, N., Teodori, S.-P., and Yashima, A.: Reconnaissance Investigation on the Damage of the 2009 L'Aquila, Central Italy Earthquake, J. Earthq. Eng., 14, 817–841, https://doi.org/10.1080/13632460903584055, 2010. a
Kent, J. D. and Dunaway, L.: Real-Time GPS Network Monitors Bayou Corne Sinkhole Event, Eos, 94, 1–2, https://doi.org/10.1002/2013EO430002, 2013. a
Kersten, T., Kobe, M., Gabriel, G., Timmen, L., Schön, S., and Vogel, D.: Geodetic monitoring of subrosion-induced subsidence processes in urban areas, J. Appl. Geodesy, 11, 21–29, https://doi.org/10.1515/jag-2016-0029, 2017. a
Klees, R., Reudink, R. H. C., and Flikweert, P. L. M.: Tilt Susceptibility of the Scintrex CG-5 Autograv Gravity Meter Revisited, in: International Association of Geodesy Symposia, https://doi.org/10.1007/1345_2017_4, 2017. a
Knolle, F., Kempe, S., Vogel, B., and Rupp, H.: World-wide largest Biosphere Reserve on sulphate karst and the schlotten caves – endangered geo- and biodiversity hotspots in the South Harz, Germany, in: Proceedings of the 17th International Speleology Congress, Sydney, Australia, edited by: Moore, S. and White, K., vol. 1, 149–152, 2017. a
Krawczyk, C. M., Polom, U., Trabs, S., and Dahm, T.: Sinkholes in the city of Hamburg – new urban shear-wave reflection seismic system enables high-resolution imaging of subrosion structures, J. Appl. Geophys., 78, 133–143, https://doi.org/10.1016/j.jappgeo.2011.02.003, 2012. a, b
Krawczyk, C. M., Polom, U., and Buness, H.: Geophysikalische Schlüsselparameter zur Überwachung von Erdfällen – Stand und Ziele der aktiven Seismik, in: DGG-Sonderband Geohazards/Sinkholes I/2015, Deutsche Geophysikalische Gesellschaft (DGG), Hannover, 19–30, 2015. a
Kugler, H.: Studien zur pleistozänen Formung der Hainleite, der Windleite, des Wippertals und des Frankenhäuser Beckens, Wissenschaftliche Zeitschrift der Karl-Marx-Universität Leipzig, 2, 355–385, 1958. a
Kupetz, M. and Mucke, D.: Beitrage zur Geologie und Genese der Barbarossahohle bei Rottleben am Kyffhäuser und Mansfelder Mulde, Wissenschaftlich-Technischer Informationsdienst des Zentralen Geologischen Instituts der DDR, 30, Reihe A, Heft 2, 96–103, 1989. a
Lambrecht, J. L., Miller, R. D., and Durrant, S.: Time-Lapse High Resolution Seismic Imaging of A Catastrophic Salt Dissolution Sinkhole In Central Kansas, in: Symposium on the Application of Geophysics to Engineering and Environmental Problems 2005, Society of Exploration Geophysicists, 943–951, 2005. a
Lee, E. J., Shin, S. Y., Ko, B. C., and Chang, C.: Early sinkhole detection using a drone-based thermal camera and image processing, Infrared Phys. Techn., 78, 223–232, https://doi.org/10.1016/j.infrared.2016.08.009, 2016. a
Lei, M., Gao, Y., Jiang, X., and Guan, Z.: Emergency investigation of extremely large sinkholes, Maohe, Guangxi, China, in: Proceedings of the 13th Multidisciplinary Conference on Sinkholes and the Engineering and Environmetal Impacts of Karst, Carlsbad, New Mexico, edited by: Land, L., Doctor, D. H., and Stephenson, J. B., 293–297, 2013. a
Leica Geosystems AG, S.: Leica DNA03/DNA10 User Manual, 2nd Edn., available at: http://surveyequipment.com/assets/index/download/id/59/ (last access: 1 April 2019), 2006. a
Lollino, P., Martimucci, V., and Parise, M.: Geological survey and numerical modeling of the potential failure mechanisms of underground caves, Geosys. Engin., 16, 100–112, https://doi.org/10.1080/12269328.2013.780721, 2013. a
Mäkinen, J. and Tattari, S.: Soil moisture and groundwater: Two sources of gravity variations, Bull. Info. Mar. Terr., 62, 103–110, 1988. a, b
Meng, L. and Quiring, S. M.: A Comparison of Soil Moisture Models Using Soil Climate Analysis Network Observations, J. Hydrometeorol., 9, 641–659, https://doi.org/10.1175/2008JHM916.1, 2008. a
Mesescu, A. A.: The Ocnele Mari salt mine collapsing sinkhole – A NATECH breakdown in the Romanian sub-carpathians, Carpath, J. Earth. Env., 6, 215–220, 2011. a
Messerklinger, S.: Formation mechanism of large subsidence sinkholes in the Lar valley in Iran, Q. J. Eng. Geol. Hydroge., 47, 237–250, https://doi.org/10.1144/qjegh2012-062, 2014. a
Miao, X., Qiu, X., Wu, S.-S., Luo, J., Gouzie, D. R., and Xie, H.: Developing Efficient Procedures for Automated Sinkhole Extraction from Lidar DEMs, Photogramm. Eng. Rem. S., 79, 545–554, https://doi.org/10.14358/PERS.79.6.545, 2013. a
Miensopust, M. P., Igel, J., Günther, T., Dlugosch, R., and Hupfer, S.: Electric and Electromagnetic Investigation of a Karst System, in: Near Surface Geoscience 2015 – 21st European Meeting of Environmental and Engineering Geophysics, https://doi.org/10.3997/2214-4609.201413704, 2015. a
Milanovic, P.: The environmental impacts of human activities and engineering constructions in karst regions, Episodes, 25, 13–21, 2002. a
Naujoks, M., Weise, A., Kroner, C., and Jahr, T.: Detection of small hydrological variations in gravity by repeated observations with relative gravimeters, J. Geodesy, 82, 543–553, https://doi.org/10.1007/s00190-007-0202-9, 2008. a, b, c
Nof, R. N., Baer, G., Ziv, A., Raz, E., Atzori, S., and Salvi, S.: Sinkhole precursors along the Dead Sea, Israel, revealed by SAR interferometry, Geology, 41, 1019–1022, https://doi.org/10.1130/G34505.1, 2013. a
Nooner, S. L., Eiken, O., Hermanrud, C., Sasagawa, G. S., Stenvold, T., and Zumberge, M. A.: Constraints on the in situ density of CO2 within the Utsira formation from time-lapse seafloor gravity measurements, Int. J. Greenh. Gas Con., 1, 198–214, https://doi.org/10.1016/S1750-5836(07)00018-7, 2007. a
Parise, M. and Lollino, P.: A preliminary analysis of failure mechanisms in karst and man-made underground caves in Southern Italy, Geomorphology, 134, 132–143, https://doi.org/10.1016/j.geomorph.2011.06.008, 2011. a, b
Patterson, D., Davey, J. C., Cooper, A. H., and Ferris, J. K.: The application of microgravity geophysics in a phased investigation of dissolution subsidence at Ripon, Yorkshire, Q. J. Eng. Geol., 28, 83–94, https://doi.org/10.1144/GSL.QJEGH.1995.028.P1.08, 1995. a
Pazzi, V., Di Filippo, M., Di Nezza, M., Carlà, T., Bardi, F., Marini, F., Fontanelli, K., Intrieri, E., and Fanti, R.: Integrated geophysical survey in a sinkhole-prone area: Microgravity, electrical resistivity tomographies, and seismic noise measurements to delimit its extension, Eng. Geol., 243, 282–293, https://doi.org/10.1016/j.enggeo.2018.07.016, 2018. a
Pfeffer, J., Champollion, C., Favreau, G., Cappelaere, B., Hinderer, J., Boucher, M., Nazoumou, Y., Oï, M., Mouyen, M., Henri, C., Le Moigne, N., Deroussi, S., Demarty, J., Boulain, N., Benarrosh, N., and Robert, O.: Evaluating surface and subsurface water storage variations at small time and space scales from relative gravity measurements in semiarid Niger, Water Resour. Res., 49, 3276–3291, https://doi.org/10.1002/wrcr.20235, 2013. a
Pivetta, T. and Braitenberg, C.: Laser-scan and gravity joint investigation for subsurface cavity exploration – The Grotta Gigante benchmark, Geophysics, 80, B83–B94, https://doi.org/10.1190/GEO2014-0601.1, 2015. a
Polom, U., Alrshdan, H., Al-Halbouni, D., Holohan, E. P., Dahm, T., Sawarieh, A., Atallah, M. Y., and Krawczyk, C. M.: Shear wave reflection seismic yields subsurface dissolution and subrosion patterns: application to the Ghor Al-Haditha sinkhole site, Dead Sea, Jordan, Solid Earth, 9, 1079–1098, https://doi.org/10.5194/se-9-1079-2018, 2018. a
Reudink, R., Klees, R., Francis, O., Kusche, J., Schlesinger, R., Shabanloui, A., Sneeuw, N., and Timmen, L.: High tilt susceptibility of the Scintrex CG-5 relative gravimeters, J. Geodesy, 88, 617–622, https://doi.org/10.1007/s00190-014-0705-0, 2014. a
Richter, B. and Bernburg, G.: Stratigraphische Gliederung des deutschen Zechsteins, Zeitschrift der Deutschen Geologischen Gesellschaft, 105, 843–854, 1953. a
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The global land data assimilation system, B. Am. Meteorol. Soc., 85, 381–394, https://doi.org/10.1175/BAMS-85-3-381, 2004. a, b
Rybakov, M., Goldshmidt, V., Fleischer, L., and Rotstein, Y.: Cave detection and 4-D monitoring: A microgravity case history near the Dead Sea, The Leading Edge, 20, 896–900, https://doi.org/10.1190/1.1487303, 2001. a
Rybakov, M., Rotstein, Y., Shirman, B., and Al-Zoubi, A.: Cave detection near the Dead Sea – a micromagnetic feasibility study, The Leading Edge, 24, 585–590, https://doi.org/10.1190/1.1946210, 2005. a
Sahu, P. and Lokhande, R. D.: An Investigation of Sinkhole Subsidence and its Preventive Measures in Underground Coal Mining, Proced. Earth Plan. Sc., 11, 63–75, https://doi.org/10.1016/j.proeps.2015.06.009, 2015. a
Sandia National Laboratories: September 2016 Bayou Choctaw Subsidence Report, available at: https://prod.sandia.gov/techlib-noauth/access-control.cgi/2017/175688r.pdf (last access: 1 April 2019), 2016. a
Sargent, C. and Goulty, N. R.: Seismic reflection survey for investigation of gypsum dissolution and subsidence at Hell Kettles, Darlington, UK, Q. J. Eng. Geol. Hydroge., 42, 31–38, https://doi.org/10.1144/1470-9236/07-071, 2009. a
Schmidt, W.: Geological and Geotechnical Investigation Procedures for Evaluation of the Causes of Subsidence Damage in Florida, Flor. Geol. Sur. Spec. Publ., 57, 1–28, 2005. a
Schriel, W. and Bülow, K. V.: Geologische Karte von Preußen und benachbarten deutschen Ländern. Map Frankenhausen 4632, Lieferung 9, 2. Auflage, Preußische Geologische Landesanstalt, Berlin, Germany, 1926a. a, b, c
Schriel, W. and Bülow, K. V.: Geologische Karte von Preußen und benachbarten deutschen Ländern. Map Kelbra 4532, Lieferung 9, 2. Auflage, Preußische Geologische Landesanstalt, Berlin, Germany, 1926b. a, b
Scintrex: CG-3/3M Autograv – Automated Gravity Meter Operator Manual, available at: https://scintrexltd.com/wp-content/uploads/2017/02/CG3-Manual.pdf (last access: 1 April 2019), 1995. a
Scintrex: CG5 Scintrex Autograv System Operation Manual, available at: https://www.aseg.org.au/sites/default/files/Scintrex-CG5manualrelease1.pdf (last access: 1 April 2019), 2006. a
Seidel, G.: Geologie von Thüringen (The Geology of Thuringia), E. Schweizerbart'sche Verlagsbuchhandlung, Stuttgart, Germany, 2nd Edn., 2003. a
Sevil, J., Gutiérrez, F., Zarroca, M., Desir, G., Carbonel, D., Guerrero, J., Linares, R., Roque, C., and Fabregat, I.: Sinkhole investigation in an urban area by trenching in combination with GPR, ERT and high-precision leveling. Mantled evaporite karst of Zaragoza city, NE Spain, Eng. Geol., 231, 9–20, https://doi.org/10.1016/j.enggeo.2017.10.009, 2017. a
Shviro, M., Haviv, I., and Baer, G.: High-resolution InSAR constraints on flood-related subsidence and evaporite dissolution along the Dead Sea shores: Interplay between hydrology and rheology, Geomorphology, 293, 53–68, https://doi.org/10.1016/j.geomorph.2017.04.033, 2017. a
Song, K.-I., Cho, G.-C., and Chang, S.-B.: Identification, remediation, and analysis of karst sinkholes in the longest railroad tunnel in South Korea, Eng. Geol., 135-136, 92–105, https://doi.org/10.1016/j.enggeo.2012.02.018, 2012. a, b
Timmen, L.: Absolute and Relative Gravimetry, in: Sciences in Geodesy I – Advances and Future Directions, edited by: Xu, G., Springer-Verlag, Berlin, Heidelberg, 1–43, 2010. a, b
Timmen, L., Falk, R., Gabriel, G., Lothhammer, A., Schilling, M., and Vogel, D.: The Relative Gravimeter Calibration System Hannover for 10−4 Scale Determination, avn – allgemeine vermessungs-nachrichten, 125, 140–150, 2018. a
Torge, W.: Gravimetry, Walter de Gruyter, Berlin, New York, 465 pp., 1989. a, b, c, d
TrukkSoft: Nigra – Special Software for Levellings, available at: http://www.nivellement.de/files/Nigra 0Manual.pdf (last access: 1 April 2019), 2018. a
Tuckwell, G., Grossey, T., Owen, S., and Stearns, P.: The use of microgravity to detect small distributed voids and low-density ground, Q. J. Eng. Geol. Hydroge., 41, 371–380, https://doi.org/10.1144/1470-9236/07-224, 2008. a
Van Camp, M., Meus, P., Quinif, Y., Kaufmann, O., van Ruymbeke, M., Vandiepenbeeck, M., and Camelbeek, T.: Karst aquifer investigation using absolute gravity, Eos, 87, 294–299, https://doi.org/10.1029/2006EO300005, 2006. a
Wadas, S. H., Polom, U., and Krawczyk, C. M.: High-resolution shear-wave seismic reflection as a tool to image near-surface subrosion structures – a case study in Bad Frankenhausen, Germany, Solid Earth, 7, 1491–1508, https://doi.org/10.5194/se-7-1491-2016, 2016. a, b, c, d, e
Wadas, S. H., Tanner, D. C., Polom, U., and Krawczyk, C. M.: Structural analysis of S-wave seismics around an urban sinkhole: evidence of enhanced dissolution in a strike-slip fault zone, Nat. Hazards Earth Syst. Sci., 17, 2335–2350, https://doi.org/10.5194/nhess-17-2335-2017, 2017. a, b, c
Waltham, A. C. and Fookes, P. G.: Engineering classification of karst ground conditions, Q. J. Eng. Geol. Hydroge., 36, 101–118, https://doi.org/10.1144/1470-9236/2002-33, 2003. a
Waltham, T.: Control the drainage: the gospel accorded to sinkholes, Q. J. Eng. Geol. Hydroge., 49, 5–20, https://doi.org/10.1144/qjegh2015-088, 2016. a
Waltham, T., Bell, F. G., and Culshaw, M. G.: Sinkholes and Subsidence: Karst and Cavernous Rocks in Engineering and Construction, Springer, Berlin, Heidelberg, https://doi.org/10.1007/b138363, 2005. a, b, c
Weise, A., Kersten, T., Timmen, L., Gabriel, G., Schön, S., and Vogel, D.: Ein integrativer geodätisch-gravimetrischer Ansatz zur Erkundung von Subrosion im Erdfallgebiet Hamburg-Flottbek – Oberflächendeformation und Massentransfer, avn – allgemeine vermessungs-nachrichten, 125, 244–254, 2018. a, b
Wenzel, H. G.: Schwerenetze, in: Geodätische Netze in Landes- und Ingenieurvermessung II: Vorträge des Kontaktstudiums Februar 1985 in Hannover, Vermessungswesen bei Konrad Wittwer, edited by: Pelzer, H., vol. 13, p. 475 ff., 1985. a, b
Wilkinson, M., Mouli-Castillo, J., Morgan, P., and Eid, R.: Time-lapse gravity surveying as a monitoring tool for CO2 storage, Int. J. Greenh. Gas Con., 60, 93–99, https://doi.org/10.1016/j.ijggc.2017.03.006, 2017. a
Williams, P.: Encyclopedia of Caves and Karst Science, chap. Dolines, Fitzroy Dearborn, NYC, US, 628–641, 2004. a
Wolf, H.: Ausgleichungsrechnung. Formeln zur praktischen Anwendung., Ferdinand Dümmlers Verlag, Bonn, 1975. a
Yechieli, Y., Abelson, M., Wachs, D., Shtivelman, V., Crouvi, O., and Baer, G.: Formation of Sinkholes along the Shore of the Dead Sea – Preliminary Investigation, in: Ninth Multidisciplinary Conference on Sinkholes and the Engineering and Environmental Impacts of Karst, Geotechnical Special Publication, 184–194, https://doi.org/10.1061/40698(2003)16, 2003. a
Zini, L., Calligaris, C., Forte, E., Petronio, L., Zavagno, E., Boccali, C., and Cucchi, F.: A multidisciplinary approach in sinkhole analysis: The Quinis village case study (NE-Italy), Eng. Geol., 197, 132–144, https://doi.org/10.1016/j.enggeo.2015.07.004, 2015. a
acc – accuracy for a single measurement of a gravity difference under urban conditions in our local network derived from least squares adjustments per campaign