Relative timing of uplift along the Zagros Mountain Front Flexure (Kurdistan Region of Iraq): Constrained by geomorphic indices and landscape evolution modeling

The Mountain Front Flexure marks a dominant topographic step in the frontal part of the Zagros Fold–Thrust Belt. It is characterized by numerous active anticlines atop of a basement fault. So far, little is known about the relative activity of the anticlines, about their evolution, or about how crustal deformation migrates over time. We assessed the relative landscape maturity of three along-strike anticlines (from SE to NW: Harir, Perat, and Akre) located on the hanging wall of the Mountain Front Flexure in the Kurdistan Region of Iraq to identify the most active structures and to gain insights into the evolution of the fold–thrust belt. Landscape maturity was evaluated using geomorphic indices such as hypsometric curves, hypsometric integral, surface roughness, and surface index. Subsequently, numerical landscape evolution models were run to estimate the relative time difference between the onset of growth of the anticlines, using the present-day topography of the Harir Anticline as a base model. A stream power equation was used to introduce fluvial erosion, and a hillslope diffusion equation was applied to account for colluvial sediment transport. For different time steps of model evolution, we calculated the geomorphic indices generated from the base model. While Akre Anticline shows deeply incised valleys and advanced erosion, Harir and Perat anticlines have relatively smoother surfaces and are supposedly younger than the Akre Anticline. The landscape maturity level decreases from NW to SE. A comparison of the geomorphic indices of the model output to those of the present-day topography of Perat and Akre anticlines revealed that it would take the Harir Anticline about 80–100 and 160–200 kyr to reach the maturity level of the Perat and Akre anticlines, respectively, assuming erosion under constant conditions and constant rock uplift rates along the three anticlines. Since the factors controlling geomorphology (lithology, structural setting, and climate) are similar for all three anticlines, and under the assumption of constant growth and erosion conditions, we infer that uplift of the Akre Anticline started 160–200 kyr before that of the Harir Anticline, with the Perat Anticline showing an intermediate age. A NW-ward propagation of the Harir Anticline itself implies that the uplift has been independent within different segments. Our method of estimating the relative age difference can be applied to many other anticlines in the Mountain Front Flexure region to construct a model of temporal evolution of this belt.

1 Introduction

The Zagros Fold–Thrust Belt (hereafter referred to as Zagros) is an active orogen that resulted from the collision between the Arabian and Eurasian plates and contains the deformed portions of the NE part of the former Arabian passive margin (Fig. 1; Berberian, 1995; Mouthereau et al., 2012). Many aspects of the structural configuration and the evolution of the Zagros Fold–Thrust Belt are by now satisfactorily constrained, but the detailed spatial and temporal distribution of deformation across the belt is not yet well understood. This concerns especially the NW part of the belt in the Kurdistan Region of Iraq (KRI) due to a lack of comprehensive studies and for geopolitical reasons that make access to the field challenging. The style, timing, and relative activity of front thrusts, deformation propagation, and along-strike variations have not been sufficiently studied. It is not well known which structures are currently the most active ones either.

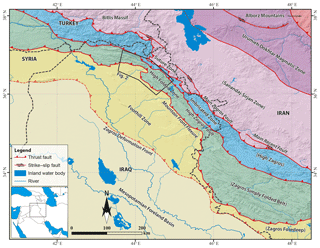
Figure 1 Tectonic subdivision of the NW segment of the Zagros Fold–Thrust Belt (modified after Berberian, 1995; Emre et al., 2013; Koshnaw et al., 2017; Zebari and Burberry, 2015). Names within the parentheses are known in the Iranian part of Zagros.

One of the morphologically most conspicuous structural elements of the Zagros Fold–Thrust Belt is the Mountain Front Flexure (MFF), which separates the High Folded Zone and the Foothill Zone (known in Iran as the Zagros Simply Folded Belt and Zagros Foredeep, respectively; Figs. 1 and 2; Berberian, 1995; Jassim and Goff, 2006; McQuarrie, 2004; Mouthereau et al., 2012; Vergés et al., 2011). In most parts of the Zagros Mountains, the MFF marks a pronounced topographic step, separating folds with high amplitudes, narrow wavelengths, and higher topography in the High Folded Zone from folds with relatively low amplitudes, long wavelengths, and lower topography in the Foothill Zone (Fig. 2). The MFF is characterized by numerous active anticlines atop of fault strands emerging from a basement fault. It was suggested that the onset of the MFF activity in the NW Zagros was about 5±1 Ma based on low-temperature thermochronology (Koshnaw et al., 2017). The timing of this activity is expected to differ along-strike of the belt and, hence, the initiation of uplift of the anticlines on the hanging wall of the MFF is the key to understand this temporal and spatial evolution. In the neighboring Iranian part, the MFF was a relatively long-lived structure active from 8.1 to 7.2 Ma to about the Pliocene–Pleistocene boundary. After that, only the southwesternmost anticline remained active in front of the MFF. This was inferred from progressive unconformities and magnetostratigraphy (Hessami et al., 2001, 2006; Homke et al., 2004).

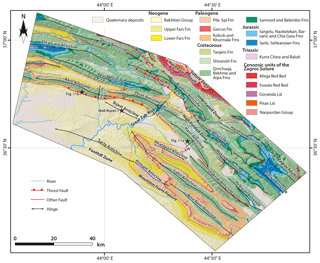
Figure 2 Geological map of the Zagros Fold–Thrust Belt in KRI showing the location of the three anticlines Harir, Perat, and Akre with respect to the MFF that separates the High Folded Zone from the Foothill Zone (modified after Csontos et al., 2012; Sissakian, 1997; Zebari and Burberry, 2015).

In active orogens, the main factor that contributes to building up topography is ongoing convergence (e.g., Bishop, 2007; Burbank and Anderson, 2012; Whittaker, 2012). Recent advancements in the availability of high-resolution digital elevation models (DEMs) and geographic information system (GIS) software allows us to quantitatively analyze the landscape (Bishop, 2007; Tarolli, 2014). Tectonic geomorphology approaches and landscape maturity studies have been used extensively and proven to be efficient in studying the relative tectonic activity of different areas in contractional settings (Cheng et al., 2012; Mahmood and Gloaguen, 2012; Ramsey et al., 2008; Regard et al., 2009). Nevertheless, the NW part of the Zagros lacks modern studies on tectonic geomorphology – with few exceptions. Bretis et al. (2011) detected sets of wind gaps (i.e., segments of river valleys abandoned due to lateral and vertical fold growth) in the High Folded Belt, NE of the MFF, suggesting that larger folds grew by linkage of smaller, shorter folds. Zebari and Burberry (2015) performed detailed analyses of various geomorphic indices for numerous anticlines in the High Folded Zone, concluding that the combination of clearly asymmetric drainage patterns and the mountain front sinuosity index (Bull, 2007; Keller et al., 1999) is a valuable tool for identifying putatively active fault-related folds. Obaid and Allen (2017) studied the landscape maturity of various anticlines within the Zagros Foothill Zone and constrained the order of deformation of these anticlines by proposing an out-of-sequence propagation of underlying faults into the foreland. They proposed that the Zagros Deformation Front was among the earliest faults that have been reactivated within the Foothill Zone.

In an active orogen such as the Zagros, a better understanding of the temporal and spatial distribution of deformation due to ongoing tectonics can be achieved with landscape modeling. In the last 2 decades, numerical models have been extensively used to study landscape evolution (Chen et al., 2014; Tucker and Hancock, 2010) and several software packages were specifically developed for this purpose (e.g., Hancock and Willgoose, 2002; Hobley et al., 2017; Refice et al., 2012; Salles and Hardiman, 2016; Tucker et al., 2001). Most of these models include algorithms for bedrock fluvial incision and hillslope creep as input parameters. Several studies have constrained the landscape evolution with the involvement of the corresponding tectonics and structures elsewhere (Collignon et al., 2016; Cowie et al., 2006; Miller et al., 2007; Refice et al., 2012).

In this study, we assessed variations in the landscape maturity of three anticlines (from SE to NW, the Harir, Perat, and Akre anticlines) located on the hanging wall of the MFF by quantitatively analyzing landscape indices (hypsometric curve, hypsometric integral, surface roughness, and surface index) in order to distinguish more mature segments from less mature ones, and to reconstruct the relative variation in uplift time and/or rate along these anticlines. We then computed the difference in the onset of uplift between more mature anticlines and less mature ones using a landscape evolution model. The present-day topography of the least mature anticline served as an input model for computing the time that it takes this anticline to reach the same state as the most mature one. Also, three structural cross sections were constructed across the three anticlines to delineate their structural style and to link it with their landscape maturity.

2 Geological setting

The Zagros Fold–Thrust Belt is the result of the collision between the Arabian and Eurasian plates (Fig. 1; Berberian, 1995; Mouthereau et al., 2012). Continental collision started in the Early Miocene following the progressive subduction of Neo-Tethyan oceanic lithosphere underneath Eurasia (Agard et al., 2011; Csontos et al., 2012; Koshnaw et al., 2017; Mouthereau et al., 2012). The Zagros Fold–Thrust Belt extends for about 2000 km from the Strait of Hormuz in southern Iran to the KRI and further into SE Turkey. Since the onset of collision, the deformation front has propagated 250–350 km southwestward, involving the northeastern margin of the Mesopotamian Foreland Basin and the Persian Gulf into a largely NW–SE-trending foreland fold–thrust belt (Mouthereau, 2011; Mouthereau et al., 2007). The shortening across different sectors of the Zagros Fold–Thrust Belt is estimated to range between 10 % and 32 % (Blanc et al., 2003; McQuarrie, 2004; Molinaro et al., 2005; Mouthereau et al., 2007; Vergés et al., 2011). GPS-derived horizontal velocities between Arabia and Eurasia show present-day convergence rates between 19 and 23 mm yr⁻¹ (McClusky et al., 2003). It is suggested that deformation partitioning occurs between the external and internal portions of the Iranian part of the Zagros Fold–Thrust Belt. While the internal Zagros Fold–Thrust Belt currently accommodates 3–4 mm yr⁻¹ of right-lateral displacement along the Main Recent Fault (Fig. 1; Reilinger et al., 2006; Vernant et al., 2004), the external part accommodates 7–10 mm yr⁻¹ of shortening by thrusting and folding (Hessami et al., 2006; Vernant et al., 2004), 2–4 mm yr⁻¹ of which is taken up by the MFF in the Fars Arc (Oveisi et al., 2009). However, no such estimates are available for the Iraqi segment of the Zagros. It is hence not known how much of the total Arabia–Eurasia plate convergence is being accommodated across the Iraqi part of the Zagros Fold–Thrust Belt.

The NW segment of the Zagros Fold–Thrust Belt in the KRI is subdivided into several NW-trending morphotectonic zones. These zones from NE to SW are (i) Zagros Suture Zone, (ii) Imbricated Zone, (iii) High Folded Zone, and (iv) Foothill Zone (Figs. 1 and 2; Jassim and Goff, 2006). These zones are bounded by major faults in the area. The faults include Main Zagros Fault separating the Zagros Suture Zone from the Imbricated Zone, High Zagros Fault that separates the Imbricated Zone from the High Folded Zone, and the Mountain Front Flexure that separates the High Folded Zone from the Foothill Zone (Figs. 1 and 2; Berberian, 1995; Jassim and Goff, 2006).

The deformed sedimentary succession is composed of 8–12 km thick Paleozoic to Cenozoic strata that rest on the Precambrian crystalline basement (Aqrawi et al., 2010; Jassim and Goff, 2006). The thick sedimentary cover consists of various competent and incompetent rock successions separated by detachment horizons. The infra-Cambrian Hormuz salt, which acts as a basal detachment in much of the southern and central Zagros in Iran, pinches out towards the northwest (Hinsch and Bretis, 2015; Kent, 2010). Other intermediate detachment horizons influence the structural style of the central Zagros in Iran (e.g., Sepehr et al., 2006; Sherkati et al., 2006), but their behavior is uncertain in NW Zagros due to limitations in outcrops and insufficient seismic profiles southwest of the Main Zagros Fault. Some proposed detachment levels include Ordovician and Silurian shales (Aqrawi et al., 2010), Triassic–Jurassic anhydrites (Aqrawi et al., 2010; Hinsch and Bretis, 2015; Zebari, 2013; Zebari and Burberry, 2015), and Lower Miocene anhydrite (Aqrawi et al., 2010; Csontos et al., 2012; Jassim and Goff, 2006; Kent, 2010; Zebari and Burberry, 2015).

The exposed geological units within the High Folded Zone are limited to ca. 5 km thick Upper Triassic–Quaternary stratigraphic succession (Fig. 2; Jassim and Goff, 2006; Law et al., 2014). Most anticlines are made up of Cretaceous carbonate rocks, while Upper Triassic–Lower Cretaceous strata are only exposed in the core of some anticlines. The Tertiary clastic rocks are preserved within the adjacent synclines. Within the studied structures, the Upper Jurassic–Lower Cretaceous Chia Gara and Lower Cretaceous Sarmord formations only crop out in Bekhme and Zinta gorges and consist of medium to thick bedded marly limestone, dolomitic limestone, and shale (Figs. 2 and 3). The Lower Cretaceous succession of Qamchuqa and Upper Cretaceous Bekhme and Aqra formations consist of thick bedded and massive reef limestone, dolomitic limestone, and dolomite. These units are generally rigid and resistant to erosion. Thus, they build the raised cores of anticlines. The Upper Cretaceous–Tertiary succession consists primarily of clastic rocks, which are mostly denuded, and alternating upper Paleocene and upper Eocene limestone of Khurmala and Pila Spi formations, respectively. They form a ridge surrounding the anticlines (Figs. 2 and 3). Unconsolidated Quaternary sediments in the study area consist of slope deposits, residual soil, alluvial fan deposits, and river terraces.

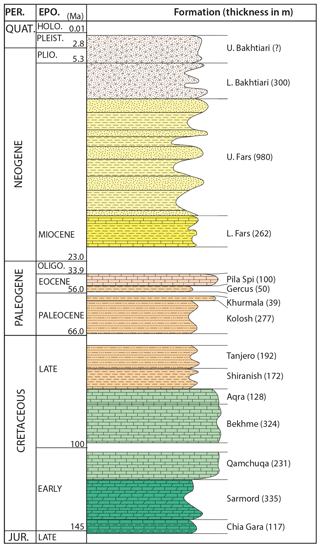
Figure 3 Stratigraphic column of the exposed rock units in the area. Thicknesses are given as in well Bijeel-1 (Fig. 2), which is located 5 km to the south of Perat Anticline (modified after Law et al., 2014). The column is scaled to the stratigraphic thicknesses.

There is no agreement concerning the overall structural style of the NW Zagros in KRI. Several authors (Al-Qayim et al., 2012; Ameen, 1991; Fouad, 2014; Jassim and Goff, 2006; Numan, 1997) suggested that the Iraqi part of the Zagros Fold–Thrust Belt reveals a combination of both thin- and thick-skinned deformation. Partly relying on reflection seismic data, it was also suggested that contraction has been localized on inherited passive-margin normal faults in the basement, which were inverted during the late stage of deformation since ca. 5 Ma (Abdulnaby et al., 2014; Burberry, 2015; Koshnaw et al., 2017). The structural relief across the MFF (Fig. 2) is likely linked to blind thrusts in the basement (Al-Qayim et al., 2012; Ameen, 1991, 1992; Fouad, 2014; Koshnaw et al., 2017; Numan, 1997). The same linkage between structural relief and a regional basement blind thrust is also documented in the Iranian Zagros (Blanc et al., 2003; Emami et al., 2010; Leturmy et al., 2010; Sherkati et al., 2006). Alternatively, Hinsch and Bretis (2015) argued that the structural relief in the hanging wall of the MFF is related to an underlying duplex structure that is linked to a stepped detachment horizon rooting in a lower Paleozoic detachment in the internal parts of the orogen. The relief has been attributed to the accumulation of the Hormuz salt in the Iranian Zagros (McQuarrie, 2004). Even though the MFF is believed to be a major blind thrust in the basement (Berberian, 1995), it is usually mapped along the southwestern limb of the last high anticline where the Pila Spi limestones or the Bekhme and Aqra limestones crop out (Fouad, 2014; Jassim and Goff, 2006; Numan, 1997). Given that landforms in the vicinity of the MFF indicate ongoing tectonic deformation, we suspect that these blind faults might be active at present. Unfortunately, however, instrumental seismicity in the entire region is too diffusely distributed to be attributed to any particular faults (Jassim and Goff, 2006).

Structurally, this segment of the Zagros Fold–Thrust Belt is dominated by NW–SE trending fault-related folds, the trend of folds changes to nearly E–W to the west of the Great Zab river (a.k.a. Greater Zab River; Fig. 2). The folds are usually S-verging and the related faults emerge to the surface within both the Imbricated Zone and High Folded Zone, while they remain blind within the Foothill Zone (Fouad, 2014; Hinsch and Bretis, 2015).

3 Data and methods

We calculated and analyzed landscape indices from DEMs for the studied anticlines and built a landscape evolution model that simulates progressive uplift and erosion of the landscape. We also constructed structural cross sections across these anticlines based on literature data and our own field observations.

3.1 Geomorphic indices

The present-day relief in the study area resulted from a competition between rock uplift triggered by horizontal contraction and erosion destroying it. Parameters controlling these competing processes are the rate of tectonic accretion, rock erodibility, and climate (Bishop, 2007; Burbank and Anderson, 2012).

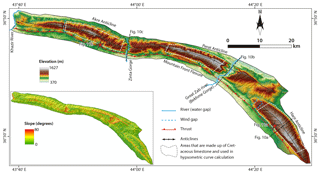
In order to quantitatively analyze the landscape for the Harir, Perat, and Akre anticlines (Figs. 2 and 4), we calculated hypsometric curves and determined three geomorphic indices: (i) hypsometric integral, (ii) surface roughness, and (iii) surface index. These are considered proxies for the relative maturity of a particular landscape. The hypsometric curve and integral refer to the distribution of surface area of a landscape with respect to the elevation (Strahler, 1952). The surface roughness value is mainly sensitive to incision (Andreani et al., 2014; Andreani and Gloaguen, 2016; Pike and Wilson, 1971); the surface index is a measure for the amount of erosion. When referring to the results obtained by using this set of geomorphic indices, we colloquially refer to them as “landscape maturity” parameters.

3.1.1 Hypsometric curve

The hypsometric curve for a basin is the frequency distribution of elevation of the watershed area below a given height (Strahler, 1952). Convex-shaped hypsometric curves represent relatively youthful stages of the basin, S-shaped and concave curves refer to more mature and old stages (Strahler, 1952). Hypsometric curves are usually calculated for a specific drainage basin. In this study, we calculated the weighted mean of the hypsometric curves for basins with areas > 0.25 km² within each anticlinal ridge, weighted by the basin area within the anticline. We restricted our analyses to those basins where Upper Cretaceous carbonates are exposed (Fig. 4). This allowed us to make realistic comparisons between the three anticlines, neglecting the differences in rock erodibility that arise when varying lithologies are included. Wind gaps and water gaps as well as the plunging crests of the anticlines were also excluded from the calculation.

Figure 4 Topography and slope maps of the studied anticlines obtained from 30 m resolution SRTM1 DEM data showing the location of water and wind gaps across these anticlines.

3.1.2 Hypsometric integral

The hypsometric integral (HI) is the ratio of area under the hypsometric curve (Strahler, 1952). It is used to highlight the erosional stage of a landscape with high values corresponding to less mature landscapes and low values indicating advanced stages of erosion. The hypsometric integral is computed for a certain area by the following equation (Pike and Wilson, 1971):

$$\begin{array}{}\text{(1)}& \mathrm{HI}={\displaystyle \frac{h_{\mathrm{mean}}-h_{\min }}{h_{\max }-h_{\min }}},\end{array}$$

where h_mean, h_min, and h_max are the mean, minimum, and maximum elevations (m) of the examined area.

3.1.3 Surface roughness

The surface roughness (SR) measures how much an area deviates from being totally flat. It differentiates flat planar surfaces with values close to 1 from irregular surfaces with higher values. It increases with the increase in incision by streams. The surface roughness is calculated using the following equation (Grohmann, 2004; Hobson, 1972):

$$\begin{array}{}\text{(2)}& \mathrm{SR}={\displaystyle \frac{\mathrm{TS}}{\mathrm{FS}}},\end{array}$$

where TS and FS are the areas (m²) of the actual topographic surface and the corresponding projection of that surface onto a planar surface, respectively.

3.1.4 Surface index

The surface index (SI; Andreani et al., 2014) combines elevations, hypsometric integral, and surface roughness to map simultaneously preserved and eroded portions of an elevated landscape. It is calculated using Eq. (3) (Andreani and Gloaguen, 2016):

$$\begin{array}{}\text{(3)}& \mathrm{SI}=(N_{\mathrm{HI}}\cdot N_{\mathrm{h}})-N_{\mathrm{SR}},\end{array}$$

where N_HI, N_h, and N_SR are the normalized hypsometric integral, elevations, and surface roughness values, respectively. Elevated and poorly incised landscapes with high hypsometric integral and low surface roughness show positive surface index values. Highly dissected landscapes with a high surface roughness yield negative surface index values. This means that the surface index is also sensitive to elevation.

3.2 Digital elevation models

The geomorphic indices for this study were calculated from the 12 m resolution TanDEM-X DEM (Krieger et al., 2007) obtained from the German Aerospace Center (DLR) and the 30 m resolution SRTM1 (Shuttle Radar Topography Mission Global 1 arc second Data) DEM (NASA JPL, 2013); these two inputs were used since different DEM inputs give slightly different geomorphic results (Andreani et al., 2014; Koukouvelas et al., 2018; Obaid and Allen, 2017). Geomorphic indices were calculated using both the TanDEM-X and the SRTM1 data. However, the TanDEM-X data revealed numerous artifacts and voids, which made calculations unstable and results unreliable (also see the comparison in the Supplement). All results of the geomorphic indices and subsequent calculations presented in the following sections were calculated from a 100×100 cell (3 km×3 km) moving window on the 30 m resolution SRTM1 data. A larger moving window makes the obtained measurements smoother and vice versa. The size of the moving window must be chosen based on the scale of the target; here we targeted anticlines with wavelengths varying from 5 to 8 km. A 3 km moving window covered almost an entire limb of an anticline. We also tested the method proposed by Pérez-Peña et al. (2009) in order to account for the neighboring cells in the calculation of the geomorphic indices. Rather than using a moving window, this approach uses a spatial autocorrelation of neighboring cells and maps clusters of high and low values of indices using Moran's I statistic (Moran, 1950) and Gi^* statistics (Ord and Getis, 1995). We have tested the same method here by calculating the HI for a 500 m×500 m grid of the SRTM data. We applied a hot spot analysis using Gi^* statistics with a distance of 1.5 km to define neighbor cells. Then, we resampled the HI map calculated from a 100×100 cell (3 km×3 km) moving window to 500 m×500 m grid from SRTM data. The calculations were performed using the focal and zonal tool sets in ESRI ArcGIS 10.4 software. In addition, the SRTM DEMs with 30 m resolution were used to extract topographic profiles, drainage networks, watersheds, stream slopes, and upstream drainage areas wherever required.

3.3 Modeling landscape evolution

We built a landscape evolution model to quantify the time difference in between the maturity level of the more mature and less mature anticlines by comparing the geomorphic indices of the evolved landscape with those of both anticlines based upon the open-source Landlab toolkit (Hobley et al., 2017; http://landlab.github.io, last access: 13 March 2019).

We used two components in our model: one simulating erosion due to fluvial action and another simulating sediment transport along slopes due to hillslope diffusion processes. Chen et al. (2014) showed that consideration of only these two components is sufficient for many landscapes but cannot model fluvial sedimentation. However, from field observations and from satellite imagery, we know that no significant fluvial sedimentation takes place on the slopes of the analyzed anticlines. On slopes of anticline flanks, the detachment-limited erosion due to the fluvial system tends to be the dominant process (Howard, 1994). To detect changes in the landscape due to fluvial erosion through time, we applied the commonly accepted idea that the rate of stream incision is directly proportional to the hydraulic shear stress of a stream (Braun and Willett, 2013). Consequently, we used the stream power incision law (Sklar and Dietrich, 1998; Whipple and Tucker, 1999):

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial z}{\partial t}}=K{A}^m{S}^n,\end{array}$$

where $\partial z/\partial t$ is the erosion rate (m yr⁻¹); K is an erodibility coefficient (yr⁻¹ m^(1−2 m)) that encompasses the influence of climate, lithology, and sediment transport processes; A is the upstream drainage area (m²) and is typically taken as a proxy for discharge (Wobus et al., 2006); $S=\partial z/\partial x$ is the local channel slope (m m⁻¹); z is the elevation (m); and m and n are the area and slope exponents, respectively. The stream power incision law (Eq. 4) is derived since the upstream drainage area A scales with channel discharge and channel width. The magnitude of the sediment flux in the channel is assumed to equal unity in the standard detachment-limited stream power model (Perron, 2017; Whipple, 2002). In the model, an incision threshold (C) was included, below which no incision occurs (Hobley et al., 2017).

To account for the provision of sediment due to hillslope diffusion processes from slopes outside the river system, we used the hillslope diffusion equation (Culling, 1963; Tucker and Bras, 1998):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\partial z}{\partial t}}=K_{\mathrm{d}}{\mathrm{\nabla }}^{\mathrm{2}}z,\end{array}$$

where K_d is the diffusivity coefficient (m² yr⁻¹), z is the elevation (m), and ∇² is the Laplace operator, i.e., the divergence of the gradient.

Finally, the overall evolution of the landscape in different time steps was calculated as the uplift rate subtracted by the changes due to both fluvial erosion and the hillslope diffusion (Temme et al., 2017):

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\partial z}{\partial t}}=U-K{A}^m{S}^n-K_d{\mathrm{\nabla }}^{\mathrm{2}}z,\end{array}$$

where U is the uplift rate (m yr⁻¹).

A DEM raster grid of the present-day less mature anticline (Harir) and the surrounding basins (Fig. 5a) served as model input. The advantage of using Harir Anticline was that the evolved drainage network overprinted the pre-existing one. The boundary conditions were set as closed on all sides except in pre-existing outlets in the input grid. The basins surrounding Harir Anticline were also included in the input grid to minimize the effect of the boundary conditions on the Harir Anticline itself. In the input raster grid, a flow route of each cell was connected with neighboring cells both diagonally and orthogonally. This means that each cell had the possibility to be linked with eight surrounding cells across its sides and corners (Hobley et al., 2017; Tucker et al., 2016).

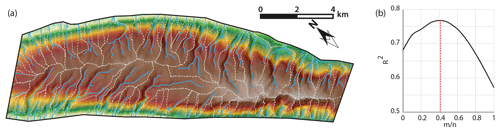
Figure 5 (a) DEM grid, drainage network, and basins for the present-day Harir Anticline that is used as an input for the model. White lines are basin divides; (b) m∕n plotted against regression values of elevation–X plot for streams in the Harir Anticline. The highest regression is achieved for $m/n=\mathrm{0.41}$.

Concerning the parameter used in the model, the value of m∕n, n, and K were found following the methodology described by Harel et al. (2016), Mudd et al. (2014), and Perron and Royden (2013), and by comparison with data from Harel et al. (2016). The value of m∕n was found by plotting the elevation against X (elevation–X plot) for streams in the input grid (Fig. 5a), where X is found following the equation described by Perron and Royden (2013):

$$\begin{array}{}\text{(7)}& X=\underset{xb}{\overset{x}{\int }}{\left({\displaystyle \frac{A_{\mathrm{0}}}{A\left(x\right)}}\right)}^{m/n}\mathrm{d}x,\end{array}$$

where A₀ is the reference drainage area (m²) of 166 160 m² and x is the horizontal upstream distance (m). In this approach, we ascribed values for m∕n range from zero to one, and X was calculated for each time from Eq. (7). The value of m∕n with maximum regression (R²) value in the elevation–X plot was taken as the best-fitting value, which was 0.41 in our case for the present-day Harir Anticline's drainages (Fig. 5b). This value of m∕n is located within the theoretically predicted values of m∕n, which ranges from 0.3 to 0.7, based on the stream power incision model (Kwang and Parker, 2017; Temme et al., 2017; Whipple and Tucker, 1999).

In the model, n=1.7 and $K=\mathrm{3.0}\times {\mathrm{10}}^{-\mathrm{6}}$ yr⁻¹ m^−0.4 were used; these values were estimated as mean of K and n in Harel et al. (2016) for those areas that are comparable with our study area in aspect of lithology, climate, and precipitation. The value of m was 0.7. We used an incision threshold of $C=\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{5}}$ m yr⁻¹, which is widely adopted for erosion of an upland landscape (Hobley et al., 2017). A present-day annual mean precipitation of ca. 0.7 m yr⁻¹ was used through the time due to the lack of nearby paleoclimate data with good quality. The average of the modeled precipitation anomaly data for Lake Van in SE Turkey (200 km to the NNW of the studied anticlines) is close to zero (Stockhecke et al., 2016; Supplement). The current elevation of the Bekhme and Aqra formations in the crest of Harir Anticline is about 1500 m a.s.l. Above that, 2070 m of Upper Cretaceous–Miocene units (Law et al., 2014) and 300 m of upper Miocene Lower Bakhtiari were exhumed before exposure of the Bekhme and Aqra formations. If we consider that the Lower Bakhtiari have been deposited close to sea level before onset of the MFF ca. 5 Ma, there would be 3872 m of rock uplift at a rate of ∼0.0007 m yr⁻¹, which was used in the model. This rate of vertical uplift is reasonable for the area and it matches with the vertical uplift in Kurdistan that has been presented by Tozer et al. (2019). Since soil (regolith) is rare and very thin when present on the slopes, a low diffusivity coefficient of K_d=0.001 m² yr⁻¹ was used (Fernandes and Dietrich, 1997).

There are minor variations in lithology between the three anticlines (they consist of a thick pile of dominantly Cretaceous carbonate) and no variation in climate can be expected on such a relatively local scale. Therefore, no significant variances are expected in the used parameters. Lastly, the parameters were calibrated by comparing the nature of the evolved landscape to other anticlines within the High Folded Zone that are cored by Cretaceous carbonates and more mature than the Harir Anticline to evaluate how realistic the evolved landscape is.

4 Results

4.1 Landscape maturity

The three studied anticlines are composed of the raised Cretaceous carbonates in their crests, whereas the Tertiary clastic rocks have been denuded, but conserved in the adjacent synclines. The three anticlines are dissected by rivers that form water gaps across them. Bekhme and Zinta gorges cut the Perat and Akre anticlines, respectively. We also observed wind gaps, such as those in the NW end of Harir Anticline (Zebari and Burberry, 2015). Therefore, neither the location of these water and wind gaps nor the plunging tips of anticlines have been considered in interpreting the geomorphic indices as proxies for relative landscape maturity.

The anticlines reach up to ca. 1500 m a.s.l. The minimum altitude is ca. 700 in the adjacent synclines and ca. 400 m in the Great Zab river (a.k.a. Greater Zab River) course. The hypsometric curves for the three anticlines are presented in Fig. 6. Harir Anticline's curve is more convex, and its shape is close to the youthful stage of Strahler's diagram (Ohmori, 1993; Strahler, 1952) with 78 % of the area above the mean elevation, while Akre Anticline is less convex and close to a mature stage with only 50 % of the area above the mean elevation. Perat Anticline's values are located in between and closer to the Harir Anticline curve with 64 % of its area above the mean elevation.

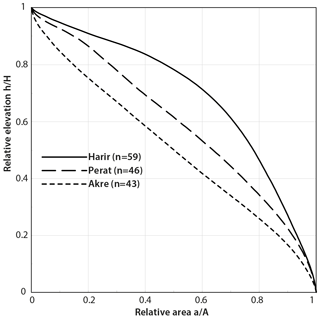
Figure 6 Present-day hypsometric curves of the studied anticlines. The curves are calculated as a total weighted mean for drainage basins within each anticline. We only use those parts where Upper Cretaceous carbonate rocks crop out and we exclude wind gaps, water gaps, and the plunging tips of anticlines. n is the number of basins used in the calculation of the hypsometric curve for each anticline.

The three calculated geomorphic indices (HI, SR, and SI) seem to be substantially influenced by the local structure, and wind and water gaps (Fig. 7). Hypsometric integral values vary between 0.2 and 0.77, with lower values in the adjacent synclines and higher values in the crest of the anticlines. The HI values decrease toward the plunging ends of the anticlines and at gorges, e.g., Perat Anticline's HI values are minimum at the Great Zab river. In general, Harir Anticline shows higher values than the other two anticlines. Harir Anticline has a broad crest and has been incised by narrow valleys. This makes the mean elevation within the moving window in the calculation close to the maximum elevation and, thus, causes higher values of the hypsometric integral. Perat Anticline shows high values of HI on its crest to the west of Bekhme Gorge. Among the three anticlines, Akre Anticline shows the lowest values of HI in its central part, which is due to the presence of more incised and wider valleys. Elevation drops rapidly from the hinge of the anticline toward the limbs, which causes the mean elevation within the window to fall.

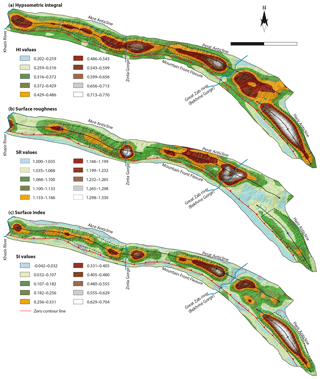
Figure 7 Surface index maps for the three anticlines calculated from 100×100 cell (3 km×3 km) and moving windows; (a) hypsometric integral, (b) surface roughness, and (c) surface index.

The surface roughness values range between 1 and 1.33 in the area. The lowest values of the SR are also present in the adjacent synclines and in the plunging tips of the anticlines. The highest values are associated with the location of water gaps. These are areas where rivers are deeply incised at both Bekhme and Zinta gorges. Harir Anticline has lowest surface roughness values. Perat Anticline shows the highest value of SR especially in its northern limb. Akre Anticline has moderate SR values in its central segment and western side where a wind gap is present.

The results of the surface index range between −0.04 to 0.70 in the three anticlines studied. Few locations show negative values. These are associated partly with adjacent synclines and with Bekhme Gorge. Apart from these locations, the area shows positive surface indices. Harir Anticline exhibits higher values on its broad crest. Perat Anticline shows moderate values of SI on its crest to the west and east of Bekhme Gorge. For Akre Anticline, SI values are lower than in both Harir and Perat anticlines, with highest values on its crest east of Zinta Gorge. These high values of SI highlight the flat areas with high elevation and high hypsometric integral. The surface index values also highlight the Pila Spi and Khurmala limestone ridges encircling the anticlines with values close to zero.

In our calculation, the results of geomorphic indices change with changing the size of the moving window and the resolution of the input data (see the Supplement). This was also detected by Andreani et al. (2014) and Obaid and Allen (2017). Andreani et al. (2014) found that the DEM resolution does not affect the hypsometric integral but it affects the surface roughness, while the size of the moving window affects both hypsometric integral and surface roughness. The results become smoother with an increasing size of the moving window. Here, we found that it is reasonable to use a 100×100 cell (3 km×3 km) moving window, which covers approximately one limb of the anticline with 6–7 km width. It therefore highlights the desirable signal. The cluster map for the HI Gi^* statistics was calculated following the approach by Pérez-Peña et al. (2009) for the 500 m×500 m grid. We obtained results similar to the HI map calculated from a 100×100 cell (3 km×3 km) moving window and resampled to 500 m×500 m grid in terms of highlighting the cluster of high and low HI values (Fig. S19a and b in the Supplement). This comparison proves that our method is equally applicable and valid. We therefore ran all analyses based on the 100×100 cell moving window as described above.

According to the hypsometric curves and the geomorphic indices, we found that there is a measurable difference in landscape maturity between the three anticlines. We classified our anticlines as relatively mature (Akre Anticline), moderately mature (Perat Anticline), and less mature (Harir Anticline). The difference in the maturity level must be due to a difference in one or more of the factors tectonics, climate, or rock erodibility. No variation in the climate is expected for the scale of the studied area, therefore its impact on the landscape maturity can be neglected. The three anticlines show essentially the same lithology (Figs. 2 and 3), i.e., similar lateral rock type and erodibility. Thus, the only factors that may vary along the anticlines are uplift rate or onset time of the uplift. This can be interpreted with one of the following scenarios: either the anticlines started to uplift in the order (1) Akre, (2) Perat, and (3) Harir from west to east or all of them started at the same time but with different rates. In the latter case, the uplift rate would have been highest at Akre and lowest at Harir, exposing Akre to erosion earlier than Harir.

4.2 Landscape evolution model

The aged landscape from the model run (Figs. 8 and 9) is the result of fluvial erosion and hillslope diffusion on the one hand and uplift due to folding on the other hand. In the landscape modeling, various simulations with different parameters and time spans were performed (Figs. S24–S27). Harir Anticline was used as an input model and the landscape evolution model was run for a time span of 10 up to 100 kyr and then it was run for a time span of 20 kyr. The evolving drainage system overprints the pre-existing one in the input and gradually becomes more deeply incised from the anticline flanks carving toward its core (Fig. 8). Harir Anticline is a box-shaped anticline with a wide and flat crest area. With ongoing incision towards the core of the anticline, this plain crest narrowed gradually and finally became a sharp ridge that divided the drainage basins of the SW flank from those of the NE.

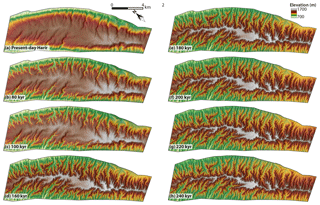
Figure 8 The input landscape (a), which is the present-day Harir topography, and the evolved landscape through time; (b) 80, (c) 100, (d) 160, (e) 180, (f) 200, (g) 220, and (h) 240 kyr.

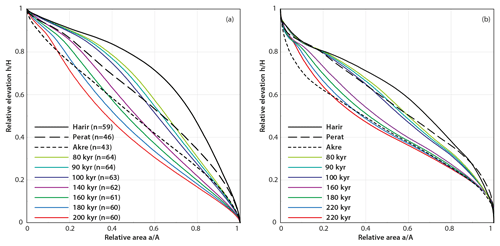
Figure 9 Hypsometric curves of the studied anticlines and those of the evolved Harir landscape from the model for different time spans. (a) The curves were calculated using the total weighted mean for drainage basin within each anticline, indicating that the evolved landscapes after 100 and 160 kyr are the closest ones to the present-day Perat and Akre anticlines, respectively. n is the number of basins used in the calculation of the hypsometric curve for each time; (b) the curves were calculated for the entire anticline, indicating that the evolved landscapes after 80 and 200 kyr are the closest ones to the present-day Perat and Akre anticlines, respectively.

We compared the hypsometric curves of the model outputs to the present-day curves of the anticlines. The hypsometric curves were calculated first as total weighted mean for basins within the anticline and later calculated for the entire anticlinal ridges (Fig. 9). Statistically (with minimum RMS), the hypsometric curve of Harir Anticline was closest to the present-day Perat Anticline after 100 and 80 kyr of erosion when using total weighted mean and entire anticlinal ridge, respectively, in the calculation of the hypsometric curves. The output curve after 160 and 200 kyr matched best with present-day Akre Anticline, when using total weighted mean and entire anticlinal ridge, respectively, in the calculation of the hypsometric curves. We conclude that it will take Harir Anticline roughly 80–100 kyr to reach the maturity level of Perat Anticline and about 160–200 kyr to reach the level of Akre Anticline based on our model and comparison of the hypsometric curves if the uplift rates of the three anticlines were the same. The other possibility is that the anticlines started to grow at the same time but with different uplift rates. In this case, it is not possible to find the difference in uplift rates via our landscape modeling. Since the factors that control geomorphology (lithology, structural setting, and climate) were similar for all three anticlines, and under the assumption of constant growth and erosional conditions, we infer that uplift of Akre and Perat anticlines started, respectively, 160–200 and 80–100 kyr before Harir started to grow if their uplift rates were the same.

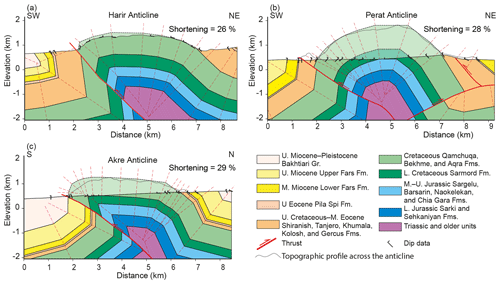
Figure 10 Structural cross sections across the three studied anticlines; (a) Harir section (modified after Syan, 2014), (b) Perat section constructed from field data and thrusts inferred from a seismic line by Csontos et al. (2012), and (c) Akre section constructed from field data (see Figs. 2 and 4 for the locations). In Akre and Perat anticlines the data were collected along gorges and the topographic profile across the anticline along an adjacent transect to the gorges are delineated by a dotted line. The shortening percentage since Late Miocene is shown on each cross section.

4.3 Geometry of the studied anticlines

The structural cross sections for the three anticlines (Fig. 10) constructed from field data and literature (Syan, 2014) show that the anticlines are box-shaped with broad crests. They are asymmetrical verging toward the SW with a nearly vertical or overturned forelimb. The three anticlines are thrust-related, in accordance with published studies of the area (Csontos et al., 2012), and have a thrust in their forelimb. Perat Anticline additionally exhibits a back thrust in its NE limb. The shortening across the three anticlines was calculated using line-length balancing. We found 26 %, 28 %, and 29 % shortening for Harir, Perat, and Akre anticlines, respectively, and conclude that there is no significant variation. A difference in the fold amplitude between the three anticlines can be discerned in the cross sections. The amplitude of Perat Anticline is higher than that of both Harir and Akre anticlines. Another difference concerns the thickness of the Upper Cretaceous–middle Eocene clastic succession, which dwindles toward the Akre Anticline. The whole Miocene succession, however, is the thickest in the Akre Anticline. Both the Upper Cretaceous–Middle Eocene and Miocene successions consist of highly erodible clastic rocks, and the thicker Miocene succession in the Akre Anticline counterbalances the thinner Upper Cretaceous–middle Eocene succession. Therefore, it is not expected that these variations in the structural geometry and stratigraphic thickness have a great impact on the variation in the landscape maturity in the three anticlines and the landscape model.

5 Discussion

5.1 Landscape maturity and modeling

Any relative change in the base level induced by tectonics or climate leads to a change of erosion rates. A relict landscape survives when its uplift is not completely counterbalanced by erosion (Andreani and Gloaguen, 2016; Burbank and Anderson, 2012; Pérez-Peña et al., 2015). The relative relict landscape and its distribution on these three anticlines atop the MFF reveal clues about underlying tectonics since there is no significant variation in climate and lithology.

Within the three studied anticlines, the geomorphic indices effectively highlighted their incision. The surface index, which combines both hypsometric integral and surface roughness, sets apart relict landscapes of positive and high values from transient landscapes of negative values that are preferentially incised (Andreani et al., 2014). There is a notable relative deviation in areas where anticlines are crossed by rivers, e.g., Bekhme and Zinta gorges which show high surface roughness. Also, variations in surface index are found in comparable areas in the three anticlines. Focussing on the crest of the anticlines, we observe that the Harir Anticline shows higher values than the two others. The lowest values are found in Akre Anticline. Harir has low incision at elevated surfaces while Akre has a more incised uneven landscape, because erosion has worked deeper into the core of the anticline. This can also be inferred from the valley shapes. We observe tight V-shape valleys in the flanks of Harir and open V-shape valleys in Akre (Fig. 11a and b). We relate this difference to the tectonic uplift and to the effects of longer erosion acting on Akre. The observation can be interpreted with one of the following two premises: either the anticlines started to uplift successively (first Akre, then Perat, and finally Harir) or all of them started at the same time but with different uplift and exhumation rates (Akre the fastest, Harir the slowest). In other words, the Cretaceous carbonates in Harir Anticline were exposed to the erosion later than in Akre Anticline and, consequently, incised less.

Figure 11 Different shape of valleys in the Harir (a) and Akre anticlines (b). See Figs. 2 and 4 for the locations.

The current landscape of these anticlines exposes Cretaceous carbonates of the Qamchuqa, Bekhme, and Aqra formations, which became exposed to erosion only after unroofing of the entire Palaeogene–Neogene succession. The upper Miocene–Pliocene Bakhtiari Group, which is the youngest stratigraphic unit in the area, is affected by folding, as observed from growth strata (Csontos et al., 2012). This has also been observed in the upper Bakhtiari (Pliocene–Pleistocene) close to the MFF (Koshnaw et al., 2017). In between Bekhme and Aqra and the Upper Bakhtiari formations, 2.37 km of the Upper Cretaceous–Miocene clastic rocks interbedded with thin units of limestone (Law et al., 2014) have been exhumed due to successive rock uplift in the crest of the studied anticlines, triggered by shortening and erosion. They are only preserved in the adjacent synclines. The Cretaceous carbonates themselves have been exposed in the crests of Akre, Perat, and Harir anticlines for ca. 0.9 km above the level of the other exhumed units. Based on the thickness, the amount of the exposed Cretaceous carbonate makes ca. 28 % of the total exhumed and exposed thickness in the crest of the anticlines. Therefore, with both scenarios (different uplift time or different uplift rate) and with assumption of constant (linear) rock uplift rate through time, the Cretaceous carbonate in Harir Anticline was exposed to erosion later than in the Akre Anticline (Fig. 12a).

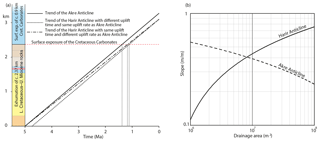
Figure 12 (a) Diagram showing the exposure time of the Upper Cretaceous carbonates in Akre and Harir Anticlines. Two different scenarios are plotted for Harir: having a slower uplift rate than Akre or onset of uplift later than Akre. (b) Channel slope–drainage area plots for streams in both Akre and Harir Anticlines.

The steeper valley flanks in Harir Anticline compared to those of Akre also support higher uplift rates of the Harir Anticline. Furthermore, the relationship between stream slope and upstream drainage area at any given point of the streams in the Harir Anticline is positive (Fig. 12b). This means that the streams have a convex shape and the streams' segments with steeper slopes are still located in the flanks of the anticline. In the Akre Anticline, this relationship is negative (Fig. 12b), which means that the streams have a concave shape and the segments with steeper slopes have migrated toward the core of the anticline. This implies that tectonic activity in the Harir Anticline is younger than in the Akre Anticline; in other words, the Harir Anticline was exposed to erosion later than the Akre Anticline. Therefore, the premise of having Harir Anticline starting its uplift later than Akre Anticline is most likely. This is our preferred scenario in the model for the successive tectonic evolution of the study area presented below.

The geomorphic indices have been widely used to assess the landscape maturity and, subsequently, active tectonics (Andreani and Gloaguen, 2016; Mahmood and Gloaguen, 2012; Pérez-Peña et al., 2009). The challenging aspect of landscape maturity modeling is to obtain an absolute quantification of tectonics and the relevant time spans. The same holds true with using a landscape evolution model to estimate the relative time difference between two landscapes, because it is difficult to compare two landscapes in terms of maturity by absolute means. The results of the landscape modeling approach yielded a numerically derived estimate on the relative age difference between the studied anticlines but without absolute growth ages.

In the model, various parameters and two well-known landscape evolution equations for the fluvial erosion and hillslope diffusion were used, but in general it is impossible to mimic nature perfectly. The relative time difference of landscape evolution of these anticlines was estimated from the model assuming that the climate has not changed much during the evolution of the landscape since there was not much variation in the precipitation based on the modeled data (Stockhecke et al., 2016) and for the sake of simplicity, admitting that climatic change has a significant impact on the landscape. In addition, neither rock fall nor karstification were included in the model for simplicity. Field observations suggest that karstification does not have a significant impact on the landscape. Overall, the evolved landscape from the model seems to be plausible in comparison with the other anticlines that surround Harir Anticline, and the landscape models are more mature with respect to the developed topography and to the overall drainage patterns.

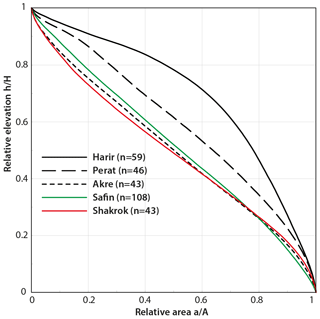
Figure 13 Total weighted mean hypsometric curves for drainage basin within the studied anticlines as compared to those of the Shakrok and Safin anticlines. The Harir's curve is more convex than those of both Shakrok and Safin. n is the number of basins used in the calculation of the hypsometric curve for each anticline.

Figure 14 Simplified history of the formation of anticlines during the propagation of the deformation front over time in the study area. The Harir anticline is likely the latest to have formed within the High Folded Zone in its SE end. It occupies the position of a relay structure during the linkage of two adjacent, but overlapping, segments of the deformation front. The anticlines were outlined based on the exposure of Cretaceous carbonates.

5.2 Structural style and regional tectonics

An orogenic bend is depicted in the area where the trend of structures changes across the Great Zab river from NW–SE at the eastern side of the river to nearly E–W at its western side. The course of the Great Zab River is suggested to overlie a NE-trending transversal basement fault with right-lateral displacement (Ameen, 1992; Burberry, 2015; Jassim and Goff, 2006) evidenced by an offset of the High Folded Zone propagation forelandward. At the eastern side of the river the deformation has propagated for about 25 km further than on its western side (Figs. 1 and 2). The origin of this fault reaches back to the late Proterozoic tectonic history of the Arabian Plate. This fault has been reactivated later in subsequent tectonic events (Ameen, 1992; Aqrawi et al., 2010; Burberry, 2015; Jassim and Goff, 2006). This can also be noticed in the thickness of the sedimentary cover, which is thinner to the west of the Great Zab River (Ameen, 1992; Zebari and Burberry, 2015). This change in thickness is attributed to a series of uplift events and erosional or non-depositional gaps during the Mesozoic (Ameen, 1992; Aqrawi et al., 2010). Further propagation of the deformation (Mountain Front) in the eastern side of the Great Zab River may be due to the existence of a thicker sedimentary cover than on the western side, which in turn may have influenced the foreland-ward propagation of deformation (Marshak and Wilkerson, 1992). The deference in propagation of deformation may also be due to the convergence being accommodated differently across the curved fold–thrust belt (Csontos et al., 2012). In the eastern side of the Great Zab River, the convergence is accommodated across NW–SE trending structures through belt-normal slip and right-lateral strike–slip components, while in the western side of the river the convergence is accommodated only by a belt-normal slip across E–W trending structures (Csontos et al., 2012; Reilinger et al., 2006).

Zebari and Burberry (2015) found that anticlines to the east of the Great Zab River (Harir, Shakrok and Safin anticlines) demonstrate pronounced NW-ward propagation based on their geomorphic criteria, and the start point of the NW-ward propagation of the Harir Anticline is close to its SE end. This implies that progressing uplift in the hanging wall of the MFF was not gradually continuing from the Akre Anticline towards the Perat Anticline and further SE-ward to the Harir Anticline. The uplift progress is probably rather partitioned into segments along the belt. In addition, other anticlines to the south (Safin Anticline) and to the southwest (Shakrok Anticline) of Harir Anticline are more mature than Harir Anticline itself, based on their hypsometric curves (Fig. 13) and geomorphic indices (Figs. S1–S18), implying that the forelandward propagation of the deformation was also out of sequence in this part of the High Folded Zone. This has also been noted in the Foothill Zone based on thermochronological dating (Koshnaw et al., 2017) and landscape maturity (Obaid and Allen, 2017). Thus, the most plausible scenario is that deformation in the Harir segment started sometime after that in Akre segment (160–200 kyr according to our landscape evolution modeling). Harir Anticline uplift would also postdate Perat Anticline uplift (80–100 kyr) to the west and the onset of Safin and Shakrok anticlines to the south and southeast, which are not included in the model (Fig. 14). As discussed by Csontos et al. (2012), the fold relay corresponds to the change in strain partitioning and rotation of the horizontal stress direction from NE–SW to N–S in Late Pliocene (Navabpour et al., 2008; Navabpour and Barrier, 2012). During the latest stage of the N–S convergence, a right-lateral shear and superposed folding along the NW–SE trending anticlines (Csontos et al., 2012) can be observed from the relay of the Shakrok, Harir, and Perat anticlines (Figs. 2 and 14). Applying this concept requires a comprehensive paleostress analysis investigation especially within these studied anticlines, which is beyond the scope of this paper.

6 Conclusions

The geomorphic indices used in this study allowed us to quantitatively differentiate between variably degraded landforms in the frontal Zagros Mountains of NE Iraq. This area is characterized by active folding due to ongoing convergence between the Eurasian and Arabian plates. Three active thrust-related anticlines that are aligned along-strike of the MFF were studied in detail. While the Akre Anticline shows deeply incised valleys indicative of advanced erosion, the Harir and Perat anticlines have relatively smooth surfaces and show younger landscape than Akre. We related this difference to the underlying tectonics. This can be interpreted with one of the following concepts: either anticlinal growth started at different times or all of them started to grow at the same time, but with different surface uplift and exhumation rates.

A comparison of the geomorphic index values of the model output with those of the present-day topography of Akre and Perat anticlines revealed that it will take Harir Anticline about 160–200 kyr to reach the maturity level of today's Akre Anticline, and about 80–100 kyr to reach the maturity level of the Perat Anticline, assuming constant uplift rates along the three anticlines. Due to similarity in the lithology, structural setting, and climate along the three anticlines, and by assuming constant growth and erosion conditions, we infer that Akre Anticline started to grow 160–200 kyr before Harir Anticline. The onset of growth of Perat Anticline lies in between that of Harir and Akre anticlines. A NW-ward propagation of Harir Anticline itself implies that the uplift has been independent within different segments rather than having been continuous from the NW to the SE. Our method of estimating relative age differences in variously degraded anticlines can be applied to many other anticlines along the MFF and could eventually develop into a model of the temporal evolution of this fold and thrust belt.