Bromine speciation and partitioning in slab-derived aqueous fluids and silicate melts and implications for halogen transfer in subduction zones

Understanding the behavior of halogens (Cl, Br, and I) in subduction zones is critical to constrain the geochemical cycle of these volatiles and associated trace metals, as well as to quantify the halogen fluxes to the atmosphere via volcanic degassing. Here, the partitioning of bromine between coexisting aqueous fluids and hydrous granitic melts and its speciation in slab-derived fluids have been investigated in situ up to 840 ^∘C and 2.2 GPa by synchrotron x-ray fluorescence (SXRF) and x-ray absorption spectroscopy (XAS) in diamond anvil cells. The partition coefficients $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ range from ∼2 to ∼15, with an average value of 6.7±3.6 (1σ) over the whole pressure–temperature (P–T) range, indicating a moderate Br enrichment in aqueous fluids, in agreement with previous work. Extended x-ray-absorption fine-structure (EXAFS) analysis further evidences a gradual evolution of Br speciation from hydrated Br ions [Br(H₂O)₆]⁻ in slab dehydration fluids to more complex structures involving both Na ions and water molecules, [BrNa_x(H₂O)_y], in hydrous silicate melts and supercritical fluids released at greater depth (> 200 km). In denser fluids (ρ > 1.5 g cm⁻³) containing 60 wt % dissolved alkali–silicates and in hydrous Na₂Si₂O₅ melts (10 wt % H₂O), Br is found to be in a “salt-like” structure involving the six nearest Na ions and several next-nearest O neighbors that are either from water molecules and/or the silicate network. Bromine (and likely chlorine and iodine) complexing with alkalis is thus an efficient mechanism for the mobilization and transport of halogens by hydrous silicate melts and silica-rich supercritical fluids. Our results suggest that both shallow dehydration fluids and deeper silicate-bearing fluids efficiently remove halogens from the slab in the sub-arc region, thus favoring an efficient transfer of halogens across subduction zones.

1 Introduction

The fluxes of volatile elements (water, carbon, sulfur, and halogens) in subduction zones play a critical role in the Earth's chemical evolution; however, the mechanisms and extent of their transfer from slab components to the mantle wedge, the volcanic arc, and ultimately the atmosphere remain poorly understood. Although halogens (F, Cl, Br, and I) are rather minor volatiles compared to H₂O and CO₂, their effect on the physical and chemical properties of slab-derived fluids and arc magmas (e.g., phase equilibria, viscosity, density), as well as their ability to bind to trace elements and base metals (e.g., Au, Cu, Zn, Pb, REE), makes them key players in chemical transfer in subduction zones and the formation of ore deposits (e.g., Zellmer et al., 2015; Barnes et al., 2018). Furthermore, their emission to the troposphere and stratosphere at volcanic arc centers may have a significant environmental impact, including ozone depletion by Br (Bobrowski et al., 2003; von Glasow et al., 2009; Kutterolf et al., 2013). Constraining the halogen cycle in subduction zones is thus crucial for assessing their impact on the global atmospheric chemistry and climate.

In the last decade, new developments in quantification techniques on pore fluids, fluid inclusions, and rocks as well as in detection methods for halogens species in volcanic gases enabled better estimates of halogen fluxes in subduction zones (Wallace, 2005; Pyle and Mather, 2009; John et al., 2011; Kendrick et al., 2013, 2015; Chavrit et al., 2016; Barnes et al., 2018). For example, comparisons of the input from the subducted sediments, altered oceanic crust, and serpentinized oceanic lithosphere to the output along volcanic arcs point to a significant imbalance between fluorine input and output, suggesting that a significant amount of F may be transferred to the deep mantle (Roberge et al., 2015; Grutzner et al., 2017). In contrast, Cl, Br, and I appear to be efficiently recycled up to the surface either through shallow loss of fluids to the fore-arc region (Br and especially I) or deeper release upon slab dehydration (especially Cl and Br, and to a lesser extent I) (Kendrick et al., 2018). Yet, the poor understanding of the transfer mechanisms and pathways of halogens limits the development of numerical models constraining the role of fluids in the global cycling of elements in subduction zones (Ikemoto and Iwamori, 2014; Kimura et al., 2016). There is, for instance, virtually no constraint on the amounts of residual halogens that may be stored in the dehydrated slab or lost to the continental crust through hidden hydrothermal activity and passive degassing. Similarly, current knowledge of halogen solubility and speciation in fluids and melts is mostly limited to pressures below 0.3 GPa (equivalent to ∼10 km of depth), which are relevant to volcanic degassing and ore deposit formation in the shallow crust (Webster, 1990, 1992; Métrich and Rutherford, 1992; Bureau et al., 2000; Signorelli and Carroll, 2002; Bureau and Métrich, 2003; Carroll, 2005; Evans et al., 2009; Cadoux et al., 2018) but not to slab dehydration or melting beneath arcs at far greater depth. Only recently did Bureau et al. (2010, 2016) report fluid–melt partition coefficients for Br and I in the haplogranite–H₂O system up to 1.7 GPa, while Cochain et al. (2015) investigated the speciation of Br in haplogranitic melts up to 7.6 GPa. Nevertheless, the effect of fluid chemistry on the speciation and partitioning of halogens at high pressures and temperatures (P–T) remains unknown in subduction zones. To fill this gap, we combined synchrotron x-ray fluorescence (SXRF) and x-ray absorption spectroscopy (XAS) measurements in a hydrothermal diamond anvil cell (HDAC) to investigate Br fluid–melt partitioning and speciation in aqueous fluids and hydrous silicate melts that mimic the mobile phases released by the slab at sub-arc depths (Manning, 2004; Frezzotti and Ferrando, 2015). Bromine is employed here as an analog of chlorine amenable to SXRF and XAS studies through the diamond window of the HDAC due to its higher absorption edge energy (13.47 keV for bromine K edge compared to 2.82 keV for chlorine K edge; Sanchez-Valle, 2013). Furthermore, among the halogens, bromine displays the closest behavior to chlorine in terms of solubility, partitioning, and speciation in silicate melts, at least at shallow depth (Bureau et al., 2000. 2010; Bureau and Metrich, 2003; Wasik et al., 2005; Cadoux et al., 2018). Bromine therefore represents the best analog of Cl for in situ studies at high-pressure (P) and high-temperature (T) conditions. Our experimental results reveal systematic changes in Br speciation that reflect changes in fluid composition with depth; these new findings enable better constraints on the mechanisms controlling the transfer of halogens from the slab to arc magmas.

Table 1 Synthesis conditions and chemical compositions of the Na₂Si₂O₅ (NS2) and haplogranite (Hpg) glasses employed as starting materials in this study.

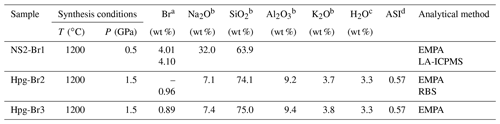
EMPA: electron microprobe analysis; LA-ICPMS: laser ablation inductively couple plasma mass spectrometry; RBS: Rutherford backscattering spectroscopy. ^a Standard deviations (1σ) are 0.04 wt % for RBS analysis, 0.3 wt % for LA-ICPMS, and 0.03 wt % for EMPA. ^b Average from 10 to 25 analyses performed on each glass composition. Standard deviations (1σ) are < 0.1 wt % for Na₂O, Al₂O₃, and K₂O and < 0.3 wt % for SiO₂. ^c Nominal H₂O concentration (not analyzed). ^d Aluminum saturation index (ASI) $=\frac{{\mathrm{Al}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{3}}}{{\mathrm{Na}}_{\mathrm{2}}\mathrm{O}+{\mathrm{K}}_{\mathrm{2}}\mathrm{O}}$ (in moles).

2 Methods

2.1 Starting materials

The speciation and fluid–melt partitioning experiments were conducted using 3 wt % NaBr aqueous solutions and synthetic sodium disilicate (NS2: Na₂Si₂O₅) or haplogranite (Hpg) glasses doped with 1 wt % to 4 wt % Br as starting materials (Table 1). The 3 wt % NaBr aqueous solution was freshly prepared from distilled deionized water and analytical grade NaBr powder, sealed in tight containers, and refrigerated until the experiments. The NS2 and Hpg glasses were synthesized in a piston–cylinder apparatus at 1200 ^∘C and 0.5 and 1.5 GPa, respectively, following the method described in Louvel et al. (2013). Briefly, reagent-grade SiO₂ and Na₂SiO₃ were employed for the NS2 glasses, whereas reagent-grade SiO₂, Al₂O₃, and the alkali–carbonates K₂CO₃ and Na₂CO₃ were mixed for the haplogranite glass synthesis. Bromine was added as NaBr together with 3.3 wt % H₂O for the synthesis of the haplogranite glass to ensure complete melting and homogenization of the sample at run conditions.

Major element (Si, Al, K, and Na) contents and distribution in the glass were measured by electron microprobe analysis (EMPA) using a JEOL JXA-8200 microprobe with an accelerating voltage of 15 keV, a 10 nA beam current, and a defocused beam of 30 µm to avoid element migration during the analysis (Table 1). The probe was calibrated using wollastonite–quartz (Si), corundum (Al), aegirine (Na), K-feldspar (K), and a counting time set to 40 s. The homogeneity of the glasses was confirmed by elemental profiles collected across the sample and by the absence of microscopic mineral phases. EMPA measurements of Br are hindered by (i) the high ionization potential for the K lines of Br resulting in low count rates; (ii) the peak overlap between the L lines of Br and the K lines of Al; and (iii) the lack of matrix-matched standards. To overcome these limitations, the concentration of Br in the Hpg-Br2 glass sample was first determined by Rutherford backscattering spectroscopy (RBS) at the Department of Physics of ETH Zurich. This technique provides absolute elemental concentrations and is particularly appropriated for quantifying heavy elements in a light matrix, as is the case of Br in silicate glasses (Feldman and Mayer, 1986; Chu and Liu, 1996). A 3.5 mm diameter disk of Hpg-Br2 glass, mounted in epoxy and carbon-coated, was exposed to a 2 MeV ⁴He ion beam. The concentration of Br in the sample was determined from the energy of the backscattered alpha particles ⁴He²⁺, yielding a Br concentration of 0.96±0.04 wt %, which is identical to the nominal Br concentration within analytical uncertainties (Table 1). This well-characterized sample was then used as a standard for Br analysis by EMPA and LA-ICPMS in the other glass samples (NS2 and Hpg-Br3 – Table 1). EMPA characterization of Br was conducted with an accelerating voltage of 25 keV, a 90 nA beam current, and a defocused beam of 30 µm. The signal from Br (and Na) was carefully monitored during the measurements and found to be stable for these conditions. Br concentrations in NS2-Br1 were also cross-checked by LA-ICPMS analyses that were conducted using a 193 nm ArF excimer laser coupled with an ELAN 6100 DRC ICP quadrupole mass spectrometer (Heinrich et al., 2003) and a beam diameter of 40 µm. All analyses were bracketed by measuring an external standard (NIST 610) to allow for linear drift correction, and the average SiO₂ and Br content determined by EMPA for the Hpg-Br2 glass was used as the internal standard.

2.2 Hydrothermal diamond anvil cell experiments

All experiments were conducted in Bassett-type hydrothermal diamond anvil cells (HDACs; Bassett et al., 1993) widely used for in situ SXRF and XAS measurements on aqueous fluids and silicate melts up to 1000 ^∘C at about 3 GPa (e.g., Borchert et al., 2009; Louvel et al., 2013, 2014). The HDACs were mounted with a thinner diamond (1.2 mm thick) on the detector side to reduce the x-ray path through the diamonds and widen the collection angle of the XAS analysis (Sanchez-Valle et al., 2004). This configuration permits (i) the reduction of the attenuation of the fluorescence x-rays in the anvil and (ii) lowering the fluorescence background arising from the Compton and Rayleigh scattering in the thick diamond anvils, hence increasing the signal-to-noise ratio and thus the overall quality of the analysis. The sample chamber, a 300 µm hole drilled in a 250 µm rhenium gasket compressed between the two diamond anvils, was heated externally with molybdenum wires wrapped around two tungsten carbide seats supporting the diamond anvils. Temperature was measured to within 2 ^∘C with K-type thermocouples attached to each anvil as close as possible to the sample chamber. The temperature gradient between thermocouples and the sample chamber was calibrated for each HDAC prior to experiments using the melting temperature at the ambient pressure of S (115.4 ^∘C), NaNO₃ (308.0 ^∘C), and NaCl (800.5 ^∘C). Overall, the T gradient remains < 35 ^∘C at the highest temperature reached (850 ^∘C). Pressure was determined from the equation of state of the gold internal pressure standard (Jamieson et al., 1982) whose x-ray diffraction pattern was measured during the experiment.

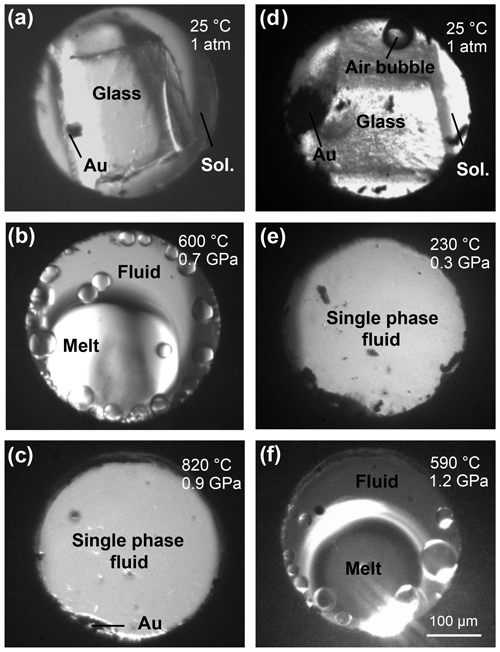
Figure 1 Microphotographs of the compression chamber of the HDAC showing the haplogranite–H₂O (a, b, c) and NS2–H₂O (d, e, f) systems at the indicated pressure and temperature conditions. Images are taken through the diamond along the x-ray path. (a) Haplogranite glass and 3 wt % NaBr aqueous solution at room conditions; (b) globulus of hydrous silicate melt in equilibrium with the aqueous fluid; (c) supercritical liquid (single fluid phase); (d) NS2 glass and 3 wt % NaBr aqueous solution at room conditions; (e) supercritical liquid (low-temperature supercriticality); (f) hydrous NS2 melt coexisting with aqueous fluid (high-temperature subcriticality).

Fluid–melt partitioning experiments were conducted by loading the sample chamber with a piece of Br-bearing Hpg glass and either pure H₂O or an aqueous 3 wt % NaBr solution (Fig. 1). For the speciation measurements by XAS, loadings included either Br aqueous solutions or a piece of Br-bearing NS2 or Hpg glass loaded together with deionized water. In all runs, a pellet of a mixture of Au and Al₂O₃ powders was added to be used for pressure calibration (Louvel et al., 2013, 2014). The volumetric proportions of glass and aqueous fluid in the different loadings were adjusted by adding double-sided polished glass pieces of known dimensions (Fig. 1). Upon heating, the haplogranite melt–aqueous fluid system followed the classical phase transitions described in previous studies (Bureau and Keppler, 1999; Louvel et al., 2013), with initial hydrous melting recorded between 550 and 700 ^∘C (Fig. 1b) and complete miscibility reached within the 700–850 ^∘C range, depending on the pressure (Fig. 1c). In contrast, the NS2–H₂O system displayed distinct and rather unusual phase relations in the investigated P–T range (Fig. 1d–f): the NS2 glass first dissolved completely in the aqueous solution between 150 and 250 ^∘C to produce a single fluid phase containing 30 wt % to 60 wt % dissolved Na₂O and SiO₂ solutes, an analog for slab-derived so-called supercritical fluids (Fig. 1e). Upon further heating between 500 and 750 ^∘C, the fluid unmixed into two phases, a hydrous melt and an aqueous fluid (Fig. 1f). This immiscibility gap remained open up to the highest temperatures reached with the HDAC (800–900 ^∘C), as also previously observed for the haploandesite ${\mathrm{Na}}_{\mathrm{2}}{\mathrm{Si}}_{\mathrm{4}}{\mathrm{O}}_{\mathrm{9}}-{\mathrm{Na}}_{\mathrm{2}}(\mathrm{Si},\mathrm{Al}{)}_{\mathrm{4}}{\mathrm{O}}_{\mathrm{9}}$ join and the K₂O–SiO₂–H₂O system (Mysen and Cody, 2004).

Table 2 Bromine fluid–melt partition coefficients at different P–T conditions. Calculated fluid and melt compositions as well as densities are also reported.

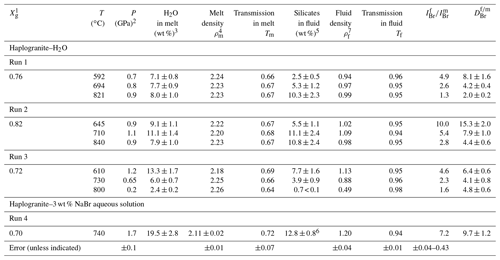
¹ Initial weight fraction of glass in the loading. ² Maximum estimated uncertainty on pressure for the calculations was 10 %. ³ H₂O solubility in the haplogranite melt calculated from the solubility data of Mysen and Wheeler (2000). ⁴ Melt density (g cm⁻³) calculated as a function of P–T conditions and melt composition using Malfait et al. (2014). ⁵ Solubility of silicate components (SiO₂, Na₂O, Al₂O₃, and K₂O) in the aqueous fluid coexisting with haplogranite melt calculated from the albite solubility data of Anderson and Burnham (1983). ⁶ Silicate solubility in the aqueous fluid estimated from Wohlers et al. (2011) for P > 1.2 GPa. ⁷ Fluid density (g cm⁻³) calculated as a function of P–T conditions from the data of Mantegazzi et al. (2013).

The composition of the high-pressure fluids (wt % cations dissolved) and melts (wt % H₂O) was determined from available solubility studies (Table 2) as follows. The water content of haplogranite melts at equilibrium with aqueous fluids (Fig. 1b) was calculated from the water solubility data for aluminosilicate melts reported by Mysen and Wheeler (2000) and extrapolated to our experimental conditions. The composition of the aqueous fluid phase in equilibrium with the haplogranite melt (i.e., total silicate content including SiO₂, Al₂O₃, Na₂O, and K₂O) was estimated by extrapolating to the P–T conditions of our experiments the solubility data reported for the albite–H₂O system between 0.20 and 0.84 GPa at 600 and 700 ^∘C (Anderson and Burnham, 1983), except for Run 4, for which the high-pressure (1–2 GPa) solubility data of Wolhers et al. (2011) were employed. Uncertainties in the calculated dissolved silicate content mostly arise from the compositional differences between solubility models (albite) and our experimental system (peralkaline haplogranite), but they cannot be rigorously quantified here due to a lack of information on Si, Na, K, and Al partitioning between silicate melts and water. To account for potential uncertainties on calculated silicate contents in the fluid phase we thus considered a 10 % error on pressure values, which translates to an overall uncertainty of 20 %–22 % for all investigated conditions, except in Run 4 (Table 2). The compositions of the aqueous fluids in the NS2–H₂O system were determined from the initial volumetric proportions of the NS2 glass and the aqueous fluid loaded in the compression chamber. The mass of the glass was calculated from its measured volume using a density of 2.52(5) g cm⁻³ (Yamashita et al., 2008) and that of the fluid determined from the volume left in the compression chamber (Fig. 1d). The amount of water dissolved in the hydrous NS2 melt in equilibrium with the aqueous fluid at 700 ^∘C and 0.4 GPa (Fig. 1f) was calculated from water solubility data in sodium silicate melts reported by Mysen and Cody (2004). The overall error in the calculated bulk compositions is within 10 % of the total concentration value.

2.3 In situ SXRF and XAS measurements and data analysis

The SXRF and XAS measurements were performed at the microXAS beamline (X05LA) of the Swiss Light Source (SLS, Paul Scherrer Institute; Borca et al., 2009). Measurements at the Br K edge were conducted with an incident energy of 13.6 keV tuned by a Si(111) double-crystal monochromator and focused down to 5×8 (V × H) µm² size by a set of Rh-coated Kirkpatrick–Baez mirrors. This configuration ensured a photon flux of 2×10¹¹ photons per second at the measurements conditions. The intensity of the incident beam was monitored throughout the experiments using an Ar-filled micro-ion chamber placed between the Kirkpatrick–Baez mirrors and the HDAC. Before measurements, temperature was stabilized for about 30 min after each heating stage to ensure that chemical equilibrium was achieved inside the cell (Louvel et al., 2014). In the case of coexisting melt and fluid, measurements were only performed when the melt globule was stationary and bridging both diamonds (Fig. 1f). This configuration ensured that spectra were only collected from pure phases (fluid or melt), thus avoiding any contamination of the SXRF and XAS signals by the other coexisting phase. SXRF and XAS spectra were collected in fluorescence mode in a forward scattering geometry with an energy dispersive single-element silicon drift diode (SDD) detector (Ketek^®, 139 eV resolution at Mn-K_α=5.89 keV) set at 22^∘ from the incident beam in the horizontal plane (Sanchez-Valle et al., 2003; Louvel et al., 2013, 2014). Angle-dispersive x-ray diffraction spectra were collected on the gold pressure calibrant before and after XAS and SXRF measurements using a high-resolution charge-coupled device (CCD) camera set in transmission geometry. A microscope equipped with a video camera was used to monitor the compression chamber during the heating and cooling cycles (Fig. 1).

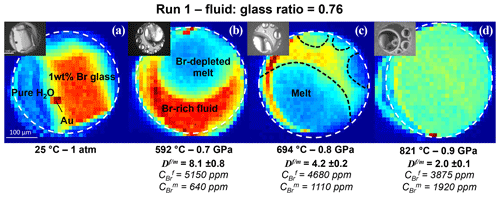
Figure 2 2D SXRF Br K_α intensity maps of Run 1 showing the distribution of Br between coexisting aqueous fluid and haplogranite melt at different P–T conditions. The fluid : glass ratio refers to the weight fraction calculated from the volumetric proportions of loaded glass and the sample chamber. The white dashed line delimits the edge of the Re gasket. Br-enriched phases appear in red and yellow, Br-depleted areas in blue and green. At the beginning of the experiment (a), all the Br is concentrated in the glass. After the glass melts (b), Br strongly partitions into the fluid phase ($D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{8.07}\pm \mathrm{0.79}$). As temperature increases, the Br concentration in the melt increases, while the Br concentrations in the fluid decreases (c). At 821 ^∘C and 0.9 GPa, the I_f∕_m ratio appears homogeneous as the Br concentrations per volume are almost similar ($I_{\mathrm{f}}{/}_{\mathrm{m}}=\mathrm{1.3}\pm \mathrm{0.1}$). However, per weight, Br still partitions preferentially into the fluid ($D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{2.02}\pm \mathrm{0.14}$).

2D SXRF maps were acquired across the sample chamber to qualitatively monitor the distribution of Br between the coexisting aqueous fluid and haplogranite melt (Fig. 2). Then, at least three fluorescence spectra were collected from each phase to further determine the Br fluid–melt partition coefficients $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ at each P–T condition (Table 2). Counting times were set to 100 or 300 s, depending on the signal intensity. Spectra were always recorded far away from the Au pressure calibrant (Fig. 2) to suppress the contribution of the Au L_β line (11.442 keV) to the Br K_α line (11.924 keV) used for the quantifications. Note that the Au L_β line was only observed in the spectra when the beam spot was positioned less than 5 µm away from the Au chip (horizontal beam size 8 µm), thus demonstrating the well-defined beam shape and appropriate spatial resolution of the x-ray beam.

The fluid–melt partition coefficients, $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$, which correspond to the ratio of the Br concentration in coexisting fluid ($C_{\mathrm{Br}}^{\mathrm{f}}$) and melt ($C_{\mathrm{Br}}^{\mathrm{m}}$) at each P–T, were derived from the integrated intensities of the Br fluorescence emission line recorded in the fluid and melt, I_f and I_m, after normalization to the incident beam intensity and counting times, as well as background removal with the Peakfit v4.12 software (SeaSolve Software, USA), following the method described in Louvel et al. (2014). This method relies on the fixed geometry of the HDAC setup and takes into account the different composition, density (ρ), and effective transmission (A) of the aqueous fluid and melt to normalize the fluorescence signal and calculate $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ according to the equation

$$\begin{array}{}\text{(1)}& D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}={\displaystyle \frac{C_{\mathrm{Br}}^{\mathrm{f}}}{C_{\mathrm{Br}}^{\mathrm{m}}}}={\displaystyle \frac{I_{\mathrm{f}}}{I_{\mathrm{m}}}}\times {\displaystyle \frac{A_{\mathrm{m}}}{A_{\mathrm{f}}}}\times {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{m}}}{{\mathit{\rho }}_{\mathrm{f}}}}.\end{array}$$

The standard deviation of the intensity ratios I_f∕_m is smaller than 10 % (Table 2). The fluid and melt densities were calculated for the relevant pressure, temperature, and fluid or melt compositions using density relations determined by in situ techniques for comparable fluid and melt compositions by Mantegazzi et al. (2013) and Malfait et al. (2014) and assuming a 10 % uncertainty on pressure determination and by propagating this error on the fluid and melt compositions. The effective transmission A_f and A_m, which accounts for the probability that the fluorescent radiation reaches the detector depending on the phase composition, density, and thickness of the sample at the incident energy, was calculated from the compositionally dependent attenuation lengths λ determined below and above the Br K-edge energy as a function of melt–fluid compositions and densities for all P–T conditions using the Hephaestus software (Ravel and Newville, 2005). The sample thickness t was set as an average of the thickness of the sample chamber after each run (∼200 µm). A variation of the sample thickness by 50 µm induces a deviation smaller than 10 % of the absolute value of the A_m∕A_f ratio. Note that the corrections in Eq. (1) significantly affect $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$. Because the XRF intensities correlate with the Br concentration and the melts are denser than the fluids, the values for $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ are consistently higher than the I_f∕_m ratio itself (Table 2). Partition coefficients derived in this study are reported with 2σ uncertainty that takes into account the analytical uncertainty on the intensity ratios I_f∕_m and an extra 10 % error on pressure determination and its propagation on the fluid and melt compositions, densities, and effective transmission.

XAS measurements were conducted on 3 wt % NaBr aqueous solution, “solute-poor” fluids equilibrated with hydrous haplogranite melt (Fig. 1b), supercritical fluids containing different amounts of dissolved NS2 (Fig. 1e), and hydrous NS2 melt (Fig. 1f). XAS analyses on the haplogranite melt were precluded by the lower Br concentration of these melts (< 0.2 wt %). For each composition, three to five XAS spectra were collected with counting times of 1 s per point in the pre-edge region to 3 s in the x-ray absorption near-edge-structure (XANES) and extended x-ray-absorption fine-structure (EXAFS) regions. The contribution of Bragg reflections arising from the diamond anvils was avoided in the energy range of interest by changing the orientation of the diamond anvil cell by 0.5 to 1^∘ with respect to the incident x-ray beam direction (Bassett et al., 2000). The edge position was calibrated using a pellet of NaBr, and no significant drift of the energy was observed during measurements. XAS spectra were also collected at ambient conditions on an approximately 200×200 µm² double-side polished section of the NS2 and Hpg glasses.

Data reduction was performed using the Athena and Artemis packages (Ravel and Newville, 2005) based on the IFEFFIT program (Newville, 2001). Averaged experimental spectra were normalized to the absorption edge height and background removed using the automatic background subtraction routine AUTOBK included in the Athena software. To minimize the contribution of features at distances below the atom–atom contact distance, the R_bkg parameter, which represents the minimum distance for which information is provided by the signal, was set to 1.3 Å. For all spectra, the absorption energy E₀ was set to 13.474 keV, which corresponds to the maximum of the first derivative of the absorption edge. Based on previous studies of Br and Cl speciation in aqueous solutions and silicate glasses (Ayala et al., 2002; D'Angelo et al., 1993; Evans et al., 2008; Ferlat et al., 2001; McKeown et al., 2011; Ramos et al., 2000; Sandland et al., 2004; Stebbins and Du, 2002), our EXAFS analysis included the Br–O and Br–Na scattering paths to describe the evolution of the local structure around Br from the high P–T fluids to the hydrous melts and silicate glasses. Although Na cannot be easily distinguished from Al or Si by EXAFS under our experimental conditions, the presence of network cations in the nearest coordination shell of Br is deemed unlikely, as shown for Cl by magic-angle spinning nuclear magnetic resonance (MAS-NMR) and XAS studies (Evans et al., 2008; McKeown et al., 2011; Sandland et al., 2004; Stebbins and Du, 2002). The theoretical backscattering amplitudes, mean free paths, and phase-shift functions for these paths were calculated with the FEFF6.0 ab initio code (Mustre de Leon et al., 1991) using an aqueous Br ion [Br(H₂O)₆]⁻ with a mean Br–O distance of 3.37 Å and the NaBr salt crystallographic structure with a Br–Na distance of 2.98 Å (Deshpande, 1961; Makino, 1995). Multiple scattering within a linear Br^…H−O cluster was also included to model the hydration shell around Br, with the H–O distance fixed to 1.0 Å (Silvestrelli and Parrinello, 1999; Soper and Benmore, 2008). The χ(k) EXAFS functions were Fourier filtered over the 1.5–6.0 Å⁻¹ k range for most spectra. For all samples, modeling of the EXAFS oscillations was performed using four variables: average coordination number (N), distance to nearest neighbor (R), Debye–Waller factor σ², and the energy shift ΔE (which is a nonstructural parameter). The amplitude reduction factor $S_{\mathrm{0}}^{\mathrm{2}}$ was set to 1 based on previous fits of aqueous NaBr, KBr, and GaBr₃ solutions (Da Silva et al., 2009; Ferlat et al., 2002). All fits were performed simultaneously with k weighting of 1, 2, and 3 in order to decrease correlations between N and σ² and between R and ΔE (Pokrovski et al., 2009a, b). The multi-electronic excitations (MEE) at 34 and 90 (±1) eV above the Br K edge (D'Angelo et al., 1993) were neglected as they did not significantly contribute to the EXAFS spectra. The variation of ΔE values between different fitted samples was less than ±4 eV, further confirming the validity of the fitting procedure and the accuracy of the derived interatomic distances.

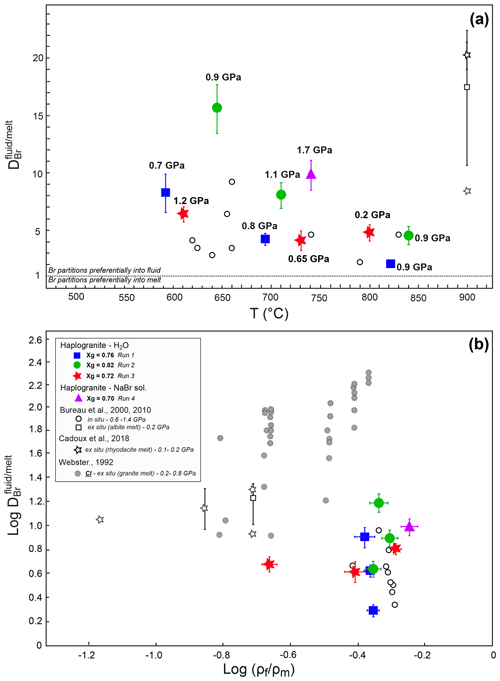
Figure 3 Evolution of the Br partition coefficients $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ with (a) increasing temperature at different pressure conditions and (b) density ratio of coexisting fluids and melts for given P–T. The different symbols and colors account for separate experimental runs involving different glass proportions. The errors reported on $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ take into account analytical uncertainties on the SXRF signal intensities in fluid and melt and an additional uncertainty of 10 % on pressure determination. The Br and Cl fluid–melt partition coefficients from Bureau et al. (2000, 2010), Cadoux et al. (2018), and Webster (1992) are shown for comparison. For Cadoux et al., note that both average values from several experiments ($D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{20.2}\pm \mathrm{1.2}$) and the minimum value for a single experiment ($D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{8.6}$) are reported. For Webster (1992), the solid and dotted symbols are for experiments in which Cl in glass was < 0.01 wt % and 0.01 wt %–0.03 wt %, respectively.

3 Results and discussion

3.1 Bromine partition coefficients in the haplogranite–fluid system

The distribution of Br between aqueous fluids and silicate melts at high P–T conditions has been constrained by measuring fluid–melt partition coefficients $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ from 592 to 840 ^∘C and from 0.2 to 1.7 GPa in four experimental runs. For all investigated conditions, the $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ values are always higher than 1 (Table 2), confirming the preferential partitioning of Br into the fluid phase, which is also qualitatively evident from the in situ Br distribution maps reported in Fig. 2. The $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ values vary between 2.0±0.1 and 15.3±1.0, and they fall within the range reported in a previous HDAC study by Bureau et al. (2010) at similar P–T conditions (Fig. 3). Our limited set of $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ values does not display any clear and systematic pressure, composition, or density dependence (Fig. 3b) as would generally be expected for vapor–liquid and fluid–melt equilibrium partitioning of elements, which postulates that a partition coefficient should tend to 1 when approaching the critical point at which the compositions and densities of both phases are identical by definition (e.g., Bureau and Keppler, 1999; Pokrovski et al., 2013, and references therein). While such a trend is indeed vaguely apparent for Runs 1 and 2, in which the partition coefficients decrease with increasing P–T, Runs 3 and 4 do not show such a trend (Fig. 3a). The lack of a pressure–density trend and the apparent data scatter might be partially related to larger uncertainties on the pressure calibration when employing the equation of state of gold at low pressures. Yet, large differences between Br chemical speciation in the melt and fluid phases (see Sect. 3.2) may also contribute to the apparent data scatter, obscuring the simple water activity-, density-, or pressure-dependent partitioning trends as reported for vapor–liquid partitioning (Pokrovski et al., 2013) and ultimately driving the system towards nonideal, non-Henrian behavior, as for instance reported for the fluid–melt partitioning of Cl under crustal magmatic conditions (cf. data from Webster, 1992 in Fig. 3b). In this regard, the large $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{9.7}$ obtained at 1.7 GPa in Run 4, when the system should be close to miscibility and $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}\sim \mathrm{1}$ (Table 2, Fig. 3), may result at least partly from differences between the real fluid composition and that estimated using available data (Wohlers et al., 2011), coupled with possible non-Henrian effects, i.e., ∼2 wt % Br dissolved in the sample chamber compared to only ∼0.5 wt % for Runs 1 to 3. We further note that previous in situ high P–T measurements of $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ (Bureau et al., 2010) also do not show clear P–T dependence for pressure > 0.6 GPa, e.g., $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}=\mathrm{2.8}$–6.4 between 625 and 655 ^∘C at 1.2 GPa. Thus, the combined effect of pressure, temperature, and fluid and melt composition changes on Br fluid–melt partitioning should be more systematically investigated at P > 0.2 GPa.

Despite the current uncertainties, an important observation here is that the $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ values remain relatively small, 6.7±3.6 (1σ), over a wide range of P–T conditions. Assuming that the high P–T fluid-to-melt volumetric ratio is similar to the initial fluid-to-glass ratio for each run, we calculate between 0.04 wt % and 0.2 wt % Br to be dissolved in the high P–T hydrous melts at run conditions. This estimation suggests that hydrous granitic melts have a capacity comparable to fluids to carry Br under subduction zone P–T conditions and may thus contribute to the efficient transport of Br from the subducting slab to the mantle wedge and volcanic arc.

At lower-pressure conditions relevant to fore-arc or crustal processes (< 0.2 GPa), our in situ partition coefficients are slightly lower than those obtained from quench experiments (Fig. 3). For instance, Bureau et al. (2000) and Cadoux et al. (2018) reported average $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ of ∼17–20 for albitic and rhyodacitic melts at 900 ^∘C and 0.2 GPa, while we found $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ of ∼5 at 800 ^∘C and 0.2 GPa. The minimum $D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$ value from Cadoux et al. (2018) is ∼9, which is close to our in situ value. The small differences between our value and previous studies may stem from uncertainties in the pressure determination below 0.5 GPa in the HDAC, the quantification of Br by mass balance in Bureau et al. and Cadoux et al. (i.e., salt precipitates), or artifacts of the quench method resulting in the loss of Br to the aqueous phase upon cooling in those ex situ studies. Furthermore, slight differences in the melt composition and structure could also result in different Br speciation (Louvel et al., 2020), favoring or not the incorporation of Br in the silicate melt. The relatively low Br partition coefficients (< 20) compare favorably with those reported for Cl in experiments conducted under Cl-undersaturated conditions (i.e., Webster, 1992 – experiments with less < 0.01 wt % Cl in quenched glass; reported as solid gray circles in Fig. 3b). Nonetheless, comparison between these and our study underline the fact that additional efforts are still required to quantitatively assess the effect of halogen contents and density controls on Cl and Br fluid–melt partitioning (see Dolejs and Zajacz, 2018, and Webster et al., 2018, for reviews).

Table 3 Structural parameters derived from Br K-edge EXAFS analysis for the reference aqueous solutions and silicate glasses at ambient conditions.

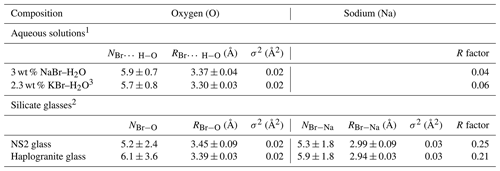
N: Br coordination number (N_Br−O or N_Br−Na); R: Br-neighbor (Na or O) mean distance (Å); σ²: squared Debye–Waller factor (Ų); R factor: goodness of the fit; $S_{\mathrm{0}}^{\mathrm{2}}=\mathrm{1}.$ ¹ Hydration shell (Br^…H−O). ² Br coordinated to oxygens from the silicate network (next-nearest coordination shell). ³ Ferlat et al. (2002), 0.2 m KBr–H₂O for comparison.

3.2 Speciation of bromine in aqueous fluids and silicate melts

3.2.1 Aqueous solutions and silicate glasses at room conditions

The XANES and EXAFS spectra collected at ambient conditions from the 3 wt % NaBr aqueous solution and Br-bearing silicate glasses are respectively reported in Figs. 4 and 5, together with data for a KBr aqueous solution from Ferlat et al. (2002). These spectra were employed to validate the theoretical backscattering amplitude and phase shift functions for Br–O and Br–Na scattering paths used in EXAFS modeling. The XANES spectrum of the 3 wt % NaBr aqueous solution is characterized by an absorption edge at 13.474 keV and a white line that peaks at 13.478 keV (Fig. 4). It displays close similarities to that of the KBr aqueous solution from Ferlat et al. (2002) and overall resembles other alkali bromide aqueous solutions reported in the literature (Wallen et al., 1997; Ferlat et al., 2001; Evans et al., 2007). The EXAFS spectra from the KBr and NaBr aqueous solutions are accurately modeled with a hydration shell of 5.7±0.8 and 5.9±0.7 water molecules (N_Br…H−O) at a Br–O distance of 3.30±0.03 and 3.37±0.04 Å, respectively (Table 3). Note that multiple scattering paths from the linear Br^…H−O cluster are needed to accurately reproduce the experimental data; when only Br–O interactions are considered, the model fails to reproduce the amplitude of the EXAFS oscillations unless an unrealistic hydration shell of ∼12 H₂O molecules is adopted. The structural parameters fitted for the KBr aqueous solution from Ferlat et al. (2002) are, within errors, similar to those reported by the authors. Together with the EXAFS fits of the NaBr aqueous solution, they confirm that Br speciation in aqueous solution at room conditions is dominated by a sixfold coordinated hydration shell with the H–O bond of the water molecule radially aligned towards the Br ion (Ferlat et al., 2001; Ramos et al., 2000).

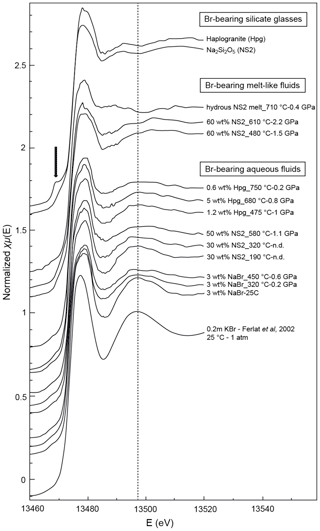
Figure 4 Normalized Br K-edge XANES spectra collected on Br-bearing silicate glasses, aqueous fluids, and hydrous silicate melts at various pressure and temperature conditions. Spectra are offset for clarity. The vertical dashed line is a visual guide to appreciate phase shifts. The black arrow shows the pre-edge feature in the haplogranite glass spectrum corresponding to the 1s to 4p transition in Br (Burattini et al., 1991).

EXAFS spectra collected on NS2 and Hpg glasses at room conditions display distinct oscillations, with a new feature at 2.2 Å⁻¹ in both glass samples and amplitudes nearly out of phase at > 2 Å⁻¹ in k space compared to the NaBr and KBr aqueous solutions (Fig. 5). Different combinations of Br–Na and Br–O scattering paths were tested to constrain the local structural environment of Br in the silicate glasses. Models individually considering either the Br–Na or Br–O paths do not provide a reasonable fit of the EXAFS oscillations, and the simultaneous contribution of Br–Na and Br–O bond is required to reproduce the experimental spectra. The EXAFS-derived parameters suggest that Br in NS2 and Hpg glasses is coordinated to an average of six Na cations in the first shell at an average distance of 2.95 Å and the next-nearest six O neighbors located at 3.4 Å (Table 3). The fitted Br–Na bond length is consistent, within errors, with theoretical Br–Na distances in crystalline NaBr (2.987 Å; Deshpande, 1961) and is close to that reported for aluminosilicate glasses in a previous study (Cochain et al., 2015), suggesting Br is incorporated in the silicate glasses in a salt-like structure, similar to NaBr. The similarities between the structural parameters fitted for anhydrous NS2 and hydrous Hpg (3.3 wt % H₂O) glasses also suggest that the nearest environment of Br remains largely anhydrous in glasses containing relatively low water contents and that the second O neighbors may be from the silicate network rather than more distant H₂O or OH groups. Attempts to include the effect of Br^…H−O bonds in the fitting model by taking into account multiple scattering Br^…H−O paths instead of Br–O correlations only resulted in a systematic decrease in the fit quality (higher R factor). The sole difference between the two glasses is the presence of a pre-edge feature at ∼13.468 keV in the haplogranite glass (Fig. 4). Such features have been attributed to the 1s to 4p electronic transitions in Br (Burattini et al., 1991) and reported in several covalently bonded and/or reduced Br-bearing compounds, including HBr, Br₂, and CHBr₃ (D'Angelo et al., 1993; Feiters et al., 2005). While Evans et al. (2007) suggested that this feature could arise from partial Br reduction in the presence of remaining carbon material in the sample from the synthesis, changes in the local site symmetry around Br could also contribute to the development of such feature. Recent HERFD-XAS measurements conducted on silicate glasses, however, demonstrate that this feature is absent in basaltic and andesitic glasses, and hence it may be specific to the structure of granitic glass compositions (Louvel et al., 2020).

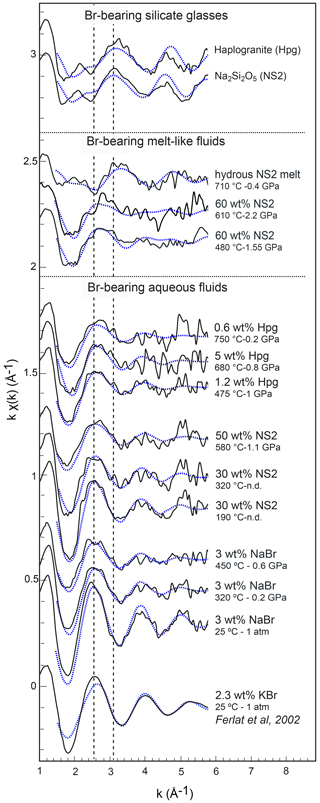
Figure 5 Normalized k¹-weighted EXAFS oscillations of the investigated Br-bearing samples (black solid lines) and corresponding least-square fits (blue dashed lines). Spectra are offset vertically for clarity. The pressure and temperature conditions and the compositions are reported to the right of each spectrum. The dashed lines underline the shift of EXAFS oscillations with a change in composition.

3.2.2 High P–T aqueous fluids and hydrous silicate melts

Bromine K-edge XANES spectra of high P–T aqueous fluids (3 wt % NaBr solution, fluids at equilibrium with haplogranite melt, and water-dominated fluids containing < 50 wt % dissolved NS2) all share a shape very similar to that of the NaBr aqueous solution at room conditions, suggesting a similar local structure of Br in H₂O-dominated phases at elevated P–T (Figs. 4 and 5). Differences in the shape of the XANES spectra become more pronounced for the supercritical fluids with > 50 wt % dissolved Si and Na and the hydrous NS2 melt (Fig. 4). Although the maximum of the white line remains at 13.478 keV, it broadens and decreases in amplitude compared to the 3 wt % NaBr aqueous solution. Also, the first post-edge resonance is shifted toward either higher (13.504 keV) or lower (13.487 keV) energies compared to the aqueous fluids. These changes may be indicative of the progressive incorporation of Na in the local structure around Br. These modifications of the Br coordination environment are also noticeable in the EXAFS oscillations (Fig. 5): while Br-bearing aqueous fluids mostly show a decrease in the amplitude of the oscillations with increasing P–T, they are shifted to higher distances (i.e., from 2.6 to 2.8 Å⁻¹ in k space for the first oscillation) for the 60 wt % NS2 fluid. Moreover, the NS2 melt bears closer resemblance to the NS2 and Hpg glasses, sharing similar oscillations at 2.2 and 3.2 Å⁻¹.

Table 4 Br K-edge EXAFS analysis of experimental high P–T fluids with various compositions.

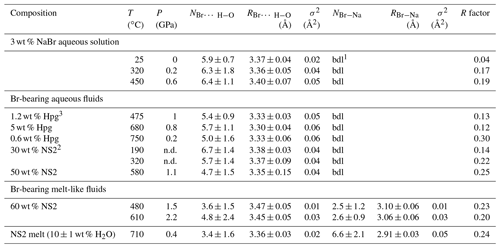
N: Br coordination number (dissociate as N_Br…_H−O and N_Br−Na); R: Br-neighbor mean distance (Å); σ²: squared Debye–Waller factor (Ų); R factor: goodness of the fit; $S_{\mathrm{0}}^{\mathrm{2}}=\mathrm{1}$. ¹ bdl: below detection limit. Detection limit corresponds to the maximum Br–Na coordination number determined for 3 wt % NaBr aqueous solution at ambient conditions. ² wt % NS2 indicates the amount of dissolved NS2 in the single phase fluid calculated from the mass of H₂O and NS2 glass. ³ wt % Hpg refers to the amount of dissolved silicate in the fluid coexisting with haplogranite melt calculated as in Table 2. Errors in temperature and pressure are ±2 ^∘C and 10 %, respectively. Errors in the composition of the analyzed fluids are within 5 % (Table 2).

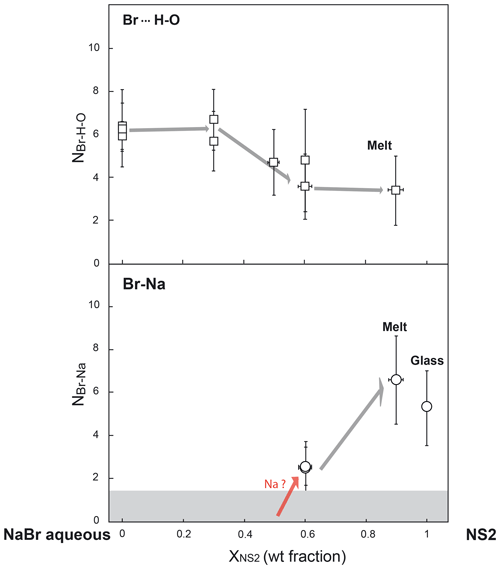
Figure 6 Evolution of bromine coordination numbers with oxygen (from H₂O molecules) and sodium (N_Br… _H−O and N_Br−Na) as a function of fluid composition (i.e., the weight fraction of NS2 dissolved in the fluid) along the NaBr aqueous solution–NS2 join. The gray field shows the detection limit (DL) for Br–Na complexes, which corresponds to the maximum Br–Na coordination number (N_Br−Na) determined for 3 wt % NaBr aqueous solution at ambient conditions and 450 ^∘C (DL < 1.5 atoms).

The structural parameters derived from the quantitative EXAFS analysis are reported in Table 4. Comparably to room conditions, the EXAFS spectra of the NaBr aqueous solution at high pressure–temperature conditions are well matched by an octahedral hydration shell including multiple scattering contributions from the Br^…H−O cluster (Fig. 6). Br–O coordination numbers and distances are respectively 6.4±1.1 and 3.40±0.07 Å at 450 ^∘C and 0.6 GPa, indicating the persistence of the sixfold coordinated hydration shell up to high temperatures. This observation contrasts with results from a number of classical EXAFS studies performed at lower pressures (< 0.07 GPa at 450 ^∘C) that reported a significant reduction in the number of water molecules around Br at supercritical conditions (Wallen et al., 1997; Da Silva et al., 2009). These differences are likely to reflect the differences in pressure (or fluid density), with higher pressures stabilizing the hydration shell around Br due to the increase in the solvent dielectric constant (Pan et al., 2013; Sverjensky et al., 2014), as also predicted for other ions such as Li⁺ (Jahn and Wunder, 2009) and Ti⁴⁺ (van Sijl et al., 2010) by molecular dynamics simulations. An exception to this trend are the experimental results of Mayanovic et al. (2001), who reported a decrease by > 60% in the number of water molecules in the solvation shell of both Br aqua ions and ${\mathrm{ZnBr}}_{\mathrm{4}}^{\mathrm{2}-}$ complexes in 1 m ZnBr₂–6 m NaBr aqueous solution from ambient conditions to 500 ^∘C and 0.5 GPa. The reason for this discrepancy is unclear at this state of our knowledge, and additional studies on the speciation of Br in aqueous electrolytes will be necessary to explain the disagreement.

There are no significant changes in Br speciation in the aqueous fluids equilibrated with haplogranitic melts, which contain only a few weight percent of dissolved silicate components, and in fluids containing up to 30 wt % dissolved NS2 (Fig. 6; Table 4). The first noticeable changes are only found for fluids containing at least 50 wt % dissolved NS2, with a small decrease in the average Br coordination number (N_Br…_H−O) to ∼4.7 compared to more dilute fluids (∼6.0). While this value stays within errors from the other compositions, the reduction of the hydration shell might define the onset of Br–Na complexation with an increasing amount of Na dissolved in the fluid. This hypothesis was tested by introducing a Br–Na contribution in the fitting model for the high-temperature data, but this resulted in a decrease in the overall fit quality. The formation of Br–Na complexes and the partial dehydration of Br, however, become evident with a further increase in the solute content to 60 wt % dissolved NS2 in the fluid (Table 4). For this composition, the best-fit model is consistent with the presence of approximately three Na atoms and four to five H₂O molecules (or OH groups) in the nearest environment of Br at 480 ^∘C and 1.5 GPa as well as 610 ^∘C and 2.2 GPa. In the NS2 hydrous melt (10 wt % H₂O), the number of Na neighbors further increases to approximately six, whereas the number of oxygens remains similar to that of the 60 wt % NS2 fluid (∼3.4). This increase in the number of Na neighbors compared to the 60 wt % NS2-bearing fluid suggests that the nearest environment of Br in silicate-rich fluids progressively approaches the local structure observed in the NS2 glass. Yet, the Br local environment remains hydrated in contrast to the NS2 and Hpg glasses. Based on results from Fourier transform infrared (FTIR) and ²⁹Si NMR studies showing that molecular H₂O is favored in aluminosilicate and sodium silicate glasses as the amount of dissolved water increases (Stolper, 1982; Uchino et al., 1992; Xue and Kanzaki, 2004; Behrens and Yamashita, 2008), we suggest that molecular H₂O, rather than OH groups, would be present around Br in the hydrous NS2 melt. Moreover, we cannot exclude the possibility that distinct “fluid-like” Br(H₂O)₆ and “glass-like” BrNa₆ complexes coexist in the hydrous melt as [yBr(H₂O)₆+ xBrNa₆] moieties, as the average signal of these structures could not be distinguished from [BrNa_x(H₂O)_y] clusters by XANES or EXAFS. Although Br speciation could not be investigated in the hydrous haplogranite melt due to lower Br concentrations (< 0.2 wt %), the similarities between the XANES and EXAFS spectra of the Hpg and NS2 glasses (Figs. 4 and 5) allow us to anticipate a similar Br local environment in the haplogranite melt dominated by alkali complexation.

4 Implications for the transport and recycling of halogens in subduction zones

The new partitioning and speciation data derived for bromine in the present study provide direct insights on the transport mechanisms of halogens (Cl, Br and I) in subduction zones. Our results suggest that the mobilization of Br (and likely Cl and I) in subduction zones is affected by the chemistry of the slab-derived mobile phases. These phases, in turn, are essentially controlled by the slab composition, the depth of fluid extraction, and hence by the P–T conditions (Poli and Schmidt, 2002; Manning, 2004; Schmidt et al., 2004; Hermann et al., 2006; Bebout, 2007; Keppler, 2017). Figure 6 illustrates a gradual transition of Br speciation from hydrated species [Br(H₂O)₆]⁻ to [BrNa_x(H₂O)_y] clusters with various stoichiometries (or a mixture of [Br(H₂O)₆] and BrNa₆ moieties) as the fluid composition evolves from diluted aqueous fluids such as those released by continuous metamorphic dehydration of the slab (< 15 wt % dissolved solutes; Manning, 2004; Rustioni et al., 2019) to Si∕Na-rich supercritical fluids that form owing to the enhanced solubility of silicate minerals at depth and/or granitic melts produced by fluid-assisted melting of subducted sediments (Hermann et al., 2006; Skora and Blundy, 2010). The increasing similarities in the local structure of Br in aqueous fluids containing large amounts of dissolved alkali–silica (> 12.5 wt % Na) and the hydrous melts (Fig. 6) are consistent with the progressive decrease in the Br fluid–melt partition coefficients ($D_{\mathrm{Br}}^{\mathrm{f}/\mathrm{m}}$) with a T increase observed in this study in each separated run (Fig. 3). Sodium complexation with Br is thus an efficient mechanism that enables not only aqueous fluids but also supercritical fluids and hydrous melts to carry significant amounts of Br at depth.

General similarities between Cl, Br, and I speciation in aqueous solutions and silicate glasses (Evans et al., 2008; McKeown et al., 2011, 2015; Shermann et al., 2010) suggest that the speciation and partitioning trends found in our study for Br may extend to Cl and I. Therefore, while early dehydration fluids should release large amounts of halogens to the fore-arc and the mantle wedge (100–200 km of depth), hydrous slab melts and supercritical fluids play a critical role in recycling the residual halogens dragged by the subducting slabs to greater depths. Such efficient recycling, whereby most of the Cl and Br subducted is transferred to the mantle wedge and ultimately returned to the surface through arc magmatism, is further supported by the recent quantification of halogens in subducted sediments, serpentinites, and altered oceanic crust. Mass balance calculations indeed show a close match, within errors, between worldwide influx to the mantle wedge, ∼13–15×10³ kt yr⁻¹ Cl and 5–70 kt yr⁻¹ Br, and calculated outflux as HCl and HBr at volcanic arcs, ∼3–22×10³ kt yr⁻¹ Cl and 5–15 kt yr⁻¹ Br (Barnes et al., 2018; Chavrit et al., 2016; Kendrick et al., 2013; Pyle and Mather, 2009). In comparison, iodine degassing at volcanic arcs is less well constrained, making it more difficult to assess its fate in the subduction factory (e.g., Bureau et al., 2016). The small imbalances remaining between Cl and Br input and output fluxes may arise from difficulties in quantifying halogen loss to the fore-arc and crustal hydrothermal systems. Recent reports of halogens enrichment in oceanic islands basalts (Barnes et al., 2018; Hanyu et al., 2019; Kendrick et al., 2017) also point to the subduction of a noticeable fraction of F, Cl, Br, and I to greater depth, to an extent that is yet to be quantified. Additional in situ experiments, like those presented here, may help better constrain the mechanisms of halogen transfer and partitioning at depth, which are inaccessible to direct observation.

5 Conclusions

In situ SXRF and XAS have been applied to quantify Br fluid–melt partition coefficients and speciation in aqueous fluids, supercritical fluids, and hydrous silicate melts up to 840 ^∘C and 2.2 GPa. Above all, our experimental results demonstrate how changes in speciation, from hydrated ions in aqueous fluids to “salt-like” structures in hydrous melts, may facilitate the uptake of high amounts of Cl, Br, and probably I by subduction zone fluids regardless of their composition. Significant efforts are, however, still needed to accurately quantify halogen cycling from the surface to the deep Earth and back. New experiments investigating the solubility of halogens in subduction zone fluids and the capacity of high-pressure minerals (e.g., micas, Ti–clinohumite, apatite, and carbonates) to incorporate these elements are still necessary to evaluate the amounts of halogen that may be returned to the volcanic arc or retained in the slab.