the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Post-entrapment modification of residual inclusion pressure and its implications for Raman elastic thermobarometry
Xin Zhong
Evangelos Moulas
Lucie Tajčmanová
Residual pressure can be preserved in mineral inclusions, e.g. quartz-in-garnet, after exhumation due to differential expansion between inclusion and host crystals. Raman spectroscopy has been applied to infer the residual pressure and provides information on the entrapment temperature and pressure conditions. However, the amount of residual pressure relaxation cannot be directly measured. An underestimation or overestimation of residual pressure may lead to significant errors between calculated and actual entrapment pressure. This study focuses on three mechanisms responsible for the residual pressure modification: (1) viscous creep; (2) plastic yield; (3) proximity of inclusion to the thin-section surface. Criteria are provided to quantify how much of the expected residual pressure is modified due to these three mechanisms. An analytical solution is introduced to demonstrate the effect of inclusion depth on the residual pressure field when the inclusion is close to the thin-section surface. It is shown that for a quartz-in-garnet system, the distance between the thin-section surface and inclusion centre needs to be at least 3 times the inclusion radius to avoid pressure release. In terms of viscous creep, representative case studies on a quartz-in-garnet system show that viscous relaxation may occur from temperatures as low as 600–700 ∘C depending on the particular pressure–temperature (P–T) path and various garnet compositions. For quartz entrapped along the prograde P–T path and subject to viscous relaxation at peak T above 600–700 ∘C, its residual pressure after exhumation may be higher than predicted from its true entrapment conditions. Moreover, such a viscous resetting effect may introduce apparent overstepping of garnet nucleation that is not related to reaction affinity.
- Article
(2570 KB) - Full-text XML
-
Supplement
(482 KB) - BibTeX
- EndNote
During metamorphism, the growth of porphyroblasts often results in the entrapment of solid or fluid inclusions, which then provide important information about the rock's history (e.g. Farber et al., 2014; Yardley and Bodnar, 2014; Ferrero and Angel, 2018). Due to the differences in the elastic compressibility and thermal expansion coefficient between the inclusion and host, residual inclusion pressures may be preserved after exhumation (e.g. Rosenfeld and Chase, 1961; Gillet et al., 1984; Zhang, 1998; Angel et al., 2015). The residual pressure can be inferred by Raman shift based on experimental calibrations, e.g. quartz inclusions (Liu and Mernagh, 1992; Schmidt and Ziemann, 2000). This allows the application of Raman thermobarometry to infer the entrapment pressure and temperature (P–T) conditions (e.g. Ashley et al., 2014; Bayet et al., 2018; Enami et al., 2007; Izraeli et al., 1999; Kohn, 2014; Spear et al., 2014; Taguchi et al., 2019a; Zhong et al., 2019a). Existing models that link residual pressure and entrapment P–T conditions are based on elastic rheology and often assume an infinite host radius (Rosenfeld and Chase, 1961; Van Der Molen and Van Roermund, 1986; Guiraud and Powell, 2006; Angel et al., 2017b). Despite these simplifications, recent experimental works have been successfully performed to compare the measured residual pressure with modelled residual pressure under well-controlled P–T conditions for synthetic samples with a quartz-in-garnet system (Thomas and Spear, 2018; Bonazzi et al., 2019).
Although many studies using Raman spectroscopy reported maximal residual pressure close to the predictions from elastic models (e.g. Ashley et al., 2014; Enami et al., 2007; Zhong et al., 2019a), a large amount of inclusion pressure estimates are lower than theoretically predicted by the elastic model (Korsakov et al., 2009; Kouketsu et al., 2016; Yamamoto et al., 2002). The modification of inclusion pressure can be due to various reasons and a systematic investigation is critical to better apply Raman thermobarometry to natural samples. Meanwhile, Raman thermobarometry has been employed to investigate the amount of overstepping for garnet growth by comparing the P–T constraints from phase equilibria and elastic thermobarometry (Spear et al., 2014; Castro and Spear, 2017; Wolfe and Spear, 2017). Particularly, when comparing the determined paleopressures based on phase equilibria and elastic barometry using a quartz-in-garnet system, careful examination of the amount of residual quartz pressure modification due to the creep of garnet host becomes critical.
When a mineral inclusion maintains residual pressure, differential stress is concomitantly developed around the inclusion on the host side to maintain mechanical equilibrium (e.g. Zhang, 1998; Tajčmanová et al., 2014). The host mineral may experience viscous creep, which is manifested by the dislocation structures (Chen et al., 1996; Yamamoto et al., 2002; Taguchi et al., 2019b). Furthermore, the host mineral may also experience rate-independent plastic yield when the differential stress exceeds the yield criterion (e.g. Zhang, 1998). In the mechanics literature, plastic deformation is commonly considered as any inelastic deformation (time-dependent and time-independent) (e.g. Kachanov, 1971). In this work, we distinguish between viscous creep, i.e. the rate-dependent inelastic deformation, and the rate-independent plastic flow. Mechanical models show that both viscous creep (dislocation or diffusion creep of host) and plastic flow during decompression and cooling can cause a significant inclusion pressure drop (Dabrowski et al., 2015; Zhang, 1998). This would lead to an underestimate of residual inclusion pressure (Zhong et al., 2018) (Fig. 1). Meanwhile, during the thin-section preparation, mineral inclusions are positioned into proximity towards the thin-section surface (Fig. 1). The thin-section surface is stress-free and may elastically release the residual pressure (Mindlin and Cheng, 1950; Seo and Mura, 1979; Zhong et al., 2019b). It is of petrological interest to study how deep the inclusion needs to be in order to preserve the residual pressure. Experimental works and numerical simulations with the finite-element method have been performed to test the safe inclusion depth (inclusion radius less than one-third of host radius) so that the residual inclusion pressure can be preserved for the application of Raman barometry (Campomenosi et al., 2018; Mazzucchelli et al., 2018).
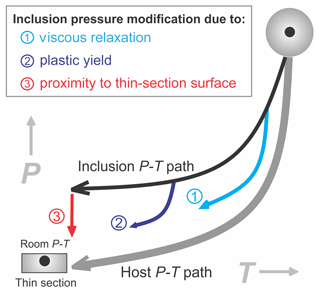
Figure 1Schematic illustration for the residual pressure. The grey and black curves are retrograde P–T paths for host and inclusion, respectively. Pressure drop is possibly due to the following reasons: (1) viscous relaxation preferentially occurs at high-temperature conditions; (2) plastic yield commonly occurs at low confining pressures where residual pressure is high; (3) thin-section preparation that drives inclusion close to the thin-section surface. Note that this illustration refers to systems where the inclusion is elastically softer than its host (e.g. quartz in garnet).
In this contribution, we systematically investigate the following mechanisms for residual inclusion pressure modification: (1) viscous creep of the host materials, (2) plastic yield within the host, and (3) pressure release due to the proximity of inclusion towards the thin-section surface. For the first and second purposes, a 1-D visco-elasto-plastic mechanical model is developed in a radially symmetric spherical coordinate frame. The derived system of equations is non-dimensionalized to extract the key parameters that control the amount of viscous relaxation and plastic yield. For the third mechanism, a simple analytical solution for the residual inclusion pressure field close to the thin-section surface is introduced based on the existing work of Seo and Mura (1979). The analytical solution demonstrates the effect of the inclusion depth that controls the amount of pressure release. This solution applies to the case where the inclusion possesses the same elastic moduli as the host. The inclusion is initially subject to an arbitrary hydrostatic pressure in an infinite host and its pressure is released as it moves towards a stress-free thin-section surface. In comparison, for a natural quartz-in-garnet system, numerical solutions are applied to investigate the safe distance that causes negligible pressure release due to the presence of the thin-section surface (stress-free boundary). In this study, both inclusion and host are treated as elastically isotropic as an assumption to put focus on the effect of these three mechanisms on preserved residual pressure. The effects of elastic anisotropy for commonly encountered quartz inclusion have been studied experimentally and theoretically by, e.g., Murri et al. (2018) and Campomenosi et al. (2018) and are discussed at the end.
2.1 Governing equations
We develop a 1-D mechanical model with spherical symmetry that is based on the conservation of mass and momentum. In 1-D radially symmetric spherical coordinate frame, mechanical equilibrium is expressed as follows:
where τrr is the radial component of deviatoric stress (Pa), P is pressure (Pa), and r is radial coordinate (m). We apply the Maxwell visco-elasto-plastic rheology as follows:
where is the radial components of the deviatoric strain rate (s−1) composed of elastic, viscous (rate-dependent) and plastic (rate-independent) parts. The elastic and viscous strain rates are expressed as
where the dot above denotes time derivative, G is shear modulus (Pa), and η is viscosity (Pa s). The non-Newtonian (effective) viscosity is expressed as follows:
where A is the temperature-dependent pre-factor and n is the stress exponent (e.g. Dabrowski et al., 2015, Eq. 10). The plastic strain rate is obtained by using the Tresca yield criterion (e.g. Kachanov, 1971):
where C is plastic yield strength (Pa) and τtt is the tangential component of deviatoric stress. Due to spherical symmetry, we have . Applying the plastic flow law (e.g. Vermeer and De Borst, 1984), we get
where λ is the plastic multiplier (s−1), which provides the amount of plastic strain (rate) that guarantees the yield criterion is not exceeded, and δ is the sign of τrr. For isotropic materials, the pressure (negative mean stress) can be expressed as a function of volume and temperature via the equation of state (EoS), and its time derivative is as follows:
where β is compressibility (Pa−1), α is the thermal expansion coefficient (K−1), and is the rate of temperature change (K s−1). Temperature is treated as homogeneous within the inclusion–host system. Einstein summation is used here for the volumetric strain rate (, where due to spherical symmetry the two tangential strain rates are equal). No viscous or plastic volumetric strain is considered. This assumption is a good approximation for non-porous, crystalline materials (e.g. Moulas et al., 2019).
Substituting Eqs. (3) and (6) into Eq. (2) and applying first-order finite difference in time to Eqs. (2) and (7) (i.e. and ), we can explicitly express τrr and P as
where is the viscoelastic coefficient, Δt is the time increment, is the radial component of deviatoric stress in the previous time step, Po is the pressure in the previous time step. If the yield criterion in Eq. (5) is exceeded (F>0), the plastic multiplier must be adjusted to drive F to zero. This can be achieved by substituting the deviatoric stress Eq. (8) into Eq. (5), and we let F=0. Therefore, we obtain λ as follows:
2.2 Non-dimensionalization
The variables in the above equations can be scaled to derive non-dimensional parameters for better understanding the behaviour of the inclusion–host system. This is done by choosing the following six parameters to non-dimensionalize the system of equations: the temperature drop in the host-inclusion system ΔT, the inclusion radius R, the time of the P–T path t∗, the host's viscosity pre-factor Ah, the host's plastic yield strength Ch, and the expected pressure perturbation Pexp that is given as follows:
where ΔP and ΔT are the confining pressure and temperature drops from entrapment to the Earth's surface, βi and βh are the compressibility of inclusion and host, αi and αh are the thermal expansion coefficients of inclusion and host, and Gh is the shear modulus of host. The number Pexp is the expected amount of residual inclusion pressure after exhumation assuming linear thermo-elasticity and an infinite host (Zhang, 1998). It is noted that this is not the actual final residual inclusion pressure but merely a scale to non-dimensionalize the stress (and pressure). By choosing Pexp as the stress scale, the inclusion residual pressure is expected to be between 0 and 1 for a case of cooling and decompression. This pressure scale allows convenient quantification for the amount of pressure modification due to viscous creep and plastic yield. The involved physical variables are scaled as shown below:
where the overhead bars indicate dimensionless properties. Substituting these scaling equations into Eqs. (1), (8), and (9), we get
where dimensionless viscosity, viscoelastic coefficient, and plastic multiplier are expressed as
Two dominant dimensionless numbers emerge after non-dimensionalization. They are the Deborah number De and dimensionless yield strength C∗ defined as follows:
The Deborah number (De) is the ratio between the characteristic viscous relaxation time () and model duration (t∗) (Reiner, 1964). If De>1, the system behaves in an elastic manner, and if viscous creep becomes important. The pre-factor of viscosity is temperature-dependent. By choosing the pre-factor Ah at peak temperature, one can directly use De to estimate the maximal amount of viscous relaxation. This is especially suitable for the process of isothermal decompression in many high-pressure (HP) rocks.
The dimensionless yield strength C∗ characterizes the ability of a host mineral to plastically yield and a high C∗ implies that the material is less prone to plastic yield given the amount of residual inclusion pressure Pexp. The viscosity of different mineral phases may vary by orders of magnitude, and the plastic yield strength of different minerals may also vary by several factors. Therefore, these two dimensionless numbers have a dominant effect on the amount of inclusion pressure modification due to viscous relaxation and plastic yield.
2.3 The numerical approach for the visco-elasto-plastic model
The dimensionless viscosity (Eq. 16), viscoelastic coefficient (Eq. 17), and plastic multiplier (Eq. 18) can be substituted into pressure equation (Eq. 14) and deviatoric stress equation (Eq. 15). Together with mechanical equilibrium equation (Eq. 13), they form a system of three equations with three unknowns, namely , , and . The numerical model is based on a finite-difference scheme over a 1-D staggered grid (on the numerical stencil, see, e.g., Gerya, 2010, chap. 7). The initial pressure is set at the beginning of the numerical model. If upon entrapment, the inclusion and host possess the same hydrostatic pressure, the deviatoric stress is zero in the inclusion and host. If pressure heterogeneity exists upon entrapment, the deviatoric stress of the host () needs to be precalculated with the elastic model to ensure that mechanical equilibrium is satisfied at the beginning of the model (Pinc is the initial inclusion pressure and Phost is the initial host pressure).
For predefined P–T path, the inclusion–host system is loaded by the increment of confining pressure and temperature. Both temperature and far-field pressure are obtained directly from the P–T–t path as prescribed. Temperature is treated as homogeneous in the model and the new pressure is set as the outer boundary value. Because viscosity, the viscoelastic coefficient, and the plastic multiplier are functions of deviatoric stress (viscosity is also a function of temperature as prescribed by the P–T path), the system of the mechanical equations is nonlinear. We solve for the three variables (, , and ) using an iterative (Picard) method. Within the iteration loop, an elastic test stress is first evaluated by letting so that the prediction for the yield function is obtained. If , no plastic yield occurs and remains zero. Otherwise the prediction of the yield function is positive and is computed based on Eq. (18). The calculated is then substituted back into Eq. (15) to adjust the amount of plastic strain rate. This will drive to zero (on the plastic yield surface). After the Picard iteration loop, the residuals of the three Eqs. (13), (14), and (15) are minimized below ca. 10−12.
The elastic moduli are updated based on pressure and temperature conditions from tabulated lookup tables within the iteration. The lookup tables are pre-computed based on EoS. We used the EoS for quartz crystal from Angel et al. (2017a) and the EoS for pyrope, grossular, and almandine crystals from Milani et al. (2015). The detailed expressions of EoS can be found in the EoSFit7c software documentation (Angel et al., 2014). The EoS for spessartine is from Gréaux and Yamada (2014). The compressibility and thermal expansion coefficient for garnet are averaged based on the molar percentage of garnet endmembers. The shear moduli of garnet endmembers are from Bass (1995). The numerical model has been benchmarked using the analytical solution with elastic, non-Newtonian viscous rheology in Zhong et al. (2018). The numerical benchmark for elasto-plastic rheology is performed by using the analytical solution of Zhang (1998) (see Supplement).
3.1 Residual pressure affected by viscous or plastic flow
The solutions of the system of equation (Eqs. 13, 14, 15) are obtained using the elasticity of a quartz-in-garnet system. The host radius is set to be 50 times the inclusion radius to make boundary effects negligible. Temperature is treated as homogeneous in space. At the beginning of the model, a pressure perturbation within the inclusion is prescribed, and the far-field host maintains zero confining pressure. The pre-factor of viscosity is fixed as temperature does not vary in this case. The amount of inclusion pressure relaxation is systematically investigated for the two inelastic deformation mechanisms (i.e. viscous creep and plastic yield) as a function of De and C∗. The results are shown in Fig. 2 with the purpose of systematically demonstrating how much the initially prescribed residual pressure can be reduced due to viscous creep and plastic yield. This diagram may assist petrological investigations because De and C∗ can be evaluated based on experimental rock deformation data for different minerals. The Deborah number can be evaluated using the experimental flow law of a single crystal, e.g. garnet (Karato et al., 1995; Wang and Ji, 1999), as given in the next section. The plastic yield strength is evaluated using microhardness test data (see Discussion below for details). The thickness of the plastic yield region is plotted as contours. The thick grey contour represents the onset of plastic yield starting from the inclusion–host interface and propagating towards the host side (Fig. 2). Based on the amount of inclusion pressure relaxation, three regimes are distinguished.
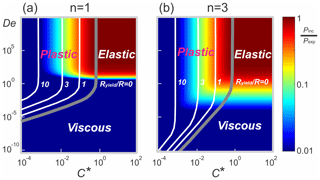
Figure 2Inclusion pressure as a function of the Deborah number and dimensionless yield strength given different stress exponents. The contours denote the radius of plastic yield region Ryield scaled by inclusion radius. The thick grey contour represents the onset of plastic yield. Three regimes are labelled: (1) elastic (De>1, ); (2) viscous (De<1 and C∗ is above the onset of plastic yield); (3) plastic (, De is above the onset of plastic yield). To obtain the results, a residual pressure is prescribed at the beginning and the confining pressure and temperature are fixed, i.e. no temporal variations in P–T conditions.
The elastic regime takes place when De and C∗ are higher than 1. Under these circumstances, no viscous relaxation and plastic yield occurs. The residual inclusion pressure is close to the expected residual pressure (Pinc≈Pexp). This regime is the most suitable for the application of Raman thermobarometry.
The viscous regime dominates when De is lower than 1, and C∗ is above the plastic onset shown by the thick grey contour. In this case, the main mechanism responsible for the inclusion pressure relaxation is the viscous creep. The effect of stress exponent on the amount of viscous relaxation is also significant. In general, a higher stress exponent delays pressure relaxation (cf. Dabrowski et al., 2015). As the viscosity of natural minerals is low at high-temperature conditions, the viscous regime may be reached at a high temperature, which leads to the relaxation of residual pressure.
The plastic regime prevails when C∗ is lower than 1 and De is above 1. Under this circumstance, the residual pressure is not significantly relaxed by viscous creep, but by plastic yield. In general, the radius of the plastic yield region is positively related to the amount of residual pressure release.
It is noted here that although viscous relaxation and plastic yield of the host mineral have the same effect in reducing the residual inclusion pressure after exhumation, there is a fundamental difference between them. Viscous relaxation is time-dependent (De includes time), which means that the residual pressure will vanish given an infinite amount of time. Plastic yield refers to a time-independent process, and it will only limit the amount of deviatoric stress supported by the host mineral. If the yield criterion is reached, plastic strain (rate) in the host immediately occurs, which leads to the inclusion pressure release. Both viscous relaxation and plastic yield are irreversible; as a consequence, if the inclusion-host system is placed back in the original entrapment condition, the stress state would be different.
3.2 Viscous relaxation of garnet host
Assuming that the thin-section surface is sufficiently far away from a quartz inclusion and no plastic yield occurs around the quartz inclusion, only viscous creep may contribute to the modification of residual pressure. Here, we show the effect of viscous relaxation, particularly influenced by the temperature, on the preserved residual pressure. Using De as a criterion to estimate the amount of viscous relaxation, we show the relationship between temperature, inclusion pressure, and relaxation time given De=1 (see Eq. 19) in Fig. 3. The flow law of garnet from Wang and Ji (1999) is applied. The pre-factor A of the effective viscosity (Eq. 4) is as follows:
where B=exp (40.1) in s−1 and g=32. The stress exponent n=3. Geometric correction based on experimental set-up (simple or pure shear) was not applied. The melting point Tm of pyrope-rich garnet, grossular, and spessartine is from the Table 1 in Karato et al. (1995). For almost pure almandine, the garnet melting point is found to be 1588 K from Mohawk Garnet Inc., which is slightly higher than 1570 K for almandine-rich (Alm0.68Prp0.20Grs0.12) garnet in Karato et al. (1995).
Figure 3Viscous relaxation time (in years) of different garnet hosts as functions of temperature and inclusion overpressure. The viscous relaxation time is calculated based on the expression of the Deborah number (De=1) in Eq. (19). The viscosity's pre-factor is T-dependent and is obtained using the flow law from Wang and Ji (1999). The melting temperature is from Karato et al. (1995) (the melting temperature of almost pure almandine is taken from the data of Mohawk Garnet Inc. to be 1588 K). Shear modulus is from Bass (1995). The flow law is given in the main text (Wang and Ji, 1999). The four garnet endmembers are almandine (Alm), grossular (Grs), pyrope (Prp), and spessartine (Sps).
Table 1Averaged plastic strength from microhardness tests for some minerals at room conditions. Strength is converted from microhardness based on , where the geometry constant Cg is taken as 3. Raw data are dependent on crystallographic orientation, composition, and applied load that are examined in some of the involved references.
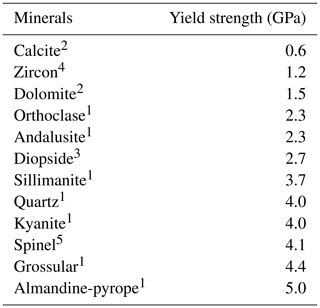
1 Data reported in Whitney et al. (2007). 2 Data reported in Wong and Bradt (1992). The reported data for calcite and dolomite are averaged from the applied load and azimuthal angle from []. 3 Data reported in Smedskjaer et al. (2008). 4 Data reported in Yuan et al. (2017) 5 Data reported in Dekker and Rieck (1974). The reported data are averaged from the applied load at [110] and [100].
As an example (Fig. 3), for a quartz inclusion possessing 0.5 GPa residual pressure maintained at 650 ∘C, significant viscous relaxation is expected during 1 Myr for almandine-rich garnet host based on the applied flow law. This temperature becomes higher (700 ∘C) for pyrope-rich garnet. If the residual pressure is used to recover the entrapment pressure given that the temperature experienced by the garnet-host system was higher than 650–700 ∘C, an underestimate of the entrapment pressure may potentially occur.
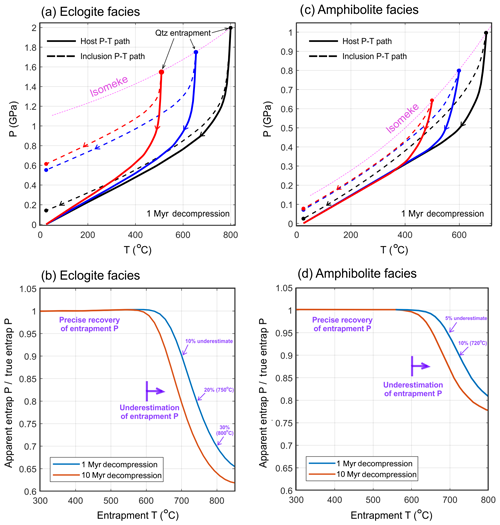
Figure 4(a) Synthetic retrograde P–T paths from eclogite-facies metamorphic conditions. The quartz inclusions are entrapped within almandine at different peak P–T conditions along the same isomeke; thus a purely-elastic model would predict the same value for the residual inclusion P. Due to viscous relaxation, the residual P is lower than the pressure predicted by an elastic model. In (b), the apparent entrapment P is calculated based on the relaxed residual inclusion pressure given different entrapment T along the elastic isomeke that is given in (a). Pressure relaxation is manifested by lower values of apparent entrapment P and it becomes more significant if the host experiences high temperatures with time. Panels (c) and (d) are the same plots for amphibolite-facies entrapment conditions. The amount of viscous relaxation is less compared to eclogite facies due to the lower magnitude of inclusion overpressure and the stress-dependent viscosity of garnet host. Pure almandine garnet is used as host, and its flow law is from Wang and Ji (1999).
In Fig. 4, synthetic retrograde P–T paths from eclogite and amphibolite-facies metamorphic conditions are prescribed with different peak temperatures. The entrapment P–T conditions for the three synthetic P–T paths are along an elastic isomeke, which is the isopleth where no relative elastic interaction exists between inclusion and host. Thus, the residual inclusion pressure would be the same if the inclusions were entrapped along the same isomeke and they were purely elastic. By involving the viscous rheology of the garnet host, different residual inclusion pressures are predicted. For the P–T path starting at 800 ∘C, 2 GPa, the quartz inclusion pressure is predicted to be less than 0.2 GPa. This reduced value of the residual pressure is then used to determine the apparent entrapment pressure (Fig. 4b). In Fig. 4b, it is shown that for the entrapment pressure within eclogite-facies conditions at 700 ∘C, and by using a purely-elastic model, a value of entrapment pressure is inferred that is approximately 10 % less than the actual value. The amount of underestimation of entrapment pressure increases to 30 % when the entrapment temperature reaches 800 ∘C. These values are conservative estimates since the total exhumation time is set to 1 Myr. Longer residence at high-temperature conditions would result in larger modifications of the residual pressure.
For amphibolite-facies entrapment conditions, the residual pressure that is preserved in the quartz inclusion is significantly lower compared to the case where the entrapment occurred at eclogites-facies conditions. As shown in Fig. 4d, ca. 5 % and 20 % underestimates of true entrapment pressure are predicted depending on whether the entrapment occurred at 700 ∘C or 800 ∘C, respectively. Similarly, the amount of underestimation will be larger if the duration of exhumation is longer than 1 Myr.
3.3 Pressure relaxation along the prograde P–T path and apparent overstepping
The pressure relaxation problem becomes more complicated when the quartz inclusion is entrapped not at the peak P–T conditions but along the prograde P–T path. In this case, viscous relaxation occurs also along the prograde P–T path and the pressure difference between host and inclusion will relax with time and increasing temperature. This effect starts before the rock reaches the peak P–T conditions. Two synthetic P–T paths are illustrated in Fig. 5. In Fig. 5a, the quartz is entrapped in the almandine-garnet host at 400 ∘C, 1 GPa, and further experiences eclogites-facies P–T conditions. During the prograde path, the quartz inclusion will develop underpressure (e.g. Angel et al., 2015, Fig. 5), which will also be subject to viscous relaxation over geological time. The quartz pressure starts to converge towards the garnet host pressure at T > 600 ∘C. Nearly complete viscous resetting is observed when the system is brought up to 800 ∘C. The prograde time is set to 1 Myr or 10 Myr to compare the amount of viscous relaxation as a function of time in Fig. 5.
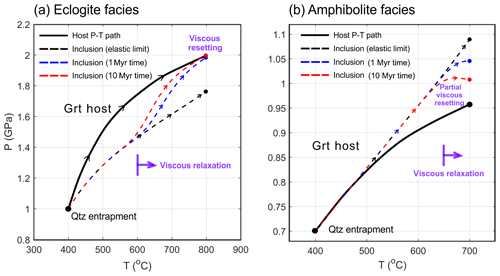
Figure 5The prograde P–T path for inclusion (dashed curve) and host (solid curve). Panel (a) is for rocks that experienced eclogite-facies peak P–T conditions. The quartz inclusion is entrapped at 400 ∘C and 1 GPa. Along the given prograde P–T path, viscous relaxation becomes significant at > 600 ∘C. The duration of the prograde P–T path is illustrated with different colours (1 and 10 Myr; see legend). At 800 ∘C, the quartz inclusion pressure is reset to the confining pressure (host). For rocks that experienced amphibolite-facies peak P–T conditions (b), viscous relaxation becomes significant at ca. 650–700 ∘C and the quartz inclusion pressure is partially reset at 700 ∘C. Pure almandine garnet is used as a host, and its flow law is from Wang and Ji (1999).
An alternative scenario is considered where the rock may also stay at the peak P–T conditions before decompression occurs. A synthetic clockwise P–T path reaching eclogite-facies metamorphic conditions is constructed as shown in Fig. 6. The quartz inclusion is entrapped in the garnet host at 400 ∘C, 0.6 GPa, which is considered to be along the entrance of the garnet stability field. Subsequently the system is brought to 700–750 ∘C, 1.8–1.9 GPa, conditions and stays there for 5 Myr. Afterwards, the retrograde P–T path takes 10 Myr. Two different P–T paths of quartz inclusions are constructed based on the implemented elastic and visco-elastic rheologies. Interestingly, the residual pressure of the inclusion that was subject to viscous relaxation is significantly higher (by 0.2 GPa) than the prediction of the pure elastic model as shown by the black dashed curve (0.14 GPa). The apparent entrapment pressure is calculated using the predicted residual pressure for the inclusion whose host experienced viscous relaxation. A large discrepancy exists between the apparent entrapment pressure (ca. 1 GPa at the entrapment T 400 ∘C) and the true entrapment pressure (0.6 GPa). The overall overestimate of true entrapment pressure (0.6 GPa) is about 0.3–0.4 GPa, which may potentially be interpreted as overstepping the garnet growth or nucleation.
Despite the importance of viscous or plastic relaxation in the post-entrapment modification of pressure, residual pressure measurements may be different when the inclusions are closer to the thin-section surface (Enami et al., 2007). When a pressurized mineral inclusion in an infinite host under mechanical equilibrium is moved towards the thin-section surface, its pressure is released and the pressure distribution within the inclusion becomes heterogeneous. Mindlin and Cheng (1950) provided a closed-form analytical solution of stress field inside and outside a spherical inclusion with thermal strain in a semi-infinite host. The analytical solution has been generalized to ellipsoidal inclusion (Seo and Mura, 1979). Substantial mathematical investigations have also been done in deriving the analytical solution of the elastic field for inclusion in half-space (e.g. Tsuchida and Nakahara, 1970; Aderogba, 1976; Jasiuk et al., 1991). Although the analytical formulations for individual stress components of inclusion are non-trivial, here, we show that the formula for the pressure distribution of a pressurized inclusion can be significantly simplified (detailed derivations are provided in the Appendix):
where Pini is the initial inclusion pressure in an infinite host under mechanical equilibrium, is the scaled inclusion depth () and is a function of position in Cartesian coordinate system (Fig. 7), and ν is the Poisson ratio of the inclusion and host. It is emphasized that in this situation the inclusion and host possess the same elastic moduli.
The released inclusion pressure due to proximity to the thin-section surface is plotted in Fig. 7b and c using Eq. (22). Pressure release is concentrated at the top of the inclusion, while the bottom of the inclusion is subject to minimal pressure releases (< 10 %). Interestingly, the top of the inclusion is subject to negative pressure (expansion) when the inclusion is very close to the thin-section surface (see, e.g., the case of ). Based on the analytical solution, the safe inclusion depth to avoid residual pressure release is ca. (the amount of pressure release is less than 3 % within the entire inclusion). Here, the simple analytical solution in Eq. (22) can precisely model the inclusion's residual pressure due to stress release at the thin-section surface, where the inclusion possesses the same elastic moduli as the host. In a natural mineral inclusion–host system, the inclusion and host possess different elastic properties. As a case study, the stress fields of quartz-in-almandine and almandine-in-quartz systems are numerically modelled using a finite-difference (FD) thermo-elastic model (model benchmarks are provided in the Supplement). These examples are chosen to investigate two endmembers: elastically stiffer host (quartz-in-almandine in Fig. 8a) and softer host (almandine-in-quartz in Fig. 8b). Pressures at three points within the inclusion (top, centre, and bottom) are contoured as a function of . The pressures evaluated at these three localities based on the analytical solution in Eq. (22) are also shown by the dashed curves for comparison with numerical solutions. With decreasing distance to the thin-section surface, the heterogeneity of the pressure field increases. It is shown that the pressure release is less significant in elastically stiffer host (garnet) than in elastically softer host (quartz).
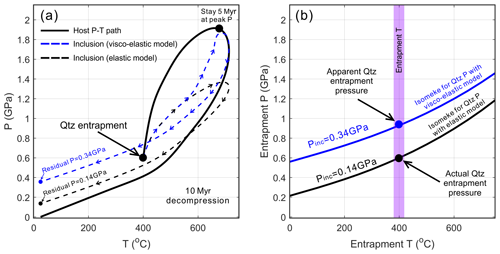
Figure 6(a) Clockwise P–T path of inclusion (dashed curve) and host (solid curve). The dashed black curve shows the inclusion P–T path based on a pure elastic model, and the blue dashed curve is based on a visco-elastic model. The quartz inclusion is entrapped in almandine garnet at 400 ∘C, 0.6 GPa. The prograde P–T path lasts 5 Myr, and the rock stays at peak P for 5 Myr before the retrograde P–T path, which lasts 10 Myr. The residual pressure preserved by the quartz inclusion that was subject to viscous relaxation is in fact higher than the elastic limit. Therefore, the apparent entrapment pressure, calculated using elastic isomeke, is higher than the actual entrapment pressure as shown in (a). This may lead to a ca. 3–4 kbar apparent overstepping effect. The almandine flow law is from Wang and Ji (1999).
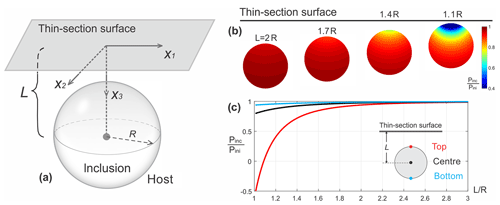
Figure 7(a) Analytical model configuration of a mineral inclusion close to the thin-section surface. The distance between the surface to the inclusion centre is denoted by L. (b) Pressure distribution on an x–z plane. The pressure is scaled by the initial inclusion pressure (Pini). The initial inclusion pressure is under force equilibrium in an infinite host. The analytical model describes the amount of pressure release when the inclusion approaches the thin-section surface. (c) Pressure at three localities (inclusion top, centre, and bottom) as a function of dimensionless depth L∕R. The analytical solution of Eq. (22) is used for the pressure plot.
It is shown that the difference between the analytical and the numerical solution due to the difference in elastic moduli becomes significant when the inclusion depth is shallow. The analytical and solutions are similar when evaluated at the bottom point at any depth (Fig. 8). For a quartz-in-garnet system, the analytical solution overestimates the amount of pressure release (Fig. 8a). Assuming 3 % pressure release as acceptable for the application of Raman barometry, the analytical solution yields a safe distance of ca. for the bottom and centre point, while the numerical solution yields ca. . For the top point, the safe distance of ca. based on the analytical solution is again higher than the prediction of ca. based on a numerical solution. The difference in safe distance between analytical and numerical solution is due to the presence of elastically stiffer garnet host.
Differential stress (|σ1−σ3|) is also shown in Fig. 8b. High differential stress at the host appears when the inclusion is close to the thin-section surface. Differential stress may also exist inside the inclusion, but it is in general smaller than that of the host. For a quartz-in-garnet system, the differential stress forms a “ring”-shaped pattern with a peak at the surface. The differential stress may reach up to 3 times the expected residual pressure. This may potentially trigger plastic failure at the thin-section surface. However, for the garnet-in-quartz system, such pattern is not observed even if the inclusion depth is shallow.
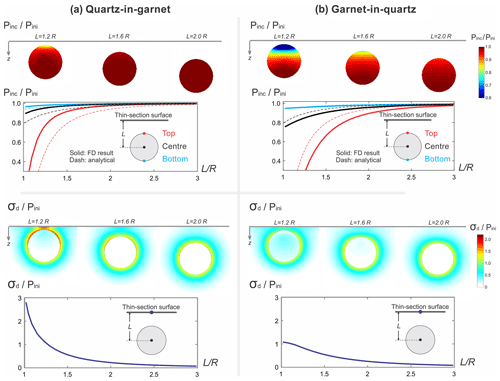
Figure 8Dimensionless pressure and differential stress plotted on an x–z plane or as a function of dimensionless depth. (a) Quartz-in-almandine system; (b) almandine-in-quartz system. For the profiles, pressure and differential stress are measured at different locations denoted by the coloured dots. In the top panel, the dashed curves in the pressure plot are based on the analytical solution in Eq. (22) considering the same elastic moduli between inclusion and host, while the solid curves are based on finite-difference results. The discrepancy between the solid (numerical solution) and dashed (analytical solution) curves in (a) is due to the fact that the host elasticity is different from the inclusion.
5.1 What may cause the residual pressure modification?
The mechanisms investigated here, i.e. visco-plastic flow of the host and proximity of the inclusion to the thin-section surface, can all be responsible for the modification of the residual inclusion pressure. The amount of inclusion pressure change due to these mechanisms is controlled by the Deborah number (De), dimensionless yield strength (C∗), and dimensionless depth (). In the examples of quartz-in-garnet systems, the residual pressure is considered to be sealed in a perfectly elastic garnet host. Based on our study, the presence (radius) of a plastic yield region and preserved residual inclusion pressure are dominated by dimensionless yield strength ) as shown in Fig. 2. Strength Ch can be converted from hardness test data using the formula below (e.g. Evans and Goetze, 1979):
where H is the measured microhardness and Cg is a constant accounting for the indenter's geometry in the experiment. Taking Cg=3 (Evans and Goetze, 1979), the yield strength of garnet host is between 4.4 and 5 GPa at room conditions (Whitney et al., 2007), which leads to given residual inclusion pressure Pexp=1 GPa. This suggests that plastic yield does not occur in an idealized scenario of isotropic, spherical quartz inclusion entrapped in an infinite garnet host. However, such an ideal scenario is highly improbable in natural samples. Localized plastic yield may still occur due to the following reasons: (1) elevated differential stress when the inclusion is close to the thin-section surface (“ring”-shaped pattern in Fig. 8); (2) stress concentration at the corners of the quartz inclusion (Whitney et al., 2000); (3) anisotropic elastic deformation of the quartz inclusion (e.g. Murri et al., 2018); (4) pre-fractures or weakness in garnet host before the entrapment of quartz inclusions that leads to the localization of dislocations. Although our model does not predict exact conditions for plastic yield due to the above possibilities, it gives a lower bound for the strength and provides information on what type of host mineral phase cannot be used for Raman barometry. Plastic yield strength of some common rock-forming minerals measured in hardness tests are compiled and provided in Table 1. As an example, given Pexp=1 GPa, the dimensionless yield strength of calcite host is ca. 0.6 and dolomite is ca. 1.5 (Wong and Bradt, 1992). This implies that plastic flow will most likely affect the residual pressure Pexp in the calcite host but not in dolomite host.
After thin-section preparation, the inclusion pressure may be (partially) released. The dimensionless depth can be evaluated by performing depth-step scan analysis with Raman spectroscopy in order to observe if the pressure gradually decreases towards the thin-section surface (Enami et al., 2007). For a quartz-in-garnet system, to avoid significant pressure release (> 3 %) in the bottom half of the inclusion, the dimensionless depth needs to be above at least 1.5 (Fig. 8). To avoid significant pressure release in the entire quartz inclusion, the dimensionless depth needs to be above ∼2. Therefore, we recommend a safe dimensionless depth of 2–2.5 (from the surface to the centre of the inclusion) for quartz-in-garnet Raman barometry (see also Mazzucchelli et al., 2018). For a 30 µm thick thin section, the maximal radius of an inclusion is ca. 6 µm (12 µm in diameter) located at the mid-point of the thin section. In practice, it is difficult to precisely measure the depth of an inclusion, and it is uncommon that an inclusion is located right in the middle of a thin section. Therefore, it is ideal to choose smaller inclusions or prepare a thicker thin section for measurement (Campomenosi et al., 2018; Mazzucchelli et al., 2018).
For commonly used quartz-in-garnet Raman barometry, our results show that below 550–600 ∘C, the effect of viscous relaxation can be negligible. Above ca. 650–750 ∘C, the effect of viscous relaxation needs to be taken into account depending on a particular P–T path, garnet composition, and timescale (Figs. 3, 4). This is similar to the empirical estimate ca. 750 ∘C in Walters and Kohn (2014). It is also shown that the preserved residual pressure may even increase due to viscous relaxation if viscous resetting occurs at peak P condition (Fig. 6). This is simply because viscous creep does not only relax the overpressure in the quartz inclusion but also the underpressure that develops along the prograde P–T path. Meanwhile, the amount of viscous relaxation is time-dependent (De is a function of the operating time of viscous relaxation). Thus, the above temperature criterion for Raman barometry applies only for exhumation lasting at a million years' timescale. A higher temperature criterion for Raman barometry (e.g. ∼1000 ∘C for garnet host at high pressure close to the coesite–quartz transition) is applicable for more rapid exhumation, e.g. xenolith ascent carried by magma (Zhong et al., 2018) or garnet synthesis experiments that lasts hours or days (Thomas and Spear, 2018; Bonazzi et al., 2019).
5.2 Implications to garnet overstepping
Quartz-in-garnet Raman barometry has been used to determine the entrapment pressure, i.e. garnet nucleation or growth conditions, and compared it to the P–T conditions determined based on phase equilibria or classical chemical thermobarometry (Castro and Spear, 2017; Spear et al., 2014). As has been shown in Fig. 6, viscous resetting occurs when the inclusion–host system is brought to high temperature (> 600–700 ∘C). Even if the quartz inclusion is entrapped at lower P–T conditions, e.g. the garnet entrance conditions, the preserved residual inclusion pressure may still be significantly higher than predicted from the actual entrapment P–T conditions using a pure elastic model. In this case, erroneous results may emerge if one uses the relaxed residual quartz inclusion pressure to determine the entrapment pressure. In case of significant viscous resetting at peak T conditions followed by decompression, as in the case of some HP rocks, apparent garnet growth overstepping will be inferred (see Fig. 6b). In that case, care must thus be taken to interpret the discrepancy between the results of quartz-in-garnet Raman barometry and phase equilibria. As shown in the example with a synthetic clockwise P–T path (Fig. 6), ca. 3–4 kbar apparent overstepping is predicted by considering viscous resetting at peak T condition. The amount of apparent overstepping will be even larger if the exhumation process happens faster (current model assumes 10 Myr decompression time).
We first presented a 1-D visco-elasto-plastic model to study the inclusion–host system undergoing a prograde or retrograde P–T path. The non-dimensionalization of the governing equations yields two controlling parameters: the Deborah number (De) and dimensionless yield strength (C∗), which control the amount of pressure drop due to viscous relaxation and plastic yield. Both De and C∗ must be higher than 1 to avoid underestimating the residual pressure. Subsequently, a simplified analytical solution for inclusion pressure (Eq. 22) close to a stress-free thin-section surface is presented based on the existing analytical solution from Seo and Mura (1979). It is suggested that the distance between the thin-section surface and inclusion must be higher than 2–3 times the inclusion radius to avoid stress release.
The relevance of our presented visco-elasto-plastic model to quartz-in-garnet elastic barometry has been systematically studied. Although plastic yield is not expected for garnet host due to its high yield strength, the residual inclusion pressure preserved in quartz inclusion can be partially modified at high temperature due to time-dependent viscous creep. It is shown that above 650–700 ∘C over a Myr timescale, viscous creep of garnet host may partially reset the quartz pressure. This may have important implications for the determination of entrapment pressure of quartz inclusion. Additionally, this may also cause apparent overstepping of garnet growth; thus care must be taken when applying quartz-in-garnet barometry at rocks which experienced high temperatures (> 600–700 ∘C).
Here, we introduce a simplified formula for the pressure distribution of an initially pressurized inclusion in an infinite host moved toward a stress-free surface based on the existing analytical solution of Seo and Mura (1979). A Cartesian coordinate system is employed as shown in Fig. 7. The full stress tensor σij of inclusion loaded with eigenstrains is represented as follows (Seo and Mura, 1979):
While for the host, stresses are given below:
where the indices of xi () are in Cartesian coordinate frame following the order of x, y, and z(see Fig. 7) and ε∗ is the isotropic eigenstrain that is expressed as the difference of volumetric strain between inclusion and host assuming that they are not bounded by each other. The elliptic integrals ψ and ϕ are expressed below:
where for host, λ=0 for inclusion, and .
where for both host and inclusion and . Here, we focus on the stress experienced by the inclusion and derive a simplified form for the pressure of inclusion. For the inclusion, the elliptic integrals are derived:
The normal stresses in the inclusion are
By substituting ψ and ϕ into the equations above, the normal stresses can be obtained. In deriving the pressure, i.e. negative mean stress, many terms in Eqs. (A7)–(A9) can be cancelled out. A simplified form is obtained as follows:
The pre-factor is in fact the initial pressure of the inclusion in an infinite host loaded by the eigenstrain ε∗ under mechanical equilibrium. Therefore, we may simplify Eq. (A10) as follows:
where Pini is the inclusion pressure in an infinite host loaded by eigenstrain ε∗ under mechanical equilibrium before moving it close to the thin-section surface. The equation can be non-dimensionalized by using R as a length scale shown below:
The analytical solution for pressure in the mineral inclusion subject to an initial residual pressure Pini is obtained. When the inclusion is far from the thin-section surface (, and ), the actual residual pressure approaches the expected residual pressure based on a classical elastic model (Pinc→Pini). Another potential application of the solution in Eq. (A12) is for benchmarking numerical solutions. Due to the simplicity of the pressure expression, it is particularly suitable for quick validation of numerical models, e.g. the finite-difference model presented in the Supplement.
The MATLAB code to reproduce the results of a quartz-in-garnet system is available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/se-11-223-2020-supplement.
XZ designed the numerical or analytical model and wrote the MATLAB code. All the co-authors contributed to discussion and wrote the manuscript together.
The authors declare that they have no conflict of interest.
This work is supported by MADE-IN-EARTH ERC starting grant (no. n.335577) to Lucie Tajčmanová and Swiss National Science Foundation (P2EZP2_172220) to Xin Zhong. We thank Viktoriya Yarushina and an anonymous reviewer for helpful comments that greatly improved the quality of this work. Taras Gerya and Susanne Buiter are acknowledged for editorial handling.
This research has been supported by the European Research Council (grant no. n.335577) and the Swiss National Science Foundation (grant no. P2EZP2_172220).
This paper was edited by Taras Gerya and reviewed by Viktoriya Yarushina and one anonymous referee.
Aderogba, K.: On eigenstresses in a semi-infinite solid, Math. Proc. Cambridge Philos. Soc., 80, 555–562, https://doi.org/10.1017/S0305004100053172, 1976.
Angel, R. J., Gonzalez-Platas, J., and Alvaro, M.: EosFit7c and a Fortran module (library) for equation of state calculations, Z. Kristallogr., 229, 405–419, https://doi.org/10.1515/zkri-2013-1711, 2014.
Angel, R. J., Nimis, P., Mazzucchelli, M. L., Alvaro, M., and Nestola, F.: How large are departures from lithostatic pressure? Constraints from host–inclusion elasticity, J. Metamorph. Geol., 33, 801–813, https://doi.org/10.1111/jmg.12138, 2015.
Angel, R. J., Alvaro, M., Miletich, R., and Nestola, F.: A simple and generalised P–T–V EoS for continuous phase transitions, implemented in EosFit and applied to quartz, Contrib. Mineral. Petrol., 172, 1–15, https://doi.org/10.1007/s00410-017-1349-x, 2017a.
Angel, R. J., Mazzucchelli, M. L., Alvaro, M., and Nestola, F.: EosFit-Pinc: A simple GUI for host-inclusion elastic thermobarometry, Am. Mineral., 102, 1957–1960, https://doi.org/10.2138/am-2017-6190, 2017b.
Ashley, K. T., Caddick, M. J., Steele-MacInnis, M. J., Bodnar, R. J., and Dragovic, B.: Geothermobarometric history of subduction recorded by quartz inclusions in garnet, Geochem. Geophy. Geosy., 15, 350–360, https://doi.org/10.1002/2013GC005106, 2014.
Bass, J. D.: Elasticity of Minerals, Glasses, and Melts, in: Mineral Physics & Crystallography: Mineral Physics & Crystallography: A Handbook of Physical Constants, 45–63, 1995.
Bayet, L., John, T., Agard, P., Gao, J., and Li, J.: Massive sediment accretion at ∼80 km depth along the subduction interface? Evidence from the southern Chinese Tianshan, Geology, 46, 495–498, 2018.
Bonazzi, M., Tumiati, S., Thomas, J., Angel, R. J., and Alvaro, M.: Assessment of the reliability of elastic geobarometry with quartz inclusions, Lithos, 350/351, 105201, https://doi.org/10.1016/j.lithos.2019.105201, 2019.
Campomenosi, N., Mazzucchelli, M. L., Mihailova, B. D., Scambelluri, M., Angel, R. J., Nestola, F., Reali, A., and Alvaro, M.: How geometry and anisotropy affect residual strain in host inclusion system: coupling experimental and numerical approaches, Am. Mineral., 103, 2032–2035, https://doi.org/10.1111/ijlh.12426, 2018.
Castro, A. E. and Spear, F. S.: Reaction overstepping and re-evaluation of peak P-T conditions of the blueschist unit Sifnos, Greece: implications for the Cyclades subduction zone, Int. Geol. Rev., 59, 548–562, https://doi.org/10.1080/00206814.2016.1200499, 2017.
Chen, J., Wang, Q., Zhai, M., and Ye, K.: Plastic deformation of garnet in eclogite, Sci. China, 39, 18–25, 1996.
Dabrowski, M., Powell, R., and Podladchikov, Y.: Viscous relaxation of grain-scale pressure variations, J. Metamorph. Geol., 33, 859–868, https://doi.org/10.1111/jmg.12142, 2015.
Dekker, E. H. L. J. and Rieck, G. D.: Microhardness investigations on manganese aluminate spinels, J. Mater. Sci., 9, 1839–1846, 1974.
Enami, M., Nishiyama, T., and Mouri, T.: Laser Raman microspectrometry of metamorphic quartz: A simple method for comparison of metamorphic pressures, Am. Mineral., 92, 1303–1315, https://doi.org/10.2138/am.2007.2438, 2007.
Evans, B. and Goetze, C.: The temperature variation of hardness of olivine and its implication for polycrystalline yield stress, J. Geophys. Res., 84, 5505–5524, https://doi.org/10.1029/JB084iB10p05505, 1979.
Farber, K., Caddick, M. J., and John, T.: Controls on solid-phase inclusion during porphyroblast growth: insights from the Barrovian sequence (Scottish Dalradian), Contrib. Mineral. Petrol., 168, 1089, https://doi.org/10.1007/s00410-014-1089-0, 2014.
Ferrero, S. and Angel, R. J.: Micropetrology: Are inclusions grains of truth?, J. Petrol., 59, 1671–1700, https://doi.org/10.1093/petrology/egy075, 2018.
Gerya, T. V.: Introduction to Numerical Geodynamic Modelling, Cambridge University Press, 345 pp., 2010.
Gillet, P., Ingrin, J., and Chopin, C.: Coesite in subducted continental crust?: P-T history deduced from an elastic model, Earth Planet. Sc. Lett., 70, 426–436, 1984.
Gréaux, S. and Yamada, A.: P-V-T equation of state of Mn3Al2Si3O12 spessartine garnet, Phys. Chem. Miner., 41, 141–149, https://doi.org/10.1007/s00269-013-0632-2, 2014.
Guiraud, M. and Powell, R.: P-V-T relationships and mineral equilibria in inclusions in minerals, Earth Planet. Sc. Lett., 244, 683–694, https://doi.org/10.1016/j.epsl.2006.02.021, 2006.
Izraeli, E. S., Harris, J. W., and Navon, O.: Raman barometry of diamond formation, Earth Planet. Sc. Lett., 173, 351–360, 1999.
Jasiuk, I., Tsuchida, E., and Mura, T.: Spheroidal sliding inclusion in an elastic half-space, Appl. Mech. Rev., 44, S143–S149, https://doi.org/10.1115/1.3121346, 1991.
Kachanov, L. A.: Foundations of the Theory of Platicity, North-Holland Publishing Company, 482 pp., 1971.
Karato, S., Wang, Z., Liu, B., and Fujino, K.: Plastic deformation of garnet: systematics and implications for the rheology of the mantle transition zone, Earth Planet. Sc. Lett., 130, 13–20, 1995.
Kohn, M. J.: “Thermoba-Raman-try”: Calibration of spectroscopic barometers and thermometers for mineral inclusions, Earth Planet. Sc. Lett., 388, 187–196, https://doi.org/10.1016/j.epsl.2013.11.054, 2014.
Korsakov, A. V., Perrakim, M., Zhukov, V. P., De Gussem, K., Vandenabeele, P., and Tomilenko, A. A.: Is quartz a potential indicator of ultrahigh-pressure metamorphism?: Laser Raman spectroscopy of quartz inclusions in ultrahigh-pressure garnets, Eur. J. Mineral., 21, 1313–1323, https://doi.org/10.1127/0935-1221/2009/0021-2006, 2009.
Kouketsu, Y., Hattori, K., Guillot, S., and Rayner, N.: Eocene to Oligocene retrogression and recrystallization of the Stak eclogite in northwest Himalaya, Lithos, 240–243, 155–166, https://doi.org/10.1016/j.lithos.2015.10.022, 2016.
Liu, L. and Mernagh, T. P.: High Pressure Raman study of the a-quartz forms of SiO2 and GeO2 at room temperature, High Temp. Press., 24, 13–21, 1992.
Mazzucchelli, M. L., Burnley, P., Angel, R. J., Morganti, S., Domeneghetti, M. C., Nestola, F., and Alvaro, M.: Elastic geothermobarometry: Corrections for the geometry of the host-inclusion system, Geology, 46, 1–4, https://doi.org/10.1130/G39807.1, 2018.
Milani, S., Nestola, F., Alvaro, M., Pasqual, D., Mazzucchelli, M. L., Domeneghetti, M. C., and Geiger, C. A.: Diamond-garnet geobarometry: The role of garnet compressibility and expansivity, Lithos, 227, 140–147, https://doi.org/10.1016/j.lithos.2015.03.017, 2015.
Mindlin, R. D. and Cheng, D. H.: Thermoelastic Stress in the Semi-Infinite Solid, J. Appl. Phys., 931, 931–933, https://doi.org/10.1063/1.1699786, 1950.
Moulas, E., Schmalholz, S. M., Podladchikov, Y., Tajčmanová, L., Kostopoulos, D., and Baumgartner, L.: Relation between mean stress, thermodynamic, and lithostatic pressure, J. Metamorph. Geol., 37, 1–14, https://doi.org/10.1111/jmg.12446, 2019.
Murri, M., Mazzucchelli, M. L., Campomenosi, N., Korsakov, A. V., Prencipe, M., Mihailova, B. D., Scambelluri, M., Angel, R. J., and Alvaro, M.: Raman elastic geobarometry for anisotropic mineral inclusions, Am. Mineral., 113, 1869–1872, 2018.
Reiner, M.: The Deborah Number, Phys. Today, 17, 62–62, 1964.
Rosenfeld, J. L. and Chase, A. B.: Pressure and temperature of crystallization from elastic effects around solid inclusions in minerals?, Am. J. Sci., 259, 519–541, https://doi.org/10.2475/ajs.259.7.519, 1961.
Schmidt, C. and Ziemann, M. A.: In situ Raman spectroscopy of quartz: A pressure sensor for hydrothermal diamond-anvil cell experiments at elevated temperatures, Am. Mineral., 85, 1725–1734, https://doi.org/10.2138/am-2000-11-1216, 2000.
Seo, K. and Mura, T.: The elastic field in a half space due to ellipsoidal inclusions with uniform dilatational eigenstrains, J. Appl. Mech., 46, 568–572, https://doi.org/10.1115/1.3424607, 1979.
Smedskjaer, M. M., Jensen, M., and Yue, Y. Z.: Theoretical calculation and measurement of the hardness of diopside, J. Am. Ceram. Soc., 91, 514–518, https://doi.org/10.1111/j.1551-2916.2007.02166.x, 2008.
Spear, F. S., Thomas, J. B., and Hallett, B. W.: Overstepping the garnet isograd?: a comparison of QuiG barometry and thermodynamic modeling, Contrib. Mineral. Petrol., 168, 1059, https://doi.org/10.1007/s00410-014-1059-6, 2014.
Taguchi, T., Igami, Y., Miyake, A., and Enami, M.: Factors affecting preservation of coesite in ultrahigh-pressure metamorphic rocks: Insights from TEM observations of dislocations within kyanite, J. Metamorph. Geol., 37, 401–414, https://doi.org/10.1111/jmg.12470, 2019a.
Taguchi, T., Enami, M., and Kouketsu, Y.: Metamorphic record of the Asemi-gawa eclogite unit in the Sanbagawa belt, southwest Japan: Constraints from inclusions study in garnet porphyroblasts, J. Metamorph. Geol., 37, 181–201, https://doi.org/10.1111/jmg.12456, 2019b.
Tajčmanová, L., Podladchikov, Y., Powell, R., Moulas, E., Vrijmoed, J. C., and Connolly, J. A. D.: Grain-scale pressure variations and chemical equilibrium in high-grade metamorphic rocks, J. Metamorph. Geol., 32, 195–207, https://doi.org/10.1111/jmg.12066, 2014.
Thomas, J. B. and Spear, F. S.: Experimental study of quartz inclusions in garnet at pressures up to 3.0 GPa: evaluating validity of the quartz-in-garnet inclusion elastic thermobarometer, Contrib. Mineral. Petrol., 173, 1–14, https://doi.org/10.1007/s00410-018-1469-y, 2018.
Tsuchida, E. and Nakahara, I.: Three dimensional stress concentration around a spherical cavity in a semi infinite elastic body, Bull. Jpn. Soc. Mech., 13, 499–508, https://doi.org/10.1299/jsme1958.13.499, 1970.
Van Der Molen, I. and Van Roermund, H. L.: The pressure path of solid inclusions in minerals?: the retention of coesite inclusions during uplift, Lithos, 19, 317–324, 1986.
Vermeer, P. A. and De Borst, R.: Non-associated plasticity for soils, concrete and rock, in: Physics of dry granular media, NATO ASI Series, 163–196, 1984.
Walters, J. B. and Kohn, M. J.: Examining the temperature range suitable for Quartz-in-Garnet Geoba-Raman-try, in: 11th International GeoRaman Conference, p. 5023, 2014.
Wang, Z. and Ji, S.: Deformation of silicate garnets: Brittle-ductile transition and its geological implications, Can. Mineral., 37, 525–541, 1999.
Whitney, D. L., Cooke, M. L., and Du Frane, S. A.: Modeling of radial microcracks at corners of inclusions in garnet using fracture mechanics, J. Geophys. Res., 105, 2843, https://doi.org/10.1029/1999JB900375, 2000.
Whitney, D. L., Broz, M., and Cook, R. F.: Hardness, toughness, and modulus of some common metamorphic minerals, Am. Mineral., 92, 281–288, https://doi.org/10.2138/am.2007.2212, 2007.
Wolfe, O. M. and Spear, F. S.: Determining the amount of overstepping required to nucleate garnet during Barrovian regional metamorphism, Connecticut Valley Synclinorium, J. Metamorph. Geol., 36, 79–94, https://doi.org/10.1111/ijlh.12426, 2017.
Wong, T. Y. and Bradt, R. C.: Microhardness anisotropy of single crystals of calcite, dolomite and magnesite on their cleavage planes, Mater. Chem. Phys., 30, 261–266, https://doi.org/10.1016/0254-0584(92)90234-Y, 1992.
Yamamoto, J., Kagi, H., Kaneoka, I., Lai, Y., Prikhod'ko, V. S., and Arai, S.: Fossil pressures of fluid inclusions in mantle xenoliths exhibiting rheology of mantle minerals: Implications for the geobarometry of mantle minerals using micro-Raman spectroscopy, Earth Planet. Sc. Lett., 198, 511–519, https://doi.org/10.1016/S0012-821X(02)00528-9, 2002.
Yardley, B. W. and Bodnar, R. J.: Fluids in the Upper Continental Crust, Front. Geofluids, 3, 1–127, https://doi.org/10.1002/9781444394900.ch17, 2014.
Yuan, X., Liu, X., Wang, L., and Lu, X.: Density and hardness of Nd-doped zircon ceramics as nuclear waste forms, IOP Conf. Ser. Earth Environ. Sci., 61, 012140, https://doi.org/10.1088/1755-1315/61/1/012140, 2017.
Zhang, Y.: Mechanical and phase equilibria in inclusion–host systems, Earth Planet. Sc. Lett., 157, 209–222, https://doi.org/10.1016/S0012-821X(98)00036-3, 1998.
Zhong, X., Moulas, E., and Tajčmanová, L.: Tiny timekeepers witnessing high-rate exhumation processes, Sci. Rep., 8, 2234, https://doi.org/10.1038/s41598-018-20291-7, 2018.
Zhong, X., Andersen, N. H., Dabrowski, M., and Jamtviet, B.: Zircon and quartz inclusions in garnet used for complimentary Raman- thermobarometry: application to the Holsnøy eclogite, Bergen Arcs, Western Norway, Contrib. Mineral. Petrol., 4, 1–17, https://doi.org/10.1007/s00410-019-1584-4, 2019a.
Zhong, X., Dabrowski, M., and Jamtveit, B.: Analytical solution for the stress field in elastic half space with a spherical pressurized cavity or inclusion containing eigenstrain, Geophys. J. Int., 216, 1100–1115, 2019b.
- Abstract
- Introduction
- 1-D mechanical model with visco-elasto-plastic rheology
- Inclusion pressure modification due to visco-plastic deformation of host
- Inclusion pressure modification due to proximity to the thin-section surface
- Discussion
- Conclusions
- Appendix A
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- 1-D mechanical model with visco-elasto-plastic rheology
- Inclusion pressure modification due to visco-plastic deformation of host
- Inclusion pressure modification due to proximity to the thin-section surface
- Discussion
- Conclusions
- Appendix A
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement





