the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Understanding controls on hydrothermal dolomitisation: insights from 3D reactive transport modelling of geothermal convection
Rungroj Benjakul
Cathy Hollis
Hamish A. Robertson
Eric L. Sonnenthal
Fiona F. Whitaker
The dominant paradigm for petrogenesis of high-temperature fault-controlled dolomite, widely known as “hydrothermal dolomite” (HTD), invokes upwelling of hot fluid along faulted and fractured conduits from a deep over-pressured aquifer. However, this model has several inherent ambiguities with respect to fluid sources and their dolomitisation potential, as well as mechanisms for delivering enough of these reactive fluids to form substantial volumes of dolomite. Here, we use generic 2D and 3D reactive transport simulations of a single transmissive fault system to evaluate an alternative conceptual model whereby dolomitisation is driven by seawater being drawn down into the subsurface and heated. We examine the evolution of fluid chemistry and the distribution of diagenetic alteration, including predictions of the rate, distribution, and temperature of HTD formation, and consider the possible contribution of this process to the Mg budget of the world's oceans.
The simulations suggest that it is possible for convection of seawater along the fault damage zone to form massive dolomite bodies that extend hundreds of metres vertically and along the fault within a timescale of a few tens of thousands of years, with no significant alteration of the country rock. Dolomitisation occurs as a gradient reaction by replacement of host limestones and minor dolomite cementation, and it results in the discharge of Mg2+-poor, Ca2+-rich fluids to the sea floor. Fluids sourced from the basement contribute to the transport of heat that is key for overcoming kinetic limitations to dolomitisation, but the entrained seawater provides the Mg2+ to drive the reaction. Dolomite fronts are sharper on the “up-flow” margin where Mg2+-rich fluids first reach the threshold temperature for dolomitisation, and the “down-flow” dolomite front tends to be broader as the fluid is depleted in Mg2+ by prior dolomitisation. The model demonstrates spatial contrasts in the temperature of dolomitisation and the relative contribution of seawater and basement-derived fluids which are also commonly observed in natural fault-controlled dolomites. In the past, such variations have been interpreted in terms of major shifts in the system driving dolomitisation. Our simulations demonstrate that such changes may also be a product of emergent behaviour within a relatively stable system, with areas that are dolomitised more slowly recording the effect of changes in fluid flow, heat, and solute transport that occur in response to diagenetic permeability modification.
Overall, our models robustly demonstrate that high-temperature fault-controlled dolomite bodies can form from mixed convection and act as a sink for Mg in the circulating seawaters. In addition, comparison of our 3D simulations with simplifications to 2D indicate that 2D models misrepresent critical aspects of the system. This has important implications for modelling of systems ranging from geothermal resources and mineralisation to carbonate diagenesis, including hydrothermal karstification and ore genesis as well as dolomitisation.
- Article
(5505 KB) - Full-text XML
- BibTeX
- EndNote
Hydrothermal dolomite (HTD) is commonly thought to form under burial conditions from fluids escaping rapidly from a deep over-pressured aquifer via normal or strike-slip faults, and it can take the form of dolomite cement, replacement of limestone, and/or overprinting of dolomitic country rocks (Gregg, 2004; Hollis et al., 2017; López-Horgue et al., 2010; Machel, 2004). The economic importance of HTD often lies in the associated hydrothermal dissolution and/or mineralisation, in particular Mississippi Valley-type Pb–Zn ore deposits (Davies and Smith, 2006; Qing and Mountjoy, 1994). More controversially, fluids thought to have formed fault-related HTDs have also been interpreted as being responsible for the formation or overprinting of large volumes of matrix-replacement dolomite that form important hydrocarbon reservoirs and infer basin-wide hydrothermal activity (Al-Aasm, 2003; Davies and Smith, 2006; Sharp et al., 2010; Weissenberger et al., 2006). Machel and Lonnee (2002) were particularly critical of this suggestion and argued strongly against the use of the term hydrothermal (as distinct from geothermal) without evidence that the dolomites formed at temperatures of at least 5–10 ∘C higher than the country rock. This would require very rapid rates of both fluid flow and precipitation, and the physics of heat transport mean that it is practically impossible to form HTD away from high-permeability conduits. The requisite temperature data to define HTD sensu stricto is rarely presented; thus, this distinction, whilst technically correct, is often ignored. Rather, the term HTD has become widely applied to describe high-temperature fault-related dolomites.
Despite a substantial body of previous work describing HTD geobody distributions and dimensions in outcrops, along with petrographical and geochemical characterisation, important questions remain regarding the process of formation. These include the origin and chemistry of the dolomitising fluids, the volumes of fluids that can be released from deep sources, and the mechanisms controlling the distribution and rate of fluid flow and, thus, the temperature and rate of dolomitisation. Over-pressured aquifers exist at depth as a result of rapid burial and/or orogenic compression, and tectonic activity can create permeable pathways for the release of such fluids (Ge and Garven, 1994; Oliver, 1986; Whitaker et al., 2004). However, these processes can release, at the most, only a single pore-volume; thus, dolomitisation requires significant focusing of flow from large reservoirs (Consonni et al., 2010; Frazer et al., 2014; Kaufman, 1994). Potential dolomitising fluids are hypothesised as brines or saline connate waters, and this is supported by high-salinity fluid inclusions in the dolomite cements in some cases (Al-Aasm, 2003; Boni et al., 2000; Davies and Smith, 2006; Luczaj et al., 2006). However, a review of the thermodynamic potential of formation waters to drive dolomitisation suggests that fluids hosted in deep aquifers are close to dolomite–calcite equilibrium and, thus, have limited dolomitisation potential.
Given the ambiguities in existing conceptual models for HTD formation, we evaluate an alternative model for the formation of high-temperature dolomites by “top-down” circulation of Mg2+-rich fluids from an effectively infinite reservoir of seawater (or modified seawater) overlying a permeable fault damage zone. In high-enthalpy areas, heating of groundwater at depth increases buoyancy and, where the critical Rayleigh number is exceeded (Nield, 1968), drives free convection that can entrain water that is cooler and therefore more dense. Controls on this flow system have been analysed numerically by means of 2D models of heat and fluid flow (Person and Garven, 1994; Simms and Garven, 2004), and they include sediment and fault permeabilities, spacing between faults, lithologic heterogeneity, and basal heat flow. These studies show convection cells that are characteristically laterally elongated, with an aspect ratio of 1.8, and inflow over broad areas but discharge focused over narrower zones. The power of this approach was demonstrated by simulations coupling large-scale free convection of groundwater flow with gravity-driven flow in the Dead Sea rift, Israel (Gvirtzman et al., 1997a, b), that replicate both thermal anomalies and the composition of springs that are mixtures of shallow groundwater with hot brine from a deep aquifer.
An increasing number of studies have suggested fault-related dolomitisation by seawater or seawater-derived fluids (Carmichael and Ferry, 2008; Corbella et al., 2014; Haeri-Ardakani et al., 2013; Hollis et al., 2017; Wilson et al., 2007). For example, in the Hammam Faraun Fault (HFF) area, Egypt, strontium isotope and rare earth element (REE) signatures suggest that massive dolostone bodies limited to the damage zone of the fault formed from Oligo-Miocene seawater during development of the Suez Rift (Hirani et al., 2018; Hollis et al., 2017). We have previously suggested a conceptual model for the formation of these dolostones whereby Mg2+-rich seawater could have been drawn down into a convection cell along the fault, heated, and then ascended to form massive dolostone (Hollis et al., 2017). Testing this hypothesis by reference to the behaviour of modern analogues is challenging using direct observation of hydrological and chemical processes, and process-based modelling provides an alternative means for rigorous evaluation in such scenarios.
Following the early work of Wilson et al. (2001) and Jones and Xiao (2005), over the past decade process-based numerical modelling of heat and fluid flow coupled with the simulation of water–rock reactions using reactive transport models (RTMs) have contributed to the understanding of shallow, relatively low-temperature dolomitisation (Al-Helal et al., 2012; Gabellone et al., 2016; Gabellone and Whitaker, 2016; Garcia-Fresca, 2009; Whitaker and Xiao, 2010; Xiao et al., 2013). RTM simulations of HTD have focused on understanding controls on the nature of dolomitisation fronts, which are characteristically sharp in fault-related dolomites, and on the development of fault-associated strata-bound dolostone bodies (Corbella et al., 2014; Xiao et al., 2013; Yapparova et al., 2017). These studies demonstrate the importance of the geometry of the fault, termination of the fault against a sealing layer, and distribution of permeability and precursor mineralogy in the country rock, but they are all predicated on a supply of hot, Mg2+-rich fluid at the base of the fault. Consonni et al. (2018) highlight some of the challenges in moving beyond these outcrop-scale models of HTD that arise from uncertainties in fluid composition and volumes, and they contrast these with the RTM simulation of reflux and thermal convection systems for which fluid flow and chemistry can be better constrained from an understanding of the geometry of the carbonate platform, relative sea-level, and climate. Where fluids are derived from compaction, the geometry of the system can help constrain fluid volumes, but specifying fluid chemistries is more challenging – even when the mineralogy of the compacting formation is known (Consonni et al., 2010; Frazer et al., 2014). This points to the need for a better understanding of deep aquifer and reservoir fluid chemistry to identify controls on dolomitisation potential among different lithological and geological settings.
Simulations of free convection within a magmatic hydrothermal system volcanic caldera system exemplified how faults can either act as conduits for focusing the discharge of high-temperature fluids or as conduits for the influx of cool shallow fluids from a shallow reservoir (Jasim et al., 2015). Recently, the study of natural fault-controlled dolomite bodies have provided evidence for the mixing of seawater and mantle-derived fluids, during dolomitisation, implying that hot, deeply sourced brines at least provide a thermal drive for dolomitisation (Breislin et al., 2020; Koeshidayatullah et al., 2020a). The mixing that occurs between such fluids expelled from a fault and host-rock pore waters of marine salinity was invoked by Smith et al. (2008) in order to explain HTD in the Trenton and Black River reservoirs of eastern North America, following 1D RTM studies by Salas et al. (2007). However, in a limestone aquifer separated from overlying seawater by a confining layer, a single pore-volume of seawater would clearly be insufficient to provide the Mg2+ required for the scale of hydrothermal dolomitisation described by Smith et al. (2008).
The objective of this study is to use RTM to evaluate whether, for a highly simplified generic single transmissive faulted system, physical and chemical constraints might allow the formation of significant volumes of dolomite by entrainment of seawater into a geothermal convection system. It is not our objective to reproduce the development of a real dolostone body; rather, we consider a generic scenario with a simple geometry under conditions that are clearly defined. The key question addressed is whether the proposed flow system could account for the volumes and geometries of dolostone geobodies and temperature characteristics observed in fault-related HTDs, given heat and solute transport, chemical thermodynamics, and kinetic constraints. We examine the evolution of fluid chemistry and the distribution of diagenetic alteration, including predictions of the rate, distribution, and temperature of dolomite formation, and the relative contribution of seawater and basement-derived fluids along with sensitivity analysis of certain model parameters. Additionally, we compare the results of our 3D simulations with those from 2D sections perpendicular to the plane of the fault (echoing this key element of many previous 2D models of HTD) as well as 2D models oriented along the plane of the fault.
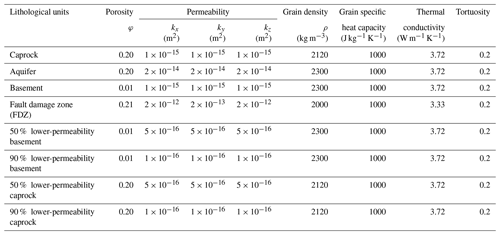
Fluid flow and reactive transport simulations were performed using TOUGHREACT (Sonnenthal et al., 2017; Xu et al., 2011), which simulates multiphase fluid flow, heat, and solute transport with physical and chemical heterogeneity and incorporates feedbacks between diagenesis and evolving porosity and permeability (Xu et al., 2004). A number of generic simulations were run to evaluate the potential of geothermal convection of seawater to form fault-related dolomites within a single transmissive fault system open to the sea surface. Fluid flow and heat transport were simulated in 2D sections oriented both parallel and perpendicular to the plane of the fault and compared with that in a 3D domain to constrain an initial condition for the reactive transport simulations. The 3D domain has a dimension of 2.7 km along the plane of the fault, 2.5 km perpendicular to the fault, and is 5 km deep (Fig. 1). A symmetry boundary along the centre of the fault damage zone (FDZ) has been assumed, and the half model is discretised into 4158 active grid blocks, 150 m wide and 250 m deep, which vary in width from 10 m within the FDZ to 500 m at the boundaries. The simulated sequence comprises a 3000 m thick carbonate unit with a permeability of m2 (≈ 20 mD) that is sandwiched between two 1000 m thick lower-permeability (10−15 m2≈1 mD) layers, herein termed “caprock” and “basement” respectively as generic terms indicating rocks of lower permeability relative to our reactive aquifer. An 80 m wide permeable FDZ extends vertically through the carbonate unit and the overlying layer to the sea floor. Matrix cells are isotropic, but within the FDZ vertical permeability is 10 times higher than horizontal permeability and the porosity is 3 % higher than that of the aquifer. The properties of all units are listed in Table 1. A full 3D flow model ( km) has validated the assumed symmetry, and, as such, the presence or absence of a low-permeability fault gouge in the core of the fault would not significantly affect the result.
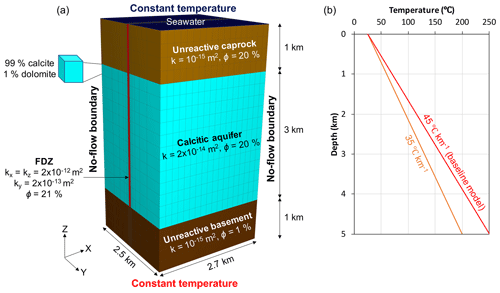
Figure 1(a) Model dimensions, material properties, and simulation grid. The permeable fault damage zone (FDZ) is displayed in red. Parallel to the FDZ, the grid is regularly discretised with dimensions of 150×250 m (width × height); perpendicular to the fault, cell thickness varies from 500 m at the edge of the model to 10 m within the FDZ. The caprock and basement are unreactive, and the aquifer is calcitic, with 1 % “seed” dolomite. The side boundaries are no-flow, and the top and bottom boundaries are constant temperature. (b) The initial conditions of the simulations. The top boundary is open to exchange with overlying seawater at 25 ∘C, and the base of the model is set at 200 and 250 ∘C (for the baseline model), giving an initial geothermal gradient of 35 and 45 ∘C km−1 respectively.
Table 1Hydrological and thermal properties of units in models. Porosity is fractional and permeability is isotropic in all units except for the fault damage zone. For the 3D model, we also evaluate sensitivity to 50 % and 90 % lower basement and caprock permeability. Permeability in SI units (m2) can be converted to approximate darcies by multiplying by 1012.
The two 2D models are based on slices through the 3D model, both perpendicular to the plane of the fault and along the FDZ (Fig. 2). The fault-perpendicular 2D model is 2.5 km wide and includes an 80 m wide FDZ from the surface to a depth of 4 km within a model that extends to a total depth of 5 km. The fault-parallel 2D model represents an 80 m wide FDZ that is one cell thick and extends 2.7 km laterally and to a depth of 4 km within a model that extends to a total depth of 5 km. Both models are discretised into grid blocks of identical dimensions and with identical rock properties to those in the 3D model; a single porosity–single permeability approach was used in all cases.
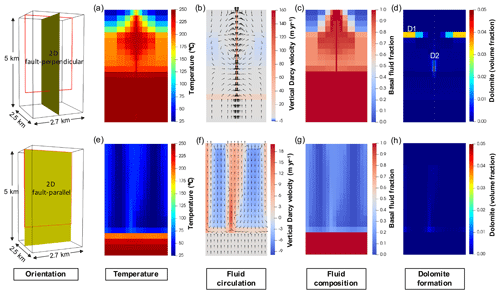
Figure 2Simulation results for 2D fault-perpendicular (a–d) and fault-parallel (e–h) models showing heat transfer, fluid flow (with representative streamlines), basal fluid fraction, and dolomite distribution at 30 kyr. The yellow planes on the left of each row represent the orientation of 2D displays, and the red outlines highlight the FDZ. Darcy velocities are positive when the flow is upward and negative when the flow is downward. Note the difference in scale for Darcy velocity between the 2D fault-perpendicular and fault-parallel models.
In all three models, the side boundaries are no-flow, and the bottom and top boundaries are constant temperature and pressure. Infinite volume cells at atmospheric pressure and 25 ∘C are implemented at the top boundary to represent a shallow overlying body of seawater. The basal cells are at 250 ∘C, giving an initial conductive temperature gradient of 45 ∘C km−1, and a hydrostatic pressure gradient is imposed. The flux of fluids into the base of the FDZ is determined by the permeability of the 1 km thick basement. Initial parameters and boundary conditions for all model runs are summarised in Fig. 1. The resulting fluid flux is expressed as a Darcy velocity (in m yr−1), also known as Darcy flux or specific discharge, and is calculated by multiplying the pore velocity by porosity where all porosity is assumed to be effective. We compare the total mass flow, differentiating seawater and basement fluid drawn into the model, and the discharge of mixed fluid to the sea floor via the 80 m wide FDZ and from the matrix. We model solute transport by diffusion as well as advection, with the same diffusion coefficient (10−9 m2 s−1) for all species.
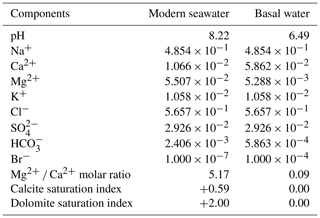
The baseline RTM was constructed using modern open-ocean seawater (Nordstrom et al., 1979) as the initial fluid throughout the reservoir and caprock. Within the basement the fluid is high-temperature (250 ∘C) modern seawater at equilibrium with calcite and dolomite and, thus, has a higher Ca2+ concentration, a lower Mg2+ concentration and alkalinity, and is slightly acidic (Table 2). Geochemical calculations include 10 primary aqueous species and two minerals, calcite and dolomite. We use the concentration of Br− to trace the contribution of fluids from the basement, hereinafter expressed as the basal fluid fraction. The upper 1 km (matrix and FDZ) and basal 1 km (basement) are assumed to be unreactive. Initial mineralogy throughout the interval, 1–4 km depth, is 99 % calcite, with 1 % dolomite as a seed. As the rate of dolomite precipitation is much slower than that of calcite dissolution, calcite was modelled as an equilibrium thermodynamic mineral (fluid and solid equilibrating within a single time step). Thus, the rate of dolomitisation is determined by the kinetics of dolomite precipitation. The kinetic rate of dolomite precipitation was constrained by the laboratory experiments of Arvidson and Mackenzie (1999) in which dolomite was precipitated at 115–196 ∘C. Thus, we include the effects of temperature on both thermodynamics and kinetics of dolomitisation, as well as the evolving fluid composition and mineralogy. The baseline simulation assumes an effective reactive surface area (RSA) of 1000 cm2 g−1, representative of 25 µm diameter idealised grains (Gabellone and Whitaker, 2016), but does not consider changes in the RSA due to diagenetic changes in texture.
Table 2Chemical composition of end-member fluids in reactive transport analysis. Primary aqueous species concentrations are in moles per kilogram (mol kg−1) of H2O; mineral saturation indices are log (IAP∕K). Br− is used as a non-reactive tracer of the contribution of basal fluid.
Porosity changes in the matrix and fractures are directly tied to the volume changes as a result of mineral precipitation and dissolution, and the model estimates changes in permeability from these. TOUGHREACT tracks diagenetic changes in both porosity and permeability that result from changes in mineral volume fractions due to water–rock interaction, and it subsequently returns this feedback to modify fluid flow. The porosity–permeability relationship for the matrix is approximated by Eq. (1), the Kozeny–Carman equation (Bear, 1972), which is one of the simplest and most widely used models for porosity–permeability relationship (Costa, 2006; Ehrenberg et al., 2006):
where ki and φi are the initial permeability and porosity respectively. Within the fracture zone, we represent changes in permeability using the cubic law relation (Steefel and Lasaga, 1994), Eq. (2):
In two additional 3D simulations, we explore the influence of heat flux on temperature, fluid flux, and dolomitisation by reducing the permeability of the basement from 10−15 m2 (≈1 mD) to either m2 (≈0.5 mD) or m2 (≈ 0.1 mD). This limits the effective flux of hot fluids from the basement whilst maintaining the same temperature at the base of the model. We further investigate the effect of basal temperature by specifying a lower temperature (200 ∘C) at the base of the model, giving an initial geothermal gradient of 35 ∘C km−1 (Fig. 1) which is comparable to the average thermal gradient of 31.3 and 32.0 ∘C km−1 in the onshore Netherlands region (Bonté et al., 2012) and geothermal areas in Germany (Agemar et al., 2012) respectively. Finally, we evaluate the sensitivity of the system to the permeability of the caprock, reducing this to 0.5 and 0.1 mD from 1 mD in the baseline model.
Post-processing data analysis includes Mg2+-flux calculation and differentiation between dolomite cementation and replacement dolomite. The Mg flux is calculated as the product of the aqueous concentration of Mg2+ (mol kg−1) and mass fluid flux (kg s−1 m−2), is reported in millimoles per second per square metre (mmol s−1 m−2), and provides both a better understanding of source–sink behaviour and a mechanism to track Mg2+ circulation and exchange. The changes in the total volume of dolomite formed by the replacement of calcite (as commonly described by the stoichiometric equation, Reaction R1) is differentiated from dolomite cementation (primary precipitation of dolomite, Reaction R2) using the reduction in the volume of calcite and adjusting for the molar volume difference between calcite (36.93 cm3 mol−1) and dolomite (64.37 cm3 mol−1).
This ignores the effect of any changes in the volume of calcite that may occur independent of dolomitisation. Because of the retrograde solubility of calcite, this calculation yields a maximum estimate of the fraction of dolomite that forms by replacement in the areas of increasing temperature in the direction of flow and a minimum estimate in areas of decreasing temperature.
3.1 Baseline 2D and 3D simulations of geothermal convection: fluid flow and heat transfer
The 2D and 3D simulations show the circulation of fluids by geothermal convection within the fault damage zone (FDZ) and the combined effects of conduction and advection of heat for a very simple planar fault (Figs. 2 and 3). Fluid circulation is driven by differences in fluid density generated by temperature contrasts between the surface and basement, mediated by the spatial distribution of permeability. The fault-perpendicular 2D model shows the FDZ acting as a conduit for advective discharge of hot fluid sourced largely from the basement, with a vertical Darcy velocity within the FDZ of up to 159 m yr−1, some 1–2 orders of magnitude higher than rates in the matrix (Fig. 2a, b). Convection and heat transfer between the matrix and the FDZ mainly occur in the aquifer zone (1–4 km depth). A combination of conduction and the ascending flow of buoyant hot fluid from the basement (average Darcy velocity of 1.1 m yr−1) elevates the temperature throughout the FDZ (185–246 ∘C) and in the lower part of the aquifer (235–245 ∘C at >2.75 km). The total discharge across the 80 m wide FDZ at 30 kyr is 3.44×103 m3 yr−1 per metre length of fault, which is equivalent to 9.30×106 m3 yr−1 for the entire 2.7 km length of the model. Water from the basement represents 97 % of this discharge, as the influx of seawater from the upper boundary through the matrix is limited by the low permeability of the caprock (with a Darcy velocity for inflow of only 0.01–0.04 m yr−1) and contributes <25 % of fluid within the matrix (Fig. 2b, c).
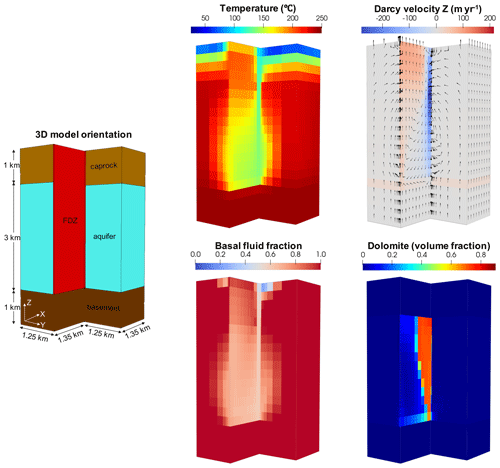
Figure 3A 3D baseline simulation illustrating heat transfer, fluid flow, basal fluid fraction, and dolomite distribution at 30 kyr. Note that the Darcy velocities are positive when the flow is upward and negative when the flow is downward. The 3D volume on the left represents the orientation and dimensions of the displays. The dolomitisation is focused along the plane of the fault for which the temporal evolution of the system is presented in Fig. 5.
The fault-parallel 2D model shows convection within the FDZ, with flow rates approximately 1 order of magnitude slower those within the FDZ in the fault-perpendicular 2D model (Fig. 2e, f). Several narrow convection cells develop which draw cold seawater downward into the FDZ across a broad zone. This circulates to the base of the aquifer, with Darcy velocities for the descending limb of up to 6 m yr−1, resulting in widespread cooling within the FDZ, and in the ascending limb of up to 16.5 m yr−1 at temperatures of up to 72 ∘C (Fig. 2e, f). The total flow of seawater drawn into the FDZ from the sea along the 2.7 km length of the model is 3.14×105 m3 yr−1, with only 15 % of this being fluid from the basement. This 2D simulation ignores fluid exchange with the matrix but allows lateral circulation along the plane of the fault and gives much lower fluid fluxes and temperatures in the system than the simulation oriented perpendicular to the fault.
The 3D simulation clearly demonstrates the importance of considering both flow along the plane of the FDZ and exchange with the surrounding matrix (Fig. 3). Fluid flux is strongly focused within the FDZ which accounts for 88 % of the total fluid circulation within the system within only 3 % of the total modelled volume. Rates of fluid flow within the FDZ in the 3D simulation are almost 1 order of magnitude higher than those of the fault-parallel 2D case. Darcy velocities reach a maximum of 280 m yr−1 within the FDZ at a depth of 1.2–1.5 km and decrease with depth below this. However, temperature within the FDZ is much higher than in the fault-parallel 2D simulation despite the 3D model predicting an influx of cold seawater within the FDZ 5 times higher (1.61×106 m3 yr−1) than that in the fault-parallel 2D model. This apparent contradiction arises from the inability of the 2D fault-parallel model to account for advective transfer of heat between the FDZ and the matrix. In the 3D model, seawater at 25 ∘C that is drawn into the FDZ results in cooling that extends to the top of the basement and laterally into the surrounding matrix at a depth of 2.5–4.0 km. High temperature at the base of the model leads to upward flow of fluid through the basement both within the FDZ and, at lower rates, throughout the aquifer (with a Darcy velocity of up to 33 and 18 m yr−1 respectively). The lower permeability of the caprock forces ascending fluid within the aquifer matrix back into the FDZ at depths shallower than 2.5 km, with a total influx from the upper aquifer to the FDZ of 1.11×107 m3 yr−1 at temperatures that range from 115 to 222 ∘C. This leads to a major contribution of basement water in mixed fluid circulated in most parts of the system, with the exception of the downwelling core (Fig. 3).
3.2 Baseline 2D and 3D reactive transport simulations of dolomitisation
The low convective flux of Mg2+-rich fluid (seawater) means that, despite the high temperature (>185 ∘C), dolomitisation in the 2D, fault-perpendicular model is very limited, with replacement of <0.05 volume fraction of the calcite within 30 kyr. Minor dolomitisation occurs where surface-derived fluids enter the reactive aquifer (“D1” in Fig. 2d) and also adjacent to the FDZ at 2.3–3 km depth (“D2” in Fig. 2d). For the 2D fault-parallel model, an even smaller amount (<0.005 volume fraction) of dolomite forms at the base of the ascending limbs of the free-convection cells close to the basement. Although there is a high convective flux of Mg2+-rich fluid, the associated cooling (<72 ∘C) means that dolomitisation is limited by sluggish kinetics. This illustrates the importance of having both a sufficient flux of Mg2+ and temperatures hot enough to overcome kinetic barriers to dolomitisation.
The 3D simulations show how a free-convection system developed within the FDZ of a simple planar fault could result in the flux of Mg2+-rich seawater across strong thermal gradients and drive dolomitisation. Reactions are largely confined to within the plane of the fault (Fig. 3), although convection also drives some exchange of fluids between the FDZ and the matrix. Flow rates within the matrix are 1–2 orders of magnitude less than those within the FDZ, yet flow from the upper part of the aquifer into the fault (at 1–2.1 km depth) is critical to maintaining temperatures within the FDZ that are kinetically favourable to dolomitisation. This “top-down” circulation of seawater drives the replacement of calcite by dolomite, reflected in a steep decline in Mg2+ along the flow path in areas of active dolomitisation within the FDZ, mirrored by an increase in Ca2+ (Fig. 4). The activity of these ions is a complex function of the effect of water–rock interaction and that of mixing between seawater and basement fluid.
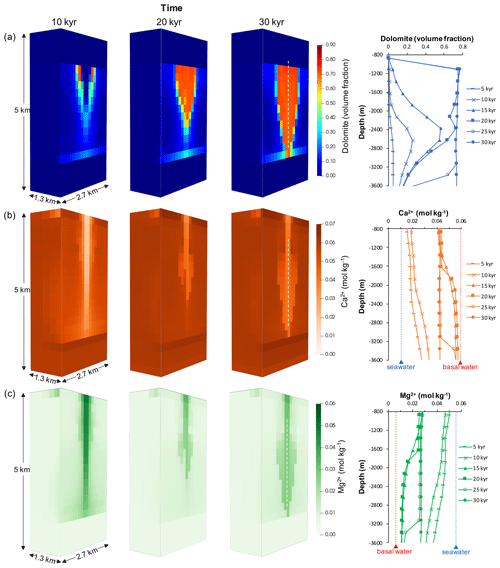
Figure 4Temporal evolution of the dolomite volume fraction (a), the Ca2+ concentration (b), and the Mg2+ concentration (c) from the 3D baseline simulation, and plots of those changes down the core of the descending limb of the convection cell within the FDZ (white dashed line). Ca2+ is enriched relative to seawater, and Mg2+ is depleted as a result of the replacement of precursor limestone by dolomite. After complete replacement, there is a minor decrease in the concentrations of both Mg2+ and Ca2+ due to dolomite cementation.
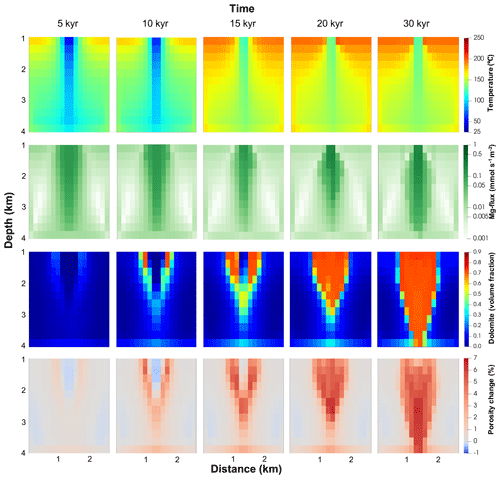
Figure 5Temporal evolution of temperature, Mg2+-flux (fluid flux × Mg2+ concentration), dolomite abundance (volume %), and change from initial porosity (volume %) along the fault plane for the 3D baseline simulation after 5, 10, 15, 20, and 30 kyr. Two separate dolomite geobodies start to form in the FDZ in the upper part of the aquifer, with large areas where more than half the calcite has been replaced by dolomite. Over time, with dolomitisation, these merge to a single massive dolomite body with relatively sharp dolomitisation fronts. The downwelling core is initially a zone of minor calcite cementation, but the dominance of replacement dolomite over dolomite cementation results in an increase in porosity of up to 7 %.
Replacement of calcite by dolomite leads to an increase in porosity of up to 7 %, controlled by the difference in molar volume between dolomite and calcite (Fig. 5). Dolomitisation initiates at a depth of 1–2 km in the FDZ, either side of the descending limb of the convection cell, where the temperature exceeds 75 ∘C. In these areas the precursor calcite is completely replaced by dolomite within 9 kyr, with a commensurate increase in porosity. Replacement dolomitisation occurs as a gradient reaction, driven by Mg2+-rich fluids flowing from cooler to warmer areas. There is minimal alteration of the surrounding matrix, even at very high temperatures (>200 ∘C in the rising limb of the convection cell), because there is insufficient flux of Mg2+-rich fluid. The dolomite front extends laterally over time, reaching a limit of 1 km from the centre of the downwelling limb. At depths >2 km within the descending limb of the convection cell, dolomitisation initially occurs at a slower rate during the period when dolomitisation “up-flow” at shallower depths consumes Mg2+. After 15 kyr, the fluids circulating to depth are less depleted in Mg2+, and complete dolomitisation gradually extends to the base of the aquifer. In addition, there is late-stage replacement of calcite in the core of the downwelling limb where low temperatures initially limited reaction rate.
Figure 6 illustrates the importance of temperature and fluid flux in controlling patterns and rates of dolomitisation at contrasting locations. There are sharp lateral differences in dolomite abundance within the shallow FDZ (1–2 km depth), with a change from 8 % to 70 % dolomite between adjacent grid cells (150 m model resolution). Where dolomite first develops, temperatures are >100 ∘C (Location B), and dolomitisation occurs at a rate of up to 10 % kyr−1 at simulation times of 3–10 kyr following an initial 1 kyr induction period of slower dolomitisation. The temperature is slightly higher 0.6 km further along the flow path at Location C, but here the dolomitisation rate is no more than 1.4 % kyr−1 within the entire simulation period, reflecting the relatively low Mg2+-flux. Dolomitisation occurs most rapidly at Location B, reflecting the ample supply of Mg2+ from seawater, paired with a sufficiently high temperature (Fig. 5). Dolomitisation within the downwelling zone at the same depth (Location A) is very limited for the first 13 kyr, and only initiates after temperatures start to increase in response to the influx of hot waters from the matrix (which leads to a doubling of heat flux from 13 to 30 kyr). Dolomite abundance decreases more gradually with depth (Fig. 6), and further insights into the behaviour of the system are provided by comparing locations at different depths in the downwelling core. Here the higher temperature at depth results in more dolomite forming in the early stages of the simulation (compare locations A, D, and E). However, dolomitisation occurs more slowly at depth, limited by the lower flux of Mg2+.
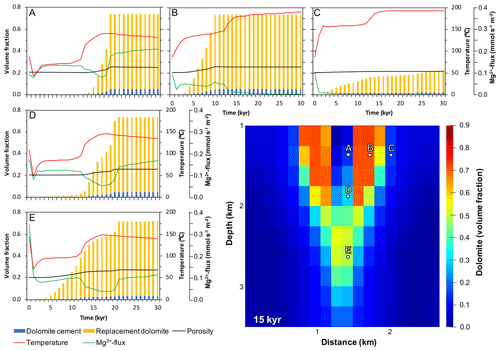
Figure 6Dolomitisation, Mg2+-flux, temperature, and porosity change in the FDZ, at locations vertically along the descending flow path (A–D–E) and laterally with distance from the core (A–B–C). Note how replacement dolomitisation is initially limited by the low temperature in the “up-flow” margin of the dolomite body (A), whereas reactions are limited by Mg2+-flux in the “down-flow” margin (C).
3.3 Role of porosity–permeability feedbacks in controlling patterns of dolomitisation
Most dolomite forms by replacement of calcite, with the associated increase in porosity moderated only slightly by precipitation of a minor amount of dolomite cement. Once all calcite has been replaced, dolomite formation continues but at a very slow rate (0.015 % kyr−1). Dolomite cement represents a minor percentage (<8 %) of the total dolomite at shallow depth (locations A and B) and decreases with depth (to 5 % at Location E) due to the lower Mg2+-flux. The baseline 3D simulation incorporates feedbacks between diagenetically controlled changes in porosity, estimated permeability, heat and solute transport, and reactions. An increase in porosity of 5.4 % which results from the complete replacement of calcite by dolomite increases the permeability by a factor of 2. One impact of this in the upper aquifer is that the later-stage dolomitisation occurs within the core of the descending limb of the convection cells due to the increased transfer of heat from the matrix. In contrast, in a 3D simulation with no porosity–permeability feedback (Fig. 7) the distribution of temperature and fluid flux do not evolve with time. The total discharge of hot fluid from the FDZ to the ocean floor amounts to 7.63×106 m3 yr−1 (reduced by 9 % relative to the baseline simulation with the porosity–permeability feedback incorporated). In absolute terms, the volume of recirculated seawater is higher, but this is outweighed by the reduction in fluids from the basement which represent 70 % of the total discharge (compared with 81 % in the baseline simulation). The result is that the FDZ in the shallow aquifer remains un-dolomitised within the descending limb of the convection cell in the simulation in which there is no increase in permeability driven by replacement dolomitisation (or reduction due to dolomite cements).
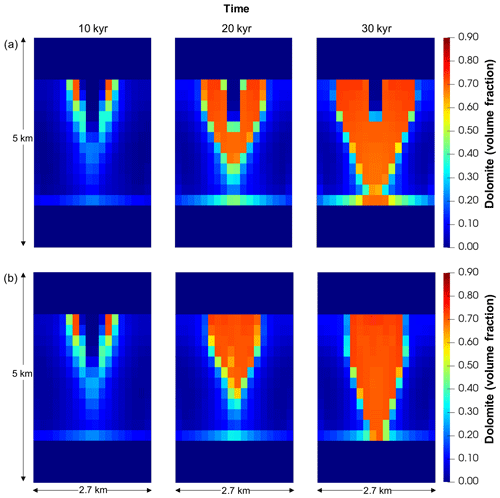
Figure 7Development of the dolomite geobody within the FDZ cutting along the middle of the fault plane: (a) the 3D simulation with the porosity–permeability feedback turned off, and (b) the baseline 3D simulation that includes feedback between porosity and permeability that results in localised advection of heat from the matrix and dolomitisation in the downwelling core.
3.4 Sensitivity of dolomitisation by geothermal convection of seawater to basement and caprock properties
Reducing permeability of the basement from 10−15 m2 (≈ 1 mD) to m2 (≈0.5 mD) and m2 (≈ 0.1 mD) significantly reduces the flux of both fluid and heat from the basement, with a drop in the maximum Darcy velocity within the FDZ from 280 m yr−1 to 155 and 64 m yr−1 respectively. This results in a rather broader zone of descending flow and a more focused discharge zone (Fig. 8). The total discharge of hot fluid from the FDZ to the ocean floor is 3.64×106 and 8.28×105 m3 yr−1 respectively, or 44 % and 10 % that of the baseline simulation. Halving the permeability of basement, the influx of seawater into the FDZ is 16 % higher, but there is a substantial (72 %) decrease in total volumetric fluid flux from the basement (Fig. 8). For a basement that is 10 times less permeable, there is a 58 % reduction in the seawater descending into the FDZ and a 97 % reduction in the basal fluid flux. Temperatures in the fault plane are lower due to reduced heat transfer from the basement to the aquifer and, subsequently, from the matrix to the fault zone. The temperature within the FDZ is consequently lower, with a broad (600 m) zone of cool (<80 ∘C) waters extending to the base of the aquifer and laterally in the FDZ within the lower part of the aquifer. There is also a reduced heat transfer from the basement into the aquifer matrix and, subsequently, to the FDZ in the upper part of the aquifer. The result of these differences is a considerably smaller volume of dolomite in the FDZ compared with the 3D baseline simulation, with only partial dolomitisation below 1750 m depth and a less sharp dolomite front in the zone of ascending flow than seen in the baseline model. There is also a marked difference in dolomite distribution, with dolomite forming in the ascending limb of the convection cell where the temperature exceeds 100 ∘C; however, as in all 3D simulations, reactions are constrained to within the FDZ. Dolomitisation occurs at temperatures lower than in the baseline simulation, ranging from 155 ∘C down to a minimum of 73 ∘C where dolomitisation rates are low. With a 90 % lower permeability basement, the very low basal heat flux and temperature significantly limit dolomitisation within FDZ (Fig. 8c).
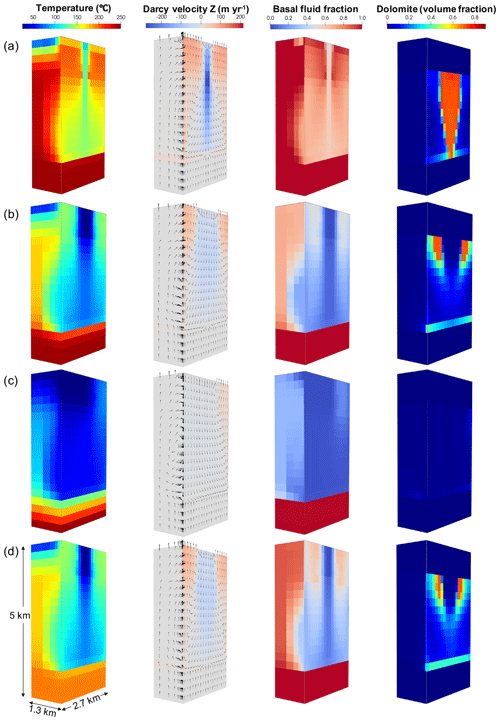
Figure 8Simulation results at 30 kyr from (a) the baseline 3D model, (b) the 50 % lower permeability basement model ( m2), (c) the 90 % lower permeability basement model (10−16 m2), and (d) the baseline model with a lower basal temperature (200 ∘C) showing heat transfer and fluid flow (black arrows), the distribution of dolomitisation, and the basal fluid fraction. The orientation of the panels is identical to Figs. 3 and 4. Darcy velocities are positive when the flow is upward and negative when the flow is downward. The lower heat flux with either a less permeable basement or lower basal temperature (200 ∘C) results in cooler conditions, lower fluid flux, and smaller dolomite bodies forming in zones of upwelling rather than a single large dolomite body in the zone of descending flow.
Reducing the temperature at the base of the model from 250 ∘C (baseline model) to 200 ∘C decreases the flux of both fluid and heat from the basement (Fig. 8d). As in the lower-permeability basement models, descending flow occurs within a broader zone and discharge is more focused than in the baseline simulation. The total discharge of hot fluid from the FDZ to the ocean floor is 55 % that of the baseline simulation (4.56×106 m3 yr−3), with a reduction in total volumetric fluid flux from the basement of 54 % (Fig. 9). This reduction in heat transfer from the basement to the aquifer and, subsequently, from the matrix to the FDZ results in a cooler FDZ. Dolomitisation within the FDZ is very limited below 75 ∘C, generating an un-dolomitised core in the zone of descending seawater, and rarely exceeds 50 % dolomite below 2000 km depth. The rate of dolomitisation is lower and dolomite fronts are more diffuse both laterally and vertically along the fault plane. Whilst the basement properties influenced dolomitisation via control on the transfer of both heat and fluid, the sensitivity of the system to caprock permeability seems negligible. There is no significant effect on fluid circulation, temperature, or dolomite distribution by reducing the permeability of caprock from 10−15 m2 in the baseline model to m2 or m2 (Figs. 9, 10).
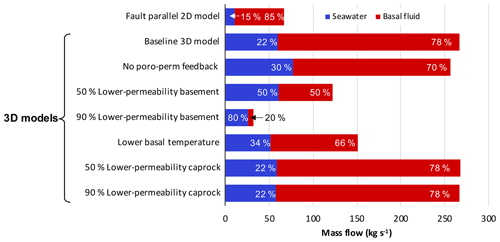
Figure 9Total discharge to the sea floor from simulations of geothermal convection within the FDZ, differentiating between the contributions of seawater drawn down into the fault-damage zone (FDZ) and basal fluid.
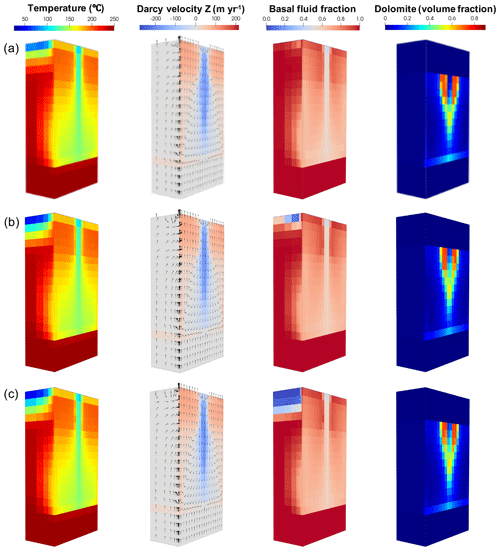
Figure 10Simulation results at 15 kyr from (a) the baseline 3D model, (b) the 50 % lower permeability caprock model ( m2), and (c) the 90 % lower permeability caprock model (10−16 m2) showing no significant difference in heat transfer, fluid flow (black arrows), distribution of dolomitisation, or basal fluid fraction. The orientation of panels is identical to Figs. 4 and 8. Note that the Darcy velocities are positive when the flow is upward and negative when the flow is downward.
It has been more than 35 years since Land (1985) recognised that seawater is the only widely available fluid with the capacity to form extensive bodies of replacement dolomite, although reaction kinetics can limit the rate of dolomitisation at near-surface temperatures (Arvidson and Mackenzie, 1999). Recent geochemical studies (Ryb and Eiler, 2018; Shalev et al., 2019) have presented isotopic data consistent with large-scale dolomitisation by convection of seawater through carbonate sediments. In contrast, a major focus of sedimentological research over the last decade has been to understand the genesis of dolostones developed along extensional or transtensional fault systems. Many of these dolomites form at high temperatures and, thus, are generally assumed to be formed from fluids that originate at depth. Release and upward escape of fluids from deep aquifers has become the dominant paradigm (Davies and Smith, 2006), despite considerable debate over the physical and chemical basis for this model and the extent to which it can account for dolomitisation of surrounding limestone (Machel, 2004; Machel and Lonnee, 2002; Robertson et al., 2015).
4.1 Comparing RTM predictions with fault-related dolomites
Whilst recognising the simplifications inherent in this narrow subset of possible 3D models, our aim is simply to evaluate the potential of the new conceptual model for fault-related high-temperature dolomitisation and capture the essence of such a system. Thus, it is important to compare the simulation results with available data describing these dolostones at outcrops. Data extracted from RTM simulations include the dimensions and position of dolomite geobodies within the permeability field, the extent to which alteration extends beyond the FDZ into the matrix, and, less commonly, the nature of reaction fronts. Outcrops provide a snapshot of dolomitisation at the time that reactions ceased, but models can provide time series maps of the development of simulated diagenetic geobodies. Rarely explored is the potential of RTM simulations to provide metrics that relate to the properties of the dolomitising fluids (temperature, salinity, and elemental concentrations and ratios) and can be directly compared with spatial variations in the geochemical and isotopic characteristics of the dolomites. In this example, we have illustrated the further insight offered from tracking changes in temperature through the progress of the reaction at specific locations, and the difficulties in interpreting evidence of such changes from the rock record alone.
4.1.1 Dolomite geobody dimensions
For a FDZ with vertical and along-fault permeability 2 orders of magnitude greater than that of the country rock, our simulations suggest dolomitisation would be constrained almost entirely within the plane of the fault. In the matrix, reactions are limited not by temperature, but by the low flux of Mg2+. Note that, sensu stricto, dolomite in the FDZ could be classified as hydrofrigid rather than hydrothermal, as the temperatures at which it forms are lower – rather than higher – than that of the country rock (Machel and Lonnee, 2002). As the free-convection system draws cool seawater down from the surface, the transfer of heat from the matrix to the FDZ contributes to dolomitisation. Here, we do not investigate systems with sufficient matrix permeability to give the potential for significant fluid flow between the matrix and the FDZ, and the rates of diffusion are insufficient to allow for dolomitisation. However, even in such scenarios, with a transmissive FDZ providing direct connectivity between overlying seawater and the geothermal heat source at depth, the drive for dolomitisation of rocks more than a few tens of metres from the FDZ is likely limited. An exception could be where a permeable matrix may allow hydraulic continuity between two or more faults, such as across a relay ramp, allowing for the development of a single-pass convection system.
The baseline simulation suggests that, for a high basal heat flux, vertically extensive dolomite bodies could form and, over time, extend laterally, merging to form a single body that might extend for >1 km along the plane of the fault. In comparison, with a lower heat flux, dolomite bodies form at a shallower depth, and these are more limited vertically and extend only a few hundred metres along the fault. This pattern of dolomitisation focused in zones within the uppermost part of the limestones sequence beneath a barrier or baffle to flow is consistent with observations in the subsurface by Smith et al. (2008) in the Trenton and Black River formations. Comparing our generic 3D simulations with the fault-controlled dolostone bodies of the Hammam Faraun Fault described by Hollis et al. (2017) and Hirani et al. (2018) shows marked geometric similarities. The dolostone bodies are constrained to the FDZ of the Hammam Faraun Fault, postdating earlier strata-bound dolostones within Eocene limestone country rock. Whilst the outcrop provides limited information about the vertical extent of the dolostone bodies (which exceed the 75–80 m height of the outcrop), they extend for up to 500 m along the plane of the fault. Similarly, fault-related dolostones in the Ranero area, northwest Spain, that extend >1 km and are defined by sharp contact within the host Aptian–Albian limestone (Dewit et al., 2012; Nader et al., 2012; Shah et al., 2012).
4.1.2 Dolomitisation timescales
Our simulations suggest that, for the combination of heat flux and permeability geometry that has been simulated, complete replacement of limestones can occur within the FDZ within a timescale of thousands to a few tens of thousands of years (Fig. 4). The unlimited supply of Mg2+ from seawater, coupled with a high geothermal heat flux in tectonically active or rifting settings, enables much more rapid reactions than suggested by previous RTM simulations of fault-controlled diagenesis that propose timescales ranging from 60 kyr to a few million years, even assuming more favourable kinetics (Abarca et al., 2019; Consonni et al., 2018; Corbella et al., 2014). Our model simulates a single event lasting a few tens of thousands of years within a fault that retains its transmissivity, but many outcrop studies suggest multiple episodes of fluid flow, each with the potential to recrystallise the previous dolomite. For example, in Hammam Faraun, Sr-isotope dating suggests that the massive dolomite formed over a 10 Myr period but likely within multiple episodes during which fault zone permeability permitted more active circulation (Hirani et al., 2018; Hollis et al., 2017). Fault transmissivity is dynamic, and the movement of large quantities of fluids within faults during earthquakes via “seismic pumping” has been linked to submarine hydrothermal mineralisation that is episodic on timescales ranging from a minutes to tens of thousands of years and is controlled by volcanic and tectonic processes (Brantut, 2020; Sibson, 2001; Sibson et al., 1975). Data on permeability changes over longer timescales are sparse (Ingebritsen and Gleeson, 2017), but the reconstruction of episodic hydrothermal flow along the Malpais Fault in Nevada suggests either intermittent fluid pulses that lasted ≈1 kyr or continuous flow that shifted in location every 1 kyr (Louis et al., 2019). Such timescales are not incompatible with those of dolomitisation suggested by our generic simulations.
4.1.3 Characterisation of dolomite fronts
Our rather simplistic simulations are not designed to evaluate the characteristics of realistic dolomite fronts within the FDZ, given the large size of the model cells both vertically and along the fault as well as the associated requirement to use effective permeabilities for cells which are known to be both highly heterogeneous and temporally variable. It would be rewarding to further explore suggestions from these simulations that at early times, and with low heat flux, large areas of the fault-bound geobody remain only partially dolomitised, particularly at depth. The model also raises important questions about contrasts between dolomite fronts in different areas of the flow system depending on whether reactions are flux or reaction rate limited. We predict that the character of the dolomite front varies between the margins that receive unmodified seawater (here termed the “up-flow” margins) and those where fluids flow out of the dolomite body (“down-flow margins”). Sharper dolomite fronts (complete alteration across a single model cell) occur in the “up-flow” dolomite front where dolomitisation is kinetically limited (Mg2+-rich fluids first reach the threshold temperature for dolomitisation). In comparison, the “down-flow” dolomite front tends to be broader, as rates here are flux-limited as a result of the depletion of Mg2+ by upstream dolomitisation. Reaction fronts perpendicular to the plane of the fault, where the model resolution is also higher, are within a single 10 m wide cell. This is in the same order of magnitude as those predicted by 2D simulations of HTDs formed by flow along through-going faults (Yapparova et al., 2017) as well as many field examples with sharp dolomitisation fronts (Grandia et al., 2003; Nurkhanuly and Dix, 2014; Shah et al., 2012). Detailed analysis of dolomitisation fronts within fault-controlled dolomite bodies in nature are remarkably understudied, however, and are likely complex; for example, Koeshidayatullah et al. (2020b) show that reaction fronts can back-step in time, as progressive phases of recrystallisation result in porosity reduction (over-dolomitisation), restricting the extent to which subsequent fluids can flux away from the fault. An obvious benefit of flow simulations such as these is that they can provide information on the controls on dolomite body termination during the earliest phases of fluid flux, before the porosity–permeability feedback becomes an important control on the extent of fluid migration and reaction.
4.1.4 Linking RTM output to dolomite geochemistry and isotopic characteristics
In addition to evaluating the concept of fault-related dolomitisation by hydrothermal seawater circulation, we hope to illustrate the insights offered by a more forensic analysis of simulation data. Specifically, changes in the temperature and chemistry of fluids during the dolomitisation process can be extracted from RTM output for a more meaningful comparison between simulations and paragenetic sequences recorded in the rock record. The contrast between two simple simulations performed at higher heat flux (baseline) and lower heat flux (reduced basement permeability) demonstrates the sensitivity of geobody size and location within the convection cell, as well as the robustness of other characteristics.
The temperature of dolomitisation across much of the dolomite body in the baseline simulation is relatively high and tightly constrained (120–150 ∘C) at depth (1–2 km). This is slightly higher but comparable to the range for the spatially more restricted dolomite bodies that form in the lower heat flux simulation (100–135 ∘C), reflecting the dominant role of temperature in controlling reaction rate. However, there are also contrasts between the core and the more marginal areas of the dolomite body, which are clear from the baseline simulation. Within the “up-flow” part of the dolomite body, dolomitisation initially occurs at considerably lower temperatures (80–100 ∘C) (e.g. locations D and E, Fig. 11), with a step change to higher temperature as the percentage of dolomite increases. Similarly, there is a sudden increase in the dolomitisation temperature in the “down-flow” margins, although here it is from ≈160 to ≈190 ∘C (e.g. Location C, Fig. 11). These changes occur at the same time, reflecting shifts in patterns of heat and solute transport that occur in response to diagenetic changes in porosity and permeability.
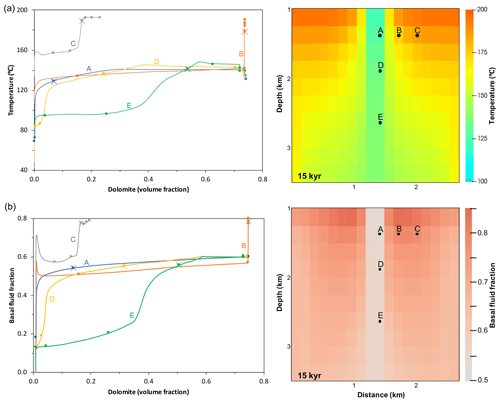
Figure 11(a) Temperature of dolomitising fluid during reaction progress at selected locations in the FDZ in the baseline 3D simulation, with lateral distance from the downwelling core (A–B–C) and vertical distance through the core (A–D–E). Locations are shown on the temperature distribution at 15 kyr. Circles represent 5 kyr intervals, with a cross to mark 15 kyr, midway through the simulation. (b) The basal fluid fraction of dolomitising fluid during reaction progress at locations A–E in the FDZ in the baseline 3D simulation. Dolomites record lower temperatures and basal fluid fraction in the core of the downwelling limb and higher temperatures and basal fluid fraction towards the upwelling limb of the convection cell. Locations where dolomite forms more slowly also show a step change in temperature with the addition of more warm water derived from the basement and delivered via the matrix as dolomitisation increases permeability in the FDZ.
The incorporation of an unreactive tracer (Br−) to our RTM allows us to evaluate the relative contribution of basal fluids and seawater (Figs. 2, 3). Chemical differences in the two fluids (Table 2), along with contrasting boundary water temperatures (250 and 25 ∘C respectively), determine their respective role in the formation of the fault-constrained dolomite bodies. Dolomite bodies develop where hydrothermal fluids are mixtures of seawater and basal fluid. Where basal fluids comprise less than half of the fluid, any dolomite that forms in the model does so very slowly. The largest volume of dolomites form from a mixture comprising 59 %–60 % basal fluid, and dolomite formed during the later stages of the simulation records up to 80 % basal fluids in some areas. The association between basally derived fluids, identified from distinctive geochemical and/or isotopic signatures, and high-temperature fault-related dolomite is one commonly observed in the rock record and is generally interpreted to indicate that there is a chemical drive for dolomitisation that is associated with the input of fluid from a deep aquifer (Al-Aasm, 2003; Boni et al., 2000; Davies and Smith, 2006; Luczaj et al., 2006). The RTM clearly calls this assumption into question, as the source of Mg2+ for dolomitisation is from the fraction of the fluid derived from the surface seawater. Instead, the basal fluid controls heat transport within the aquifer and the FDZ by advection, and thus temperature distribution. Therefore, the basal fluid plays a critical role in providing the heat required for relatively rapid formation of dolomite but is not critical to the supply of Mg2+ for dolomitisation. The geochemical and isotopic signatures of the resulting dolomites would reflect the component of basement-derived fluids. We might expect, for instance, to see mixing trends between a 87Sr ∕ 86Sr signature of downwelling fluids reflective of the seawater values, ∼ 0.7068–0.70907 (Burke et al., 1982), and more radiogenic basin-derived fluids. Fluid inclusion and isotope analysis from several studies suggest that the dolomitising fluid might be formed by an evolved seawater or its interaction with rocks and/or other fluids (Gomez-Rivas et al., 2014; Jacquemyn et al., 2014; López-Horgue et al., 2010).
When the porosity–permeability feedback is not implemented in the model, the temperature and basal fluid fraction remain constant through the simulation. With this feedback implemented, the evolution of thermal and chemical conditions for dolomitisation during reaction progress is a clear example of emergent behaviour, arising from the dynamic nature of the coupled system. However, because of spatial differences in the dolomitisation rate, this behaviour would be recorded at different stages within the paragenetic sequence of the dolomites at different locations in a natural dolomite. Thus, simulations help to explain complexities in defining a unique paragenetic sequence within some large, natural dolomite bodies.
We suggest that these thermal and geochemical trends are likely to be robust, irrespective of uncertainties in dolomite kinetics, although assumptions about reaction rates will affect the absolute temperatures (and, thus, basal fluid fractions) recorded in the simulated dolomites, as will differences in the composition of fluids modelled. Even relatively minor evaporative concentration of the overlying seawater will significantly lower the temperature of dolomitisation (Al-Helal et al., 2012; Gabellone and Whitaker, 2016). Thus, clumped isotope analyses suggesting temperatures <100 ∘C for the massive dolostone developed in the Hammam Faraun Fault (Hirani et al., 2018) could suggest formation from mesohaline seawater; this is not unreasonable as dolomitisation has been dated to the Miocene, when the Gulf of Suez was undergoing desiccation and evaporite precipitation (Hollis et al., 2017). Temperatures predicted from our simple models are consistent with fluid inclusion homogenisation temperatures of most dolomite formed in the Trenton and Black River groups (85–160 ∘C; Smith et al., 2008) and are more similar to those reported for fault-related dolomites in the Ranero area in northern Spain (120–200 ∘C; Shah et al., 2010) which are interpreted to form during multiphase dolomitisation, potentially at variable salinities of up to 22 wt % NaCl (López-Horgue et al., 2010). Numerous other studies combining petrographic, isotopic, and fluid inclusion analysis support the suggestion that HTDs with multiple populations of temperature and fluid composition are likely to be the norm. For example, Luczaj et al. (2006) report fluid inclusion temperatures of 120–150 ∘C in the HTD of the Devonian Dundee Formation of the Michigan Basin, with an average 21 ∘C difference between the interior and outer zone of individual dolomite crystals reflecting the episodic fault-controlled transport of fluids and heat which is interpreted to originate from the deeper basin. Koeshidayatullah et al. (2020a) demonstrated complex geochemical proxies within the Mount Whyte Formation in the West Canada Sedimentary Basin, suggestive of mixing between seawater and deep crustal fluids, resulting in dolomite precipitated at high temperature (>200 ∘C) from very high-salinity, metal-enriched fluids at shallow depths. This highlights the need for further work to evaluate the impact of changing composition of the end-member fluids, as well as the effect of solute concentration on density-driven circulation, which is driven solely by differences in fluid temperature in this simulation.
4.2 Model limitations and new insights from simulations of dolomitisation by hydrothermal convection of seawater
Systems that are governed by interactions between heat and solute transport and water–rock interaction are challenging to predict or quantify a priori (Ingebritsen et al., 2010). Numerical simulations that represent the coupled nature of these processes can reveal emergent behaviour that is governed by relationships between these separate components. Thus, they offer a route to evaluate conceptual models of complex systems. However, model results are inevitably affected by the chosen geometry and permeability of the system which controls solute flux and heat transport and, thus, the rate and distribution of reactions.
Simulations of structurally complex reservoirs are particularly challenging as they comprise discrete structures with properties that contrast strongly with those of the country rock and range over vastly different length scales (Matthäi et al., 2007). Variations in permeability and fault zone thickness are fundamental controls on fluid circulation and subsequent mineralisation distribution (Guillou-Frottier et al., 2020; Harcouët-Menou et al., 2009), whereas the effect on hydrothermal convection of other parameters, such as porosity, is considerably less significant (Gow et al., 2002; Kühn et al., 2006; Zhao et al., 2003). However, our models do not attempt to capture the complexities of flow within FDZs, for which the porous media formulation employed by TOUGHREACT is inappropriate. We also do not consider how the permeability of the FDZ may change due to geomechanical responses to variations in the stress field that are localised in time and space nor the physical and chemical effects of changes in state of the fluid, for example, due to boiling. Rather, we simply demonstrate that, where major discontinuities provide high-permeability pathways for flow, it is possible for interaction between heat supplied from the basement and Mg2+-rich seawaters from above to form high-temperature fault-bound dolomite bodies in high-enthalpy settings. The magnitude and anisotropy of permeability, as well as the effective reactivity, of the country rock will also influence the extent to which this fault-associated convection system could form dolomites in the adjacent matrix or, alternatively, might drive recrystallisation of a dolomite precursor formed during earlier diagenesis.
Although this model deals solely with seawater and an equivalent salinity basal fluid, there is a clear opportunity now to evaluate the reactions that occur within convective systems involving basal fluids of different geochemical characteristics and densities as well as to investigate alternative surface water compositions. More complex mineral assemblages should also be investigated, both in terms of host-rock mineralogy and diagenetic minerals that may form. Our simple simulations incorporating the effect of replacement dolomitisation on permeability demonstrate the importance of better understanding the impact of the full range of both physical and chemical controls on the evolving permeability. They also offer three substantive lessons with implications that extend beyond the contentious realm of genesis of HTD.
Firstly, although our generic models are very simple, they robustly demonstrate that, under the conditions simulated, high-temperature fault-controlled dolostone bodies can form by seawater convection. Mg2+-rich seawater is drawn downward into the permeable damage zone around a fault that extends to shallow depth, mixing with hot buoyant fluids escaping from the basement. Dolomitisation occurs within the FDZ as a gradient reaction, with the replacement of host limestones and minor dolomite cementation as circulating fluids flow across isotherms. Fluids from the basement play an important role in transporting heat into the FDZ, but the Mg2+ to drive dolomitisation comes from the entrained seawater even though this is <50 % and locally <20 % of the fluid within the FDZ. Thus, our reactive transport simulations reconcile the apparently contradictory observations that on the one hand identify geochemical and isotopic signatures for basement fluids in many high-temperature dolomites, and on the other hand indicate that almost all basement fluids are depleted in Mg2+ and, therefore, do not have the potential for dolomitisation.
Secondly, comparison of our 3D baseline model with simplifications in 2D, both perpendicular and parallel to the plane of the FDZ, illustrate how 2D models fail to represent critical aspects of system behaviour (Fig. 2a–h). The alignment of convective flow with fault planes has long been recognised (López and Smith, 1995, 1996; Murphy, 1979) and is supported by recent 3D thermal models of the Upper Rhine Graben (Armandine Les Landes et al., 2019) that show good agreement between simulated and predicted thermal anomalies. Our RTM simulations show that 2D models oriented perpendicular to the fault cannot represent the convection that occurs along the plane of the fault within the permeable damage zone, which is key to generating massive fault-constrained dolostone bodies. It is likely that prior simulations using such 2D models oriented perpendicular to the plane of the fault (Corbella et al., 2014; Frixa et al., 2014; Jones and Xiao, 2013; Xiao et al., 2013) misrepresent these important aspects of reactions driven by the circulation of fluid along the fault plane. Therefore, they might not explain the diagenetic evolution of fault-guided diagenetic reactions well, specifically overestimating the influence of fault-controlled fluid convection control on the adjacent matrix. Circulation within the FDZ is seen in the 2D model oriented along the plane of the fault (Fig. 2e–h). However, because this model fails to account for the effect of heat transfer between the matrix and the FDZ, the system appears to have been too cool for significant dolomitisation in this case. Our clear conclusion is that numerical analysis of systems where faults impact permeability must be conducted in 3D, and this has important implications for modelling a range of systems, from geothermal resources and mineralisation fluid to carbonate diagenesis, including dolomitisation and hydrothermal karstification.
Finally, dolomitisation associated with the hydrothermal and geothermal circulation of seawater has been suggested as an important but poorly constrained sink for Mg in seawater (Shalev et al., 2019). Thus, these processes have fundamental implications for understanding the global budgets of Mg, Ca, and C, which are linked by the common controls of weathering, volcanism, and carbonate precipitation (Arvidson et al., 2011; Elderfield, 2010; Holland, 2005). Combining recent magnesium isotope (26Mg) data for low-temperature hydrothermal fluids with evidence of a constant 26Mg over the past 20 Myr, Shalev et al. (2019) suggest that there is a significant unexplained flux of Mg from the modern ocean (estimated at 1.5–2.9 Tmol yr−1). Mg mass balance calculations for our simple generic models suggest that the dolomitisation that results from this mixed convection system within permeable fault zones may provide a sink for 2.0 × 107–2.6 × 107 mol Mg yr−1 for each kilometre of fault. At such rates, in order to account for all the cryptic dolomite identified by Mg-isotope studies, such a system would need to be established along total fault length of 60 × 103–150 × 103 km. For comparison, the East African Rift system extends some 6.4×103 km, with extension accommodated by numerous intra-rift faults in addition to those bordering the rift (Shillington et al., 2020, and references therein). This suggests that Mg drawdown by fault-related dolomitisation in areas of very high localised heat flux may be significant, but it is likely to be subsidiary to dolomitisation driven by geothermal (“Kohout”) convection within platform carbonates. The absence of permeable conduits or high basal heat flux mean much lower rates of dolomitisation in these systems (Whitaker and Xiao, 2010), but this is amply compensated for by the vast area of major carbonate platform systems globally (currently some 800 000 km2 of low-latitude oceans; Milliman, 1993). Further resolution of these fluxes is key to critically assessing the role of dolomitisation relative to weathering and seafloor spreading in determining secular changes in the Mg∕Ca of global ocean (Hardie, 1996; Holland and Zimmermann, 2000; Shalev et al., 2019).
Hydrothermal dolomitisation has been synonymous with dolomitisation driven by release of over-pressured fluids from depth, but our simulations offer another potential interpretation. An alternative concept considers that high-temperature dolomite could replace a precursor limestone where seawater is drawn down into a convection system that is developed within a steep high-permeability conduit during periods of high heat flux. Such a scenario may be most likely developed in extensional basins, when faults breach the seafloor and geothermal gradients are elevated. Evaluating this concept using 2D and 3D reactive transport simulations shows that when a deep-seated permeable fault extends to the sea floor, the influx of high-Mg2+ ∕ Ca2+ seawaters can drive replacement of calcite by dolomite with only minor dolomite cementation. The rate of advective transfer of heat by basally derived fluids relative to that of cold seawater from above will determine the distribution of dolomite within the flow field and the size of the dolomite geobodies that form within the convective cell. This new model provides one solution to the Mg2+ mass balance problems inherent in HTD formation by release of hot over-pressured fluids from a deep reservoir. It may also explain at least some of the missing Mg2+ from the world's oceans. The new insights and key conclusions from our study include the follows:
-
RTM simulations suggest that convection of seawater that leads to a mixture of hot basal fluids and seawater along the FDZ can form sizable (102–103 m) fault-bound dolomite bodies within timescales of thousands of years in high-enthalpy settings.
-
Reactions are largely confined to within the FDZ, and dolomitisation occurs at temperatures of 80–160 ∘C and from fluids that comprise a significant (>0.5, and locally >0.8) fraction of basally derived fluids.
-
Modification of porosity and permeability during diagenesis can lead to systematic changes in the temperature and fraction of basal fluid in the hydrothermal mixture as progress of the reaction that may be recorded in the paragenetic sequence.
-
A permeable fault damage zone provides a corridor along which fluids will preferentially flow. As this is not represented in 2D simulations perpendicular to the plane of the fault such model construction is fundamentally inappropriate and could result in misleading suggestions (e.g. about the extent of the associated alteration of the country rock).
-
Heat transfer between the fault zone and country rock plays an important role in contributing to dolomitisation within the FDZ which cannot be observed using 2D simulations along the plane of the fault.
3D RTM simulations can enhance understanding of the mechanisms and controls on dolomitisation within faulted and fractured systems, and the geometry and spatial distribution of the resulting high-temperature dolomite geobodies. RTMs offer insights into temporal evolution of reactions, and an opportunity to examine not only the geometry of diagenetic geobodies and the nature of reaction fronts but also a broader range of metrics that can be directly related to isotopic and geochemical characteristics of diagenetic products. Critically, numerical analysis of systems where faults impact permeability must be conducted in 3D, and this has important implications for the modelling of systems ranging from geothermal resources to ore formation and carbonate diagenesis, including hydrothermal karstification as well as dolomitisation.
In our experiments we used TOUGHREACT, a numerical simulation program developed by the Lawrence Berkeley National Laboratory (LBNL) which is available at https://tough.lbl.gov/software/toughreact (Sonnenthal et al., 2017, last access: 5 December 2020). The output files from TOUGHREACT are visualised using trexplot, a Python script developed by Hamish Robertson which can be found at https://github.com/hammytheham/trexplot (Robertson and Benjakul, 2019, last access: 5 December 2020). The output data from all simulation models in this article are available at https://doi.org/10.5281/zenodo.4312236 (Benjakul et al., 2020, last access: 8 December 2020).
FFW and RB wrote the article and designed and developed the conceptual model and experiments. Model construction, simulations, and analyses were conducted by RB under the supervision of FFW. ELS provided technical support with the TOUGHREACT simulator. HAR offered advice on the initial model construction and developed a Python script, trexplot, for TOUGHREACT data visualisation. CH, ELS, and HAR gave advice, feedback, and comments on the paper.
The authors declare that they have no conflict of interest.
Rungroj Benjakul is supported by a scholarship from Chiang Mai University, and this work was also partially supported by a joint industry project, PD3 (Prediction of Deposition, Deformation and Diagenesis in Carbonates). We are very grateful to the reviewers, Mercè Corbella and Taury Smith, for carefully reading our paper and providing us with valuable feedback.
This paper was edited by Kei Ogata and reviewed by Merce Corbella and Taury Smith.
Abarca, E., Idiart, A., Grandia, F., Rodríguez-Morillas, N., Pellan, C., Zen, M., Aït-Ettajer, T., and Fontanelli, L.: 3D reactive transport modeling of porosity evolution in a carbonate reservoir through dolomitization, Chem. Geol., 513, 184–199, https://doi.org/10.1016/j.chemgeo.2019.03.017, 2019.
Agemar, T., Schellschmidt, R., and Schulz, R.: Subsurface temperature distribution in Germany, Geothermics, 44, 65–77, https://doi.org/10.1016/j.geothermics.2012.07.002, 2012.
Al-Aasm, I.: Origin and characterization of hydrothermal dolomite in the Western Canada Sedimentary Basin, J. Geochem. Explor., 78/79, 9–15, https://doi.org/10.1016/S0375-6742(03)00089-X, 2003.
Al-Helal, A. B., Whitaker, F. F., and Xiao, Y.: Reactive transport modeling of brine reflux: dolomitization, anhydrite precipitation, and porosity evolution, J. Sediment. Res., 82, 196–215, https://doi.org/10.2110/jsr.2012.14, 2012.
Armandine Les Landes, A., Guillon, T., Peter-Borie, M., Blaisonneau, A., Rachez, X., and Gentier, S.: Locating Geothermal Resources: Insights from 3D Stress and Flow Models at the Upper Rhine Graben Scale, Geofluids, 2019, 1–24, https://doi.org/10.1155/2019/8494539, 2019.
Arvidson, R. S. and Mackenzie, F. T.: The dolomite problem, control of precipitation kinetics by temperature and saturation state, Am. J. Sci., 299, 257–288, https://doi.org/10.2475/ajs.299.4.257, 1999.
Arvidson, R. S., Guidry, M. W., and Mackenzie, F. T.: Dolomite Controls on Phanerozoic Seawater Chemistry, Aquat. Geochem., 17, 735–747, https://doi.org/10.1007/s10498-011-9130-7, 2011.
Bear, J.: Dynamics of fluids in porous media, available at: https://www.academia.edu/3367245/Dynamics_of_fluids_in_porous_media (last access: 6 December 2019), 1972.
Benjakul, R., Hollis, C., Robertson, H., Sonnenthal, E., and Whitaker, F.: Output Files from Reactive Transport Models (supplement to Solid Earth Manuscript “se-2020-99”), Zenodo, https://doi.org/10.5281/zenodo.4312236, 2020.
Boni, M., Parente, G., Bechstädt, T., De Vivo, B., and Iannace, A.: Hydrothermal dolomites in SW Sardinia (Italy): evidence for a widespread late-Variscan fluid flow event, Sediment. Geol., 131, 181–200, https://doi.org/10.1016/S0037-0738(99)00131-1, 2000.
Bonté, D., Wees, J.-D., and van Verweij, J. M.: Subsurface temperature of the onshore Netherlands: new temperature dataset and modelling, Netherlands J. Geosci.-Czech, 91, 491–515, https://doi.org/10.1017/S0016774600000354, 2012.
Brantut, N.: Dilatancy-induced fluid pressure drop during dynamic rupture: Direct experimental evidence and consequences for earthquake dynamics, Earth Planet. Sci. Lett., 538, 116179, https://doi.org/10.1016/j.epsl.2020.116179, 2020.
Breislin, C., Crowley, S., Banks, V. J., Marshall, J. D., Millar, I. L., Riding, J. B., and Hollis, C.: Controls on dolomitization in extensional basins: An example from the Derbyshire Platform, UK, J. Sediment. Res., 90, 1156–1174, https://doi.org/10.2110/jsr.2020.58, 2020.
Burke, W. H., Denison, R. E., Hetherington, E. A., Koepnick, R. B., Nelson, H. F., and Otto, J. B.: Variation of seawater 87Sr ∕ 86Sr throughout Phanerozoic time, Geology, 10, 516–519, https://doi.org/10.1130/0091-7613(1982)10<516:VOSSTP>2.0.CO;2, 1982.
Carmichael, S. K. and Ferry, J. M.: Formation of replacement dolomite in the Latemar carbonate buildup, Dolomites, northern Italy: Part 2, Origin of the dolomitizing fluid and the amount and duration of fluid flow, Am. J. Sci., 308, 885–904, https://doi.org/10.2475/08.2008.01, 2008.
Consonni, A., Ronchi, P., Geloni, C., Battistelli, A., Grigo, D., Biagi, S., Gherardi, F., and Gianelli, G.: Application of numerical modelling to a case of compaction-driven dolomitization: a Jurassic palaeohigh in the Po Plain, Italy, Sedimentology, 57, 209–231, https://doi.org/10.1111/j.1365-3091.2009.01103.x, 2010.
Consonni, A., Frixa, A., and Maragliulo, C.: Hydrothermal dolomitization: simulation by reaction transport modelling, J. Geol. Soc. Spec. Publ., 435, 235–244, https://doi.org/10.1144/SP435.13, 2018.
Corbella, M., Gomez-Rivas, E., Martín-Martín, J. D., Stafford, S. L., Teixell, A., Griera, A., Travé, A., Cardellach, E., and Salas, R.: Insights to controls on dolomitization by means of reactive transport models applied to the Benicàssim case study (Maestrat Basin, eastern Spain), Pet. Geosci., 20, 41–54, https://doi.org/10.1144/petgeo2012-095, 2014.
Costa, A.: Permeability-porosity relationship: A reexamination of the Kozeny-Carman equation based on a fractal pore-space geometry assumption, Geophys. Res. Lett., 33, L02318, https://doi.org/10.1029/2005GL025134, 2006.
Davies, G. R. and Smith, L. B.: Structurally controlled hydrothermal dolomite reservoir facies: An overview, AAPG Bull., 90, 1641–1690, https://doi.org/10.1306/05220605164, 2006.
Dewit, J., Huysmans, M., Muchez, P., Hunt, D. W., Thurmond, J. B., Verges, J., Saura, E., Fernandez, N., Romaire, I., Esestime, P., and Swennen, R.: Reservoir characteristics of fault-controlled hydrothermal dolomite bodies: Ramales Platform case study, J. Geol. Soc. Spec. Publ., 370, 83–109, https://doi.org/10.1144/SP370.1, 2012.
Ehrenberg, S. N., Eberli, G. P., Keramati, M., and Moallemi, S. A.: Porosity-permeability relationships in interlayered limestone-dolostone reservoirs, AAPG Bull., 90, 91–114, https://doi.org/10.1306/08100505087, 2006.
Elderfield, H.: Seawater Chemistry and Climate, Science, 327, 1092–1093, https://doi.org/10.1126/science.1186769, 2010.
Frazer, M., Whitaker, F., and Hollis, C.: Fluid expulsion from overpressured basins: Implications for Pb–Zn mineralisation and dolomitisation of the East Midlands platform, northern England, Mar. Pet. Geol., 55, 68–86, https://doi.org/10.1016/j.marpetgeo.2014.01.004, 2014.
Frixa, A., Maragliulo, C., Consonni, A., and Ortenzi, A.: Dolomitization of the lacustrine carbonates of the Toca Fm. (Kambala field, offshore Cabinda) and quantitative diagenetic modeling, in: Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 10–13 November 2014, ID: SPE-171960-MS, 2014.
Gabellone, T. and Whitaker, F.: Secular variations in seawater chemistry controlling dolomitization in shallow reflux systems: insights from reactive transport modelling, Sedimentology, 63, 1233–1259, https://doi.org/10.1111/sed.12259, 2016.
Gabellone, T., Whitaker, F., Katz, D., Griffiths, G., and Sonnenfeld, M.: Controls on reflux dolomitisation of epeiric-scale ramps: Insights from reactive transport simulations of the Mississippian Madison Formation (Montana and Wyoming), Sediment. Geol., 345, 85–102, https://doi.org/10.1016/j.sedgeo.2016.09.003, 2016.
Garcia-Fresca, B.: Outcrop-constrained flow and transport models of reflux dolomitization, PhD thesis, The University of Texas at Austin, USA, available at: https://repositories.lib.utexas.edu/handle/2152/10627 (last access: 5 March 2020), 2009.
Ge, S. and Garven, G.: A theoretical model for thrust-induced deep groundwater expulsion with application to the Canadian Rocky Mountains, J. Geophys. Res.-Sol. Ea., 99, 13851–13868, https://doi.org/10.1029/94JB00687, 1994.
Gomez-Rivas, E., Corbella, M., Martín-Martín, J. D., Stafford, S. L., Teixell, A., Bons, P. D., Griera, A., and Cardellach, E.: Reactivity of dolomitizing fluids and Mg source evaluation of fault-controlled dolomitization at the Benicàssim outcrop analogue (Maestrat basin, E Spain), Mar. Pet. Geol., 55, 26–42, https://doi.org/10.1016/j.marpetgeo.2013.12.015, 2014.
Gow, P. A., Upton, P., Zhao, C., and Hill, K. C.: Copper-gold mineralisation in New Guinea: Numerical modelling of collision, fluid flow and intrusion-related hydrothermal systems, Aust. J. Earth Sci., 49, 753–771, https://doi.org/10.1046/j.1440-0952.2002.00945.x, 2002.
Grandia, F., Cardellach, E., Canals, À., and Banks, D. A.: Geochemistry of the Fluids Related to Epigenetic Carbonate-Hosted Zn-Pb Deposits in the Maestrat Basin, Eastern Spain: Fluid Inclusion and Isotope (Cl, C, O, S, Sr) Evidence, Econ. Geol., 98, 933–954, https://doi.org/10.2113/gsecongeo.98.5.933, 2003.
Gregg, J. M.: Basin fluid flow, base-metal sulphide mineralization and the development of dolomite petroleum reservoirs, J. Geol. Soc. Spec. Publ., 235, 157–175, https://doi.org/10.1144/GSL.SP.2004.235.01.07, 2004.
Guillou-Frottier, L., Duwiquet, H., Launay, G., Taillefer, A., Roche, V., and Link, G.: On the morphology and amplitude of 2D and 3D thermal anomalies induced by buoyancy-driven flow within and around fault zones, Solid Earth, 11, 1571–1595, https://doi.org/10.5194/se-11-1571-2020, 2020.
Gvirtzman, H., Garven, G., and Gvirtzman, G.: Hydrogeological modeling of the saline hot springs at the Sea of Galilee, Israel, Water Resour. Res., 33, 913–926, https://doi.org/10.1029/96WR03191, 1997a.
Gvirtzman, H., Garven, G., and Gvirtzman, G.: Thermal anomalies associated with forced and free ground-water convection in the Dead Sea rift valley, GSA Bull., 109, 1167–1176, https://doi.org/10.1130/0016-7606(1997)109<1167:TAAWFA>2.3.CO;2, 1997b.
Haeri-Ardakani, O., Al-Aasm, I., and Coniglio, M.: Petrologic and geochemical attributes of fracture-related dolomitization in Ordovician carbonates and their spatial distribution in southwestern Ontario, Canada, Mar. Pet. Geol., 43, 409–422, https://doi.org/10.1016/j.marpetgeo.2012.12.006, 2013.
Harcouët-Menou, V., Guillou-Frottier, L., Bonneville, A., Adler, P. M., and Mourzenko, V.: Hydrothermal convection in and around mineralized fault zones: insights from two- and three-dimensional numerical modeling applied to the Ashanti belt, Ghana, Geofluids, 9, 116–137, https://doi.org/10.1111/j.1468-8123.2009.00247.x, 2009.
Hardie, L. A.: Secular variation in seawater chemistry: An explanation for the coupled secular variation in the mineralogies of marine limestones and potash evaporites over the past 600 m.y., Geology, 24, 279–283, https://doi.org/10.1130/0091-7613(1996)024<0279:SVISCA>2.3.CO;2, 1996.
Hirani, J., Bastesen, E., Boyce, A., Corlett, H., Eker, A., Gawthorpe, R., Hollis, C., Korneva, I., and Rotevatn, A.: Structural controls on non fabric-selective dolomitization within rift-related basin-bounding normal fault systems: Insights from the Hammam Faraun Fault, Gulf of Suez, Egypt, Basin Res., 30, 990–1014, https://doi.org/10.1111/bre.12290, 2018.
Holland, H. D.: Sea level, sediments and the composition of seawater, Am. J. Sci., 305, 220–239, https://doi.org/10.2475/ajs.305.3.220, 2005.
Holland, H. D. and Zimmermann, H.: The Dolomite Problem Revisited1, Int. Geol. Rev., 42, 481–490, https://doi.org/10.1080/00206810009465093, 2000.
Hollis, C., Bastesen, E., Boyce, A., Corlett, H., Gawthorpe, R., Hirani, J., Rotevatn, A., and Whitaker, F.: Fault-controlled dolomitization in a rift basin, Geology, 45, 219–222, https://doi.org/10.1130/G38s394.1, 2017.
Ingebritsen, S. and Gleeson, T.: Crustal permeability, Hydrogeol. J., 25, 2221–2224, https://doi.org/10.1007/s10040-017-1663-4, 2017.
Ingebritsen, S. E., Geiger, S., Hurwitz, S., and Driesner, T.: Numerical simulation of magmatic hydrothermal systems, Rev. Geophys., 48, RG1002, https://doi.org/10.1029/2009RG000287, 2010.
Jacquemyn, C., El Desouky, H., Hunt, D., Casini, G., and Swennen, R.: Dolomitization of the Latemar platform: Fluid flow and dolomite evolution, Mar. Pet. Geol., 55, 43–67, https://doi.org/10.1016/j.marpetgeo.2014.01.017, 2014.
Jasim, A., Whitaker, F. F., and Rust, A. C.: Impact of channelized flow on temperature distribution and fluid flow in restless calderas: Insight from Campi Flegrei caldera, Italy, J. Volcanol. Geotherm. Res., 303, 157–174, https://doi.org/10.1016/j.jvolgeores.2015.07.029, 2015.
Jones, G. D. and Xiao, Y.: Dolomitization, anhydrite cementation, and porosity evolution in a reflux system: Insights from reactive transport models, AAPG Bull., 89, 577–601, https://doi.org/10.1306/12010404078, 2005.
Jones, G. D. and Xiao, Y.: Geothermal convection in South Atlantic subsalt lacustrine carbonates: Developing diagenesis and reservoir quality predictive concepts with reactive transport modelsGeothermal Convection and Diagenesis in Lacustrine Carbonates, AAPG Bull., 97, 1249–1271, https://doi.org/10.1306/02191312162, 2013.
Kaufman, J.: Numerical models of fluid flow in carbonate platforms, implications for dolomitization, J. Sediment. Res., 64, 128–139, https://doi.org/10.1306/D4267D2F-2B26-11D7-8648000102C1865D, 1994.
Koeshidayatullah, A., Corlett, H., Stacey, J., Swart, P. K., Boyce, A., Robertson, H., Whitaker, F., and Hollis, C.: Evaluating new fault-controlled hydrothermal dolomitization models: Insights from the Cambrian Dolomite, Western Canadian Sedimentary Basin, Sedimentology, 67, 2945–2973, https://doi.org/10.1111/sed.12729, 2020a.
Koeshidayatullah, A., Corlett, H., Stacey, J., Swart, P. K., Boyce, A., and Hollis, C.: Origin and evolution of fault-controlled hydrothermal dolomitization fronts: A new insight, Earth Planet. Sc. Lett., 541, 116291, https://doi.org/10.1016/j.epsl.2020.116291, 2020b.
Kühn, M., Dobert, F., and Gessner, K.: Numerical investigation of the effect of heterogeneous permeability distributions on free convection in the hydrothermal system at Mount Isa, Australia, Earth Planet. Sc. Lett., 244, 655–671, https://doi.org/10.1016/j.epsl.2006.02.041, 2006.
Land, L. S.: The Origin of Massive Dolomite, J. Geol. Educ., 33, 112–125, https://doi.org/10.5408/0022-1368-33.2.112, 1985.
López, D. L. and Smith, L.: Fluid Flow in Fault Zones: Analysis of the Interplay of Convective Circulation and Topographically Driven Groundwater Flow, Water Resour. Res., 31, 1489–1503, https://doi.org/10.1029/95WR00422, 1995.
López, D. L. and Smith, L.: Fluid flow in fault zones: Influence of hydraulic anisotropy and heterogeneity on the fluid flow and heat transfer regime, Water Resour. Res., 32, 3227–3235, https://doi.org/10.1029/96WR02101, 1996.
López-Horgue, M. A., Iriarte, E., Schröder, S., Fernández-Mendiola, P. A., Caline, B., Corneyllie, H., Frémont, J., Sudrie, M., and Zerti, S.: Structurally controlled hydrothermal dolomites in Albian carbonates of the Asón valley, Basque Cantabrian Basin, Northern Spain, Mar. Pet. Geol., 27, 1069–1092, https://doi.org/10.1016/j.marpetgeo.2009.10.015, 2010.
Louis, S., Luijendijk, E., Dunkl, I., and Person, M.: Episodic fluid flow in an active fault, Geology, 47, 938–942, https://doi.org/10.1130/G46254.1, 2019.
Luczaj, J. A., Harrison, W. B., and Williams, N. S.: Fractured hydrothermal dolomite reservoirs in the Devonian Dundee Formation of the central Michigan Basin, AAPG Bull., 90, 1787–1801, https://doi.org/10.1306/06270605082, 2006.
Machel, H. G.: Concepts and models of dolomitization: a critical reappraisal, J. Geol. Soc. Spec. Publ., 235, 7–63, https://doi.org/10.1144/GSL.SP.2004.235.01.02, 2004.
Machel, H. G. and Lonnee, J.: Hydrothermal dolomite – a product of poor definition and imagination, Sediment. Geol., 152, 163–171, https://doi.org/10.1016/S0037-0738(02)00259-2, 2002.
Matthäi, S. K., Geiger, S., Roberts, S. G., Paluszny, A., Belayneh, M., Burri, A., Mezentsev, A., Lu, H., Coumou, D., Driesner, T., and Heinrich, C. A.: Numerical simulation of multi-phase fluid flow in structurally complex reservoirs, J. Geol. Soc. Spec. Publ., 292, 405–429, https://doi.org/10.1144/SP292.22, 2007.
Milliman, J. D.: Production and accumulation of calcium carbonate in the ocean: Budget of a nonsteady state, Global Biogeochem. Cy., 7, 927–957, https://doi.org/10.1029/93GB02524, 1993.
Murphy, H. D.: Convective instabilities in vertical fractures and faults, J. Geophys. Res.-Sol. Ea., 84, 6121–6130, https://doi.org/10.1029/JB084iB11p06121, 1979.
Nader, F. H., López-Horgue, M. A., Shah, M. M., Dewit, J., Garcia, D., Swennen, R., Iriarte, E., Muchez, P., and Caline, B.: The Ranero Hydrothermal Dolomites (Albian, Karrantza Valley, Northwest Spain): Implications on Conceptual Dolomite Models, Oil Gas Sci. Technol., 67, 9–29, https://doi.org/10.2516/ogst/2011165, 2012.
Nield, D. A.: Onset of Thermohaline Convection in a Porous Medium, Water Resour. Res., 4, 553–560, https://doi.org/10.1029/WR004i003p00553, 1968.
Nordstrom, D. K., Plummer, L. N., Wigley, T. M. L., Wolery, T. J., Ball, J. W., Jenne, E. A., Bassett, R. L., Crerar, D. A., Florence, T. M., Fritz, B., Hoffman, M., Holdren, G. R., Lafon, G. M., Mattigod, S. V., McDuff, R. E., Morel, F., Reddy, M. M., Sposito, G., and Thrailkill, J.: A Comparison of Computerized Chemical Models for Equilibrium Calculations in Aqueous Systems, in: Chemical Modeling in Aqueous Systems, Vol. 93, edited by: Jenne, E. A., American Chemical Society, Washington, DC, USA, 857–892, 1979.
Nurkhanuly, U. and Dix, G. R.: Hydrothermal Dolomitization of Upper Ordovician Limestone, Central-East Canada: Fluid Flow in a Craton-Interior Wrench-Fault System Likely Driven by Distal Taconic Tectonism, J. Geol., 122, 259–282, https://doi.org/10.1086/675666, 2014.
Oliver, J.: Fluids expelled tectonically from orogenic belts: Their role in hydrocarbon migration and other geologic phenomena, Geology, 14, 99–102, https://doi.org/10.1130/0091-7613(1986)14<99:FETFOB>2.0.CO;2, 1986.
Person, M. and Garven, G.: A sensitivity study of the driving forces on fluid flow during continental-rift basin evolution, Geol. Soc. Am. Bull., 106, 461–475, https://doi.org/10.1130/0016-7606(1994)106<0461:ASSOTD>2.3.CO;2, 1994.
Qing, H. and Mountjoy, E. W.: Formation of Coarsely Crystalline, Hydrothermal Dolomite Reservoirs in the Presqu'ile Barrier, Western Canada Sedimentary Basin, AAPG Bull., 78, 55–77, https://doi.org/10.1306/BDFF9014-1718-11D7-8645000102C1865D, 1994.
Robertson, H.: The search for fluids with HTD potential, in: 15th Bathurst Meeting of Carbonate Sedimentologists, Edinburgh, United Kingdom, 13–16 July 2015, 95–96, 2015.
Robertson, H. and Benjakul, R.: trexplot, available at: https://github.com/hammytheham/trexplot/ (last access: 5 December 2020), 2019.
Ryb, U. and Eiler, J. M.: Oxygen isotope composition of the Phanerozoic ocean and a possible solution to the dolomite problem, P. Natl. Acad. Sci. USA, 115, 6602–6607, https://doi.org/10.1073/pnas.1719681115, 2018.
Salas, J., Taberner, C., Esteban, M., and Ayora, C.: Hydrothermal dolomitization, mixing corrosion and deep burial porosity formation: numerical results from 1-D reactive transport models, Geofluids, 7, 99–111, https://doi.org/10.1111/j.1468-8123.2006.00167.x, 2007.
Shah, M. M., Nader, F. H., Dewit, J., Swennen, R., and Garcia, D.: Fault-related hydrothermal dolomites in Cretaceous carbonates (Cantabria, northern Spain): Results of petrographic, geochemical and petrophysical studies, Bull. Soc. Geol. Fr., 181, 391–407, https://doi.org/10.2113/gssgfbull.181.4.391, 2010.
Shah, M. M., Nader, F. H., Garcia, D., Swennen, R., and Ellam, R.: Hydrothermal Dolomites in the Early Albian (Cretaceous) Platform Carbonates (NW Spain): Nature and Origin of Dolomites and Dolomitising Fluids, Oil Gas Sci. Technol., 67, 97–122, https://doi.org/10.2516/ogst/2011174, 2012.
Shalev, N., Bontognali, T. R. R., Wheat, C. G., and Vance, D.: New isotope constraints on the Mg oceanic budget point to cryptic modern dolomite formation, Nat. Commun., 10, 1–10, https://doi.org/10.1038/s41467-019-13514-6, 2019.
Sharp, I., Gillespie, P., Morsalnezhad, D., Taberner, C., Karpuz, R., Vergés, J., Horbury, A., Pickard, N., Garland, J., and Hunt, D.: Stratigraphic architecture and fracture-controlled dolomitization of the Cretaceous Khami and Bangestan groups: an outcrop case study, Zagros Mountains, Iran, J. Geol. Soc. Spec. Publ., 329, 343–396, https://doi.org/10.1144/SP329.14, 2010.
Shillington, D. J., Scholz, C. A., Chindandali, P. R. N., Gaherty, J. B., Accardo, N. J., Onyango, E., Ebinger, C. J., and Nyblade, A. A.: Controls on Rift Faulting in the North Basin of the Malawi (Nyasa) Rift, East Africa, Tectonics, 39, e2019TC005633, https://doi.org/10.1029/2019TC005633, 2020.
Sibson, R. H.: Seismogenic framework for hydrothermal transport and ore deposition, Rev. Econ. Geol., 14, 25–50, 2001.
Sibson, R. H., Moore, J. M. M., and Rankin, A. H.: Seismic pumping – a hydrothermal fluid transport mechanism, J. Geol. Soc., 131, 653–659, https://doi.org/10.1144/gsjgs.131.6.0653, 1975.
Simms, M. A. and Garven, G.: Thermal convection in faulted extensional sedimentary basins: theoretical results from finite-element modeling, Geofluids, 4, 109–130, https://doi.org/10.1111/j.1468-8115.2004.00069.x, 2004.
Smith, T., Nyahay, R., and Group, R. C.: Widespread Hydrothermal Dolomitization of Trenton and Black River Groups, Eastern North America, AAPG Annual Convention, 20–23 April 2008, San Antonio, Texas, USA, 2008.
Sonnenthal, E. L., Spycher, N., and Xu, T.: TOUGHREACT V3.32-OMP, available at: https://tough.lbl.gov/software/toughreact/ (last access: 22 May 2020), 2017.
Steefel, C. I. and Lasaga, A. C.: A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems, Am. J. Sci., 294, 529–592, https://doi.org/10.2475/ajs.294.5.529, 1994.
Weissenberger, J. A. W., Wierzbicki, R. A., and Harland, N. J.: Carbonate Sequence Stratigraphy and Petroleum Geology of the Jurassic Deep Panuke Field, Offshore Nova Scotia, Canada, AAPG Memoir, 88, 395–431, https://doi.org/10.1306/1215883M883275, 2006.
Whitaker, F. F. and Xiao, Y.: Reactive transport modeling of early burial dolomitization of carbonate platforms by geothermal convection, AAPG Bull., 94, 889–917, https://doi.org/10.1306/12090909075, 2010.
Whitaker, F. F., Smart, P. L., and Jones, G. D.: Dolomitization: from conceptual to numerical models, J. Geol. Soc. Spec. Publ., 235, 99–139, https://doi.org/10.1144/GSL.SP.2004.235.01.05, 2004.
Wilson, A. M., Sanford, W., Whitaker, F., and Smart, P.: Spatial Patterns of Diagenesis during Geothermal Circulation in Carbonate Platforms, Am. J. Sci., 301, 727–752, https://doi.org/10.2475/ajs.301.8.727, 2001.
Wilson, M. E. J., Evans, M. J., Oxtoby, N. H., Nas, D. S., Donnelly, T., and Thirlwall, M.: Reservoir quality, textural evolution, and origin of fault-associated dolomites, AAPG Bull., 91, 1247–1272, https://doi.org/10.1306/05070706052, 2007.
Xiao, Y., Jones, G. D., Whitaker, F. F., Al-Helal, A. B., Stafford, S., Gomez-Rivas, E., and Guidry, S.: Fundamental Approaches to Dolomitization and Carbonate Diagenesis in Different Hydrogeological Systems and the Impact on Reservoir Quality Distribution, in: International Petroleum Technology Conference, Beijing, China, 26–28 March 2013, ID: IPTC 16579, 2013.
Xu, T., Sonnenthal, E., Spycher, N., and Pruess, K.: TOUGHREACT User's Guide: A Simulation Program for Non-isothermal Multiphase Reactive geochemical Transport in Variable Saturated Geologic Media, Lawrence Berkeley National Lab. (LBNL), Berkeley, CA, US, https://doi.org/10.2172/834237, 2004.
Xu, T., Spycher, N., Sonnenthal, E., Zhang, G., Zheng, L., and Pruess, K.: TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions, Comput. Geosci., 37, 763–774, https://doi.org/10.1016/j.cageo.2010.10.007, 2011.
Yapparova, A., Gabellone, T., Whitaker, F., Kulik, D. A., and Matthäi, S. K.: Reactive transport modelling of hydrothermal dolomitisation using the CSMPGEM coupled code: Effects of temperature and geological heterogeneity, Chem. Geol., 466, 562–574, https://doi.org/10.1016/j.chemgeo.2017.07.005, 2017.
Zhao, C., Hobbs, B. E., Mühlhaus, H. B., Ord, A., and Lin, G.: Convective instability of 3-D fluid-saturated geological fault zones heated from below, Geophys. J. Int., 155, 213–220, https://doi.org/10.1046/j.1365-246X.2003.02032.x, 2003.





