Yttrium speciation in subduction-zone fluids from ab initio molecular dynamics simulations

The rare Earth elements (REEs) are important geochemical tracers for geological processes such as high-grade metamorphism. Aqueous fluids are considered important carriers for the REEs in a variety of geological environments including settings associated with subduction zones. The capacity of a fluid to mobilize REEs strongly depends on its chemical composition and on the presence of suitable ligands such as fluoride and chloride. In this study, we present structural and thermodynamic properties of aqueous yttrium–chloride and yttrium–fluoride species at a temperature of 800 ^∘C in a pressure range between 1.3 and 4.5 GPa derived from ab initio molecular dynamics simulations. The total yttrium coordination by H₂O and halide ions changes from seven to eight within the pressure range. For the yttrium–chloride species, a maximum number of three chloride ligands was observed. The derived thermodynamic data show that aqueous yttrium–fluoride complexes are more stable than their yttrium–chloride counterparts in chloride- and fluoride-rich environments at conditions relevant to slab dehydration. Mixed Y(Cl,F) complexes are found to be unstable even on the molecular dynamics timescale. Furthermore, in contrast to field observations, thermodynamic modeling indicates that yttrium should be mobilized at rather low fluoride concentrations in high-grade metasomatic systems. These results suggest a rather low fluoride activity in the majority of subduction-zone fluids because yttrium is one of the least-mobile REEs. Additionally, the simulations indicate that yttrium drives the self-ionization of hydration water molecules as it was observed for other high-field-strength elements. This might be a general property for highly charged cations in aqueous solutions under high-temperature and high-pressure conditions.

1 Introduction

Subduction zones have been the most important sites for exchange of matter and energy between the Earth's crust and mantle for billions of years until now (Tang et al., 2016). Magnetotelluric anomalies (e.g., Worzewski et al., 2011; McGary et al., 2014) suggest the occurrence of a high proportion of melts and water-rich fluids in the subducted slabs due to partial melting (Zheng et al., 2016) and the dehydration of water-bearing minerals such as serpentine (Ulmer and Trommsdorff, 1995) and amphibole (Schmidt and Poli, 1998). Quite naturally, these fluids do not consist of pure water; much rather, they are brines with high salinity up to several mass percent of Cl (Métrich and Wallace, 2008; Newton and Manning, 2010) and contain Si, Al and alkali cations (Na, K) as major solutes with minor amounts of Ca, Fe and Mg (Manning, 2004; Hermann et al., 2013).

Aqueous fluids play an important role in subduction zones. Their interaction with minerals and rocks results in alterations including the dissolution and precipitation of minerals and/or the exchange of chemical elements and isotopes. Furthermore, fluid-mediated transport of trace elements such as high-field-strength elements (HFSEs) and rare Earth elements (REEs) is a major process of the deep element cycles (Manning, 2004). The distribution of these elements between minerals and fluids or melts is used as petrogenetic indicator for fractionation processes in igneous and metasomatic petrology (Winter, 2009). It is known that REE patterns of subducted rocks are affected by the chemical composition of the metamorphic fluid (e.g., John et al., 2008; Zhang et al., 2008) due to their chemical complexation with dissolved anions, e.g., F⁻, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, ${\mathrm{CO}}_{\mathrm{3}}^{\mathrm{2}-}$ and Cl⁻ (Tsay et al., 2014, 2017; Alt et al., 1993; Scambelluri and Philippot, 2001; Newton and Manning, 2010).

The speciation of REEs at moderate pressures (up to few 100 MPa) and high temperatures (250–300 ^∘C) was studied experimentally using in situ X-ray absorption spectroscopy (XAS) and solubility experiments (see a recent review by Migdisov et al., 2016) to understand physicochemical properties of hydrothermal fluids related to REE ore deposition focusing on chloride and fluoride complexes. Due to the high stability of fluoride complexes (Wood, 1990; Haas et al., 1995), it is a widely shared notion that fluoride complexes are most important for REE transport in hydrothermal fluids, but Migdisov and Williams-Jones (2014) suggested that REE fluoride complexes are not the major carrier of REEs due to the low solubility of REE fluoride minerals such as bastnaesite, $(\mathrm{Ce},\mathrm{La},\mathrm{Nd},\mathrm{Y})\left[{\mathrm{FCO}}_{\mathrm{3}}\right]$, and due to the low fluoride activity in low pH environments. According to Migdisov and Williams-Jones (2014), REE chloride and sulfate complexes appear to be the main species for REE transport in hydrothermal systems. However, this interpretation is questioned by other authors (Xing et al., 2018).

So far, the number of in situ studies that address the complexation or thermodynamic properties of REE aqueous species at pressure (P) and temperature (T) conditions of subduction zones is very limited due to the challenging experimental setups (Sanchez-Valle, 2013). Apart from field observations (e.g., fluid inclusion analysis), our main understanding of the behavior of REEs under high P∕T conditions is derived from fluid/mineral partitioning and solubility experiments (e.g., Bali et al., 2012; Keppler, 1996; Tsay et al., 2014; Keppler, 2017) and from numerical simulations. In a case study, van Sijl et al. (2009) modeled the hydration shell of REEs in solution by static energy calculations of an explicit first hydration shell and an implicit solvent model. Temperature effects were introduced by considering changes of the dielectric constant of the solvent and by calculations of the entropy. In this study, it is concluded that the hydration energies of all lanthanides become more similar at high P∕T conditions and that the availability of ligands becomes a controlling factor for the fractionation of light REEs (LREEs) and heavy REEs (HREEs) by subduction-zone fluids. Experiments suggest that LREEs (e.g., La) are more mobile than HREEs in chloride-rich solutions (Tropper et al., 2011; Tsay et al., 2014). The presence of fluoride in the system enhances the mobility of HREEs and this leads to fractionation processes (Tropper et al., 2013).

From a geochemical perspective, yttrium is considered a HREE¹, and as such it is very common to use yttrium as a representative of the whole group of HREEs because of their similar chemical properties. Further, the comparable behavior of Y and the majority of the HREEs in high-grade metasomatism processes (Ague, 2017) supports this assumption. The hydration shell of Y³⁺ in aqueous solutions and possible complexation of Y³⁺ with chloride has been subject to a number of studies at room temperature (e.g., Johansson and Wakita, 1985; Petrović et al., 2016). Molecular simulations in conjunction with advanced sampling methods indicate that in the absence of other ligands Y³⁺ is coordinated by eight hydration water molecules (Ikeda et al., 2005a, b), whereas at high pH [Y(OH)₃(H₂O)₃]_aq complexes are formed (Liu et al., 2012). The reported Y–O distance of 2.38 Å (Ikeda et al., 2005b) agrees with extended X-ray absorption fine structure (EXAFS) and X-ray absorption near edge structure (XANES) measurements (Näslund et al., 2000; Lindqvist-Reis et al., 2000).

The complexation of Y³⁺ with Cl⁻ was studied by Vala Ragnarsdottir et al. (1998) at hydrothermal conditions up to 340 ^∘C using in situ EXAFS spectroscopy. The authors claim that yttrium is coordinated by eight to nine neighbors at hydrothermal conditions and does not associate with chloride but rather forms polyatomic yttrium species. In another study by Mayanovic et al. (2002), a strong association of Y with chloride up to ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ at 500 ^∘C and a linear reduction of the total number of coordinating atoms from eight to four towards high temperatures are reported. The results of that study indicate that yttrium behaves like 3d transition metal ions rather than a HREE under hydrothermal conditions at high chloride activity. Solubility experiments up to 1 GPa and 800 ^∘C in a hydrothermal piston-cylinder apparatus performed by Tropper et al. (2013, 2011) indicate that yttrium is transported as [YClOH]⁻ complexes in NaCl brines and that ${\mathrm{YF}}_{\mathrm{2}}^{+}$ is the major complex in a fluorine-rich environment.

While the stability and distribution of $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ species in aqueous solutions at ambient conditions have been subject to a number of studies (e.g., Luo and Byrne, 2001, 2000, 2007), the knowledge of thermodynamic properties of yttrium species in hydrothermal fluids is limited to theoretical predictions (Haas et al., 1995; Wood, 1990) based on regressions using the Helgeson–Kirkham–Flowers (HKF) model (Helgeson et al., 1981) and one experimental study by Loges et al. (2013). Stability constants of Y−Cl and Y−F complexes at subcrustal high P∕T conditions have been barely investigated.

The capacity of a fluid to mobilize a certain element or to dissolve a certain amount of a component in the fluid depends on the chemical potential of the formed aqueous complexes (Anderson, 2009; Dolejš, 2013). For a better understanding of the mobility of Y (as a representative of the HREE group) in subduction-zone fluids at high P∕T conditions, knowledge of the relation between the concentration of the molecular species in aqueous fluids and their thermodynamic properties is required. Yttrium in general is one of the most immobile REEs (Ague, 2017; Schmidt et al., 2007b) in high-grade metasomatic environments. But the high mobility in certain locations not only associated with hydrothermal ore deposits (McPhie et al., 2011; Graupner et al., 1999) but also in metamorphic or diagenetic context (Hole et al., 1992; Moore et al., 2013; Harlov et al., 2006) indicates that the dissolution or transport of Y is constrained to a very narrow range of fluid compositions. Therefore, yttrium could be a potential indicator for certain geological fluid compositions. In this study, we use ab initio molecular dynamics (AIMD) simulations to investigate the atomic-scale structure and probe the free energy of different $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes in the P∕T range of subduction zones.

Table 1 Number of atoms in the different simulation cells together with the size of the simulation cell. A and B refer to the system density of 1072 (1.3 GPa) and 1447 kg m⁻³ (4.5 GPa)^a.

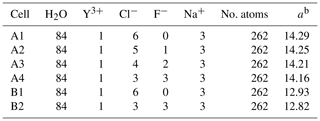
^a Volume estimated using the empirical equation of state from Mantegazzi et al. (2013) for 2 molal NaCl solution. ^b Edge length of the simulation box (Å).

2 Methods

2.1 Ab initio molecular dynamics

The AIMD simulation approach is based on a quantum-mechanical description of the electronic structure within the density functional theory (DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965). Here, we used AIMD simulations with the Car–Parrinello (Car and Parrinello, 1985) method to model the molecular structure of $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes in aqueous solutions. We performed simulations with the widely used Car–Parrinello molecular dynamics (CPMD) code (CPMD, 1990; Marx and Hutter, 2000). Within the code, the BLYP exchange correlation functional (Becke, 1988) was employed and the plane-wave expansion of the Kohn–Sham orbitals was truncated at a cutoff energy of 80 Ry. To reduce the computation effort, the core electrons of all atoms in the cubic simulation cell were approximated by Goedecker-type pseudopotentials (Goedecker et al., 1996; Hartwigsen et al., 1998; Krack, 2005). To separate the electronic and nuclear motion of the CPMD, a fictive electron mass of 600 $\mathrm{a}.\mathrm{u}.$ with fictitious kinetic energy of 0.24 $\mathrm{a}.\mathrm{u}.$ was used. All results presented here are based on simulations performed with a constant number of atoms N at constant volume V and a temperature T of 800 ^∘C (a so-called NVT ensemble) and with a time step of 0.1 fs. The temperature in the simulation was controlled using a Nosé thermostat (Nosé, 1984; Hoover, 1985). We chose two different pressure conditions of 1.3 and 4.5 GPa for this study. The volumes of the simulation cell were estimated from the correlation function provided by Mantegazzi et al. (2013) assuming 2 molal NaCl solution for all cells (see Table 1). Due to this approximation, the pressures listed in Table 1 have to be considered estimates.

The initial atomic configurations were derived from AIMD simulations of pure NaCl solutions (200 H₂O and 10 NaCl). This configuration had been equilibrated for a few tens of picoseconds (ps) at 1000 K and a simulation box size of 13.74 Å. The original NaCl solutions were generated in classical molecular dynamics simulations using Matsuoka–Clementi–Yoshimine (MCY) potentials (Matsuoka et al., 1976). We substituted one of the sodium atoms by yttrium and decreased the number of water molecules and chlorine atoms stepwise until we reached configuration A1 in Table 1. Figure 1 shows a snapshot of the simulation cell A1 with a [YCl₃(H₂O)₄]_aq complex. The chloride ions not initially bonded to the yttrium ion are constrained to remain at larger distance (6–7 Å) from the yttrium ion. All other simulation boxes (see Table 1) were generated from this initial one and equilibrated for several picoseconds.

For the fluoride-bearing cells, we used different cell compositions due to the strong association of hydrogen and fluoride at low pressures. Only initially bonded F⁻ ions were included to avoid the formation of hydrofluoric acid by the reaction ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}+{\mathrm{F}}^{-}\rightleftharpoons {\mathrm{OH}}^{-}+\mathrm{HF}$.

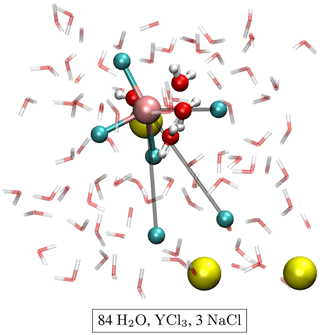
Figure 1 Snapshot of simulation cell A1 with a [YCl₃(H₂O)₄]_aq complex. The water molecules are indicated by red–white bond sticks, sodium by yellow balls and chlorine by cyan balls. The H₂O in the first hydration shell of the yttrium atom (copper colored) is presented as red–white balls and sticks. The constraint distances between the yttrium ion and the constraint Cl⁻ are colored in gray.

2.2 Analysis of interaction distances and coordination number

The average atomic structure of disordered systems such as aqueous solutions is commonly described in terms of partial radial distribution functions g_ij(r). These functions describe the probability for finding a pair of atoms of elements j and i at a distance r normalized to the particle number density ρ_N of the fluid:

$$\begin{array}{}\text{(1)}& g_{ij}\left(r\right)={\displaystyle \frac{\mathrm{1}}{c_{\mathrm{i}}{c}_j\mathrm{4}\mathit{\pi }{r}^{\mathrm{2}}{\mathit{\rho }}_{N}N}}\sum _{a=\mathrm{1}}^{N_{\mathrm{i}}}\sum _{b=\mathrm{1}}^{N_j}\mathit{\delta }(r-|{\mathit{R}}_a-{\mathit{R}}_b\left|\right),\end{array}$$

where $c_{\mathrm{i}}(=N_{\mathrm{i}}/N)$ and c_j are the concentrations of elements i and j, N is the number of particles in the simulation box, δ(x) the Dirac delta function, and R_a and R_b are the position vectors of particles a and b. In the numerical implementation of Eq. (1), the distance of each particle in respect to all other particles is calculated at every time step. The evolving list of distances is normalized to the number of particles and the volume of the simulation cell.

The positions of the first maximum of g_ij(r) represent the distances with the highest density of particles around the central position, which are usually interpreted as the nearest-neighbor distances (or bond distances) between elements i and j. The average coordination number of one element is derived from counting the number of neighbors for each atom of this element within a given cutoff distance respecting periodic boundary conditions and averaging over all particles of the same kind and over time. The cutoff distance is taken from the first minimum of the respective g_ij(r). The association of OH⁻ groups with cations is evaluated by considering oxygen atoms coordinated by one hydrogen only. To distinguish pure OH⁻ from two H₂O sharing one hydrogen, the cutoff between the oxygen and the hydrogen is set to 1.3 Å. Additionally, the distance of the hydrogen within this cutoff distance to the next oxygen is taken as the distinguishing criterion. Only if the oxygen of the next water molecule is located at a distance of >1.6 Å, the OH⁻ is counted as hydroxide. This value represents approximately the hydrogen bond distance between OH⁻ and H₂O (Stefanski et al., 2018). To evaluate the formation of a certain species during a simulation run, only complexes with a constant coordination of chloride and fluoride over at least 3 ps are considered. The average halogen ion hydration number is computed by counting the number of hydrogen oriented towards the ion of the vicinal water molecules.

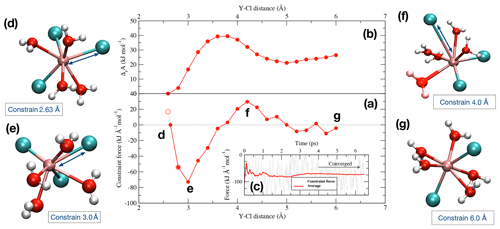
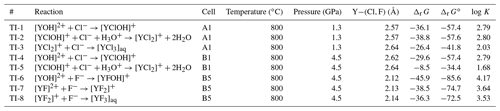
Figure 2 (a) Potential of mean force of the dissociation reaction of YCl₃ to ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ at 1.3 GPa and 800 ^∘C over a distance between 2.63 Å and 6.0 Å. The evolution of the Helmholtz free energy is shown in panel (b). In panel (c), an example of the progress of the constraint force with simulation time at a Y–Cl distance of 3.0 Å is shown (stage e). Panels (d)–(g) indicate the different stages of the dissociation of the initial complex (see text for details).

2.3 Constraint molecular dynamics simulations and thermodynamic integration

A single MD simulation only yields the total internal energy of the system. Thermodynamic integration (TI) is used to derive free energy differences between different states. This approach usually requires a number of intermediate MD simulations along a certain integration variable (Resat and Mezei, 1993). Here, we use the constrained molecular dynamics approach and thermodynamic integration in terms of the blue moon sampling (Ciccotti et al., 2005). This method has been used already by different groups to investigate the stability of metal complexes in aqueous solutions, not only at ambient pressure and temperature conditions (Bühl and Golubnychiy, 2007; Bühl and Grenthe, 2011) but also at hydrothermal (Mei et al., 2013, 2015, 2016) and deep crustal high-density fluid conditions (Mei et al., 2018).

Using this method, the Helmholtz free energy difference (Δ_rA) of a chemical dissociation reaction is obtained from the average forces F(r) between two atoms under the constraint of keeping their bond distance r constant. Δ_rA is derived from the integration of F(r) between two different distances (r₁ and r₂), which correspond to the associated and the dissociated states of the aqueous complexes (Sprik and Ciccotti, 1998):

$$\begin{array}{}\text{(2)}& {\mathrm{\Delta }}_{\mathrm{r}}{A}_{\mathrm{1}⟶\mathrm{2}}=-\underset{\mathrm{1}}{\overset{\mathrm{2}}{\int }}\langle F\left(r\right)\rangle \mathrm{d}r.\end{array}$$

The formal relation between the Helmholtz free energy and the Gibbs free energy is given by

$$\begin{array}{}\text{(3)}& {\mathrm{\Delta }}_{\mathrm{r}}G={\mathrm{\Delta }}_{\mathrm{r}}{A}_{\mathrm{1}⟶\mathrm{2}}+V\underset{\mathrm{1}}{\overset{\mathrm{2}}{\int }}\mathrm{d}P.\end{array}$$

V is the volume of the simulation cell. Here, we use an NVT ensemble, and the change in pressure averaged over the whole trajectory is approximately zero (${\int }_{\mathrm{1}}^{\mathrm{2}}\mathrm{d}P=\mathrm{0}$).

To look into the formation of $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ species in equilibrium reactions, we removed one of the ligands from the Y ion in multiple integration steps by constraining the Y−Cl and Y−F distances. During the integration, the Y−Cl and Y−F distances of the Cl or F ions that are not initially bonded to the yttrium ion are fixed at 6.0 to 7.0 Å to avoid disruptions during the integration. Figure 2 illustrates an example of the dissociation reaction in the simulation box at 1.3 GPa and 800 ^∘C:

$$\begin{array}{}\text{(R1)}& \left[{\mathrm{YCl}}_{\mathrm{3}}\right({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_{\mathrm{4}}{]}_{\mathrm{aq}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \left[{\mathrm{YCl}}_{\mathrm{2}}\right({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_{\mathrm{5}}{]}^{+}+{\mathrm{Cl}}^{-}.\end{array}$$

The integration starts at the first distance (Fig. 2d), which corresponds approximately to the equilibrium distance of the Y–Cl contact ion pair. This interatomic distance (Fig. 2a) is estimated as the intercept with the zero force line from a linear interpolation between the first and the second integration steps, the first step starting at 2.6 Å for Y–Cl (and at 2.0 Å for Y–F). With increasing displacement of the chloride ion, the constraint force is attractive (Fig. 2e) until a water molecule takes the place of the ion in the first coordination shell around the Y³⁺ (Fig. 2f). At this point, the force becomes repulsive. By integration over the potential of mean force (PMF) (Fig. 2a), the Helmholtz free energy (Δ_rA) difference between the initial complex and the product of the reaction is derived (Fig. 2b). For the Y–Cl complexes, we assume a ligand in a distance of 6.0 Å  as being dissociated, and for Y–F this distance reduces to 5.0 Å (see Fig. S1 in the Supplement ). In Fig. 2g, the dissociation is completed and [YCl₂(H₂O)₅]⁺ is formed. To estimate the convergence of the constraint force, the standard deviation of the average force is computed. As a convergence criterion, a value of 5 kJ mol⁻¹ over the last 2 ps is taken. This value is also considered as approximate error of the computed reaction free energies. To satisfy this criterion, the constraint AIMD simulations are performed for values between 4.5 and 40 ps.

2.4 Thermodynamic approaches

It is textbook knowledge that the formation of monomeric complexes in equilibrium reactions develops in steps (Atkins and De Paula, J., 2006; Brown and Ekberg, 2016). During the formation process, a ligand L is added to the metal cation M. This formation of a ML_n complex can be written as a sequence of stepwise reactions:

$$\begin{array}{c}{\displaystyle }M+L\to ML\\ {\displaystyle }ML+L\to M{L}_{\mathrm{2}}\\ {\displaystyle }\mathrm{⋮}\\ {\displaystyle }M{L}_{n-\mathrm{1}}+L\to M{L}_n,\end{array}$$

with the respective logarithmic equilibrium constants:

$$\begin{array}{}\text{(4)}& \log K_n={\displaystyle \frac{-{\mathrm{\Delta }}_{\mathrm{r}}G{{}^{\circ }}_n}{\mathrm{2.303}RT}}.\end{array}$$

Having determined equilibrium constants for all of those reactions, the stability constant (also referred to as cumulative stability constant or overall stability constant) β_n of species ML_n is defined as

$$\begin{array}{}\text{(5)}& \log {\mathit{\beta }}_n=\log K_{\mathrm{1}}+\log K_{\mathrm{2}}+\log K_{\mathrm{3}}\mathrm{\dots }\log K_n.\end{array}$$

The standard Gibbs free energy (${\mathrm{\Delta }}_{\mathrm{r}}G{{}^{\circ }}_{\mathrm{i}}$) depends on the reaction Gibbs free energy (Δ_rG_i) derived from the MD simulation, temperature T, gas constant R, molality of the ions m_i and the activity coefficient γ_i:

$$\begin{array}{}\text{(6)}& {\mathrm{\Delta }}_{\mathrm{r}}G{{}^{\circ }}_{\mathrm{i}}={\mathrm{\Delta }}_{\mathrm{r}}{G}_{\mathrm{i}}-RT\ln {\displaystyle \frac{m_{M{L}_{\mathrm{i}}}{\mathit{\gamma }}_{M{L}_{\mathrm{i}}}}{m_{M{L}_{\mathrm{i}-\mathrm{1}}}{\mathit{\gamma }}_{M{L}_{\mathrm{i}-\mathrm{1}}}\cdot m_L{\mathit{\gamma }}_L}}.\end{array}$$

The standard state for a solute in aqueous solution is a 1 molal hypothetical solution with properties of an infinitely diluted solution (IUPAC, 1982). The concentration and behavior of the solutes in the simulation cell (see Table 1) are quite different from this standard state. Therefore, we computed the activity coefficient corresponding to this hypothetical solution using the B-dot model (Helgeson et al., 1981; Helgeson, 1969), which is an empirical extension of the Debye–Hückel theory (Hückel and Debye, 1923):

$$\begin{array}{}\text{(7)}& \log {\mathit{\gamma }}_{\mathrm{i}}=-{\displaystyle \frac{z_{\mathrm{i}}^{\mathrm{2}}{A}_{\mathrm{DH}}\sqrt{I}}{\mathrm{1}+{\mathit{å}}_{\mathrm{i}}{B}_{\mathrm{DH}}\sqrt{I}}}+\dot{B}I,\end{array}$$

where z_i is the charge of ion i, å the mean distance of closest approach between the ions and I the ionic strength:

$$\begin{array}{}\text{(8)}& I=\mathrm{0.5}\sum _{i=\mathrm{1}}^n{m}_{\mathrm{i}}{z}_{\mathrm{i}}^{\mathrm{2}}.\end{array}$$

A_DH and B_DH are the Debye–Hückel parameters:

$$\begin{array}{}\text{(9)}& {\displaystyle }{A}_{\mathrm{DH}}={\displaystyle \frac{\mathrm{1.8248}\cdot {\mathrm{10}}^{\mathrm{6}}\sqrt{{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}{(T\mathit{ϵ}{)}^{\frac{\mathrm{3}}{\mathrm{2}}}}}\text{(10)}& {\displaystyle }{B}_{\mathrm{DH}}={\displaystyle \frac{\mathrm{50.292}\sqrt{{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}{(T\mathit{ϵ}{)}^{\frac{\mathrm{1}}{\mathrm{2}}}}}.\end{array}$$

They depend on temperature, density (${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) and dielectric constant (ϵ) of the solvent. ϵ is computed using the equation provided by Pan et al. (2013) and Sverjensky et al. (2014) for pure H₂O assuming a fluid density of the simulation. The value of $\dot{B}$ is calculated by the CHNOSZ software package (Dick, 2008) applying the extrapolation suggested by Manning et al. (2013). The $\stackrel{\mathrm{˚}}{a}$ parameter for the different complexes and ions (for all $\mathrm{Y}-\mathrm{Cl}/\mathrm{F}$ complexes, a constant value of 4.5 Å is applied) are taken from Kielland (1937) and Eq. (7) was solved in a Python implementation of the EQBRM program (Anderson and Crerar, 1993).

Table 2 The listed atomic distances and coordination numbers are averaged over the whole-simulation runs for all unbiased simulations. “AIMD time” corresponds to the total simulation time, whereas lifetime (“LT”) refers to persistence of the initial yttrium–halide complex. Under “formed”, the most abundant complexes^a of the last 10 ps of the simulation are listed.

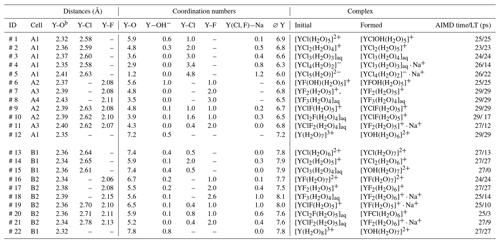
^a A list of all formed complexes observed for at least 3 ps over the AIMD is given in the Supplement in Table S3. ^b The decomposed Y−OH₂ and $\mathrm{Y}-{\mathrm{OH}}^{-}$ distances are listed in Table S1.

Note that in the simulations we modeled a dissociation reaction but to be in line with the modern nomenclature of aqueous geochemistry all the derived thermodynamic data presented below correspond to the formation reaction. In this study, we investigated two kinds of reactions:

$$\begin{array}{}\text{(R2)}& {\mathrm{Y}}^{\mathrm{3}+}+n{\mathrm{Cl}}^{-}\to {\mathrm{YCl}}_n^{\mathrm{3}-n}(n=\mathrm{1}-\mathrm{3})\end{array}$$

and

$$\begin{array}{}\text{(R3)}& {\mathrm{Y}}^{\mathrm{3}+}+n{\mathrm{F}}^{-}\to {\mathrm{YF}}_n^{\mathrm{3}-n}(n=\mathrm{1}-\mathrm{3}).\end{array}$$

In the following, all results referring to one of those reactions are indexed by TI −n. Furthermore, for reasons of clarity, we do not include the number of hydration water molecules in the formula of the aqueous complexes in some of the presented figures and tables.

3 Results

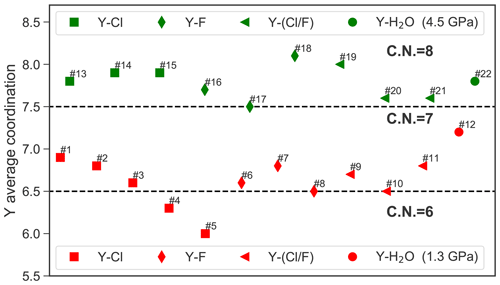
3.1 Yttrium coordination in high-density aqueous fluid

AIMD simulations were performed for the hydrated Y³⁺ and for 11 different yttrium–halogen complexes: five YCl${}_n^{\mathrm{3}-n}$, n=1–5; three YF${}_n^{\mathrm{3}-n}$, n=1, 2, 3; and three mixed $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes. Simulation conditions and obtained structural data are compiled in Table 2. Moreover, the formed aqueous species are listed in Table 2. Note that the composition of the simulation cells varies slightly as cells A1–A4, B1 and B2 contain different amounts of F and Cl.

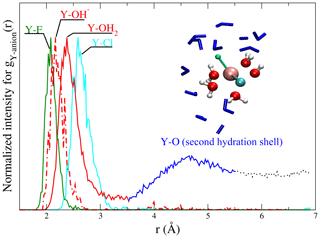
Figure 3 Radial distribution functions of $\mathrm{Y}-(\mathrm{Cl},\mathrm{O},\mathrm{F})$ scaled to the maximum of the g_ij(r) from run # 9 and 12 together with a snapshot of a [YClF(OH)(H₂O)₄] complex. In the snapshot (from a run at 1.3 GPa and 800 ^∘C), the central yttrium atom is surrounded by chlorine (cyan), fluorine (green), a hydroxyl group and water molecules (red – O and white – H balls). Water molecules of the second shell are shown as blue sticks. This visualization illustrates the relation between g_ij(r) and the atomic structure of the aqueous species. The colors of the ligands in the snapshot are equivalent to those in the g_ij(r) functions.

Different partial radial distribution functions for Y–(Cl⁻, F⁻, OH⁻ and OH₂) are shown in Fig. 3. To facilitate the comparison of the first peaks, the g_ij(r) values are scaled to equal maximum intensity. The observed sequence of atomic distances between the central metal ion and its ligands holds for all the complexes. The shortest distance is found between Y³⁺ and F⁻ (∼2.1 Å), followed by $\mathrm{Y}-{\mathrm{OH}}^{-}$ (∼2.1–2.2 Å) and Y–OH₂ (∼2.3–2.4 Å). The largest distance is observed for Y–Cl pairs (∼2.6–2.8 Å) (for an overview, see Tables 2 and S1). Further, in g_Y−O(r), a second maximum is observed. It corresponds to the second hydration shell, which is formed around all complexes at all studied P∕T conditions. For all fluid compositions, association of NaCl_n (n=1–3) and of Na⁺ with the yttrium complex is observed. The mean Na–Cl coordination, NaCl species distribution and second hydration shell positions are listed in Table S1.

Figure 4 Average yttrium coordination by chloride, fluoride and oxygen for run # 1–22.

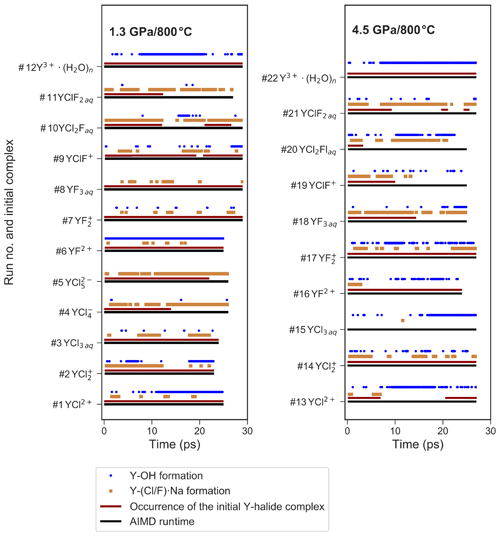
Figure 5 Presence of selected ion pairs or complexes during the different AIMD simulations. This includes the formation of OH⁻ within the first hydration shell of yttrium, the association of sodium with the coordinating halogens and the stability of the initial Y–halide complexes over AIMD time.

At 1.3 GPa, the average Y coordination by O, Cl and/or F is about seven (see Fig. 4) with two exceptions, run # 4 and 5, even if the initial coordination is lower (run # 1–3). In run # 1–3, the initial Y–Cl coordination is retained over the entire AIMD runtime, whereas for # 4 and 5, the 4-fold and 5-fold Cl coordinations do not persist and the time average yttrium coordination is below seven. The initial complex of # 5 seems to be unstable and transforms to the initial complex of # 4 after 26 ps. In # 4, after the 4-fold coordinated chloride complex is dissociated, a total coordination number of seven is reached at the end of the simulation run. Frequently, the formation of OH⁻ in the first hydration shell of yttrium is observed. The major hydroxide formation mechanism will be discussed below.

Figure 5 provides an overview over the formation and dissolution of selected structural units in the course of the simulations, i.e., the stability of the initial complexes, Y–hydroxide association and bonding of the coordinating halogen to sodium. All five chloride complexes associate with sodium. The strongest association is observed in # 2–5, where the sodium is connected to one or two chloride ligands of the Y complex. This association increases with the number of halide ligands in these complexes. Furthermore, in # 4 and 5, this association initiates the dissociation of [YCl₄(H₂O)₂]⁻ and [YCl₅(H₂O)]²⁻. Even larger clusters of sodium, constraint chlorides and the Y–chloride complex appear over timescales of less than 3 ps. Moreover, from # 1–5, the average Y coordination decreases with the increasing number of initial chloride ligands (Fig. 4). The Y–O distances do not change significantly with the increasing number of chloride ligands from # 1 to 4. Only in run # 5 is a significantly longer Y–O distance of 2.41 Å observed. The Y–chloride distances range from 2.58 Å in # 1 to 2.63 Å in # 5.

For pure Y–fluoride complexes under the same conditions (# 6–8), a slight increase of the Y–O distance with increasing number of fluoride ligands from 2.37 Å in [YF(H₂O)₆]²⁺ to 2.43 Å in [YF₃(H₂O)₄]_aq is observed. In all three runs, the initial complex persists over the whole simulation time. As in the case of Y–chloride solutions, the association of fluoride with sodium is observed but it is less pronounced. In # 6, where only one fluoride is initially bonded to the central ion, OH⁻ is formed within the first hydration shell of yttrium. The Y−F distances within the complexes are approximately 0.5 Å shorter than those of the Y−Cl species.

For the $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ mixed complexes (run # 9–11), only the run starting initially from [YClF(H₂O)₅]⁺ does not show the formation of multiple complexes over time. Here, only short separations of the Cl⁻ over ∼1 ps from the complex occur. In # 10, [YCl₂F(H₂O)₄]_aq dissociates to [YClF(H₂O)₆]⁺ after 11.5 ps. This complex is present over approximately 10 ps, in conjunction with the formation of [YClFOH(H₂O)₄]_aq, followed by the reassociation of the initial complex. In # 11, starting from [YClF₂(H₂O)₄]_aq, the initially bonded chloride is released after ∼12 ps and [YF₂(H₂O)₅]⁺ is formed. The $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ distances of the mixed complexes are comparable to those of the pure ones.

In run # 12, starting from [Y(H₂O)₇]³⁺, hydroxide is formed within the first 8 ps (see Fig. 5), which results in the formation of [YOH(H₂O)₆]²⁺ that is present over 14 ps of the AIMD time, followed by a reassociation and a redissociation, which suggests a dynamic change between these two species.

In the high-pressure runs at 4.5 GPa (# 13–22), the average Y coordination is about eight (see Fig. 4). In the case of the Y–chloride complexes, the dissociation of the 1-fold and 3-fold coordinated complexes is observed in run # 13 and 15 (see Fig. 5). Only in run # 14 does the initial Y–chloride complex [YCl₂(H₂O)₅]⁺ persist over the whole 27 ps trajectory. The higher-coordinated Y–chloride complexes break apart within the equilibration run and the results are not further analyzed. This breakdown is partly driven by the association of the coordinating chloride with sodium. For instance, in run # 13, one sodium chloride unit associates with the Y complex before the chloride dissociates from the Y complex and [NaCl₃]²⁻ is formed for ∼3 ps (Fig. 6). The resulting [Y(H₂O)₈]³⁺ associates with OH⁻ shortly afterwards. In all high P runs, the formation of OH⁻ by self-dissociation of H₂O close to the yttrium ion can be seen as in the low P runs.

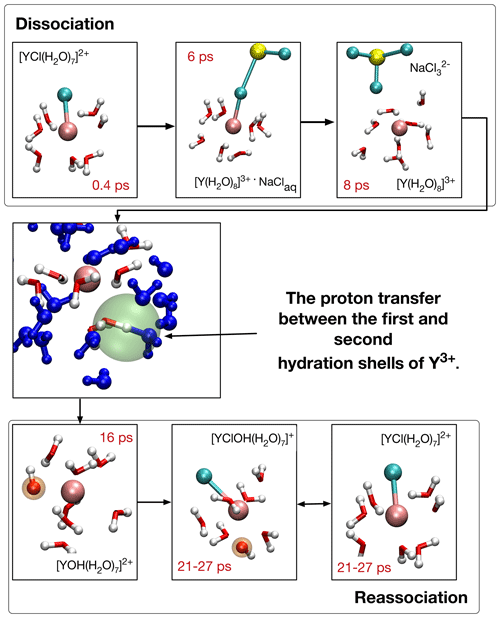
Figure 6 Formation of [YOH(H₂O)₇]²⁺ and reassociation of initial complex [YCl(H₂O)₇]²⁺ in run # 13. The blue-colored water molecules are located in the second hydration shell, red–white H₂O and OH⁻ are bonded in the first coordination shell, and sodium is colored yellow. Chloride ions are in cyan and the Y³⁺ ion is copper colored. The red numbers indicate the time progress in the AIMD simulation. In the center, the proton transfer state is highlighted with a green sphere.

Figure 6 illustrates the OH⁻ formation mechanism as it evolves for Y–chloride and Y–fluoride complexes at low- and high-pressure conditions for the example of [YCl(H₂O)₇]²⁺ in run # 13. After the initial complex dissociates within the first 7 ps into [Y(H₂O)₈]³⁺, a proton is transferred between one H₂O in the first hydration shell and a water molecule of the second shell after additional 2–3 ps. The resulting [YOH(H₂O)₇]²⁺ complex is present over 14 ps, followed by reassociation with chloride. The thus-formed [YClOH(H₂O)₆]⁺ persists during the remaining simulation time with some interruptions due to short-lived proton transfers.

For the Y–fluoride complexes, under the high-pressure conditions, the 1-fold or 2-fold Y by F coordination persists over the whole-simulation runs (# 16, 17). All complexes show association with one or two sodium ions over several picoseconds but this interaction does not lead to a dissociation of fluoride from yttrium. In # 18, the initially 3-fold coordinated complex dissociates after 14.5 ps and [YF₂(H₂O)₆]⁺ is formed. None of the mixed $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes at 4.5 GPa persist over the entire simulation run. In each of those runs, all chloride ions are dissociated from the yttrium after at most 10 ps, and pure Y−F or $\mathrm{Y}-(\mathrm{F},\mathrm{OH})$ complexes remain. As in the low-pressure run for the pure hydrated Y³⁺, a hydroxide ion is observed in the first hydration shell for a significant amount of simulation time.

The nearest Y-(O,Cl,F) distances show only small variations between both pressure conditions, typically in the range of 0.01–0.06 Å for the stable complexes (Table 2). A closer look at the distances between oxygen of the second hydration shell and the yttrium ion (see Y−O(2nd) in Table S1) reveals a continuous increase from the purely hydrated ion with increasing Cl coordination at low pressures from 4.7 to 5.2 Å. In all other cases, these distances are rather similar in a range between 4.3 and 4.6 Å.

Comparing the average halide ion coordination by H₂O molecules, differences between purely hydrated halide ions or halide ions associated with the yttrium ion as well as pressure-induced changes are observed (see Table S2). For the chloride ion at 1.3 GPa, the number of hydrating water molecules increases from two to four between ${\mathrm{YCl}}_{\mathrm{2}}^{+}-{\mathrm{YCl}}_{\mathrm{3}\mathrm{aq}}$ and dissociated Cl⁻, whereas in the mixed complexes YClF_2 aq the chloride hydration number is close to three. For YCl²⁺, ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ and ${\mathrm{YCl}}_{\mathrm{5}}^{\mathrm{2}-}$, this number lies between two and three. The fluoride ion is coordinated by one water molecule in the Y–fluoride and mixed complexes. At 4.5 GPa, F⁻ is hydrated by four H₂O and by two when associated with the metal ion, whereas the dissociated Cl⁻ coordination increases to five solvent molecules. For those Y–chloride complexes that persist for at least 10 ps in the AIMD run, the chloride ion is coordinated by three water molecules.

To conclude this section, the main findings from the AIMD simulations are summarized. Firstly, the pure Y–chloride complexes YCl²⁺, ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ and YCl_3 aq do not dissociate within the course of the simulation of at least 23 ps at a pressure of 1.3 GPa (ρ=1072 kg m⁻³) but they do at higher pressure (4.5 GPa, 1447 kg m⁻³) except for YCl${}_{\mathrm{2}}^{+}$. Furthermore, ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ and ${\mathrm{YCl}}_{\mathrm{5}}^{\mathrm{2}-}$ decompose in the unbiased AIMD simulations. Secondly, the pure Y–fluoride complexes persist over the simulation time at 1.3 GPa. It is important to state that at these conditions the formation of hydrofluoric acid is very strong when the fluoride is not associated with the metal ion. At 4.5 GPa, the neutral complex [YF₃(H₂O)₅]_aq dissociates and a lower coordinated species forms. Thirdly, OH⁻ is formed in the first hydration shell of Y–chloride and Y–fluoride complexes due to the self-dissociation of water. Its abundance increases with decreasing number halide ligands. Furthermore, chloride as well as fluoride form mixed complexes with yttrium and hydroxide at both P∕T conditions, whereas mixed $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes are rather unstable. The overall coordination of yttrium changes from ∼7 at 1.3 GPa to ∼8 at 4.5 GPa.

3.2 Free energy exploration

Although several complexes are observed in some of the runs described above, it is not feasible to derive the corresponding formation constants of the aqueous species directly from the AIMD simulations. This would require much longer simulation times to ensure the statistical significance of the relative species abundance. On the tens of picoseconds timescale, we did not observe a complete exchange of the halogen ligands of the Y–chloride or Y–fluoride complexes except for run # 15. To overcome this problem, we apply the TI approach within a constraint AIMD simulation to compute the reaction free energies of aqueous complex dissociation. As described in the previous section, the mixed $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes have a tendency to dissociate already during the conventional AIMD runs, which indicates their low stability. Therefore, no TI runs are performed for those complexes. When the constraint halide ion associates with hydrogen during the constraint MD, the simulation is stopped and the integration step is repeated from a different starting configuration. Thus, we confirm that all results are reproducible within a series of simulations. The derived Helmholtz free energies (Δ_rA) of Reactions (R2) and (R3) are listed in Table 3.

Table 3 List of the formation Gibbs free energies (kJ mol⁻¹) derived from ab initio thermodynamic integration. The error of the free energies is estimated with 5 kJ mol⁻¹.

At 1.3 GPa, in TI-1 starting from [YCl(H₂O)₆]²⁺, in nearly all TI steps close to the yttrium OH⁻ formed by the hydrolysis of water molecules within the first 2–4 ps. Therefore, the obtained dissociation energy of 36.1 kJ mol⁻¹ does not distinguish between [YCl(H₂O)₆]²⁺ and [YOHCl(H₂O)₅]⁺ complexes. For TI-2, we observe a similar dissociation energy of 38.8 kJ mol⁻¹ but much fewer hydroxide ions are formed such that in average over all integration steps $\mathrm{Y}-{\mathrm{OH}}^{-}$ appears in only 14 % of the total simulation time. The lowest dissociation energy of the Y–chloride complexes at 1.3 GPa occurs in TI-3 with 26.4 kJ mol⁻¹. In TI-3, only little amounts of OH⁻ are formed. While the integration proceeds, the yttrium–oxygen coordination changes (including OH⁻ and H₂O) for all complexes at a constraint Y−Cl distance between 3.6 and 4.0 Å. The removed chloride as well as the remaining Y–chloride complex associate with sodium during the dissociation process for a few picoseconds. Dissociation energies of the Y–fluoride complexes at 1.3 GPa could not be obtained due to the strong association of H⁺ and F⁻. The formation of hydrofluoric acid prevents the required long constraint Y–fluoride bond distances for the integration of the PMF.

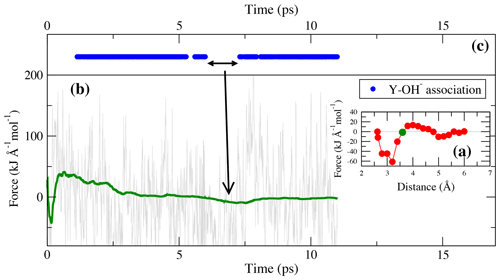
Figure 7 (a) Potential of mean force of TI-4. The green circle indicates the constraint distance of 3.6 Å for which the force and cumulative mean force is shown in panel (b). Dots in panel (c) indicate the presence of $\mathrm{Y}-{\mathrm{OH}}^{-}$ bonds during the simulation run.

As in the lower-pressure runs, the integration at high pressure does not distinguish between complexes in which OH⁻ is present or absent. In TI-4, starting from [YClOH(H₂O)₆]⁺ and forming [YOH(H₂O)₇]²⁺, a free energy difference of 29.6 kJ mol⁻¹ is obtained. As illustrated in Fig. 7, the reassociation of OH⁻ with an excess proton leads to a change of the constraint force due to the decreasing attraction of the metal cation to the constraint chloride ligand. The most frequent $\mathrm{Y}-{\mathrm{OH}}^{-}$ association is observed at constraint Y–Cl distances above 3.0 Å.

The dissociation energies of the Y–chloride complexes significantly decrease between [YCl(H₂O)₇]²⁺ and [YCl₂(H₂O)₆]⁺ at 4.5 GPa. TI-5 yields a low dissociation energy of 8.5 kJ mol⁻¹ where in several of the integration steps the second chloride ligand also dissociates and [YOH(H₂O)₇]²⁺ is formed. The Y−Cl dissociation is preceded by an $\mathrm{Y}-{\mathrm{OH}}^{-}$ association and results in the formation of $\left[{\mathrm{YOH}}_{\mathrm{0}-\mathrm{1}}\right({\mathrm{H}}_{\mathrm{2}}\mathrm{O}{)}_{\mathrm{6}-\mathrm{7}}{]}^{\mathrm{3}-\mathrm{2}+}$. In those cases, the initial complex was reset and the integration step was restarted. For [YCl₃(H₂O)₅]_aq, the dissociation energy was not derived because the initial complex dissociated at short Y−Cl constraint distances within the first picosecond of each simulation. Therefore, this complex is not considered as important at such high-pressure conditions. An approach to derive a dissociation energy for such unstable complexes was shown by Mei et al. (2016) by constraining the remaining ligands at the equilibrium distance.

Table 4 List of the logarithmic stability constants log  β^* derived from ab initio thermodynamic integration in comparison to theoretical predictions based on HKF regression.

^a Listed values involve further transition states that cannot be separated during the TI. ^b Pressure estimates assuming a 2 molal NaCl solution using the empirical equation of state by Mantegazzi et al. (2013). ^c Values computed using the DEW model (Sverjensky et al., 2014) with HKF parameters reported by Loges et al. (2013)^d for Y and Migdisov et al. (2009)^e for Ho complexes.

In TI-6 to TI-8, the dissociation energies of Y–fluoride complexes following Reaction (R3) are investigated. The equilibrium distance between the yttrium ion and its fluoride ligands is smaller than the Y–Cl bond distance. Due to this shorter distance, the integration range to reach the dissociated state was reduced to 5.0 Å. As shown in Fig. 8 (and Fig. S1), the convergence of the free energy is still reached. In each run of this simulation series, we observe the temporary formation of hydrofluoric acid by the protolysis from H₃O⁺ to one of the constraint F⁻and, compared to the low-pressure runs, to a lesser extent by the protolysis of H₂O.

The dissociation energies (Fig. 8) are quite similar between the Y–fluoride complexes. During the integration, the Y complexes as well as the removing fluoride ions interact with sodium. No self-dissociation of the complexes is observed except for [YF₃(H₂O)₅]_aq. In the latter case, at a constant distance of 2.6 Å, one of unconstrained fluorides separates from the initial complex. However, this behavior is not reproducible.

During all integration runs at both pressures, the Y−O coordination number increases in average by one during the transformation from the associated with the dissociated state. For the Y–chloride complexes, the increase in hydration happens at a Y−Cl distance between 3.6 and 4.1 Å, which is in the range of the repulsive part of the constraint force. For the dissociation of Y–fluoride complexes, this distance decreases to 3.4–3.6 Å. A significant influence of the second hydration shell on the constraint force of the reaction coordinate is not observed. All complexes and the removing halide ions interact with sodium. This interaction cannot be quantified by the PMF but the association of the yttrium complex with sodium decreases with the number of halide ligands.

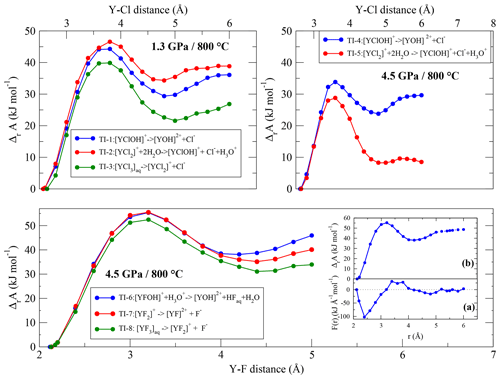
Figure 8 Evolution of the Helmholtz free energy derived from thermodynamic integration for $\mathrm{Y}-\mathrm{Cl}/\mathrm{F}$ complexes at 800 ^∘C and 1.3∕4.5 GPa Inset: (a) potential of mean force of the dissociation reaction of [YFOH]⁺ to ${\mathrm{YOH}}_{\mathrm{2}}^{+}$ for a integration length of 5.0 and 6.0 Å. (b) Resulting Helmholtz free energy along the integration pathway (for higher magnification, see Fig. S1).

3.3 Thermodynamic data

Finally, the reaction free energies derived from thermodynamic integration are transformed into standard state properties by applying the activity corrections described in the methods section above. The standard state correction yields Δ_rG^∘ values that are significantly smaller compared to Δ_rG (see Table 3). This treatment does not consider explicitly the formation of HCl and HF as well as the association of yttrium with hydroxide because their formation during TI is not systematic and it is not possible to quantify their contributions to the reaction free energies. As these contributions seem not to be negligible as shown in Fig. 7, the logarithmic stability constants include not only the reactions listed in Table 4 and are therefore indicated with a star (log  β^*). Figure 9 shows the Δ_rG^∘ and log β^* for the different species. While pressure does not affect the formation reaction of YCl²⁺, the stability of ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ decreases substantially with increasing pressure. Comparing the stability constants of chloride and fluoride species at 4.5 GPa, it is found that those of the fluoride species are higher by 1.4 ($\log {\mathit{\beta }}_{\mathrm{1}}^{*}$) to 3.3 ($\log {\mathit{\beta }}_{\mathrm{2}}^{*}$) log units.

4 Discussion

4.1 Molecular structure of the aqueous complexes

As mentioned in the introduction, the number of studies focusing on the hydration environment of yttrium or other HREEs in aqueous fluids at high T and P conditions is very limited. The average coordination of seven nearest neighbors that is observed in the simulations at 1.3 GPa fits in the range of experimental results. Vala Ragnarsdottir et al. (1998) observed eight to nine nearest neighbors at lower T of 250 ^∘C and vapor pressures in highly concentrated chloride solution. But they did not find an association of Y–chloride, whereas Mayanovic et al. (2002) reported a strong association with an average coordination of four at 500 ^∘C. The present simulations predict that ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ is not stable at high P∕T conditions. The reason for this could be the too-low average Y coordination in ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ and ${\mathrm{YCl}}_{\mathrm{5}}^{\mathrm{2}-}$. An average coordination of seven as present in the stable Y–chloride complexes of the simulations cannot be achieved in these highly chlorinated species due to steric constraints. The Y–O distances derived from EXAFS spectra by Vala Ragnarsdottir et al. (1998) in the range of 2.36–2.39 Å are in good agreement with the atomic distances from the presented simulations, while the conference abstract by Mayanovic et al. (2002) does not comprise quantitative data. Experiments and simulations are only partly comparable, as the simulations were performed at higher T (800 ^∘C) than the experiments by Vala Ragnarsdottir et al. (1998) or Mayanovic et al. (2002).

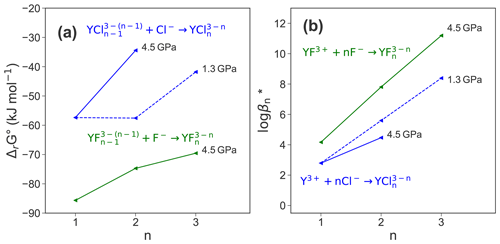
Figure 9 (a) Reaction Gibbs free energy Δ_rG^∘ of the different formation reactions; (b) change of the logarithmic stability constant of the different $\mathrm{Y}-(\mathrm{Cl},\mathrm{F})$ complexes.

The formation of stable Y−Cl species at 1.3 and 4.5 GPa is consistent with observations by, e.g., Tropper et al. (2011), Schmidt et al. (2007b) that the mobility of yttrium increases with increasing availability of Cl⁻ in aqueous systems. The Y–Cl complexes become less stable with increasing P. The destabilization of metal–halide species with rising pressure is known from a variety of systems (see overview by Manning, 2018). This is commonly explained by the increase of the dielectric constant with increasing density at constant T. The increase of ϵ (ϵ=17.1 at 1072 kg m⁻³ and ϵ=26.2 at 1447 kg m⁻³ according to Sverjensky et al., 2014) leads to a stronger hydration of the metal ion by H₂O and the stabilization of charged species. Therefore, YCl_3 aq decomposes at 4.5 GPa. The direct competition of both halide ligands in the mixed complexes shows a clear preference of yttrium to form stable bonds with F⁻ rather than with Cl⁻. Moreover, the lower reaction Gibbs free energies of the Y–fluoride species in Fig. 9a strongly support this observation.

Figure 10 shows a comparison of the $\mathrm{Y}-{\mathrm{OH}}^{-}$ formation between both pressure conditions in those aqueous complexes that persist over at least 10 ps in the unconstrained AIMD simulations. A higher abundance of hydroxide groups is observed for Y−Cl and Y−F complexes at lower P. Furthermore, the amount of formed OH⁻ decreases with increasing number of ligands and is particularly high for the purely hydrated Y³⁺ at both pressures. This observation cannot be explained by the increased self-dissociation of water, which increases with pressure (see, e.g., Rozsa et al., 2018; Goncharov et al., 2005). According to Marshall and Franck (1981), the OH⁻ molality is in the range of 10⁻⁶ to 10⁻⁵ under the investigated P∕T conditions. Therefore, the hydroxide formation in the simulation must be driven by charge compensation in the absence of other ligands around the yttrium. The low abundance of $\mathrm{Y}-{\mathrm{OH}}^{-}$ in the neutral species (e.g., YF_3 aq) supports this interpretation. It has to be stressed that the initial simulation cells do not contain excess hydroxide ions. Therefore, the $\mathrm{Y}-{\mathrm{OH}}^{-}$ association is expected to be much higher if the OH⁻ concentration increases. But it has to be underlined that the values in Fig. 10 are rather imprecise because an equilibrium distribution of Y–hydroxide bonds cannot be achieved in the rather short simulation time.

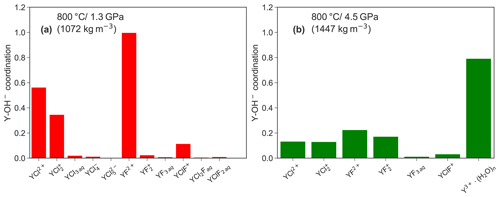
Figure 10 Comparison of the average $\mathrm{Y}-{\mathrm{OH}}^{-}$ coordination number between the different complexes that exist for at least over 10 ps in the unconstrained AIMD at 1.3 (a) and 4.5 GPa (b).

The association of yttrium with hydroxide as observed in the simulations was also noticed in high P∕T solubility experiments by Tropper et al. (2011) in NaCl brines but not in the H₂O−NaF system (Tropper et al., 2013). The authors explained the association by a geometrical effect. The smaller HREEs (in comparison to a LREE) have less attraction to a large chloride ion due to the so-called “steric hindrance”, as discussed by Mayanovic et al. (2009). However, in the case of the Y–fluoride complexes, especially for YF²⁺, the OH⁻ formation is also controlled by the protolysis of H₂O close to the metal ion. Therefore, the geometrical explanation does not hold to explain the Y–hydroxide bonding. The fact that this process was not detected in the experiments by Tropper et al. (2013) might be caused by the high fluoride content in the experiments. The majority of ${\mathrm{YF}}_{\mathrm{2}}^{+}$ in the experiments underlines this conclusion. The fact that the formation of $\mathrm{Y}-(\mathrm{F}/\mathrm{OH})$ species was not detected in solubility experiments by Loges et al. (2013) up to 250 ^∘C indicates that the protolysis of vicinal water by yttrium is a high temperature process. Protolysis at high temperatures was also reported by van Sijl et al. (2010) for Ti⁴⁺ and might be a general property of high-field-strength elements.

Entropy is an additional driving force for the ion association due to changes in the local solvent structure near the critical point and above as discussed, e.g., by Sherman (2010) and Mei et al. (2014) based on AIMD simulations. The dominant effect arises from the translational entropy through hydration changes of the ions during the aqueous reaction. Such a concept was already discussed by Mesmer et al. (1988). They proposed that the change in the electrostriction volume of the solvent controls the association of aqueous species, e.g., NH_3 aq, HCl_aq and NaCl_aq. In the present simulation study, a relation between the change of hydration of chloride and the stability of certain complexes is observed at 1.3 GPa. For example, the formation of ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ and YCl_3 aq (TI-2, TI-3) releases two inner-sphere solvation water molecules because the hydration of Cl⁻ decreases from four to two. This may explain the very similar reaction Gibbs energy of −38.8 kJ mol⁻¹ in TI-2 compared to TI-1 (−36.1 kJ mol⁻¹), where only one H₂O is released (besides the effect of OH⁻ formation). Normally, one would expect a decrease in released reaction free energy with increasing number of ligands. Due to the spontaneous formation of HF, the number of H₂O in the hydration shell of an F⁻ion cannot be derived directly from the 1.3 GPa simulations. At 4.5 GPa, two hydration H₂O are exchanged for F⁻and Cl⁻ during the dissociation of the initial complexes. This convergence of the hydration change for the halogens supports the assumptions by Mesmer et al. (1988) and Mei et al. (2015) that the entropic effect decreases with increasing density at constant temperature (≥200 ^∘C).

4.2 Comparison of the thermodynamic data with HKF regression

Experimental high P and high T thermodynamic properties of Y–chloride and Y–fluoride species are not available to compare and evaluate the present simulation results. Therefore, the Deep Earth Water (DEW) model (Sverjensky et al., 2014) is used to compute stability constants of YF²⁺ and ${\mathrm{YF}}_{\mathrm{2}}^{+}$ derived from solubility experiments up to 250 ^∘C by Loges et al. (2013) using a HKF regression to 800 ^∘C and a fluid density equal to that of the simulations. There are no stability data of Y–chloride complexes available but due to the similarities of yttrium– and holmium (Ho)–chloride complexes at room temperature (Luo and Byrne, 2001), the behavior of Y–chloride complexes is assumed to be similar to Ho–chloride complexes (Migdisov et al., 2019). The Ho–chloride HKF parameters are taken from Haas et al. (1995), Migdisov et al. (2009). In addition, $\mathrm{Y}/\mathrm{Ho}-{\mathrm{OH}}^{-}$ stabilities are derived from data of Shock et al. (1997), Haas et al. (1995). The results are shown in Fig. 11.

Comparing the results in Fig. 11a, it can be observed that the stabilities of YCl²⁺ and ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ are similar to those of the Ho–chloride species within approximately one logarithmic unit. For β₃ (Y−Cl), Y and Ho show opposite behavior. In this case, an increase in the stability of YCl_3 aq is observed, whereas the Ho β₃ (Ho−Cl) decreases (Haas et al., 1995). Migdisov et al. (2009) do not report any β₃ (Cl) values. For Y–hydroxide and Ho–hydroxide species, the stabilities are in the range of YCl²⁺. At higher density (Fig. 11b), the HKF model yields significantly lower stability constants of Ho–/Y–chloride species compared to the AIMD for YCl²⁺ and ${\mathrm{YCl}}_{\mathrm{2}}^{+}$. The formation of $\mathrm{Y}-{\mathrm{OH}}^{-}$ in the AIMD runs suggests that $\mathrm{Y}-{\mathrm{OH}}^{-}$ association may occur in high-density brines.

Due to the lack of AIMD log β_n (Y−F) data, Fig. 11c only shows values derived from the HKF parameters. Here, the Y–fluoride species (Loges et al., 2013) have the highest stability compared to Ho–fluoride (Migdisov et al., 2009; Haas et al., 1995), Y–hydroxide (Shock et al., 1997) and Ho–hydroxide (Haas et al., 1995) species. It should be mentioned here that the model from Haas et al. (1995) is suspected to overestimate the HREE-F stability (Migdisov and Williams-Jones, 2014). In Fig. 11d, it is shown that for the higher fluid density the ${\mathit{\beta }}_{\mathrm{1}}^{*}$ (Y−F) values from the simulations are consistent with regression based on experimental data (Loges et al., 2013) within one log unit. The formation constant of ${\mathrm{YF}}_{\mathrm{2}}^{-}$ from Loges et al. (2013) is higher compared to the AIMD results. On the other hand, the Ho–fluoride (Migdisov et al., 2009) complexes and the Y–/Ho–hydroxide complexes have a much lower stability. Those differences indicate a different behavior of the geochemical twins (Y and Ho) in fluoride-rich environments, which could explain the fractionation of these elements even at high P∕T conditions as it was observed, e.g., in hydrothermal systems (Bau and Dulski, 1995) and discussed by Loges et al. (2013). Furthermore, the comparable stability of both Y–chloride and Ho–chloride complexes confirms the comparable geochemical behavior of the ions in chloride-rich solutions as assumed by Migdisov et al. (2019).

In general, at lower fluid densities, we note similar stabilities of Y– and Ho–chloride complexes. The strong divergence for the neutral complexes might be explained by the origin of the HKF parameters. The data from Haas et al. (1995) were derived from thermodynamic predictions based on measurements at 25 ^∘C and 1 bar where only a very small amount of a neutral species is formed and the uncertainty of the extrapolation is large. This interpretation is supported by reported experiments of Migdisov et al. (2009) and Loges et al. (2013), who do not observe the formation of neutral complexes up to 250 ^∘C. Only in situ measurements by Mayanovic et al. (2002) show higher Cl coordination of yttrium, whereas for Ho no data are available.

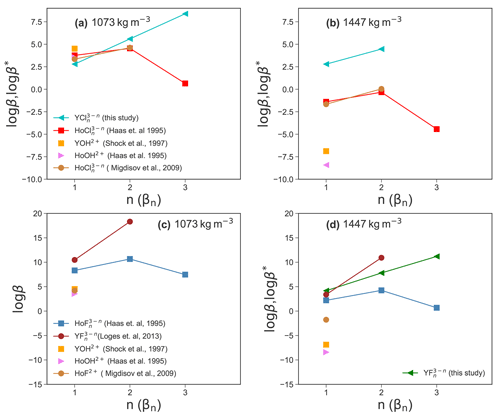
Figure 11 Comparison of the aqueous species stability derived from the AIMD simulation and HKF regression using the DEW model (Sverjensky et al., 2014) at 800 ^∘C and a fluid density of 1072 and 1447 kg m⁻³.

4.3 The role of chloride and fluoride for the mobilization of Y³⁺ under subduction-zone conditions

Stable Y–chloride and Y–fluoride complexes are found over the investigated P∕T range. Fluoride-bearing species are predominant in chloride- and fluoride-rich metamorphic fluids. This outcome is consistent with a variety of studies from the field (see, e.g., Newton et al., 1998) as well as from experiments (Hetherington et al., 2010; Tsay et al., 2014; Tropper et al., 2013). Figure 12a–c show the distribution of the Y–fluoride and Y–chloride complexes as a function of the dissolved salt concentration. In Fig. 12d, the speciation change as function of the F⁻concentration is shown. Besides the presented thermodynamic data from this study, competing aqueous reactions as the formation of HCl_aq, NaCl_aq, NaF_aq, HF_aq and NaOH_aq as expected in high-grade metamorphic fluids (Aranovich and Safonov, 2018; Galvez et al., 2016; Manning, 2018) and observed in the simulations are included. Possible complexation with silica components due to the lack of thermodynamic data as well as mineral reactions are not included. The neutral pH∕pOH is fixed by the ion product of water (Marshall and Franck, 1981). The thermodynamic properties of the competing aqueous species at high P∕T conditions are computed using the HKF model parameters reported by Mei et al. (2018), Shock and Helgeson (1988), Shock et al. (1997) and Shock et al. (1989) using the DEW model (Sverjensky et al., 2014). For this simple model, a Y concentration of 23 ppm in solution is assumed. This amount corresponds to measurements in subducted material such as mid-ocean-ridge basalt (Sun and McDonough, 1989) and is in the range of Y solubility in Cl⁻-bearing brines reported by Tropper et al. (2011); Schmidt et al. (2007a).

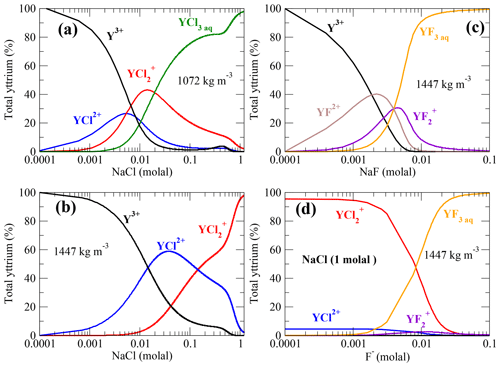
Figure 12 Y–chloride and Y–fluoride species distribution computed from the AIMD data assuming 23 ppm dissolved yttrium in aqueous solution at 800 ^∘C. (a, b) Y–chloride species distribution versus the logarithmic sodium chloride concentration in low- and high-density fluid; (c) Y–fluoride species versus the amount of dissolved NaF and (d) $\mathrm{Y}-\mathrm{Cl}/\mathrm{F}$ species in a 1 molal NaCl solution with increasing F⁻ concentration. The pH of the solutions is changing in a range of ±1.7 over the concentration ranges.

Comparing the Y–chloride speciation in Fig. 12a–b, it can be noted that yttrium is mainly associated with Cl⁻ at an NaCl concentration of ∼0.005 molal in the lower-density fluid, whereas under higher-density conditions this state is reached at ∼0.01 molal NaCl in solution. For a fluid density of 1072 kg m⁻³, YCl₃ is the main species above an NaCl concentration of 0.01 molal. Under high-density conditions, ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ is the major species at a higher NaCl concentration of 0.14 molal. This shows that rather small amounts of dissolved NaCl are needed to form Y–chloride species under subduction-zone P∕T conditions if the yttrium is in solution. The required amounts of chloride presumably occur in subduction fluids as demonstrated in a variety of studies (Barnes et al., 2018; Aranovich and Safonov, 2018). However, it has been discussed by Tropper et al. (2013) that fluoride aqueous complexes are much more capable to mobilize significant amounts of yttrium. As shown in Fig. 12c for a fluid-bearing Y+NaF (in the absence of other ligands) at an NaF concentration of about 0.0014 molal, Y–fluoride complexes are the majority species. Deep aqueous fluids in the Earth's crust are presumed to be mixtures of H₂O plus salt (mainly NaCl, CaCl₂ and KCl) (Manning, 2018). Therefore, in Fig. 12d, the speciation in a 1 molal NaCl brine with increasing amount of fluoride in the solution at a density of 1447 kg m⁻³ is computed. Here, ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ and YF_3aq are the dominant species. Below a F⁻ concentration of approximately 0.01 molal, Y–chloride complexes are formed, and above this concentration, Y–fluoride becomes more important, at least in high-density brines. At lower densities, the formation of Y–fluoride evolves at lower fluoride concentration due to the strong increase of complex stability as shown in Fig. 11c.

Estimates of the fluoride content in aqueous phases evolving in subducting slabs are given in the range of ∼0.003–0.18 molal derived from analysis of melt inclusions and metamorphic rocks (Portnyagin et al., 2007; Hughes et al., 2018; Aranovich and Safonov, 2018), thermodynamic modeling (Zhu and Sverjensky, 1991) and the fugacity ratio $f_{\mathrm{HF}}/f_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ based on partitioning data between mineral and fluid (Sallet, 2000; Yardley, 1985). The simple model outlined above shows that only a low fluoride concentration in the metamorphic aqueous fluids is needed to change the yttrium speciation and therefore its mobility. This outcome is in line with recent thermodynamic modeling by Xing et al. (2018) that shows that a small amount of dissolved F⁻ (tens of ppm) in ore-forming solutions in equilibrium with a granite assemblage is able to mobilize significant amount of REEs. But the high immobility of yttrium in crustal as well as subduction-zone metasomatism (Ague, 2017) might reflect a low fluorine activity in the majority of metasomatic fluids due to formation of fluoride species, e.g., HF_aq, ${\mathrm{HF}}_{\mathrm{2}}^{-}$, ${\mathrm{SiF}}_{\mathrm{6}}^{\mathrm{2}-}$ or Si(OH)₂F_2 aq. Therefore, the included thermodynamic properties of HF from Shock et al. (1989) might underestimate its stability. A very low solubility of yttrium-bearing minerals as suggested by Migdisov et al. (2016) and the retrograde solubility of REE phosphates (Schmidt et al., 2007a; Cetiner et al., 2005) could play an important role in the fixation of yttrium and other HREEs.

At high densities, the stability of Y–hydroxide complexes might be higher than the HKF regression indicates. As shown by Liu et al. (2012), at room temperature, the $\mathrm{Y}-{\mathrm{OH}}^{-}$ complexation is sensitive to pH changes and could evolve under more alkaline conditions as presumed for deep metasomatism (Galvez et al., 2016). But with the applied methods in this study, no further statement can be made due to the limitations of the PMF thermodynamic integration approach to extract reaction free energies for all relevant individual reactions including different intermediate states and dynamic changes such as proton transfer. To overcome this problem, multiple constraints could be applied as suggested by Ivanov et al. (2006) but this would lead to even longer simulation times and might require more than the available computation resources for reaching sufficient convergence of structures and energies (Mark et al., 1994). Therefore, other free energy sampling methods could be promising alternatives, e.g., the metadynamics approach (Laio and Parrinello, 2002). This method has been successfully applied to compute acid constant (pK_a) in combination with quantum mechanical molecular dynamics (e.g., Sakti et al., 2018; Tummanapelli and Vasudevan, 2015) and to find new reaction pathways (see Pérez de Alba Ortíz et al., 2018; Pietrucci et al., 2018). To probe aqueous systems or mineral–fluid interactions of more realistic size and composition, classical molecular dynamics simulations in combination with force field interaction potentials or/and machine learning potentials (Behler and Parrinello, 2007; Cheng et al., 2019) certainly have potential to provide significant progress in this field.

5 Conclusions

The results of the ab initio molecular dynamics simulations provide new insight into the Y−Cl, Y−F and $\mathrm{Y}-{\mathrm{OH}}^{-}$ complexation in highly saline solutions, as they occur in geological settings, e.g., of subduction zones. Firstly, Y–chloride aqueous complexes are observed at 800 ^∘C and 1.3 or 4.5 GPa where YCl₃ and ${\mathrm{YCl}}_{\mathrm{2}}^{+}$ are the major species. Moreover, the destabilization of ${\mathrm{YCl}}_{\mathrm{4}}^{-}$ and ${\mathrm{YCl}}_{\mathrm{5}}^{\mathrm{2}-}$ indicates that there are no other Y–chloride species that have to be considered at least in high-grade metamorphic processes.

The extracted thermodynamic properties of Y–chloride species presented in this study are the first published data set to our knowledge. The stability of Ho–chloride complexes derived from thermodynamic calculations based on an HKF regression (Migdisov et al., 2009) at a solution density of 1073 kg m⁻³ suggests that Y and Ho behave very similar in Cl⁻ rich solutions but with increasing solution density Y–chloride complexes are more favorable than Ho–chloride complexes. On the contrary, Y shows a much stronger association with fluoride compared to Ho, which could explain their different behavior in F-rich aqueous environments. A different association behavior of both elements with respect to OH⁻ would have an even higher impact on the Y∕Ho fractionation because mineral solubilities and mineral surface adsorption are much more controlled by the pH and pOH values than the halide content of the aqueous fluid.

The formation of Y–fluoride complexes in high-density aqueous fluids happens even at very low F⁻concentrations and should lead to a high mobility of Y (HREE) as observed in natural samples. Only in very fluorine-rich environments (e.g., Pan and Fleet, 1996; Harlov et al., 2006) significant amounts of HREEs are mobilized. This finding may indicate that the fluoride activity in the majority of metamorphic aqueous fluids is rather low. The reason for that could be the high affinity of fluorine to silicate (Dolejš and Zajacz, 2018; Dalou et al., 2015), which is one of the main components of aqueous phases in metamorphic processes (Manning, 2018; Hermann et al., 2006). In high-grade metamorphic fluids, it is also necessary to consider that more cations are competing for fluoride to form, e.g., MgF⁺ and CaF⁺. This leads to a decrease of the F⁺ activity as well.

As discussed by Ague (2017), the HREE mass change by fluid–rock interaction is much more determined by the mineral assemblages and phosphate mobility and therefore the halide content of the fluid phase might not be the only controlling factor for the HREE mobility. Nevertheless, the thermodynamic data reported here are consistent with the results of the HKF regression. Furthermore, the stability constants are affected by the formation of hydroxide mixed complexes and HCl∕HF formation during the thermodynamic integration. Therefore, the presented thermodynamic quantities can only be considered as semi-quantitative. Furthermore, it must be emphasized that the applied activity correction could be a source of huge uncertainty. As demonstrated by Hünenberger and McCammon (1999), the Ewald summation, that is used to build up the periodic boundary condition within the simulation, disrupts the solvation free energy of highly charged ions. But this kind of perturbation is not accounted in the Debye–Hückel approach. Therefore, a more systematic evaluation of the impact of artificial periodic electrostatics and neutralizing background charge on the computed thermodynamic properties derived from AIMD simulations especially at high temperatures is required in future studies.