Azimuth-, angle- and frequency-dependent seismic velocities of cracked rocks due to squirt flow

Understanding the properties of cracked rocks is of great importance in scenarios involving CO₂ geological sequestration, nuclear waste disposal, geothermal energy, and hydrocarbon exploration and production. Developing noninvasive detecting and monitoring methods for such geological formations is crucial. Many studies show that seismic waves exhibit strong dispersion and attenuation across a broad frequency range due to fluid flow at the pore scale known as squirt flow. Nevertheless, how and to what extent squirt flow affects seismic waves is still a matter of investigation. To fully understand its angle- and frequency-dependent behavior for specific geometries, appropriate numerical simulations are needed. We perform a three-dimensional numerical study of the fluid–solid deformation at the pore scale based on coupled Lamé–Navier and Navier–Stokes linear quasistatic equations. We show that seismic wave velocities exhibit strong azimuth-, angle- and frequency-dependent behavior due to squirt flow between interconnected cracks. Furthermore, the overall anisotropy of a medium mainly increases due to squirt flow, but in some specific planes the anisotropy can locally decrease. We analyze the Thomsen-type anisotropic parameters and adopt another scalar parameter which can be used to measure the anisotropy strength of a model with any elastic symmetry. This work significantly clarifies the impact of squirt flow on seismic wave anisotropy in three dimensions and can potentially be used to improve the geophysical monitoring and surveying of fluid-filled cracked porous zones in the subsurface.

1 Introduction

Wave propagation is controlled by the effective rock properties. Wave velocity and attenuation can be estimated from seismic data in scenarios such as seismic exploration, seismology, borehole measurements and tomography. Rock physics could then be used to estimate different rock properties, such as mineral composition, elastic moduli, the presence of a fluid, and pore space connectivity (and hence permeability) from seismic measurements. Thus, investigation of how cracks and fluids affect seismic properties has many practical applications. In activities including nuclear waste disposal, CO₂ geological sequestration, hydrocarbon exploration and production, geothermal energy production, and seismotectonics, a quantification of the fluid content, porosity and permeability of rocks are of great interest. All these activities can benefit from rock physics studies, and that is why cracked rocks have been under intensive studies during the last decades.

Cracks and grain-scale discontinuities are the key rock parameters which control effective elastic and hydraulic properties of such rocks. Many studies show that seismic waves exhibit significant dispersion and attenuation in cracked porous rocks due to pore-scale fluid flow (O'Connell and Budiansky, 1977; Dvorkin et al., 1995; Gurevich et al., 2010; Müller et al., 2010). Furthermore, cracks cause significant seismic wave anisotropy (Schoenberg and Sayers, 1995; Sayers and Kachanov, 1995; Sayers, 2002; Chapman, 2003; Maultzsch et al., 2003; Tsvankin and Grechka, 2011).

Fluid flow due to a passing wave may happen at different scales: at the wavelength scale, at the mesoscopic scale and at the pore scale (Müller et al., 2010). Biot's theory (Biot, 1962) describes the so-called global flow at the wavelength scale, but its overall effect on a passing wave at seismic frequencies is usually much smaller than that of fluid flow at the mesoscopic and pore scales (Pride et al., 2004). The mesoscopic scale is that much larger than the pore-scale but smaller than the wavelength. At this scale, studies are performed in the framework of Biot theory, assuming heterogeneous rock properties. One can define fractures as discontinuities at the mesoscopic scale and cracks as discontinuities at the pore scale. There are several analytical and numerical studies on the effect of wave-induced fluid flow between mesoscopic fractures and a porous rock background and between interconnected fractures using Biot's equations (Brajanovski et al., 2005; Rubino et al., 2013; Quintal et al., 2014; Masson and Pride, 2014; Grab et al., 2017; Hunziker et al., 2018; Caspari et al., 2019) as well as on the comparison between the numerical and analytical results (Guo et al., 2017, 2018). Experimental studies of synthetic rock samples showed the impact of fluid-saturated fractures on seismic velocities (Amalokwu et al., 2016; Tillotson et al., 2012, 2014). The resulting frequency-dependent anisotropy was analyzed by Carcione et al. (2013), Rubino et al. (2017) and Barbosa et al. (2017). The last two also considered fracture-to-fracture flow, in addition to fracture-to-background flow.

At the pore scale, a passing wave induces fluid pressure gradients which occur between interconnected cracks, as well as between cracks and stiffer pores. Such pressure gradients force fluid to move between different cracks and pores until the pore pressure equilibrates throughout the connected pore space. This phenomenon, known as squirt flow (Mavko and Nur, 1975), causes strong energy dissipation due to the viscosity of the fluid and the associated viscous friction. Several experimental studies confirmed the importance of squirt flow at different frequency ranges (Mayr and Burkhardt, 2006; Best et al., 2007; Adelinet et al., 2010; Mikhaltsevitch et al., 2015; Pimienta et al., 2015; Subramaniyan et al., 2015; Chapman et al., 2019). There are several analytical solutions for squirt flow (O'Connell and Budiansky, 1977; Dvorkin et al., 1995; Chapman et al., 2002; Guéguen and Sarout, 2009, 2011; Gurevich et al., 2010), which are based on simplified pore geometries and many physical assumptions.

Dispersion and attenuation caused by squirt flow can be simulated numerically by solving the coupled fluid–solid deformation at the pore scale using Lamé–Navier and Navier–Stokes equations with appropriate boundary conditions and then calculating effective frequency-dependent viscoelastic properties. During the last decades, many studies used numerical methods to solve mechanical problems (Andrä et al., 2013a, b; Saxena and Mavko, 2016). Recently, some numerical studies appeared in the geophysical literature aiming to solve the coupled fluid–solid deformation and hence studying dispersion and attenuation caused by squirt flow (Zhang et al., 2010; Zhang and Toksöz, 2012; Quintal et al., 2016, 2019; Das et al., 2019; Alkhimenkov et al., 2020). Das et al. (2019) numerically simulated a fully coupled fluid–solid interaction at the pore scale for digital rock samples. They modeled the pore fluids as Newtonian fluids using the Navier–Stokes equation with appropriate coupling between both the solid and liquid phases, accounting for inertial effects. Quintal et al. (2016, 2019) simplified the Navier–Stokes equations by neglecting the inertial term and hence used the linearized quasistatic Navier–Stokes equation.

We numerically simulate squirt flow in three dimensions and calculate frequency-dependent effective stiffness moduli using the finite-element method to solve the quasistatic Lamé–Navier equations coupled to the linearized quasistatic Navier–Stokes equations (Quintal et al., 2016, 2019; Alkhimenkov et al., 2020). We apply an oscillatory deformation to certain boundaries of the numerical model, and, assuming that the wavelength is much larger than the size of individual cracks, we calculate the volume-average stress and strain fields and the resulting effective stiffness moduli. Then, we calculate the associated azimuth-, angle- and frequency-dependent seismic velocities by solving the Christoffel equation. The main goal of this study is to analyze seismic anisotropy due to squirt flow in three dimensions since the previous numerical studies of seismic anisotropy were performed only in two dimensions and in the framework of Biot's theory (Rubino et al., 2017; Barbosa et al., 2017).

This paper is organized as follows. First, we briefly describe the numerical methodology. Then, we describe the numerical model and show the numerical results – frequency-dependent effective stiffness moduli. After, by solving the Christoffel equation, we evaluate the angle-, azimuth- and frequency dependent velocities of the model. Lastly, we quantify the anisotropy strength of the models analyzing the conventional Thomsen-type anisotropy parameters and also by adopting another scalar parameter.

2 Numerical methodology

We consider that at the pore scale, a rock is composed of a solid material (grains) and a fluid-saturated pore space (cracks). The numerical methodology is described by Quintal et al. (2016, 2019) and Alkhimenkov et al. (2020), and here we briefly outline the main equations. The solid phase is described as a linear isotropic elastic material for which the conservation of momentum is (e.g., Landau and Lifshitz, 1959b and Nemat-Nasser and Hori, 2013)

$$\begin{array}{}\text{(1)}& \mathrm{\nabla }\cdot \mathit{\sigma }=\mathrm{0},\end{array}$$

where “∇⋅” denotes the divergence operator acting on the stress tensor σ. The infinitesimal stress–strain relation for an elastic material can be written as

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\sigma }=& (K-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mathit{\mu })\text{tr}\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left((\mathrm{\nabla }\otimes \mathit{u})+(\mathrm{\nabla }\otimes \mathit{u}{)}^{\text{T}}\right)\right){\mathbf{I}}_{\mathrm{2}}\\ +& \mathrm{2}\mathit{\mu }\left({\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left((\mathrm{\nabla }\otimes \mathit{u})+(\mathrm{\nabla }\otimes \mathit{u}{)}^{\text{T}}\right)\right),\end{array}\end{array}$$

where I₂ is the second-order identity tensor, tr is the trace operator, “⊗” defines the tensor product, the superscript “T” corresponds to the transpose operator, u is the displacement vector, and K and μ are respectively the bulk and shear moduli.

The fluid phase is described by the quasistatic linearized compressible Navier–Stokes momentum equation (Landau and Lifshitz, 1959a):

$$\begin{array}{}\text{(3)}& -\mathrm{\nabla }p+\mathit{\eta }{\mathrm{\nabla }}^{\mathrm{2}}\mathit{v}+{\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\mathit{\eta }\mathrm{\nabla }\left(\mathrm{\nabla }\cdot \mathit{v}\right)=\mathrm{0},\end{array}$$

where v is the particle velocity, p is the fluid pressure and η is the shear viscosity. Equation (3) is valid for the laminar flow of a Newtonian fluid. In the finite-element numerical solver, Eqs. (2)–(3) are combined in the space–frequency domain

$$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{ij}=\mathit{\lambda }e{\mathit{\delta }}_{ij}+\mathrm{2}\mathit{\mu }{\mathit{ϵ}}_{ij}+i\mathit{\omega }\left(\mathrm{2}\mathit{\eta }{\mathit{ϵ}}_{ij}-{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}\mathit{\eta }e{\mathit{\delta }}_{ij}\right),\end{array}$$

where ϵ_ij represents the components of the strain tensor ${\mathit{ϵ}}_{ij}=\mathrm{0.5}\left(u_{i,j}+u_{j,i}\right)$, e is the trace of the strain tensor, λ and μ are the Lame parameters, u_i is the displacement in the ith direction, δ_ij is the Kronecker delta, i is the imaginary unit, and ω is the angular frequency. In the domain representing a solid material, Eq. (4) reduces to Eq. (2) by setting the shear viscosity η to zero. In the domain representing compressible viscous fluid, Eq. (3) is recovered by setting the shear modulus μ to zero. The solid and fluid displacements are described by the same variable, and thus they are naturally coupled at the boundaries between subdomains (Quintal et al., 2016, 2019). In the simulations, the energy dissipation is caused only by fluid pressure diffusion, since inertial terms are neglected.

The COMSOL Multiphysics partial differential equation module is used for implementing Eqs. (1) and (4) (displacement-stress formulation) in a weak form. Our numerical results can be fully reproduced by using any open-access software which includes mesh generation and finite-element implementation with a corresponding solver for a linear system of equations. The whole spatial domain is discretized using an unstructured mesh with tetrahedral elements. A direct PARDISO solver (Schenk and Gärtner, 2004) is used for solving the linear system of equations. Direct relaxation tests are performed to compute all components of the stiffness matrix (in Voigt notation) c_ij. The basic idea of the direct relaxation tests is that a displacement boundary condition of the form $u={\mathrm{10}}^{-\mathrm{6}}\times \exp \left(i\mathit{\omega }t\right)$ is applied to a certain external wall of the model and in a certain direction, while at other walls of the model the displacements are set to zero or let free to change. In the direct tests that we perform, only one component of the stiffness matrix c_ij can be directly calculated after one numerical simulation. A detailed description of the boundary conditions is given in Alkhimenkov et al. (2020). The initial conditions for displacements are set to zero. The resulting stress and strains are averaged over the spatial domain for each frequency. Then, the complex-valued c_ii(ω) components (diagonal) are calculated for each frequency (in Voigt notation, no index summation):

$$\begin{array}{}\text{(5)}& c_{ii}\left(\mathit{\omega }\right)={\displaystyle \frac{\langle {\mathit{\sigma }}_i\left(\mathit{\omega }\right)\rangle }{\langle {\mathit{ϵ}}_i\left(\mathit{\omega }\right)\rangle }},\end{array}$$

where 〈⋅〉 represents the volume averaging over the sample volume. For calculating the P-wave modulus ($ii=\mathrm{11},\mathrm{22},\mathrm{33}$), a harmonic displacement on the i direction is applied perpendicularly to a wall of the model. At the other walls of the model, the normal component of the displacement is set to zero. For calculating shear components of the stiffness matrix ($ii=\mathrm{44},\mathrm{55},\mathrm{66}$), the boundary conditions applied are those of a simple shear test. For the c₁₂(ω), c₁₃(ω) and c₂₃(ω) components (off-diagonal), mixed direct tests are needed, and the corresponding boundary conditions are given in Appendix A. The corresponding inverse quality factor is (O'connell and Budiansky, 1978)

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{\mathrm{1}}{Q_{ij}\left(\mathit{\omega }\right)}}={\displaystyle \frac{\text{Im}\left(c_{ij}\left(\mathit{\omega }\right)\right)}{\text{Re}\left(c_{ij}\left(\mathit{\omega }\right)\right)}}.\end{array}$$

Note that usually the inverse quality factor is used as a measure of attenuation (O'connell and Budiansky, 1978). In this study, we show the inverse quality factor for each component of the stiffness tensor, even though the ratio Im(c_ij(ω))∕Re(c_ij(ω)) does not represent attenuation of any corresponding wave mode for some components.

3 Numerical model

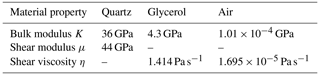
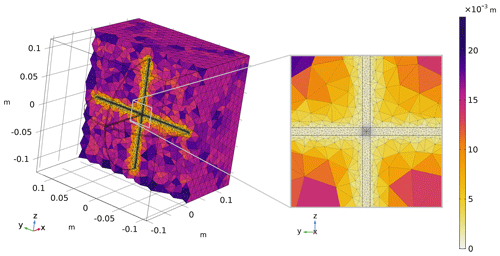
Two 3D numerical models are constructed, which consist of a pore space embedded into an elastic solid grain material (Fig. 1). The solid grain material is represented by a cuboid whose size is ($\mathrm{0.24}\times \mathrm{0.24}\times \mathrm{0.24}$) m³. The pore space consists of two perpendicular cracks represented by thin cylinders of 0.002 m thickness, 0.1 m radius (i.e., the aspect ratio is thickness divided by diameter – 0.01) and fully saturated with a liquid. In the first model, the two cracks are disconnected, while, in the second model, the two cracks are connected (cross sections in Fig. 1). The employed liquid properties are those of glycerol, and the grain material has properties of quartz (Table 1).

A fine, regular mesh is used inside the crack to accurately account for dissipation, while in the grain material the mesh is coarser (Fig. 2). The total number of elements is 3.3×10⁶. The simulation is performed for 12 different frequencies from 10¹ to 10^6.5 Hz for each of the nine components of the stiffness matrix (c₁₁, c₂₂, c₃₃, c₁₂, c₁₃, c₂₃, c₄₄, c₅₅, c₆₆). For each frequency, the solver uses approximately 0.95 TB (terabytes) of RAM memory and takes approximately 2.5 h on 32 Intel dual-socket E5-2683 v4 2.1 GHz (1024 GB RAM) cores.

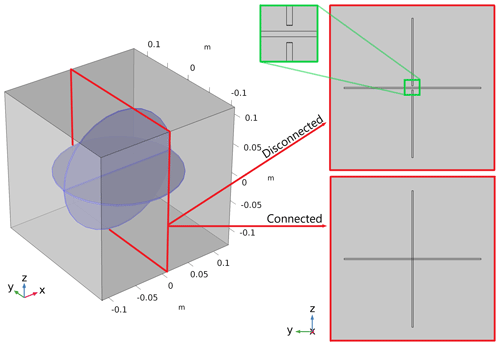
Figure 1 Sketch illustrating two flat cylinders representing two cracks. The blue region represents the pore space saturated with a fluid and the transparent gray area corresponds to the solid grain material. In the first model, the two cracks are disconnected as illustrated by the upper right sketch. In the second model, the two cracks are connected as illustrated by the lower right sketch.

One crack embedded into an isotropic background induces a transverse isotropy (five independent components of the stiffness tensor, e.g., Mavko et al., 2009). If the crack is parallel to the x–y plane, then the symmetry is vertical and the medium exhibits vertical transverse isotropy – VTI symmetry. If the crack is parallel to the x–z plane, then the symmetry is horizontal and the medium exhibits horizontal transverse isotropy – HTI symmetry. If two cracks, perpendicular to each other, are embedded into an isotropic material and the crack compliances are different, then the medium exhibits orthorhombic symmetry (nine independent components of the stiffness tensor). If the crack compliances are the same, then the medium symmetry is tetragonal (six independent components of the stiffness tensor); some authors attribute this geometry to a special case of orthorhombic symmetry (e.g., Bakulin et al., 2000b), while tetragonal and orthorhombic symmetry classes are different. On the other hand, one can argue that an orthorhombic medium (created by two perpendicular sets of cracks) degenerates into a tetragonal medium if the crack compliances are the same.

The symmetry of the saturated numerical model with connected cracks is tetragonal (Fig. 1), because the crack compliances are the same. Thus, there are only six independent components of the stiffness tensor. We will see that the symmetry of the saturated numerical model with disconnected cracks is orthorhombic, because one crack is stiffer than the other one due to its separation into two parts. However, the difference between c₂₂ and c₃₃ stiffness components is less then 0.3 %, thus the divergence from the tetragonal symmetry is negligible, and therefore this model is considered tetragonal as well.

Table 1 Material properties of the numerical model.

4 Results

4.1 Dry stiffness moduli

Let us first consider the geometry shown in Fig. 1 with a pore space filled with air (i.e., dry). We perform nine relaxation tests to calculate the full stiffness tensor for each of the two models with connected and disconnected cracks. The resulting effective stiffness moduli for the model with connected cracks are (in Voigt notation)

$$\begin{array}{}\text{(7)}& c_{ij}^{\text{Con}}=\left[\begin{array}{cccccc}\mathrm{93.53}& \mathrm{4.65}& \mathrm{4.65}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{4.65}& \mathrm{63.91}& \mathrm{5.46}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{4.65}& \mathrm{5.46}& \mathrm{63.91}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{31.62}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{35.16}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{35.16}\end{array}\right]\left(\text{GPa}\right).\end{array}$$

For the model with disconnected cracks, the effective stiffness moduli are (in Voigt notation)

$$\begin{array}{}\text{(8)}& c_{ij}^{\text{Dis}}=\left[\begin{array}{cccccc}\mathrm{93.55}& \mathrm{4.92}& \mathrm{4.60}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{4.92}& \mathrm{69.21}& \mathrm{4.40}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{4.60}& \mathrm{4.40}& \mathrm{64.06}& \mathrm{0}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{31.95}& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{35.16}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{0}& \mathrm{36.96}\end{array}\right]\left(\text{GPa}\right).\end{array}$$

The effective stiffness moduli of the two models are different. Zero values are written if the value is below 0.0002 GPa (i.e., up to numerical precision). The $c_{ij}^{\text{Con}}$ stiffness matrix precisely belongs to the tetragonal symmetry class, while the $c_{ij}^{\text{Dis}}$ stiffness matrix has all diagonal components different from each other; thus, it represents the orthorhombic symmetry class. The largest difference between $c_{ij}^{\text{Con}}$ and $c_{ij}^{\text{Dis}}$ is in the c₂₂ component; i.e., $\mathrm{\Delta }{c}_{\mathrm{22}}=c_{\mathrm{22}}^{\text{Dis}}-c_{\mathrm{22}}^{\text{Con}}=\mathrm{5.3}$ GPa. That is a significant difference and it is only due to the vertical crack separation. There are two different features which must be clearly separated. (1) The effect of crack intersection without changing the crack geometry on the effective elastic properties. In this case, the crack intersection is achieved by changing the spatial position of the cracks. Grechka and Kachanov (2006) studied numerically the effect of crack intersection without changing the crack geometry. They concluded that crack intersection has a very little impact on the effective elastic moduli. (2) The effect of the crack partition into two “halves” on the effective elastic properties. In this case, the partitioned crack has a long, thin contact area across the whole diameter (Fig. 1). It is well known that the contact areas inside a crack significantly reduce crack compliance (Trofimov et al., 2017; Kachanov and Sevostianov, 2018; Markov et al., 2019; Lissa et al., 2019). Comparing Eqs. (7) and (8), we also observe that the thin contact area significantly reduces the crack compliance: the effective dry moduli of the model with disconnected cracks are much higher compared to the model with connected cracks. An intuitive explanation is the following: if crack surfaces have not been changed by changing the spatial position of the cracks in the volume, the effect of crack intersection is negligible (Grechka and Kachanov, 2006); if the crack surfaces have been changed – as we did in the present study by partitioning the vertical crack into two pieces (and introducing a thin additional contact area) – the effective elastic moduli would become much stiffer compared to the model where the crack surfaces have not been changed.

Figure 2 Sketch illustrating the element's size distribution for the model with connected cracks. The element's size in the crack is $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}-\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$ m, and in the surrounding grain material it is $\mathrm{2.4}\times {\mathrm{10}}^{-\mathrm{3}}-\mathrm{1.6}\times {\mathrm{10}}^{-\mathrm{2}}$ m. The element's size distribution for the model with disconnected cracks is the same.

4.2 Fluid pressure fields

Here and later on we deal only with a liquid-saturated pore space. The liquid has properties of glycerol (Table 1). A direct P-wave modulus test is performed to calculate dispersion and attenuation for the c₃₃ component. (A harmonic displacement is applied to the top wall of the model in the z direction, while the normal component of the displacement is set to zero on all the other walls.) Figure 3 shows snapshots of the fluid pressure P_f in the cracks at three different frequencies, in the vertical middle slice of the model (the y–z plane, red frame in Fig. 1a). For the model with connected cracks, at low frequencies, there is enough time for pressure equilibration between the cracks; thus, the pore pressure is uniform throughout the pore space (Fig. 3, LF (connected)). This is called the relaxed state. At intermediate frequencies, there is a large pressure gradient in the cracks, which corresponds to the maximum attenuation due to squirt flow between cracks (Fig. 3, Fc (connected)). At high frequencies, there is no time for fluid to move; hence, there is no fluid pressure equilibration between the vertical and horizontal cracks (Fig. 3, HF (connected)). This is called the unrelaxed state. Therefore, at high frequencies, the connected cracks behave as hydraulically isolated and the fluid highly stiffens the crack.

In the model with disconnected cracks, the fluid pressure in the cracks is the same in all three regimes, which corresponds to the unrelaxed state in the model with connected cracks. The unrelaxed state can be interpreted as the elastic limit because there is no fluid flow between the cracks, and the effective properties of the two models (connected and disconnected cracks) are the same, as will be shown in the next subsection.

4.3 Dispersion and attenuation

4.3.1 Elastic moduli

Figure 4 shows the numerical results for the complex-valued frequency-dependent components of the stiffness matrix c_ij(ω) (in Voigt notation) for the models with connected and disconnected cracks filled with glycerol. In the model with connected cracks, the real part of the c_ij component and the corresponding inverse quality factor (Eq. 6) curves show strong frequency-dependent behavior of the c₂₂, c₃₃ and c₂₃ components (Fig. 4a and c). The inverse quality factor and dispersion of the c₂₂ and c₃₃ components coincide because the geometrical properties of the two cracks are the same (Fig. 4a) and the model is symmetric. The c₁₁ component is nondispersive and exhibits zero attenuation. The dispersion of the c₄₄, c₅₅ and c₆₆ components is negligible and these components also exhibit negligible attenuation (Fig. 4b). The c₁₂ and c₁₃ components are nondispersive, the c₂₃ component exhibits strong negative dispersion and a negative inverse quality factor peak is shifted towards high frequencies compared to that of the c₂₂ and c₃₃ components. A similar phenomenon has been reported by Guo et al. (2017) in the context of two-dimensional simulations. The c₂₃ component does not correspond to a wave mode alone; it is always used together with c₂₂ and/or c₃₃ components. Therefore, no wave will gain energy. This negative inverse quality factor sign for the c₂₃ component was also verified using Kramers–Kronig relations. In other words, different components of the stiffness tensor might have positive or negative values of the ratio Im(c₂₃)∕Re(c₂₃) but, when we calculate the velocity and the inverse quality factor of a wave, the cumulative effect of all c_ij components must be physical and no negative attenuation will be observed.

Note that the width of the inverse quality factor peak (at half amplitude) for the components c₂₂ and c₃₃ has a 1.5 order of magnitude (Fig. 4a and 4c). It means that attenuation and dispersion due to squirt flow play a significant role over a broad frequency range even for cracks with a single aspect ratio.

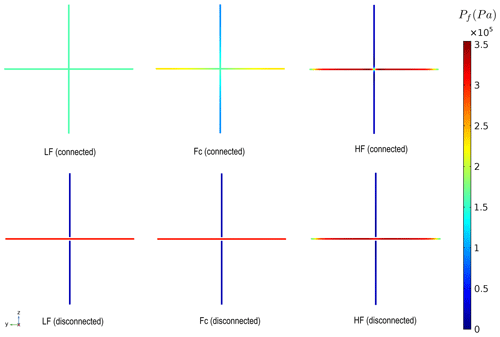
Figure 3 Snapshots of the fluid pressure P_f in the cracks at three different frequencies: LF – the low-frequency limit (corresponds to 10¹ Hz, relaxed state), Fc – intermediate frequency snapshot (corresponds to 10⁴ Hz, close to the characteristic frequency) and HF – the high-frequency limit (corresponds to 10^6.5 Hz, unrelaxed state).

In the model with disconnected cracks, all components of the stiffness tensor c_ij(ω) (Fig. 4a and 4c) are constant across the whole frequency range and exhibit zero inverse quality factor. Furthermore, all components are approximately equal to the high-frequency values of the model with connected cracks. This is expected in the unrelaxed state because the connected cracks behave as hydraulically isolated with respect to fluid flow. A very small discrepancy between the two models at high frequencies is associated with the vertical crack partition (two thin regions of pore space replaced with stiffer grain material).

4.3.2 P- and S-wave velocities

Figure 5 shows the P-wave (primary wave) phase velocity as a function of the phase angle of the numerical model with connected and disconnected cracks (Fig. 1), where the zero phase angle corresponds to the vertical wave propagation (along z axis). The P- and S-wave phase velocities are calculated by solving the Christoffel equation, which represents an eigenvalue problem relating the stiffness components c_ij, the phase velocities of plane waves that propagate in the medium and the polarization of the waves (Fedorov, 1968; Tsvankin, 2012). Considering the plane Y–Z, the P-wave velocity is the same for phase angles of 0 and 90^∘; it changes with frequency only for phase angles between 0 and 90^∘ and is maximal in the high-frequency limit at phase angle of $\mathit{\theta }=\mathrm{90}(\pm \mathrm{90})$^∘ (Fig. 5a). Furthermore, in the high-frequency limit the P-wave phase velocity coincides for the models with connected and disconnected cracks. As frequency decreases, the P-wave velocity decreases, and at 10⁴ Hz the P-wave velocity is almost angle independent (yellow curve, Fig. 5a). It is interesting that this “local” isotropy corresponds to the maximum attenuation of the c₂₂ and c₃₃ components (Fig. 4). As frequency further decreases, the P-wave velocity decreases and stays nearly unchanged for the frequencies below 10^3.5 Hz. In the X–Z plane, the P-wave phase velocity is the same for the models with connected and disconnected cracks in the high-frequency limit (Fig. 5b). For the model with connected cracks, as frequency decreases, the P-wave velocity decreases, reaching its minimum at low frequencies (10¹–10^3.5 Hz).

Figures 6–7 show the quasi-shear (SV) and the pure shear (SH) phase velocities as functions of the phase angle of the numerical models with connected and disconnected cracks (Fig. 1). The SV wave velocity is strongly frequency dependent in both the X–Z and Y–Z planes. The SH wave exhibits some frequency-dependent behavior in the X–Z plane and is angle and frequency independent in the Y–Z plane. It is interesting that the SV waves in two different planes have different velocities at 0 and 90^∘ phase angles, which is due to their different wave polarization. The SV wave in the Y–Z plane has the same polarization as the SH wave in the X–Z plane; their velocities are equivalent at the 0 and 90^∘ phase angles. The same conclusion is valid for the SV wave in the X–Z plane and the SH wave in the Y–Z plane. A slight discrepancy (around 0.5 %) between the SV wave velocities for the disconnected crack model (Fig. 6, dashed red line) and the high-frequency velocity for the connected crack model (Fig. 6, green line) at phase angles of 0, 90 and 180^∘ is due to the crack separation.

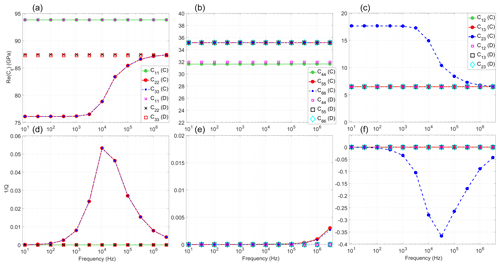
Figure 4 Numerical results for the connected (C) and disconnected (D) crack models: real part of the c_ij components versus frequency (a–c), dimensionless inverse quality factor of the c_ij components versus frequency (d–f). Each symbol corresponds to the test result of one numerical simulation and lines correspond to linear interpolation between discrete numerical results.

Due to the symmetry of the model, the behaviors of the P-, SV-, SH-wave phase velocities in the X–Z and X–Y planes are identical; thus, the results in the X–Y plane are not shown here.

4.4 Quantitative analysis of the frequency-dependent anisotropy

First, we quantify the Thomsen-type anisotropic parameters (Thomsen, 1986) for orthorhombic media (Tsvankin, 1997; Bakulin et al., 2000a). Then, we quantify the universal elastic anisotropy index (Ranganathan and Ostoja-Starzewski, 2008) and the two parameters which define the anisotropy strength in bulk and shear modes. All these anisotropy measures highlight different frequency-dependent features of the models. Our results shown in Fig. 4 (frequency-dependent elastic moduli) are used as input to quantify these anisotropy measures.

4.4.1 Thomsen-type parameters

Thomsen-type anisotropic parameters (ϵ, δ, γ) describe the P-wave anisotropy – ϵ, the shape of the P-wave phase velocity at different phase angles – δ and the S-wave anisotropy – γ: each set of three parameters corresponds to one plane. Thus, for our model symmetry, there are two different planes – Y–Z and X–Z (because the X–Z plane is equivalent to the X–Y plane). In this study, we refer to Thomsen parameters $\left|\mathit{ϵ}\right|,\left|\mathit{\delta }\right|,\left|\mathit{\gamma }\right|\in \left[\mathrm{0},\mathrm{0.1}\right]$ as to weak elastic anisotropy ($|\cdot |$ corresponds to the absolute value), $\left|\mathit{ϵ}\right|,\left|\mathit{\delta }\right|,\left|\mathit{\gamma }\right|\in \left[\mathrm{0.1},\mathrm{0.15}\right]$ as moderate elastic anisotropy and $\left|\mathit{ϵ}\right|,\left|\mathit{\delta }\right|,\left|\mathit{\gamma }\right|\in \left[\mathrm{0.15},+\mathrm{\infty }\right]$ as strong elastic anisotropy. The choice of these intervals is based on the divergence between the exact and approximate (by using Thomsen parameters) equations for the P-wave phase velocities in cracked media.

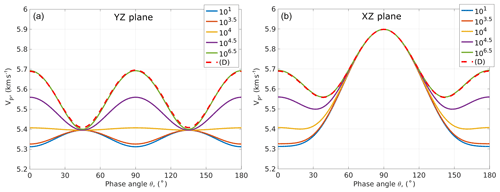
Figure 5 P-wave phase velocity versus phase angle in the Y–Z plane (a) and the X–Z plane (b). Curves 10¹–10^6.5 denote the frequency of the P wave for the model with connected cracks. (D) denotes the P wave for the model with disconnected cracks.

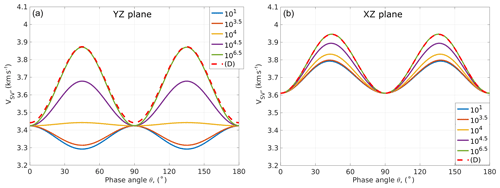
Figure 6 SV-wave phase velocity versus phase angle in the Y–Z plane (a) and the X–Z plane (b). Curves 10¹−10^6.5 denote the frequency of the P wave for the model with connected cracks. (D) denotes the P wave for the model with disconnected cracks.

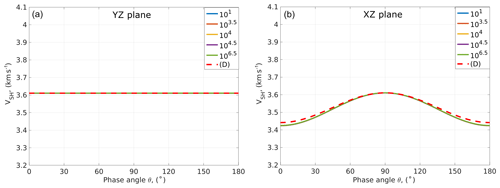
Figure 7 SH-wave phase velocity versus phase angle in the Y–Z plane (a) and the X–Z plane (b). Curves 10¹−10^6.5 denote the frequency of the P wave for the model with connected cracks. (D) denotes the P wave for the model with disconnected cracks.

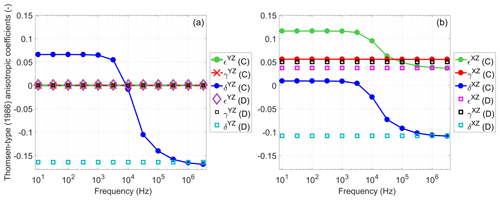
Figure 8 shows the Thomsen-type anisotropy parameters in the Y–Z and X–Z planes (formulas are given in Appendix B). In the high-frequency limit, all anisotropy parameters are the same for both models with connected and disconnected cracks. Furthermore, for the model with disconnected cracks, all anisotropy parameters are frequency independent, because the stiffness tensor is frequency independent. For the model with connected cracks, several anisotropy parameters are frequency dependent due to squirt flow.

In the Y–Z plane, parameters ϵ^YZ and γ^YZ are zero for both models. The parameter δ^YZ is frequency dependent and controls the shape of the P-wave phase velocity between 0 and 90^∘. In the high-frequency limit, δ^YZ exhibits the maximum negative value which corresponds to strong elastic anisotropy. As frequency decreases, δ^YZ also decreases reaching a zero value around 10⁴ Hz, and then δ^YZ increases reaching its positive maximum at low frequencies, which corresponds to weak elastic anisotropy; the positive maximum is approximately one-third of the absolute value of its negative maximum. It is interesting that δ^YZ changes sign from negative to positive, which is indeed observed in the P-wave velocity behavior (Fig. 5a) as P-wave velocity changes polarity with frequency. This was also observed by Barbosa et al. (2017) in the framework of Biot's theory. This polarity change has a fully mechanical nature. In the high-frequency limit, cracks behave as hydraulically isolated and fluid highly stiffens the normal compliance of the cracks (not tangential). As frequency decreases, fluid started to flow from more compliant to stiffer cracks as a response to the applied displacement boundary condition. δ^(yz)=0 corresponds to zero anisotropy; the numerator of δ^YZ is ${\left[c_{\mathrm{23}}\left(\mathit{\omega }\right)+c_{\mathrm{44}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}-{\left[c_{\mathrm{33}}\left(\mathit{\omega }\right)-c_{\mathrm{44}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}$ (see Appendix B). Therefore, for zero anisotropy, c₂₃(ω)+c₄₄(ω) must be equal to c₃₃(ω)−c₄₄(ω). The function c₄₄(ω) is constant across the whole frequency range, c₂₃(ω) is strictly decreasing with frequency and c₃₃(ω) is strictly increasing with frequency (Fig. 4). At a certain frequency (here it is at ∼10⁴ Hz), the c₃₃ and c₂₃ components are in such a combination that $c_{\mathrm{23}}\left({\mathrm{10}}^{\mathrm{4}}\right)+c_{\mathrm{44}}\left({\mathrm{10}}^{\mathrm{4}}\right)\approx c_{\mathrm{33}}\left({\mathrm{10}}^{\mathrm{4}}\right)-c_{\mathrm{44}}\left({\mathrm{10}}^{\mathrm{4}}\right)$, so δ^YZ=0, and the P-wave velocity in the Y–Z plane behaves as in a fully isotropic media.

In the X–Z plane, ϵ^XZ and δ^XZ are frequency dependent in the model with connected cracks. ϵ^XZ exhibits moderate elastic anisotropy at low frequencies, while δ^XZ exhibits moderate elastic anisotropy at high frequencies. Other parameters are frequency independent and exhibit certain nonzero values from weak to moderate elastic anisotropy.

Figure 8 Thomsen-type anisotropic parameters in the Y–Z (a) and X–Z (b) planes.

4.4.2 The universal elastic anisotropy index

The universal elastic anisotropy index A^U (Ranganathan and Ostoja-Starzewski, 2008) is widely used to measure the anisotropy strength in crystallography, engineering and materials science. This parameter is designed to evaluate the anisotropy strength of crystals having any elastic symmetry class (Ranganathan and Ostoja-Starzewski, 2008). Since A^U is a scalar, it gives a simple and fast identification of the overall anisotropy strength of a model. A^U=0 corresponds to zero anisotropy of a model, while the discrepancy of A^U from zero defines the anisotropy strength and accounts for both the shear and the bulk contributions simultaneously. In analogy to the universal elastic anisotropy index, two other parameters are adopted which define the anisotropy strength in bulk A^bulk and in shear A^shear. As far as we are concerned, these parameters have not been widely used in earth sciences: only a few studies were found. Almqvist and Mainprice (2017) applied the universal elastic anisotropy index and two similar parameters for bulk and shear to study seismic properties and anisotropy of the continental crust. Kube and De Jong (2016), Duffy (2018) and Vieira et al. (2019) applied A^U to quantify the elastic anisotropy of polycrystals. A brief review of these anisotropic measures and all necessary equations for their calculation are provided in Appendix C.

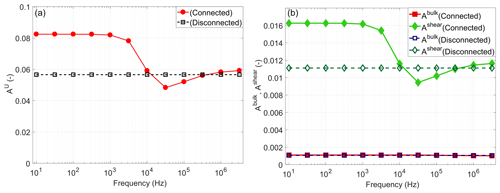
Figure 9 shows the universal elastic anisotropy index A^U and the anisotropy measures in bulk A^bulk(ω) and shear A^shear. For the model with disconnected cracks, A^U is constant and frequency independent (Fig. 9, black line). Because A^U has a certain small value (about 0.058), the model with disconnected cracks exhibits a certain small anisotropy. For the model with connected cracks, A^U in the high-frequency limit is almost the same as for the model with disconnected cracks (Fig. 9, red line). (The nature of the discrepancy is related to the region containing the crack intersection.) For the model with connected cracks, the overall anisotropy slightly decreases towards lower frequencies until 10^4.3 Hz, reaching its minimum of 0.048 (Fig. 9, red line). This local minimum indeed corresponds to the c₂₃ attenuation peak (Fig. 4c). Then, still towards lower frequencies, A^U(ω) increases reaching its maximum of 0.083 at frequencies below 10³ Hz (Fig. 9, red line). Thus, the overall anisotropy of the model mainly increases due to squirt flow between the cracks, so the crack connectivity increases the overall anisotropy of the model towards low frequencies.

The anisotropy measure in bulk A^bulk is constant and frequency independent for the models with connected and disconnected cracks (Fig. 9b). It means that fluid flow does not affect bulk properties of the model or the anisotropy strength in bulk. On the other hand, the anisotropy measure in shear A^shear(ω) basically reproduces the behavior of the universal elastic anisotropy index measure A^U. Therefore, one can conclude that the fluid flow changes anisotropy in shear mode but not in bulk mode.

Figure 9 The universal elastic anisotropy index measure A^U versus frequency (a) and the anisotropy measures in bulk and shear (A^bulk and A^shear) (b). These plots show that the overall anisotropy of the model increases in the low frequencies due to fluid flow.

5 Discussion

5.1 Elastic anisotropy

Thomsen-type anisotropic parameters provide a very detailed description of the velocity anisotropy in different planes. Most importantly, only a limited number of the stiffness tensor coefficients are needed to calculate ϵ, δ and γ in each plane. Thus, Thomsen parameters can be used to quantify the medium anisotropy using seismic data. On the other hand, when all components of the stiffness tensor are known and the model's symmetry is low, it is difficult to analyze the overall anisotropy due to a large number of Thomsen parameters. For example, if the model exhibits orthorhombic symmetry, one should analyze nine Thomsen anisotropic parameters (three in each plane). Due to a large number of Thomsen parameters in this study, it is difficult to evaluate whether the overall medium's anisotropy is increasing or decreasing with frequency and how far the current model is from the closest isotropy. Thus, in addition to (or instead of) the Thomsen-type anisotropic parameters, the universal elastic anisotropy index can be used. The universal elastic anisotropy index A^U and the related measures in bulk, A^bulk, and shear, A^shear, provide the overall description of the anisotropy strength regardless of the model's complexity. The calculation of these parameters is as simple as the calculation of the Thomsen parameters. An obvious disadvantage of the universal elastic anisotropy index (and related measures) is that it requires knowledge of the full stiffness tensor. Thus, this anisotropic measure can be useful to evaluate results of numerical simulations of laboratory experiments and for measuring the anisotropy of single crystals.

The analysis of two sets of anisotropic measures shows that (i) the overall anisotropy of the model with connected cracks (Fig. 1) mainly increases due to squirt flow towards low frequencies with a slight local decrease at intermediate frequencies (Fig. 9a); (ii) in the Y–Z plane, the magnitude of the “delta” anisotropy parameter decreases, reaches zero, and then increases again (reaching approximately one-third of its high-frequency value) towards low frequencies (Fig. 8a, blue curve); and (iii) in the X–Z plane, the “delta” anisotropy parameter decreases towards low frequencies (Fig. 8b, blue curve), while the “epsilon” anisotropy parameter increases (Fig. 8b, green curve).

5.2 Comparison with previous works

In this study, we numerically solve a coupled fluid–solid deformation problem at the pore scale. If we consider the mesoscopic scale scenario and use Biot's (1941) equations, the fluid flow effects on the effective moduli are equivalent to that of the coupled elastic Stokes equations (as in the present study), as it was shown by Quintal et al. (2016). The frequency-dependent anisotropy due to fluid flow at the mesoscopic scale for orthogonal fracture sets with different degrees of connectivity was numerically studied by Rubino et al. (2017), but their study was limited to two dimensions. The main conclusion of Rubino et al. (2017) is that the anisotropy decreases with fracture connectivity in the seismic frequency band due to fluid flow between connected fractures. The Y–Z plane in the present 3D numerical model is reasonably equivalent to the 2D numerical model of Rubino et al. (2017) as well as the physical mechanism under consideration. The results of Rubino et al. (2017) are reflected in Fig. 5 of this study. However, a more in-depth analysis shows that the anisotropy in the Y–Z plane decreases, reaches zero and then increases again towards low frequencies due to squirt flow (Fig. 5a, green, yellow and blue curves, respectively). Moreover, our present study shows that the overall anisotropy of the model with cracks of finite length actually increases due to fluid flow between interconnected cracks (Figs. 8, 9). This conclusion is not universal and is valid only for a specific set of model parameters.

Barbosa et al. (2017) performed a more detailed study of seismic anisotropy for a similar fracture geometry in two dimensions, as in the study of Rubino et al. (2017), specifying that the decrease in anisotropy is described by the anisotropy parameter δ while ϵ is zero. Furthermore, they observed a polarity change of the P-wave phase velocity behavior with frequency. In the present study, the “delta” anisotropy parameter in the Y–Z plane is more pronounced in the low-frequency limit (Fig. 5a, blue curve) compared to the work of Barbosa et al. (2017) due to different material properties and the three-dimensional nature of the present model configuration.

In summary, fluid flow effects on seismic anisotropy are nonlinear with a possible increase or decrease in the elastic anisotropy at different frequencies. These two extreme cases, the maximum negative and the maximum positive δ parameter (and hence P-wave velocity) in the Y–Z plane, correspond to the relaxed and unrelaxed states. In other words, seismic anisotropy may behave completely different in different scenarios; therefore, more studies should be performed, especially with the sensitivity analysis of model parameters.

5.3 A qualitative comparison against analytical models

Numerical simulations are useful but analytical models are especially attractive since they help us to better understand the physics and do not require sophisticated numerical simulations. The limitations of the analytical solutions are restricted to simple pore space geometry, and some assumptions related to physics are needed to derive the closed form analytical formulas. Such a comparison of the numerical results against an analytical solution has been performed by Alkhimenkov et al. (2020) for a different pore space geometry. Unfortunately, there is no analytical solution for the present study considering a periodic distribution of intersecting cracks in three dimensions. But the qualitative comparison of the low- and high-frequency limits (which correspond to relaxed and unrelaxed states) is possible (Mavko and Jizba, 1991). Several analytical studies show that the anisotropy (described by Thompson's parameters) is, in general, more pronounced at high frequencies than at low frequencies (Guéguen and Sarout, 2009, 2011). In the relaxed state, one can calculate the effective dry elastic moduli and use Gassmann's equations to obtain the effective moduli of the saturated medium. In the unrelaxed state, one can calculate the effective elastic moduli by restricting fluid flow (by using zero displacement boundary conditions in the crack intersections). The low- and high-frequency limits for elastic moduli have been calculated using these semi-analytical approaches, and numerical results have been reproduced.

6 Conclusions

We have numerically calculated the frequency-dependent elastic moduli of a fluid-saturated porous medium caused by squirt flow. The considered 3D numerical models consist of two perpendicular connected or disconnected cracks embedded in a solid grain material. Cracks are represented by very flat cylinders filled with a fluid. Grains are described as a linear isotropic elastic material, while the fluid phase is described by the quasistatic linearized compressible Navier–Stokes momentum equation.

We showed that seismic velocities are azimuth, angle and frequency dependent due to squirt flow between connected cracks. The resulting elastic frequency-dependent anisotropy was analyzed by using the Thomsen-type anisotropic parameters and the universal elastic anisotropy index. The latter is a scalar parameter which can be used to analyze the overall anisotropy of the model and its divergence from the closest isotropy. We showed that the seismic anisotropy may locally decrease as well as increase due to squirt flow in one specific plane. However, the overall anisotropy of the model mainly increases due to squirt flow between the cracks towards low frequencies. In the model with disconnected cracks, no fluid flow occurs, and thus the effective properties of the model correspond to the elastic limit. The elastic limit is equivalent to the high-frequency limit for the model with connected cracks. Seismic velocities are only azimuth and angle dependent as for a fully elastic material, and they are independent of frequency. In summary, squirt flow does affect effective mechanical properties of cracked rocks and thus seismic velocity anisotropy. Given that seismic anisotropy variations with frequency are very sensitive to the pore space geometry and material properties, it is difficult to make a general prediction. According to our study, the effective frequency-dependent response of a cracked medium is different in different planes. The local response (in a certain plane) is controlled by crack orientation, which is the key parameter. The magnitude of the frequency-dependent response (i.e., the dispersion and attenuation) is controlled by crack compliances, crack porosity and their fluid content. (Dry or liquid-saturation conditions will cause completely different behavior.) Most importantly, crack porosity is a very important parameter in fluid-saturated rocks (contrary to dry rocks) since it defines the volume of fluid which may flow due to wave propagation, causing wave attenuation and dispersion.

Appendix A: Boundary conditions for c_ij off-diagonal components

Let us consider a cuboid, volume $V=(\mathrm{0},Lx)\times (\mathrm{0},Ly)\times (\mathrm{0},Lz)$ and Γ its boundary, $\mathrm{\Gamma }={\mathrm{\Gamma }}^{xz\mathrm{0}}\cup {\mathrm{\Gamma }}^{xzL}\cup {\mathrm{\Gamma }}^{yz\mathrm{0}}\cup {\mathrm{\Gamma }}^{yzL}\cup {\mathrm{\Gamma }}^{xy\mathrm{0}}\cup {\mathrm{\Gamma }}^{xyL}$, where Γ^xz0 represents an x–z with zero coordinate, Γ^xzL represents an x–z with Ly coordinate, etc. There are six planes in total.

The mixed test for the c₁₃ component can be derived from the anisotropic stress–strain relation (Hooke's law) (similarly to the c₁₃ component in a VTI medium; Alkhimenkov et al., 2020); Γ^xyL is set to u_zz=Δu; u_xx and u_yy are free;
Γ^yzL is set to u_xx=Δu; and u_zz and u_yy are free,
where $\mathrm{\Delta }u={\mathrm{10}}^{-\mathrm{6}}$. In the other four planes, the normal component of the displacement is set to zero and other components are free. The the stress–strain relation for the 〈σ₁〉 stress component is

$$\begin{array}{}\text{(A1)}& \langle {\mathit{\sigma }}_{\mathrm{1}}\rangle =c_{\mathrm{11}}\langle {\mathit{ϵ}}_{\mathrm{1}}\rangle +c_{\mathrm{12}}\langle {\mathit{ϵ}}_{\mathrm{2}}\rangle +c_{\mathrm{13}}\langle {\mathit{ϵ}}_{\mathrm{3}}\rangle .\end{array}$$

Using the abovementioned boundary conditions and setting 〈ϵ₂〉=0, Eq. (A1) becomes

$$\begin{array}{}\text{(A2)}& \langle {\mathit{\sigma }}_{\mathrm{1}}\rangle =c_{\mathrm{11}}\langle {\mathit{ϵ}}_{\mathrm{1}}\rangle +c_{\mathrm{13}}\langle {\mathit{ϵ}}_{\mathrm{3}}\rangle .\end{array}$$

Equation (A2) can be solved for the c₁₃ component; the solution is

$$\begin{array}{}\text{(A3)}& c_{\mathrm{13}}={\displaystyle \frac{\langle {\mathit{\sigma }}_{\mathrm{1}}\rangle }{\langle {\mathit{ϵ}}_{\mathrm{1}}\rangle }}-c_{\mathrm{11}}.\end{array}$$

Equation (A3) is used to calculate the c₁₃ component (c₁₁ is taken from the direct tests).

The mixed test for the c₂₃ (in this numerical model, the c₂₃ is dispersive) component again can be derived from the anisotropic stress–strain relation (Hooke's law) (similarly to the previous test). Γ^xyL is set to u_zz=Δu; u_xx,u_yy are free;
Γ^xzL is set to u_yy=Δu; and u_zz and u_xx are free.

In the other four planes, the normal component of the displacement is set to zero, other components are free. Then, using the following equation

$$\begin{array}{}\text{(A4)}& c_{\mathrm{23}}={\displaystyle \frac{\langle {\mathit{\sigma }}_{\mathrm{2}}\rangle }{\langle {\mathit{ϵ}}_{\mathrm{2}}\rangle }}-c_{\mathrm{22}},\end{array}$$

the c₂₃ component is calculated (c₂₂ is taken from the direct test). Equations (A3)–(A4) are found from Hooke's law considering nonzero strains in the x and z (in y and z) directions and then solving a system of two equations analytically.

Appendix B: Thomsen-type anisotropic parameters

Thomsen-type anisotropic parameters (Thomsen, 1986) are widely used in the applied geophysics community. Thomsen weak anisotropy parameters were originally developed for vertical transverse isotropic media (Thomsen, 1986). A natural extension of these parameters to orthorhombic media was suggested by Tsvankin (1997) and Bakulin et al. (2000a). These parameters correspond to the anisotropy of the compression and shear waves in orthorhombic media in different Cartesian propagation planes. In the Y–Z plane, Thomsen-type anisotropic parameters are

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}{\mathit{ϵ}}^{\left(YZ\right)}\left(\mathit{\omega }\right)=& {\displaystyle \frac{c_{\mathrm{22}}\left(\mathit{\omega }\right)-c_{\mathrm{33}}\left(\mathit{\omega }\right)}{\mathrm{2}{c}_{\mathrm{33}}\left(\mathit{\omega }\right)}},{\mathit{\gamma }}^{\left(YZ\right)}\left(\mathit{\omega }\right)\\ =& {\displaystyle \frac{c_{\mathrm{66}}\left(\mathit{\omega }\right)-c_{\mathrm{55}}\left(\mathit{\omega }\right)}{\mathrm{2}{c}_{\mathrm{55}}\left(\mathit{\omega }\right)}},\end{array}\end{array}$$

and

$$\begin{array}{}\text{(B2)}& {\mathit{\delta }}^{\left(YZ\right)}\left(\mathit{\omega }\right)={\displaystyle \frac{{\left[c_{\mathrm{23}}\left(\mathit{\omega }\right)+c_{\mathrm{44}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}-{\left[c_{\mathrm{33}}\left(\mathit{\omega }\right)-c_{\mathrm{44}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}}{\mathrm{2}{c}_{\mathrm{33}}\left(\mathit{\omega }\right)\left[c_{\mathrm{33}}\left(\mathit{\omega }\right)-c_{\mathrm{44}}\left(\mathit{\omega }\right)\right]}}.\end{array}$$

In the X–Z plane, Thomsen-type anisotropic parameters are

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}{\mathit{ϵ}}^{\left(XZ\right)}\left(\mathit{\omega }\right)=& {\displaystyle \frac{c_{\mathrm{11}}\left(\mathit{\omega }\right)-c_{\mathrm{33}}\left(\mathit{\omega }\right)}{\mathrm{2}{c}_{\mathrm{33}}\left(\mathit{\omega }\right)}},{\mathit{\gamma }}^{\left(XZ\right)}\left(\mathit{\omega }\right)\\ =& {\displaystyle \frac{c_{\mathrm{66}}\left(\mathit{\omega }\right)-c_{\mathrm{44}}\left(\mathit{\omega }\right)}{\mathrm{2}{c}_{\mathrm{44}}\left(\mathit{\omega }\right)}},\end{array}\end{array}$$

and

$$\begin{array}{}\text{(B4)}& {\mathit{\delta }}^{\left(XZ\right)}\left(\mathit{\omega }\right)={\displaystyle \frac{{\left[c_{\mathrm{13}}\left(\mathit{\omega }\right)+c_{\mathrm{55}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}-{\left[c_{\mathrm{33}}\left(\mathit{\omega }\right)-c_{\mathrm{55}}\left(\mathit{\omega }\right)\right]}^{\mathrm{2}}}{\mathrm{2}{c}_{\mathrm{33}}\left(\mathit{\omega }\right)\left[c_{\mathrm{33}}\left(\mathit{\omega }\right)-c_{\mathrm{55}}\left(\mathit{\omega }\right)\right]}}.\end{array}$$

Appendix C: The universal elastic anisotropy index parameter

Assuming that one deals with an anisotropic frequency-dependent effective fourth-rank stiffness tensor C (might be frequency dependent C⇒C(ω)), a compliance tensor is defined as $\mathbf{S}\left(\mathit{\omega }\right)=\mathbf{C}(\mathit{\omega }{)}^{-\mathrm{1}}$. Then, for each frequency, the effective single orientation fourth-rank stiffness and compliance tensors are uniformly distributed and the isotropic stiffness and compliance tensors are calculated. Averaging the single orientation stiffness tensor belongs to the Voigt assumption, which is the theoretical maximum value of the isotropic elastic moduli. On the other hand, averaging the single orientation compliance tensor belongs to the Reuss assumption which is the theoretical minimum value of the isotropic elastic moduli. The resulting isotropic tensors can be expressed in terms of the spherical and deviatoric parts corresponding to bulk K and shear moduli μ:

$$\begin{array}{}\text{(C1)}& {\mathbf{C}}^{\mathrm{V}}\left(\mathit{\omega }\right)=\mathrm{3}{K}^{\mathrm{V}}\mathbf{J}+\mathrm{2}{\mathit{\mu }}^{\mathrm{V}}\mathbf{D}\end{array}$$

and

$$\begin{array}{}\text{(C2)}& {\mathbf{S}}^{\mathrm{R}}\left(\mathit{\omega }\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{3}{K}^{\mathrm{R}}}}\mathbf{J}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{\mathit{\mu }}^{\mathrm{R}}}}\mathbf{D},\end{array}$$

where the superscripts “V” and “R” correspond to Voigt and Reuss estimates, respectively. J and D are the spherical (volumetric) and deviatoric parts of the symmetric unit fourth-order tensor.

The double contraction of the scalar product (quadruple contraction) of Eqs. (C1) and (C2) gives

$$\begin{array}{}\text{(C3)}& {\mathbf{C}}^{\mathrm{V}}\left(\mathit{\omega }\right)::{\mathbf{S}}^{\mathrm{R}}\left(\mathit{\omega }\right)={\displaystyle \frac{K^{\mathrm{V}}\left(\mathit{\omega }\right)}{K^{\mathrm{R}}\left(\mathit{\omega }\right)}}+\mathrm{5}{\displaystyle \frac{{\mathit{\mu }}^{\mathrm{V}}\left(\mathit{\omega }\right)}{{\mathit{\mu }}^{\mathrm{R}}\left(\mathit{\omega }\right)}}.\end{array}$$

If the effective stiffness tensor is isotropic, then ${\mathbf{C}}^{\mathrm{V}}\left(\mathit{\omega }\right)={\left({\mathbf{S}}^{\mathrm{R}}\left(\mathit{\omega }\right)\right)}^{-\mathrm{1}}$ and $K^{\mathrm{V}}/K^{\mathrm{R}}={\mathit{\mu }}^{\mathrm{V}}/{\mathit{\mu }}^{\mathrm{R}}=\mathrm{1}$. Therefore, when the effective stiffness tensor is isotropic, the value of Eq. C3 equals to 6 and this value increases when the effective stiffness tensor becomes anisotropic. Thus, the universal elastic anisotropy index measure A^U is defined as (Ranganathan and Ostoja-Starzewski, 2008):

$$\begin{array}{}\text{(C4)}& A^{\mathrm{U}}\left(\mathit{\omega }\right)={\displaystyle \frac{K^{\mathrm{V}}\left(\mathit{\omega }\right)}{K^{\mathrm{R}}\left(\mathit{\omega }\right)}}+\mathrm{5}{\displaystyle \frac{{\mathit{\mu }}^{\mathrm{V}}\left(\mathit{\omega }\right)}{{\mathit{\mu }}^{\mathrm{R}}\left(\mathit{\omega }\right)}}-\mathrm{6}\ge \mathrm{0},\end{array}$$

In geophysics, the separation of the elastic anisotropy measure in bulk and shear modes is necessary because rocks might exhibit different frequency dependencies due to bulk and shear deformations. Therefore, in analogy to the universal elastic anisotropy index measure A^U, the anisotropy measures in bulk A^bulk(ω) and shear A^shear(ω) can be defined as

$$\begin{array}{}\text{(C5)}& A^{\text{bulk}}\left(\mathit{\omega }\right)={\displaystyle \frac{K^{\mathrm{V}}\left(\mathit{\omega }\right)}{K^{\mathrm{R}}\left(\mathit{\omega }\right)}}-\mathrm{1}\end{array}$$

and

$$\begin{array}{}\text{(C6)}& A^{\text{shear}}\left(\mathit{\omega }\right)={\displaystyle \frac{G^{\mathrm{V}}\left(\mathit{\omega }\right)}{G^{\mathrm{R}}\left(\mathit{\omega }\right)}}-\mathrm{1}.\end{array}$$

These two parameters, A^bulk(ω) and A^shear(ω), obey the same interpretation as the universal elastic anisotropy index measure: A^bulk=0 (A^shear=0) corresponds to zero bulk (shear) anisotropy of the model, while the discrepancy of A^bulk (A^shear) from zero anisotropy defines the anisotropy strength in bulk (shear). The Voigt and Reuss estimates (K^V, K^R, μ^V and μ^R) can be calculated via simple algebraic formulas for different symmetry classes which can be found elsewhere, e.g., in Ravindran et al. (1998) for orthorhombic symmetry, in Feng et al. (2012) for tetragonal symmetry and in Duffy (2018) for cubic symmetry. Thus, for orthorhombic symmetry (lowest possible symmetry created by two perpendicular sets of cracks embedded into an isotropic material), the Voigt and Reuss bulk moduli are (written for the components of stiffness (compliance) matrices c_ij(s_ij), in Voigt notation)

$$\begin{array}{}\text{(C7)}& K^{\mathrm{V}}={\displaystyle \frac{\mathrm{1}}{\mathrm{9}}}\left[\left(c_{\mathrm{11}}+c_{\mathrm{22}}+c_{\mathrm{33}}\right)+\mathrm{2}\left(c_{\mathrm{12}}+c_{\mathrm{13}}+c_{\mathrm{23}}\right)\right]\end{array}$$

and

$$\begin{array}{}\text{(C8)}& K^{\mathrm{R}}={\left[\left(s_{\mathrm{11}}+s_{\mathrm{22}}+s_{\mathrm{33}}\right)+\mathrm{2}\left(s_{\mathrm{12}}+s_{\mathrm{13}}+s_{\mathrm{23}}\right)\right]}^{-\mathrm{1}}.\end{array}$$

Similarly, the Voigt and Reuss shear moduli are (in Voigt notation)

$$\begin{array}{}\text{(C9)}& \begin{array}{rl}{\mathit{\mu }}^{\mathrm{V}}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{15}}}\left[\left(c_{\mathrm{11}}+c_{\mathrm{22}}+c_{\mathrm{33}}-c_{\mathrm{12}}-c_{\mathrm{13}}-c_{\mathrm{23}}\right)\right.\\ +& \mathrm{3}\left(c_{\mathrm{44}}+c_{\mathrm{55}}+c_{\mathrm{66}}\right)\left.\right]\end{array}\end{array}$$

and

$$\begin{array}{}\text{(C10)}& \begin{array}{rl}{\mathit{\mu }}^{\mathrm{R}}=& \mathrm{15}\left[\mathrm{4}\left(s_{\mathrm{11}}+s_{\mathrm{22}}+s_{\mathrm{33}}-s_{\mathrm{12}}-s_{\mathrm{13}}-s_{\mathrm{23}}\right)\right.\\ +& \mathrm{3}\left(s_{\mathrm{44}}+s_{\mathrm{55}}+s_{\mathrm{66}}\right){}^{-\mathrm{1}}.\end{array}\end{array}$$

Equations (C7)–(C10) are valid for orthorhombic symmetry and for higher symmetries: tetragonal, transverse isotropy and cubic. Thus, for evaluating the universal elastic anisotropy index A^U and the anisotropy measures in bulk A^bulk(ω) and shear A^shear(ω), one can use Eqs. (C7)–(C10) to calculate the Voigt and Reuss estimates (K^V, K^R, μ^V and μ^R) and then calculate A^U using Eq. (C4) and A^bulk(ω) and A^shear(ω) using Eqs. (C5) and (C6), respectively.