Potential influence of overpressurized gas on the induced seismicity in the St. Gallen deep geothermal project (Switzerland)

In July 2013, the city of St. Gallen conducted a deep geothermal project that aimed to exploit energy for district heating and generating power. A few days after an injection test and two acid stimulations that caused only minor seismicity, a gas kick forced the operators to inject drilling mud to combat the kick. Subsequently, multiple earthquakes were induced on a fault several hundred meters away from the well, including a M_L 3.5 event that was felt throughout the nearby population centers. Given the occurrence of a gas kick and a felt seismic sequence with low total injected fluid volumes (∼1200 m³), the St. Gallen deep geothermal project represents a particularly interesting case study of induced seismicity. Here, we first present a conceptual model based on seismic, borehole, and seismological data suggesting a hydraulic connection between the well and the fault. The overpressurized gas, which is assumed to be initially sealed by the fault, may have been released due to the stimulations before entering the well via the hydraulic connection. We test this hypothesis with a numerical model calibrated against the borehole pressure of the injection test. We successfully reproduce the gas kick and spatiotemporal characteristics of the main seismicity sequence following the well control operation. The results indicate that the gas may have destabilized the fault during and after the injection operations and could have enhanced the resulting seismicity. This study may have implications for future deep hydrothermal projects conducted in similar geological conditions with potentially overpressurized in-place gas.

1 Introduction

Industrial injection and extraction projects causing anthropogenic earthquakes have increased during recent years and have been conducted closer to densely populated areas (Foulger et al., 2018). As a result, both the nonscientific and scientific community's interest in induced seismicity has risen dramatically. Anthropogenic earthquakes have been observed related to water impoundment, mining, geothermal power production, hydrocarbon extraction, hydraulic fracturing for shale gas extraction, CO₂ sequestration, wastewater injection, and cyclic injection and extraction operations at underground gas storage (UGS) sites (Ellsworth, 2013; Grigoli et al., 2017; Foulger et al., 2018). Industrial and societal problems arising from induced seismicity are 2-fold. On the one hand, large induced seismic events can be a risk to the population and cause damage to structures. For instance, in the United States mid-continent, several M>5 events have been recorded after wastewater injection, causing substantial damage to structures and harm to people (Yeck et al., 2017). On the other hand, geo-energy projects may be jeopardized by lack of public support due to felt but only slightly damaging seismic events. A striking example is the Enhanced Geothermal System (EGS) project in Basel, Switzerland, where seismicity was induced immediately below the city, which led to the suspension of the entire project (e.g., Giardini, 2009). Recent history clearly shows that the success of geo-energy, in particular geothermal projects, largely depends on the level at which we are able to control induced seismicity (Kraft et al., 2009; Kwiatek et al., 2019). There is an urgent need to communicate transparently with the public and employ methods that will safely keep the seismicity to a tolerable level (Giardini, 2009; Lee et al., 2019). Understanding the physics behind the induced seismicity is an important step necessary to assess the hazard and risk of geo-energy projects and to develop methods to mitigate the seismicity. Hence, it is crucial to get a more accurate understanding of the thermo-hydromechanical–chemical interactions occurring at reservoir depths.

To date, two main mechanisms are thought to be responsible for man-made earthquakes: (i) removing or adding mass (e.g., mining, water impoundment) and (ii) injection or withdrawal of fluid (e.g., geothermal power, hydrocarbon extraction, wastewater injection, and CO₂ sequestration; Foulger et al., 2018). For injection or extraction activities, pressure and temperature changes influence the state of stress in the subsurface zones. This process is considered to be the main mechanism employed in deep geothermal projects, where cold water injection and hot water or steam production can change the effective stress in and around the reservoir and hence induce earthquakes. Several geothermal projects globally have induced seismicity (e.g., Baisch et al., 2015; Evans et al., 2012; Grigoli et al., 2018; Jeanne et al., 2015); recently, a M_w 5.5 earthquake struck the city of Pohang (South Korea) (Ellsworth et al., 2019; Grigoli et al., 2018), the largest earthquake recorded at an EGS site to date (Kim et al., 2018). This earthquake has challenged recently proposed models that relate the maximum expected seismic magnitude to the total injected fluid volume (Galis et al., 2017; McGarr, 2014). In contrast to the majority of geo-energy projects conducted so far, the main shock in Pohang lies well beyond the magnitude threshold given by such models.

The deep geothermal project in St. Gallen conducted in 2013 shows some similarity with the Pohang event, given the relatively strong induced seismicity (in terms of total released seismic moment) after the injection of rather small volumes of fluid. A few days after an injection test and two acid stimulations that caused only minor seismicity, gas entered the borehole from an unidentified source at a pressure greater than the one exerted by the fluid column in the borehole (a so-called gas kick). The gas kick was fought by pumping fresh water and heavier drilling mud into the well (e.g., Moeck et al., 2015). The well control injection induced multiple seismic events (Fig. 1), including a local magnitude M_L 3.5 (moment magnitude M_w 3.3; Diehl et al., 2014) earthquake that was distinctly felt throughout the population centers adjacent to the well (e.g., Edwards et al., 2015). For St. Gallen, using McGarr's model (McGarr, 2014) that relates the maximum expected magnitude M_max to the product of the shear modulus G (30 GPa following McGarr, 2014) and the total injected volume V (ca. 1200 m³ neglecting additional mud losses; Alber and Backers, 2015, and references therein), gives a M_max of 3.0. Despite the assumption of a relatively stiff fault, the main event (M_w 3.3) is above the theoretically derived threshold. This calls for a more thorough analysis of the hydromechanical processes taking into account multiphase fluid flow to evaluate the potential influence of the gas. Since we only have a limited knowledge of the deep subsurface (e.g., from boreholes and nondestructive geophysical methods), numerical modeling can help shed light on otherwise hidden processes.

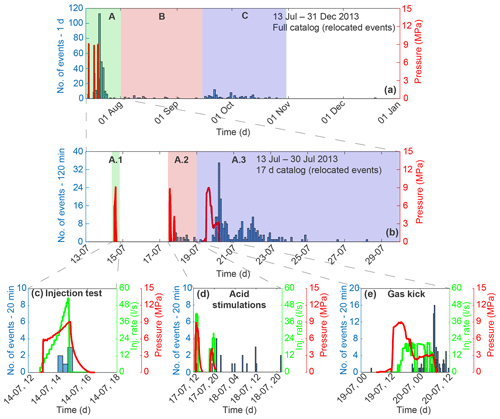
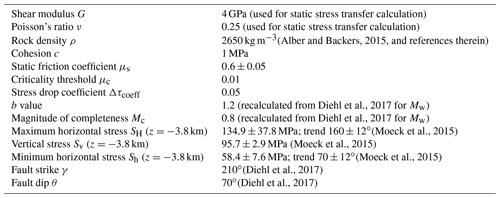
Figure 1 The St. Gallen induced seismicity sequence: (a) time series of the wellhead pressure in SG GT-1 and number of relocated events of the full catalog from July to the end of 2013. A: main seismicity sequence; B: more quiet post-injection period; C: seismic activity restarts due to cleaning and fishing operations. (b) Time series of the wellhead pressure in SG GT-1 and number of relocated events from 13 July to the end of July 2013. A.1: injection test; A.2: acid stimulations; A.3: gas kick and well control measures. (c, d, e) Time series of the injection rates and wellhead pressure in SG GT-1, as well as the number of relocated seismic events for the (c) injection test (14 July), (d) acid stimulations (17 July), and gas kick including the well control injection (19–20 July). The full relocated catalog is taken from Diehl et al. (2017).

In this study, we perform hydromechanical simulations to more accurately understand the causes of the induced seismicity during the St. Gallen deep geothermal project. Our aim is to propose and evaluate potential mechanisms that led to the seismicity and to reproduce the characteristics of the main sequence in July 2013 (denoted as phase A in Fig. 1a). Firstly, we describe the temporal and spatial evolution of the seismic sequence associated with the injection. Secondly, we present a conceptual model for the induced seismicity in St. Gallen based on the earthquake catalog (Diehl et al., 2017), data from a 3D seismic campaign (Heuberger et al., 2016), and data from the borehole St. Gallen (SG) GT-1 (Wolfgramm et al., 2015). We then present a 3D numerical model using TOUGH2-seed (Rinaldi and Nespoli, 2017) that combines the multicomponent and multiphase fluid flow simulator TOUGH2 (Pruess et al., 2012) with a geomechanical–stochastic model (Catalli et al., 2016; Gischig and Wiemer, 2013; Gischig et al., 2014; Goertz-Allmann and Wiemer, 2013). Our model is calibrated to the well pressure response during the injection test and the gas kick. We simulate the injection test, the gas kick, and the well control injection to reproduce the main seismic sequence at the end of July 2013. In our simulations, the primary focus is the potential effect of gas on the induced seismicity. Finally, we discuss our results in the context of future deep hydrothermal projects.

2 The deep geothermal project in St. Gallen

The St. Gallen deep geothermal project was conducted in the North Alpine Foreland Basin a few kilometers west of the city of St. Gallen (Fig. 2). The plan was to drill into the fractured damage zone within the St. Gallen Fault Zone (SFZ), a 20 km long fault system consisting of several steeply dipping normal and subsidiary apparent reverse faults striking NNE–SSW (Heuberger et al., 2016). The target formation was chosen to be the Malm carbonate layer (Upper Jurassic, top of the Mesozoic sediments at this site) located in the damage zone of two normal faults of the SFZ at a depth of about 4 km. The formation was expected to be sufficiently permeable to circulate water at rate of at least 50 L s⁻¹ (e.g., Hirschberg et al., 2015) per 200 m of drawdown in the well (∼2 MPa; Thomas Bloch, personal communication, 7 September 2019) without requiring permeability enhancement by EGS-type hydraulic stimulation. Although the St. Gallen deep geothermal project has been considered an EGS in some studies (e.g., Breede et al., 2013), we here clearly classify it as a hydrothermal project, since no hydraulic stimulation for the targeted shearing of fractures (hydro-shearing) was performed adjacent to the injection well (see below). The choice of the reservoir was motivated by the fact that at different sites in southeastern Germany, multiple hydrothermal systems are currently running successfully in similar geological conditions (Wolfgramm et al., 2015). A 3D seismic survey carried out between 2009 and 2010 revealed that the SFZ tapers off in the crystalline basement, probably bounding a Permo-Carboniferous trough (PCT) below the Mesozoic sediments (Heuberger et al., 2016). The PCT is poorly defined in the seismic survey, since strong reflections from the sediments above prevented a detailed interpretation of the deeper horizons (Heuberger et al., 2016).

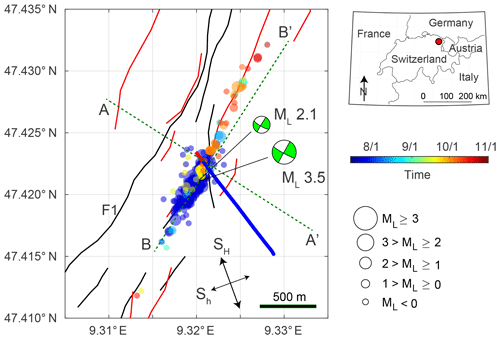
Figure 2 Map view of the relocated events color-coded by origin time (format month/day). The fault plane solutions of the M_L 3.5 and M_L 2.1 events (Diehl et al., 2017) are denoted by the green focal mechanisms. Red (top Malm) and black (bottom Muschelkalk) lines illustrate the faults of the SFZ including a large fault (F1) bounding the Permo-Carboniferous trough (Heuberger et al., 2016). The cased and open section of borehole GT-1 are denoted by the thick blue and red lines, respectively. The black arrows sketch the orientation of the minimum and maximum principal stress after Moeck et al. (2015). The red dot in the European map (top right) marks the location of the St. Gallen deep geothermal project.

The St. Gallen region had experienced only minor natural seismicity prior to the project, with the largest being a M_L 3.2 earthquake since 1984 (Diehl et al., 2017). Only two historic earthquakes with M_w>4.0 were reported in the vicinity of the geothermal site (Fäh et al., 2011). Nevertheless, in anticipation of a possible induced microseismic activity, the regional seismic network was densified locally at the beginning of 2012 with a short-period borehole sensor and five broadband surface stations within a radius of 12 km around the geothermal well. During the stimulation phase in July 2013, the network was further extended by seven short-period surface stations (Diehl et al., 2017; Edwards et al., 2015).

In the beginning of July 2013, the drilling of the SG GT-1 well was completed to a true vertical depth (TVD) of about 4.2 km without inducing any seismic events (depth is defined relative to the top of the borehole throughout the paper). The open section extended from 3.8 to 4.2 km TVD within the Malm formation. In order to get an estimate of the hydraulic properties of the reservoir, an injection test was performed on 14 July (phase A.1 in Fig. 1b and Fig. 1c). Water was injected with a stepwise increasing rate reaching a maximum of 53 L s⁻¹. A total of 175 m³ of water was pumped into the subsurface, leading to a pressure increase from 36.7 to 46.5 MPa (ΔP=9.8 MPa) and inducing some microearthquakes with six being precisely located (Diehl et al., 2017). These were the first seismic events recorded since microseismic monitoring began in 2012. On 17 July, two acid stimulations were performed in sections where permeable fractures were expected, and a total of 150 m³ hydrochloric acid and 140 m³ of water was injected (phase A.2 in Fig. 1b and Fig. 1d). The first acid stimulation was conducted in the Lower Malm at a depth of 4.15 km, reaching maximum injection rates of 42 L s⁻¹ and a wellhead pressure increase of 8.8 MPa. The second acid stimulation was performed in the Upper Malm with injection rates of up to 24 L s⁻¹ and a pressure increase of up to 6.3 MPa. During the first acid stimulation, only a few microearthquakes with M_L<0.0 were recorded, two of them being relocated at a depth of approx. 4.9 km. The second acid stimulation led to much more seismicity; 19 microearthquakes with M_L<0.5 were relocated until the morning of 19 July at an average depth of ca. 4.6 km (Diehl et al., 2017), i.e., shallower than the microevents during the first acid stimulation. The number and magnitude of the seismic events was well within the range expected for the injected fluid volumes. On 19 July at noon, gas (roughly 90 % methane; Wolfgramm et al., 2015) entered the well from an unknown source; for security reasons, the well was closed immediately. Since the wellhead pressure increased to between 8 and 9 MPa due to the inflowing gas, fresh water and heavier fluids were pumped into the well at rates of up to 20 L s⁻¹ over 15 h (total volume of approx. 700 m³) to prevent further gas inflow (phase A.3 in Fig. 1b and Fig. 1e). This injection successfully decreased the wellhead pressure. However, numerous seismic events were induced in the evening on 19 July, one triggering the yellow threshold of the installed traffic light system (TLS), meaning that injection should be stopped immediately (e.g., Diehl et al., 2017; Obermann et al., 2015). Nevertheless, injection was continued until the early morning of 20 July to keep the wellhead pressure at about 3 MPa; stopping the injection would probably have led to an increase in the wellhead pressure due to further gas inflow. Seismicity continued, and a M_L 2.1 event was induced at 02:40 am on 20 July, followed by multiple smaller events. At 05:30 am, after more water, including heavy components, was injected, a M_L 3.5 event was induced. Subsequently, the pressure normalized and the injection was stopped. The main shock was followed by almost 200 seismic events (relocated) until the end of July (Diehl et al., 2017) (Fig. 1b). After a preliminary analysis of the incidents, the geothermal project was temporally suspended. The main seismic sequence was followed by only minor seismicity between August and mid-September 2013 (phase B in Fig. 1a). Cleaning and fishing operations in the borehole from mid-September to mid-October likely led to a temporal increase in the seismicity rate due to some mud losses (phase C in Fig. 1a). During a production test conducted at the end of October, the seismicity ceased completely. Thereafter, the operators decided to permanently suspend the project because the permeability of the reservoir was much too low (flow rate <6 L s⁻¹ for a drawdown of approx. 1500 m in the borehole (∼15 MPa); Wolfgramm et al., 2015), and the gas content was found to be too high to maintain flow rates sufficient for economic feasibility of a hydrothermal power plant. EGS-type hydraulic stimulation (i.e., hydro-shearing) was not considered because the risk of further seismicity was judged to be too high (e.g., Moeck et al., 2015).

The spatial distribution and evolution over time of the induced seismicity is illustrated in Fig. 2. The seismic sequence extends along a relatively narrow band (width of several hundreds of meters) striking SSW–NNE and dipping approximately 70^∘ to WNW. During the injections in July 2013, the seismicity mainly propagated in the southwest direction from the borehole. Only from August to October 2013 did the seismicity start to propagate to the northeast but at much smaller propagation velocities (Diehl et al., 2017). The main focal mechanism in St. Gallen is strike-slip, which can be deduced from the two largest events of the sequence (Fig. 2). To measure the local stress field, Moeck et al. (2015) performed in situ stress estimations for borehole SG GT-1 and determined that the maximum (S_H) and minimum (S_h) principal stresses were horizontal trending 160±12 and 70±12^∘, respectively. The vertical stress (S_v) was estimated to be intermediate with a magnitude of 98 MPa at a depth of ca. 3.9 km. Furthermore, the mean stress ratios of $S_{\mathrm{H}}=\mathrm{1.41}\cdot S_{\mathrm{v}}$ and $S_{\mathrm{h}}=\mathrm{0.61}\cdot S_{\mathrm{v}}$ were calculated at 4.1 km TVD. On a more regional scale, Kastrup et al. (2004) inverted focal mechanisms of naturally occurring earthquakes over the last 50 years to obtain the orientation of the three principal stresses in the Northern Alpine Foreland. They obtained a trend of about 160 to 170^∘ for the maximum horizontal stress – in good agreement with the in situ stress estimations. Assuming a straight planar fault, we calculate the best-fit strike orientation (least-squares regression) to be approximately 210^∘ (Fig. 2), coinciding with the focal mechanisms of the two largest induced events. Hence, in comparison to the local stress field, S_H intersects the fault with an angle of about 50^∘.

3 Conceptual model

First, we describe the conceptual model of the stimulation phase, the gas kick, and the subsequent well control injection in July 2013. Clearly, there is a temporal correlation between the seismicity and the fluid injected during the injection test, the acid stimulations, and the well control measures (Fig. 1). With regard to the spatial distribution, despite the estimated vertical and horizontal absolute location uncertainties of 0.15 and 0.1 km, respectively (Diehl et al., 2017), most of the seismicity occurred in the pre-Mesozoic basement below a depth of 4.4 km (Fig. 3). Hence, considering the mean locations, the seismicity is separated from the well bottom (at a depth of ca. 4.2 km) by a minimum distance of about 0.3 km. The main shock (M_L 3.5) was located at a depth of about 4.6 km, 0.2 km further southwest with respect to the top of the open well section. The spatial gap between the borehole and the seismicity suggests that the seismic events were triggered either remotely by poroelastic stress changes or by a hydraulic connection (e.g., a fracture zone or a damage zone of a fault; Zbinden et al., 2020). Temperature and gamma-ray anomalies from borehole logs support a connection to the Lower Mesozoic sediments and possibly to the pre-Mesozoic basement (Wolfgramm et al., 2015). The temperature anomalies indicate the presence of major inflow zones intersecting with the borehole, the most prominent one at the upper part of the Malm (at a depth of 3.9 km). In the gamma-ray log, thorium anomalies suggest a connection between the borehole and the Dogger layer (underlying the Malm reservoir) or deeper (Wolfgramm et al., 2015). From a geometrical analysis, Diehl et al. (2017) suggested that at least one fault mapped by the seismic survey (Heuberger et al., 2016) might act as a hydraulic connection. The presence of a hydraulic connection would suggest that the injected fluid moved from the borehole toward the fault, resulting in an increase in pore pressure and a decrease in effective normal stress, eventually destabilizing the fault and leading to seismicity (Zbinden et al., 2020). Models have shown that the seismicity can be significantly stronger for hydraulically connected faults than for unconnected faults (Chang and Segall, 2016). Since the seismic response in St. Gallen was unexpectedly intense, it would support the hypothesis of a hydraulic connection.

Figure 3 Conceptual model of the stimulation phase, the gas kick, and the well control measures in July 2013. (a, b) Seismicity of the injection test (14 July) on a profile (a) normal to (A–A^′ in Fig. 2) and (b) along (B–B^′ in Fig. 2) the fault. The blue shaded area denotes the region affected by the direct pressurization, while the red shaded area depicts the possible location of the gas as described in the text (shown in all subfigures). The question mark next to the deeper events indicates that their location is probably an artifact that can be removed considering a local v_p∕v_s velocity anomaly (Diehl et al., 2017). (c, d) Seismicity due to the acid stimulations (17 July) on a profile (c) normal to and (d) along the fault. The yellow dots correspond to the seismicity induced during the first acid stimulation, while the cyan dots mark the events induced during the second acid stimulation. The red shaded area in (d) is the region affected by the proposed seal breach through which the gas may have migrated. (e, f) Seismicity during and after the well control measures (19–31 July) on a profile (e) normal to and (f) along the fault. The injected fluid and the gas that is intruding into the fault could have caused the seismic sequence including the M_L 3.5 main shock. Depth is defined relative to the top of the borehole (i.e., the free surface).

With respect to the gas kick, the gas may have originated from the PCT located below the Mesozoic sediments, which contains high concentrations of organic carbon (Heuberger et al., 2016; Wolfgramm et al., 2015). The gas might then have migrated upwards over geologic time, eventually reaching an impermeable seal preventing the gas from moving higher up. The stratigraphy in the St. Gallen region indicates that the Lower Mesozoic sediments (Keuper, Lias, and Dogger) could serve as a caprock to the gas reservoir. Additionally, the fault may have acted as a lateral seal to prevent the gas from reaching the hydraulic connection prior to the stimulations (Fig. 3). The gas kick first occurred 2 d after the acid stimulations and 5 d after the injection test, whereas no gas was observed during the drilling of the well (Naef, 2015). This is an indication that a hydraulic connection was indeed present, enabling the gas to enter the borehole from a greater depth. On the other hand, it implies that the hydraulic connection was only established after the injection test and the acid stimulations. Possibly, the stimulations enhanced the permeability of the hydraulic connection; the resulting seismicity as well as the acidification breached the fault seal, opening up a pathway for the gas to reach the well. This would imply that the gas took the same path as the injected fluid but in the opposite direction (Fig. 3).

In summary, we propose that the following processes could have led to the main seismicity sequence (14–31 July 2013) in St. Gallen.

1. During the injection test and the acid stimulations, the fault was pressurized by a highly permeable hydraulic connection (whose permeability is enhanced by the pressurization and the acid treatment).

2. The pressure increase on the fault led to a decrease in the effective normal stress and caused minor seismicity (Fig. 3a–d).

3. Due to the acidification and shear slip associated with the fault reactivation, a pathway opened up for the gas to reach the borehole through the hydraulic connection and caused the gas kick (Fig. 3c and d).

4. The fluid injected into the well during the control measures and the gas destabilized a larger patch on the fault leading to the seismic sequence that included the M_L 3.5 event (Fig. 3e and f).

5. The injection of water and drilling mud during the well control measures probably clogged the hydraulic connection and stopped the gas kick.

In our conceptual model, we show one distinct fracture zone that intersects with the borehole at the Upper Malm where a strong temperature anomaly was observed. However, the logs show that other permeable structures might exist at the depth of the Lower Malm. Moreover, for both the injection test and the first acid stimulation, Diehl et al. (2017) observed that the seismicity was initiated at a greater depth (between 4.8 and 5.0 km) compared to later events. The first acid stimulation was performed in the lower section of the Malm and induced two microearthquakes at a depth of about 4.9 km (Fig. 3c and Fig. 3d). The second acid stimulation was performed in the Upper Malm section, inducing seismic events above a depth of 4.7 km. For the injection test and the well control measures, where water and drilling mud was injected into the cased section and the well was pressurized equally, seismic event locations ranged from a depth of approximately 4.4 to 4.9 km. Given these observations, the presence of a second permeable connection seems possible; the first structure connects the Upper Malm at the borehole with the reactivated fault at a depth of about 4.5 km, while a second permeable structure may connect the Lower Malm with the fault at a depth of about 4.8 km. The second hydraulic connection could then explain the fast seismic response to the stimulations in the lower part of the fault. However, despite these observations, Diehl et al. (2017) proposed that the vertical offset of this cluster is a location artifact, which can be removed considering the presence of a local v_p∕v_s velocity anomaly. For this reason, we choose to perform the numerical simulations with only one hydraulic connection.

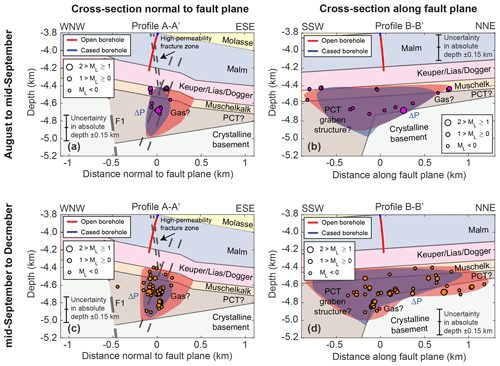
Figure 4 Conceptual model of the post-stimulation phase from August to December 2013. (a, b) Seismicity for the period 1 August to 15 September on a profile (a) normal to (A–A^′ in Fig. 2) and (b) along (B–B^′ in Fig. 2) the fault. The blue shaded area denotes the region affected by the direct pressurization, while the red shaded area depicts the possible location of the gas (shown in all subfigures). The seismicity in July is mainly located on the southwestern side of the borehole, whereas the seismic events after 1 August start to propagate to the northeast. (c, d) Seismicity of the period from 16 September to the end of 2013 on a profile (c) normal to and (d) along the fault. Borehole operations associated with some mud loss may be responsible for the increase in seismicity in September and October. The seismicity propagates further to the northeast but ceases during a production test at the end of October. Depth is defined relative to the top of the borehole (i.e., the free surface).

Figure 4 shows the conceptual model for the post-stimulation phase from August to December 2013. The seismicity of the main sequence (July 2013) was mainly distributed southwest of the injection well, whereas some minor events induced between August and mid-September 2013 were located northeast of it (Fig. 4a and b). In order to explain this observation, Diehl et al. (2017) argued that a seal, represented by a mapped fault intersecting with the reactivated fault in the area immediately beneath the borehole (Heuberger et al., 2016), may have been breached by the 20 July main shock. Only after this event could the fluid flow to the northeast. Alternatively, it can be argued that the permeability of the reactivated fault was lower to the northeast, since the PCT probably tapers off in this direction (Fig. 4b and Fig. 4d, see also Fig. 11 in Heuberger et al., 2016), and hence the fault may contain lower-permeability components from the suggested crystalline horst. In this case, the pressure front would then propagate slower to the northeast, consistent with the seismic observations. From mid-September to the end of October 2013, the seismicity increased again in the area below the borehole, although not drastically (Fig. 4c and d). At the same time, mud loss was observed in borehole SG GT-1 due to some fishing and cleaning operations. This indicates that the hydraulic connection, possibly clogged by the well control injection, may have been reopened, and the mud was able to reach the fault plane. Subsequently, the seismicity continued to propagate further to the northeast, while no seismic activity was observed southwest of the borehole. This may be associated with renewed gas movement due to the pressure changes caused by the mud. It is possible that the mud clogged potential pathways to the southwest, and hence the gas could only propagate to the northeast, inducing the seismicity in this region. Alternatively, the mud itself and some gas may have propagated to both the southwest and northeast but only induced seismic events in the northeast because the fault might possibly terminate in the southwest. We do not have data that supports any of these hypotheses, and, therefore, we cannot assess whether the seismicity in the post-injection period was induced by the gas, the mud, or a mixture of both. The seismicity in St. Gallen ceased during a production test at the end of October 2013. It was observed that the entire seismic sequence was constrained below a depth of about 4.4 km (Figs. 3 and 4), which coincides with the top boundary of the Muschelkalk. The reason for this may be (i) a stiffness contrast of the softer Keuper, Lias, and Dogger layers with respect to the stiffer Muschelkalk and Malm layers, which absorb most of the tectonic stress, leading to a lower differential stress in the softer layers and therefore to a less critically stressed fault in this region (Hergert et al., 2015), or (ii) a lower permeability of the reactivated fault due to the surrounding low-permeability layers (Keuper, Lias, and Dogger) and thus a smaller pressurization above the Muschelkalk – as assumed in our conceptual model.

4 Model setup and calibration

The numerical simulations are performed using TOUGH2-seed (Rinaldi and Nespoli, 2017). The seismic module of TOUGH2-seed is switched off during the simulation of the injection test and the gas kick to simplify the calibration of the model; however, we use the full model during the simulation of the main seismic sequence.

4.1 TOUGH2-seed

TOUGH2-seed couples TOUGH2 with a stochastic–geomechanical model (Catalli et al., 2016; Gischig and Wiemer, 2013; Gischig et al., 2014; Goertz-Allmann and Wiemer, 2013). TOUGH2 is a multiphase, multicomponent, and heat transport numerical simulator based on a first-order implicit finite difference scheme in time and an integral finite difference method in space (Pruess et al., 2012). After the computation of the pressure field in TOUGH2, the solution is passed on to the seed model for each time step. TOUGH2-seed incorporates two different modules: (i) the hydraulic module that is similar to TOUGH2 but accounts for pressure-dependent permeability and (ii) a seismic module that simulates induced seismicity and can be switched off if no seeds are distributed in the model. Seeds are uniformly randomly distributed potential failure points with prescribed stress and failure conditions. The hydraulic and seismic modules can be fully coupled if the permeability is chosen to be dependent on the seismicity (Gischig et al., 2014; Rinaldi and Nespoli, 2017). TOUGH2-seed has been successfully applied to the EGS project in Basel, where most of the characteristic behavior of the induced seismicity could be reproduced (Rinaldi and Nespoli, 2017). The main advantage of using a stochastic model is that uncertainties can be assigned to different model parameters (e.g., stress magnitude, fault orientation, friction) depending on how well they are constrained by field data. Synthetic earthquake catalogs can be obtained after each simulation, allowing a comparison to observed earthquake data.

In this study, the pressure P strictly refers to the average pore pressure (summation over fluid phases) exerted by the gas and liquid phases (e.g., Kim et al., 2013), written as

$$\begin{array}{}\text{(1)}& P=S_{\mathrm{g}}\cdot P_{\mathrm{g}}+(\mathrm{1}-S_{\mathrm{g}})\cdot P_{\mathrm{w}},\end{array}$$

where S_g is the gas saturation, P_g the gas pressure, and P_w the water pressure. Here we ignore the interfacial energy caused by the two-phase system (Kim et al., 2013, and references therein). For the hydraulic module, we account for pressure-dependent permeability following Rinaldi and Nespoli (2017):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\kappa }}_{\mathrm{hm}}=\mathit{\kappa }\cdot \exp \left[C_{\mathrm{1}}\left({\displaystyle \frac{{\mathit{\varphi }}_{\mathrm{hm}}}{{\mathit{\varphi }}_{\mathrm{0}}}}-\mathrm{1}\right)\right]\text{(3)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{hm}}=(\mathit{\varphi }-{\mathit{\varphi }}_{\mathrm{r}})\cdot \exp \left(\mathit{\alpha }\mathrm{\Delta }P\right)+{\mathit{\varphi }}_{\mathrm{r}},\end{array}$$

where C₁ and α (Pa⁻¹) are scaling parameters. The updated permeability κ_hm is a function of the initial permeability κ and the ratio of the actual porosity ϕ_hm and the initial porosity ϕ. ϕ_hm is exponentially dependent on the pore pressure change ΔP and linearly dependent on the difference between ϕ and the residual porosity ϕ_r. Note that the permeability and porosity changes in Eqs. (2) and (3) are reversible (i.e., purely elastic). For the seismic module, TOUGH2-seed takes into account the full 3D stress state formulation as well as the static Coulomb stress transfer (Catalli et al., 2016; Rinaldi and Nespoli, 2017). TOUGH2 solves for the pore pressure in each model element and transfers it to the seed model, where the new stress state of the seeds is computed according to the analysis of effective stress (Terzaghi, 1923):

$$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{ij}^{\prime }={\mathit{\sigma }}_{ij}-P,\end{array}$$

where ${\mathit{\sigma }}_{ij}^{\prime }$ is the effective stress tensor, and σ_ij is the total stress tensor. The current version of TOUGH2-seed does not account for poroelasticity; i.e., the total stresses do not change due to pressure and vice versa. The initial stress state on the seeds follows a normal distribution around a mean regional stress field in order to account for stress heterogeneity that can be present in reality. The seeds are distributed on a fault, and their orientation is normally distributed around the strike (γ) and dip (θ) of the fault. From the orientation and the given effective stress tensor of the seeds, the effective normal stress ${\mathit{\sigma }}_{\mathrm{n}}^{\prime }$ and the shear stress τ can be computed (e.g., Zoback, 2010). A seed is triggered if a Mohr–Coulomb failure criterion is reached, i.e., when the shear stress exceeds the shear strength τ_s (critical shear stress):

$$\begin{array}{}\text{(5)}& {\mathit{\tau }}_{\mathrm{s}}=c+{\mathit{\mu }}_{\mathrm{s}}\cdot {\mathit{\sigma }}_{\mathrm{n}}^{\prime },\end{array}$$

where c is the cohesion and μ_s the static friction coefficient, which follows a normal distribution (i.e., the strength of the seeds varies). Moreover, following Gischig and Wiemer (2013), we define a criticality threshold μ_c, so that the stress states of the seeds at the beginning of the simulation have a certain gap to the failure criterion. A moment magnitude is assigned to each triggered seed, randomly chosen from a Gutenberg–Richter (GR) distribution with a fixed b value of 1.2 and a magnitude of completeness (M_c) of 0.8 obtained from the St. Gallen catalog and recalculated for M_w using a corrected maximum likelihood method (e.g., Marzocchi and Sandri, 2003, and references therein). A shear stress drop Δτ is calculated for each reactivation given by Gischig et al. (2014)

$$\begin{array}{}\text{(6)}& \mathrm{\Delta }\mathit{\tau }=\mathrm{\Delta }{\mathit{\tau }}_{\mathrm{coeff}}\cdot \left({\displaystyle \frac{\mathit{\tau }-c}{{\mathit{\mu }}_{\mathrm{s}}}}\right),\end{array}$$

where Δτ_coeff is a coefficient determining how much shear stress is released. A new stress state is then computed on the reactivated seed and on all neighboring seeds that are affected by the static stress transfer. After the evaluation of the triggered seeds, the permeability is updated, and TOUGH2 solves for the pressure distribution of a new time step before the coupling is repeated.

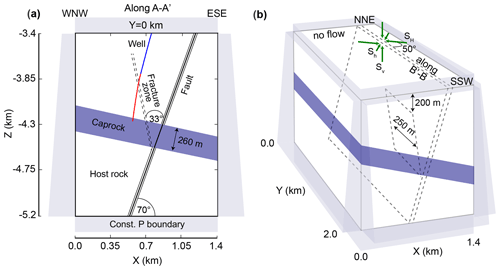
Figure 5 Schematic of the 3D numerical model: (a) slice at y=0 km (along profile A–A^′ in Fig. 2). The well is indicated by the blue (cased section) and red lines (open section). (b) Entire 3D model along the strike of the fracture zone and fault (along profile B–B^′ in Fig. 2). The dark green arrows indicate the orientation of the mean stress field used for the TOUGH2-seed simulations.

4.2 Numerical model setup

The 3D hydrogeological model consists of a fracture zone connecting the upper part of the open section of the borehole (at a depth of approx. 3.9 km) with a fault plane intersecting a caprock layer (Fig. 5). The fracture zone dips 77^∘ and is therefore a conjugate plane of the reactivated fault, which itself dips 70^∘ toward the WNW. The fracture zone extends over a length of about 920 m along the dip from a depth of 3.6 to 4.5 km, where it is bound by the fault. The top corresponds to the base of the Molasse sediments (not modeled), where the fracture zone is presumed to taper off. Furthermore, the fracture zone is assumed to have an along-strike length of 250 m. The fracture zone is modeled as a high-permeability, low-porosity, and high-compressibility equivalent porous medium with a thickness of 20 m. The permeability in the fracture zone is pressure-dependent to account for fracture opening during injection (initial permeability, pore compressibility, and α in Eq. 3 are calibration parameters). We assume a very small initial porosity of $\mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}$, corresponding to a total void space of 600 µm within the 20 m thick equivalent porous medium domain (e.g., 10 fractures with an aperture of 60 µm each). The fault zone consists of a two-sided, 2×20 m wide permeable damage zone ($\mathit{\kappa }={\mathrm{10}}^{-\mathrm{14}}$ m²) and a 5 m wide, impermeable fault core ($\mathit{\kappa }={\mathrm{10}}^{-\mathrm{22}}$ m²), and it extends over the entire width and length of the model (2 km in the y and ca. 1.9 km in the z direction). The fault intersects a slightly inclined, very low permeability caprock ($\mathit{\kappa }={\mathrm{10}}^{-\mathrm{22}}$ m²) corresponding to the Lower Mesozoic sediments (Keuper, Lias, and Dogger). A host rock layer representing the Malm reservoir surrounds the open section of the well. For simplicity, we assume that the domain below the caprock has the same properties as the host rock (Fig. 5a). The well is approximated as a high-porosity and high-permeability porous medium, under the assumption of negligible dynamic pressures within the wellbore (well permeability is a calibration parameter; Rinaldi et al., 2017). For the multiphase flow modeling, we use the relative permeability curves of Corey (1954) and capillary pressure functions of van Genuchten (1980). A summary of the hydraulic parameters is given in Table 1.

van Genuchten (1980)van Genuchten (1980)

Table 1 Predefined and calibrated hydraulic parameters of the numerical model.

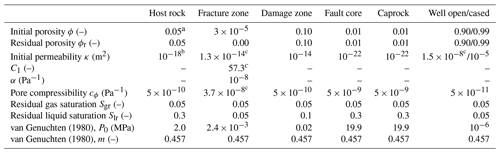
^a Moeck et al. (2015) and Wolfgramm et al. (2015). ^b Wolfgramm et al. (2015). ^c calibrated.

In accordance with the in situ conditions measured in borehole SG GT-1 in St. Gallen (Wolfgramm et al., 2015), we initialize the pressure at approx. 37 MPa and the temperature at 143 ^∘C at the top of the open well section. The temperature linearly increases with depth by 35.5 ^∘C km⁻¹ and is held constant during the injection. Although injection of low-temperature fluid can cool the rock and influence both the stress and pressure conditions (e.g., Ghassemi and Tao, 2016; Hopp et al., 2019; Rinaldi et al., 2015), we do not expect a significant cooling effect over the relatively short-term and small-volume injection that occurred in St. Gallen. We choose the boundaries to be open for fluid flow everywhere except at the boundary y=0 km (symmetry boundary), where we apply no flow conditions (Fig. 5b). In order to model the multiphase fluid system, we employ an equation of state with water and air as liquid and gas phase, respectively. Methane and nitrogen (air contains approx. 78 % nitrogen by volume) are both in a supercritical state at reservoir conditions (e.g., Nasrifar and Bolland, 2006); i.e., their dynamic viscosity is similar to a gas, and their density is between a liquid and a gas. We therefore consider the use of air instead of methane to be an appropriate approximation for the purposes of this study. We create an initial steady-state condition of a gas plume below the caprock on the right side of the fault by simulating gas inflow with a pressure of 70 MPa at the lower boundary into the right damage zone for 1 Myr (0.1 km long line source along the y axis). To prevent gas leakage, we assign a high capillary entry pressure to the fault core and the caprock. Figure 6 shows the initial pressure distribution and gas saturation at three different vertical cross sections. The pressure increase is approximately linear with depth (approx. 9.1 MPa km⁻¹) above the caprock, while it is highly disturbed below the caprock by the overpressurized gas plume (i.e., pressurized with respect to an undisturbed state without gas). At the fracture zone/fault intersection at y=0 km (at a depth of 4.5 km), the pressure on the right side of the fault exceeds the pressure on the left by about 7 MPa. This pressure difference becomes less pronounced toward the boundary at y=2 km (Fig. 6a to c). The plume is completely gas saturated in the right damage zone and in the adjacent host rock at y=0 km, while the size of the plume decreases along the strike of the fault (Fig. 6d to f). The domain below the caprock on the left side of the fault has an initial gas saturation of 5 %.

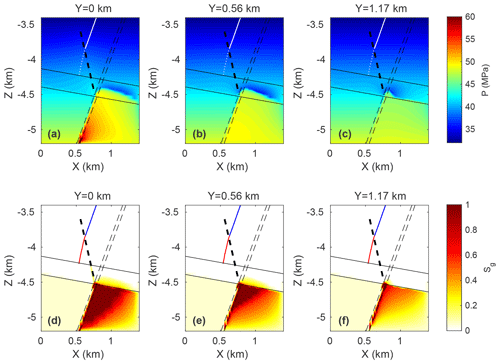
Figure 6 Initial conditions of the model: (a–c) Pressure at (a) y=0, (b) y=0.56, and (c) y=1.17 km along profile A–A^′ in Fig. 2 (normal to the strike of the fault). The well is denoted by the dotted (open section) and solid (cased section) white line. (d–f) Gas saturation at (d) y=0, (e) y=0.56, and (f) y=1.17 km along the profile A–A^′ in Fig. 2. The well is denoted by the red (open section) and blue (cased section) lines. The fault is illustrated by the thin dashed black lines, the fracture zone by the thick dashed black line, and the caprock by the solid black lines.

The stress input for the seed model is based on the findings of Moeck et al. (2015). The maximum principal stress S₁ is horizontal and has a mean trend of 160^∘; the intermediate principal stress S₂ is equal to the vertical stress S_v, and the minimum principal stress S₃ is horizontal with a trend of 70^∘. The seeds are randomly distributed on the lower part of the fault ($z\le -\mathrm{4.5}$ and y≤1.0 km) and in the immediate surroundings, not more than 90 m normal distance to the fault core. Due to uncertainties in the exact orientation of the principal stresses with respect to the reactivated fault plane, we assign a standard deviation of 12^∘ on both the dip (mean of 70^∘) and the strike of the seeds (the latter is equivalent to a 12^∘ uncertainty in the horizontal stress orientations). The mean strike of the seeds is 210^∘, thus exhibiting an average angle of 50^∘ with respect to S₁. We assume the seeds to have a coefficient of friction of 0.6±0.05 and a cohesion of 1 MPa. For the vertical stress magnitude, starting from S_v=85.3 MPa at a depth of 3.4 km, we use a stress gradient of 26.0 MPa km⁻¹ according to density estimations from borehole samples (rock density ρ=2650 kg m⁻³; Alber and Backers, 2015, and references therein). We set $S_{\mathrm{H}}=(\mathrm{1.41}\pm \mathrm{0.39})\cdot S_{\mathrm{v}}$ and $S_{\mathrm{h}}=(\mathrm{0.61}\pm \mathrm{0.08})\cdot S_{\mathrm{v}}$, while the standard deviation of S_v is set to 0.03. Note that all parameters in the seed model, except for the coefficient of friction and the state of stress that follow a normal distribution, are assumed to be constant. A list of the seed model parameters is given in Table 2.

(Alber and Backers, 2015, and references therein)Diehl et al., 2017Diehl et al., 2017(Moeck et al., 2015)(Moeck et al., 2015)(Moeck et al., 2015)(Diehl et al., 2017)(Diehl et al., 2017)

Table 2 Parameters used for the seed model.

4.3 Model calibration

We calibrate some of the hydraulic parameters against the bottom hole and wellhead pressure of the injection test, while the remaining parameters are taken from data or are reasonably assumed from the literature. We use iTOUGH2-PEST (Finsterle and Zhang, 2011) for the calibration according to the approach of a recent study using a coupled hydromechanical model (Rinaldi et al., 2017). The injection test is best suited for model calibration, since the area surrounding the borehole was not affected by previous stimulation. In addition, bottom hole pressures, probably more representative of the reservoir properties, are only available for the injection test. The pressure data from the acid stimulations are less useful for calibration, since the acidification may have changed the permeability of the carbonate rocks by dissolution, which is not considered in this study. Similarly, pressure data from the gas kick and well control injection are strongly affected by multiphase fluid interactions, which prevents a straightforward calibration.

The misfit between the observed and simulated bottom hole and wellhead pressure data is minimized using a Levenberg–Marquardt algorithm. We put 4 times more weight on the bottom hole data, since they are directly coupled to the hydraulic properties of the reservoir. We account for the wellhead pressure to obtain realistic well properties, because the injection occurs in the upper part of the cased borehole. The parameters we invert for are (i) the initial fracture zone permeability, (ii) the parameter C₁ in the permeability–pressure relationship for the fracture zone (Eq. 2), (iii) the fracture zone compressibility, and (iv) the permeability of the open section of the well.

In order to get a reasonably good fit for the pressure curve, we need to capture the typical fracture opening behavior at ΔP≃6 MPa (sharp kink shortly after the start of injection) as well as the post-shut-in behavior that is observed in the data (Fig. 7a). These two observations can be reproduced with an initial fracture zone permeability of $\mathrm{1.3}\times {\mathrm{10}}^{-\mathrm{14}}$ m² that increases to a maximum permeability of $\mathrm{5.4}\times {\mathrm{10}}^{-\mathrm{13}}$ m² at ΔP=9.4 MPa (C₁=57.3, $\mathit{\alpha }={\mathrm{10}}^{-\mathrm{8}}$) after 2 h of injection. Using the cubic law (Witherspoon et al., 1980), these permeabilities correspond to 10 fractures, each with a hydraulic aperture of about 70 (initial) and 235 µm (fully pressurized). Both the absolute fracture permeability and its changes are within expected ranges derived from in situ data in fractured rock (e.g., Rutqvist, 2015). For the remaining two inversion parameters, we obtain a fracture zone compressibility of $\mathrm{3.7}\times {\mathrm{10}}^{-\mathrm{8}}$ Pa⁻¹ and a permeability of the open well section of $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{8}}$ m².

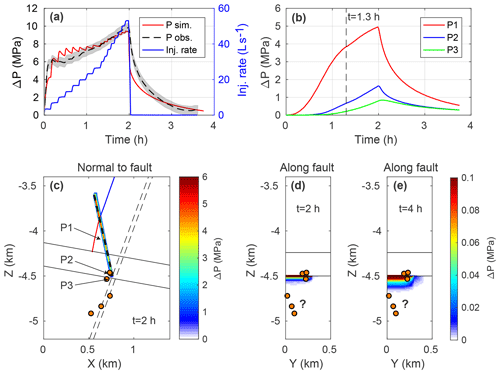
Figure 7 Simulated pressure change during the injection test. (a) Comparison of the measured and simulated pressure at the open section of the well after the model calibration with iTOUGH2-PEST. The shaded area denotes an error bound of 0.5 MPa of the measured pressure. (b) Pressure change over time at different points marked in (c): P1 in the fracture zone at a depth of ca. 4.2 km, P2 at the fracture zone/fault intersection in the fracture zone, and P3 at the fracture zone/fault intersection in the fault. The dashed black line marks the onset of seismicity at about 1.3 h. (c) Pressure change after 2 h at y=0 km (along profile A–A^′ in Fig. 2). The well is denoted by the red (open section) and blue (cased section) lines. The orange dots are the projections of the relocated events recorded during the injection test. (d–e) Pressure change after (d) 2 and (e) ca. 4 h along the fault (left damage zone, along profile B^′–B in Fig. 2). The orange dots are the projections of the relocated events recorded during the injection test. The location of the three deeper events is probably an artifact that can be corrected taking into account a local v_p∕v_s velocity anomaly (Diehl et al., 2017).

5 Numerical results and discussion

5.1 Injection test

We use the simulation run of the model calibration to quantify the timing and the magnitude of the pressure changes within the fracture zone and on the fault during the injection test. Figure 7b shows the pressure change over time at different points in the fracture zone (P1 and P2) and in the fault (P3), whose locations are specified in Fig. 7c. For all three points, a delay and an attenuation of the pressure response with respect to the well (Fig. 7a) can be observed. While the pressure at the center of the fracture zone (P1) increases by a maximum of about 5 MPa, the change is only about 1.6 MPa further down in the fracture zone (P2) and 0.8 MPa on the fault (P3). Despite the delayed response on the fault, an increase of about 0.2 MPa is observed after 1.3 h when the seismicity in St. Gallen was initiated (Diehl et al., 2017). Figure 7c illustrates the pressure change and the relocated seismic events of the injection test on a cross section normal to the fault (y=0 km) after 2 h of simulation time. The uppermost three events are close to the fracture zone/fault intersection and can be explained by the direct effect of the pressure caused by the injection, whereas the deeper events are outside the pressurized region. This can also be seen in Fig. 7d and e, where the pressure change and the induced events are shown along the fault after 2 and ca. 4 h, respectively. The three deeper events could be explained by a second fracture zone connecting the well with the reactivated fault at greater depth. However, as mentioned in Sect. 3, the location of the deeper events is probably an artifact (Diehl et al., 2017), which would allow an explanation of all the induced events with only one fracture zone.

Recently, Zbinden et al. (2020) used a hydromechanically coupled model to compare different scenarios with and without hydraulic connection. In the case of no connection, stress changes on the fault were purely governed by poroelasticity. Although the results showed that the induced events of the injection test all lay in regions of positive Coulomb stress change (i.e., in regions promoting failure), the magnitude of the stress changes was on the order of 10⁻³ MPa or lower, which is about 3 orders of magnitude smaller than in the case of a hydraulic connection (Fig. 7). In order to explain the induced seismicity, Zbinden et al. (2020) concluded that the reactivated fault in St. Gallen was most probably hydraulically connected to the well. This interpretation was in contrast to another study in which the St. Gallen deep geothermal project was classified as a site where poroelastic effects, rather than the direct influence of the injection and the associated increase in pore pressure, predominate at a greater distance from the well (Goebel and Brodsky, 2018). However, in view of our conceptual model with its supporting observations for a hydraulic connection and the results from previous simulations (Zbinden et al., 2020), a scenario without hydraulic connection is much less plausible than the fracture zone scenario examined here.

The results show that the small injection volume of 175 m³ during the injection test is sufficient to cause a significant increase in pore pressure on the distant fault and can thus promote fault reactivation. Although not modeled here, the same mechanism may have occurred for the acid stimulations, where more fluid was injected (roughly 290 m³; Alber and Backers, 2015, and references therein), and hence more seismicity was induced. Zbinden et al. (2020) found that several fracture zone parameters affect the pressure response at the well and on the fault. For calibrated models, however, the response in terms of pressure and stress changes was comparable, thus leading to similar conclusions. The strong pressure increase during the injection test raises the question why the connecting fracture zone was not reactivated itself, since in our model, it underwent pressure changes of several megapascals . On the one hand, a higher shear strength (i.e., higher friction or cohesion) of the fracture zone may be sufficient to prevent reactivation. Moreover, stress modeling has shown that the differential stress acting on the weaker Keuper, Lias, and Dogger formation, where the fracture zone mainly cuts through, may be lower than in other formations (Hergert et al., 2015). Hence, the fracture zone may be less critically stressed than the reactivated fault. On the other hand, we cannot exclude that the fracture zone was indeed reactivated but underwent only aseismic deformation that did not induce any seismic events.

In addition to the potential to reactivate a fault several hundreds of meters away from the well, such a hydraulic connection could also significantly affect the flow conditions during the operation of a geothermal power plant. If fluid were extracted from the well, the produced fluid would mainly be governed by inflow from the most permeable structure, i.e., from the highly permeable fracture zone in our model. The porosity, which determines the amount of fluid contained in the rock, can be very low in fractured rock. Thus, if production targets such a fracture zone, high flow rates are unlikely to last long, which is consistent with the low flow rates measured during the production test in St. Gallen (Wolfgramm et al., 2015). In the case of a second well drilled for fluid production and using the first well for injection (i.e., a geothermal doublet), the injected fluid would flow rapidly out of the well into the hydraulic connection. Hence, the open section of the production well would need to intersect the fracture zone at another location to efficiently produce the injected fluid. In our model, a potential location of the production well could be close to the fracture zone/fault intersection. However, since the efficiency of a geothermal plant strongly depends on the temperature of the produced fluid (e.g., Schechinger and Kissling, 2015), which is a function of the residence time of the fluid in the reservoir, a single, highly permeable flow path between the production well and the injection well would be far from appropriate as the fluid could not heat up sufficiently and the efficiency of the geothermal plant would be low.

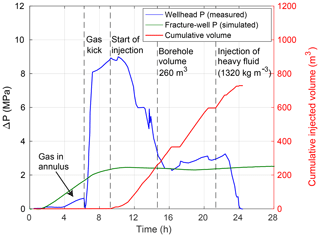
Figure 8 Measured wellhead pressure, simulated bottom hole pressure (fracture zone/well intersection inside fracture zone), and cumulative injected volume with time during the gas kick and well control injection. The vertical dashed black lines mark important events during the well operation (see text for more detailed explanations). The simulated overpressure at the bottom hole does not exceed the wellhead pressure prior to the injection of heavy fluids. Zero-time corresponds to the breach of the seal to initiate the gas kick in the simulation. Note that the injection is not modeled here.

5.2 Gas kick

For the gas kick simulation, we follow the hypothesis that the seismicity caused by the initial stimulations breached a seal to an overpressurized gas reservoir. In order to initiate the kick, we assume a sudden large change in permeability (from 10⁻²² to 10⁻¹⁵ m²) in the fault core right below the caprock (at a depth of 4.5 km). This enables the gas to pressurize the fracture zone and the bottom hole (i.e., the fracture zone/well intersection), where the pressure starts to increase after about 2 h (modeled curve in Fig. 8). We do not intend to completely fit the pressure curve measured in St. Gallen, because our high-permeability approach used for the well does not cover the physics of gas lifting, dynamic pressures, and pipe friction, which can play an important role during a kick (e.g., Pan et al., 2018). Instead, we focus on approximately matching the overpressure at the bottom hole and the timing of the gas kick. Since the pressure monitoring tool at the well bottom could not be retrieved after the gas kick and well control measures (Thomas Bloch, personal communication, 7 September 2019), we have to reconstruct the pressure change over time from the available wellhead pressure P_wh and injection data. The gas kick occurred shortly after the release by the operating crew of some gas that had accumulated in the annulus (ΔP≃0.6 MPa). After closing the well, the pressure rapidly increased to 8 MPa, then slowly rose to about 9 MPa (Fig. 8). At this point, the well was partially gas-filled and the weight of the fluid column was therefore below the hydrostatic equilibrium. During the injection of fresh water to combat the gas kick, the overpressure dropped to a plateau of 3 MPa shortly after the amount of injected water corresponded to the volume of the borehole (V_bh=260 m³; Fig. 8). Subsequently, since continuing water injection would not reduce the pressure further, the borehole was probably almost completely water-filled again (i.e., in hydrostatic equilibrium). Therefore, the overpressure at the bottom hole caused by the gas may have approximately corresponded to the wellhead pressure of the plateau, i.e., about 3 MPa. Since we cannot rule out that the well was still partially filled with gas, this value is assumed to be a maximum overpressure that could have been caused by the gas. For the simulation, the bottom hole pressure reaches a steady plateau of ca. 2.4 MPa after about 10 h, which is similar to the value of the reconstructed bottom hole overpressure (note that injection is not modeled here). The well could finally be killed (P_wh=0) by the injection of dense (ρ_m=1320 kg m⁻³) K₂CO₃-based drilling fluid (Alber and Backers, 2015; Naef, 2015, and references therein). Assuming a fully fluid-filled borehole, a drilling mud injection volume of V_m=100 m³ (Alber and Backers, 2015, and references therein), and a water density of ρ_w=1000 kg m⁻³, the average fluid density can be calculated as

$$\begin{array}{}\text{(7)}& {\mathit{\rho }}_{\mathrm{avg}}={\displaystyle \frac{\left[V_{\mathrm{m}}\cdot {\mathit{\rho }}_{\mathrm{m}}+(V_{\mathrm{bh}}-V_{\mathrm{m}})\cdot {\mathit{\rho }}_{\mathrm{w}}\right]}{V_{\mathrm{bh}}}}=\mathrm{1123}{\mathrm{kg}\mathrm{m}}^{-\mathrm{3}},\end{array}$$

which results in a pressure of about 42 MPa at a depth of 3.8 km. This corresponds to an overpressure of approximately 5 MPa with respect to the initial undisturbed reservoir pressure, which is indeed sufficient to prevent gas with an overpressure of 3 MPa from entering the well.

The change in overpressure over time at the well bottom and the timing of the gas kick is dependent on different parameters such as the overpressure of the gas reservoir, the capillary pressure in the fault and in the fracture zone, and the permeability of the breached fault core. Here, we consider the effect of different permeabilities for the breached fault core, as this does not require reinitialization of the gas plume (Fig. 9). For the base case shown in Fig. 8, we set the permeability of the breached seal to 10⁻¹⁵ m². Reducing the permeability by 1 order of magnitude leads to a significantly slower and weaker pressure response at the fracture zone/well intersection, whereas a 10-fold increase yields a similar overpressure as in the base case (Fig. 9a). In the latter case, the peak pressure is reached about 0.2 d before, followed by a pressure drop that is not observed for the base case. Similar to the permeability of the breached fault seal, we expect the thickness of the fault core to influence the strength of the gas kick, because reducing the thickness would result in a higher pressure gradient between the two reservoir compartments, which would cause more fluid flow across the fault after the seal has been breached. In our numerical model, the thickness of 5 m corresponds to the width of the fault core elements. Individual fault cores are usually thinner than 1 m (e.g., Shipton et al., 2006), but faults may contain multiple narrow cores (e.g., Faulkner et al., 2010) so that the sealing part of the fault can be thicker, which can justify our assumption in the model. Moreover, note that according to Darcy's law, an increase (decrease) in permeability of the breached fault core would correspond to a decrease (increase) in thickness of the fault core, since in both cases the fluid flow across the fault would be equally affected. For instance, decreasing the fault core thickness by 1 order would correspond to the scenario with a breached-fault-seal permeability of 10⁻¹⁴ m². Hence, the sensitivity study on the permeability of the breached fault seal is equivalent to examining the effect of fault core thickness on the strength of the gas kick. The permeability also has an effect on the timing of the gas kick, as illustrated in Fig. 9b. In the case of $\mathit{\kappa }={\mathrm{10}}^{-\mathrm{14}}$ m², the gas reaches the fracture zone/well intersection after about 0.2 d, whereas it takes 0.26 and 0.5 d for the cases of medium (10⁻¹⁵ m²) and low (10⁻¹⁶ m²) permeability, respectively. A second increase in gas saturation can be observed for the medium and high-permeability cases after about 0.8 d, which occurs when the gas starts to accumulate in the upper part of the fracture zone between a depth of 3.6 and 3.8 km. The change in pressure at the fracture zone/fault intersection that is located in the vicinity of the breached seal follows a similar trend when compared to the pressure simulated at the fracture zone/well intersection (Fig. 9c). Figure 9d shows the gas saturation of the base case at y=0 km after 0.4 d, i.e., about 3 h after the gas has reached the well. At this time, the entire fracture zone has a gas saturation of about 30 %.

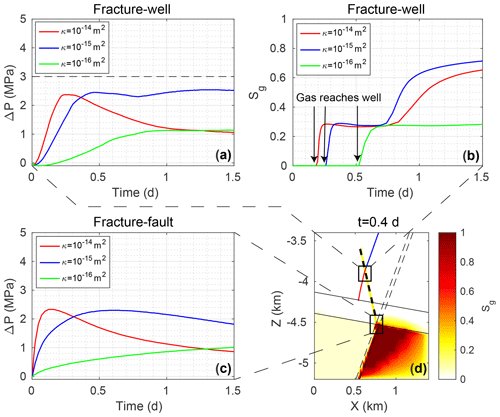
Figure 9 (a) Pressure change over time for different permeability values of the broken fault seal at the fracture zone/well intersection ($z\simeq -\mathrm{3.9}$ km). The dashed black line at 3 MPa marks the approximate pressure of the plateau in Fig. 8, which is considered as a maximum overpressure that could have been caused by the gas (see text). Zero-time corresponds to the breach of the seal to initiate the gas kick. (b) Gas saturation over time for different permeability values of the broken fault seal at the fracture zone/well intersection ($z\simeq -\mathrm{3.9}$ km). (c) Pressure change over time for different permeability values of the broken fault seal at the fracture zone/fault intersection ($z\simeq -\mathrm{4.5}$ km, i.e., close to the breached seal). (d) Gas saturation after ca. 0.4 d at y=0 km (normal to the fault, along profile A–A^′ in Fig. 2).

5.3 Well control injection and associated seismicity

Starting from the same conditions as for the gas kick simulation (base case), we start to inject water after about 0.4 d, i.e., about 3 h after the gas has reached the well – consistent with the observations illustrated in Fig. 8. We then follow the recorded injection protocol but ignore the injection of heavy mud at the end of the well control exercise. Using a total of 40 000 seeds, we simulate 1000 realizations of the entire sequence for a simulation time of 10 d. During the sequence, we assume further permeability changes in the fault core associated with the M_L 2.1 and M_L 3.5 events, the two largest earthquakes in the sequence. For the sake of simplicity, we set a permeability of 10⁻¹⁵ m² after 0.9 d (M_L 2.1) and 1.0 d (M_L 3.5) on rectangular areas around the corresponding hypocenters that may have slipped (Fig. 10). Additionally, we account for the fact that the fracture zone/fault intersection has encountered some stress drop due to the seismicity induced by the previous activities (see Fig. 3) using a slightly higher criticality threshold in this region (μ_c=0.015).

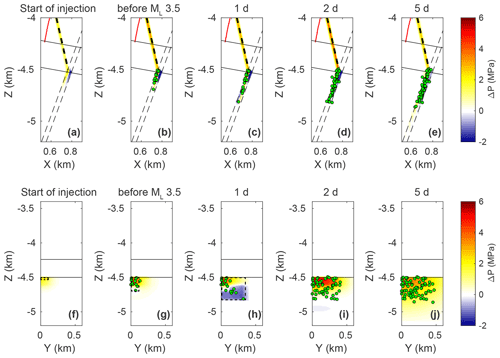
Figure 10 (a–e) Pressure change and simulated seismicity (single realization) during the gas kick and well control measures at y=0 km after (a) ca. 0.4 d (start of injection), (b) 0.99 d (shortly before the M_L 3.5 event), (c) 1 d (immediately after the M_L 3.5 event), (d) 2 d, and (e) 5 d of simulation time along profile A–A^′ in Fig. 2 (normal to the fault). The open section of the well is denoted by the red line. The fault is illustrated by the thin dashed black lines, the fracture zone by the thick dashed black line, and the caprock by the solid black lines. (f–j) Pressure change and simulated seismicity (single realization) on the fault (left damage zone) after (f) approx. 0.4 d (start of injection), (g) 0.99 d (shortly before the M_L 3.5 event), (h) 1 d (immediately after the M_L 3.5 event), (i) 2 d, and (j) 5 d of simulation time along profile B^′–B in Fig. 2 (along fault). The solid black lines indicate the caprock. The dashed black rectangles denote the area of permeability change to (f) initiate the gas kick, due to (g) the M_L 2.1 event, and because of (h) the M_L 3.5 event.

Figure 10 shows the pressure change on the left damage zone of the fault together with the simulated seismicity of a single model realization at different times. No seismicity is observed before the gas kick, whereas a few events are induced at a depth of about 4.6 km after the M_L 2.1 and immediately before the M_L 3.5 event (Fig. 10a, b, f and g). Shortly after the main shock (after 1 d), seismicity has propagated further along the horizontal direction and to greater depth, mainly in regions where the permeability of the fault core has changed (Fig. 10c and h). During the following days, significantly more seismicity is induced, extending on a patch between a depth of 4.5 and 4.8 km and up to 0.5 km in the y axis (Fig. 10d, e, i and j). Regarding the spatial distribution of the seismicity, our model approximately reproduces the extent of the observed seismicity cloud (Fig. 3e and f), although the simulated seismicity cloud is somewhat smaller than the observed one; the mean extent of the seismicity of the 1000 model realizations is 0.133 km² with a standard deviation of 0.025 km², while the area of the observed seismic events (with magnitudes greater than M_c, see below) is 0.214 km². The pressure is strongly affected by the permeability changes adopted in the model. The pressure in the left damage zone increases after the M_L 2.1 event in the upper part of the fault (at a depth of approx. 4.6 km) due to gas inflow, whereas the M_L 3.5 event causes the pressure to decrease in the lower part of the rupture area because water flows across the fault (Fig. 10g and h). On the other hand, the pressure in the fault core increases after the main shock, which leads to the reactivation of seeds at greater depth (Fig. 10c). The negative change in pressure is compensated by water and gas inflow, and after 5 d the pressure change becomes positive along the entire fault (Fig. 10j).

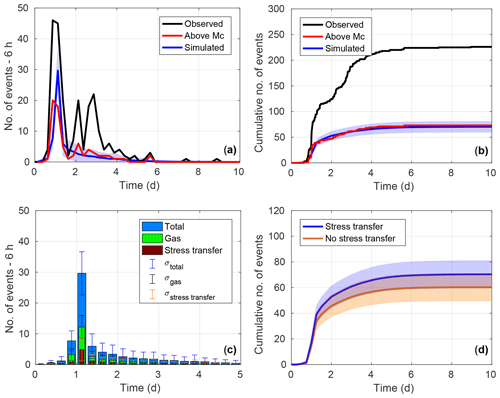
Figure 11 Statistical analysis of the main sequence simulation. (a) Number of events for every 6 h compared to the entire relocated catalog and events above M_c. (b) Cumulative number of events with time compared to the entire relocated catalog and events above M_c. (c) Number of events for every 6 h induced in total, by the gas and by static stress transfer. (d) Comparison of simulated cumulative number of events with and without stress transfer. The shaded area in (a), (b), and (d) and the error bars in (c) indicate 1 standard deviation over a total of 1000 realizations. Zero-time corresponds to the breach of the seal to initiate the gas kick.

With the given number of seeds, our model fits the temporal evolution of the seismicity (Fig. 11). Since the relocated catalog is incomplete for events with magnitudes M_c<0.8, we only model events with M_w≥M_c in order to properly compare the data. We obtain a good match both for the number of events per time interval (Fig. 11a) and for the cumulative number of events (Fig. 11b). For the latter, the observations lie well within 1 standard deviation of the 1000 realizations of the seed model. Due to the permeability changes in the fault core associated with the two largest seismic events, the simulation captures the strong increase in seismicity after the main shock at about 1 d. In order to quantify the influence of the gas on the seismicity, we introduce a criterion to assess whether the seeds were triggered by gas or water. We determine a seed to be gas-triggered if the change in gas saturation ΔS_g with respect to the initial state is positive (i.e., ΔS_g>0), which is equivalent to ΔP>ΔP_w and ΔP<ΔP_g. A seed is also classified as gas-triggered if the region around it is fully gas saturated, and thus ΔS_g≥0. If seeds rupture due to static stress transfer, they are classified as neither gas- nor water-triggered. Figure 11c illustrates the gas-triggered events and the seeds reactivated by static stress transfer in comparison to the total number of events. On average, 39 % of the seeds are triggered by the gas, while another 16 % are triggered by the static stress transfer. Hence, a significant number of seeds are triggered by an increase in gas pressure. The influence of static stress interactions is more complex to assess, as triggered seeds may cause both negative (stress shadow) and positive Coulomb stress changes on adjacent seeds, bringing them closer or farther away from failure (Catalli et al., 2016; King et al., 1994). Hence, some seeds can be triggered by a change in fluid pressure (i.e., counted as gas or water-triggered) as a consequence of positive Coulomb stress change, while other seeds can be prevented from failure due to a negative change in the Coulomb stress, although they would have been triggered by fluid flow if stress transfer was ignored. An alternative approach to assess the influence of earthquake interaction is to run a model completely ignoring static stress transfer (Fig. 11d). The result shows that stress transfer starts to play an important role after about 1 d of simulation time (i.e., after the main shock). At the end of the simulation, disregarding stress transfer reduces the total number of triggered seeds by about 14 % (note the difference of 2 % to the approach above). Compared to the modeling results obtained for the EGS project in Basel, the influence of stress transfer is less but still of the same order (24 %; Catalli et al., 2016).

In our simulation, most of the seismicity is induced after the fault core breached during the two main events. In order to determine the effect of the gas and the well control injection on the induced seismicity without the a priori assumption of a breached fault seal, we consider scenarios where permeability is only changed to initiate the gas kick but not afterwards. In Fig. 12a, we plot the time of the first simulated earthquake (onset) for three different scenarios (1000 realizations each): (i) water injection according to the injection protocol of the well control measures, (ii) no injection, and (iii) opening the wellhead (P_wh=0.1 MPa) and no injection. In all three scenarios, the median onset of seismicity occurs a few hours after the time of the actual well control injection. The onset differs only slightly between the three scenarios (0.5 to 0.6 d), whereas the uncertainty bars given by the first and third quartile show that the seismicity is increasingly delayed without water injection, particularly for the scenario with an open well, where the onset can become larger than 1 d. For the scenarios without injection, in 77 and 96 (open well) realizations no seismicity is induced at all, whereas for the case of injection, in only 21 instances is seismicity absent. In the simulations, although the gas has to cross the fault to cause the gas kick in the well, seismicity does not start immediately after the fault seal breached. This occurs because a certain increase in pressure is required to reactivate even the most critically stressed seeds (because of the criticality threshold described in Sect. 4.1). The pressure change over time of the analyzed scenarios is shown in Fig. 12b to d. The injection has a large effect at the fracture zone/well intersection, while it is less pronounced further away from the well. At the fracture zone/fault intersection and further down on the fault (at a depth of 4.6 km), the additional pressure increase caused by the water injection is only a few tenths of a megapascal. This strong attenuation of the pressure response is mainly caused by the highly compressible gas in the fracture zone and in the fault that damps the effect of the injection. Opening the well merely has an effect at the fracture zone/well intersection, while no influence can be observed on the fault. Overall, the scenarios suggest that without injection, the seismicity is delayed but in most cases not absent, which is another indication that the gas significantly affected the induced seismicity. On average, only four events are induced for the injection case, whereas less than three events occur for the scenarios without injection. These small numbers roughly agree with the relocated catalog, where only seven events with a magnitude larger than M_c occurred before the M_L 2.1 event.

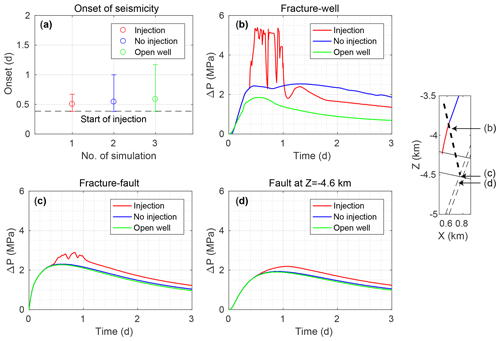
Figure 12 Comparison of scenarios with injection, without injection, and with an open well and no injection (1000 realizations each). (a) Onset of seismicity with error bars showing the first and third quartile around the median. The dashed line indicates the start of injection (ca. 0.4 d). (b–d) Pressure change at (b) the fracture zone/well intersection, (c) the fracture zone/fault intersection, and (d) within the fault at a depth of 4.6 km. The model sketch on the right shows the locations of the pressure monitoring points.

5.4 Effect of the gas on the induced seismicity

Our simulations suggest that overpressurized gas played an important role during the St. Gallen induced seismicity sequence. Using our definition of gas-triggered events, the simulation that includes permeability changes due to the two main events shows that about 40 % of the seeds were reactivated by the presence of the gas. Note that seeds are triggered not only directly by an increase in gas pressure but also indirectly by gas that dissipates the water, which can pressurize more distant regions with unchanged gas saturation. On the other hand, the observed absence of seismicity in the beginning of the gas kick could be seen as an indicator that the gas did not directly affect the induced seismicity. However, our simulation can reproduce the delay of the onset of the seismicity (Fig. 12a) even though the gas has to cross the fault to initiate the gas kick. A delay of about 6 h was observed between the onset of the seismicity and the start of the well control injection, as opposed to the injection test where seismicity begins after 1 h. Hence, the reason for the delay could be that the part of the fault that was pressurized first had been reactivated by the previous stimulations and was thus not as critically stressed (as assumed in our model). In the simulation, most of the seismicity occurs after a hydraulic connection between the left and right fault damage zones has been established, implying that these events are induced by multiphase fluid flow caused by the strong pressure gradient between the two compartments. Indeed, simulations ignoring further permeability changes (Fig. 12) produced significantly less events. Thus, in terms of seismicity, the simulation of the main sequence (Figs. 10 and 11) including the permeability changes in the two main events corresponds to a worst-case scenario with overpressurized gas. These results are supported by a maximum loss of waveform coherence in the ambient seismic noise field that was observed prior to the main shock, indicating a significant medium change due to fluid flow and associated pore pressure changes possibly caused by overpressurized gas (Obermann et al., 2015). Nevertheless, since most events are induced after the main shock and thus after our assumption of increased fault core permeability, the effect of the gas on a larger event remains unclear. From a physics-based point of view, our results suggest that the additional pressure increase due to the M_L 2.1 event could have promoted an even larger event, since overpressurized fluid can have a direct influence on the rupture area of induced earthquakes (Galis et al., 2017). Hence, overpressurized gas could explain the large magnitude of the main shock that exceeded the theoretical threshold of the expected maximum magnitude (McGarr, 2014). In this study, because of the random assignment of magnitudes in the model, we cannot further elaborate on this. A physics-based model accounting for multiphase fluid conditions and explicitly simulating fault rupture may address this open question (e.g., Zbinden et al., 2017, 2018).

The extensive permeability change assumed in this model refers to a breach of the fault seal, as suggested by other field and modeling studies (e.g., Lyon et al., 2005; Miller et al., 2004). Additionally, enhanced permeability can be caused by shear dilation of pre-existing fractures (e.g., Lee and Cho, 2002; Rinaldi and Rutqvist, 2019). The sudden change in the hydraulic properties and associated fluid flow can explain the aftershock sequence of the M_L 3.5 event. Such permeability changes in sealing faults due to induced seismicity can have implications for other geo-energy applications, such as CO₂ sequestration and UGS. For instance, the large Hutubi underground gas storage (HUGS) facility in northwestern China is bound by multiple faults sealing the reservoir (e.g., Jiang et al., 2020). These seals may be damaged by small induced earthquakes reported in the field (Zhou et al., 2019), which could cause gas leakage. In addition to fluid flow, another important mechanism for aftershocks is static stress transfer, which can lead to stress redistribution around the sliding surface of the main shock, leading to further seismicity (Catalli et al., 2016; King and Devès, 2015). In our simulations, the contribution of static stress transfer is smaller than the influence of the gas (Fig. 11). Király-Proag et al. (2019) have recently analyzed the slip pattern of the main shock by back-projecting relative source time functions of the main events onto the reactivated fault plane. They found that most aftershocks that occurred within 5 d after the main shock are located at the edge of the M_L 3.5 slip area, suggesting that stress concentration due to stress transfer may have played a major role. Here, with the exception of the assumed permeability changes, we do not explicitly model the main event with the associated stress drop and stress redistribution. Moreover, we treat fault strength as a static parameter excluding time-dependent failure caused by static stress transfer. Thus, a detailed geomechanical modeling of the M_L 3.5 event that accounts for time-dependent failure is required to more accurately quantify the relative contribution of static stress transfer and fluid flow to the aftershock sequence.

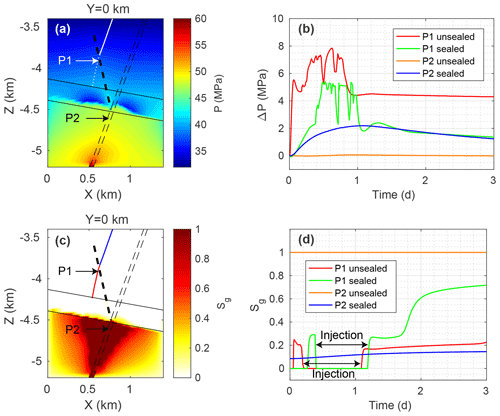
Figure 13 Scenario without a fault seal. (a) Initial pressure conditions at y=0 km (along profile A–A^′, normal to the fault, in Fig. 2). The well is denoted by the dotted (open section) and solid (cased section) white line. (b) Pressure change with time at the fracture zone/well intersection and on the fault ($z=-\mathrm{4.6}$ km) in comparison to the scenario with a sealing fault. (c) Initial gas saturation at y=0 km (along profile A–A^′ (normal to the fault) in Fig. 2). The well is denoted by the red (open section) and blue (cased section) lines. (d) Gas saturation over time at the fracture zone/well intersection and on the fault ($z=-\mathrm{4.6}$ km) in comparison to the scenario with a sealing fault. (a, c) The fault is illustrated by the thin dashed black lines, the fracture zone by the thick dashed black line, and the caprock by the solid black lines.

The suggested model depends largely upon the initial conditions with a compartmentalized gas reservoir. To further investigate the effect of this assumption, we performed simulations with a model without a fault seal, where the gas reservoir equally pressurizes the left and right damage zones of the fault (Fig. 13a). In contrast to the case with a sealed fault, in the scenario without a fault seal the gas kick is initiated after a caprock seal breaks at the fracture zone/fault intersection. The results show that the gas kick at the bottom hole is stronger for the unsealed fault (Fig. 13b), because the gas plume is initially located slightly closer to the fracture zone, and the gas does not need to penetrate the broken fault seal (Fig. 13c), which has a 10-fold lower permeability than the rest of the fault. Hence, the gas reaches the well about 0.2 d (approx. 5 h) earlier compared to the scenario that includes a fault seal (Fig.  13d). Note that the injection is started 3 h after the gas kick and thus not simultaneously for the two scenarios. A comparison of the pressure change at the left damage zone of the fault (at a depth of 4.6 km) shows that the scenarios are inherently different. For the case of a sealing fault core, the pressure increases shortly after the gas kick is initiated, because the overpressurized gas intrudes into a previously undisturbed region (i.e., P close to hydrostatic, S_g≃0.1). For the case without a seal, the pressure is affected neither by the gas kick nor by the fluid injection, because the fault is fully gas-filled (S_g=1) and already in an overpressurized condition. Hence, the pressure is largely unaffected during the gas kick, whereas during the injection, the gas is compressed with almost no effect on the pressure. Due to the near-zero pressure changes, we did not perform simulations with the seed model. The comparison shows that the scenario with a sealing fault and sudden permeability changes can more accurately describe the seismicity observed in St. Gallen. Nevertheless, the scenario with an unsealed fault also shows that gas does not necessarily enhance the seismicity, as it can damp the effect of the fluid injection.

Another possible explanation for the seismicity would be purely poroelastic stress changes without any hydraulic connection. In such a case, it was shown that stress changes on the fault are much smaller than in the case of a hydraulic connection (Zbinden et al., 2020), implying that the fault needs to be in a highly critical stress state (i.e., only a few 10⁻³ MPa or less away from failure). In addition to the reasons already provided for the injection test, the following observations would be inconsistent with a poroelastic scenario.

1. Since there is no connection, the gas would probably be stored in the Malm layer or in the Upper Dogger in the vicinity of the well (e.g., Wolfgramm et al., 2015), which raises the question of why the gas did not enter the well during drilling or shortly after the injection test/acid stimulations.

2. The fault is oriented at an angle of about 50^∘ with respect to the maximum principal stress. According to the Mohr–Coulomb theory, an optimally oriented fault would exhibit an angle of 30^∘ (assuming μ_s=0.6). Hence, the fault in St. Gallen may not be that critically stressed.

3. The seismicity of the post-injection period (September to October 2013) shows diffusion-like propagation characteristics (Diehl et al., 2017) commonly observed for fluid flow.

For these reasons, we did not attempt a model simulation that accounted for poroelastic stress changes. Due to the complex interaction of multiphase fluid flow and seismicity at St. Gallen, we cannot rule out the possibility that the gas was stored at a different location and was therefore not directly linked to the seismicity. For instance, the gas could have been stored halfway between the well and the fault, implying that the gas would not directly pressurize the fault during the gas kick. Still, the scenario simulated here is the most likely from our point of view.

5.5 Implications for future deep hydrothermal projects

In Switzerland and elsewhere, target reservoirs for future hydrothermal projects may be located at a similar depth and in similar geological conditions as the St. Gallen region. For instance, ongoing projects in the Western Alpine Molasse basin (WAMB) at the border between France and Switzerland aim to generate heat and electricity using the high geothermal potential of the area (Chelle-Michou et al., 2017). Due to the similar stratigraphy and the potential presence of Permo-Carboniferous troughs serving as source rocks for gas, the probability of encountering gas during the drilling and stimulation of deep wells could be relatively high. The simulations of fault seal architecture (Fig. 13) indicate that the effect of gas on the induced seismicity highly depends on the location of the plume and the initial pressure and gas saturation of the fault. Although it is difficult to accurately evaluate potential locations of gas prior to any stimulation, the presence of a PCT can be a strong indication of gas and should be identified as early as possible in the project, for instance with an active 3D seismic survey (Heuberger et al., 2016) and gravimetric methods (e.g., Altwegg et al., 2015) as was done in the St. Gallen region. Furthermore, if natural gas is expected to be present at the reservoir depth, it is important to record parameters such as multiphase flow rates in the well and bottom hole pressure during the entire project to enable a more accurate hydromechanical analysis in both real-time and retrospectively. In St. Gallen, pressure at the well bottom was recorded with a memory tool, which unfortunately could not be retrieved after the well control measures. With regard to fluid injection, although our simulations strongly suggest that the effect of the well control injection was damped by the compressible gas in the fracture zone and the fault (even in the scenario of a compartmentalized gas reservoir), uncontrolled injection in future projects may greatly increase seismicity and the likelihood of inducing a felt event and should therefore be avoided where possible. In St. Gallen, stopping the injection of the well control operation during the gas kick was not an option due to safety reasons at the drilling site.

The simulation of the injection test shows that a hydraulic connection can lead to rapid pressure changes several hundreds of meters away from the well. Since this can lead to problems in the efficient operation of a geothermal power plant (see Sect. 5.1), an option for future hydrothermal projects may for instance be to seal such permeable structures with hydraulic packers. This may provide more uniform flow during injection and production operations and may increase the residence time of injected fluids, meaning that they can be extracted at a higher temperature from a nearby production well. The installation of packers during the stimulation phase could also help to more locally (i.e, more accurately) characterize the hydraulic properties of the reservoir. Hydraulic testing of small intervals in the open section of the borehole (e.g., individual fractures and faults intersecting the borehole) could significantly improve hydromechanical analyses and would provide more detailed input data for numerical models. Although expensive, such a multistage approach was recently carried out in an EGS project in Finland (e.g., Kwiatek et al., 2019) and could potentially also be used for hydrothermal systems.

In St. Gallen, the seismicity ceased during a production test conducted in October 2013. While long-term fluid production from porous reservoirs may lead to compaction and induce seismicity on faults intersecting the reservoir (e.g., van Thienen-Visser and Breunese, 2015; Zbinden et al., 2017), in the short term, production associated with a decrease in pore pressure can increase the effective normal stress and thus stabilize faults close to the reservoir. Moreover, in the case of a fractured low-porosity reservoir like St. Gallen, poroelastic compaction effects may be much less pronounced (e.g., Moeck et al., 2015). Hence, an initial production phase prior to any fluid injection operation may be a strategy to reduce the potential for fault reactivation in such hydrothermal reservoirs.

Finally, since faults can act as conduits for hot fluids from greater depth and can cause positive temperature anomalies (e.g., Chelle-Michou et al., 2017), they are often considered beneficial for geothermal heat production. Such temperature anomalies can be enhanced if a PCT is present, as the rising fluids may form convective cells in the permeable sediments of the Permo-Carboniferous grabens (Chelle-Michou et al., 2017). Nevertheless, operators must be aware that drilling and injecting into fault zones is always associated with a high probability of inducing felt seismicity, especially in the case of overpressurized gas as shown by the project in St. Gallen.

6 Conclusions

We have performed a detailed hydromechanical analysis of the multiphase fluid processes and the induced seismicity at the St. Gallen deep geothermal project with the following results:

1. Based on borehole logs, a seismic survey, and the earthquake catalog, we have developed a conceptual model that suggests a highly permeable connection between the injection well and the reactivated fault that is located at several hundreds of meters distance from the well.

2. We implement our concept in a numerical model that is calibrated against the measured well pressure of the injection test. The model shows that the small fluid volumes of the injection test (175 m³) are sufficient to yield a fast and significant pressure increase on the fault (ΔP≃0.8 MPa within 1 h).

3. We simulate the gas kick using the calibrated model and assuming an overpressurized gas reservoir laterally sealed by the fault and released due to the stimulations. The model reproduces the reconstructed overpressure at the bottom hole during the gas kick (ΔP≃3 MPa).

4. We are able to reproduce the temporal and spatial evolution of the main seismicity sequence following the well control injection. In order to match the aftershock sequence of the M_L 3.5 event, we assume that the fault core is breached during the two largest events of the sequence, which results in strong pressure gradients and associated multiphase fluid flow.

5. The simulations show that the gas may have played a major role: based on the assumption of a breached fault and the initial conditions in our model, ca. 40 % of the events were directly induced by the gas, while 16 % were triggered by static stress transfer. Moreover, simulations without an injection delayed the onset of seismicity but in most cases still induced seismic events. Whether the gas increased the probability of inducing a larger event remains unclear and a more physics-based model regarding fault rupture could provide an answer.

6. In prospect of future deep hydrothermal projects, an initial phase of fluid production could stabilize faults in the vicinity of the reservoir and thus reduce the potential for fault reactivation. Additionally, since highly permeable fractures intersecting the borehole could become problematic during the long-term operation of a project in terms of heat exchange between the injected fluids and the reservoir rock, hydraulic packers could be used to seal such fractures and thus achieve more uniform flow behavior. Also, prior knowledge of the location of potential source rocks for gas (e.g., PCT) may help to better assess the hazards not only for gas kicks but also for induced seismicity. A 3D seismic survey in combination with other methods (e.g., gravimetric data), as carried out in the St. Gallen area, is therefore strongly recommended prior to any deep hydrothermal project.