Conditional probability of distributed surface rupturing during normal-faulting earthquakes

Coseismic surface faulting is a significant source of hazard for critical plants and distributive infrastructure; it may occur either on the principal fault or as distributed rupture on nearby faults. Hazard assessment for distributed faulting is based on empirical relations which, in the case of normal faults, were derived almost 15 years ago using a dataset of US earthquakes. We collected additional case histories worldwide, for a total of 21 earthquakes, and calculated the conditional probability of distributed faulting as a function of distance from the principal fault. We found no clear dependency on the magnitude nor the time of occurrence of the earthquakes, but our data consistently show a higher probability of rupture when compared with the scaling relations currently adopted in engineering practice. We derive updated empirical regressions and show that the results are strongly conditioned by the averaging of earthquakes effectively generating distributed faulting at a given distance and those which did not generate faulting; thus, we introduce a more conservative scenario that can be included in a logic tree approach to consider the full spectrum of potential ruptures. Our results can be applied in the framework of probabilistic assessment of fault displacement hazard.

1 Introduction

Surface faulting is a significant source of hazard following moderate to strong earthquakes (i.e., $M>\mathrm{ca}.\mathrm{6}$). The quantification of fault displacement hazard is critical for the engineering design of infrastructure and land use planning close to active faults. The avoidance criterion is usually applied for mitigating fault displacement hazard when a fault strand's location is certain; however, there are situations where crossing an active fault cannot be avoided (e.g., distributive infrastructure, pipelines). Moreover, faulting can occur either on the principal fault or on secondary fault strands. Currently, a probabilistic approach (i.e., PFDHA – probabilistic fault displacement hazard analysis) is the suggested method to calculate the expected displacement due to surface faulting for siting nuclear power plants and critical facilities (e.g., ANSI/ANS-2.30, 2015). This approach was firstly proposed by Youngs et al. (2003) for the high-level nuclear waste repository in the Yucca Mountain, Nevada. The method is directly derived from probabilistic seismic hazard analysis (PSHA), firstly developed by Cornell (1968), which determines the annual rate of earthquakes in which a ground motion parameter exceeds a specific value, at a given location.

The earthquake approach for assessing PFDHA (Youngs et al., 2003) expresses the rate of displacement exceeding a given value as a function of (i) the annual rate of occurrence of earthquakes with a given magnitude, (ii) the probability of surface rupture along the principal fault, and (iii) the probability that off-fault rupture at a given distance from the principal fault exceeds a given displacement value.

According to Youngs et al. (2003), the attenuation function for fault displacement, i.e., the term (iii) of the general PFDHA function, can be split into two terms (Eq. 1):

$$\begin{array}{}\text{(1)}& P_{kn}(D>d\mathrm{|}m,r)=P_{kn}(\mathrm{Slip}\mathrm{|}m,r)\times P_{kn}(D>d\mathrm{|}m,r,\mathrm{Slip}),\end{array}$$

where k is the position of the site of interest, n is the seismogenic source, D is displacement at the site, d is a given displacement threshold, m is magnitude, and r is distance from the principal fault to the site.

The first term is the conditional probability that some amount of displacement occurs at site k, i.e., it represents the actual occurrence of distributed faulting (D>0). The second term is the conditional probability of exceeding a given level of displacement (d). In this paper, we focus exclusively on the first term in Eq. (1); this choice was driven by the fact that surface faulting can be an exclusion criterion for some plants (e.g., nuclear power plants).

While several efforts have been devoted to describing and measuring surface faulting along the main rupture after strong earthquakes (e.g., Wells and Coppersmith, 1994; Pezzopane and Dawson, 1996; Field et al., 2015), less information is available on distributed faulting. Following the pivotal work of Youngs et al. (2003) on normal faults, the PFDHA approach was applied to strike-slip (Petersen et al., 2011) and reverse faults (Moss and Ross, 2011; Boncio et al., 2018; Nurminen et al., 2020). Regional datasets were built as well (e.g., Takao et al., 2013, and Inoue et al., 2019, for Japan strike-slip and reverse faults). Slightly different methods and procedures were adopted for developing empirical relations of the probability of faulting. The decrease in the probability of faulting with distance from the principal fault was unequivocally identified by all of the studies; for other driving parameters, a general consensus has still not been achieved – for instance, a magnitude dependency was included by Youngs et al. (2003) but not by Petersen et al. (2011). The hanging wall and footwall are considered separately by most of the authors dealing with dip-slip ruptures (but not by Takao et al., 2013).

The role of the local structural setting, fault architecture at depth, and near-surface geology (e.g., cut lithologies, overburden load) has been highlighted after the analysis of recent earthquakes, which caused a complex pattern of rupture at the surface (e.g., Bray et al., 1994; Milliner et al., 2015; Teran et al., 2015).

Concerning normal faults, the reference paper for PFDHA is still the work by Youngs et al. (2003), which was published almost 20 years ago and analyzed a dataset of US earthquakes. Since then, additional datasets have been acquired (see Baize et al. 2019, for a comprehensive review on the efforts devoted to building a unified database of fault displacement), and a general underestimation of the relations of Youngs et al. (2003) in the far field was recently pointed out by Ferrario and Livio (2018). In this work, we present data and improved regression equations for the conditional probability of off-fault rupture. We supplemented the earthquakes already analyzed by Youngs et al. (2003) with additional case histories, for a total of 21 earthquakes. This figure more than doubled the dataset considered in the original work.

We provide an updated version of the conditional probability of distributed faulting as a function of distance from the principal fault. Our results broadly agree with those of Youngs et al. (2003) but systematically show a probability of occurrence higher than expected. Thus, we introduced a conservative scenario, to fully account for the range of observed probabilities, that can be handled in a logic tree approach, as commonly done for PSHA studies.

2 Materials and methods

2.1 Dataset

We analyzed 21 events that occurred between 1887 and 2016, ranging in magnitude (M_w) from 6.0 to 7.5. Nine of them are from the western US and have already been analyzed in terms of PFDHA by Youngs et al. (2003), who, in turn, used data compiled by Pezzopane and Dawson (1996). Data for the remaining 12 earthquakes were collected from the scientific literature or available databases (i.e., the SURE Project; Baize et al., 2019). Table 1 lists the main details and the data source for each earthquake.

Table 1 Details on the 21 earthquakes analyzed in the present study. The references list the sources for the map of surface ruptures. “^*” in the reference column highlights the events that were included in the work by Youngs et al. (2003).

The considered events occurred in different countries, and all five continents are represented with at least one case history: nine earthquakes are from the US, six are from Italy, two are from Greece, and Kenya, Turkey, New Zealand, and China are all represented by one event (Fig. 1). The geographical distribution of the events reflects either the regional seismotectonic setting or the availability and accessibility of data: the US, Italy, and Greece are frequently hit by normal-faulting events; other regions, like China, are less represented in our database despite strong earthquake activity. For the first time, an event from the African continent is included. We stress that the addition of events from different tectonic provinces and climatic conditions will enable a better characterization of distributed faulting, resulting in an overall more reliable scaling relation. In this sense, we follow the recommendation of Baize et al. (2019) and uploaded a shapefile with the rupture sections for the 13 events not already available in the SURE database to an online repository (see the “Data Availability” section of this paper for further details).

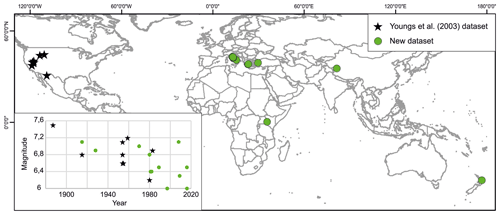
Figure 1 Location of the analyzed events. The inset shows the distribution of the events according to magnitude and time of occurrence.

The earthquakes' magnitude and year are plotted in the inset of Fig. 1: the mean magnitude of the events analyzed by Youngs et al. (2003) was 6.86, whereas the mean magnitude of the additional events is 6.58. The additional case histories are generally more recent in time with respect to those considered by Youngs, with the exception of the 1915 Fucino (Italy) and 1928 Subukia Valley earthquake (Kenya) events. Particular effort was devoted to the collection of data on M<6.5 earthquakes; they were not adequately represented in the Youngs' database but pose a significant threat to society, as they are much more frequent than stronger earthquakes (Baize et al., 2019).

2.2 Methods

Our methodological workflow is illustrated in Fig. 2a. The input data are shapefiles mapping the traces of surface ruptures; these were available in a ready-to-use form (8 events included in Baize et al., 2019), or were created from georeferencing and digitization of maps published in the scientific literature (13 events). We handled the maps with the best possible accuracy; as a general rule, the digitization of surface ruptures was performed at a scale ranging from 1:50 000 to 1:10 000, depending on the accuracy of the original maps.

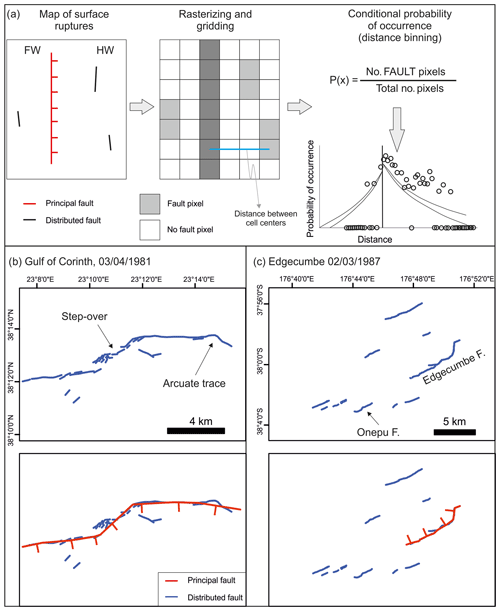
Figure 2 (a) Methodology for computing the conditional probability of faulting using the gridding approach. FW denotes footwall, and HW denotes hanging wall. (b) Example of a complex trace at the surface following the 1981 Gulf of Corinth (Greece) earthquake; ruptures are digitized from a map published by Jackson et al. (1982). (c) Example of a complex trace at the surface following the 1987 Edgecumbe (New Zealand) earthquakes; ruptures are from the SURE database (Baize et al., 2019).

We then divided the ruptures into principal and distributed faults. “Principal” faulting shows longer continuity and higher displacement with respect to distributed faults and corresponds to the surface expression of the rupture along the seismogenic source at depth. Consequently, we classified all of the ground breaks along structures irrespective of their connection to the main fault, which occurred in response to principal faulting, as “distributed faults” (DFs; e.g., Youngs et al., 2003; ANSI/ANS-2.30, 2015). We only discarded ruptures explicitly referred to gravitational phenomena, according to the reports. Different approaches have been adopted in the literature for defining the ruptures to be processed in further analyses – for example, Petersen et al. (2011) discarded the “triggered” ruptures (i.e., not structurally connected to the principal fault), whereas Nurminen et al. (2020) ranked ruptures due to reverse earthquakes into different categories (ranked from 1 to 3). We did not attempt to further categorize the distributed ruptures in our database due to the lack of reliable information for some of the case histories; moreover, from an engineering perspective the occurrence of DFs is much more relevant than the nature of the triggering process (e.g., Youngs et al., 2003).

The conditional probability of distributed faulting was computed following the earthquake approach, as defined by Youngs et al. (2003). This was the first work to introduce PFDHA and can be categorized as a gridding approach (Nurminen et al., 2020). We derived a raster of the Euclidean distance from the principal fault with a 500 m grid resolution and counted the number of pixels for each distance class, up to 20 km in the hanging wall and 15 km in the footwall; these limits allow one to encompass all of the observed DFs, which reached the 15–15.5 km bin in the hanging wall and the 12–12.5 km bin in the footwall. The conditional probability of faulting (P) is defined as the number of pixels containing distributed faulting divided by the total number of pixels in each distance class (Fig. 2a) and was calculated separately for the hanging wall and footwall blocks.

Firstly, for each event, we computed the probability of DFs as a function of distance from the principal rupture – P(x). We also investigated the possible influence of magnitude range and year of occurrence (i.e., historical or modern events), assessing whether to include these parameters in the analyses or not (see Sect. 2.3). We then calculated the mean value for each distance class and fitted empirical regression to the dataset. We tested different functional forms, following those proposed in the literature (i.e., power form – Petersen et al., 2011; exponential form – Youngs et al., 2003). In the following, we provide the fitting coefficients for Eq. (2), a functional form equivalent to that used by Youngs et al. (2003), which showed better performance in terms of fitting.

$$\begin{array}{}\text{(2)}& P\left(x\right)={\displaystyle \frac{e^{(a+b\cdot (\ln (x+c))}}{\mathrm{1}+e^{(a+b\cdot (\ln (x+c))}}},\end{array}$$

where x is distance from the principal fault in kilometers, and a, b, and c are fitting coefficients.

2.3 Assumptions and limitations

Overall, PFDHA analysis requires a significant number of subjective choices, and a common methodology or thorough comparison of different methods is still lacking. The gridding method adopted in the current research is not devoid of limitations, which we address in the following. Nevertheless, our primary goal was to assess the performance of the only scaling relation available for normal faults and to update such regression with new case histories. For this reason, we basically replicated the work of Youngs et al. (2003).

An initial issue with respect to the scale is the resolution and completeness of the original maps and data. Detailed rupture maps are available for all of the selected events; nevertheless, large variability in the quality of data is present, as we investigated events that occurred between 1887 and 2016. An increasing quality of the reported data for more recent events could be expected: modern technology and integrated approaches encompassing extensive fieldwork and remote sensing (e.g., interferometric synthetic-aperture radar, optical correlation techniques) can capture ground deformation of few centimeters, which could have easily gone undetected in the past (see Livio et al., 2017, for a more detailed discussion). A working hypothesis is that older events are characterized by a higher epistemic uncertainty due to less reliable technologies or natural censoring of smaller displacements if measurements are taken long after the earthquake occurrence (e.g., Stirling et al., 2002). The variability of modern events should indeed be aleatory. We explored this issue by dividing the dataset in two subsets, namely events that occurred in the 21st century (4 events) and those that occurred before this period (17 events).

A second issue is related to the definition of the principal fault, which subsequently affects the computation of distances. The delineation of the principal fault can be straightforward in some rupture sections but can be more complex in other sections (Petersen et al., 2011), where the surface rupture is discontinuous or structural complexities (multiple parallel strands, gaps between ruptures) are present. Figure 2 shows examples from the Gulf of Corinth (Greece) and Edgecumbe (New Zealand) events. In the first case, the principal fault shows a relatively simple trace at the two ends, while a complex pattern of ruptures is present in the central part. The Edgecumbe event ruptured the Edgecumbe Fault and 10 secondary segments. In the assessment of the principal fault, we referred to the fault plane modeled by Beanland et al. (1990), which defines the Edgecumbe Fault as the main fault rupture; the Onepu Fault (see Fig. 2c) lies along-strike of the Edgecumbe Fault, but it shows a much smaller displacement (maximum values of 2.5 m and 26 cm, respectively) and is therefore considered as a secondary rupture.

The issues defined above are not trivial, because the gridding method implicitly assumes that the mapping data for the ruptures are complete, and results depend on the grid size. The grid size of 500 m is quite coarse in order to compensate for the possible underestimation due to incomplete mapping (Youngs et al., 2003). Other approaches have been explored in the literature, such as considering different grid sizes (e.g., Petersen et al., 2011). More recently, a “slicing” approach has been introduced in the analysis of reverse earthquakes (Boncio et al., 2018; Nurminen et al., 2020); this method makes no assumptions regarding the completeness of the database and does not depend on the grid size.

Finally, in case of multiple earthquakes in few days/months (e.g., 1981 Gulf of Corinth – Jackson et al., 1982; 2016 central Italy – Brozzetti et al., 2019), it may not be possible to attribute each surface rupture to its causative event. Repeated rupture of the same fault strand is certainly a theme to be investigated, but we believe that this kind of uncertainty does not heavily affect our results.

3 Results

We initially computed the conditional probability of distributed faulting for each single event; we then explored the role of magnitude and year of occurrence as factors affecting this value.

3.1 The role of magnitude

To establish the role of magnitude, we grouped the case histories into magnitude classes (i.e., M<6.5; $\mathrm{6.5}\le M<\mathrm{7.0}$; M≥7.0). Figure 3 shows the conditional probability of faulting as a function of the distance from the principal fault. Positive values correspond to the hanging wall, whereas negative values refer to the footwall. Each symbol represents P(x) at a specific distance for a single earthquake. Points on the x axis indicate that no distributed faulting occurred in the given distance class; black asterisks show the mean values. The probability of rupture drops off quickly with distance away from the main fault, with a steeper decrease in the footwall than in the hanging wall. The ratio between the probability of faulting in the 0–500 and 1000–1500 m classes is 7:1 for the hanging wall and 14:1 for the footwall, pointing to a fundamental difference between the near and far fields. Some peaks in the far field are visible as well (e.g., in Fig. 3a at distance of 7–8 km in the hanging wall).

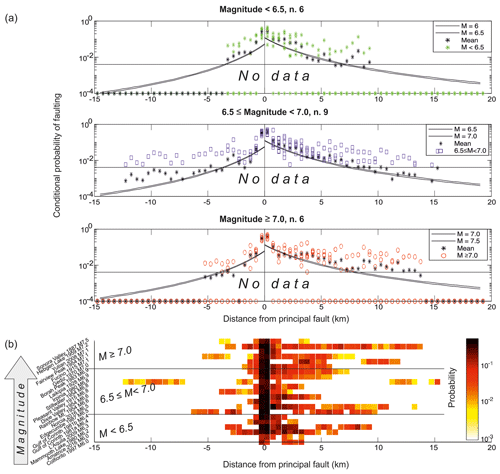
Figure 3 (a) Conditional probability of faulting as a function of distance from the principal fault. Earthquakes are grouped according to their magnitude (M<6.5; $\mathrm{6.5}\le M<\mathrm{7.0}$; M≥7.0); colored symbols represent the values for each earthquake and distance class, and black asterisks represent the mean values. Black lines are the scaling relations from Youngs et al. (2003; their Eq. 7). The “No data” field illustrates the region where no empirical observations are present, and probabilities are extrapolated by fitting. (b) Comparison between the 21 earthquakes, ranked according to magnitude; each line represents a single event.

Figure 3b shows the stacked values of conditional probability, with earthquakes ordered according to magnitude; again, it the decrease in P(x) with distance is clear, but no clear trend is apparent for increasing magnitude values. Thus, we do not explicitly include a magnitude term in the scaling relations in the following analyses; moreover, it is important to highlight the relatively small sample set as well as the fact that the magnitude determination for the older events (which go back to the end of the 19th century) may bear a significant degree of uncertainty.

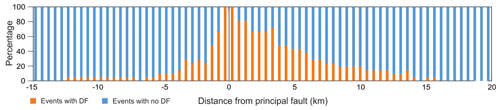
Figure 4 Percentage of earthquakes showing distributed faulting vs. no faulting for each distance class.

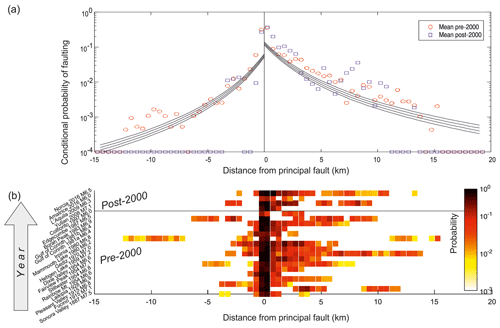
Figure 5 (a) Conditional probability of faulting for the 17 events that occurred before the year 2000 and the 4 events that occurred after 2000; colored symbols represent the mean values. Black lines are the scaling relations from Youngs et al. (2003; their Eq. 7). The “No data” field illustrates the region where no empirical observations are present, and probabilities are extrapolated by fitting. (b) Comparison between the 21 earthquakes, ranked according to the year of occurrence; each line represents a single event.

The mean values shown in Fig. 3 correspond quite well to the scaling relations by Youngs et al. (2003), but we underline that mean values are derived from balancing a dichotomous variable, as distributed rupture can either occur or not occur. On the one hand, earthquakes actually producing distributed faulting show probabilities much higher than the mean value; on the other hand, several earthquakes do not produce faulting at all at a certain distance from the principal fault. Figure 4 better clarifies this point: we calculated the percentage of earthquakes generating distributed faulting for each distance class (“events with no DF” corresponds to the points on the x axis in Fig. 3). Most earthquakes produce distributed faulting in the first few kilometers from the principal fault, whereas only 30 % generate surface faulting at 7 km in the hanging wall; this value decreases to 3 km in the footwall. Another aspect worth mentioning is that real data are constrained down to probabilities as low as ca. 10⁻² (see the “No data” field in Fig. 3a); this lower threshold is constrained by the number of pixels for each distance bin, which in turn depends on the grid size of the analysis and the length of the principal fault. Probabilities lower than this threshold derive from the averaging of the earthquakes producing DFs with those not producing DFs.

3.2 The role of the dataset age

To establish the role of the dataset age, we then grouped the case histories according to the year of occurrence, i.e., 17 earthquakes that occurred before the year 2000 (mean magnitude: 6.75) and 4 more recent earthquakes (mean magnitude: 6.47). We tested the hypothesis that older earthquakes may show a lower probability of distributed faulting due to the incompleteness of the dataset or less reliable measures. However, we found no systematic bias between the two subsets and no clear pattern arises when stacking the events according to the year of occurrence (Fig. 5).

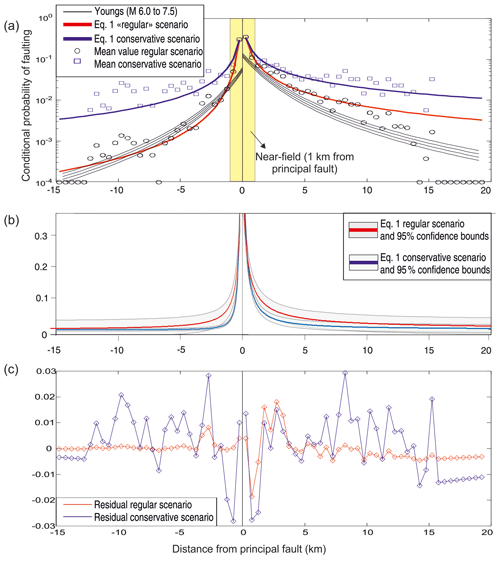
Figure 6 (a) Conditional probability of faulting as a function of distance from the principal fault. Black lines are the scaling relations by Youngs et al. (2003; their Eq. 7). Colored lines are the equations proposed in the present research (“regular” and “conservative” scenarios). Panel (b) shows the proposed equations and 95 % confidence bounds (y axis: linear scale). Panel (c) shows the residual plot (observed – predicted).

3.3 Deriving scaling relations: regular and conservative scenarios

In the following, we derive the equations of the conditional probability of distributed faulting as a function of distance from the principal fault. We calculate the mean probability values for each class distance and fit the data with Eq. (2). When trying to fit all of the data, we found a trade-off between the near and far field: including the points in the vicinity of the principal fault in the regression gives birth to higher residuals in the far field. This drawback has already been pointed out by Petersen et al. (2011), who excluded the first two off-fault rupture probability measurements. We tested several functional forms, and we selected Eq. (2) because it showed the best performance in the different scenarios. The obtained regression coefficients and goodness-of-fit parameters are provided in Table 2, and the curves are plotted in Fig. 6. The overall pattern matches the results of Youngs et al. (2003), but we note that observed data are consistently higher than predicted by their equations, in particular in the hanging wall.

Table 2 Data-fitting and goodness-of-fit parameters for the traditional and conservative scenarios (see Eq. 2); regressed parameters, with 95 % confidence bounds, are indicated. HW denotes hanging wall, FW denotes footwall, SSE denotes the sum of squares due to error, and RMSE denotes the root-mean-square error.

As pointed out earlier, computing the mean value of all of the earthquakes for each distance bin results in the average of two end-members: events without distributed faulting at a given distance and events that generated distributed faulting at that distance. The conditional probability of faulting is zero for the former category, whereas it is variable, within a certain range, for the latter; thus, when events that generate distributed faulting at that distance occur, the probability of distributed faulting is much higher than the mean value. For this reason, we introduced a conservative scenario, computing the conditional probability only for those data that recorded distributed faulting at a given distance. The points are shown in Fig. 6 along with the curves obtained in the same way as for the regular scenario. The relevance of this conservative scenario lies in the fact that for some projects it may be necessary to consider the worst-case scenario or a return period longer than the norm (Wells and Kulkarni, 2014; Cline et al., 2018).

Between 1 and 5 km from the principal fault, the conservative scenario predicts a probability of faulting that is ca. 3 times the regular scenario, whereas the conservative scenario is 1 order of magnitude higher than the regular one at about 10 km from the principal fault. The residual plots (observed minus predicted values; Fig. 6c) show that observed values better match with the predicted values for the regular scenario, with a higher discrepancy at 1–3 km in the hanging wall; beyond ca. 10 km in the hanging wall, residuals are always negative (i.e., the equation overpredicts the values). The conservative scenario shows a higher dispersion of the values, resulting in overall higher residuals and lower goodness-of-fit parameters (Table 2). In the database used to derive the equations, distributed faulting was observed up to 15 and 12 km from the principal fault in the hanging wall and footwall, respectively. Due to the limited numbers of observation points beyond ca. 10 km, extrapolation beyond such limits should be considered carefully.

4 Discussion

We compute the conditional probability of distributed faulting for a dataset of 21 normal-faulting earthquakes and provide updated empirical relations assessing the decrease in faulting with distance. Our data show a very steep decrease in the probability of faulting at distances higher than 1 km from the principal fault, pointing to a fundamental difference between near and far fields. The pattern of fault rupture in the near field has been recently explored by several authors using observation of actual faulting or numerical or analytical models (e.g., Fletcher and Spelz, 2009; Teran et al., 2015; Gold et al., 2015; Loukidis et al., 2009; Treiman, 2010). Several factors have been pointed out as conditioning the surface expression of faulting, including type of fault movement, fault dip, amount of displacement, geometrical complexity of fault traces, rock type, thickness, and nature of the materials above bedrock (Bray et al., 1994; Avar and Hudyma, 2019). The integration of modern field and remote technologies has allowed for the capture of the finer details of surface rupture; a geologically sound interpretation of such data is pivotal to the understanding of surface rupture, which, in turn, is essential for engineering design and eventually mitigation measures. The regressions presented in the current work derive from a global dataset; we stress that site-specific data should be properly considered if they are available. For instance, different behavior has been identified between Japan and US ruptures (Inoue et al., 2018; Petersen and Chen, 2018; Suzuki and Annaka, 2018); if such variations are systematic, they can, to some extent, be predictable and thus help in assessing the hazard.

From a methodological point of view, the biggest caveat in our analysis is arguably the 500 m grid size, which is quite coarse and possibly smooths differences between events. We adopted this size because we wanted to verify the performance of the regressions by Youngs et al. (2003). The assumption that any distributed faulting in the 500 m × 500 m cell is the same as the occurrence of rupture at the point of interest leads to an overestimation of the rate of occurrence; the large pixel size was chosen by Youngs et al. (2003) as a compromise between this effect and the possible incomplete mapping.

Beside the grid size, the definition of principal faulting itself can be tricky. Several earthquakes may occur in a short time interval, making it difficult to identify the causative event for each ground rupture. Discontinuous, subparallel strands with similar displacement or a complex pattern of faulting are a challenge with respect to defining principal vs. distributed faulting. The updated empirical regressions broadly confirm the results obtained by Youngs et al. (2003), highlighting the soundness of their approach and its wide applicability in different regions worldwide. The addition of new case histories only allows for an incremental improvement in the equations. The conditional probability of faulting does not show dependency on magnitude or time of occurrence, thereby allowing for the combination of all of the events in a single dataset to obtain empirical regressions. The lack of dependency on magnitude can be explained by the fact that we analyze a global dataset, whereas Youngs et al. (2003) focused their work on earthquakes that occurred in the western US. Moreover, it has been shown that the choice of the grid size has a much larger effect than the moment magnitude of the events (Suzuki and Annaka, 2018; Takao et al., 2018).

Concerning the year of occurrence, in a previous analysis of Italian Apennines events, we claim that older events and maps may be affected by higher epistemic uncertainties (Ferrario and Livio, 2018). In the current study, we again tested this hypothesis and found no systematic difference between earthquakes that occurred several decades apart; thus, we argue that the issue of data completeness is not simply a matter of the time of occurrence but is also influenced by other factors like the territorial and climatic setting (e.g., arid vs. humid climate) and the potential for the preservation of surface ruptures. Another possible explanation for the lack of dependency on the year of occurrence is the limited number of modern case histories (only four events post-2000). The acquisition of future datasets is critical for the assessment of eventual systematic biases and will allow different grid sizes to be tested.

The most striking observation when analyzing the updated regressions is the systematic higher probabilities of faulting, in particular in the hanging wall, with respect to the original formulation by Youngs et al. (2003). The output of the analysis is strongly influenced by the bins where no distributed faulting was observed (i.e., points on the x axis in Figs. 3 and 5). In order to account for the full spectrum of potential occurrences, we introduce a conservative scenario, where conditional probabilities of faulting are computed without the bins with no distributed faulting. This scenario results in higher expected probabilities, and the residual plot (Fig. 6c) shows that observed values are lower than expected between 3 and 7 km in the hanging wall, whereas they are higher than expected at distances of 7–12 km. A possible explanation for this behavior may be the structural architecture of normal faults, which commonly show a horst and graben setting: the 3–7 km sector may correspond to the block that undergoes lowering and/or tilting, and the 7–12 km sector may correspond to the location of the antithetic structure. This hypothesis can be tested on well-documented case histories, where detailed information is available on the structural architecture of the shallow subsoil. As a first approximation, this pattern is quite evident for the 1980 Irpinia and 2016 Norcia earthquakes, whereas it is more subdued for the 1954 Fairview Peak, 1959 Hebgen Lake, 1970 Gediz, and 1987 Edgecumbe events. The position at the surface of the antithetic structure is driven by factors such as the change in dip of the principal fault at depth (e.g., Caskey et al., 1996); this points to the possibility of introducing deterministic constraints in the estimation of the expected distributed faulting. Thus, we point out that the use of elastic dislocation models of deformation (e.g., Okada, 1985) and, in turn, of induced Coulomb stress transfer on receiving preexisting faults (e.g., Toda et al., 2011) may be useful for more accurately predicting the probability of DF (e.g., Gürpinar et al., 2017; Livio et al., 2017), especially where the current models show higher residuals (e.g., at ca. 7–12 km in the hanging wall).

We claim that the regular and conservative scenarios can be seen as alternative branches in a logic tree; the relative weights of the two branches can be tuned according to the degree of conservatively of the project and to professional judgment. We argue that the conservative scenario can be particularly important in the analysis of normal faults, for two main reasons: (i) normal faults have a higher probability of generating surface faulting along the principal fault when compared to strike-slip and reverse faults (Moss and Ross, 2011; Suzuki and Annaka, 2018; Takao et al., 2018); (ii) the conditional probability of distributed faulting for normal events is much higher than for strike-slip and reverse earthquakes. The latter point is better illustrated in Fig. 7, where we compare our regressions for normal faulting with the original formulation of Youngs et al. (2003) and the one proposed by Takao et al. (2018) for strike-slip and reverse Japanese events, developed using the same grid size of 500 m.

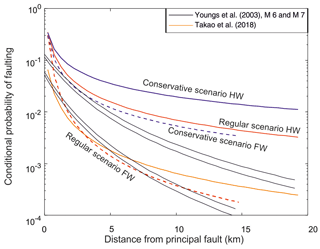
Figure 7 Comparison between the conditional probability of faulting for normal events obtained in this study and those from Youngs et al. (2003; the curves for M6 and 7 are shown as a reference) and for strike-slip and reverse events in Japan (Takao et al., 2018); full lines represent the hanging wall, and dashed lines represent the footwall.

5 Conclusions

We develop an updated regression for the conditional probability of distributed faulting as a function of distance. We propose two alternative scenarios to take the wide range of ruptures into account: the regular scenario computes the average value of all of the analyzed events, whereas the second scenario provides a more conservative estimate. We believe that a periodic update of the database allows for more robust relations to be derived: for this reason, measures of distributed faulting and data implementation in a common framework (e.g., Baize et al., 2019) should be a standard practice following every ground-rupturing event. In order to support common data mining, the shapefiles of ruptures for the new case histories and the table containing conditional probabilities of faulting derived in the present research are made available in an open repository (see the “Data Availability” section of this paper for further details).

Here, we focus on the conditional probability of faulting and do not consider the amount of faulting (i.e., we treat faulting as a binomial yes/no variable). Future research should also consider the amount of displacement in order to fully implement our results in a PFDHA perspective. PFDHA is a young science relying on empirical data; thus, it still holds a significant degree of epistemic uncertainty that can be reduced by enlarging the dataset of case histories.

The assessment of uncertainties in PFDHA analyses is not yet fully developed and methodological choices have a substantial effect on the total hazard (Moss and Ross, 2011; Treiman, 2010; Wells and Kulkarni, 2014; Cline et al., 2018); logic trees can be used to consider the full distribution of rupture characteristics. Finally, a critical comparison of different methods and procedures should be pursued and the comparability with the original works (e.g., Youngs et al., 2003) should be guaranteed.