the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Cross-diffusion waves resulting from multiscale, multiphysics instabilities: application to earthquakes
Manman Hu
Christoph Schrank
Xiao Chen
Santiago Peña Clavijo
Ulrich Kelka
Ali Karrech
Oliver Gaede
Tomasz Blach
Hamid Roshan
Antoine B. Jacquey
Piotr Szymczak
Qingpei Sun
Theoretical approaches to earthquake instabilities propose shear-dominated source mechanisms. Here we take a fresh look at the role of possible volumetric instabilities preceding a shear instability. We investigate the phenomena that may prepare earthquake instabilities using the coupling of thermo-hydro-mechano-chemical reaction–diffusion equations in a THMC diffusion matrix. We show that the off-diagonal cross-diffusivities can give rise to a new class of waves known as cross-diffusion or quasi-soliton waves. Their unique property is that for critical conditions cross-diffusion waves can funnel wave energy into a stationary wave focus from large to small scale. We show that the rich solution space of the reaction–cross-diffusion approach to earthquake instabilities can recover classical Turing instabilities (periodic in space instabilities), Hopf bifurcations (spring-slider-like earthquake models), and a new class of quasi-soliton waves. Only the quasi-soliton waves can lead to extreme focussing of the wave energy into short-wavelength instabilities of short duration. The equivalent extreme event in ocean waves and optical fibres leads to the appearance of “rogue waves” and high energy pulses of light in photonics. In the context of hydromechanical coupling, a rogue wave would appear as a sudden fluid pressure spike. This spike is likely to cause unstable slip on a pre-existing (near-critically stressed) fault acting as a trigger for the ultimate (shear) seismic moment release.
- Article
(4399 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
Part 1 (Regenauer-Lieb et al., 2021) introduced a (geo-)wave-mechanics- and physics-based formulation for deciphering patterns of multiphase material instabilities from the molecular scale to any larger scale. Although the paper is formulated for Earth sciences the approach constitutes a generic theory for any material. In this paper (Part 2) we investigate whether the approach can be applied to a real-world geological system.
Patterns in geological systems are thought to encode information on reaction–diffusion processes repeating themselves over multiple scales such that a magnified view of the structure looks like a copy of the structure itself called self-affinity or self-similarity if no affine transformation is required (Hobbs et al., 2011; Hobbs and Ord, 2015; Aifantis, 2021). The connection between these patterns as dissipative structures of reaction–diffusion systems (Ball, 2012) and their role in thermodynamic far-from-equilibrium systems was originally described by Prigogine and co-workers (Kondepudi and Prigogine, 1998). An application of self-diffusing reaction–diffusion equations to mineralizing systems has been proposed recently (Oberst et al., 2018). This contribution investigates geological applications of the possible relation to the reaction–cross-diffusion wave phenomenon due to the new addition of the cross-diffusion term proposed in Part 1 (Regenauer-Lieb et al., 2021). In this contribution we will show why the addition of the cross-diffusion term may be an important element for the earthquake source mechanism.
Along the same vein, the paper also attempts to give a somewhat simpler description of the theory from a mesoscale perspective, putting Part 1 into the context of non-local processes summarized in recent developments on size-dependent continuum mechanics approaches (Shaar and Ghavanloo, 2021). We identify that these ideas can be amalgamated with new concepts in physics and mathematics on non-local reaction (Rubinstein and Sternberg, 1992) and diffusion (Amdreo-Valle et al., 2010) processes. Such formulations provide a more rigorous framework for the consideration of processes that happen in between scales. These processes are loosely called the “mesoscale” without precise definition.
In continuum mechanics non-local processes are found to be important for introducing internal length scales for localization phenomena (Aifantis, 2021). We emphasize here that consideration of the non-local cross-diffusion terms is particularly important to link the feedbacks between different self-diffusion length scales which are normally not considered in the coarse-graining homogenization approaches discussed later.
In order to explain the physics of non-local diffusion processes, consider an assembly of solid and fluid particles/molecules in a fully saturated porous medium. The particles are subject to a thermodynamic force exerted by the stress supported by the solid matrix and the pressure of the pore fluid. If we further consider a chemical dissolution–precipitation process as an example the concentration of solid and fluid particles/molecules depend on their position in space and the gradients of their concentrations which with an equation of state approach can be interpreted as fluid pressure. Cross-diffusion describes the non-local effect of the convolution of the concentrations of solid and fluid particles. This convolution occurs because the release of a fluid particle relies on the dissolution of a solid particle and the growth of a solid particle needs the precipitation of a fluid particle. The probability distribution to jump from one location to another is then defined as the non-local diffusion. In the context of Part 1 these mesoscale or non-local jump conditions may under certain scenarios be incompatible with the large-scale thermodynamic forces and violate the equilibrium condition. Such violation then necessarily leads to the nucleation of acceleration waves radiating the local energetic incompatibilities into the far field. In the discussed example of dissolution-precipitation reactions a molecular reaction may therefore radiate solid and fluid pressure pulses into the far field and act as a perturbation to the coupled non-local phenomena at the next scale up, thus triggering the full cascade of THMC non-local reaction–diffusion processes and leading to a multifractal cascade of instabilities (Turiel et al., 2006; Koronovsky et al., 2019).
A prime example of how the physics of the very small appears to influence the physics of the very large is the earthquake instability (Sornette, 1999; Crampin and Gao, 2013). We therefore use earthquakes as a topic to discuss the roots of self-affinity underpinning the log-frequency–log-magnitude relationship (Fig. 1) and many other similar relationships in nature (examples are shown in Fig. 1 of Part 1; Regenauer-Lieb et al., 2021). To simplify the equations and address a frequently overlooked deformation mode we use the Helmholtz decomposition presented in Part 1 (Regenauer-Lieb et al., 2021) and only discuss examples for dissipative pressure (P) waves. The rich dynamics of superposing dissipative pressure (P) – and shear (S) – waves will be subject of future research. For simplifying the discussion we also focus on just considering hydromechanical (HM) coupling and refer to Part 1 for the generalized THMC formulation.
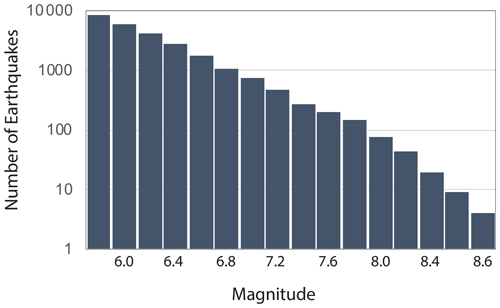
Figure 1Earthquake frequency–magnitude histogram prepared from the Global Instrumental Earthquake Catalogue, Version 7.0 – released on 9 April 2020 by the ISC-GEM (Di Giacomo et al., 2018; Storchak et al., 2015, 2013). Global quakes have a fractal power-law relationship of with an R2=0.98. The log–log relationship between numbers of earthquakes and their moment magnitude on all sizes of completeness of the catalogue suggests a simple underlying reason why the physics of the very small influences the physics of the very large in a multifractal cascade of instabilities. Sethna et al. (2001) postulates that this can be explained by the existence of a critical thermodynamics force above which an earthquake starts to slip. Accordingly, plate motions self-regulate (Sornette and Pisarenko, 2003) to be exactly at this critical point for potential failure at all scales.
This paper develops the working hypothesis that geological patterns encode information of dissipative structures in the form of standing or travelling dissipative waves that can appear with (Berenstein and Beta, 2012) or without cross-diffusion terms (Regenauer-Lieb et al., 2013a; Veveakis and Regenauer-Lieb, 2015). We develop a continuation of a solid mechanical cross-diffusion formulation in which slow damage waves (Hu et al., 2020) have been identified as a precursor phenomenon to macroscopic failure of porous materials under load. Diffusion waves prepare a material for failure as they lead to internal material damage. Developing detection methods of these newly predicted slow damage waves may point to new avenues of forecasting material failure. Additionally, the failure pattern induced by these waves can imprint a characteristic bar-code-like signature around the main failure zone. If it is possible to decipher these patterns as frozen-in stationary states of reaction–diffusion systems, the approach may provide new avenues to investigate one of the most difficult unsolved problems in Earth sciences through direct geological observations.
Other avenues for detecting these waves could be through laboratory experiments. Unfortunately, complex Earth/material dynamic reaction–diffusion processes occur under extreme temperature and pressure conditions and on timescales inaccessible to the direct human observer (Kohlstedt and Holtzman, 2009). Therefore, reliable empirical experimental engineering approaches for estimating the risk of failure of Earth materials under both engineering and plate tectonic loads are missing (Grigoli et al., 2018). A particular challenge is to replicate nature's pattern-forming, self-organized critical conditions (Fig. 1) at micro-scale in the lab, as the Earth's long-range feedbacks are missing.
To solve this problem we use a thermodynamic-based continuum mechanics approach where we consider conservation of mass, conservation of linear momentum, conservation of angular momentum, conservation of energy, and the second law of thermodynamics as the basic set of coupled partial differential equations (PDEs). These equations form the basis of deterministic continuum mechanics while the strong form of the second law is used as a bridge between statistical mechanics and continuum approaches (Ostoja-Starzewski, 2008). In this respect the thermal (T) PDE has a special role as it is tied to the entropy evolution and thereby encapsulates the uncertainty quantification for time-dependent processes through the fluctuation theorem (Evans and Searle, 2002). For a complete approach, we must look for a mathematical description that comprises all four coupled partial differential equations in a holistic way including the important uncertainty quantification.
The wave-mechanics approach offers just this opportunity as it encompasses all conservation laws. The wave mechanics approach of Part 1 (Regenauer-Lieb et al., 2021) gives, in particular, a fundamental physics-based first guess to investigate these critical domains that are not directly accessible. We thereby identify critical conditions for many important Earth science problems such as the physics of earthquakes, extraction of geothermal energy, safety of nuclear waste disposal, reservoir engineering for oil and gas, the formation of mineral deposits, induced seismicity, natural hazards, groundwater management, and CO2 sequestration and utilization. In sections to come, we will formulate a simple non-local reaction–diffusion formulation for HM coupling, illustrate the potential first application of the theory and depict its relation to other similar approaches in different disciplines.
The decoupling of dynamic processes on vastly different length scales and timescales is one of the most powerful methods of upscaling techniques. The objective, thereby, is to reduce the level of complexity by coarse-graining (Sethna, 2006b; Hanasoge et al., 2017) a complex thermodynamic system to a larger system, such that the dynamics of the lower scale can be homogenized into an effective material property for the larger scale (see Fig. 2). The dynamical system maps onto itself in a self-affine fashion so that the dynamic behaviour under external loads is the same irrespective of the scale considered. This so-called coarse-graining approach leads to time-evolution of the thermodynamically averaged larger systems that have significantly simpler time-evolution equations. The dynamic processes at lower scale are assumed to have relaxed to a quasi-steady state (local thermodynamic equilibrium) and contribute to the larger system through what is described in statistical physics by an order parameter characterizing the scale-invariant free energy of the statistical volume considered (Sethna, 2006a). This situation can lead to a cascade-like hierarchy of singularities described by a series of local power laws.
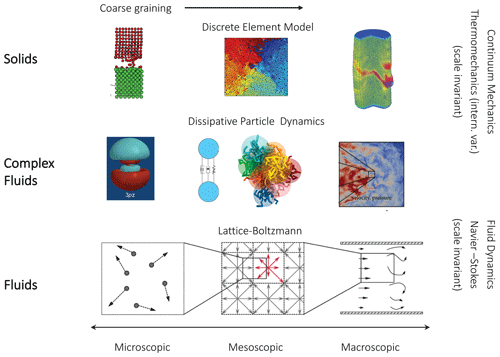
Figure 2Coarse-graining approaches in continuum and fluid dynamics. The microscale has the richest information and highest degrees of freedom. Coarse graining reduces the complex dynamics to time-evolution equations with a less detailed level of description. In the continuum scale only reduced variables are retained. In the case of the Navier–Stokes equation for fluid dynamics, these are pressure and velocity. The wave mechanics approach presented here is a meso-scale approach that opens the path for an analytical reduction of variables rather than a computational coarse-graining method based on averages. Examples for three different methods are shown. The top row illustrates the simulation of a solid body with a particle flow code (PFC, modified after Durrleman et al., 2006) and the continuum damage model (modified after Lyakhovsky et al., 2015). An incorporation of Arrhenius-dependent thermal regularization on the continuum damage model can be found in Hu et al. (2017). The middle row shows a dissipative particle dynamics approach (modified after Español and Warren, 2017) and the bottom row a lattice Boltzmann homogenization technique (modified after Fitzgerald et al., 2019). Our approach replaces the explicit simulations by considering the meso-scale processes through consideration of non-local effects of cross-diffusion. These effects enrich the upscaling of physics-based macro-scale constitutive equations at the continuum scale. The approach is complementary to the numerical coarse-graining techniques shown in this figure.
The system would then be expected to feature a multiscale combination of local power laws of thermo-hydro-mechano-chemical (THMC) reaction–diffusion equations leading to multifractal distributions, where different scales have different fractal properties (Stanley and Meakin, 1988). This multifractality relies on a random multiplicative process of each underlying physical element and a coupling of the critical point phenomena into the universality relationships of the THMC-coupled processes. The combination of a thermally activated rupture with a long memory stress relaxation was proposed as a possible mechanism to explain the multifractal scaling of the Californian earthquake catalogue (Sornette and Ouillon, 2005). The multifractality hypothesis of the Californian dataset has been reinvestigated in a more recent multiscale analysis of the micro-, meso-, and macro-scale subsequences showing that the macro-scale spectrum indeed has the strongest multifractality of the three scales, thus strongly supporting the hierarchy of scales (Fan and Lin, 2017). This finding calls for a true multiscale formulation for earthquake physics, where the largest-scale geodynamic driver is coupled to the smallest-scale singularity in a multiphysics hierarchical cascade of instabilities. In sections to come we will illustrate how the non-local cross-diffusion terms provide the missing glue between the scales. We will discuss analytical solutions showing that cross-diffusion can focus wave energy from the large scale to small scales in short sharp instabilities first discovered in hydrodynamics (Peregrine, 1983).
When extrapolating the findings from the Californian dataset to the global earthquake dataset we infer that the multifractal, so-called singularity spectrum (Turiel et al., 2006) contains most – but unfortunately not all – information about the physics of earthquakes (Koronovsky et al., 2019). The continuous spectrum of multiscale exponents contained in the global singularity spectrum suggests that there is a mechanism that is capable of coupling the various THMC reaction–diffusion equations. Individual coupling mechanisms have been discussed such as a creep activation mechanism (Sornette and Ouillon, 2005), shear heating (Ogawa, 1987; Regenauer-Lieb and Yuen, 1998; Braeck and Podladchikov, 2007), thermally induced fluid pressurization (Vardoulakis, 2001; Rice, 2006) and a mixed process between frictional slip failure and the shear fracture of intact rock (Ohnaka, 2003). A generic physics-based formulation for investigating multifractality of the earthquake mechanism that does not single out individual processes is still lacking. Part 1 (Regenauer-Lieb et al., 2021) has presented such a generic framework and here we illustrate its application to the hydromechanically coupled reaction–cross-diffusion which may be used as a simple first approach to earthquake instabilities (Crampin and Gao, 2015).
A possible candidate for cross-scale communication could be the propagation of cross-diffusional waves which can tie several or all THMC reaction processes together in a convolution operation as discussed in Part 1 (Regenauer-Lieb et al., 2021). The time-domain convolution operation of THMC waves can be seen in the frequency domain as a filter for the dominant earthquake coupling mechanism, sharpening or smoothing certain waves controlled by cross-diffusion. In this sense, the earthquake physics problem may, therefore, be condensed to the problem of how to couple instabilities across scales such that a dominant wave can lead to a self-affine macro-scale instability mechanism which we propose to be an extreme form of a sharpening filter in the language of signal processing. In the physics field, this phenomenon is known as a rogue wave (Eberhard et al., 2017). To verify the rogue-wave hypothesis as a potential earthquake trigger mechanism, we need to discuss the interplay of the vastly different timescales and length scales of the THMC reaction–diffusion processes.
The characteristic timescales and length scales of the thermodynamic THMC processes can be evaluated by calculating the relaxation time of a random perturbation from the THMC reaction term . Please refer to Table 1 in Part 1 (Regenauer-Lieb et al., 2021) for a definition of the THMC reaction terms. Characteristic timescales and length scales emerge from quasi-steady-state (time-independent) solutions of the diffusive (relaxation) response of the reaction–diffusion system characterized by the equation
where Ci stands for the diffusing species/processes (e.g. temperature, fluid or mechanical pressure, chemical species) and ζ′ for the respective diffusivity with the subscript i denoting the THMC processes. Linearizing the diffusion equation we obtain
The timescale or the relaxation process is now entirely characterized by the self-diffusion coefficients and the reaction rates Ri. Please refer to the Part 1 (Regenauer-Lieb et al., 2021) for a definition of self-diffusion and cross-diffusion coefficients.
For the benefit of the reader wishing to recap the well-known facts about the topic of reaction–self-diffusion waves including their astonishing behaviour of revealing THMC material properties through their propagation velocity, we summarize in the Appendix an example of an autocatalytic reaction and its role in the nucleation of reaction–self-diffusion waves. The reader familiar with the literature on reaction–diffusion waves may wish to continue straight into the following application of the equation to characteristic earthquakes.
The results summarized in the Appendix were based on the generalization of a first-order autocatalytic reaction. Very few practical examples will be first order, and we need to consider the generalized case of a reaction that depends on the concentrations of a second-order reaction of one component or any number of additional reactions and their equivalent THMC processes. When considering more than one reaction the concentration of second- or higher-order reactions depends on the concentration of a second- or higher-order number of species. This will add additional dynamics to the system response. In the case of two reactions the system can display a perfectly regular oscillator. A situation where two reaction–self-diffusion equations are coupled will be discussed next. In the example discussed the two reaction terms are a pressure source term from a chemical dissolution reaction and a temperature source term from shear heating.
2.1 Application of two reaction–self-diffusion equations to characteristic earthquakes
Characteristic earthquakes with some typical regularity in their recurrence have been a matter of special interest in seismology. Prominent examples of earthquakes with characteristic recurrence periods are the Parkfield earthquake sequence (Wiemer and Wyss, 1997) and also the episodic tremor and slip (ETS) events recorded in Japan, Cascadia, and Hikurangi subduction systems (Gomberg, 2010). Such events are typically modelled by spring-slider models based on empirical friction data (Ohtani et al., 2019). However, attempts have also been made to explain the friction evolution by the dehydration reaction of serpentinite explaining the phenomenon of ETS events by coupling two reaction–self-diffusion equations resulting in a perfectly periodic thermo-chemical TC oscillator model (Poulet et al., 2014b) shown in Fig. 3.
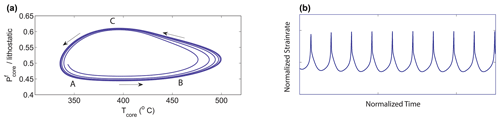
Figure 3The characteristic period of the Cascadia ETS sequence interpreted with a reaction–diffusion oscillator model (Poulet et al., 2014b). (a) The phase diagram between A and B corresponds to the slow creep of the serpentinite slowly raising the temperature to the critical level for the onset of the dehydration reaction. The segment between B and C corresponds to the dehydration reaction that coincides with the tremor and slips event. The following segment between C and A is the diffusion-dominated field. (b) The corresponding normalized strain rate with the sharp peak corresponding to the tremor event.
The approach relies on the tight coupling of the temperature reaction–self-diffusion equation with a chemical reaction–self-diffusion equation (Alevizos et al., 2014; Veveakis et al., 2014) which can lead for a highly non-linear source term to excitation waves with a characteristic perfectly periodic oscillatory response in the temperature-pressure plot (Fig. 3). The authors also show an example where, by considering an additional oscillator, a transition to chaos can be modelled (Poulet et al., 2014b). The basic element of the model is a chemical decomposition function of the type AB⇄A+B. This dissolution–decomposition reaction is different to the autocatalytic reaction discussed in the Appendix. The non-linear element which is necessary to trigger excitation waves is not stemming from the linear chemical dehydration reaction but introduced through shear heating feedback during power-law creep. Shear heating in turn drives the thermally induced dissolution. Poulet et al. (2014b) numerically investigated the potential candidate source mechanism of a thermally induced dissolution reaction of serpentinite in the fault zone originally proposed by Obara (2002). In that model solid serpentinite (phase AB) decomposes into a solid phase A (Antigorite) and a fluid phase B (water) upon application of a heat source from shear heating.
It is encouraging that a simple chemical reaction model of the normally fine-grained serpentine crystal at say millimetre scale can be used to model an ETS instability at plate scale, say around 100–1000 km scale. Communication of information over 8 to 9 orders of magnitude may hence be possible under special circumstances bearing in mind that initial material or environmental heterogeneities at multiple scales will tend to complicate the picture. We therefore propose that progress can be made by investigating the multiscale physics of the THMC reaction–diffusion system in the Earth in further detail. In addition to the timing and displacement information obtained from GPS and seismic stations, the spatial information related to the diffusion term could be investigated to verify the model. A key observable would be the propagating wavefront that would be expected from the above discussion on reaction–diffusion timescales as illustrated in the Appendix (Fig. A1).
In the case of the serpentinite decomposition reaction, the diffusive wavefront would propagate normal to the main fault plane as the chemical decomposition reaction involves significant volume reduction which would lead to a contraction of the central fault plane and a characteristic width of the fault plane. This process zone is not exposed in active subduction systems but can be found in geological exposures of fossil faults. An excellent example is the Glarus thrust which has been modelled by the same perfectly periodic two reaction–self-diffusion equation oscillator approach using a carbonate decomposition reaction (Poulet et al., 2014a). The model includes self-diffusion and therefore the expected spatial response can be tested as well. The model is shown to be capable of reproducing the process zone around the central fault plane which is documented in many fault zones (Chester et al., 2013). Another textbook example is the Punchbowl Fault in California, where a series of deformation mechanisms were described (Schulz and Evans, 2000). We would like to emphasize at this point that chemical dehydration reaction–diffusion processes are only a special case of THMC feedback. A number of other recently proposed feedback processes need to be investigated for completeness, e.g. shear heating and phase changes triggered on asperity contacts (Hayward et al., 2016; Aharonov and Scholz, 2019).
2.2 Consideration of cross-diffusion
Before introducing the concept of cross-diffusion, we might consider what is lacking for investigating the earthquake source mechanism by the reaction–self-diffusion equation without the cross-diffusion term. If indeed the reaction–self-diffusion equation were sufficient to describe the earthquake source mechanism the approach would allow a significant simplification through the coarse-graining approach. The exponential rate of approaching the self-oscillating wavefront of the Fisher–Kolmogorov–Petrovsky–Piskunov (FKPP) wave discussed in the Appendix (Fig. A1) could be used as a simplification and any non-local effects could be ignored. The above example of the reaction–self-diffusion equation for ETS sequences explains the earthquake source mechanism by a similar mechanism to the one proposed for landslides (Vardoulakis, 2001). If indeed the fluid release due to chemical dissolution were a universal mechanism that leads directly to earthquakes, coarse-graining approaches may be able to use the FKPP wave velocity limit to allow a characterization of the important physics of the dehydration mechanism. At coarse-grained level the wave velocity would just be defined through the limit velocity derived in the Appendix (Eq. A3) and may be detected from the seismic records of the episodic tremors. This offers a significant simplification as the approach would not only allow a non-linear effect of a local reactive source term (thermal pressurization) to be turned into a propagating waveform that propagates at constant speed but would also ensure that the wave velocity is governed by the dissipative material properties irrespective of the initial conditions. Excitation waves supported by local reactions will by themselves recover a characteristic wave field dictated by the reaction–diffusion rate constants.
The reaction–self-diffusion model for the ETS sequences effectively singles out a chemical dissolution process which, as emphasized above, is proposed to operate over all scales. The multifractal nature of earthquakes discussed earlier shows that this is not the general case. What is therefore missing is a means to couple the propagating multiscale and multiphysics waves of different THMC processes. The problem can be addressed by a statistical mechanics approach to the coarse-graining problem. In Fig. 2 we proposed that the missing element for considering mesoscopic complexity in a physics-based earthquake model is a meso-scale approach that captures the link between the vast differences in the diffusional length scale (listed in Table A1 in the Appendix) of THMC processes. In Part 1 (Regenauer-Lieb et al., 2021) we proposed that a meso-scale approach can be developed by decomposing the large-scale reaction term Ri into a meso-scale reaction term which requires a meso-scale cross-diffusion term for mass (momentum, energy) balance. This is because the aforementioned cross-scale coupling introduces meso-scale source/sink terms in the individual conservation laws identified by rT, rH, rM and rC, respectively. The conservation laws must, therefore, be extended to close the equations and allow a multitude of THMC processes to occur simultaneously, which introduces cross-diffusion fluxes. We therefore postulate here that these terms are the critical ingredients that provide the capacity to fire off waves that are controlled by cross-diffusion at different THMC length scales and thus explain the observed multifractal nature of earthquakes.
The synchronizing effect of cross-diffusion is well studied for the simple FitzHugh–Nagumo relaxation electrical oscillator, where the self-diffusion terms are replaced by linear cross-diffusion terms (Biktashev and Tsyganov, 2016). The electrical nerve impulses that drive a regular heart beat are an example. Antonioletti et al. (2017) describe how the characteristic recovery of the reaction–cross-diffusion excitation waveform after a random perturbation can be used, for instance, for defibrillation strategies (a small electrical stimulus applied through a pacemaker) for treatment of life-threatening heart arrhythmia. In this sense, earthquake physics might profit from an understanding of the partial differential equations developed in mathematical biology, epidemiology (wave-like propagation of viruses), and other biomedical applications for which numerical open-source tools are available. One such tool is the “heart beat box” (Antonioletti et al., 2017), which uses a mathematical formulation of the human heart in terms of a FitzHugh–Nagumo cross-diffusion formulation.
Similar cross-coupling terms are also used in other fields of physics, where the explicit cross-diffusion formulation response of the system to wave perturbations is tested by a complex-valued wave function. The complex-valued function embeds cross-diffusion as it expresses the bi-directional response of each diffusively coupled system through a mutually cross-coupled diffusion problem. The generalization to a multi-component system with N-coupled components (note no summation convention assumed here) is also known as an order parameter fluctuation analysis. The analysis uses the response functions of Fourier component variational perturbations (Balluffi et al., 2005) in the sense that
where iψ(k,t) denotes the complex position-space wave function, and A(k,t) denotes the amplitudes associated with each Fourier mode. The amplification factor R(k) depends on the Fourier mode k and the direction of the amplification controlled by the diffusivities . Assuming , we recover the cross-diffusion type relationship of Eq. (24) in Part 1 (Regenauer-Lieb et al., 2021), where the probability amplitude of the u wave depends on the cross-diffusional coupling to the v wave. Vice versa, the probability amplitude of the v wave depends on the cross-diffusion of u:
This bi-directional relationship between u and v waves has provided a robust approach to investigate kinetics of order parameters, phase transitions, and fluctuations (Sethna, 2006b). We will use this transformation later to show how our cross-diffusion formulation converts into the non-linear Schrödinger equation for a specific set of parameters. We will also show how an explicit consideration of the cross-diffusion terms can trigger a new class of waves which has not yet been described for the Earth system.
In what follows we first add the important reaction term to this approach to provide a link to the generalized approach in Part 1 (Regenauer-Lieb et al., 2021), then present laboratory examples of diffusion waves, followed by an extension of the HM coupled cross-diffusion model (Hu et al., 2020) into a specific non-local formulation that may be relevant for studying the physics of earthquakes (Crampin and Gao, 2015). We conclude with a presentation on how this set of equations may lead to or trigger a catastrophic instability.
2.3 Cross-diffusion and its role in coupling of instabilities across scales
We can now extend the reaction self-diffusion equation for full space–time coupling for multiple reaction–diffusion equations and re-introduce reactions. An exemplary convolution of the mesoscopic oscillators is the self-similar Gaussian wavelet in space and time, which is also the Green's function of the local equilibrium statistical mechanics approach. In the linear case, any number of wavelets can be superposed, and a Fourier transform is an ideal procedure to capture the effect of multiple oscillators and local heterogeneities on the macro-system. In Part 1 (Regenauer-Lieb et al., 2021) we proposed to generalize the cross-diffusion approach, which is well known in chemistry (Manning, 1970), to more general THMC terms defining cross-diffusion as the phenomenon where a gradient of one generalized thermodynamic force of species Cj drives another generalized thermodynamic flux of species Ci, described by (using explicit summation instead of Einstein convention)
The species j is identified as the cross-diffusion species other than the species i. Introducing a fully populated (N×N) diffusion matrix (Eq. 5) can also be written as
whereby the classical (self-)diffusive length scale of each THMC process is defined by . The cross-diffusion approach introduces also a new meso-scale coupling length scale that can provide a link between the large-scale self-diffusion length scales of the THMC processes. In Part 1 (Regenauer-Lieb et al., 2021) we have shown that the cross-diffusion length scale is defined by the kinetic material properties which can be evaluated by measuring the velocity of cross-diffusion waves in analogy to the generalization of Eq. (A3) for the FKPP wave. This leads to the equation for the wave speed in Eq. (A3) defined by the generalized Damköhler number and the cross-diffusion length scale . Using the alternative mechanical formulation the cross-diffusional wave speed turns out to be (Coleman and Gurtin, 1965)
where ρ is the instantaneous density and C is the eigenvalue of the material stiffness tensor also known as the acoustic tensor discussed in Part 1 (Regenauer-Lieb et al., 2021). The stability criterion of the diffusion problem is fully characterized by the diffusion matrix with the diagonal elements describing the normal self-diffusion and the off-diagonal elements the cross-diffusion processes enabling coupling across scales. For consistency with the second law, all eigenvalues of the diffusion matrix must be real and positive, and hence the determinant of the diffusion matrix as well as the trace of the diffusion matrix must be larger than zero. Complex eigenvalues of result in oscillatory relaxation of any small perturbation to the equilibrium state, even in the absence of reaction (Vanag and Epstein, 2009).
For a given sufficiently non-linear reactive source term that supports nucleation of excitation waves any local thermodynamic incompatibility that leads to complex eigenvalues of radiates energy in oscillatory instabilities by so-called acceleration waves (Regenauer-Lieb et al., 2021), relaxing to the equilibrium state (Vanag and Epstein, 2009) to recover the second law of thermodynamics at large scale. This statement is at the heart of the nucleation of the cross-diffusional wave phenomenon. We will show in the following sections that the above-described cross-diffusion formulation (Vanag and Epstein, 2009) can be extended to develop a generic multiphysics and multiscale THMC coupling approach to earthquake instabilities. This formulation implies a coupled cascade of THMC feedbacks over multiple diffusional length scales honouring the reciprocal multiscale interplay of thermodynamic forces and fluxes.
By extending the diagonal diffusion matrix through the cross-diffusion coefficients in Eq. (6), a cross-diffusion wave phenomenon is revealed as shown in Part 1 (Regenauer-Lieb et al., 2021). For the simple case of hydro-mechanical (HM) coupling, we have recently reported that the upscaled volumetric chemical strains can result in a hydromechanically coupled cross-diffusional pressure wave phenomenon (Hu et al., 2020). The important element of cross-diffusion terms for earthquake physics is their capability to link one thermodynamic force with a thermodynamic flux at a different scale, thus synchronizing the dynamics over vastly different diffusional timescales and length scales. This important aspect of earthquake physics was previously overlooked. The approach not only explains the multifractal nature of earthquakes but raises the possibility that dissipative waves can be detected before earthquake instabilities. Before discussing the potential earthquake application, we summarize observations from laboratory experiments and propose a coupled HM reaction–cross-diffusion equation which may be used as a simplification for the fully coupled THMC problem.
In Part 1 (Regenauer-Lieb et al., 2021) we have discussed reaction–diffusion waves from an idealized continuum mechanics viewpoint, and in this paper we have employed a non-local coarse-graining approach. However, both viewpoints are based on mathematically ideal worlds. For real laboratory and field applications, the processes are often occluded to direct observations and need to be derived by data assimilation methods.
This paper proposes that earthquakes are a THMC convolution of all of instabilities that cause volumetric and shear strains due to their different micromechanics. In the following, we will address the three problems sequentially using field and laboratory examples before exploring a simple analytical solution applied to earthquake physics.
3.1 Diffusion waves at mechanical scale
Oscillatory propagating deformation bands are well documented in deformation experiments of plastic materials such as steel. Perhaps the most well-studied effect is the development of characteristic Portevin–Le Chatelier (PLC) bands which show rhythmic bands of volumetric strain in metals deformed under tensile conditions. The banding is attributed to a damped runaway effect induced by a critical (negative) strain-rate sensitivity (Zaiser and Hähner, 1997). In PLC the transition from smooth to oscillatory deformation is understood as a critical point phenomenon, where mesoscopic fluctuations manifest themselves at the macro-scale due to strain-rate softening. This approach is similar to the spring-slider model discussed earlier for modelling earthquakes. A recent discussion of the PLC bands modelled by an alternative non-local internal length gradient approach is presented in Aifantis (2021).
A comprehensive review of theoretical approaches to model the phenomenon of an oscillatory material response of plastic materials with a serrated stress–strain response (or jerky flow) can also be found in Zaiser and Hähner (1997). According to the review, models first have been developed based on a phenomenological approach proposing that the effective stress applied at the boundary of the deformed sample is a non-linear function of the strain rate which can become negative. In the following, we will briefly discuss the metal deformation examples and the physical processes that are thought to underpin this peculiar constitutive behaviour. The physics appears to rely on reaction–diffusion processes that in fact can be described by an excitation wave phenomenon of the FKPP type (Zuev and Barannikova, 2010). We also present observation of diffusion waves in rock analogues which are perhaps more relevant to the earthquake application.
3.1.1 Oscillatory deformation bands in plastic deformation of materials with internal structure
The phenomenological approach where the strength weakens with an increasing strain rate is ill-posed as it leads to a runaway effect when a small local perturbation in the strain rate grows without bounds in an ever-increasing manner. Various approaches have been proposed to address this problem. In the context of relating the phenomenological approach to a physics-based model, the most interesting approach is the one by Estrin and Kubin (1995). The authors proposed to regularize the ill-posed localized runaway strain by introducing a pseudo-diffusivity; the function that was proposed as an extension of Orowan's equation as
where b is the Burgers vector, |b| is the norm of the Burgers vector ρm is the dislocation density, vd is the dislocation velocity, and D is a diffusivity of the strain ε. This heuristic approach was later shown to be the 1-D solution obtained from the coarse-graining of the time-evolution gradient flow dynamics of dislocations which results in a fractional reaction–diffusion equation (Monneau and Patrizi, 2012). The well-studied jerky flow phenomenon associated with PLC band formation is now understood as the result of initially independent, statistically distributed non-local-scale dislocation mills ultimately coalescing and propagating into a macroscopic band. The best analysed mechanism for these mesoscopic fluctuations is dynamic strain ageing which gives rise to an additional characteristic retardation timescale to dislocation glide. Dynamic strain ageing operates by diffusing atoms (solute clouds) that pin dislocations and temporarily arrest the glide dislocation segments. Therefore, the plastic strain rate cannot respond instantaneously to changes of the stress, and a meso-scale diffusion length/timescale emerges which stabilizes the slip. The key to the oscillatory behaviour is the opposite strain-rate softening effect, where the effect of retardation by diffusion is overcome through the increased mobilization of additional dislocations (increasing the reaction rate) aided by thermal activation, hence increasing the disorder and thereby the average flow stress (Zaiser and Hähner, 1997). A similar effect of competing reaction–diffusion processes has been found in many other materials such as metal alloys (Brechet and Estrin, 1996) and self-oscillating polymer materials (Masuda et al., 2016).
In an elegant discourse about possible earthquake nucleation mechanisms, Orowan (1960) postulated that earthquakes may indeed be triggered by the equivalent effect of an oscillatory response of creeping rocks at depth in the crust or mantle. Orowan (1960) drew the analogy of creep failure of an annealed steel, where the stress oscillates between upper and lower yield stress forming oscillatory bands called “Lüders” bands. Plastic materials, in general, are capable of arresting such small-scale fluctuations when slip tends to localize the meso-scale flow localization and strain hardening ensures that the instability mechanism cannot go catastrophic. Orowan (1960) appealed therefore to the synchronizing effect of thermal feedback at depths in the Earth's mantle, where self-acceleration of creep is conceivable through an avalanche-like increase in deformation where shear heating occurs faster than conduction of heat away from the shear plane, finally resulting in a localized melting event as an earthquake instability.
While runaway melting instabilities have indeed been postulated as a possible source mechanism for extremely deep earthquakes such as the great 1994 Bolivian earthquake (Kanamori et al., 1998), the mechanism may be considered another extreme end-member of earthquake mechanisms in addition to the one proposed for ETS sequences (Poulet et al., 2014b). Kanamori and Brodsky (2001) proposed that there are a great number of other possible earthquakes micro-instabilities without invoking a melting instability; however, the critical aspect remains to identify the physics of connecting small and large scales. If we consider THMC feedback as a source mechanism for earthquakes, we conclude that the largest-scale coupling effect is again the temperature. This becomes obvious from inspecting Table 1 in the Appendix, where the thermal diffusion process defines the largest diffusional length scale. Thermal coupling is so efficient that a material can be considered macroscopically homogeneous and at thermostatic equilibrium, while at the mesoscopic scale it still shows widespread thermal fluctuations. If we refer again to the PLC effect as an analogy of a thermally activated material it has been recognized that these statistically uncorrelated fluctuations may, for certain critical conditions, be coordinated in the shape of a thermal wavefront that propagates through the material (Zaiser and Hähner, 1997). These wavefronts are typical acceleration waves illustrated in Fig. 4 of Part 1 (Regenauer-Lieb et al., 2021). While metals and rocks at depth are thermally activated materials, we need to discuss acceleration waves in brittle materials, where the thermal activation process is less obvious.
3.1.2 Compression of rocks and rock analogues in the laboratory
Crushable granular materials show a similar strain-rate weakening behaviour to metals. This effect may lead to the phenomenon of propagating compaction waves in crushed snow (Barraclough et al., 2017) and puffed rice (Guillard et al., 2015), where the propagation of compaction waves is well documented. The generic experimental configuration is shown in Fig. 4. Travelling compaction waves that reflect from boundaries or release their energy by acoustic emission at the top boundary have been recorded by optical and acoustic means (Guillard et al., 2015; Barraclough et al., 2017). The puffed rice experiment is an excellent illustration of diffusion waves that can be easily replicated for demonstration purposes (Fig. 5). Experiments have also been performed by partially soaking the puffed rice at the bottom of the experimental set-up (Einav and Guillard, 2018). The interference of the compaction in unsaturated compaction and capillary-driven crushing of the puffed rice led to oscillatory catastrophic events of global compaction with acoustic emissions perceptive as loud audible beats termed “rice-quakes” by the authors (Einav and Guillard, 2018).
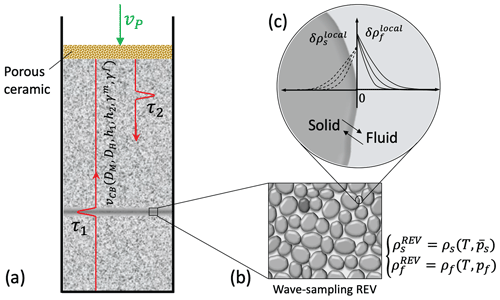
Figure 4Experimental set-up for crushing a granular strain-rate weakening medium. (a) The problem is here formulated in analogy to the Terzaghi consolidation problem, where a pore-filling fluid is diffusing out of the compacting region and crushed grains (solids) are replacing the collapsed pores. (b, c) The non-local mesoscale process sampled by a wave-scale representative elementary volume (REV). The cross-diffusion of the solid into the fluid phase leads to an increase in density, and hence an increase in fluid pressure through the equation of state. The reciprocal cross-diffusion of fluids into the solid skeleton leads likewise to an increase in solid pressure assuming that the deformation of the solid is constrained. The macro-scale continuum-scale REV for a thermostatic formulation is defined in Fig. 2.
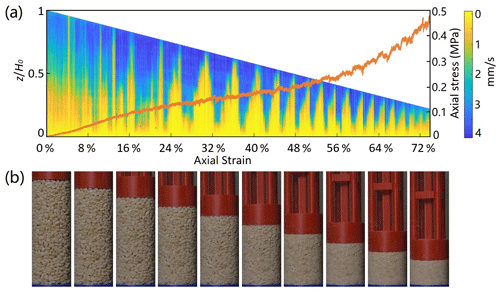
Figure 5Recreation of Guillard et al. (2015) experiment with puffed rice. (a) Time–space plot averaged over a horizontal cross section of the tube showing compaction waves travelling at less than 1 mm s−1 up and down the tube. The overlay shows the axial stress–strain curve, where stress drops correspond to nucleation of new compaction bands at the bottom of the rice pack. (b) Snapshots of the compressed puffed rice at 0 %, 8 %, 16 %, 24 %, 32 %, 40 %, 48 %, 56 %, 64 %, and 72 % axial strain (from left to right). At the termination of the experiment the rice pack is reduced to powder.
An important aspect of the interpretation of the laboratory experiments is that, when going from a perspective of propagating chemical or thermal acceleration wavefronts to a recording of the mechanical response of the medium, a coarse-graining step is made. We are, therefore, in most cases, not able to record the expected individual multiscale THMC wavefronts but are more likely to record the cumulative, convolved effect of the waveforms that underpin and support the mechanical deformation that can ultimately lead to macroscopic failure. From a mechanical perspective, we encounter two different dynamical regimes: in the first regime the dynamics of chemical, hydraulic, elastodynamic mechanical, and thermal wavefronts is still important, and the system cannot be simplified by a thermostatic assumption. The other regime is where the thermostatic assumption holds, and the problem can be described by a quasi-static framework, where the time dependence of the system can be neglected and the problem reduces to an ideal plastic time-independent one, only controlled by the kinematic boundary conditions, e.g. the position of the porous ceramic platen applying the compression in Fig. 4.
The thermomechanical theory of internal variables (Maugin and Muschik, 1999) is a variance of classical plasticity theory as it allows for additional time-dependent processes describing the evolution of local thermostatic equilibrium states through internal state variables. The introduction of additional time-dependent processes leads to a relative difference from the ideal plastic kinematic reference frame, and the localization band can move with respect to the static, ideal plastic solution which is fixed concerning the kinematic boundary conditions in a self-similar way. We can identify the two theoretical end-member cases by recording the dependence of the velocity of the optically recorded compaction waves on the velocity applied to the boundary of the experiments. If there is a positive correlation with the velocity applied to the boundary, the thermostatic end-member applies (Barraclough et al., 2017), whereas if the velocity of the wave proves to be a material constant and independent of the boundary velocity, the dynamic solution applies.
Theoretical approaches to the physics of earthquake instabilities originally were conceived as a shear instability on a frictional sliding surface (Brace and Byerlee, 1966). The role of pressure on the dynamics of the slider was derived empirically by laboratory experiments defining a rate-and-state variable friction law (Dieterich, 1972, 1987; Ruina, 1983; Tse and Rice, 1986; Rice et al., 2001). Instabilities through shear heating feedback were later considered to play an important role (Ogawa, 1987; Regenauer-Lieb and Yuen, 1998; Braeck and Podladchikov, 2007). Additionally, a thermally induced fluid pressurization term was found to be an important component for accelerated creep (Vardoulakis, 2001; Rice, 2006). Another important ingredient of the earthquake instability was thought to be the coupling of scales, where at least two different processes, operating at different timescales and length scales, interact (Ohnaka, 2003). The approach presented here summarizes these effects in the diffusion matrix (Eq. 6) and enables upscaling via renormalization group theory (Regenauer-Lieb et al., 2013b; Hanasoge et al., 2017).
4.1 The effect of cross-diffusion
A fully populated diffusion matrix provides the opportunity to extend the postulate of coupling different scale processes in earthquake mechanics (Ohnaka, 2003). For the mathematical discussion we consider a poromechanical formulation introduced earlier (Hu et al., 2020) which describes cross-diffusion between solid and fluid particles as illustrated in Fig. 4. Of particular interest for the earthquake problem is whether the hydro-mechanically coupled cross-diffusion can lead to the formation of a standing wave of significant amplitude as observed in other fields (Berenstein and Beta, 2012). In order to investigate whether cross-diffusion can lead, for certain parameters, to a sharp concentration of wave energy into a single short-lived spike we follow a recent generalization of the original formulation of Hu et al. (2020), which allowed a linear stability analysis as well as a numerical assessment of the parametric space presented elsewhere (Sun et al., 2021b). The article including the supporting numerical code is available as a preprint on the Earth and Space Science Open Archive (ESSOAr).
Before discussing the significance of the results for the earthquake problems we summarize briefly the rationale for the choice of the particular reaction–cross-diffusion equation. The generic type of reaction–cross-diffusion equation for a fully saturated hydromechanically coupled porous medium has been introduced by Hu et al. (2020):
where DH and DM are the solid and fluid pressure self-diffusion coefficients and dH and dM are the corresponding cross-diffusion coefficients. Following the discussion on non-locality in the diffusion explained in the introduction we also acknowledge a non-local coupling of the reaction as shown in the inset in Fig. 4. The specific source term for fluid pressure is assumed to be a simple linear combination of the decomposing solid and the fluid pressure production rates , with a21 and a22 the respective rate constants. In geomechanical laboratory experiments the solid matrix is known to respond to external forces by a non-linear reaction commonly expressed in a power law which serves as a source term for generating excitation self-diffusion waves in the characteristic earthquake example discussed earlier (Poulet et al., 2014b). Both chemical and mechanical reaction source terms are dissipative kinetic processes, and our approach can lead to the same laboratory-derived results. The difference is that the laboratory laws can strictly only be extrapolated for the laboratory conditions, while the physics-based approach is more generic.
In order to generalize the approach we expand the pressure reaction rate R1 in a power series truncated at third-order . Third- and higher-order reactions were found to be necessary to sustain excitation waves. We introduce following dimensionless parameters:
where denotes the reference strain rate, the reference stress and l0 the reference length. As we use the Perzyna overstress formulation (Perzyna, 1966) the reference strain rate is the background strain rate post yield, the reference stress the yield stress and the reference length determines the size of the material that has yielded. The dimensionless equation then becomes
4.1.1 Three different fundamental wave solutions and the long-wavelength cross-diffusion limit
Depending on the parameters chosen the solution space presented in Sun et al. (2021b) recovers three fundamentally different types of excitation waves which are Turing patterns, Hopf bifurcations, and quasi-soliton waves.
- i.
Turing patterns appear because around the bifurcation point in the reaction–self-diffusion system, linearly unstable eigenfunctions exist that grow exponentially with time. While analytical solutions can be obtained using the Weierstrass functions the numerical solution is traditionally difficult. To regularize the problem, finely tuned non-linear terms need to be introduced in the reaction–diffusion equation (such as in the non-linear Schrödinger equation discussed later) or, more conveniently, as is done in our approach (Sun et al., 2021b), linear cross-diffusion-like terms need to be considered in a coupled system of equations. THMC Turing patterns are indeed the most obvious patterns that have been postulated in the literature on wave-like Earth instabilities (Ball, 2012). The framework developed here offers an ideal tool for inversion of the effective self-diffusion THMC coefficients and their implicit reaction rates. Interpreting geological structures in terms of these process parameters may allow identification of principal processes underpinning the earthquake mechanism. A first attempt has been made to derive the self-diffusion coefficients of the Turing-style structures shown in Fig. 3 of Part 1 (Regenauer-Lieb et al., 2021) from field observation, but the use of the 1-D approach has been unsuccessful so far (Elphick et al., 2021).
In terms of earthquake physics Turing patterns presumably only play a minor role as they are slow deformation features that require long geological times to form a deformation pattern that is stationary in space and time. Due to their longevity and periodicity they cannot focus wave energy into a sharp single transient event. Their role in earthquake instabilities is to create heterogeneities that may be picked up by subsequent failure mechanisms.
- ii.
For the suggested reaction–cross-diffusion in Eq. (11) the broadest parameter space is covered by waves having discrete frequency content with logarithmic decaying amplitudes for higher frequencies (Hopf bifurcations). In our simulations (Sun et al., 2021b) these waves nucleate from small perturbations on the (elastic-plastic) model boundary and propagate dynamically to the opposite boundary at distance l0, where their energy is absorbed. They can obtain a stable orbit (supercritical Hopf) leading to cumulative damage on the opposite boundary including logarithmically spaced (i.e. narrowing) compaction bands towards the opposite boundary. Hopf bifurcations are perhaps the most prominently discussed candidates for earthquake source mechanism in, for example, spring-slider models (Gu et al., 1984). Our results suggest that supercritical Hopf bifurcations are likely to prepare a given internal structure for failure. Such a boundary may be a pre-existing fault which would correspond to the opposite boundary separating an elastic domain from a domain yielding under the background strain rate. In the context of the above-discussed laboratory experiments Hopf bifurcations may also explain the acoustic bursts reported in the puffed rice compression experiment (Guillard et al., 2015). However, Hopf bifurcations themselves do not have the capacity to enhance the amplitude of a given excitation wave over the initial excitation amplitude as they do not have the capacity to sample energy from the environment. The only way to amplify the magnitude of a Hopf wave is to have two waves collide. In this case the peak magnitude is simply the sum of the two waves.
- iii.
The third class of waves that is recovered from Eq. (11) is the quasi-soliton solution that has been introduced in Part 1 (Regenauer-Lieb et al., 2021). It is encountered for very small fluid (or crushed rock) production rates which should be observed under slow loading conditions such as geodynamic loads. The quasi-soliton wave reflects from boundaries often changing and reforming after reflection on boundaries or collision with other waves. The quasi-soliton wave has been identified as a new class of waves (Tsyganov et al., 2007).
For the classification of the quasi-soliton solution of Eq. (11) we follow a systematic study by Tsyganov and Biktashev (2014), who used the analogous FitzHugh–Nagumo equation to study the solution space. A typical feature of quasi-solitons is that wave-packet solutions emerge when the wave energy is concentrated around a finite wavenumber. When the dispersion is weak, the envelope travels with a uniform group velocity. Linear cross-diffusion can create non-linear dispersion, where – depending on the coefficients – three different wave types have been classified: (1) fixed-shape propagating waves, (2) envelope waves, (3a) multi-envelope waves, and (3b) intermediate regimes appearing as multi-envelope waves propagating as fixed shape most of the time but undergoing restructuring from time to time (Tsyganov and Biktashev, 2014).
The collisional behaviour of these classes of cross-diffusional waves is complicated. When a quasi-soliton wave hits an interface (including another quasi-soliton wave) the amplitude of the quasi-soliton changes, and there is a temporary diminution of the amplitude or in extreme cases an annihilation. In most cases, they recover their original form gradually. This is another feature that is different from true solitons which do not change on impact. In two-dimensional systems, additional complexities arise as they can penetrate, break apart on collision, or reflect into different directions (Tsyganov and Biktashev, 2014). Zakharov et al. (2004) compare quasi-solitons with unstable particles in nuclear physics. This describes their behaviour on collision but does not capture their capability to coordinate wave energy into a standing rogue wave (Regenauer-Lieb et al., 2021). Before discussing the formation of a rogue wave it is useful to have a closer look at the cross-diffusion waveforms.
4.1.2 Quasi-soliton waveforms, wavenumber, and short-wavelength amplitude magnification
THMC quasi-soliton waves discussed in this work stem from multiscale fluctuations as possible wave sources with the superposition of multiple waves in a wide frequency spectrum. The convolution of these waves results in interesting dispersion patterns that bear similar characteristics to quasi-solitons encountered in optical systems, where chromatic dispersion is strong, leading to anomalous dispersion patterns that, unlike solitons, come in discrete portions (Paschotta, 2008). Quasi-solitons encountered in photonics have two oscillating tails, one going to the left with a different wavenumber to the one going to the right. If the amplitudes of the tails are small, quasi-solitons can be treated as slowly decaying real solitons which lose their energy by radiation to form the tail (Zakharov et al., 2004).
Of specific interest for the earthquake problem is the aspect of the fate of the accelerations carried by the waves as discussed in Part 1 (Regenauer-Lieb et al., 2021) for cases where the wave collides and collapses after the collision. Another important aspect is the cross-scale coupling of the full spectrum of diffusion waves which may be seen as an energy cascade from extremely short-wavelength chemical quasi-soliton waves to the longest wavelength which in most cases is modulated by the thermal and mechanical diffusion length scale as shown in Table A1 of the Appendix. The spectral content of THMC wave interactions is extremely rich, and we have emphasized in Part 1 (Regenauer-Lieb et al., 2021) that it is perhaps best compared to a convolution sharpening filter for cases of instabilities, where wave energy focusses on specific locations.
The wavenumbers of the quasi-soliton waves are controlled by the competition of the diffusion processes determining the diffusion length and number of possible oscillations per unit length. The 1-D linear stability analysis for just two coupled reaction–diffusion equations discussed in Sun et al. (2021b) illustrates the role of the wavelength (or its inverse the wavenumber) for the nucleation of quasi-soliton waves. The linear stability analysis (Sun et al., 2021b) shows that cross-diffusional waves nucleate if and are nonzero, of opposite sign, and sufficiently large to overcome the self-diffusion processes in the first term, which is always positive.
The instability criterion also suggests a critical lower limit kmin (longest wavelength) for which no quasi-soliton wave can nucleate as the self-diffusion term becomes dominant. This minimum wavenumber (longest wavelength) can be constrained further by the system size. We argue that the longest wavelength is a fraction of the system size, defined by long-wavelength solution (Regenauer-Lieb et al., 2013a; Veveakis and Regenauer-Lieb, 2015), where the cross-diffusion coefficients are adiabatically eliminated. This is the Turing-style long-wave soliton solution that turns cross-diffusional waves into a standing wave Korteweg–de Vries-type cnoidal solution in normal resonance mode.
For investigating the opposite scenario where shorter wavelength cross-diffusional waves might cascade to a small dispersion limit of a coordinated short timescale instability around a dominant small wavelength with a maximum amplification factor we look at an idealized solution where we assume that there is no self-diffusion and the Eq. (11) is only controlled by cross-diffusion. For further simplification we normalize both cross-diffusion coefficients to unity. We also use the compact form of the Kramers–Kronig relationship and test the solution by a perturbation new complex wave function . In summary we investigate following parameters:
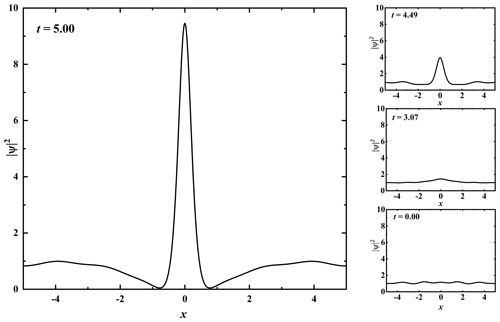
Figure 6Numerical calculation of the Peregrine soliton using the approach of Yang (2010) and Ward et al. (2019). The solution is an extreme end-member short-wavelength and short-timescale compression of wave energy . In the context of the selected parameters the soliton is understood as a fluid pressure spike likely to cause unstable slip on a pre-existing (near-critically stressed) fault plane that triggers the ultimate (shear) seismic moment release.
Setting self-diffusion to zero implies that non-local cross-diffusion processes are happening very fast and trigger large internal fluxes between solid and fluid. Additionally, the cross-coupled fluxes are maximized, in a normative sense by setting the cross-diffusion coefficients to unity and opposite sign. In other words we consider the extreme condition where the ratio of cross-diffusion over self-diffusion coefficients tends to infinity. For these parameters our reaction–cross-diffusion equation becomes the integrable non-linear Schrödinger equation.
The cross-diffusion equation then is analytically tractable, and as the solution is relevant for nucleation of earthquakes we obtain the Peregrine soliton with a simple solution for the lowest order given by Peregrine (1983) as
This classical rogue-wave soliton solution features a self-focussing wave that appears from low background oscillations for t<0, suddenly reaches a peak at x=0 and t=0, and vanishes quickly into the background noise. The criticality condition for the Peregrine soliton requires the wavelength of the background perturbation to be very large, which has been used as an argument for forecasting Peregrine solitons simply by the absence or presence of such long-wavelength perturbations in measurement of wave spectra (Shrira and Geogjaev, 2010). This criticality condition also shows that the Peregrine soliton achieves maximum spatial and temporal compression of wave energy by sampling energy from the far field. Its peak intensity is ∼ 9 times the background value. A numerical simulation of the wave is shown in Fig. 6. The Peregrine soliton solution is the simplest rogue wave that stems from the physics of cross-diffusion.
The Peregrine soliton is by no means the only rogue-wave phenomenon that stems from the non-local cross-diffusion terms in the non-linear Schrödinger equation. A higher-order cascade mechanism for coupling 7 orders of the length scale of quasi-solitary waves has for instance been discovered in the analogous problem of rogue waves in optical fibres (Eberhard et al., 2017). This resonant-like scattering mode has been argued to arise through inelastic collision of cross-diffusional waves colliding with other or reflected cross-diffusional waves. Eberhard et al. (2017) numerically investigated higher non-linear terms in the Schrödinger equation and found a similar criticality condition to for the simple Peregrine rogue wave. In the numerical experiments the emergence of the rogue wave is always preceded by a period of reduced short-wavelength amplitude described as a “calm before the storm”. Figure 6 is available as a video in the Supplement.
Since the theoretical discovery of the rogue-wave phenomenon in optics and hydrodynamics there has now been ample proof of their existence in controlled experiments. Solli et al. (2007) has provided high-resolution measurements of optical rogue waves with picosecond resolution and Dudley et al. (2019) have provided a rigorous comparison and review of rogue waves in fibre optics and rogue waves in hydrodynamic tank experiments. Although the media that the waves are travelling through are completely different the basic phenomenon is identical. We propose here that rogue waves stemming from cross-diffusion terms and quasi-soliton collisions in hydromechanically coupled media of the solid Earth provide a source mechanism for earthquakes.
We have introduced a new approach to THMC instabilities using the concept of cross-diffusion. To simplify the application, we have so far only focussed on dissipative cross-diffusional P waves. We may now discuss the inclusion of cross-diffusional S waves and speculate about the interaction with the P waves. We have shown in Part 1 (Regenauer-Lieb et al., 2021) that the wave equations can be decomposed by using the Helmholtz decomposition of the equation of motion, into P (compressional) and S (shear) quasi-soliton waves. The analysis suggests that cross-diffusion provides a crucial link to allow cross-scale coupling of the multiphysics processes potentially leading to earthquake instabilities. For critical cross-diffusion coefficients and associated reaction terms, a bi-directional energy cascade of acceleration cross-diffusion P waves, from small-scale thermo-chemical (TC) and chemo-mechanical (CM) dissipative waves to meso-scale hydro-mechanical (HM) dissipative waves, can be triggered by a geodynamic driving force. This in turn may nucleate shear-quasi-soliton waves in the form of a thermo-mechanical (TM) shear-wave instability.
We have also presented a derivation of the Peregrine soliton solution as the extreme short-wavelength standing wave end-member of the cross-diffusion approach. The Peregrine soliton has been used to explain the iconic Draupner wave example recorded on 1 January 1995 by a downward looking laser beam on an oil platform in the North Sea. The exceptional nature of these rogue waves bears many similarities with earthquake events in terms of predictability. A hindcast analysis of the Draupner wave came to the conclusion that rogue waves are not predictable with current statistical means (Cavaleri et al., 2016). Records at a specific location are often misleading, and the probability of detecting a rogue wave must be considered both in space and time; they are thought to be accepted as part of the reality of the ocean at a given sea state (Cavaleri et al., 2016). Recent work refutes this conclusion and raises hopes that a statistical analysis is possible based on large deviation theory combined with the simplified non-linear Schrödinger equation solution of the quasi-soliton waves using random initial data (Dematteis et al., 2019). This may be useful for earthquake research but it will take some time, acknowledging that it took nearly 15 years of research on the Draupner wave to come to this point.
The yardstick used to measure the length scales of diffusion fronts in reaction–diffusion equations is the diffusional length scale. Any scale that is significantly larger than the diffusional length scale is considered to be unaffected by the diffusion front for a given diffusion time td. We will later on reinterpret the diffusion length as an uncertainty measure. The characteristic diffusion length scale for a 1-D problem is
The diffusion length scale Ld allows definition of a normalized Gaussian scale space ensuring that the area under the Gaussian distribution always remains the same. The Gaussian probability density function (here called a Gaussian wavelet) is often used in probability theory, where the diffusion length is related to the standard deviation, its square to the variance, and the function centroid to the mean.
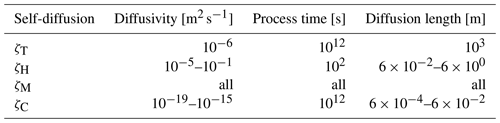
Table A1Typical diffusion length scales for geological THMC processes (Regenauer-Lieb et al., 2013a). Equation (A1) is used to calculate length scales for a given reaction time. For thermal and chemical processes a geodynamic timescale of 1012 s is chosen. Geodynamic processes are assumed to cause fluid flow at pore level in less than 100 s. Note that the mechanical diffusion length scale can range over all timescales and length scales. As an example, the visco-elastic diffusion length scale for elasto-dynamic earthquake events is very short. However, prior to the catastrophic event stress diffusion can range over all scales and can couple all processes through elasto-visco-plastic creep processes.
The simple diffusion process without reaction leads to a decaying and broadening diffusion front of an initial perturbation. When considering an active source term, the solution turns into a propagating wavefront which was first discovered in 1906 by Robert Luther. An English translation of the original article appeared in the Journal of Chemical Education (Luther, 1987). The same phenomenon was rediscovered 30 years later and is now known as Fisher or Fisher–Kolmogorov–Petrovsky–Piskunov (FKPP) equation (Kolmogorov et al., 1937). Fisher originally discussed the reaction–diffusion equation to calculate the propagation of a mutant virus in an infinite domain (Fisher, 1937).
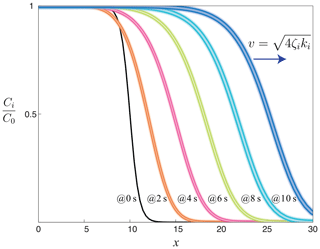
Figure A1Illustration of the propagating wavefront of the Fisher–Kolmogorov reaction–diffusion equation, which has a non-linear source term . Kolmogorov et al. (1937) showed that any initial concentration vanishes for large x and evolves to a travelling wave solution with a minimal velocity . The reaction–diffusion exhibits a bistable equilibrium. One stable equilibrium is achieved when the initial concentration is below the activation of a wave and the system is resting and the other is the travelling-wave solution with a minimal velocity v. We show here the non-dimensional solution for the example of a tanh initial condition (black curve) which quickly converges to a travelling waveform with a non-dimensional speed of 2. Various solution techniques exist. A convenient method is to turn the partial differential equation (Eq. 2) into an ordinary differential equation by using Chebyshev polynomials (Towers and Jovanoski, 2008).
The addition of a reactive non-linear source term (e.g. for the Fisher–Kolmogorov equation) into the diffusion equation leads to the interesting phenomenon of the generation of a self-oscillatory excitation wave, where after Fisher's work on the topic progress was mainly made in the Russian literature, triggered by the seminal work of Kolmogorov et al. (1937) discussed in Fig. A1.
In Russian literature, the term “autowave” was introduced (Ostrovski\ĭ, 2015; Molotkov and Vakulenko, 1993; Zuev and Barannikova, 2010). The self-excitation wave constitutes a fundamental class of waves encountered in all reaction–diffusion systems in physics, biology, and chemistry (Vasil'ev, 1979). The principal difference to classical wave equations that are based on hyperbolic differential equations is that the autowave phenomenon arises from a non-linear source term in parabolic equations.
The reaction–diffusion timescales of a single reaction–diffusion equation can be expressed by a generalization of the Damköhler number for chemical reaction–diffusion processes to all THMC couplings. The Damköhler number describes the ratio of the diffusion over the reaction time or the equivalent ratio of the reaction rate over the considered diffusion rate
This ratio thus considers an additional rate of the chemical reaction. This is illustrated here only for an infinite autocatalytic source term in the reaction–diffusion system (Fig. A1). For a finite autocatalytic reaction the reactive source term has a growth function which is sigmoid, also called a logistic function. This means that the reactant initially grows exponentially, similar to the infinite source, followed by linear reactant growth and a final zero growth branch. These general solutions imply different shapes of the self-supporting propagating wave and, depending on the value of the diffusivities, also a finite lifetime of the wave.
This geologically more relevant situation is described in Molotkov and Vakulenko (1993). The authors describe generalized reaction–diffusion systems and find that the wave behaviour depends on only three parameters. For small wavefront curvature the autowave is described by the two parameters of the infinite source term solution discussed above, while for the more general case the normal velocity of the front may contain the front curvature as an additional parameter. The additional dependence of the wave function on the curvature of the concentration field arises because of the fact that is proportional to the curvature of the wavefront. For regions of the wavefront where the curvature is negative the concentration must decrease at a rate proportional to the magnitude of the curvature. Conversely, the concentration must increase where the wavefront curvature is positive.
Summarizing the above findings, we can now characterize the reaction–diffusion thermodynamic system by five key features: (i) a bistable or multistable (for several reactions) region has a stable stationary mode and a mode for the nucleation of propagating autowaves above a critical activation threshold. (ii) In the activated state, the wavefront separates two regions, a local region characterized by the particular THMC diffusional length scale Ld affected by the reactions Ri, and a large region at >Ld which is outside the reaction–diffusion wave. (iii) For long timescales, the wavefield is governed by characteristic self-oscillatory motions which for bistable systems are described by just three parameters. For multistable systems chaotic oscillations are expected (Molotkov and Vakulenko, 1993). For the analysis of this complicated system we will propose to use perturbation theory and illustrate the approach through some basic concepts of signal processing. In the bistable system the Fisher–Kolmogorov wave is a self-propagation dissipative wave at a characteristic wave speed whose lower limit can be quantified by the square root of the Damköhler number times the diffusivity normalized by the characteristic diffusion length scale Ld. (iv) The propagating wave exponentially scatters information about its initial condition, and the wavefield only carries information about the dissipative properties into the far-field; this is an important differentiation from waves in the conservative system (e.g. elastic waves), where the wave at a long-distance still carries information about its initial conditions. (v) The wave speed thus becomes a fundamental material constant defined by the rates of the dissipative THMC processes as
As the spreading wavefronts are self-supporting and can propagate upwards in scale, we propose that this material velocity not only applies to the above-discussed chemical reaction–diffusion equations but to all reaction–diffusion equations of the THMC-coupled system. In this proposition, the propagating multiscale and multiphysics waves provide the capacity to link the different THMC length scales and could explain the multifractal nature of earthquakes. The approach allows a significant simplification of the earthquake physics problem as the exponential rate of approaching the Kolmogorov limit of a self-oscillating wavefront shown in Fig. A1 for a given scale allows a characterization of the important physics in terms of the wave velocity. With the autowave approach, one can turn any non-linear perturbation of the local source into a linearly propagating waveform only governed by the dissipative material properties. Autowaves will by themselves recover a characteristic wavefield dictated by the reaction–diffusion rate constants.
This characteristic behaviour is used, for instance, in medicine, where autowaves are encountered in many fields. The electrical nerve impulses that drive a regular heart beat are an example (Antonioletti et al., 2017). The authors describe how the characteristic recovery of the autowave waveform after a random perturbation can be used, for instance, for defibrillation strategies (a small electrical stimulus applied through a pacemaker) for treatment of life-threatening heart arrhythmia. In this sense, earthquake physics might profit from an understanding of the partial differential equations developed in mathematical biology, epidemiology (wave-like propagation of viruses), and other biomedical applications for which numerical open-source tools are available. One such tool is the “heart beat box” (Antonioletti et al., 2017) which uses a mathematical formulation of the human heart in terms of a coupled electro-mechanical reaction–diffusion equations similar to the coupled reaction–diffusion equations discussed above.
The code used for this study is available at https://doi.org/10.17632/9mkcsbk78x.2 (Sun et al., 2021a).
A linear stability analysis and a discussion of the solution domain are available on the open archive in a preprint under consideration at https://doi.org/10.1002/essoar.10507265.1 (Sun et al., 2021b).
A video animation of the Peregrine soliton solution is available on https://tinyurl.com/sz783szy (Sun and Manman, 2021), showing the rogue wave phenomenon that seems to appear as background noise. Note that before emergence of the soliton there is a slight reduction of background oscillations (calm before the storm).
KRL together with MH and CS secured research funding. KRL, MH, and CS developed the research plan. KRL prepared the first draft of the paper, and all authors contributed to subsequent revisions and interpretations of the applications.
The authors declare that they have no conflict of interest.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Thermo-hydro-mechanical-chemical (THMC) processes in natural and induced seismicity”. It is a result of the The 7th International Conference on Coupled THMC Processes, Utrecht, Netherlands, 3–5 July 2019.
We would especially like to acknowledge the thought-provoking experimental work of Francois Guillard and Itai Einav, as well as Barraclough et al., which may provide a new method for identification of dissipative material parameters. Further laboratory work is urgently needed to explore this new avenue. Finally, we would like to thank the careful review by Angelo de Santis and especially the suggestions by an anonymous reviewer.
This work was supported by the Australian Research Council (ARC DP170104550, DP170104557, 30 LP170100233), the strategic SPF01 fund of UNSW, Sydney, and the Research Grant Council of Hong Kong (ECS 27203720 and GRF 17206521). Piotr Szymczak was supported by the National Science Centre (Poland) under the research grant 2016/21/B/ST3/01373.
This paper was edited by Andre R. Niemeijer and reviewed by Angelo De Santis and two anonymous referees.
Aharonov, E. and Scholz, C. H.: The Brittle–Ductile Transition Predicted by a Physics-Based Friction Law, J. Geophys. Res.-Sol. Ea., 124, 2721–2737, https://doi.org/10.1029/2018JB016878, 2019. a
Aifantis, E. C.: Gradient Extension of Classical Material Models: From Nuclear and Condensed Matter Scales to Earth and Cosmological Scales, Springer Tracts in Mechanical Engineering, 1, 417–452, Springer, Zurich, https://doi.org/10.1007/978-3-030-63050-8_15, 2021. a, b, c
Alevizos, S., Poulet, T., and Veveakis, E.: Thermo-poro-mechanics of chemically active creeping faults. 1: Theory and steady state considerations, J. Geophys. Res.-Sol. Ea., 119, 4558–4582, https://doi.org/10.1002/2013JB010070, 2014. a
Amdreo-Valle, F., Mazon, J., Rossi, D., and Toledo-Molero, J.: Nonlocal Diffusion Processes, Mathematical Surveys and Monographs, 165, American Mathematical Society, Providence, Rhode Island, https://doi.org/10.1090/surv/165, 2010. a
Antonioletti, M., Biktashev, V. N., Jackson, A., Kharche, S. R., Stary, T., and Biktasheva, I. V.: BeatBox – HPC simulation environment for biophysically and anatomically realistic cardiac electrophysiology, PLOS ONE, 12, e0172 292, https://doi.org/10.1371/journal.pone.0172292, 2017. a, b, c, d
Ball, P.: Pattern Formation in Nature: Physical Constraints and Self-Organising Characteristics, Archit. Design, 82, 22–27, https://doi.org/10.1002/ad.1375, 2012. a, b
Balluffi, R. W., Allen, S. M., and Carter, W. C.: Kinetics of Materials, John Wiley & Sons Inc., Hoboken, https://doi.org/10.1002/0471749311, 2005. a
Barraclough, T. W., Blackford, J. R., Liebenstein, S., Sandfeld, S., Stratford, T. J., Weinländer, G., and Zaiser, M.: Propagating compaction bands in confined compression of snow, Nat. Phys., 13, 272–275, https://doi.org/10.1038/nphys3966, 2017. a, b, c
Berenstein, I. and Beta, C.: Spatiotemporal chaos arising from standing waves in a reaction-diffusion system with cross-diffusion, J. Chem. Phys., 136, 034 903, https://doi.org/10.1063/1.3676577, 2012. a, b
Biktashev, V. N. and Tsyganov, M. A.: Quasisolitons in self-diffusive excitable systems, or Why asymmetric diffusivity obeys the Second Law, Sci. Rep., 6, 30 879, https://doi.org/10.1038/srep30879, 2016. a
Brace, W. and Byerlee, J.: Stick-slip as a mechanism for earthquakes, Science, 153, 990–992, 1966. a
Braeck, S. and Podladchikov, Y. Y.: Spontaneous Thermal Runaway as an Ultimate Failure Mechanism of Materials, Phys. Rev. Lett., 98, 095 504, https://doi.org/10.1103/PhysRevLett.98.095504, 2007. a, b
Brechet, Y. and Estrin, Y.: Pseudo-portevin-le châtelier effect in ordered alloys, Scripta Mater., 35, 217–223, https://doi.org/10.1016/1359-6462(96)00126-1, 1996. a
Cavaleri, L., Barbariol, F., Benetazzo, A., Bertotti, L., Bidlot, J.-R., Janssen, P., and Wedi, N.: The Draupner wave: A fresh look and the emerging view, J. Geophys. Res.-Oceans, 121, 6061–6075, https://doi.org/10.1002/2016JC011649, 2016. a, b
Chester, F. M., Rowe, C., Ujiie, K., Kirkpatrick, J., Regalla, C., Remitti, F., Moore, J. C., Toy, V., Wolfson-Schwehr, M., Bose, S., Kameda, J., Mori, J. J., Brodsky, E. E., Eguchi, N., Toczko, S., Expedition 343, and 343T Scientists: Structure and Composition of the Plate-Boundary Slip Zone for the 2011 Tohoku-Oki Earthquake, Science, 342, 1208–1211, https://doi.org/10.1126/science.1243719, 2013. a
Coleman, B. D. and Gurtin, M. E.: Thermodynamics and the Velocity of General Acceleration Waves, in: Wave Propagation in Dissipative Materials, edited by: Coleman, B. D., Gurtin, M. E., Herrera R, I., and Truesdell, C., 83–104, Springer Berlin Heidelberg, 1965. a
Crampin, S. and Gao, Y.: The New Geophysics, Terra Nova, 25, 173–180, https://doi.org/10.1111/ter.12030, 2013. a
Crampin, S. and Gao, Y.: The physics underlying Gutenberg-Richter in the earth and in the moon, J. Earth Sci., 26, 134–139, https://doi.org/10.1007/s12583-015-0513-3, 2015. a, b
Dematteis, G., Grafke, T., Onorato, M., and Vanden-Eijnden, E.: Experimental Evidence of Hydrodynamic Instantons: The Universal Route to Rogue Waves, Phys. Rev. X, 9, 041 057, https://doi.org/10.1103/PhysRevX.9.041057, 2019. a
Di Giacomo, D., Engdahl, E. R., and Storchak, D. A.: The ISC-GEM Earthquake Catalogue (1904–2014): status after the Extension Project, Earth Syst. Sci. Data, 10, 1877–1899, https://doi.org/10.5194/essd-10-1877-2018, 2018. a
Dieterich, J.: Time-dependent friction in rocks., J. Geophys. Res., 377, 3690–3697, 1972. a
Dieterich, J.: Constitutive properties of faults with simulated gouge, in: Mechanical Behavior of Crustal Rocks, Geophys. Monogr. Ser., 24, edited by: Carter, N. L., Friedman, M., Logan, J. M., and Stearns D. W., https://doi.org/10.1029/GM024p0103, 1987. a
Dudley, J. M., Genty, G., Mussot, A., Chabchoub, A., and Dias, F.: Rogue waves and analogies in optics and oceanography, Nature Reviews Physics, 1, 675–689, https://doi.org/10.1038/s42254-019-0100-0, 2019. a
Durrleman, S., Boschetti, F., Ord, A., and Regenauer-Lieb, K.: Automatic detection of particle aggregation in particle code simulations of rock deformation, Geochem. Geophy. Geosy., 7, Q05006, https://doi.org/10.1029/2005GC001063, 2006. a
Eberhard, M., Savojardo, A., Maruta, A., and Römer, R. A.: Rogue wave generation by inelastic quasi-soliton collisions in optical fibres, Opt. Express, 25, 28 086, https://doi.org/10.1364/OE.25.028086, 2017. a, b, c
Einav, I. and Guillard, F.: Tracking time with ricequakes in partially soaked brittle porous media, Science Advances, 4, eaat6961, https://doi.org/10.1126/sciadv.aat6961, 2018. a, b
Elphick, K. E., Sloss, C. R., Regenauer-Lieb, K., and Schrank, C. E.: Distribution, microphysical properties, and tectonic controls of deformation bands in the Miocene subduction wedge (Whakataki Formation) of the Hikurangi subduction zone, Solid Earth, 12, 141–170, https://doi.org/10.5194/se-12-141-2021, 2021. a
Español, P. and Warren, P. B.: Perspective: Dissipative particle dynamics, J. Chem. Phys., 146, 150 901, https://doi.org/10.1063/1.4979514, 2017. a
Estrin, Y. and Kubin, L.: Spatial Coupling and Propagative Plastic Instabilities, 1, 395–450, John Wiley and Sons, United States, 1995. a
Evans, D. and Searle, D.: The fluctuation theorem, Adv. Phys., 51, 1529–1585, 2002. a
Fan, X. and Lin, M.: Multiscale multifractal detrended fluctuation analysis of earthquake magnitude series of Southern California, Physica A, 479, 225–235, https://doi.org/10.1016/j.physa.2017.03.003, 2017. a
Fisher, R. A.: The wave of advance of advantageous genes, Ann. Eugenic., 7, 355–369, https://doi.org/10.1111/j.1469-1809.1937.tb02153.x, 1937. a
Fitzgerald, B. W., Zarghami, A., Mahajan, V. V., Sanjeevi, S. K. P., Mema, I., Verma, V., El Hasadi, Y. M. F., and Padding, J. T.: Multiscale simulation of elongated particles in fluidised beds, Chem. Eng. Sci. X, 2, 100 019, https://doi.org/10.1016/j.cesx.2019.100019, 2019. a
Gomberg, J.: Slow slip phenomena in Cascadia from 2007 and beyond: a review, GSA Bulletin, 122, 963–978, https://doi.org/10.1130/B30287.1, 2010. a
Grigoli, F., Cesca, S., Rinaldi, A. P., Manconi, A., López-Comino, J. A., Clinton, J. F., Westaway, R., Cauzzi, C., Dahm, T., and Wiemer, S.: The November 2017 5.5 Pohang earthquake: A possible case of induced seismicity in South Korea, Science, 360, 1003, https://doi.org/10.1126/science.aat2010, 2018. a
Gu, J., Rice, J. R., Ruina, A. L., and Tse, S. T.: Slip Motion and Stability of a Single Degree of Freedom Elastic System with Rate and State Dependent Friction, J. Mech. Phys. Solids, 32, 167–196, 1984. a
Guillard, F., Golshan, P., Shen, L., Valdes, J. R., and Einav, I.: Dynamic patterns of compaction in brittle porous media, Nat. Phys., 11, 835–838, 2015. a, b, c, d
Hanasoge, S., Agarwal, U., Tandon, K., and Koelman, J. M. V. A.: Renormalization group theory outperforms other approaches in statistical comparison between upscaling techniques for porous media, Phys. Rev. E, 96, 033 313, https://doi.org/10.1103/PhysRevE.96.033313, 2017. a, b
Hayward, K. S., Cox, S. F., Fitz Gerald, J. D., Slagmolen, B. J., Shaddock, D. A., Forsyth, P. W., Salmon, M. L., and Hawkins, R. P.: Mechanical amorphization, flash heating, and frictional melting: Dramatic changes to fault surfaces during the first millisecond of earthquake slip, Geology, 44, 1043–1046, https://doi.org/10.1130/g38242.1, 2016. a
Hobbs, B. and Ord, A.: Structural Geology: The Mechanics of Deforming Metamorphic Rocks, Elsevier, Oxford, https://doi.org/10.1016/B978-0-12-407820-8.00015-1, 2015. a
Hobbs, B., Ord, A., and Regenauer-Lieb, K.: The Thermodynamics of deformed metamorphic rocks: A Review, J. Struct. Geol., 33, 758–818, 2011. a
Hu, M., Veveakis, M., Poulet, T., and Regenauer-Lieb, K.: The Role of Temperature in Shear Instability and Bifurcation of Internally Pressurized Deep Boreholes, Rock Mech. Rock Eng., 50, 3003–3017, https://doi.org/10.1007/s00603-017-1291-2, 2017. a
Hu, M., Schrank, C., and Regenauer-Lieb, K.: Cross-diffusion waves in hydro-poro-mechanics, J. Mech. Phys. Solids, 135, 103 632, https://doi.org/10.1016/j.jmps.2019.05.015, 2020. a, b, c, d, e, f
Kanamori, H. and Brodsky, E. E.: The physics of earthquakes, Phys. Today, 54, 34–40, 2001. a
Kanamori, H., Anderson, D. L., and Heaton, T. H.: Frictional melting during the rupture of the 1994 Bolivian earthquake, Science, 279, 839–842, 1998. a
Kohlstedt, D. and Holtzman, B.: Shearing Melt out of the Earth: An Experimentalist's Perspective on the Influence of Deformation on Melt Extraction, Annu. Rev. Earth Pl. Sc., 37, 561–593, https://doi.org/10.1146/annurev.earth.031208.100104, 2009. a
Kolmogorov, A., Petrovsky, I., and Piskunov, N.: Etude de l'equation de la diffusion avec croissance de la quantite de matiere et son application a un probleme biologique, Bulletin Universite de Etat a Moscow, 1, 1–26, 1937. a, b, c
Kondepudi, D. and Prigogine, I.: Modern Thermodynamics: From Heat Engines to Dissipative Structures, John Wiley and Sons, Chichester, 1998. a
Koronovsky, N. V., Zakharov, V. S., and Naimark, A. A.: Short-Term Earthquake Prediction: Reality, Research Promise, or a Phantom Project?, Moscow University Geology Bulletin, 74, 333–341, https://doi.org/10.3103/S0145875219040057, 2019. a, b
Luther, R.: Propagation of chemical reactions in space, J. Chem. Educ., 64, 740, https://doi.org/10.1021/ed064p740, 1987. a
Lyakhovsky, V., Zhu, W., and Shalev, E.: Visco-poroelastic damage model for brittle-ductile failure of porous rocks, J. Geophys. Res.-Sol. Ea., 120, 2179–2199, https://doi.org/10.1002/2014JB011805, 2015. a
Manning, J. R.: Cross terms in the thermodynamic diffusion equations for multicomponent alloys, Metall. Mater. Trans. B, 1, 499–505, https://doi.org/10.1007/BF02811561, 1970. a
Masuda, T., Akimoto, A. M., and Yoshida, R.: 5.1 – Self-Oscillating Polymer Materials, 219–236, William Andrew Publishing, Norwich , https://doi.org/10.1016/B978-0-323-37127-8.00013-3, 2016. a
Maugin, G. and Muschik, W.: Thermodynamics with internal variables, vol. WSS Nonlin. Sci. Ser. A, 27, 77–105, https://doi.org/10.1142/9789812796271_0004, 1999. a
Molotkov, I. A. and Vakulenko, S. A.: Autowave propagation for general reaction diffusion systems, Wave Motion, 17, 255–266, https://doi.org/10.1016/0165-2125(93)90005-Z, 1993. a, b, c
Monneau, R. and Patrizi, S.: Homogenization of the Peierls–Nabarro model for dislocation dynamics, J. Differ. Equations, 253, 2064–2105, https://doi.org/10.1016/j.jde.2012.06.019, 2012. a
Obara, K.: Nonvolcanic deep tremor associated with subduction in southwest Japan, Science, 296, 1679–1681, 2002. a
Oberst, S., Niven, R. K., Lester, D. R., Ord, A., Hobbs, B., and Hoffmann, N.: Detection of unstable periodic orbits in mineralising geological systems, Chaos, 28, 085 711, https://doi.org/10.1063/1.5024134, 2018. a
Ogawa, M.: Shear instability in a viscoelastic material as the cause of deep focus earthquakes, J. Geophys. Res., 92, 13801–13810, 1987. a, b
Ohnaka, M.: A constitutive scaling law and a unified comprehension for frictional slip failure, shear fracture of intact rock, and earthquake rupture, J. Geophys. Res.-Sol. Ea., 108, ESE 6–21, https://doi.org/10.1029/2000JB000123, 2003. a, b, c
Ohtani, M., Kame, N., and Nakatani, M.: Synchronization of megathrust earthquakes to periodic slow slip events in a single-degree-of-freedom spring-slider model, Sci. Rep., 9, 8285, https://doi.org/10.1038/s41598-019-44684-4, 2019. a
Orowan, E.: Mechanism of seismic faulting, Geol. Soc. Am. Mem., 79, 323–346, Washington, 1960. a, b, c
Ostoja-Starzewski, M.: Microstructural Randomness and Scaling in Mechanics of Materials, Chapman & Hall/CRC, London, New York, 2008. a
Ostrovski, L. A.: Asymptotic perturbation theory of waves, London, England: Imperial College Press, London, England, Singapore, 2015. a
Paschotta, R.: Quasi-Soliton pulses, Wiley-VCH, 1st edition, Hoboken, 2008. a
Peregrine, D. H.: Water waves, nonlinear Schrödinger equations and their solutions, J. Aust. Math. Soc. B, 25, 16–43, https://doi.org/10.1017/S0334270000003891, 1983. a, b
Perzyna, P.: Fundamental problems in viscoplasticity, Adv. Appl. Mech., 9, 243–377, 1966. a
Poulet, T., Veveakis, E., Herwegh, M., Buckingham, T., and Regenauer-Lieb, K.: Modeling episodic fluid-release events in the ductile carbonates of the Glarus thrust, Geophys. Res. Lett., 41, 7121–7128, 2014a. a
Poulet, T., Veveakis, E., Regenauer-Lieb, K., and Yuen, D. A.: Thermo-poro-mechanics of chemically active creeping faults: 3. The role of serpentinite in episodic tremor and slip sequences, and transition to chaos, J. Geophys. Res.-Sol. Ea., 119, 4606–4625, https://doi.org/10.1002/2014JB011004, 2014b. a, b, c, d, e, f
Regenauer-Lieb, K. and Yuen, D. A.: Rapid conversion of elastic energy into plastic shear heating during incipient necking of the lithosphere, Geophys. Res. Lett., 25, 2737–2740, 1998. a, b
Regenauer-Lieb, K., Veveakis, M., Poulet, T., Wellmann, F., Karrech, A., Liu, J., Hauser, J., Schrank, C., Gaede, O., and Fusseis, F.: Multiscale coupling and multiphysics approaches in earth sciences: Applications, Journal of Coupled Systems and Multiscale Dynamics, 1, 2330–152X/2013/001/042, https://doi.org/10.1166/jcsmd.2013.1021, 2013a. a, b, c
Regenauer-Lieb, K., Veveakis, M., Poulet, T., Wellmann, F., Karrech, A., Liu, J., Hauser, J., Schrank, C., Gaede, O., and Trefry, M.: Multiscale coupling and multiphysics approaches in Earth sciences: theory, Journal of Coupled Systems and Multiscale Dynamics, 1, 2330–152X, https://doi.org/10.1166/jcsmd.2013.1012, 2013b. a
Regenauer-Lieb, K., Hu, M., Schrank, C., Chen, X., Clavijo, S. P., Kelka, U., Karrech, A., Gaede, O., Blach, T., Roshan, H., and Jacquey, A. B.: Cross-diffusion waves resulting from multiscale, multi-physics instabilities: theory, Solid Earth, 12, 869–883, https://doi.org/10.5194/se-12-869-2021, 2021. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y
Rice, J. R.: Heating and weakening of faults during earthquake slip, J. Geophys. Res., 111, B05311, https://doi.org/10.1029/2005JB004006, 2006. a, b
Rice, J. R., Lapusta, N., and Ranjith, K.: Rate and state dependent friction and the stability of sliding between elastically deformable solids, J. Mech. Phys. Solids, 49, 1865–1898, 2001. a
Rubinstein, J. and Sternberg, P.: Nonlocal reaction–diffusion equations and nucleation, IMA J. Appl. Math., 48, 249–264, https://doi.org/10.1093/imamat/48.3.249, 1992. a
Ruina, A.: Slip instability and state variable friction laws., J. Geophys. Res., 88, 10359–10370, 1983. a
Schulz, S. E. and Evans, J. P.: Mesoscopic structure of the Punchbowl Fault, Southern California and the geologic and geophysical structure of active strike-slip faults, J. Struct. Geol., 22, 913–930, https://doi.org/10.1016/S0191-8141(00)00019-5, 2000. a
Sethna, J. P.: Statistical Mechanics: Entropy, Order Parameters and Complexity, Oxford University Press, Great Clarendon Street, Oxford OX2 6DP, first edition, 2006a. a
Sethna, J. P.: Statistical mechanics : entropy, order parameters, and complexity, Oxford, New York: Oxford University Press, formerly CIP, 2006b. a, b
Sethna, J. P., Dahmen, K. A., and Myers, C. R.: Crackling noise, Nature, 410, 242–250, 2001. a
Shaar, M. and Ghavanloo, E.: Nonlocal Mechanics in the Framework of the General Nonlocal Theory, Springer Tracts in Mechanical Engineering, 1, 95–122, Springer, Zürich, https://doi.org/10.1007/978-3-030-63050-8_3, 2021. a
Shrira, V. I. and Geogjaev, V. V.: What makes the Peregrine soliton so special as a prototype of freak waves?, J. Eng. Math., 67, 11–22, https://doi.org/10.1007/s10665-009-9347-2, 2010. a
Solli, D. R., Ropers, C., Koonath, P., and Jalali, B.: Optical rogue waves, Nature, 450, 1054, https://doi.org/10.1038/nature06402, 2007. a
Sornette, D.: Earthquakes: from chemical alteration to mechanical rupture, Phys. Rep., 313, 238–291, 1999. a
Sornette, D. and Ouillon, G.: Multifractal scaling of thermally activated rupture processes, Phys. Rev. Lett., 94, 038501, https://doi.org/10.1103/PhysRevLett.94.038501, 2005. a, b
Sornette, D. and Pisarenko, V.: Fractal plate tectonics, Geophys. Res. Lett., 30, 1105, https://doi.org/10.1029/2002GL015043, 2003. a
Stanley, H. E. and Meakin, P.: Multifractal phenomena in physics and chemistry, Nature, 335, 405–409, https://doi.org/10.1038/335405a0, 1988. a
Storchak, D. A., Di Giacomo, D., Bondára, I., Engdahl, E. R., Harris, J., Lee, W. H. K., Villaseñor, A., and Bormann, P.: Public release of the ISC-GEM Global Instrumental Earthquake Catalogue (1900-2009), Seismol. Res. Lett., 84, 810–815, https://doi.org/10.1785/0220130034, 2013. a
Storchak, D. A., Di Giacomo, D., Engdahl, E. R., Harris, J., Bondár, I., Lee, W. H. K., Bormann, P., and Villaseñor, A.: The ISC-GEM Global Instrumental Earthquake Catalogue (1900–2009): Introduction, Phys. Earth Planet. In., 239, 48–63, https://doi.org/10.1016/j.pepi.2014.06.009, 2015. a
Sun, Q. and Manman, M.: Animation of Figure 6, available at: https://tinyurl.com/sz783szy, last access: 30 July 2021. a
Sun, Q., Hu, M., and Regenauer-Lieb, K.: FDM simulation of Turing-, Hopf-, Quasi-soliton instabilities, Mendeley Data [code], v2 https://doi.org/10.17632/9mkcsbk78x.2, 2021a. a
Sun, Q., Hu, M., Schrank, C., and Regenauer-Lieb, K.: Reaction–diffusion waves in hydro-mechanically coupled porous solids, Geophys. Res. Lett., https://doi.org/10.1002/essoar.10507265.1, submitted, 2021b. a, b, c, d, e, f, g
Towers, I. and Jovanoski, Z.: Application of rational Chebyshev polynomials to optical problems, ANZIAM J., 50, 60–74, https://doi.org/10.21914/anziamj.v50i0.1396, 2008. a
Tse, S. T. and Rice, J. R.: Crustal Earthquake Instability in Relation to the Depth Variation of Frictional Slip Properties, J. Geophys. Res.-Solid, 91, 9452–9472, 1986. a
Tsyganov, M. A. and Biktashev, V. N.: Classification of wave regimes in excitable systems with linear cross diffusion, Phys. Rev. E, 90, 062912, https://doi.org/10.1103/PhysRevE.90.062912, 2014. a, b, c
Tsyganov, M. A., Biktashev, V. N., Brindley, J., Holden, A. V., and Genrikh, R. I.: Waves in systems with cross-diffusion as a new class of nonlinear waves, Physics-Usp+, 50, 263, https://doi.org/10.1070/pu2007v050n03abeh006114, 2007. a
Turiel, A., Pérez-Vicente, C. J., and Grazzini, J.: Numerical methods for the estimation of multifractal singularity spectra on sampled data: A comparative study, J. Comput. Phys., 216, 362–390, https://doi.org/10.1016/j.jcp.2005.12.004, 2006. a, b
Vanag, V. K. and Epstein, I. R.: Cross-diffusion and pattern formation in reaction–diffusion systems, Phys. Chem. Chem. Phys., 11, 897–912, https://doi.org/10.1039/B813825G, 2009. a, b, c
Vardoulakis, I.: Thermo-poro-mechanics of rapid fault shearing, pp. 63–74, Springer Berlin Heidelberg, Berlin, Heidelberg, https://doi.org/10.1007/3-540-44424-6_5, 2001. a, b, c
Vasil'ev, V. A.: Autowave processes in distributed kinetic systems, Sov. Phys. Uspekhi, 22, 615–639, https://doi.org/10.1070/PU1979v022n08ABEH005591, 1979. a
Veveakis, E. and Regenauer-Lieb, K.: Cnoidal waves in solids, J. Mech. Phys. Solids, 78, 231–248, 2015. a, b
Veveakis, E., Poulet, T., and Alevizos, S.: Thermo-poro-mechanics of chemically active creeping faults: 2. Transient considerations, J. Geophys. Res.-Sol. Ea., 119, 4583–4605, https://doi.org/10.1002/2013JB010071, 2014. a
Ward, C. B., Kevrekidis, P. G., and Whitaker, N.: Evaluating the robustness of rogue waves under perturbations, Phys. Lett. A, 383, 2584–2588, https://doi.org/10.1016/j.physleta.2019.05.030, 2019. a
Wiemer, S. and Wyss, M.: Mapping the frequency-magnitude distribution in asperities: An improved technique to calculate recurrence times?, J. Geophys. Res.-Sol. Ea., 102, 15115–15128, 1997. a
Yang, J.: Nonlinear Waves in Integrable and Non-integrable Systems, Society for Industrial and Applied Mathematics, USA, 2010. a
Zaiser, M. and Hähner, P.: Oscillatory Modes of Plastic Deformation: Theoretical Concepts, Phys. Status solidi B, 199, 267–330, https://doi.org/10.1002/1521-3951(199702)199:2<267::AID-PSSB267>3.0.CO;2-Q, 1997. a, b, c, d
Zakharov, V., Dias, F., and Pushkarev, A.: One-dimensional wave turbulence, Phys. Rep., 398, 1–65, https://doi.org/10.1016/j.physrep.2004.04.002, 2004. a, b
Zuev, L. and Barannikova, S.: Plastic Flow Macrolocalization: Autowave and Quasi-Particle, Journal of Modern Physics, 1, 1–8, https://doi.org/10.4236/jmp.2010.11001, 2010. a, b
- Abstract
- Introduction
- Coarse-graining techniques in the light of the earthquake problem
- Laboratory and field observations of diffusion waves
- Application to earthquake physics
- Discussion and conclusions
- Appendix A: Reaction-diffusion length scale and timescale
- Code availability
- Data availability
- Video supplement
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Coarse-graining techniques in the light of the earthquake problem
- Laboratory and field observations of diffusion waves
- Application to earthquake physics
- Discussion and conclusions
- Appendix A: Reaction-diffusion length scale and timescale
- Code availability
- Data availability
- Video supplement
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References





