A systems-based approach to parameterise seismic hazard in regions with little historical or instrumental seismicity: active fault and seismogenic source databases for southern Malawi

Seismic hazard is commonly characterised using instrumental seismic records. However, these records are short relative to earthquake repeat times, and extrapolating to estimate seismic hazard can misrepresent the probable location, magnitude, and frequency of future large earthquakes. Although paleoseismology can address this challenge, this approach requires certain geomorphic setting, is resource intensive, and can carry large inherent uncertainties. Here, we outline how fault slip rates and recurrence intervals can be estimated by combining fault geometry, earthquake-scaling relationships, geodetically derived regional strain rates, and geological constraints of regional strain distribution. We apply this approach to southern Malawi, near the southern end of the East African Rift, and where, although no on-fault slip rate measurements exist, there are constraints on strain partitioning between border and intra-basin faults. This has led to the development of the South Malawi Active Fault Database (SMAFD), a geographical database of 23 active fault traces, and the South Malawi Seismogenic Source Database (SMSSD), in which we apply our systems-based approach to estimate earthquake magnitudes and recurrence intervals for the faults compiled in the SMAFD. We estimate earthquake magnitudes of M_W 5.4–7.2 for individual fault sections in the SMSSD and M_W 5.6–7.8 for whole-fault ruptures. However, low fault slip rates (intermediate estimates ∼ 0.05–0.8 mm/yr) imply long recurrence intervals between events: 10²–10⁵ years for border faults and 10³–10⁶ years for intra-basin faults. Sensitivity analysis indicates that the large range of these estimates can best be reduced with improved geodetic constraints in southern Malawi. The SMAFD and SMSSD provide a framework for using geological and geodetic information to characterise seismic hazard in regions with few on-fault slip rate measurements, and they could be adapted for use elsewhere in the East African Rift and globally.

1 Introduction

Earthquake ruptures tend to occur on pre-existing faults (Brace and Byerlee, 1966; Jackson, 2001; Scholz, 2002; Sibson, 1989). Thus, the identification and systematic mapping of active faults, which are then compiled with other fault attributes (e.g. slip rate and slip sense) into a geospatial active fault database, provide an important tool for assessing regional seismic hazard (Christophersen et al., 2015; Hart and Bryant, 1999; Langridge et al., 2016; Shyu et al., 2016; Styron et al., 2020; Styron and Pagani, 2020; Taylor and Yin, 2009). Not only can these databases provide information on the surface rupture risk (Hart and Bryant, 1999; Villamor et al., 2012), they can also be converted into earthquake sources for probabilistic seismic hazard analysis (PSHA) to forecast future levels of ground shaking (Beauval et al., 2018; Cornell, 1968; Gerstenberger et al., 2020; Hodge et al., 2015; Morell et al., 2020; Stirling et al., 2012). Furthermore, the data contained in active fault databases are inherently useful for understanding regional geological evolution (Agostini et al., 2011b; Basili et al., 2008; Taylor and Yin, 2009).

Active fault databases with worldwide coverage have been compiled (Christophersen et al., 2015; Yeats, 2012), including recent development of the Global Earthquake Model Foundation Global Active Fault Database (Styron and Pagani, 2020). However, in some regions, the fault mapping in these databases has only been performed at a coarse scale, and the fault attributes (e.g. slip rates, earthquake recurrence intervals) that are required to use them as earthquake sources in PSHA have not been measured. This partly reflects that obtaining these attributes from dating faulted surfaces and/or paleoseismology is time-intensive, requires certain geomorphic settings, and can involve large uncertainties (Cowie et al., 2012; McCalpin, 2009; Nicol et al., 2016b). Alternatively, decadal timescale fault slip rates can be estimated using geodetic data and block models where the crust is divided by mapped faults (e.g. Field et al., 2014; Wallace et al., 2012; Zeng and Shen, 2014). However, not all fault systems are covered by sufficiently dense geodetic networks to perform this analysis, the resulting slip rates may be biased by the short time over which these data have been collected relative to earthquake cycles, and/or sometimes geodetic data cannot resolve how strain is distributed (Calais et al., 2016; Morell et al., 2020; Stein et al., 2012).

In this study, we first describe the South Malawi Active Fault Database (SMAFD), which is a systematic attempt to map active faults and collate their geomorphic attributes in southern Malawi. Located within the East African Rift System (EARS), southern Malawi lies in a region specifically highlighted by Styron and Pagani (2020) as a priority area for future active fault mapping; population growth in this region as well as seismically vulnerable building stock is also driving an increased exposure to seismic hazard (Tectonic Shift RIFT2018 Report, 2019; Goda et al., 2016; Hodge et al., 2015; Kloukinas et al., 2020; Ngoma et al., 2019; Novelli et al., 2019).

Within southern Malawi itself, faults capable of hosting M_W 7–8 earthquakes have been previously identified (Hodge et al., 2019, 2020; Jackson and Blenkinsop, 1997; Wedmore et al., 2020a). However, there are currently no reports of historical surface-rupturing earthquakes, on-fault slip rate measurements, or paleoseismic investigations. Thus, in the second part of this study, we describe a new systems-based approach for combining geodetic and geological information to estimate slip rates and earthquake recurrence intervals. In particular, it may be useful for low-slip-rate interplate regions (regional slip rates ∼ 1–10 mm/yr; Scholz et al., 1986) where the instrumental record is relatively short compared with fault recurrence intervals and where earthquakes may be especially damaging (England and Jackson, 2011). It would not, however, be appropriate for low-strain intraplate settings where geodetic data cannot resolve deformation rates (Calais et al., 2016),

By applying this approach to southern Malawi, we have developed the South Malawi Seismogenic Source Database (SMSSD), which is a complementary database to the SMAFD but where the attributes (e.g. fault segmentation, earthquake recurrence intervals) are (1) targeted towards its inclusion in PSHA and (2) derived from modelling (and are therefore mutable). Notably, previous PSHA in the EARS has typically been conducted using the ∼ 65-year-long instrumental seismic record alone (Ayele, 2017; Goitom et al., 2017; Midzi et al., 1999; Poggi et al., 2017). However, fault-based earthquake sources, such as the SMSSD, may play an important role in characterising the EARS's ever-increasing seismic risk (Goda et al., 2016; Hodge et al., 2015).

We describe the SMAFD and SMSSD together here so that the assumptions and uncertainties of our approach are clear, particularly for hazard modellers who may wish to incorporate these databases into a PSHA. This study first describes the seismotectonic setting of southern Malawi (Sect. 2), and the approach used for mapping its active faults in the SMAFD (Sect. 3). In Sect. 4, we then describe the method used to estimate fault slip rates, earthquake magnitudes, and recurrence intervals, and whose application to southern Malawi has resulted in the development of the SMSSD. The SMAFD is described in Sect. 5 along with an evaluation of fault slip rate estimates and sensitivity analysis in the SMSSD. Finally, in Sect. 6, we discuss the implication of these databases in terms of southern Malawi's seismic hazard, and the strategies needed to reduce uncertainties in these databases.

2 Southern Malawi seismotectonics

The SMAFD and SMSSD cover the geopolitical term “southern Malawi”; thus, they include all active faults between the southern end of Lake Malawi and the border between Mozambique and Malawi. Faults that lie close to or cross this national boundary are also included. The extent of these databases does not therefore correspond directly to the geological region of the “southern Malawi Rift”, whose definition has varied in previous studies (Chapola and Kaphwiyo, 1992; Ebinger et al., 1987; Laõ-Dávila et al., 2015; Williams et al., 2019). In this section, we briefly summarise the tectonic history and seismic record in the region.

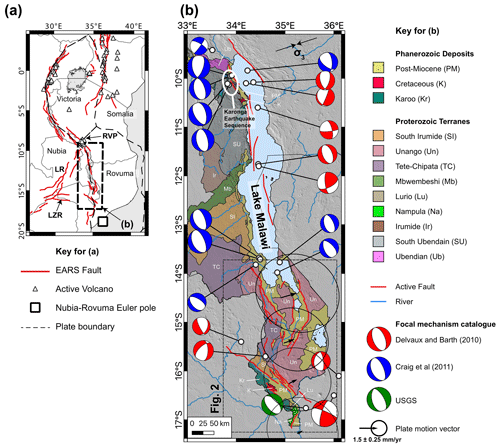
Figure 1 (a) The location of Malawi in the context of major faults in the East African Rift (Daly et al., 2020; Hodge et al., 2018a; Macgregor, 2015) and plate boundaries proposed by Saria et al. (2013). LZR represents the Lower Zambezi Rift, LR represents the Luangwa Rift, and RVP represents the Rungwe Volcanic Province. (b) A simplified geological map of Malawi, with Proterozoic terranes after Fullgraf et al. (2017). The map is underlain by the Shuttle Radar Topography Mission (SRTM) 30 m digital elevation model (DEM; Sandwell et al., 2011). The extent of Fig. 2 is also shown. Active faults within this area are those included in the South Malawi Active Fault Database (SMAFD). Active faults outside this region are mapped as in panel (a). Focal mechanisms collated from Delvaux and Barth (2010), Craig et al. (2011), and the U.S. Department of the Interior U.S. Geological Survey (2018). Minimum principal compressive stress (σ₃) trend from focal mechanism stress inversion (Williams et al., 2019). Plate motion vector for central point of each basin in southern Malawi (Fig. S1) for the Nubia–Rovuma Euler pole (Saria et al., 2013), modelled using methods described in Robertson et al. (2016).

2.1 Southern Malawi tectonic setting

Southern Malawi lies towards the southern incipient end of the EARS Western Branch, where it channels the Shire River from Lake Malawi to its confluence with the Zambezi River (Dulanya, 2017; Ivory et al., 2016). This portion of the EARS is typically considered to represent the divergent boundary between the Rovuma and Nubia plates (Fig. 1a; Saria et al., 2013; Stamps et al., 2008, 2018, 2020). However, recent seismotectonic analysis suggests that the Nubia Plate can be further divided by the Lower Zambezi and Luangwa rifts into the San and Angoni plates, with the EARS in Malawi forming the Angoni–Rovuma plate boundary (Fig. 1a; Daly et al., 2020). EARS activity in southern Malawi is unlikely to have initiated prior to the mid-Pliocene (∼ 4.5 Ma) onset of sediment accumulation in Lake Malawi's south basin (Delvaux, 1995; McCartney and Scholz, 2016; Scholz et al., 2020) and almost certainly not before the Oligocene (23–25 Ma) age of the Rungwe Volcanic Province (RVP) in southern Tanzania (Mesko, 2020; Mortimer et al., 2016; Roberts et al., 2012). The RVP, 700 km to the north (Fig. 1a), marks the closest surface volcanism to southern Malawi; hence, this rift section is considered to be amagmatic.

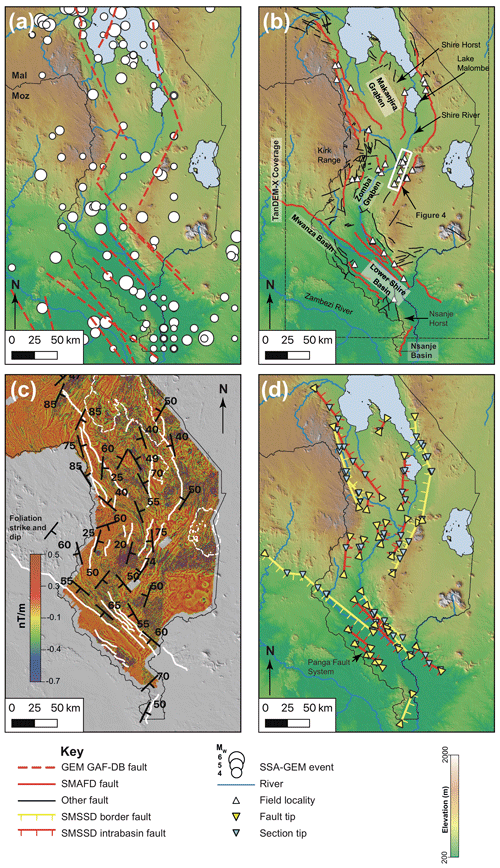
Figure 2 (a) Global Earthquake Model Global Active Fault Database map for southern Malawi (GAF-DB; Macgregor, 2015; Styron and Pagani, 2020). The sub-Saharan African Global Earthquake Model (SSA-GEM; Poggi et al., 2017) event locations are also shown. (b) Map of active fault traces compiled in the South Malawi Active Fault Database (SMAFD) with field locations and TanDEM-X coverage. Faults not interpreted to be active are also shown. (c) Aeromagnetic image created from the vertical derivative, with foliation orientations digitised from geological maps (Bloomfield, 1958, 1965; Bloomfield and Garson, 1965; Habgood et al., 1973; Walshaw, 1965). SMAFD faults shown in white and the outline of lakes are shown by dashed white lines. For full details of the acquisition of the aeromagnetic data, see Laõ-Dávila et al. (2015). (d) Simplified geometry of faults in the South Malawi Seismogenic Source Database (SMSSD), with faults sorted into border and intra-basin faults. Ticks indicate fault hanging wall. The extent of all maps is equivalent and is outlined in Fig. 1b. All maps are underlain by the SRTM 30 m digital elevation model. “Mal” denotes Malawi, and “Moz” denotes Mozambique.

Like elsewhere in the Western Branch, the EARS in southern Malawi follows Proterozoic orogenic belts and can be divided along strike into a number of 50–150 km long linked basins (Ebinger, 1989). Immediately south of Lake Malawi, the EARS bifurcates around the Shire Horst within the NW–SE trending Makanjira Graben before following an arcuate bend in regional Proterozoic fabrics to form the NNE–SSW trending Zomba Graben (Fig. 2; Dulanya, 2017; Fullgraf et al., 2017; Laõ-Dávila et al., 2015; Wedmore et al., 2020a; Williams et al., 2019). Along strike to the south, the EARS then intersects the Lower Shire Basin, a reactivated Karoo-age (i.e. Permo-Triassic) basin (Castaing, 1991; Chisenga et al., 2019; Habgood, 1963; Habgood et al., 1973; Wedmore et al., 2020b), before bending around the Nsanje Horst to link up with the Urema Graben in Mozambique (Bloomfield, 1958; Steinbruch, 2010). Daly et al. (2020) proposed that the Lower Shire Basin also extends to the west along the Mwanza Basin into Mozambique where it links with the Lower Zambezi Rift and forms the San–Angoni plate boundary (Fig. 1a).

Prior to this study, the only systematic active fault mapping in southern Malawi had been conducted by Chapola and Kaphwiyo (1992) and, for the Lower Shire Basin, by Castaing (1991). These maps were subsequently incorporated by Macgregor (2015) into EARS-scale maps, and later into the Global Earthquake Model Global Active Fault Database (Styron and Pagani, 2020). However, the faults are mapped at a coarse scale (Fig. 2a), and this database does not include active faults traces identified in legacy geological maps (Bloomfield, 1965; Bloomfield and Garson, 1965; Habgood et al., 1973; Walshaw, 1965) and high-resolution digital elevation models (Hodge et al., 2019, 2020; Wedmore et al., 2020a, b).

2.2 Southern Malawi seismicity

There are no known historical accounts of surface-rupturing earthquakes in southern Malawi, although a continuous written record only extends to ca. 1870 (Pike, 1965; Stahl, 2010). However, in northern Malawi, the previously unrecognised St Mary Fault exhibited surface rupture following the 2009 Karonga earthquakes, a sequence consisting primarily of four shallow (focal depths < 8 km) M_W 5.5–5.9 events over a 13 d period (Fig. 1b; Biggs et al., 2010; Gaherty et al., 2019; Hamiel et al., 2012; Kolawole et al., 2018b; Macheyeki et al., 2015).

The International Seismological Centre (ISC) record for Malawi is complete from 1965 to present for events with M_W>4.5 (Figs. 1b, 2a; Hodge et al., 2015), with the largest event in this record being the 1989 M_W 6.3 Salima earthquake (Jackson and Blenkinsop, 1993). Notably, seismicity in Malawi is commonly observed to depths far greater (30–35 km; Craig et al., 2011; Delvaux and Barth, 2010; Jackson and Blenkinsop, 1993) than would be expected for continental crust of typical composition and geothermal gradient (10–15 km). Thick cold anhydrous lower crust (Craig et al., 2011; Jackson and Blenkinsop, 1997; Njinju et al., 2019; Nyblade and Langston, 1995), localised weak viscous zones embedded within strong lower crust (Fagereng, 2013), and/or volumes of mafic material in the lower crust (Shudofsky et al., 1987) that are velocity weakening at temperatures < 700 ^∘C (Hellebrekers et al., 2019) have been proposed as explanations for this unusually deep seismicity.

Earthquake focal mechanism stress inversions that encompass events from across Malawi indicate a normal fault stress state (i.e. vertical maximum principal compressive stress) with an ENE–WSW to E–W trending minimum principal compressive stress (σ₃, Fig. 1b; Delvaux and Barth, 2010; Ebinger et al., 2019; Williams et al., 2019). This σ₃ orientation is comparable to the σ₃ direction inferred from regional joint orientations (Williams et al., 2019) and the geodetically derived extension direction between the Nubia and Rovuma plates (Fig. 1b; Saria et al., 2014; Stamps et al., 2018, 2020).

Using instrumental catalogues, probabilistic seismic hazard analysis (PSHA) finds that there is a 10 % probability of exceeding 0.15 g peak ground acceleration in the next 50 years in southern Malawi (Midzi et al., 1999; Poggi et al., 2017). Through the SMAFD and SMSSD, we outline how geological and geodetic data can be collated and assessed so that they may also be incorporated into PSHA in southern Malawi.

3 Mapping and describing active faults in the South Malawi Active Fault Database (SMAFD)

An active fault database consists of an active fault map, where for each fault, attributes are added that detail geomorphic, kinematic, geometric, and geological information about the fault (Christophersen et al., 2015; Styron and Pagani, 2020). Typically, an active fault database is stored in a geographic information system (GIS) environment, in which the fault attributes are assigned to a linear feature that represents the fault's geomorphic trace (e.g. Langridge et al., 2016; Machette et al., 2004; Styron et al., 2020). In this section, we describe how active faults were mapped in the South Malawi Active Fault Database (SMAFD) as well as the geomorphic attributes that were assigned to them. Estimates of associated earthquake source parameters, which are collated separately in the South Malawi Seismogenic Source Database (SMSSD), are described in Sect. 4.

3.1 Identifying active and inactive faults in southern Malawi

There are many inherent limitations in mapping active faults. Even in countries with well-developed databases, such as Italy and New Zealand, their success in accurately predicting the locations of future surface-rupturing earthquakes is, at best, mixed (Basili et al., 2008; Nicol et al., 2016a). An active fault might not be recognised because evidence of previous surface rupture is subsequently buried, eroded (Wallace, 1980), or the fault itself is blind (e.g. Quigley et al., 2012), which in turn depends on earthquake magnitude, focal depth, thickness of the seismogenic crust, and the local geology. Furthermore, although active and inactive faults are typically differentiated by the age of the most recent earthquake, the precise maximum age that is used to define “active” varies between different active fault databases depending on the regional strain rate (i.e. plate boundary vs. stable craton) and the prevalence of youthful sediments (Clark et al., 2012; Jomard et al., 2017; Langridge et al., 2016; Machette et al., 2004). Indeed, it may not always be possible to reliably determine if an exposed fault has been recently active or not (Cox et al., 2012; Nicol et al., 2016a).

Each of these issues has relevance to mapping active faults in southern Malawi. Firstly, active faults may be buried by sediments deposited due to tectonic subsidence (Gawthorpe and Leeder, 2000) and/or by regular (10–100 ka) climate-driven ∼ 100 m scale fluctuations in the level of Lake Malawi, which would likely flood the Zomba and Makanjira basins (Ivory et al., 2016; Lyons et al., 2015; Wedmore et al., 2020a). Alternatively, the relatively thick (30–35 km) seismogenic crust in southern Malawi means that even moderate–large earthquakes (M_W>6) do not necessarily result in surface rupture, as illustrated by the M_W 6.3 Salima earthquake (Gupta, 1992; Jackson and Blenkinsop, 1993). Finally, except for studies around Lake Malombe (Van Bocxlaer et al., 2012), there is no chronostratigraphic control for this section of the EARS to help differentiate between inactive and active faults (Dulanya, 2017; Wedmore et al., 2020a).

Thus, for the SMAFD, we define active faults based on evidence of activity within the current tectonic regime. Such an approach has been advocated elsewhere in the EARS (Delvaux et al., 2017) and in other areas with low levels of seismicity, few paleoseismic studies, and/or where there are faults that are favourably oriented for failure in the current stress regime but that have no definitive evidence of recent activity (Nicol et al., 2016a; De Pascale et al., 2017; Villamor et al., 2018). In practice, this means that faults will be included in the SMAFD if they can be demonstrated to have been active during East African rifting. This evidence can vary from the accumulation of post-Miocene hanging-wall sediments to the presence of a steep fault scarp, offset alluvial fans, and/or knickpoints in rivers that have migrated only a short vertical distance (< 100 m) upstream (Hodge et al., 2019, 2020; Jackson and Blenkinsop, 1997; Wedmore et al., 2020a). We note that the absence of post-Miocene sediments in the hanging wall of a normal fault does not necessarily imply that it is inactive, if, for example, faults are closely spaced across strike so that sediments are eroded during subsequent footwall uplift of an interior normal fault (e.g. Chirobwe–Ncheu Fault, Fig. 3c; see also Mortimer et al., 2016; Muirhead et al., 2016). In these cases, if there is other evidence of recent activity (e.g. scarp, triangular facets), these faults are still included.

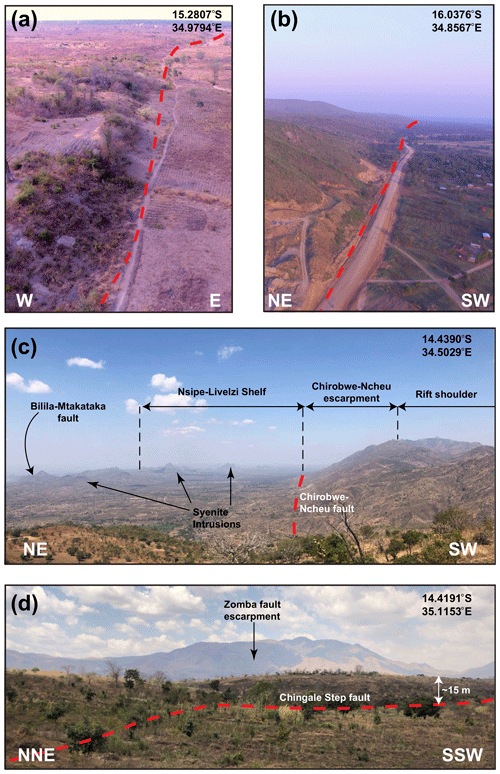
Figure 3 Field examples of border and intra-basin faults in southern Malawi. Unmanned aerial vehicle (UAV) images of scarps (dashed red line) along the (a) intra-basin Mlungusi Fault in the Zomba Graben as well as (b) the Thyolo Fault – the border fault for the Lower Shire Basin. (c) View across the western edge of the Makanjira Graben showing the Chirobwe–Ncheu and Bilila–Mtakataka faults as well as Proterozoic syenite intrusions (Walshaw, 1965). (d) Minor step in the scarp along the intra-basin Chingale Step fault, with the escarpment of the Zomba border fault behind.

For the sake of completeness, major faults that control modern-day topography but that do not fit the criteria of being active (e.g. Karoo faults) were mapped separately (Fig. 2a). However, this map is not necessarily complete for all other faults in southern Malawi, and we also cannot definitively exclude the possibility that some of these faults are still active although they display no evidence for it. The relatively broad definition of an active fault may also mean that some inactive faults are included in the SMAFD. However, in applying the opposite approach (i.e. requiring an absolute age for the most recent activity on a fault) there is a greater risk that faults mistakenly interpreted to be inactive subsequently rupture in a future earthquake (Litchfield et al., 2018; Nicol et al., 2016a).

3.2 Datasets for mapping faults in southern Malawi

3.2.1 Legacy geological maps

Between the 1950s and 1970s, the geology of southern Malawi was systematically mapped at a 1:100 000 scale. These studies noted evidence of recent displacement on the Thyolo (Habgood et al., 1973), Bilila–Mtakataka, Tsikulamowa (Walshaw, 1965), and Mankanjira faults (King and Dawson, 1976). However, they did not systematically distinguish between active and inactive faults. Furthermore, these studies are in places ambiguous with equivalent structures in the Zomba Graben being variably described as “terrace features” (Bloomfield, 1965), active fault scarps (Dixey, 1926), and Late Jurassic–Early Cretaceous faults (Dixey, 1938).

3.2.2 Geophysical datasets

Regional-scale aeromagnetic data were acquired across Malawi in 2013 by the Geological Survey Department of Malawi (Fig. 2c; Kolawole et al., 2018a; Laõ-Dávila et al., 2015). These survey data were used to refine fault mapping in cases where features interpreted as faults in the aeromagnetic survey extended beyond their surface expression. Gravity surveys have also been used to map blind faults in the Lower Shire Basin (Chisenga et al., 2019), and these have been incorporated into the SMAFD.

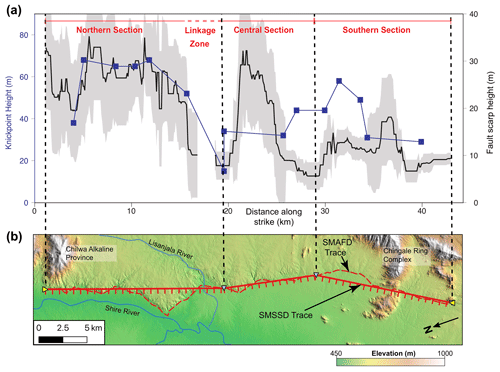
Figure 4 Fault segmentation along the Chingale Step fault, modified after Wedmore et al. (2020a). (a) Along-strike variation in stream knickpoint (blue points) and fault scarp height (black line), with the gap due to erosion by the Lisanjala River. Grey shading represents 1 standard deviation error in scarp height measurements (Wedmore et al., 2020a). (b) A map of the Chingale Step fault underlain by TanDEM-X DEM, with the extent of the area shown in Fig. 2b. The dashed red line shows the surface trace of the fault as per the South Malawi Active Fault Database (SMAFD). The solid red line shows the simplified geometry of the fault in the South Malawi Seismogenic Source Database (SMSSD), where it is defined by straight lines between section end points (blue triangles). Ticks indicate fault hanging wall. An along-strike scarp height minima at the boundary between the northern and central section occurs at a bend in the fault scarp; however, there is no obvious geometrical complexity at the along-strike scarp height minima between the southern and central sections. Topography associated with the Proterozoic Chingale Ring Structure and Chilwa Alkaline Province (Bloomfield, 1965; Manda et al., 2019) is also indicated. For full details on panel (a), see Wedmore et al. (2020a).

3.2.3 Digital elevation models

The topography of southern Malawi is primarily controlled by EARS faulting (Dulanya, 2017; Laõ-Dávila et al., 2015; Wedmore et al., 2020a) except in the case of the Kirk Range (Fig. 2b) as well as readily identifiable igneous intrusions and Karoo faults (Figs. 3c, 4b). To exploit this interaction between topography and active faulting, TanDEM-X digital elevation models (DEMs) with a 12.5 m horizontal resolution and an absolute vertical mean error of ±0.2 m (Wessel et al., 2018) were acquired for southern Malawi (Fig. 2b). This small error means that the TanDEM-X data perform better at identifying the metre-scale scarps common in southern Malawi (Hodge et al., 2019; Wedmore et al., 2020a) than the more widely used but lower-resolution Shuttle Radar Topography Mission (SRTM) 30 m DEMs (Sandwell et al., 2011). Furthermore, TanDEM-X data can be used to assess variations in along-strike scarp height (Hodge et al., 2018a, 2019; Wedmore et al., 2020a, b) and the interactions between footwall uplift and fluvial incision (Fig. 4a; Wedmore et al., 2020a). The Mwanza and Nsanje faults partly extended out of the region of TanDEM-X coverage, and these sections were mapped using the SRTM 30 m resolution DEM (Fig. 2b).

3.2.4 Fieldwork

To corroborate evidence of recent faulting recognised in DEMs and geological reports, fieldwork was conducted on several faults (Fig. 2b). This ranged from documenting features indicative of recent displacement on the faults, such as scarps, triangular facets, and displaced Quaternary–recent sediments, to comprehensively sampling the fault and surveying it with an unmanned aerial vehicle (Fig. 3; see also: Hodge et al., 2018a; Wedmore et al., 2020a, b; Williams et al., 2019).

3.3 Strategy for mapping and describing active faults in the SMAFD

Following the active fault definition and synthesis of the datasets described above, faults in southern Malawi are mapped following the approach outlined for the Global Earthquake Model Global Active Fault Database (GAF-DB) where each fault constitutes a single continuous GIS feature (Styron and Pagani, 2020). Therefore, the SMAFD differs from other active fault databases where each distinct geomorphic (i.e. traces) or geometric (i.e. sections) part of a fault is mapped as a separate GIS feature (Christophersen et al., 2015; Machette et al., 2004).

Table 1 List and brief description of attributes in the SMAFD. Attributes are based on the Global Earthquake Model Global Active Faults Database (Styron and Pagani, 2020).

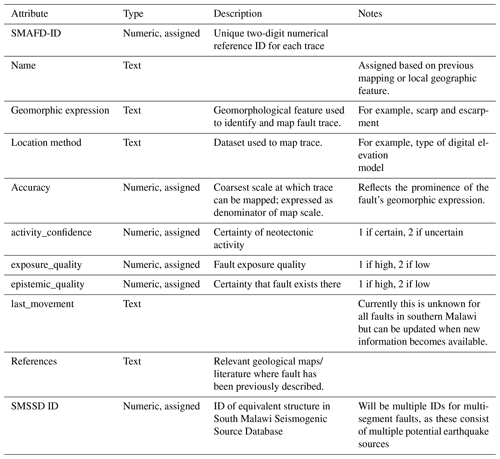
The attributes associated with each fault in the SMAFD are listed and briefly described in Table 1. These resemble the attributes in the GEM GAF-DB that describe a fault's geomorphic attributes and confidence that it is still active (Styron and Pagani, 2020). To incorporate the multidisciplinary approach that we have used to map faults in southern Malawi, we also include a “Location method” attribute, which details how the fault was mapped (Table 1). Some fault attributes used in the GEM GAF-DB, such as slip rates, are not included in the SMAFD, as these data have not been collected in southern Malawi. We instead derive these attributes as outlined in Sect. 4 and incorporate them separately into the SMSSD (Table 2). However, within each database, a numerical ID system is used make the two databases compatible (Tables 1, 2).

4 A systems-based approach to estimating seismic source parameters: application to southern Malawi

Typically, estimates of fault slip rate, earthquake magnitudes, and recurrence intervals are derived from paleoseismology, geodesy, historical records of past earthquakes, or considerations of the seismic moment rate (Basili et al., 2008; Field et al., 2014; Langridge et al., 2016; McCalpin, 2009; Molnar, 1979; Youngs and Coppersmith, 1985). However, as noted in Sect. 1, these types of data have not been collected in southern Malawi. Indeed, very few such records currently exist across the entire EARS (Delvaux et al., 2017; Muirhead et al., 2016; Siegburg et al., 2020; Zielke and Strecker, 2009), and even in regions with well-developed active fault databases, such as California and New Zealand, only a small number of faults have directly measured slip rates and paleoseismic information (Field et al., 2014; Langridge et al., 2016).

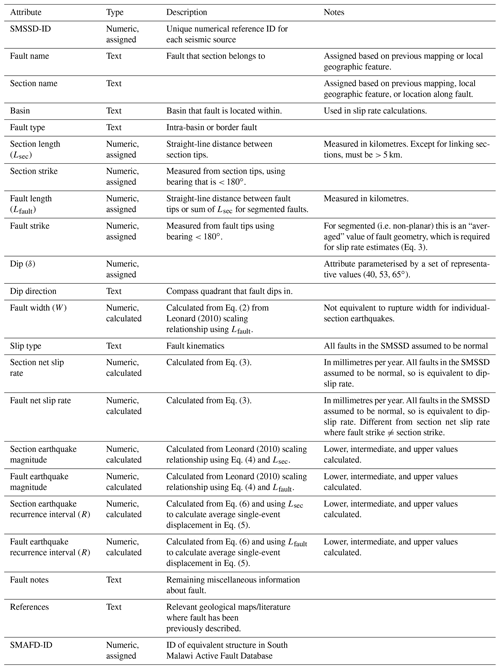
Table 2 List and brief description of fault geometry, slip rate estimates, and earthquake source attributes in the SMSSD.

In the absence of direct on-fault slip rate estimates, we suggest that they can be estimated through a systems-level approach in which geodetically derived plate motion rates are partitioned across faults in a manner consistent with their geomorphology and regional tectonic regime. Although such an approach has been used before over small regions (Cox et al., 2012; Litchfield et al., 2014), it has not been applied to an entire fault system. In addition, we outline how the uncertainties and alternative hypotheses that are inherent to this approach can, in common with seismic hazard practice elsewhere, be explored with a logic tree approach (Fig. 6; Field et al., 2014; Vallage and Bollinger, 2019; Villamor et al., 2018). We use the South Malawi Seismogenic Source Database (SMSSD) as an example of how this approach can be applied to narrow (< 100 km width; Buck, 1991) amagmatic continental rifts, where the distribution of regional strain between border faults and intra-basin faults is well constrained by previous studies (Agostini et al., 2011a; Corti, 2012; Gupta et al., 1998; Morley, 1988; Muirhead et al., 2016, 2019; Nicol et al., 1997; Shillington et al., 2020; Wedmore et al., 2020a; Wright et al., 2020).

4.1 Earthquake source geometry

Faults may rupture both along their entire length and in smaller individual-section ruptures that are often bounded by changes in fault geometry (DuRoss et al., 2016; Goda et al., 2018; Gómez-Vasconcelos et al., 2018; Hodge et al., 2015; Iezzi et al., 2019; Valentini et al., 2020). Therefore, the basic GIS feature in the SMSSD is a fault section, where individual faults from the SMAFD may be divided into multiple sections by bends in their fault trace (Fig. 2d; DuRoss et al., 2016; Jackson and White, 1989; Wesnousky, 2008; Zhang et al., 1991). Along-strike minima in fault displacement (e.g. scarp or knickpoint height) may also be indicative of segmentation (Willemse, 1997), but these do not always coincide with geometrical complexities in southern Malawi (Fig. 4; Hodge et al., 2018a, 2019; Wedmore et al., 2020a, b). This may indicate that deeper structures, not visible in the surficial fault geometry, are also influencing fault segmentation (Wedmore et al., 2020b). Therefore, where along-strike scarp height measurements exist, these local minima are also used to define fault sections (Figs. 2d, 4).

Faults that are closely spaced across strike but are not physically connected may also rupture together through “soft linkages” (Childs et al., 1995; Wesnousky, 2008; Willemse, 1997; Zhang et al., 1991). In the SMSSD, we follow empirical observations and Coulomb stress modelling that suggests that normal fault earthquakes may rupture across steps whose width is < 20 % of the combined length of the interacting sections, up to a maximum separation of 10 km (Biasi and Wesnousky, 2016; Hodge et al., 2018b), and we use this as a criteria to assign whether two en echelon faults in the SMSSD may rupture together.

A number of geometrical attributes are then assigned to both individual sections and whole faults in the SMSSD (Table 2). Section length (L_sec) is defined as the straight-line distance between section end points (Fig. 4b). This approach avoids the difficulty of measuring the length of fractal features, and it accounts for the hypothesis that small-scale (less than kilometre-scale) variations in fault geometry in southern Malawi may represent only near-surface complexity (depths < 5 km) and that the faults are relatively planar at depth (Hodge et al., 2018a). However, it only provides a minimum estimate of section length. For segmented faults in the SMSSD, fault length (L_fault) is the sum of L_sec, otherwise L_fault is the distance between its tips (Fig. 4b). As each GIS feature in the SMSSD represents a distinct earthquake source, we consider that L_sec and/or L_fault must be > ∼ 5 km, except in the case of linking sections that rupture only in whole-fault ruptures. (Christophersen et al., 2015).

In southern Malawi, fault dip is either unknown or uncertain, because fault planes are rarely exposed, surface processes affect scarp angle (Hodge et al., 2020), and/or dip at depth is not constrained. This difficulty in measuring fault dip is common, and dip has been parameterised using a range of reasonable values in these cases (Christophersen et al., 2015; Langridge et al., 2016; Styron et al., 2020). Thus, we assign minimum, intermediate, and maximum dip values in the SMSSD of 40, 53, and 65^∘ respectively, which encapsulate dip estimates from field data in southern Malawi (Hodge et al., 2018a; Williams et al., 2019), and earthquake focal mechanisms (Biggs et al., 2010; Ebinger et al., 2019), seismic reflection data (Mortimer et al., 2007; Wheeler and Rosendahl, 1994), and aeromagnetic surveys (Kolawole et al., 2018a) elsewhere in Malawi.

It is typically assumed that fault width (W) can be estimated by projecting the difference in lower and upper seismogenic depth into fault dip (δ), with the assumption that faults are equidimensional up to the point where W is limited by the thickness of the seismogenic crust (Christophersen et al., 2015):

$$\begin{array}{}\text{(1)}& W=\left\{\begin{array}{l}{L}_{\text{fault}},\text{where}{L}_{\text{fault}}\le \frac{z}{\sin \mathit{\delta }};\\ \frac{z}{\sin \mathit{\delta }},\text{where}{L}_{\text{fault}}>\frac{z}{\sin \mathit{\delta }}\end{array}\right.\end{array}$$

In southern Malawi, both seismogenic thickness, z (30–35 km; Jackson and Blenkinsop, 1993; Craig et al., 2011), and δ (40–65^∘, as justified above) are poorly constrained, so a range of W values must be considered. Furthermore, ruptures unlimited by z are not necessarily equidimensional (Leonard, 2010; Wesnousky, 2008). Therefore, in the SMSSD, we estimate W from an empirical scaling relationship between fault length and W (Leonard, 2010):

$$\begin{array}{}\text{(2)}& W=C_{\mathrm{1}}{L}_{\text{fault}}^{\mathit{\beta }},\end{array}$$

where L_fault>5 km, and C₁ and β are empirically derived constants that are equal to 17.5 and 0.66 respectively for interplate dip-slip earthquakes (Leonard, 2010). As shown in Fig. 5c, when applying Eq. (2), estimates of W in the SMSSD are consistent with (1) observations of >1 length-to-width ratios for dip-slip earthquakes (Fig. 5c) and (2) the thick seismogenic crust in East Africa (i.e. W∼40 km, Fig. 5c; Craig et al., 2011; Ebinger et al., 2019; Jackson and Blenkinsop, 1993; Lavayssière et al., 2019; Nyblade and Langston, 1995).

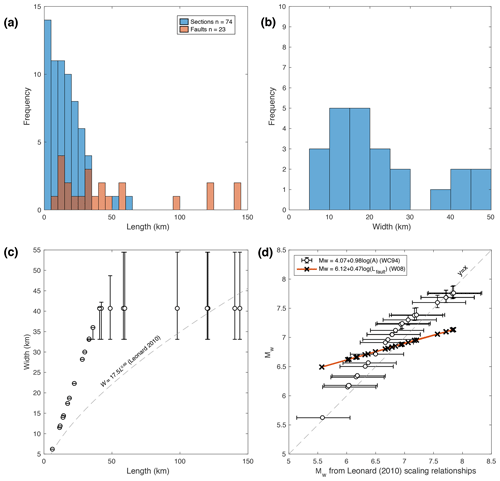
Figure 5 Assessment of fault geometry in the SMSSD. (a) Histograms showing the distribution of (a) fault (L_fault) and section (L_sec) lengths in the SMSSD. (b) Histogram of fault widths in the SMSSD as derived from the Leonard (2010) scaling relationship (Eq. 2); in panel (c), the predicted aspect ratio of faults following this relationship (dashed grey line) in comparison to an alternative method to estimate W using Eq. (1) (white circles). (d) A comparison of empirical scaling relationships used to estimate earthquake magnitudes (M_W) from fault geometry in the SMSSD. Leonard (2010) magnitudes estimated using Eq. (4), with error bars representing range of C₁ and C₂ values derived for interplate dip-slip faults. A is the fault area calculated from L_fault and W using Eq. (1), WC94 is from Wells and Coppersmith (1994), and W08 is from Wesnousky (2008).

4.2 Estimating fault slip rates

For a narrow amagmatic continental rift such as the EARS in southern Malawi, the first step to estimate slip rates is to divide the rift along its axis into its basins (Fig. 2b); within each basin, the mapped faults are then divided into border and intra-basin faults. We define border faults geometrically, as a fault located at the edge of the rift with the implicit assumption that all other mapped active faults are intra-basin faults (Fig. 2d; Ebinger, 1989; Gawthorpe and Leeder, 2000; Muirhead et al., 2019; Wedmore et al., 2020b). These geometric definitions have no direct implications for how displacement is partitioned among border and intra-basin faults.

The slip rate for each fault or fault section i is then estimated using the following equation:

$$\begin{array}{}\text{(3)}& \text{Slip}\text{rate}\left(i\right)=\left\{\begin{array}{l}\frac{{\mathit{\alpha }}_{\text{bf}}v\cos \left(\mathit{\theta }\left(i\right)-\mathit{\varphi }\right)}{n_{\text{bf}}\cos \mathit{\delta }},\text{for border faults}\\ \frac{{\mathit{\alpha }}_{\text{if}}v\cos \left(\mathit{\theta }\left(i\right)-\mathit{\varphi }\right)}{n_{\text{if}}\cos \mathit{\delta }},\text{for intra-basin faults}\end{array}\right.\end{array}$$

Here, θ(i) is the fault or fault section slip azimuth, v and φ are the respective horizontal rift extension rate and azimuth, α is a weighting applied to each fault depending on whether it is a border (α_bf) or intra-basin (α_if) fault, and it is divided by the number of mapped border faults (n_bf) or intra-basin faults (n_if) in each basin (Fig. 6). Although Eq. (3) is specific for rifts, it could be adapted in other tectonic settings where there is an a priori understanding of the rate and distribution of regional strain – for example, to distribute regional strain between the basal detachment and thrust ramps in a fold and thrust belt (Poblet and Lisle, 2011), to distribute regional strain between multiple subparallel faults in a strike-slip system, or to assess more complex strain partitioning between kinematically distinct fault populations in transtensional or transpressional systems (Braun and Beaumont, 1995).

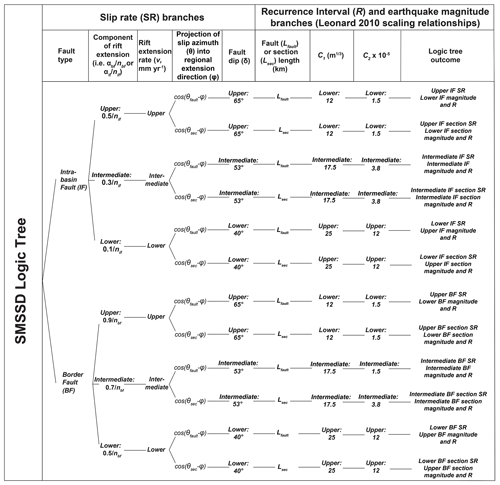
Figure 6 Logic tree for calculating lower, intermediate, and upper estimates of fault slip rates and earthquake magnitudes and recurrence intervals in the SMSSD; α_bf and α_if are the rift extension weighting assigned to border faults (BF) and intra-basin faults (IF) respectively; n_bf and n_if are the number of border or intra-basin faults in a basin respectively; and θ_fault and θ_sec are the respective whole-fault and individual-section slip azimuth values.

The distribution of v between border (α_bf) and intra-basin faults (α_if) in an amagmatic narrow rift depends on factors such as total rift extension (Ebinger, 2005; Muirhead et al., 2016, 2019), rift obliquity (Agostini et al., 2011b), hanging-wall flexure (Muirhead et al., 2016; Shillington et al., 2020), lower crustal rheology (Heimpel and Olson, 1996; Wedmore et al., 2020a), and whether border faults have attained their maximum theoretical displacement (Accardo et al., 2018; Olive et al., 2014; Scholz and Contreras, 1998). In some incipient rifts like southern Malawi, extensional strain is observed to be localised (∼ 80 %–90 %) on its border faults (Muirhead et al., 2019; Wright et al., 2020). Furthermore, evidence from boreholes and topography indicates that border faults in southern Malawi have relatively small throws (< 1000 m, Fig. S1), which combined with its thick seismogenic crust indicates that the flexural extensional strain on its intra-basin faults is likely to be negligible (Billings and Kattenhorn, 2005; Muirhead et al., 2016; Wedmore et al., 2020a). However, detailed analysis of fault scarp heights across the Zomba Graben indicates that ∼ 50 % of extensional strain is currently distributed onto its intra-basin faults (Wedmore et al., 2020a). To account for this uncertainty in the SMSSD, lower, intermediate, and upper estimates of α_bf are set to 0.5, 0.7, and 0.9 respectively (Fig. 6). As ${\mathit{\alpha }}_{\text{if}}=\mathrm{1}-{\mathit{\alpha }}_{\text{bf}}$, respective lower, intermediate, and upper estimates are 0.1, 0.3, and 0.5 (Fig. 6).

Where distinct intra-basin faults kinematically interact across steps, we consider these as one fault in Eq. (3), as this equation accounts for strain across, not along, the rift. For the Mwanza and Nsanje basins, no intra-basin faults are identified (Fig. 2b), so all the extension strain is assigned to their border faults (i.e. α_bf=1). In the case of the Nsanje Basin, however, this is extension is divided into increments of 30 %, 50 %, and 70 % between the Nsanje Fault and a border fault identified 25 km along strike in Mozambique (Fig. S1; Macgregor, 2015) to estimate its lower, intermediate, and upper slip rate.

Table 3 Coordinates from which the Nubia–Rovuma plate motion vector for different basins in southern Malawi was derived (Fig. 1b). The velocity, azimuth, and uncertainties of each vector are also reported given the Nubia–Rovuma Euler poles in Saria et al. (2013) (S13) or in Stamps et al. (2008) (S08; Fig. A1) and where the uncertainties associated with the Euler pole are derived from the methods presented in Robertson et al. (2016). For justification of basin centre locations, see Fig. S1.

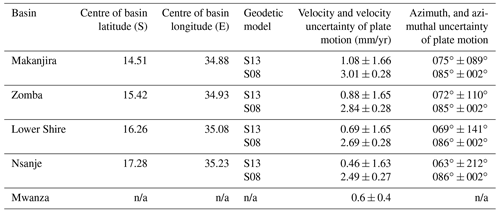
n/a: “not applicable”.

In the SMSSD, the horizontal extension rate, v, is taken from the plate motion vector between the Rovuma and Nubia plates at the centre of each individual basin (Table 3, Figs. 1b, S1) using the Euler poles reported by Saria et al. (2013). We use the Euler pole (as defined by a location and rotation rate) and the uncertainties associated with the Euler pole (defined by an error ellipse; Fig. A1) to calculate the plate motion and the plate motion uncertainty between the Rovuma and Nubia plates for each basin (Table 3, Fig. 1b) following the methods outlined in Robertson et al. (2016). With this approach, the lower bound of v is negative (i.e. the plate motion is contractional; Table 3). However, the topography and seismicity of southern Malawi clearly indicate that it is not a contractional regime nor is it a stable craton. Therefore, a lower bound of 0.2 mm/yr horizontal extension is assigned in the SMSSD, which is considered the minimum strain accrual that is measurable using geodesy (Calais et al., 2016). There are no geodetic constraints for the extension rate across the Mwanza Basin as it lies along the poorly defined Angoni–San plate boundary (Daly et al., 2020). Therefore, we assign this basin an extension rate of 0.2–1 mm/yr. This reflects the smaller escarpment height along its border fault (250 m vs. ∼ 750 m; Fig. 2b) relative to the Lower Shire Basin, which indicates a slower average extension rate over geological time.

The rift extension azimuth (φ) in southern Malawi is derived from a regional focal mechanism stress ($\mathrm{073}{}^{\circ }\pm \mathrm{012}{}^{\circ }$, Fig. 1b; Delvaux and Barth, 2010; Ebinger et al., 2019; Williams et al., 2019), as there is considerable uncertainty in this parameter from geodesy (Table 3; Saria et al., 2013). Faults in southern Malawi are considered to be normal (Delvaux and Barth, 2010; Hodge et al., 2015; Williams et al., 2019). Therefore, the slip azimuth (θ(i)) is the dip direction of each fault or fault section, where it is then projected into φ in Eq. (3). Although this sets up an apparent inconsistency in which variably striking faults accommodate normal dip-slip under a uniform extension direction, this phenomena that can be explained by lateral heterogeneity in the lower crust in southern Malawi (Corti et al., 2013; Philippon et al., 2015; Wedmore et al., 2020a; Williams et al., 2019). To account for the uncertainty in φ, upper and lower extension rates are obtained by varying $\mathit{\phi }\pm \mathrm{012}{}^{\circ }$ depending on the fault's dip direction (e.g. upper slip rate estimates for NE and NW dipping fault are estimated with φ set to 061 and 085^∘ respectively). An example of these slip rate calculations for the central section of the Chingale Step fault is provided in Fig. 7.

4.3 Earthquake magnitudes and recurrence intervals

We estimate earthquake magnitudes in the SMSSD by applying empirically derived scaling relationships between fault length and earthquake magnitude. Scaling relationships between fault length and average single-event displacement ($\stackrel{\mathrm{‾}}{D}$) can then be combined with slip rate estimates to calculate earthquake recurrence intervals (R) through the relationship $R=\stackrel{\mathrm{‾}}{D}$ ∕ slip rate (Wallace, 1970). To select an appropriate set of earthquake-scaling relationships for the SMSSD, we consider three previously reported regressions and apply them to its mapped faults: (1) between normal fault length and M_W (Wesnousky, 2008), (2) interplate dip-slip fault length and M_W (Leonard, 2010), and (3) fault area and M_W (Wells and Coppersmith, 1994) where A is calculated using W derived from Eq. (1).

We find that although generally comparable for M_W<7.5, the Wells and Coppersmith (1994) regression overestimates magnitudes relative to Leonard (2010) (Fig. 5d). This likely reflects the discrepancy in W between applying Eq. (1) and the Leonard (2010) regression (Eq. 2; Fig. 5c; Sect. 4.1). The Wesnousky (2008) regression overestimates magnitudes for M_W<6.9 relative to Leonard (2010) equations and underestimates them at larger magnitudes (Fig. 5d). This may reflect that the Wesnousky (2008) regression is derived from only six events, and these events show a poor correlation between length and M_W (Pearson's regression coefficient = 0.36). Given these considerations, the Leonard (2010) regressions are used in the SMSSD. Furthermore, these regressions are used to estimate W (Sect. 4.1) and are self-consistent when estimating M_W and $\stackrel{\mathrm{‾}}{D}$ from L_fault, which is not necessarily true for the other cases.

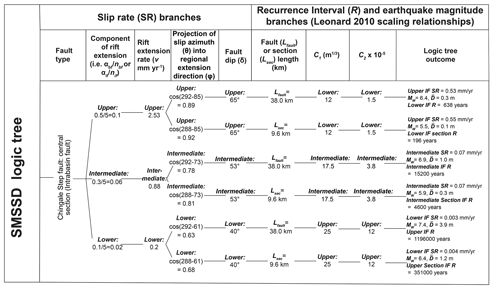
Figure 7 Example of the calculations in the SMSSD logic tree (Fig. 6), performed for the central section of the Chingale Step Fault (Fig. 4b). This is an intra-basin fault in the Zomba Graben, where the number of intra-basin faults (n_if) is five. A multiparameter sensitivity analysis for these calculations is documented in Appendix A.

Thus, M_W and $\stackrel{\mathrm{‾}}{D}$ are estimated in the SMSSD by

$$\begin{array}{}\text{(4)}& {\displaystyle }\begin{array}{rl}& M_{\text{W}}\left(i\right)=\\ & \left\{\begin{array}{l}\frac{\left(\frac{\mathrm{5}}{\mathrm{2}}\log L_{\text{sec}}+\frac{\mathrm{3}}{\mathrm{2}}\log C_{\mathrm{1}}+\log C_{\mathrm{2}}\mathit{\mu }\right)-\mathrm{9.09}}{\mathrm{1.5}}\mathrm{\text{for individual-section ruptures and}}\\ \frac{\left(\frac{\mathrm{5}}{\mathrm{2}}\log L_{\text{fault}}+\frac{\mathrm{3}}{\mathrm{2}}\log C_{\mathrm{1}}+\log C_{\mathrm{2}}\mathit{\mu }\right)-\mathrm{9.09}}{\mathrm{1.5}}\mathrm{\text{for whole-fault ruptures, and}}\end{array}\right.\end{array}\text{(5)}& {\displaystyle }\begin{array}{rl}& \log \stackrel{\mathrm{‾}}{D}\left(i\right)=\\ & \left\{\begin{array}{l}\frac{\mathrm{5}}{\mathrm{6}}\log L_{\text{sec}}+\frac{\mathrm{1}}{\mathrm{2}}\log C_{\mathrm{1}}+\log C_{\mathrm{2}}\mathit{\mu }\mathrm{\text{for individual-section ruptures and}}\\ \frac{\mathrm{5}}{\mathrm{6}}\log L_{\text{fault}}+\frac{\mathrm{1}}{\mathrm{2}}\log C_{\mathrm{1}}+\log C_{\mathrm{2}}\mathit{\mu }\mathrm{\text{for whole-fault ruptures,}}\end{array}\right.\end{array}\end{array}$$

where μ is the shear modulus (3.3×10¹⁰ Pa), C₁ is as defined for Eq. (2), and C₂ is another constant derived by Leonard (2010). Both constants are varied between the full range of values derived in a least square analysis (Leonard, 2010) to obtain lower, intermediate, and upper estimates of M_W and $\stackrel{\mathrm{‾}}{D}$ (Figs. 6, 7). Following Eq. (5), recurrence intervals R(i) can be calculated as follows:

$$\begin{array}{}\text{(6)}& R\left(i\right)={\displaystyle \frac{\stackrel{\mathrm{‾}}{D}\left(i\right)}{\text{Slip rate}\left(i\right)}},\end{array}$$

where upper estimates of R are calculated by dividing the upper estimate of $\stackrel{\mathrm{‾}}{D}$ by the lowest estimate of fault or section slip rate and vice versa (Fig. 6). An example of these earthquake source calculations for the central section of the Chingale Step fault is provided in Fig. 7.

5 Key features of the SMAFD and SMSSD

In this section, we briefly describe the fault mapping collated in the SMAFD and then the present fault slip rates, earthquake magnitudes, and recurrence intervals in the SMSSD as estimated by our systems-based approach.

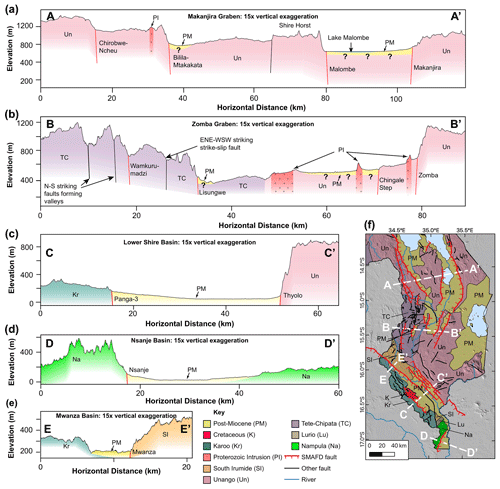
Figure 8 (a–e) Cross sections through each basin in southern Malawi. Topography from the TanDEM-X 12 m digital elevation model (DEM) except for panel (d) which is from the SRTM 30 m DEM. Tectonic terranes are from Fullgraf et al. (2017), except for Proterozoic intrusions (Bloomfield, 1965; Walshaw, 1965). All normal faults in cross sections inferred to dip at 60^∘. Post-Miocene deposits in panels (a) and (b) are shown to be 50–100 m thick, as estimated by borehole data (Fig. S1). (f) A simplified geological map for southern Malawi showing extent of cross sections that is underlain by the SRTM 30 m DEM.

5.1 Border and intra-basin faults in southern Malawi

The SMAFD contains 23 active faults across five EARS basins. The northernmost faults lie in the NW–SE trending Makanjira Graben, a full graben where two border faults, the Makanjira and Chirobwe–Ncheu, clearly define either side of the rift (Fig. 8a). Four intra-basin faults are identified, with, two of them, the Bilila–Mtakataka and Malombe faults, exhibiting steep scarps (Hodge et al., 2018a, 2019). In particular, one-dimensional diffusional models of scarp degradation suggest that the Bilila–Mtakataka Fault scarp formed within the past 10 000 years (Hodge et al., 2020). The Malombe Fault forms a ∼ 500 m high escarpment that bounds the Shire Horst and divides post-Miocene deposits in the Makanjira Graben across strike (Fig. 8a; Hodge et al., 2019; Laõ-Dávila et al., 2015).

Along strike to the south, the NNE–SSW trending Zomba Graben contains a prominent border fault, the Zomba Fault, on its eastern edge, and three well-defined intra-basin fault scarps in its interior (Fig. 8b; Bloomfield, 1965; Wedmore et al., 2020a). The western edge of the Zomba Graben grades onto the Kirk Plateau where there are several deeply incised N–S trending valleys that have been previously mapped as “rift valley faults” (Fig. 8b; Bloomfield and Garson, 1965). However, only one of these faults has an active scarp and accumulated post-Miocene sediments (the Lisungwe Fault; Wedmore et al., 2020a). In addition, the Wamkurumadzi Fault, which lies to the west of the Lisungwe, is also included in the SMAFD – albeit with low confidence – as evidence of recent activity is noted by Bloomfield and Garson (1965), and any recent sediments may have been eroded by the Wamkurumadzi River that flows along its base. Given the complex topography and ambiguity on fault activity, we tentatively interpret these faults as intra-basin faults in the SMSSD and note that the western Zomba Graben should be a priority area for future fault mapping.

The floor of the NW–SE trending Lower Shire Basin lies at an elevation 350 m lower than the floor of the Zomba Graben. Between these two EARS sections basement is exposed, and there is no evidence of tectonic activity that falls within the SMAFD definition of an active fault. Gravity surveys and topographic data indicate that the Lower Shire Basin exhibits a half-graben structure, with the Thyolo Fault bounding it to the northeast (Fig. 8d; Chisenga et al., 2019; Wedmore et al., 2020b). A number of intra-basin faults have been identified in the hanging wall of the Thyolo Fault (Chisenga et al., 2019), although none are identified in the Nsanje and Mwanza basins (Fig. 8d, e).

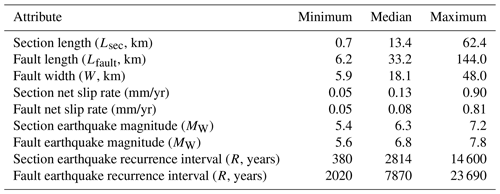
Table 4 Range of selected numeric attributes across all faults and sections in the SMSSD. To demonstrate how calculated attributes vary across different faults in the SMSSD, as opposed to variation from the set of parameters used to calculate them, the values shown are for the intermediate branches in the SMSSD logic tree (Fig. 6).

5.2 Fault slip rates, and earthquake magnitudes and recurrence intervals in the SMSSD

By implementing a logic tree approach to assess uncertainty in the SMSSD, three values (lower, intermediate, and upper) are derived for each calculated attribute (Table 2, Fig. 6). However, it is implicit that the upper and lower values have a low probability as they require a unique, and possibly unrealistic, combination of parameters. Therefore, we primarily report values obtained from applying the intermediate branches in the logic tree but discuss the uncertainties in Sect. 5.4.

Although the SMAFD contains 23 active faults, these are further subdivided into 74 sections in the SMSSD – of which 13 are linking sections. Section lengths (L_sec) range between 0.7 and 62 km, whereas fault lengths (L_fault) vary from 6.2 to 144 km (Fig. 5a, Table 4). The highest slip rates are estimated to be on the Thyolo and Zomba faults (intermediate estimates of 0.6–0.8 mm/yr). On intra-basin faults in the SMSSD, intermediate slip rate estimates are 0.05–0.1 mm/yr (Fig. 9). Slip rates tend to be relatively fast in the Makanjira Graben (Fig. 9c), as the extension rate is higher (Table 3), and its NNW–SSE striking faults are more optimally oriented to the regional extension direction (Fig. 2). The difference between upper and lower slip rate estimates in the SMSSD logic tree is 2 orders of magnitude: ∼ 0.05–5 mm/yr for the border faults and ∼ 0.005–0.5 mm/yr on the intra-basin faults (Fig. 9).

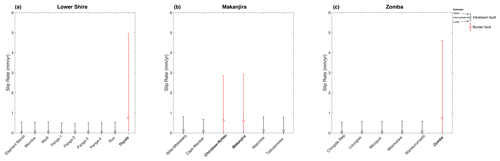
Figure 9 Fault slip rate estimates in the SMSSD, calculated following the approach outlined in Fig. 6 and sorted into different basins in southern Malawi.

For whole-fault ruptures along border faults, intermediate estimates of earthquake recurrence intervals (R) are between 2000 and 5000 years, whereas they are between 10 000 and 30 000 years for intra-basin whole-fault ruptures (Fig. 10a–c). Considerable uncertainty exists in these values, with the upper and lower estimates for R varying from 10² to 10⁵ years and from ∼ 10³ to 10⁶ years for border and intra-basin whole-fault ruptures respectively (Fig. 10a–c). Furthermore, if these faults rupture in individual sections, R may be reduced by up to an order of magnitude (Fig. 10d–f). Intermediate estimates of earthquake magnitudes range from M_W 5.4 to M_W 7.2 for individual-section ruptures and from M_W 5.6 to M_W 7.8 for faults that rupture their entire length (Table 4, Fig. 11b). The SMSSD also includes one example where multiple en echelon faults, the Panga Fault system (Fig. 2d), could rupture together given the constraints outlined in Sect. 4.1.

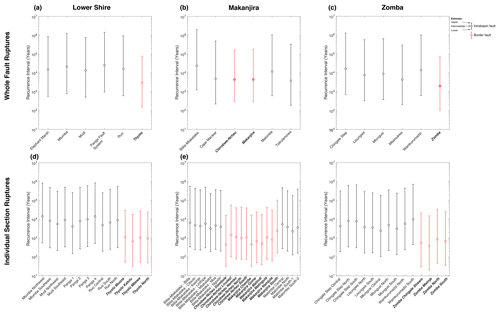
Figure 10 Recurrence interval (R) estimates in the SMSSD for (a–c) whole-fault ruptures and (d–f) individual-section ruptures. Note, R estimates for each Panga Fault are included in panel (d), and a multi-fault rupture is shown in panel (a).

Table 5 Parameters and their associated upper and lower levels used in the sensitivity analysis for recurrence interval (R) calculations for the Chingale Step fault central section using the Stamps et al. (2008) (S08) and Saria et al. (2013) (S13) Nubia–Rovuma Euler poles (Fig. A1). The main effect of each parameter (A) for each geodetic model is then also reported. See Appendix A for full details of this analysis.

5.3 Robustness of fault slip rate estimates

It is possible that slip rate estimates in the SMSSD are effectively upper bounds, as some proportion of the geodetically derived rift extension may be accommodated by aseismic creep or along unrecognised faults. With regards to aseismic creep, the discrepancy between geodetic and seismic moment rates in Malawi implies that its faults are strongly coupled (Ebinger et al., 2019; Hodge et al., 2015). This is also consistent with the velocity-weakening behaviour of some samples from the rift in deformation experiments at lower crustal pressure–temperature conditions (Hellebrekers et al., 2019).

Conversely, the possible inclusion of inactive faults in the SMAFD and SMSSD would mean that individual fault slip rates may be lower bounds. Without paleoseismic investigations and dating of offset surfaces in southern Malawi, it is difficult to test this point. Nevertheless, reactivation analysis that encompasses the range of fault orientations in southern Malawi indicates that these faults are favourably oriented in the current stress field (Williams et al., 2019). Therefore, even faults that have been inactive for a considerable time (up to the entire age of the EARS) could still theoretically be reactivated. We also note that slip rates of intra-basin faults in the North Basin of Lake Malawi over the last 75 ka (0.15–0.7 mm/yr; Shillington et al., 2020) are within the range of estimates of intra-basin faults in the SMSSD (Fig. 9).

5.4 Sensitivity analysis

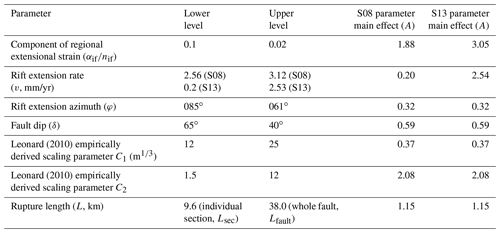
Upper and lower estimates of R differ by up to 3 orders of magnitude in the SMSSD (Fig. 10). To investigate these uncertainties, we performed a multiparameter sensitivity analysis following the methods presented in Box et al. (1978) and Rabinowitz and Steinberg (1991). Full details of this analysis are given in Appendix A. In summary, seven parameters that contribute to uncertainty in R for the central section of the Chingale Step fault are considered (Table 5). By exploring all possible combinations in which these seven parameters are set at their upper or lower estimates, 128 (i.e. 2⁷) different values of R can be calculated. However, we instead considered 64 parameter combinations that were chosen following a fractional factorial design (Table S1; Box et al., 1978). In this way, parameter combinations that offer little insight into how a system works are omitted, thereby increasing the efficiency of this analysis at minimal cost to its validity (Rabinowitz and Steinberg, 1991). From these combinations, the natural log of the average value of R when a parameter (k) is set at its upper ($\stackrel{\mathrm{‾}}{\ln R}(k+)$) and lower ($\stackrel{\mathrm{‾}}{\ln R}(k-$)) value is calculated and the difference between these values defines the parameter effect (A; Rabinowitz and Steinberg, 1991):

$$\begin{array}{}\text{(7)}& A=\stackrel{\mathrm{‾}}{\ln R}\left(k+\right)-\stackrel{\mathrm{‾}}{\ln R}\left(k-\right)\end{array}$$

This analysis indicates that R is most sensitive to uncertainties in the partitioning of strain between border and intra-basin faults in the rift (i.e. α_if∕n_if), the rift extension rate (v), and the C₂ parameter in Eq. (5), and it is least sensitive to uncertainties in the rift's extension azimuth and the C₁ parameter in Eq. (5) (Table 5). If, however, v and its associated uncertainties were estimated using a different Nubia–Rovuma Euler pole solution (Fig. A1; Table 3; Stamps et al., 2008), R estimates are least sensitive to v and most sensitive to C₂ (Table 5). There are no interaction effects between two separate parameters that may influence their effect on R (Table S2).

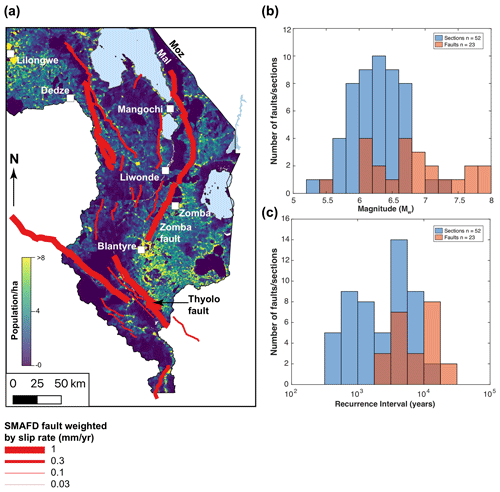
Figure 11 (a) Faults in the SMAFD with lines weighted by intermediate estimates of fault slip rate in the SMSSD. The fault map is underlain by population density, where the pixel size is 3 arcsec (approximately 1 ha), as derived from WorldPop predicted 2020 datasets for Malawi (WorldPop, 2018) with major population centres also highlighted. Note that the population density in these places may exceed 100 people per hectare. The area shown is the same as in Fig. 2. Histograms show the range of (b) earthquake magnitudes and (c) recurrence interval estimates in the SMSSD from intermediate branches in Fig. 6.

6 Discussion

6.1 Implications for seismic hazard in southern Malawi

The existence of active faults within southern Malawi poses a significant risk to the 7.75 million people living in this region (Malawi National Statistics Office, 2018) as well as those living adjacent to the rift in northern Mozambique (Fig. 11a). Furthermore, with population growth at an annual rate of 2.7 % in southern Malawi (Malawi National Statistics Office, 2018), this risk will increase over the coming decades. The rapidly growing city of Blantyre (population of 800 000; Malawi National Statistics Office, 2018), which is in the footwall of both the relatively fast slipping (intermediate estimates ∼ 0.8 mm/yr) Zomba and Thyolo faults is at a particularly high risk (Fig. 11a).

Intermediate estimates in the SMSSD for M_W 5.4–7.8 earthquakes and fault recurrence intervals (R) of 10³–10⁴ years (Fig. 11) imply that southern Malawi's seismic hazard is characterised by infrequent large-magnitude events. Indeed, faults in this region may host earthquakes comparable to the largest historical continental normal fault earthquakes (∼ M_W 7.5; Valentini et al., 2020); although relatively rare, >150 km long normal faults have been mapped elsewhere, and these would be capable of even larger events (Styron and Pagani, 2020).

6.2 Improving earthquake source estimates in the SMSSD

One of the purposes of collating the SMSSD was to identify current knowledge gaps in our understanding of active faulting and seismic hazard in southern Malawi. Our sensitivity analysis (Sect. 5.4) indicates that the two biggest factors contributing to uncertainty in R in the SMSSD is related to our understanding of the distribution and rate of extension (v) in southern Malawi (Table 5). In particular, there is considerable uncertainty in the position of the Nubia–Rovuma Euler pole (Fig. A1; Saria et al., 2013), and we would not expect such large differences between upper and lower fault slip rate estimates by following our systems-based approach elsewhere. Although the uncertainties associated with v in the SMSSD could be reduced if an alternative solution for the Nubia–Rovuma Euler pole was applied (Fig. A1, Tables 5, S2; Stamps et al., 2008), this solution uses fewer Global Positioning System (GPS) sites and a shorter position time series (Saria et al., 2013). Therefore, in the short term, the best refinements to R estimates may come from new regional geodetic data and further high-resolution topographic analysis (e.g. Daly et al., 2020; Stamps et al., 2020; Wedmore et al., 2020a).

Directly measuring on-fault slip rates and paleoseismicity would provide more robust R estimates than the model-derived estimates in SMSSD. However, careful site selection would be required for these analyses in southern Malawi because of its potential for large (∼ 10 m) single-event displacements (Hodge et al., 2020). Furthermore, these investigations carry large inherent uncertainties in low-strain-rate regions like southern Malawi if only a few earthquakes are sampled, as these events may be temporally clustered (Nicol et al., 2006, 2016b; Pérouse and Wernicke, 2017; Taylor-Silva et al., 2020).

When considering how different rupture magnitude estimates in the SMSSD influence R, the main source of uncertainty is the C₂ parameter from the Leonard (2010) regressions (Table 5). This factor controls the amount of displacement for a given rupture area (Leonard, 2010). It is therefore likely related to earthquake stress drops, and uncertainty in C₂ in southern Malawi will only be reduced by recording more events here or in similar tectonic environments – i.e. normal fault earthquakes in regions with low (∼ 1–10 mm/yr) extension rates and thick (20–35 km) seismogenic crust.

7 Incorporation of the SMSSD into probabilistic seismic hazard analysis

The SMSSD contains the attributes (earthquake magnitudes and R estimates) that allow it to be used as a source model for future PSHA in southern Malawi. However, in common with other low-strain-rate regions with limited paleoseismic information (e.g. Cox et al., 2012; Villamor et al., 2018), there are various aleatory (i.e. the uncertainty related to unpredictable nature of future event) and epistemic (i.e. the uncertainty due to incomplete knowledge and data) uncertainties. Firstly, as noted in Sect. 5.2, it is unrealistic that the intermediate, lower, and upper value of each attribute in the SMSSD logic tree has an equal probability (Fig. 6). This could be formalised by treating these attributes as continuous variables and assigning probability distribution functions to them.

Implicit in the R estimates in the SMSSD is that each earthquake source can only host events of two sizes: “individual sections” and “whole faults”. Therefore, it does not consider multi-segment ruptures that do not rupture the entire fault. Although not strictly the same, the SMSSD therefore follows many aspects of the characteristic earthquake model (i.e. each earthquake source only hosts event of one size) whose applicability remains contentious (Kagan et al., 2012; Page and Felzer, 2015; Stirling and Gerstenberger, 2018). An alternative approach to model R in southern Malawi would be to allow each fault to host a range of earthquake sizes that follow a frequency–magnitude distribution that is consistent with its moment rate (Youngs and Coppersmith, 1985), with this moment rate derived from the instrumental record and data incorporated into the SMSSD.

Finally, there are likely active faults in Malawi that are not included in the SMAFD and SMSSD. Thus, we recommend that future PSHA in southern Malawi should also consider “off-fault” areal seismic sources by using the instrumental record (e.g. Field et al., 2014; Gerstenberger et al., 2020; Hodge et al., 2015; Morell et al., 2020; Stirling et al., 2012). Many of the challenges discussed above can be addressed through the creation of synthetic seismic catalogues, which are then used as a PSHA source (Hodge et al., 2015).

8 Conclusions

We describe a new systems-based approach that combines geologic and geodetic data to estimate fault slip rates and earthquake recurrence intervals in regions with little historical or paleoseismic earthquake data. This approach is used to develop the South Malawi Active Fault Database (SMAFD) and South Malawi Seismogenic Source Database (SMSSD), geospatial databases designed to direct future research and aid seismic hazard analysis and planning.

In the SMAFD, we document 23 active faults that have accumulated displacement during East African rifting in southern Malawi. In the SMSSD, fault slip rates, earthquake magnitudes, and recurrence intervals are estimated for the active faults compiled in the SMAFD. The SMSSD indicates the potential for M_W 6.5–7.8 earthquakes throughout southern Malawi. However, slow geodetically derived extension rates (∼ 1 mm/yr) imply low fault slip rates (0.001–5 mm/yr), and so the recurrence intervals of M_W>7 events are estimated to be 10²–10⁶ years. The large range of these estimated recurrence times reflects aleatory uncertainty on fault rupture scenarios and epistemic uncertainties in fault-scaling relationships, fault slip rates, and fault geometry. Sensitivity analysis suggests the biggest reduction in uncertainties would come from improved knowledge of fault slip rates through paleoseismic investigations or geodetic studies. Nevertheless, the combination of long, highly coupled, low-slip-rate faults and a short (< 65 years) instrumental record imply that the SMAFD and SMSSD are important sources of information for future seismic hazard analyses in the region. In this respect, the development of SMSSD is timely as the seismic risk of southern Malawi is growing due to rapid population growth, urbanisation, and seismically vulnerable building stock. Similar challenges exist elsewhere along the EARS, which may also be partially addressed by following the framework provided by the SMAFD and SMSSD.

Appendix A: A multiparameter sensitivity analysis for recurrence interval estimates in the South Malawi Active Fault Database

Recurrence interval estimates in the South Malawi Seismogenic Database (SMSSD) vary by over 3 orders of magnitude (Fig. 10). These uncertainties are not unexpected in a region like Malawi with no paleoseismic data and an incomplete instrumental seismic record (Cox et al., 2012; Villamor et al., 2018), and they can be accounted for in probabilistic seismic hazard analysis (PSHA) using synthetic seismicity catalogues (Hodge et al., 2015). Nevertheless, by conducting a sensitivity analysis on the logic tree approach used to calculate these recurrence intervals (Fig. 6), it is possible to determine which parameters contribute most to this uncertainty and, in turn, guide future research directions that will help constrain them in future iterations of the SMSSD. This analysis is briefly described in the main text (Sect. 5.4, Table 5) and is documented fully below.

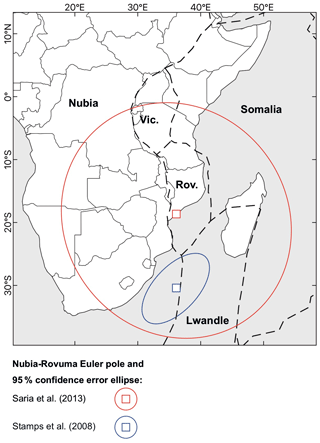
Figure A1 Plate boundaries in East Africa with location and uncertainty of the Nubia–Rovuma Euler pole derived by Saria et al. (2013) and Stamps et al. (2008). “Vic.” denotes Victoria, and “Rov.” denotes Rovuma. Modified after Saria et al. (2013).

Here, we follow the multiparameter sensitivity analysis presented by Rabinowitz and Steinberg (1991). This study conducted sensitivity analysis for the parameters that feed into PSHA, where the output metric is the probability of exceedance of a given level of ground shaken. For the SMSSD, we adapt this method to test the sensitivity of seven parameters that are used to calculate earthquake recurrence intervals (R; Eq. A1; Table 5). This metric is chosen as it fully incorporates the aleatory uncertainties in rupture length as well as epistemic uncertainties in fault slip rates and the Leonard (2010) scaling relationships (Fig. 6). This analysis is performed for the Chingale Step fault central section (Fig. 4), where like all intra-basin faults in the SMSSD, R is calculated by

$$\begin{array}{}\text{(A1)}& R={\displaystyle \frac{\left(\frac{\mathrm{5}}{\mathrm{6}}\log L+\frac{\mathrm{1}}{\mathrm{2}}\log C_{\mathrm{1}}+\log C_{\mathrm{2}}\right)\left(n_{\text{if}}\cos \mathit{\delta }\right)}{{\mathit{\alpha }}_{\text{if}}v\cos \left(\mathit{\theta }-\mathit{\varphi }\right)}}\end{array}$$

Here, L is rupture length and depends on whether an individual-section (L_sec) or whole-fault (L_fault) rupture is considered, C₁ and C₂ are empirically derived constants from Leonard (2010), δ is fault dip, θ is the fault slip azimuth, v and φ are the rift extension rate and azimuth respectively, α_if is a weighting of rift extension for intra-basin faults, and n_if is the number of mapped intra-basin faults (n_if) in the basin.

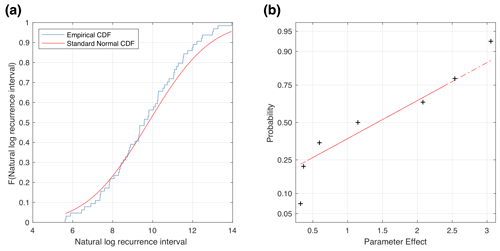
Figure A2 (a) Cumulative distribution function (CDF) of the natural log of the recurrence intervals calculated for the Chingale Step fault central section using the various parameter combinations listed in Table S1 (blue line). This CDF is compared to a standard normal CDF (red line) with the same mean value and standard deviation as the values in Table S1. (b) A normal probability plot of the parameter effects assessed in the sensitivity analysis and reported in Table 5. The most important effects are those that plot above a standard normal distribution (red line). The line is solid when within the first and third quartiles of data and is dashed when outside of this region.

Equation (A1) is essentially a combination of Eqs. (3), (5), and (6) in the main text, and its application with the SMSSD logic tree to calculate R for the Chingale Step fault central section is shown in Fig. 7. There are five intra-basin faults in the Zomba Graben where the Chingale Step fault is situated (Fig. 2), and this parameter is not treated as an uncertainty in this analysis. However, for simplicity, it is combined with α_if to give the “component of rift extensional strain” parameter, which is defined by α_if∕n_if (Table 5). Assuming that the Chingale Step fault is a normal fault (Wedmore et al., 2020a; Williams et al., 2019), θ is the fault dip direction, and differs by only 4^∘ depending on whether the whole fault ruptures or just the central section (Fig. 7). Hence, uncertainty in this parameter is not considered here, and it is set at 290^∘, which is the average value for these two rupture scenarios. When assessing the influence of v, we consider two geodetic models (Fig. A1; Saria et al., 2013; Stamps et al., 2008) and perform this sensitivity analysis for both.

The method presented by Rabinowitz and Steinberg (1991) involves a two-level fractional factorial multiparameter design, where each parameter is restricted to the two levels which will give lower or upper estimates of R (Table 5). Ideally, these levels would be symmetric about the intermediate case; however, in the SMSSD this is not possible for the v, L, and C₂. Compared with a “one-at-a-time (OAT)” parameter analysis, a multiparameter analysis allows us to assess how different parameters interact with each other and, thus, more fully explore the parameter space (Rabinowitz and Steinberg, 1991). This is achieved through a factorial design, which for the seven parameters (k) tested here would generate 128 (i.e. 2⁷) possible combinations in a full two-level factorial approach. However, in a fractional factorial design, just a subset of these combinations is assessed. This approach recognises that many of the combinations in a full factorial design offer little insight into how a system works and that this can instead be achieved at minimal cost to the results by considering a carefully selected subset of these combinations (Box et al., 1978; Rabinowitz and Steinberg, 1991). In this analysis, 2^k−p combinations are assessed, where p is the number of generators and is set at one. This results in the assessment of 64 combinations (Table S1) and a “resolution” of five, which means it is possible to estimate the main effects of each parameter (Eq. A2), interactions between two parameters (Eq. A3), but not interactions between three parameters (Box et al., 1978).

The main effect (A) of one parameter (e.g. fault dip, δ) is quantified from the difference between the average of the natural log of recurrence interval ($\stackrel{\mathrm{‾}}{\ln R}$) for the 32 combinations in Table S1 when a parameter was at its upper level (i.e. $\mathit{\delta }+=\mathrm{40}{}^{\circ }$) and $\stackrel{\mathrm{‾}}{\ln R}$ for the 32 combinations when the parameter was at its low level (i.e. $\mathit{\delta }-=\mathrm{65}{}^{\circ }$):

$$\begin{array}{}\text{(A2)}& A=\stackrel{\mathrm{‾}}{\ln R}\left(\mathit{\delta }+\right)-\stackrel{\mathrm{‾}}{\ln R}\left(\mathit{\delta }-\right)\end{array}$$

By applying a multiparameter approach it is also possible to quantify the parameter–parameter interaction effects – for example, if the effect of δ depends on the choice of rift extension azimuth (φ). To do this, the results in Table S1 can be divided into two sets with 2${}^{k-p-\mathrm{1}}$ combinations each depending on which level of δ was applied. Following the table designs developed by Box et al. (1978), each set of 32 combinations will have 16 combinations when φ was at is upper level (φ+) and 16 combinations when φ was at its lower level (φ−). The effect of δ on each level of φ (i.e. δφ) is then calculated from the corresponding differences in $\stackrel{\mathrm{‾}}{\ln R}$ (Rabinowitz and Steinberg, 1991):

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}& \mathit{\delta }\mathit{\varphi }=\left(\stackrel{\mathrm{‾}}{\ln R}\left(\mathit{\delta }+\mathit{\varphi }+\right)-\stackrel{\mathrm{‾}}{\ln R}\left(\mathit{\delta }-\mathit{\varphi }+\right)\right)\\ & -\left(\ln \stackrel{\mathrm{‾}}{R}\left(\mathit{\delta }+\mathit{\varphi }-\right)-\stackrel{\mathrm{‾}}{\ln R}\left(\mathit{\delta }-\mathit{\varphi }-\right)\right)\end{array}\end{array}$$

If there is no interaction effect between these two parameters, δφ is zero; otherwise, the size of the effect is proportional to the magnitude of δφ. In addition, we demonstrate our results in terms of an empirical cumulative distribution function for the values of lnR reported in Table 1 (Fig. A2a) and, following Rabinowitz and Steinberg (1991), values of A in a normal probability plot (Fig. A2b).

If the Saria et al. (2013) model is used to provide estimates of v in this sensitivity analysis, the parameter that contributes most to uncertainties of R in the SMSSD is the component of regional extensional strain that each fault accommodates (A=3.05, Table 5). This essentially means that lnR is higher by 3.05 when this component is set at its high value compared with its lower value, or, in other words, that R is ∼ 21 times (e^3.05) higher when 10 % of regional extensional strain is assigned to the Chingale Step fault as opposed to 2 %. The importance of this parameter is also demonstrated by the fact that it does not plot close to the normal distribution line in Fig. A2b. The parameters with the next highest main effect on R are v and C₂, whereas estimates of R are least sensitive to uncertainties in φ (Table 5). If, however, estimates of v are provided by the Stamps et al. (2008) model (Fig. A1), estimates of R are considerably less sensitive to uncertainties in rift extension rates, and the C₂ parameter has the biggest influence on R (Table 5). Multiparameter effects are all equal to zero (Table S2) regardless of geodetic model; thus, the sensitivity of each of these parameters is independent of changes in other parameters.

The results of the sensitivity analysis reported here are specific to estimates of R for the Chingale Step fault central section; however, results should be broadly applicable to all other faults in the SMSSD, as R was calculated following the same steps. Nevertheless, there will be differences for faults that are not segmented (where L is not an uncertainty) or that have more than the three sections mapped along the Chingale Step fault (e.g. the seven-section Bilila–Mtakataka Fault). The uncertainty in the weighting of rift extension may also be different for border faults, as the weighting factor (α_bf) is varied between 0.5 and 0.9 in these cases. The results of this analysis are discussed further in Sect. 5.4 and 6.2 in the main text.