The Subhercynian Basin: an example of an intraplate foreland basin due to a broken plate

The Late Cretaceous intraplate shortening event in central western Europe is associated with a number of marine basins of relatively high amplitude and short wavelength (2–3 km depth and 20–100 km width). In particular, the Harz Mountains, a basement uplift on a single, relatively steeply dipping basement thrust, have filled the adjacent Subhercynian Cretaceous Basin with their erosive product, proving that the two were related and synchronous. The problem of generating subsidence of this general style and geometry in an intraplate setting is dealt with here by using an elastic flexural model conditioned to take account of basement thrusts as weak zones in the lithosphere. Using a relatively simple configuration of this kind, we reproduce many of the basic features of the Subhercynian Cretaceous Basin and related basement thrusts. As a result, we suggest that overall, it shares many characteristics with larger-scale foreland basins associated with collisional orogens on plate boundaries.

1 Introduction

The Subhercynian Cretaceous Basin (SCB) is a narrow (∼ 20 km) but relatively thick (∼ 2500 m at its depocentre), mostly shallow marine trough with a WNW–ESE-oriented subsidence axis extending ∼ 90 km along the northern edge of the Harz Mountains in central Germany (von Eynatten et al., 2008; Voigt et al., 2008). It is bounded on its southern margin by the Harz Northern Boundary Fault (HNBF) and partly to the north by a series of three anticlines (Huy, Fallstein, Hakel), and it also contains a number of syn-depositional structures (Figs. 1, 2). The HNBF is a WNW–ESE-trending basement thrust that offsets a “Variscan” basement (Devonian to Carboniferous metasedimentary rocks with some granitic intrusions deformed by the Variscan orogeny) and its Late Paleozic and Mesozoic cover along a ∼ 100 km long zone. A further basement uplift, the Flechtingen high, occurs some 70 km north of the HNBF (Figs. 1, 2, 3).

The main phase of Harz Mountains uplift had been considered a well-constrained Late Cretaceous (Santonian–Campanian) event based on biostratigraphy of their eroded product captured by the basin infill (Voigt et al., 2006; von Eynatten et al., 2008). A more recent multi-method thermochronological analysis (von Eynatten et al., 2019) using zircon and apatite fission-track as well as (U–Th) $/$ He methods yields a slightly broader age spectrum for Harz exhumation (90–60 Ma), with the earliest age corresponding to initial uplift with little erosion, a main pulse of thrusting and basin filling between 86 and 82 Ma, and a further erosion of up to 4 km of material stretching into the early Cenozoic.

The Harz uplift forms part of a much wider Late Cretaceous deformation event extending across central western Europe from the North Sea in the west to the Mid-Polish Swell in the east (Kley and Voigt, 2008; Krzywiec, 2002; Voigt, 1963; Voigt et al., 2008; Scheck et al., 2002). Late Cretaceous depocentres are associated with various basement thrusts forming parts of this system (Fig. 1), such as the Osning fault (Voigt et al., 2008), a south-directed basement thrust overriding the Munsterland basin, the Lausitz anticline, which overthrusts both the Saxony–Bohemian Cretaceous Basin and the Northern Sudetic Cretaceous Basin (Voigt, 2009), and the basins adjacent to the Mid-Polish Swell (Krzywiec, 2002).

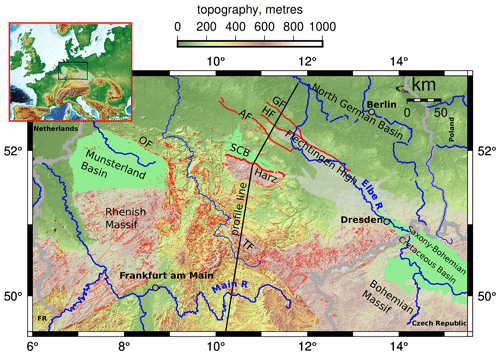
Figure 1 Overview of Late Cretaceous basins in central western Europe and associated basement structures and massifs. The line of cross section from Fig. 3a is shown. The inset shows the figure location (black square). Abbreviations: OF – Osning Fault; GF – Gardelegen Fault; HF Haldensleben Fault; AF – Allertal Fault; TF – Thuringian Forest. Topography is from EU-DEM v1.0 (Mouratidis and Ampatzidis, 2019). Faults are from GÜK200 (Zitzmann, 2003), and Malz et al. (2020).

An often overlooked aspect of these basins is the mechanism by which they are able to subside and accumulate large thicknesses of marine sediments in intraplate, compressional settings. In particular, the SCB has a depocentre directly adjacent to the Harz Northern Boundary Fault (HNBF), and despite being syn-tectonically folded, the Late Cretaceous infill is clearly asymmetrically distributed, with its maximum sedimentary thickness along the HNBF, wedging out to the north over a minimum of 25 km distance (Fig. 2). In this way, the basin geometry resembles a foreland basin, which is a unique example of marine basins in compressional settings on Earth. One of the first people to recognize the distinct character of these Late Cretaceous basins (Voigt, 1963) also used the term “Vortiefe” (foredeep), although this does not refer to the much later concept of foreland basins, and the Voigt (1963) discussion of subsidence mechanisms is limited to an analogy with much larger pre-plate tectonic “geosynclines”.

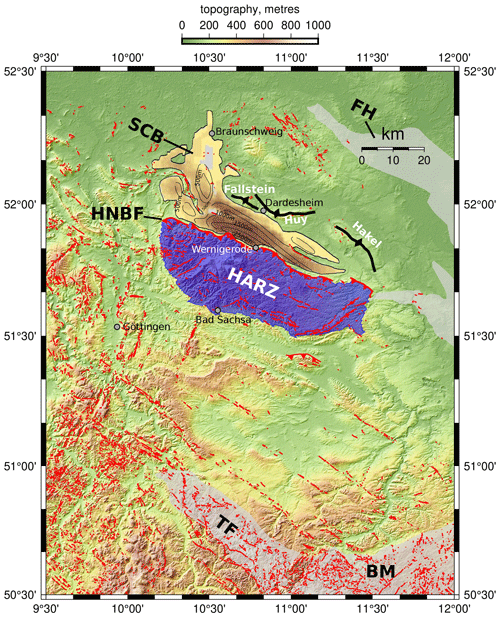
Figure 2 Overview of the Harz Mountains and the Subhercynian Cretaceous Basin (SCB), showing the positions of the northern bounding structures of the SCB (Fallstein–Huy–Hakel anticlines). The SCB outline is adapted from the Southern Permian Basin Atlas (Doornenbal and Stevenson, 2010). Contours of Late Cretaceous total thickness are from Voigt et al. (2008). Abbreviations: SCB – Subhercynian Cretaceous Basin; FH – Flechtingen High; HNBF – Harz Northern Boundary Fault; TF – Thuringian Forest Basement Uplift; BM – Bohemian Massif. Topography is from EU-DEM v1.0 (Mouratidis and Ampatzidis, 2019). Faults are from GÜK200 (Zitzmann, 2003).

Although more recently, a number of different mechanisms (Voigt et al., 2008; von Eynatten et al., 2008) have been associated with SCB formation and to a lesser degree subsidence, an explicit analysis of the mechanics of elastic flexural bending has not been presented.

2 Foreland Basin character of the SCB

The SCB is underlain by a Mesozoic cover of Triassic, Jurassic, and some Lower Cretaceous material, which in turn overlies upper Permian Zechstein evaporites that act as a décollement horizon accommodating some Late Cretaceous shortening (Fig. 3). The latter formed during a transgression, which led to a regional unconformity on a denuded and flattened surface of Variscan basement punctuated by transtensional Rotliegend basins (Ziegler and Dèzes, 2006). This cover was also present across the Harz Mountains prior to uplift, but it has since been removed by erosion estimated at as much as ∼ 6 km (von Eynatten et al., 2019). The Mesozoic sequences beneath the SCB form a structural marker recording the total effect of Upper Cretaceous deformation, including both shortening and detachment folding related to movement on the HNBF and subsidence of the SCB. They have a strongly asymmetric, synclinal geometry, with a nearly vertical, sometimes overturned southern limb along the HNBF (see also the Appendix) and a gently dipping northern limb locally disturbed by internal basin structures. The syn-tectonic, Late Cretaceous deposits of the SCB are thus sometimes strongly affected by syn-sedimentary deformation. The regional base Zechstein unconformity which lies below the detachment horizon is, by contrast, mostly unaffected by the shortening of the Mesozoic cover except where it is offset by major basement thrusts. Assuming it started as a relatively horizontal surface and underwent fairly even amounts of Mesozoic subsidence, its present-day geometry thus mostly records the effects of Late Cretaceous subsidence (Fig. 3a).

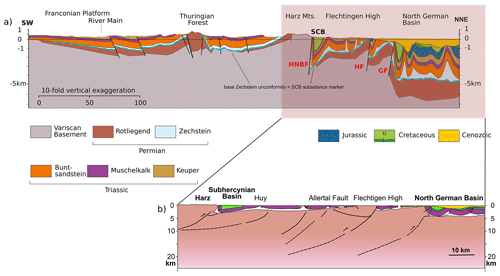
Figure 3 Cross sections across the study area. (a) Vertically exaggerated section emphasizing the geometry of Paleozoic and Mesozoic cover across central and northern Germany. (b) Details of interpreted basement thrusts are adapted from a section of Kley et al. (2008).

Large, classical foreland basins are often associated with a progressive syn-sedimentary deformation synchronous with subsidence, usually consisting of increased tilting of older units, often a lateral migration of the basin margin, and hence prograding onlap away from an orogen as large thrust systems evolve and grow (Allen et al., 1986; Homewood et al., 1986; Burkhard and Sommaruga, 1998; DeCelles and Giles, 1996). In the case of the SCB however, due to its smaller scale and the relatively stationary nature of the thrust load, we might expect such effects to be weaker. Recognizing any characteristic sedimentary geometries is further complicated by the combination of erosion and syn-sedimentary internal deformation of the basin fill due to detachment folding of the Mesozoic cover above Zechstein evaporites, which has led to the formation of a series of unconformities within the Upper Cretaceous fill of the SCB (Voigt et al., 2004, 2006; von Eynatten et al., 2008). It is, however, interesting that Turonian and lower Coniacian marly limestones and micrites thicken somewhat towards the southern margin of the SCB, perhaps indicating a slightly earlier, probably submarine initiation of subsidence and thrusting than is generally assumed based on the first arrival of eroded material from the uplifting Harz Mountains (von Eynatten et al., 2008). A broader insight into the distribution of subsidence can be deduced from the isopachs of Upper Cretaceous sediments, which show a pronounced depocentre up to 2500 m deep directly adjacent to the central portion of the HNBF in the area of Wernigerode (Fig. 2), part of the ∼ 40 km long main SCB.

Systematic change in sediment type throughout a basin's history is an often-cited characteristic of foreland basins. It has been argued that early sedimentation as orogenic wedge development begins adjacent to the basin is characterized by relatively deepwater sediments, often turbiditic in character, with little or no clastic input due to the underdeveloped initial thrust wedge and lack of significant erosional product (Allen et al., 1986). Such basins are sometimes referred to as “underfilled” (Sinclair, 1997): for example, the earliest stages of the western Alpine foreland in Switzerland in the form of the Helvetic flysch and Lower Marine Molasse (Burkhard and Sommaruga, 1998; Homewood et al., 1986). Later, as the orogenic load develops, sedimentation becomes increasingly clastic-dominated and the basin fills with eroded product of the orogenic wedge. Eventually, sedimentation may change from marine to lacustrine as the basin becomes overfilled, and sedimentary bypassing may begin. In the SCB, a relatively deepwater to shallow-water transition during basin development could be argued for if the Turonian (deeper water, pelagic limestones, no clastic input) and Coniacian (marly limestones, with some clastics) (Voigt et al., 2004) are considered to be related to the earlier stages of basin subsidence and flexure in an underfilled state, succeeded by Santonian age and later shallow-water facies, generally interpreted as tidal plain and estuarine deposits (Voigt et al., 2008) associated with the main phase of erosion of the Harz Mountains.

In summary, the SCB may have some of the sedimentary characteristics of larger orogenic foreland basins, but they are probably not as pronounced due to the much smaller scale of the system and its relative structural simplicity (single basement thrust).

3 Flexure of plates, flexural amplitudes, wavelengths, and loads

Gunn (1943a, b) developed the first models for elastic bending of the lithosphere as part of wider studies of gravity anomalies (Watts, 2001). Quite remarkably in the pre-plate tectonic era, Gunn created endmember models of elastic bending of “plates” both continuous and broken with both point and distributed loads (Fig. 4a and b). For instance, Gunn (1943a) modelled the Hawaiian island chain as a distributed load sitting upon an unbroken portion of the Pacific plate. Gunn (1947) also modelled flexure of oceanic lithosphere in subduction zones using an end-loaded plate with a “free” end, again without realizing the plate tectonic implications of his work (Fig. 4c). Later, as the idea of lithospheric plates developed, studies of flexural bending continued (Walcott, 1970a, b, c) with the aim of better determining the magnitude and temporal evolution of elastic parameters of the lithosphere like flexural rigidity and elastic thickness.

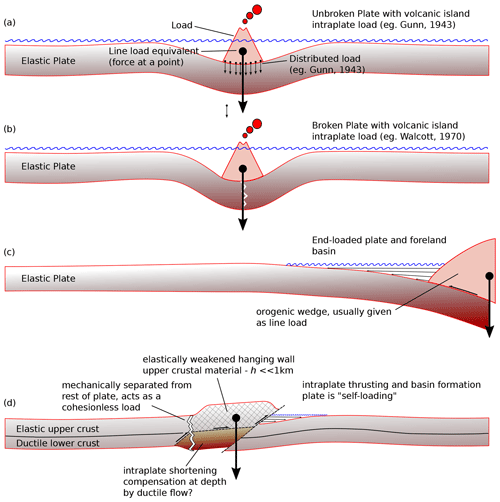
Figure 4 Traditional endmember models of flexural basins and details of a new intraplate flexural basin from this paper. (a) Mid-plate load on an unbroken plate after Gunn (1943a). (b) Mid-plate load on a broken plate after Gunn (1943a). (c) Edge load on the end of a plate typical of subduction zones after Gunn (1947). (d) Intraplate deformation-associated flexural basin from this paper with an assumed elastically weakened hanging wall and a basement thrust transecting most or all of the elastic crust and possible local weakening of the rest of the lithosphere.

In collisional belts and orogens such as the Alps, the elastic bending causing foreland basin development on their margins due to the vertical loading of the underthrust continental lithosphere by an overriding stack of nappes or thrust sheets (Allen et al., 1986) has often been studied by using some kind of edge-loaded plate with the load set to correspond to the force exerted by the weight of the orogenic wedge (Fig. 4c). This type of model makes intuitive sense in these cases, since there are two plates interacting and the edge of the underthrust plate is depressed and bent into an elastic curve, which is thought to be the main mechanism of foreland basin subsidence (Burkhard and Sommaruga, 1998; Homewood et al., 1986).

These elastic flexural endmember models also neatly illustrate the problem posed by an intraplate thrust and associated basin. In the case of the Harz and the SCB, for instance, the Harz basement uplift represents the load generating subsidence for, and at the same time is part of the same plate as, the SCB (Fig. 4d and e). Effectively, this means the plate is loading itself. The fundamentally different response of edge-loaded (or broken) plate models compared to intraplate-loaded, continuous plate models is also important in this context. Elastic flexural models assume that the lithosphere has a finite elastic thickness (h_o) which supports loads applied locally over a wider area by transferring the resistance to the load into more widespread elastic bending of the plate. In this context, an unbroken plate loaded in its middle by a relatively small load would usually be characterized by a broad, long-wavelength, shallow, low-amplitude flexural response, forming two similarly proportioned sedimentary basins either side of the load due to flexure. By contrast, an edge-loaded plate supports the load in a cantilever type of configuration, loaded at one end, and clamped at the other, thus maximizing the moment of the load and lithospheric bending (see Gunn, 1943b).

The geometry of the SCB is notable for its short wavelength of ∼ 25–40 km and high amplitude of ∼2500 m (compare to the Swiss Molasse Basin, with an “original” ∼ 120 km and ∼ 5–7 km; Burkhard and Sommaruga, 1998; Homewood et al., 1986). In this respect, the subsidence profile of the SCB is skewed towards the end load or broken plate situation. This question then naturally arises: can we imagine an end-loaded, intraplate basement uplift to be a natural analogue for the HNBF and SCB?

4 Broken lithosphere and the structural evolution of the HNBF and SCB

At the present day, as shown by the DEKORP deep seismic profile (Group, 1999) as well as global and local GPS and seismic data (Sella et al., 2002; Tesauro et al., 2006), the central western European lithosphere in the region of the Late Cretaceous intraplate shortening structures is an integral, stable part of the European portion of the Eurasian plate. Viewed from today's perspective, there is no reason to assume anything other than a continuous, elastic, lithospheric underpinning for the region, including that of the Harz and SCB (Pérez-Gussinyé and Watts, 2005).

In the Late Cretaceous, however, the situation was quite different, with active basement thrusting affecting a portion of the crust and lithosphere. In general, the geometry and magnitude of shortening on the HNBF are difficult to constrain due to a variety of factors, mostly related to erosional loss of hanging wall cut-off marker beds and hence direct geometric constraints on any fault offset. To try to mitigate this and gain some insight into the structural evolution of the HNBF and SCB, we have produced a composite, forward kinematic, and retro-deformed balanced section across the HNBF and SCB (Fig. 5). We use a forward kinematic model for the HNBF itself and its hanging wall (Fig. 5) using a fault-parallel flow deformation algorithm (Erslev, 1986). Total displacement of the hanging wall was adjusted iteratively to best match exhumation estimates from thermochronology (von Eynatten et al., 2019, 2021). For the steep southern limb of the SCB, we employ a trishear model, varying the opening angle over time to best match the southern limb geometry. The gently dipping northern portion of the SCB and the Fallstein salt pillow were derived from stepwise restoration of Sects. E–F from Voigt et al. (2008) using a flexural slip algorithm. The details of the restoration procedure are given in the Appendix.

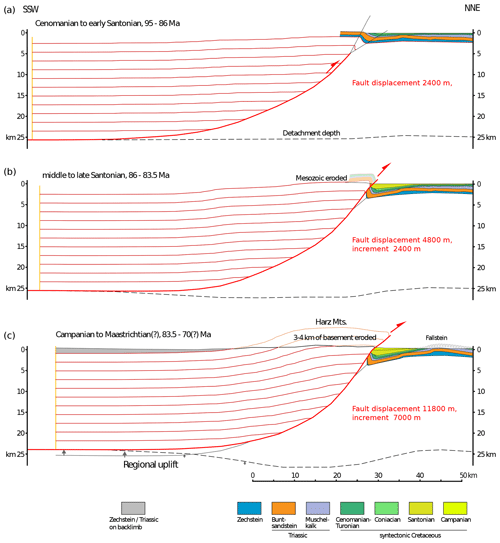
Figure 5 Three-stage geometric model of the Harz basement uplift. A listric thrust dipping 50^∘ near the surface and reaching 25 km of depth creates the Harz anticline with a reasonable exhumation depth (constrained by thermochronological data) after 12 000 m of total displacement. Red marker lines illustrate the gentle deformation of the hanging wall block. The cross-sectional geometry of the Subhercynian Basin and Fallstein salt anticline is from Voigt et al. (2008) (their Sects. E–F). The evolution of the gentle northern flank and Fallstein anticline was obtained by reversing a stepwise restoration of the cross section. (a) The growing Harz anticline is modelled using a trishear triangle with its apex fixed to the footwall and a trishear angle of 30^∘ (thin black lines). (b, c) The steep limb of the footwall syncline is further modelled with a trishear angle decreasing to 25^∘ and then 20^∘. The hanging wall in these steps requires more displacement than predicted by the trishear algorithm to satisfy the indicated exhumation constraints.

Our cross section (Fig. 5) thus consists of a composite image of the three separate components we have modelled. We present the section in three evolutionary time steps. In an initial Cenomanian to early Santonian step (95–86 Ma), approximately 2.4 km of displacement on the HNBF produces gentle folding of the Mesozoic cover north of the HNBF, which behaves effectively as a blind thrust in this period. A second increment of 2.4 km displacement is modelled in the middle to late Santonian (86–83.5 Ma), at which point the HNBF reaches the surface and begins to offset the Mesozoic strata forming the southern limb of the SCB. Finally, from the Campanian to Maastrichtian (83.5–70 Ma), a further 7 km increment of thrust displacement occurs. Our final geometry shows a depth to detachment for the HNBF of 24 km, very similar to the 23 km result of Tanner and Krawczyk (2017), who used a simple shear algorithm. The major difference from our result is the total fault displacement of 12 km (compared to 3 km for Tanner and Krawczyk, 2017). This is due to our section being made consistent with exhumation documented by thermochronology (von Eynatten et al., 2019). Another poorly constrained parameter affecting detachment depth estimates is the length of the back limb. The Harz experienced regional domal uplift after thrusting (von Eynatten et al., 2021), which we have accounted for in our cross section (Fig. 5c). As a result, at the present day, its back limb is elevated above the regional elevation of the foreland (Fig. 3, regional cross section). In our model, we placed the southern end of the back limb at the transition from the very gentle dip of the Thuringian syncline to the slightly steeper one of the southern Harz. A longer back limb would give an even deeper detachment.

Our structural model suggests continuous thrust movements on a discrete HNBF for at least 25 Myr, most of which overlapped the flexural subsidence documented by the SCB. It is likely that fault movement was associated with seismicity, causing rupture and discrete slip. Movement of hanging wall material over the basement thrust ramp led to pervasive deformation and weakening of the hanging wall, producing a non-cohesive topographic load. We therefore suggest that in the Late Cretaceous intraplate shortening on the HNBF resulted in a broken plate, which led to a situation resembling that shown in Fig. 4d. Hence, the deformed hanging wall material of the HNBF formed an end load on the on the edge of the SCB and caused its flexural subsidence (Fig. 6).

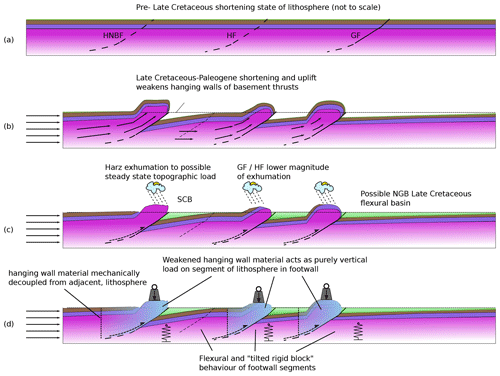
Figure 6 Cartoons of the mechanics of flexure, structural evolution, and basin evolution in the Late Cretaceous deformation system of the SCB and other basins. (a) The initial set of thrusts evolve either newly initiated or from pre-existing structures. (b) The majority of shortening occurs on the HNBF, but overthrusting also occurs on both the HF and GF. (c) Erosion of the Harz has removed all Mesozoic cover and probably led to a steady-state topography and load, balancing uplift and erosion. GF may have formed a flexural basin on the NGB since being distorted by Cenozoic subsidence. (d) Loads formed by hanging wall material are assumed to become non-cohesive due to internal deformation and elastic weakening, and they only act downwards on the footwall part of the adjacent lithospheric segment.

Figure 3 shows a number of Late Cretaceous basement faults besides the HNBF to the north of the SCB. These are, from south to north, a possible blind basement thrust below the Huy anticline, the Allertal Fault or lineament (AF), the Haldensleben Fault (HF), and the Gardelegen Fault (GF). Of these, the HF and GF are associated with basement thrusting and hence have the potential for the intraplate self-loading of adjacent lithosphere we have already discussed for the HNBF and SCB (Fig. 6). These structures are considered to transect most of the upper crust even if their precise geometry at depth and total displacement are uncertain (Group, 1999; Scheck et al., 2002; Kossow and Krawczyk, 2002). Hence, we assume that like the HNBF, they form elastic breaks in the lithosphere. North of the GF, the North German Basin (NGB) is a region of reduced crustal thickness and persistent subsidence throughout the Mesozoic, which continued into the Cenozoic (Malz et al., 2020). Hence, the NGB and its crust are generally considered to have been mechanically distinct from those of the region south of the GF throughout this period.

The base Zechstein unconformity, which, as we have already noted, can be regarded as a passive marker of post-Variscan deformation excluding the disturbance of Late Cretaceous detachment folding of the Mesozoic cover, effectively records the net effect of Late Cretaceous subsidence associated with this set of basement structures. Figure 3 shows that the base Zechstein unconformity makes a number of ramps with abrupt kinks and changes of angle corresponding closely to the positions of each of the basement faults. The HF and GF both offset this basal unconformity.

In general, the kinked geometry described by the basal unconformity in the region from the HNBF to the NGB resembles a series of tilted and sometimes abruptly bent rigid blocks. A similar situation was already described by McQueen and Beaumont (1989) for the Late Cretaceous–Paleogene Laramide orogeny of the western United States. Their model sought to explain basin formation and basement uplift by tilting of crustal blocks or segments due to differential horizontal, compressive forces acting across segment bounding, dipping, and/or thrust faults.

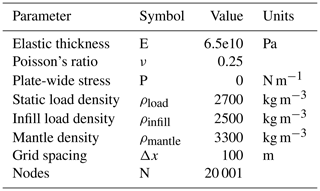
We propose a similar scheme to model Late Cretaceous subsidence of the SCB and the region north of it. However, we draw some conceptual distinctions from McQueen and Beaumont (1989). Firstly, we use a modified numerical solution of the elastic flexure equation to allow for large and abrupt discontinuities in elastic thickness within a plate (Hindle and Besson, 2021) to simulate the effect of Late Cretaceous basement thrusts on the elastic strength of the lithosphere. Breaks in the plate are simulated in the flexure model by sharp reductions of the elastic thickness to very low values (≪100 m) over short distances (<1 km). A succession of these breaks effectively splits the elastic lithosphere into independent (basement-fault-bounded) elastic segments. We then simulate basement-thrust-induced loading of the end of any segment by placing a load to one side only of the elastic break. In this way, we consider the hanging wall material of the thrust to be mechanically weak, decoupled elastically from adjacent crust, and to act as a vertical load on the footwall of the structure (Figs. 4d and 6). Our model thus calculates the isostatic and flexural response of elastic crustal blocks or segments to thrust-emplaced loads. Our model thus focuses on calculating the basin subsidence due to imposed thrust loads, which we take to be the consequence of horizontal shortening (of quite large magnitude in the case of the HNBF) rather than explaining both subsidence and uplift as a consequence of rigid block rotation. Our model uses a specific finite-difference formulation referred to as a “half-station” method (Cyrus and Fulton, 1968) applied to the fourth-order differential equation for elastic flexure of the lithosphere with a spatially varying elastic thickness h(x) and hence coefficient of flexural rigidity, D(x). The numerical method is described in the Appendix.

5 Flexure models of the broken central European lithosphere

A flexure model corresponding to the situation at the end of Late Cretaceous thrusting in the region extending from the Harz and the HNBF northwards to the North German Basin (Fig. 3 and cartoons in Fig. 6) is shown in Fig. 7. We apply simple loads with a constant overburden (3–5 km) corresponding to the basement thrusts (HNBF, HF, GF). We add elastic breaks to the lithosphere representing the HNBF, the Huy basement fault at the edge of the SCB, the AF, the HF, and the GF bordering the NGB. Flexural subsidence of approximately the correct magnitude and width at the position of the SCB (∼ 3 km deep and ∼ 15 km wide) is generated. The flexural profile closely matches the base Zechstein geometry shown in Fig. 7 between the HNBF and the GF and reproduces the series of kinks and relatively constant dipping segments. Our model also shows flexural subsidence on the edge of the NGB. Figure 3 shows a synclinally folded Late Cretaceous sequence in the footwall of the GF, with more Late Cretaceous deposits further north. Clearly, since the Late Cretaceous, the NGB has been affected by differential Cenozoic subsidence, which is again reflected in the geometry of the base Zechstein unconformity, and hence the present-day geometry of the NGB is not able to be matched by an elastic model that only accounts for Late Cretaceous flexure. However, our model suggests that the load of either the GF or perhaps the HF and GF combined could have generated an initial flexural subsidence on the NGB's margin. In general, the empirical success of the elastic model is surprising given its relative simplicity. We therefore suggest that much of the Late Cretaceous subsidence in the SCB and the basins north of it is probably due to a combination of a lithosphere discretely weakened by active basement faulting and a “tilted-rigid-block” response to thrust loading of short segments of crust.

A second model is shown in Fig. 8. Here, we remove the Huy basement fault to see what effect its western termination may have on basin width. The SCB becomes noticeably wider in the area around Braunschweig, from 15 km along the Huy anticline to 30–40 km east of its eastern termination near Braunschweig (Fig. 2). In this case, our model also produces the expected widening of the basin, suggesting that the Huy basement weak zone may indeed be critical in controlling the SCB's three-dimensional geometry. This is an important observation for this problem since it clearly shows the likely effects of the three-dimensional interactions of weak zones with loads. A more complete model of this situation could be created with a two-dimensional “thin elastic sheet” model based on the same numerical scheme as the current “thin elastic beam model”.

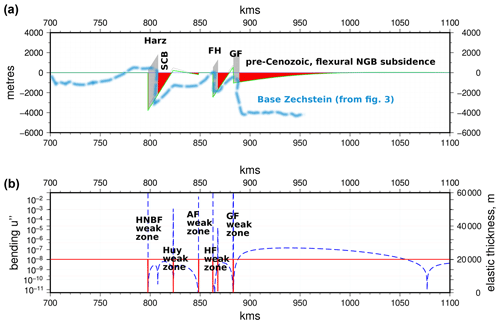
Figure 7 Flexure model of broken central European lithosphere during Late Cretaceous compression. (a) Flexural subsidence of an originally horizontal marker within the lithosphere. The black dashed line is the initial subsidence due to static thrust load (grey shade), and the green solid line is the final subsidence including iteratively calculated basin fill (red shading). The light blue dashed line shows base Zechstein unconformity for comparison. Model includes a Harz, Flechtingen, and Gardelegen (Calvörde) “load” and breaks in the lithosphere. (b) Bending (blue dashed) and elastic thickness (red dashed) curves for the model. Elastic breaks at the HNBF, Huy, AF, HF, and GF basement faults are shown. Abbreviations: HNBF – Harz Northern Boundary Fault; AF – Allertal Fault; HF – Haldensleben Fault; GF – Gardelegen Fault; SCB – Subhercynian Cretaceous Basin.

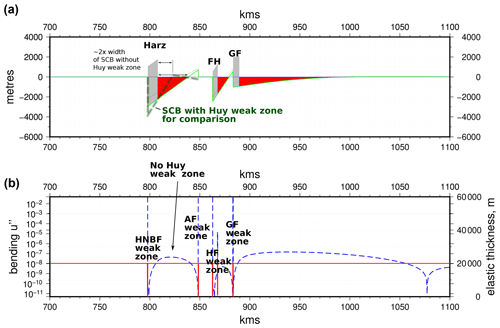
Figure 8 Flexure model (same as Fig. 7 but not including the Huy weak zone) to simulate the situation in the western part of the basin. The basin width of the model including the Huy weak zone is shown for comparison (dark green dashed line). Abbreviations: HNBF – Harz Northern Boundary Fault; AF – Allertal Fault; HF – Haldensleben Fault; GF – Gardelegen Fault; SCB – Subhercynian Cretaceous Basin.

It is interesting to consider the meaning of the parameters we vary in these models. A load can be applied anywhere along the plate, and although it is given in terms of a load density and thickness, is actually a force acting at a point. In flexure models these forces are often implicitly understood to be due to things like the sedimentary infill of a basin created by flexure of the plate or additional material placed on part of a plate by overthrusting and stacking of the crust or wholesale overriding of one plate by another. However, we can also imagine loads to be due to the elastic stress across fault planes resolved into the vertical direction (Gunn, 1943b). Hence, any force, regardless of its origin, can be expressed as an equivalent crustal or sedimentary load, which can even be negative in the case of erosional removal of material. The absolute values of the loads applied in our models are thus not necessarily indicative of a simple vertical loading condition. For the Harz and SCB, we consider the magnitude of the thrust emplaced load to be controlled by shortening and erosion rates. Uplift due to shortening builds hanging wall relief and increases loading. However, it is countered by erosion (Fig. 6). Some of the erosive product from the Harz ends up in the SCB and also forms part of the flexure-inducing load in our model. Our structural restoration (Fig. 5) implies a basement thrust which does not advance toward the foreland and a steady-state equilibrium being reached between uplift and erosion, at which point the topography of the Harz and hence the instantaneous load would be constant. In our flexure models we apply a fixed load, the top and width of which could be seen as equivalent to the flexurally supported topography of the Harz uplift at the end of the Late Cretaceous. Our models use a 20 km wide load, in reasonable agreement with hanging wall dimensions in the section in Fig. 5c and also the present-day Harz Mountains. The average topography produced (for an arbitrarily constant load thickness of 4000 m) is ∼ 1000 m, which is somewhat greater than the present day. In general, our estimated Late Cretaceous Harz load remains within reasonable bounds and perhaps implies that the vertically imposed load of hanging wall material was far more significant than any loading due to horizontal stresses interacting with the basement thrust. The FH and GF loads are more speculative, especially given the fact that the NGB has undergone substantial Cenozoic subsidence, which masks the signal of at least the GF-related flexural subsidence. However, our model suggests that some portion of the Late Cretaceous subsidence in the NGB could be due to flexural subsidence due to elastically broken lithosphere in a manner analogous to the SCB.

The effective elastic thickness is generally understood as a parameter dependent on lithospheric structure and rheology which characterizes the elastic response of the lithosphere to loading (Burov and Diament, 1995). It is usually indirectly determined by a combination of flexure modelling and gravity data (Walcott, 1970a; Pérez-Gussinyé and Watts, 2005; Stewart and Watts, 1997). Our flexure model defines a value of effective elastic thickness at each node along a plate. One consistent result of our models is the requirement for a value of nearly zero elastic thickness at the positions of basement faults to generate appropriate flexural subsidence. This effectively corresponds to splitting the lithosphere in the model into discrete fault-bounded segments, with loading applied as previously described. Thus, we find our model naturally replicates the idea of “tilted rigid blocks” (McQueen and Beaumont, 1989). However, it is important to emphasize that in our opinion, the “uplift” component in the case of the Harz and the wider Late Cretaceous deformation system is explained by hanging wall deformation and relief as a consequence of crustal shortening (see Fig. 5) and not rigid block rotation as was implied by McQueen and Beaumont (1989). In our view, the hanging wall material of the basement overthrusts is mechanically weak and non-cohesive as a consequence of pervasive deformation during thrust emplacement. Hence, we apply the hanging wall load in the models to one side only of the elastic break, representing the vertical force on the end of a lithospheric segment due to hanging wall material that is mechanically detached from the rest of the lithosphere. The tilted block portions of the system thus correspond to the basement underlying the various Late Cretaceous basins, which is not part of the deformed hanging walls of the thrusts (Fig. 6d).

6 Implications of the model

The major insight of our models is the role flexural subsidence plays in a plate interior when the lithosphere is weakened or broken due to basement faulting. In the case of the Late Cretaceous deformation system north of the Harz, our model shows the likelihood that, in addition to the SCB, the NGB has also undergone some flexural subsidence on its margins. Thus, in the foreland of the Harz Mountains, a system of marginal basins with, in the case of the SCB at least, sedimentary characteristics similar to classical foreland basins has developed.

As was already noted by McQueen and Beaumont (1989), the length of fault-bounded segments is critical in determining their flexural response. In the case of the Harz foreland, segments are very short (15–20 km), at which point they effectively respond to loading as rigid blocks. This rigid block geometry with sharp kinks seems to be recorded by the base Zechstein unconformity, which acts as a passive marker for flexural subsidence in the system and is unaffected by contemporaneous shortening and folding of the Mesozoic cover.

The flexural model (Fig. 7) matches the base Zechstein geometry remarkably closely by placing discrete breaks in the lithosphere at the position of basement faults, with narrow zones of nearly zero elastic thickness. Hence, whatever the meaning of the elastic thickness parameter in these cases, the empirical result appears broadly correct. One aspect of basement faulting that may help explain the associated nearly zero value of elastic thickness is seismic activity. The present-day central European lithosphere apparently shows no evidence of segmentation, although whether this would be easily detectable by the usual spectral methods is perhaps debatable (Pérez-Gussinyé and Watts, 2005). However, there is also almost no seismic activity across central western Europe today and certainly no major active basement thrusts. Seismicity is a highly discrete process, with strain accumulated over hundreds or even thousands of years released in a few seconds. Slip during earthquakes is also associated with a breakdown of friction across a fault plane, which, if it reaches deep into the crust and down to the brittle–ductile transition, would also be equivalent to a momentary drop of elastic strength to zero. This may be sufficient for a flexural load accumulated over a seismic cycle to re-equilibrate with the momentarily low friction and elastic strength of the lithosphere. Hence, extremely short-period reductions of elastic strength may be the dominant factor controlling flexural subsidence in these circumstances.

Our elastic model may also be applicable to other regions of intraplate shortening. Intraplate basins have been recognized or suspected in many places on Earth (Rodgers, 1987). Presently active systems include parts of the Andean Cordillera (Kley et al., 1999) and many parts of central Asia linked to the ongoing India–Eurasia convergence (Cobbold et al., 1996). Fossil systems include the wider Late Cretaceous central European basin system (Voigt, 1963; Voigt et al., 2008; Krzywiec, 2006) and the Laramide orogeny of the western United States (Hagen et al., 1985; Jordan, 1981).

We suggest calling the SCB an intraplate foreland basin, since this conveys the compressional setting of the subsidence and the basin's likely sedimentary evolution as well as the fact that it will contain large amounts of the eroded product of adjacent basement uplifts and their sedimentary cover if any is present.

7 Conclusions

The Subhercynian Cretaceous Basin is part of a wider system of intraplate, compressional basins across western central Europe whose subsidence and geometry can be well explained by a combination of elastic flexure and rigid tilting of lithosphere that has been tectonically segmented by basement thrusting. A relatively simple modification of the elastic flexure equations gives a reasonable first-order model of this process. These basins are likely to be relatively narrow, and deep relative to load size, although their dimensions will be strongly influenced by the frequency of individual basement thrusts and hence the length of plate segments.

Appendix A: A broken plate formulation for intraplate loading

The general problem of variable thickness elastic lithosphere in elastic flexure equations has been discussed in several papers (Van Wees and Cloetingh, 1994; Manríquez et al., 2013; Garcia et al., 2014). It is not generally amenable to an analytical solution, which has been the preference of most flexure studies. Our approach starts with a general formulation of the problem as follows:

$$\begin{array}{}\text{(A1)}& (D{u}^{\prime \prime }{)}^{\prime \prime }+P{u}^{\prime \prime }+ku=q(u),\end{array}$$

where u(x) is the deflection of the plate at any position x along its length. D (the flexural rigidity) varies in space and is implicitly a function of x. The value of D is given by $E{h}^{\mathrm{3}}/(\mathrm{12}\cdot (\mathrm{1}-{\mathit{\nu }}^{\mathrm{2}}\left)\right)$, where E is the elastic modulus of the lithosphere, h is the effective elastic thickness of the lithosphere and is actually the parameter in D that varies in space, and ν is Poisson's ratio. P is a constant representing a plate-wide horizontal stress. $k={\mathit{\rho }}_{\mathrm{mantle}}\cdot g$ and represents a restoring force due to displaced mantle, and q(u) is the load term, which consists of fixed, imposed loads generating subsidence $q_{\mathrm{load}}\cdot {\mathit{\rho }}_{\mathrm{load}}\cdot g$ and also infill loads of the resulting basins $q(u{)}_{\mathrm{infill}}\cdot {\mathit{\rho }}_{\mathrm{infill}}\cdot g$. For instance, as shown in Fig. A1, a load due to an orogenic wedge on the edge of a plate would constitute the “fixed” load q_o in our model and is given directly at each node. The subsidence this load causes generates basins, which are then “filled” by q(u)_infill with material of density usually corresponding to water or sediments. This formulation of the load term and the restoring force results in a non-linear equation in which the infill and resulting elastic equilibrium have to be calculated iteratively. The model results in this paper show this process by plotting the initial calculated subsidence due to static loads as a black line, with the final iteratively derived subsidence, including the infill, plotted as a red curve. Static loads are shown in grey, whilst infill is shown with vertical red lines. The most common analytical formulation of the flexure equation actually combines the restoring force due to displaced mantle with the infill as a load as part of the constant k, thus making the equation apparently linear. In fact, the equation should only be treated as linear under certain special conditions, although this is rarely stated (see Gunn, 1943a).

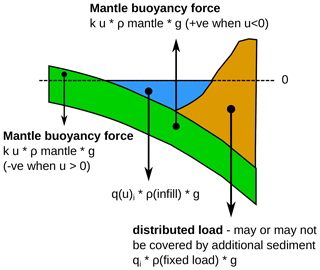
Figure A1 Sketch showing the different components of the total load q(u) and the restoring force due to mantle displacement in the model.

Table A1 Standard parameters used in numerical models

We apply a finite-difference operator for the second derivative directly to the term in brackets, which is itself discretized as a second derivative finite-difference scheme, something referred to as the half-station method (Cyrus and Fulton, 1968).

Hence, if

$$\begin{array}{}\text{(A2)}& f^{\prime \prime }\approx d^{\mathrm{2}}f=\left(f_{i+\mathrm{1}}-\mathrm{2}{f}_i+f_{i-\mathrm{1}}\right)/\mathrm{\Delta }{x}^{\mathrm{2}},\end{array}$$

where Δx is the grid spacing and i is the node number, then

$$\begin{array}{}\text{(A3)}& (D{u}^{\prime \prime }{)}^{\prime \prime }\approx d^{\mathrm{2}}\left(D{d}^{\mathrm{2}}u\right).\end{array}$$

We discretize the whole term in brackets first on a grid $i=\mathrm{1},\mathrm{\dots },N$.

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}{d}^{\mathrm{2}}\left(D{d}^{\mathrm{2}}u\right)& =({\left(D{d}^{\mathrm{2}}u\right)}_{i+\mathrm{1}}-\mathrm{2}{\left(D{d}^{\mathrm{2}}u\right)}_i\\ & +{\left(D{d}^{\mathrm{2}}u\right)}_{i-\mathrm{1}})/\mathrm{\Delta }{x}^{\mathrm{2}}\end{array}\end{array}$$

Then, substituting the terms in brackets and advancing the indices leads to the following.

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}{d}^{\mathrm{2}}\left(D{d}^{\mathrm{2}}u\right)& =\left(D_{i+\mathrm{1}}\left(u_{i+\mathrm{2}}-\mathrm{2}{u}_{i+\mathrm{1}}+u_i\right)\right)\\ & -\mathrm{2}\left(D_i\left(u_{i+\mathrm{1}}-\mathrm{2}{u}_i+u_{i-\mathrm{1}}\right)\right)\\ & +\left(D_{i-\mathrm{1}}\left(u_i-\mathrm{2}{u}_{i-\mathrm{1}}+u_{i-\mathrm{2}}\right)\right)/\mathrm{\Delta }{x}^{\mathrm{4}}\end{array}\end{array}$$

Collecting terms, we obtain the following.

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}{d}^{\mathrm{2}}\left(D{d}^{\mathrm{2}}u\right)& =(D_{i+\mathrm{1}}{u}_{i+\mathrm{2}}-\mathrm{2}\left(D_{i+\mathrm{1}}+D_i\right)u_{i+\mathrm{1}}\\ & +\left(D_{i+\mathrm{1}}+\mathrm{4}{D}_i+D_{i-\mathrm{1}}\right)u_i\\ & -\mathrm{2}\left(D_{i-\mathrm{1}}+D_i\right)u_{i-\mathrm{1}}+D_{i-\mathrm{1}}{u}_{i-\mathrm{2}})/\mathrm{\Delta }{x}^{\mathrm{4}}\end{array}\end{array}$$

Discretizing the remaining parts of the equation then gives the following.

$$\begin{array}{}\text{(A7)}& {\displaystyle }(D_{i+\mathrm{1}}{u}_{i+\mathrm{2}}-\mathrm{2}\left(D_{i+\mathrm{1}}+D_i-\mathrm{\Delta }{x}^{\mathrm{2}}{P}_i/\mathrm{2}\right)u_{i+\mathrm{1}}\text{(A8)}& {\displaystyle }+\left(D_{i+\mathrm{1}}+\mathrm{4}{D}_i+D_{i-\mathrm{1}}+\mathrm{\Delta }{x}^{\mathrm{4}}{k}_i-\mathrm{\Delta }{x}^{\mathrm{2}}{P}_i\right)u_i\text{(A9)}& {\displaystyle }\begin{array}{rl}& -\mathrm{2}\left(D_{i-\mathrm{1}}+D_i-\mathrm{\Delta }{x}^{\mathrm{2}}{P}_i/\mathrm{2}\right)u_{i-\mathrm{1}}+D_{i-\mathrm{1}}{u}_{i-\mathrm{2}})/\\ & \mathrm{\Delta }{x}^{\mathrm{4}}={\left(q_o\right)}_i+q\left(u_i\right)\end{array}\end{array}$$

Here, the two load terms (q_o)_i and q(u_i) represent the static fixed load and the iteratively calculated infill load, respectively.

If we gather all coefficients into a matrix A and form a matrix equation, the resulting system is of the form

$$\begin{array}{}\text{(A10)}& \mathbf{A}u=q\left(u\right),\end{array}$$

which is a non-linear series of equations in u. We reformulate this as a recursive matrix fixed point problem of the form

$$\begin{array}{}\text{(A11)}& {\mathbf{A}}^{-\mathbf{1}}q(u{)}^{\left(r\right)}=u^{(r+\mathrm{1})},\end{array}$$

where r is the iteration step, and solve.

An alternative finite-difference scheme can be derived by instead applying the product rule of differentiation to the problem before discretization. For instance, Buiter (2000) shows the following.

$$\begin{array}{}\text{(A12)}& D{u}^{\prime \prime \prime \prime }+\mathrm{2}{D}^{\prime }{u}^{\prime \prime \prime }+D^{\prime \prime }{u}^{\prime \prime }+P{u}^{\prime \prime }+ku=q\left(u\right)\end{array}$$

Crucially, however, this form of the equation assumes a smoothly varying elastic thickness function. Hence, for our problem with abrupt variations in elastic thickness, it is not applicable. It can easily be verified that a finite-difference scheme derived from this form of the equation will give an identical set of equations as the half-station method if D is constant everywhere.

Appendix B: An estimate of Harz shortening and fault geometry from kinematic modelling

Our three-step geometric model of the Harz basement uplift was created with PETEX's MOVE software. Three parts of the cross section were modelled separately: (1) the general listric geometry of the fault was found by trial-and-error fitting of the Harz back limb with a near-surface fault dip of 50^∘ and using a fault-parallel flow algorithm. (2) The steep southern limb of the footwall syncline in the Subhercynian Basin was created using the trishear algorithm. The fit shown in Fig. 5 was obtained with a trishear triangle having its apex fixed to the footwall (propagation-to-slip ratio 0) about 5 km below the top basement surface and an initial opening angle of 30^∘ that decreased to 25 and 20^∘ in the two following steps. In each step the trishear triangle was rotated along with the fault, which became steeper due to footwall subsidence. The trishear parameters of the steep limb were chosen to obtain matching geological contacts across the synclinal axial plane. In the first modelling step, a trishear solution fits both the footwall and hanging wall (Fig. 5a). In the second and particularly the third step, however, the hanging wall displacement required to satisfy the exhumation history of the Harz (von Eynatten et al., 2019, 2008) exceeds the displacement recorded by footwall folding (Fig. 5b and c). (3) The gently dipping northern flank of the Subhercynian Basin and the Fallstein salt pillow were created by stepwise restoration of cross section “E–F” in Voigt et al. (2008) using the flexural slip algorithm. The redistribution and loss of Zechstein salt due to flow and subsurface dissolution had to be implemented manually; the spatial and temporal details of these processes are not well constrained. Running the stepwise restoration of the Subhercynian Basin infill in reverse constrains the evolving footwall geometry with an increasing southward dip. We constructed a hypothetical deep structure beneath the Harz by letting the detachment level follow the foreland basement dip before returning to its elevation beneath the back limb. Overall, our modelled Harz NBF becomes steeper and, at shallow levels, more discrete over time.