Analogue modelling of basin inversion: a review and future perspectives

Basin inversion involves the reversal of subsidence in a basin due to compressional tectonic forces, leading to uplift of the basin's sedimentary infill. Detailed knowledge of basin inversion is of great importance for scientific, societal, and economic reasons, spurring continued research efforts to better understand the processes involved. Analogue tectonic modelling forms a key part of these efforts, and analogue modellers have conducted numerous studies of basin inversion. In this review paper we recap the advances in our knowledge of basin inversion processes acquired through analogue modelling studies, providing an up-to-date summary of the state of analogue modelling of basin inversion. We describe the different definitions of basin inversion that are being applied by researchers, why basin inversion has been historically an important research topic and what the general mechanics involved in basin inversion are. We subsequently treat the wide range of different experimental approaches used for basin inversion modelling, with attention to the various materials, set-ups, and techniques used for model monitoring and analysing the model results. Our new systematic overviews of generalized model results reveal the diversity of these results, which depend greatly on the chosen set-up, model layering and (oblique) kinematics of inversion, and 3D along-strike structural and kinematic variations in the system. We show how analogue modelling results are in good agreement with numerical models, and how these results help researchers to better understand natural examples of basin inversion. In addition to reviewing the past efforts in the field of analogue modelling, we also shed light on future modelling challenges and identify a number of opportunities for follow-up research. These include the testing of force boundary conditions, adding geological processes such as sedimentation, transport, and erosion; applying state-of-the-art modelling and quantification techniques; and establishing best modelling practices. We also suggest expanding the scope of basin inversion modelling beyond the traditional upper crustal “North Sea style” of inversion, which may contribute to the ongoing search for clean energy resources. It follows that basin inversion modelling can bring valuable new insights, providing a great incentive to continue our efforts in this field. We therefore hope that this review paper will form an inspiration for future analogue modelling studies of basin inversion.

1 Introduction

1.1 Definition of basin inversion

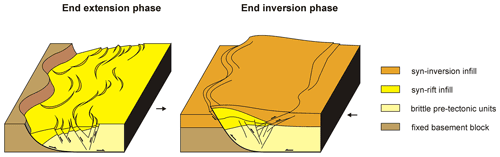
The development of extensional tectonic systems leads to the formation of (fault-bounded) basins, followed by crustal necking and eventually continental break-up and oceanic spreading (e.g. Lavier and Manatschal, 2006; Wilson et al., 2019). However, at any time during continental break-up, changes in the tectonic regime may halt rifting and lead to subsequent compression, causing the inversion of the previously established basins (Fig. 1).

Even though the concept of basin inversion has been used since over a century ago (e.g. Lamplugh, 1919), the term “inversion” appears to have been initially introduced by Glennie and Boegner (1981), who used “inversion tectonics” or “structural inversion” to explain the evolution of the Sole Pit structure in the North Sea, which involved “conversion of a basin area into a structural high”. These terms were subsequently used more restrictively by Williams et al. (1989), who considered that “structural inversion (or inversion tectonics) occurs when basin-controlling extensional faults reverse their movement during compressional tectonics, and to varying degrees, basins are turned inside out to become positive features”. Although inversion is generally assumed to involve compression, some authors make a distinction between “positive” and “negative” inversion, with the former being defined as “the reversal of extensional fault movement during contractional tectonics”, and the latter as “the reactivation in extension of a significant portion of an existing contractional system” by Williams et al. (1989). At the same time, Cooper et al. (1989) used the term “basin inversion” to describe “a basin controlled by a fault system that has been subsequently compressed-transpressed producing uplift and partial extrusion of the basin fill”, without being specific as to whether pre-existing faults need to reverse their movement or whether new faults are formed. As becomes clear from the above, there is no generally accepted definition of the term “inversion” (see also Buchanan and Buchanan, 1995), although the term is widely used.

In the context of this review of analogue modelling of basin inversion, we define the process of “basin inversion” rather broadly as: “the reversal of subsidence in a (rift) basin due to compressional tectonics, so that the sedimentary infill of the basin is uplifted and/or exhumed, with or without reactivation of previously established normal faults”. We must also point out that basin inversion has traditionally been considered to refer to the inversion of continental basins that did not yet reach the stage of necking and continental break-up, which is also the general context of this review paper.

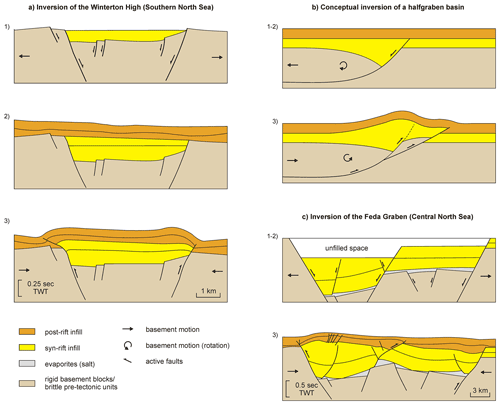
Figure 1 Schematic examples of the three main stages of basin inversion: (1) syn-rift, (2) post-rift, and (3) inversion. (a) Formation and inversion of a symmetric graben (Winterton High in the Southern North Sea), where bounding normal faults were reactivated and propagated into the overburden at a shallow angle during Cenozoic basin inversion. Redrawn after Panien et al. (2006a), based on Badley et al. (1989), with permission from the Geological Society, London. (b) Schematic example of an inverted half-graben related to a listric fault. Inversion causes uplift of the basin fill and reactivation of the listric fault that propagates upward into the previously undeformed post-rift units, as well as the development of a new thrust fault (i.e. a “footwall shortcut”). Modified after Cooper et al. (1989), with permission from the Geological Society, London. (c) Simplified development of the salt-bearing Feda Graben in the central North Sea. The salt (Upper Permian Zechstein evaporites) decouples the basin infill from the basement. Based on Gowers et al. (1993) and Stewart and Clark (1999), with permission from the Geological Society, London. TWT stands for two-way travel time.

1.2 Importance of basin inversion tectonics

Inverted basins are very common geological features and are found in multiple locations, for instance the North Sea area (Lamplugh, 1919; Glennie and Boegner, 1981; Nalpas et al., 1995; Evans et al., 2003; De Jager, 2003; Hansen et al., 2021), the Pyrenees and European Alps (Pfiffner, 1993; Ziegler et al., 1995; Kiss et al., 2020; Mencos et al., 2015; Lescoutre and Manatschal, 2020; Musso Piantelli et al., 2022), the Atlas Mountains (Vially et al., 1994), Iran (Boutoux et al., 2021), the Araripe Basin in northeastern Brazil (Marques et al., 2014), the Andes (Ferrer et al., 2022b, and references therein), offshore of Korea (Park et al., 2021), and China (Yu et al., 2021), as well as many other places around the globe (Letouzey, 1990; Lowell, 1995; Iaffa et al., 2011; Gibson and Edwards, 2020; Bosworth and Tari, 2021; Dooley and Hudec, 2020).

A thorough understanding of the geological processes associated with basin inversion is not only relevant for scientific purposes but is also of great importance for societal and economic reasons. First, the ongoing tectonic deformation in many inverted basins, which are often incorporated into active mountain belts, causes seismic hazards that need to be assessed and monitored (Plenefisch and Bonjer, 1997; Edwards et al., 2015; Mock and Herwegh, 2017; Madritsch et al., 2018; Deckers et al., 2021). Second, knowledge of processes related to basin inversion is important for petroleum geologists. Basin inversion allows for hydrocarbon trap formation, whereas the associated uplift and exhumation can shut down hydrocarbon generation from deeply buried source rocks, which are often poorly imaged on seismic data (Tari et al., 2020). Determining the timing and impact of basin inversion has therefore always been a crucial challenge to petroleum geologists (De Jager, 2003; Evans et al., 2003; Turner and Williams, 2004; De Jager and Geluk, 2007; Cooper and Warren, 2010, 2020; Tari et al., 2020, as also demonstrated in two special volumes edited by Cooper and Williams, 1989; Buchanan and Buchanan, 1995). Third, since (emptied) hydrocarbon reservoirs can subsequently be used for CO₂ sequestration (Voormeij and Simandl, 2004; Li et al., 2006), knowledge of inversion tectonics can be applied to mitigate the impact of greenhouse gas emissions. Fourth, basin inversion processes and related fluid flow may furthermore lead to the development of economical mineral resources and ore deposits (e.g. Pb–Z mineralizations and Fe–Cu–Au deposits, Sibson and Scott, 1998; Groves and Bierlein, 2007; Hageman et al., 2016; Gibson et al., 2017; Gibson and Edwards, 2020; Liang et al., 2021). Finally, a thorough understanding of basin evolution, including basin inversion, is also of great interest for geothermal energy projects since tectonic displacements can strongly affect the thermal profile of the subsurface (Sandiford, 1999; Edwards et al., 2015; Vidal and Genter, 2018; Doornenbal et al., 2019; Békési et al., 2020; Weibel et al., 2020; Willems et al., 2020). Possible future applications, including exploration for natural hydrogen, are presented in Sect. 7.

1.3 Analogue modelling of basin inversion

When studying tectonic processes, researchers must face a couple of major obstacles. Firstly, the size of the systems involved is massive, meaning that a thorough (structural) mapping is a major challenge. Secondly, large parts of these systems are simply inaccessible as they are deep below the surface, covered by thick sedimentary sequences or situated far offshore. Recent advances in mapping techniques and geophysical methods have mitigated these obstacles to a certain degree, yet the most challenging impediment on the path to a thorough understanding of tectonic processes is the vast timescales involved. It is simply impossible to directly observe the evolution of a tectonic system in a human lifetime.

To circumvent these limitations, geologists have for over 2 centuries applied analogue modelling techniques with the aim of simulating large-scale tectonic processes at convenient timescales and length scales in the laboratory. By using relatively simple model materials representing the different layers in the lithosphere that are subsequently deformed in experimental apparatus, such large-scale tectonic processes can be reproduced on a small scale within a matter of hours or days. In addition to simulating the dynamic aspects of tectonic processes, researchers can also systematically test the influence of specific parameters in their models and compare the model results to natural examples. As such, analogue modelling is an excellent tool to study tectonic processes and has greatly contributed to our understanding of the evolution of our dynamic planet.

Analogue modelling as an approach to study tectonic processes has been applied since the early 19th century (Hall, 1815; Cadell, 1889; Hubbert 1937; see also the reviews by Koyi, 1997; Ranalli, 2001; Bonini et al., 2012; Graveleau et al., 2012; Schellart and Strak, 2016; Reber et al., 2020; Zwaan and Schreurs, 2022a). However, the first experimental studies aiming at basin inversion were only performed in the second half of the 20th century (Lowell, 1974; Koopman et al., 1987; McClay and Buchanan, 1992; Mitra, 1993; McClay, 1995; Bonini et al., 2012). This relatively late start may have been caused by a late interest in basin inversion processes in general, which only flared up in the 1980s, as well as the relative complexity of these models, which require sophisticated experimental machines capable of simulating multiple deformation phases. Nevertheless, the field of basin inversion modelling has steadily advanced over the past decades, following the same trends as other analogue tectonic modelling fields. These trends include a shift of focus from qualitative to quantitative modelling practices through the use of new and improved model materials, experimental set-ups, and monitoring techniques and analyses (see e.g. Koyi, 1997; Ranalli, 2001; Bonini et al., 2012; Graveleau et al., 2012; Zwaan and Schreurs, 2022a, and references therein).

1.4 Aim of this review

The main aim of this review is to recap the advances in knowledge of basin inversion tectonics acquired through analogue modelling efforts since the previous reviews by McClay (1995) and, more recently, by Bonini et al. (2012). In this work we systematically review over 70 analogue modelling studies of basin inversion, providing an up-to-date summary of the different set-ups, materials, tested parameters, and results. We also assess how these results compare to numerical models of basin inversion tectonics and to natural examples of inverted basins. We furthermore identify the various perspectives and opportunities in the field, which we hope will serve as an inspiration for future analogue modelling studies of basin inversion.

2 Mechanics of basin inversion

For a basin to be inverted, it needs to form a mechanically weak region in comparison to its immediate surroundings. Mechanical weakness may stem from the basin fill, allowing uplift and folding of the incompetent sedimentary layers upon shortening, and from extensional faults formed during initial basin formation. Basin inversion is generally well expressed in the upper crust, where brittle deformation dominates. The rheology of the brittle materials involved is commonly regarded as time-independent, roughly obeying a Mohr–Coulomb criterion of failure (Coulomb, 1773) that describes the relation between the shear stress (τ) parallel to a (potential) fault plane required for fault activation, the stress normal to the fault plane (σ_n), and the cohesion (C₀) and angle of internal friction (φ) of the material as follows (Fig. 2a):

$$\begin{array}{}\text{(1)}& \mathit{\tau }=C_{\mathrm{0}}+{\mathit{\sigma }}_{\mathrm{n}}\tan \mathit{\phi }.\end{array}$$

Basin inversion generally implies a change from an extensional setting with the maximum compressive stress, σ₁, oriented vertically and the minimum compressive stress, σ₃, oriented horizontally (Fig. 2a), to a shortening setting with σ₁ oriented horizontally and σ₃ vertically (Fig. 2b). As such, Coulomb-style normal faults related to initial basin formation form at Coulomb dip angles of ca. 60^∘ (for a φ=30^∘) (Figs. 2a, 3a), whereas reverse faults related to subsequent shortening preferentially form at dip angles of ca. 30^∘ (Fig. 2b). It follows that normal faults are, under ordinary circumstances, misoriented for reactivation in shortening (Figs. 2b, 3b).

However, fault reactivation of normal faults in shortening has been observed in nature and can be explained by four mechanisms. Firstly, normal faults that formed at lower dip angles with the horizontal (e.g. Roscoe or Arthur dip angles, Roscoe, 1970; Arthur, 1977, or low-angle detachment faults) are more readily reactivated, since lower stresses are required for fault reactivation than for the formation of a new thrust fault (Fig. 2c). Secondly, a lowering of fault strength by fluids or mineral alignment (strain softening, Sibson, 1985, 1995, 2009) can reduce the internal friction angle, thus flattening the reactivation envelope and promoting normal fault reactivation (Fig. 2c). Thirdly, thrusts may form close to normal faults, thus using the normal fault as a structural heterogeneity, but not strictly reactivating (all parts of) the normal fault (Fig. 1b). Finally, oblique shortening facilitates normal fault inversion. Here the plane containing the maximum and minimum principal stresses σ₁ and σ₃ is oriented at an angle to the normal fault, meaning that the effective fault angle is reduced and part of the deformation is accounted for by a strike-slip component (Dubois et al., 2002) (Fig. 3c).

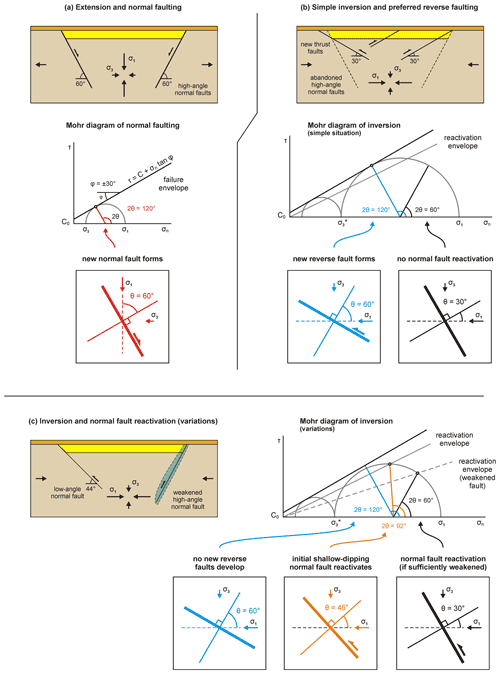
Figure 2 Schematic 2D illustration of (a) basin development, (b) inversion with preferential new reverse fault development over reactivation of steep normal faults, and (c) inversion style variations involving normal fault reactivation due to reduced normal fault dip and fault strength, including schematic Mohr diagrams of the changing states of stress in these systems (σ₁= maximum compressive stress; σ₃= minimum compressive stress; θ= angle between normal to fault plane and orientation of the maximum compressive stress (σ₁); φ = angle of internal friction; C₀= cohesion; τ= shear stress; σ_n= normal stress). The reactivation envelope concerns the reactivation of a pre-existing fault plane, which is considered to involve negligible cohesion (C₀= 0 Pa) so that the envelope starts from the origin. (^*) Note that σ₁ (vertical loading) during extension becomes σ₃ during subsequent inversion in 2D (as indicated by the small semi-circles in the Mohr diagrams in panels b and c). Inspired by Bonini et al. (2012).

It should be stressed that even though the brittle behaviour of the upper crustal layers is generally considered to dominate deformation during inversion, the ductile parts of the lithosphere can also play an important role. Such ductile layers (e.g. evaporites, shales, or on a larger scale the lower crust) can decouple different parts of the lithosphere. The degree of decoupling may depend on the viscous layer thickness and distribution, its viscosity as a function of compositional changes throughout a basin, and the tectonic strain rate (e.g. Brun, 1999, 2002; Zwaan et al., 2019). Such decoupling enables the development of significant differences in deformation in the units above and below the viscous layer (thin- vs. thick-skinned deformation). Furthermore, in the case of salt, reactivation of inherited passive diapirs can occur due to major subsalt fault movement. Excellent examples of the effect of such decoupling can be observed in the North Sea area or in the Pyrenees (Stewart and Coward, 1995; Stewart and Clark, 1999; Stewart, 2007; Mencos et al., 2015; Van Winden et al., 2018) (Fig. 1c).

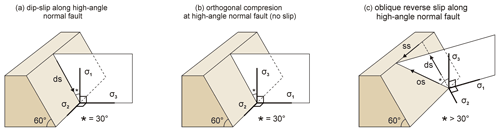
Figure 3 Oblique reactivation of a high-angle normal fault due to the reduced effective fault angle (^*). Components of deformation are as follows: ds stands for dip-slip, os stands for oblique slip, and ss stands for strike-slip. σ₁ is maximum compressive stress, σ₂ is intermediate compressive stress, and σ₃ is minimum compressive stress. Inspired by Dubois et al. (2002). Note, however, that actual displacements along pre-existing structures can deviate from the directions of the principal stresses (Withjack and Jamison, 1986; Morley, 2010).

3 Analogue modelling techniques

In this section we address the different model materials, set-ups, scaling principles, and monitoring techniques that are used in analogue modelling laboratories around the globe. It may be noted that most of these techniques are very similar to those used for analogue modelling of extensional tectonics, since the first phase of deformation involved the development of a basin (see the reviews of analogue modelling of extensional tectonics by Vendeville et al., 1987; McClay, 1990, 1996; Naylor et al., 1994; Koyi, 1997; Brun, 1999, 2002; Corti et al., 2003; Bahroudi et al., 2003; Corti, 2012; Zwaan et al., 2019; Zwaan and Schreurs, 2022a).

3.1 Materials and rheology

In analogue modelling studies, brittle and ductile layers in the lithosphere are simulated with various brittle and viscous model materials (Fig. 4). The properties of these model materials can be determined in detail using ring shear testers and rheometers (e.g. Panien et al., 2006b; Klinkmüller et al., 2016; Rudolf et al., 2016; Ritter et al., 2018a, b; Zwaan et al., 2018b). Below we describe the general characteristics of materials that are commonly used in analogue models of basin inversion.

3.1.1 Brittle materials

Granular materials are often used to reproduce the behaviour of brittle parts of the lithosphere (Fig. 4). When deformed, granular materials will form shear zones at similar angles to faults in rocks and soils in nature (see Sect. 3.5). A standard granular material, used to simulate bulk brittle rocks in most basin inversion models included in this review, is quartz sand of some sort (McClay and Buchanan, 1992). Other granular materials include feldspar sand (Munteanu et al., 2013) and corundum sand (Panien et al., 2006b), or mixtures of various granular materials (Abdelmalak et al., 2016; Montanari et al., 2017; Dooley and Hudec, 2020). Although these materials may have slightly different properties with respect to quartz sand (notably grain size, density, cohesion and angle of friction), they generally deform in the same fashion. Granular materials should be sieved from a minimum height into the model apparatus to ensure a homogeneous density distribution (Krantz, 1991b; Schellart, 2000; Klinkmüller et al., 2016; Schmid et al., 2020). Notably, the rheology of granular materials can generally be considered to be strain rate independent, even though there are some complexities that can be of importance (Vermeer, 1990; Ritter et al., 2016; Montanari et al., 2017, and references therein; see also Sect. 3.5).

Modellers regularly combine different types of granular materials in their experiments. Coloured or dyed sand is used to create (thin) layering that will be visible on side view images or cross-sections (Sect. 3.6). This is generally the same sand as used for bulk brittle rock layers, but in some cases other materials are used, such as corundum sand or Pyrex (all visible on X-ray computed tomography (CT) scans, Letouzey et al., 1995; Panien et al., 2006a, Sect. 3.6). These thin horizons of different materials in the bulk sand layers are not considered to significantly affect the bulk model behaviour. By contrast, materials such as micas and micro-beads have a significant lower angle of internal friction and deform more readily. Weaker mica layers are used to facilitate interlayer slip, while conveniently creating visible layering in sections as well (McClay, 1989, 1996; Buchanan and McClay, 1991, 1992, see Sect. 3.6), whereas micro-beads have been used to simulate basal detachment layers (Panien et al., 2006a). Micro-beads can also serve as weak sedimentary infill of a rift basin that may be more easily deformed during inversion (Martínez and Cristallini, 2017; Panien et al., 2005; Yagupsky et al., 2008).

Other modellers have applied wet clay to simulate brittle rocks (Mitra, 1993; Mitra and Islam, 1994; Eisenstadt and Withjack, 1995; Eisenstadt and Sims, 2005). Clay behaves somewhat differently from granular materials as its behaviour has a strain-rate-dependent component (Oertel, 1965; Eisenstadt and Sims, 2005, and references therein), which makes it appropriate for modelling the uppermost parts of the lithosphere, creating more intricate fault structures when deformed than sand (Eisenstadt and Sims, 2005). Similar to their granular counterparts, coloured clay can be used to highlight layering and to distinguish syn-tectonic infill. Buchanan and McClay (1992) have also used a mixture of clay and sand to simulate layers of higher competence. In contrast to sand, clay can readily be modelled into shape, but it is crucial to control its water content as this significantly affects the material's rheology (Arch et al., 1988; Eisenstadt and Sims, 2005, and references therein). This is also true for the wet sand–cement mixtures applied by Mandal and Chattopadhyay (1995).

3.1.2 Viscous materials

In analogue modelling studies, the ductile parts of the lithosphere are generally simulated by means of viscous materials (Fig. 4c, d). Typical viscous materials include silicone oils, such as polydimethylsiloxane (PDMS, e.g. SGM 36) and “putties” (e.g. Dow Corning 3179 Dilatant Compound or Rhône-Poulenc Gomme Spéciale GS1R), and various types of mixtures of such viscous materials with granular materials, acids, and other substances (e.g. Schellart and Strak, 2016; Di Giuseppe, 2018; Reber et al., 2020; Zwaan et al., 2020a). When deformed, these viscous materials flow rather than forming discrete fault structures, and in contrast to the granular materials, their behaviour is strongly strain rate dependent. Importantly, viscous materials are much weaker than their brittle counterparts, and in basin inversion models they are often used to simulate intra-crustal (salt) detachments (Letouzey, 1995; Brun and Nalpas, 1996; Dooley and Hudec, 2020) or the weak ductile lower crust and lower lithospheric mantle layers (Gartrell et al., 2005; Konstantinovskaya et al., 2007; Mattioni et al., 2007; Cerca et al., 2010; Munteanu et al., 2013, 2014) (Fig. 4). Viscous model materials used in basin inversion experiments commonly have a near-Newtonian rheology at typical model deformation rates, which aims to represent dislocation creep over geological timescales (Weijermars, 1986; Weijermars and Schmeling, 1986; Rudolf et al., 2016, and references therein).

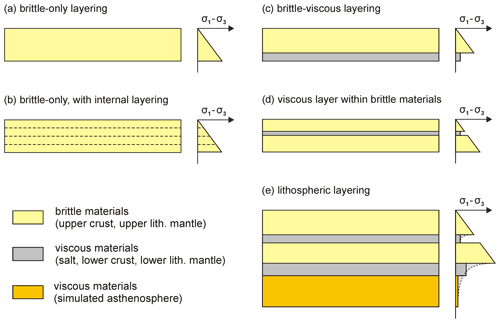
Figure 4 Examples of model layering used for basin inversion experiments seen in section view, including schematic strength profiles. (a–d) Crustal-scale layering options. (a) Homogeneous layer of brittle model material. (b) Brittle model material interlayered with other brittle materials for visualization or to simulate brittle-style detachments (e.g. Buchanan and McClay, 1991). (c) Brittle–viscous layering, with a cover of brittle model material overlying a viscous detachment layer that decouples the brittle cover from the (rigid) model base. (d) Viscous detachment within the brittle model materials (such as a weak shale or salt layer, e.g. Brun and Nalpas, 1996). (e) Brittle–viscous multilayer arrangement representing the whole of the lithosphere (e.g. Cerca et al., 2010). The dotted line in the strength profile of panel (e) indicates a schematic lithospheric strength profile that is approximated in the model (see, e.g. Brun, 1999).

3.2 Overview of general basin inversion set-ups

When modelling basin inversion, a basic necessity is choosing a set-up that can induce the type of deformation required for both the initial extensional phase and the subsequent compressional (inversion) phase (Fig. 5). Both deformation phases are generally induced by deformation rigs that move basement blocks, base plates, rubber sheets, or sidewalls and backstops below or into the analogue model materials representing (parts of) the Earth's lithosphere. An exception are the models by Gartrell et al. (2005) and Konstantinovskaya et al. (2007), who instead applied a system of pulleys and weights to drive deformation (force boundary condition). Most inversion models focus on the crustal scale, where the set-up may reflect specific assumptions regarding the properties of the basement or mantle below (see Zwaan et al., 2019, 2021, 2022, for a discussion on this topic), but some modellers have also simulated basin inversion on a lithospheric scale (Gartrell et al., 2005; Cerca et al., 2010).

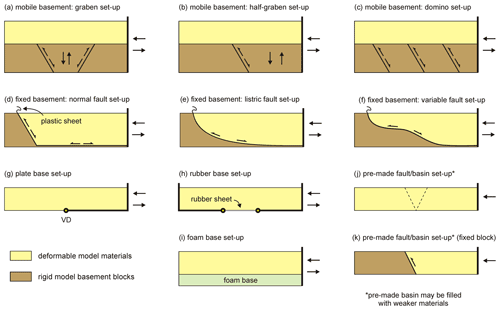
Figure 5 Examples of basin inversion model set-ups illustrated in section view. (a–c) Mobile basement block set-ups. (a) Full-graben set-up. Note that the graben boundary faults can be set to have different dip angles (e.g. Koopman et al., 1987). (b) Half-graben set-up. (c) Domino block set-up (e.g. Buchanan and McClay, 1992). (d–e) Fixed basement (footwall) block set-ups. (d) Steep normal fault set-up (e.g. Buchanan and McClay 1991). (e) Listric fault set-up (e.g. Buchanan and McClay, 1991). (f) Variable geometries of the basement block can also be applied (e.g. McClay, 1995; Ferrer et al., 2016). (g) Plate base set-up, with the edge of the plate base inducing a velocity discontinuity (VD) (e.g. Mitra and Islam, 1994). (h–i) Distributed deformation set-ups. (h) Rubber base set-up, with a rubber sheet spanned between two base plates creating a zone of distributed deformations (e.g. Amilibia et al., 2005). Note that the rubber sheet may also cover the whole base of the model (McClay, 1989). (i) Foam base set-up (e.g. Guillaume et al., 2022; Richetti et al., 2022). (j–k) Pre-made fault or basin set-up, with either (j) a pre-made fault or basin within the deformable model materials, potentially filled with weaker material (e.g. Panien et al., 2006a), or (k) a basin built next to a fixed footwall block (e.g. Letouzey et al., 1995).

The first basin inversion experiments by Lowell (1974) and Koopman et al. (1987) involved mobile basement blocks (Fig. 5a–c). Such set-ups are used to simulate the deformation of a sedimentary cover on top of a rift basin or normal fault developing in the basement (Sanford et al., 1959; Naylor et al., 1994; Dooley et al., 2003; Burliga et al., 2012a). By moving a hanging wall basement block downward between two footwall blocks, or along a single footwall block for a full-graben setting or a halfgraben setting, respectively, the overlying model materials are deformed and a basin is generated. This basin can subsequently be inverted by simply moving the hanging wall block upward again (Koopman et al., 1987; Mitra, 1993; Mitra and Islam, 1994; Burliga et al., 2012b; Moragas et al., 2017). Koopman et al. (1987) also simulated half-graben development above a tilting basement block, and a more complex version of this set-up, used by Buchanan and McClay (1992), McClay (1995), Jagger and McClay (2016), and Ferrer et al. (2022a), involves a series of basement blocks that can be tilted simultaneously (domino faulting) to form a broad extensional basin rather than a single half-graben (Fig. 5c). The basement block motion in both of these set-ups can simply be reversed to induce inversion.

Modellers have also regularly used set-ups with fixed basement (footwall) blocks (Fig. 5d–f). In these models, a plastic sheet between the basement block and the model materials is connected to a moving sidewall or backstop so that the outward motion of the sidewall caused normal faulting above the footwall block. The resulting rift structures are subsequently inverted by moving the sidewall inward again (McClay, 1989, 1995; Buchanan and McClay, 1991; Mitra 1993; Mitra and Islam, 1994; Gomes et al., 2006, 2010). Alternatively, one can also move the footwall block itself (Yamada and McClay, 2004; Ferrer et al., 2016), which is however mostly a change of reference frame (see discussion in Zwaan et al., 2019). Various authors have applied complex footwall block geometries (McClay, 1995; Ferrer et al., 2016; Roma et al., 2018a, b) (Fig. 5f) or different backstop geometries (Gomes et al., 2010).

Base plate or conveyer belt set-ups have been commonly used for modelling extensional tectonics (Allemand et al., 1989; Allemand and Brun, 1991; Brun and Tron, 1993; Keep and McClay, 1997; Michon and Merle, 2000, 2003; Gabrielsen et al., 2016; Zwaan et al., 2019) (Fig. 5g). The edge of the base plate or conveyor belt creates a velocity discontinuity (VD) representing a fault or shear zone in the basement or upper mantle that localizes deformation in the overlying model materials as the plate is pulled out from under them, resulting in the development of a rift basin (Fig. 5g). Subsequently, the motion of the base plate can be reversed, inducing compression along the VD and in the previously established rift basin (Mitra and Islam, 1994; Eisenstadt and Withjack, 1995; Nalpas et al., 1995; Brun and Nalpas, 1996; Bonini, 1998; Dubois et al., 2002; Mattioni et al., 2007; Konstantinovskaya et al., 2007; Pinto et al., 2010; Muñoz-Sáez et al., 2014). Some models include two plates on both sides of the model that move apart in opposite directions during both extension and compression (Munteanu et al., 2014). Panien et al. (2005), Del Ventisette et al. (2005, 2006), Yagupsky et al. (2008), Granado et al. (2017), and Miró et al. (2022) applied a base plate mechanism to induce a rift basin, which was subsequently inverted by moving a backstop into the model.

Other basin inversion set-ups involve distributed basal deformation, for instance by means of a basal rubber sheet. This rubber sheet is generally inserted between two base plates (Amilibia et al., 2005; Dooley and Hudec, 2020; Yu et al., 2021) (Fig. 5h), even though some authors have also used a rubber sheet covering the full length of the model (McClay, 1989). By pulling apart the base plates or sidewalls between which the rubber is fixed, the rubber is stretched and creates a distributed type of deformation at the model base, rather than the highly localized deformation induced by a VD (Vendeville et al., 1987; Withjack and Jamison, 1986; McClay, 1990; McClay et al., 2002; Corti et al., 2007; Henza et al., 2010, 2011; Zwaan et al., 2019). Similar to the base plate models, the resulting rift structure can be simply inverted by moving the plates (or sidewalls) together again so that the rubber base contracts (Amilibia et al., 2005; Dooley and Hudec, 2020). Alternatively, foam or a combination of foam and plexiglass bars can be used to reproduce distributed deformation at the model base (Scheurs and Colletta, 1998; Zwaan et al., 2016; Guillaume et al., 2022; Richetti et al., 2022). Instead of being stretched, the foam or foam and plexiglass assemblage needs to be compressed between sidewalls first, and as the model sidewalls are moved apart or together, the foam extends or contracts in a distributed fashion, deforming the overlying materials (Zwaan et al., 2019, 2020b; Guillaume et al., 2022; Richetti et al., 2022).

Some researchers simplify the modelling procedure by establishing the basin or normal fault(s) already during model preparation (Fig. 5j), obtaining inversion by subsequently moving a backstop into the model (Sassi et al., 1993; McClay et al., 2000; Panien et al., 2006a; Marques and Nogueira, 2008; Di Domenica et al., 2014; Martínez et al., 2016, 2018; Martínez and Cristallini, 2017; Lebinson et al., 2020). Such backstop models can be combined with fixed basement blocks that represent the footwall block of a rift boundary fault or half-graben structure (Vially et al., 1994; Letouzey et al., 1995; Philippe, 1995; Lebinson et al., 2020, Fig. 5k). Vially et al. (1994), Letouzey et al. (1995), and Roure and Colletta (1996) have also inverted pre-built basins in a deformable basement block set-up (Fig. 5b), where only inversion of the pre-built basin was applied. Buchanan and McClay (1992) used a domino rig (Fig. 5c) for inverting a series of pre-built basins instead. It may be noted that these moving sidewall models, which include pre-built basins or faults, may overlap to a degree with thrust wedge experiments (e.g. Colletta et al., 1991; Cotton and Koyi, 2000; Graveleau et al., 2012; Payrola et al., 2012; Oriolo et al., 2015; Villarroel et al., 2020; Borderie et al., 2018, 2019; Schori et al., 2021).

Finally, some modellers have simulated basin inversion on a lithospheric scale rather than on the more standard (upper) crustal scale (Gartrell et al., 2005; Cerca et al., 2010). Lithospheric-scale modelling of rifting in a normal gravity field (in contrast to centrifuge methods with enhanced gravity conditions, e.g. Corti et al., 2003; Agostini et al., 2009; Zwaan et al., 2020a) is generally done with set-ups involving mobile sidewalls (Allemand et al., 1991; Brun and Beslier, 1996; Nestola et al., 2013, 2015; Beniest et al., 2018; Zwaan and Schreurs, 2022a, b). By moving the sidewalls apart, the model, with layers representing the whole lithosphere floating on a dense liquid or weak viscous layer simulating the underlying asthenospheric mantle (Fig. 4e), is stretched. By simply reversing the motion of the sidewalls, rift basins that developed during the initial extension phase may be inverted. The available lithospheric-scale basin inversion model results come from very specific set-ups (involving complex lithospheric inheritance in the case of Cerca et al., 2010, and the oblique reactivation of a transfer fault system in the case of Gartrell et al., 2005), preventing generalized insights so far. We therefore do not address these models in further detail in this review.

3.3 Additional model set-up variations

We described the general model set-ups and model materials in the previous section. However, there are numerous possible variations and adaptations, especially regarding model layering and structural inheritance in both 2D and 3D (Fig. 6).

Even though many basin inversion set-ups are essentially 2D, the three-dimensional nature of tectonic processes is an important consideration when running basin inversion models. Plate motion directions are known to change over time, which can lead to changes in tectonic regimes (Sibuet et al., 2004; Philippon and Corti, 2016; Schmid et al., 2017; Brune et al., 2018; Angrand et al., 2020). To account for such changes in direction between deformation phases, modellers need modelling machines that can reproduce these kinematic changes (Fig. 6a–c). This can be done by simply repositioning the motor that controls the inward and outward motion of the moving parts with respect to the model (Dubois et al., 2002; Nalpas et al., 1995; Brun and Nalpas, 1996; Pinto et al., 2010), or by combining perpendicular and lateral motion to allow for oblique extension and oblique compression (Schreurs and Colletta, 1998; Mattioni et al., 2007) (Fig. 6a–c). Some authors have even applied rotational extension and compression in their inversion models (Jara et al., 2015, 2018) (Fig. 6d–f).

A further option to add 3D complexity is the inclusion of different along-strike base plate geometries, such as oblique VD's (Panien et al., 2005; Ustaszewski et al., 2005; Munteanu et al., 2014; Jara et al., 2015, 2018; Granado et al., 2017; Wang et al., 2017; Deng et al., 2019), transfer fault structures (Konstantinovskaya et al., 2007; Likerman et al., 2013), and pull-apart systems (Wang et al., 2017, Fig. 6g–i). Similarly, complex 3D variations such as along-strike curving geometries have been applied in basement block set-ups (Yamada and McClay, 2003a, b, 2004). Modellers have also tilted the model base to accomplish complex layered geometries and heterogeneous normal stresses (Philippe, 1995; Granado et al., 2017; Borderie et al., 2019).

Additional variations can be made to the general model layering (Fig. 4). Weak granular materials (Sect. 3.1.2) can be used to simulate (basal) detachment layers (Buchanan and McClay, 1991; Panien et al., 2006a). Viscous materials are often used to simulate weak layers or detachments in basin inversion models (Fig. 4). For instance, Vially et al. (1994), Letouzey et al. (1995), Nalpas et al. (1995), Brun and Nalpas (1996), Dubois et al. (2002), Ferrer et al. (2016) Granado et al. (2017), Roma et al. (2018a, b), and Dooley and Hudec (2020) added layers of viscous material to their sand pack for simulating weak (salt) intervals in their basin inversion experiments, decoupling the simulated sedimentary cover from the basement units (Fig. 4c, d). Patches of viscous materials are used as a handy method to distribute crustal deformation above an VD that would otherwise (too) strongly localize this deformation in crustal-scale base plate models (Brun and Nalpas, 1996; Del Ventisette et al., 2005, 2006; Sani et al., 2007; Pinto et al., 2010; Muñoz-Sáez et al., 2014; Likerman et al., 2013; Jara et al., 2015, 2018), even though deformation may also be focussed along the edges of these patches. Other researchers have applied a viscous layer throughout the model to simulate a ductile lower crustal layer underlying the brittle upper crust (Konstantinovskaya et al., 2007; Mattioni et al., 2007; Bonini et al., 2012; Munteanu et al., 2013, 2014, Fig. 4d).

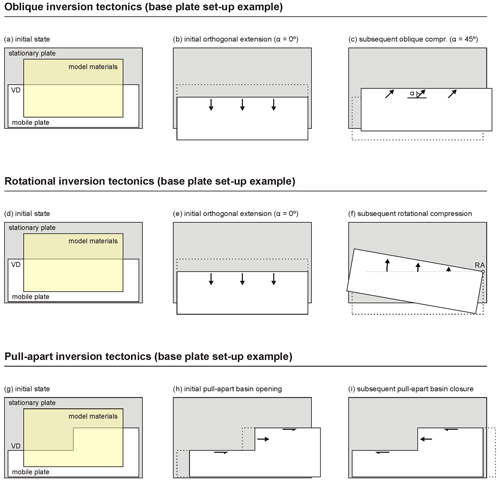
Figure 6 Examples of 3D kinematics in basin inversion models. (a–c) Oblique inversion tectonics example based on Brun and Nalpas (1996). The plate motion direction is defined as angle α, the angle between the normal to the model axis and plate motion direction (e.g. Zwaan et al., 2016; Brune et al., 2018, and references therein). VD stands for velocity discontinuity (mobile base plate edge). (d–f) Rotational inversion tectonics example based on Jara et al. (2015, 2018). RA stands for rotation axis. (g–i) Inverted pull-apart basin example based on Wang et al. (2017). Modellers have used a wide variety of other base plate geometries for basin inversion experiments (see Sect. 3.3.).

Furthermore, variations within the model layers allow for the simulation of complex 3D structural inheritance. For instance, weak granular materials can serve to simulate sedimentary basin infill (Martínez and Cristallini, 2017; Panien et al., 2005; Yagupsky et al., 2008). Pre-cut fault planes in brittle layers serve to localize deformation (Panien et al., 2006a; Di Domenica et al., 2014). Marques and Nogueira (2008) even embedded viscous material in such pre-existing faults during model preparation, reproducing the effects of salt injected along a fault plane during deformation. Additional methods to generate complex weaknesses is the application of patches or “seeds” of viscous material to locally weaken the overlying sand layers, thus localizing deformation (Munteanu et al., 2013; Dooley and Hudec, 2020).

3.4 Inclusion of additional geological processes

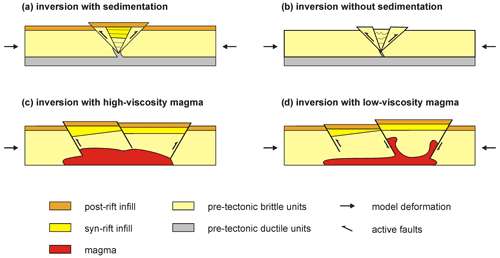
Surface processes (i.e. erosion, transport, and syn-kinematic sedimentation) can have important impacts on the evolution of both extensional and compressional tectonic systems (Koons, 1990; Burov and Cloetingh, 1997; Buiter et al., 2008; Graveleau et al., 2012; Zwaan et al., 2018a; Borderie et al., 2019) and are thus naturally of importance for basin inversion too. Often modellers simulate extension by filling in the rift basin with (weaker) brittle model materials during or after the initial extensional deformation phase (Panien et al., 2005; Pinto et al., 2010; Muñoz-Sáez et al., 2014; Ferrer et al., 2016; Granado et al., 2017; Moragas et al., 2017; Richetti et al., 2022). In addition, some studies have included the deposition of sediments during the inversion stage (e.g. Buchanan and McClay, 1991; McClay, 1995; Yamada and McClay, 2004; Jagger and McClay, 2016; Roma et al., 2018a, b). Including sedimentation in most cases is done by filling in the negative topography formed in the model or by adding a blanket layer covering the whole model, either by sieving or by pouring granular materials, although Moragas et al. (2017) included the simulation of prograding sequences. Adding erosional processes is however a challenging undertaking. Either one must determine where erosion is taking place in the model, and how much model material needs to be removed, or one needs to develop a physical method to directly include active surface processes in tectonic experiments (including precipitation, erosion, transport, and sedimentation, e.g. Graveleau et al., 2011, 2015; Reitano et al, 2020, 2022). To our knowledge, these more complex methods to simulate surface processes have not been used for typical basin inversion modelling so far due to their natural and technical complexity, although Strzerzynski et al. (2021) applied such methods in an analogue modelling study of inversion along the Algerian Margin.

Magmatism is a further important geological process that has been frequently studied in analogue models (Corti et al., 2003, 2004; Poppe et al., 2019; Maestrelli et al., 2021). However, so far only a few studies have included magmatic processes in basin inversion models (Martínez et al., 2016, 2018). Magmatism in these inversion models is achieved by injecting vegetable oil from the bottom of the model set-up during the inversion phase.

3.5 Model scaling

Scaling of analogue models is necessary to guarantee the similitude between a model and its natural equivalent or prototype (Hubbert, 1937; Ramberg, 1981), allowing for accurate model–nature comparisons. Similitude is achieved by ensuring (1) geometrical, (2) kinematic, and (3) dynamic similarity between the model and prototype. Geometrical similarity requires that all distances (length, width, depth, layer thickness) in the analogue model must have the same proportions as the natural example. Kinematic similarity signifies geometric and temporal similarity of the model and prototype, realized through similarity of velocities. Finally, dynamic similarity is established when all forces, stresses, and material strengths are properly translated from the natural example to the model scale. Although it is practically impossible to incorporate all detailed complexities that characterize natural geological settings into a small laboratory experiment, a correct scaling of the dominant factors controlling deformation will allow the scaling criteria to be fulfilled. The geological setting is usually approximated with a relatively simple model that uses as few parameters as possible to simulate the system in a meaningful way.

3.5.1 Scaling of brittle materials

Although in the past analogue modellers have generally assumed that granular materials behave according to the Coulomb failure criterion (Coulomb, 1773) (Eq. 1) with constant frictional properties, these materials show a more complex behaviour. Shear tests on granular materials reveal an elastic or frictional plastic behaviour with a phase of strain hardening until peak strength, corresponding to shear zone initiation, with a subsequent phase or strain softening until a dynamic-stable strength value is reached. If shearing is paused and subsequently resumed, shear stress increases to a second peak strength (reactivation peak strength), which corresponds to shear zone reactivation and occurs at a lower stress value than the one required for new shear zone initiation (Lohrmann et al., 2003; Panien et al., 2006b; Klinkmüller et al., 2016). From these shear tests, internal friction angles at first peak strength, dynamic-stable strength and reactivation peak strength can be deduced for a particular granular material, generally with the highest values of internal friction angle at first peak strength, lowest values at dynamic-stable strength, and intermediate values at reactivation peak strength (Panien et al., 2006b; Klinkmüller et al., 2016).

In this context, the brittle behaviour of the upper crust is roughly characterized by angles of internal friction between ca. 30 and 40^∘ and cohesion values between 0 and 50 MPa (Byerlee, 1978). In order to be properly scaled, model materials must have similar angles of internal friction as the upper crust, as well as an appropriate (low) cohesion value (Abdelmalak et al., 2016). These criteria are met by many granular materials, which have angles of internal friction between ca. 30 and 40^∘ and negligible cohesion (Krantz, 1991b; Schellart, 2000; Lohrmann et al., 2003; Panien et al., 2006b; Klinkmüller et al., 2016). Standard granular materials therefore generally produce shear zones that have similar geometries as faults in intact brittle lithosphere (Schellart and Strak, 2016, and references therein), ensuring proper geometrical and dynamic similarity between models and nature (Hubbert, 1937, 1951; Sanford, 1959). Brittle materials used to implement detachments (micro-beads) have an angle of internal friction at peak strength of ca. 20^∘ or lower (Panien et al., 2006b; Bonini et al., 2012; Klinkmüller et al., 2016), reflecting the relative weakness of such detachment layers in nature. In addition, brittle materials with higher cohesion values (e.g. mixtures of granular materials or wet clay) are appropriate for models simulating the uppermost parts of the crust (Arch et al., 1988; Abdelmalak et al., 2016; Montanari et al., 2017; Eisenstadt and Sims, 2005).

Brittle dynamic similarity can furthermore be secured by comparing the dimensionless ratio (R_s) between gravitational stresses and cohesive strength of the model and the natural prototype, which, if similar, indicates proper scaling:

$$\begin{array}{}\text{(2)}& R_{\mathrm{s}}={\displaystyle \frac{\mathrm{gravitational}\mathrm{stress}}{\mathrm{cohesive}\mathrm{strength}}}={\displaystyle \frac{\mathit{\rho }\cdot g\cdot h}{C_{\mathrm{0}}}}.\end{array}$$

Here ρ is density, g gravitational acceleration, h a representative length scale, and C₀ cohesion.

3.5.2 Scaling of viscous materials

In contrast to their brittle counterparts, viscous materials show time-dependent behaviour. When no strain hardening or softening occurs (as is the case for most viscous materials used in basin inversion models), the material's viscosity remains constant and its rheology is characterized by Newtonian flow. We can then apply the following formulas to determine the stress ratio σ^* (convention for ratios: ${\mathit{\sigma }}^{*}={\mathit{\sigma }}_{\mathrm{model}}/{\mathit{\sigma }}_{\mathrm{nature}}$) (Weijermars and Schmeling, 1986):

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}^{*}={\mathit{\eta }}^{*}\cdot {\dot{\mathit{\epsilon }}}^{*}={\mathit{\rho }}^{*}\cdot g^{*}\cdot h^{*}.\end{array}$$

Here ${\dot{\mathit{\epsilon }}}^{*}$ is the strain rate ratio and h^* the viscosity ratio. Subsequently, the velocity ratio (v^*) and the time ratio (t^*) are obtained so that a deformation rate or a time span in the laboratory can be translated to their respective values in nature and vice versa:

$$\begin{array}{}\text{(4)}& {\dot{\mathit{\epsilon }}}^{*}={\displaystyle \frac{v^{*}}{h^{*}}}={\displaystyle \frac{\mathrm{1}}{t^{*}}}.\end{array}$$

In order to secure proper dynamic similarity, the dimensionless Ramberg number (R_m), involving the ratio between gravitational stress and viscous stress of the model, and its natural equivalent can be compared (Weijermars and Schmeling, 1986):

$$\begin{array}{}\text{(5)}& R_m={\displaystyle \frac{\mathrm{graviational}\mathrm{stress}}{\mathrm{viscous}\mathrm{stress}}}={\displaystyle \frac{\mathit{\rho }\cdot g\cdot h}{\dot{\mathit{\epsilon }}\cdot v}}={\displaystyle \frac{\mathit{\rho }\cdot g\cdot h^{\mathrm{2}}}{\mathit{\eta }\cdot v}}.\end{array}$$

3.5.3 Typical scaling parameters for inversion models

Although every basin inversion modelling study has its own specific scaling parameters, these parameters generally fall in a clear range (which are in fact quite typical of analogue models in general, and are summarized in Table 1). Basin inversion models are generally several decimetres, up to perhaps a metre in size (width and length), with model layer thicknesses on the order of several to perhaps tens of centimetres. A centimetre in these models may represent one to several kilometres in nature, and model material densities are often on the order of 1000–2000 kg m⁻³, whereas rock densities range between 2300 and 3000 kg m⁻³. Basin inversion models mostly involve viscous materials with viscosities on the order of 10³ to 10⁵ Pa s, whereas weak ductile layers in the upper crust may have viscosities on the order of 10¹⁴ to 10¹⁸ Pa s (e.g. evaporites and shales; see, e.g. Warren, 2016), and ductile parts of the lower crust have viscosities between 10¹⁹ and 10²³ Pa s (e.g. Buck, 1991; Warren, 2016). Deformation rates in terms of imposed sidewall or base plate displacements are generally a few millimetres to a couple of centimetres per hour, which for models involving viscous layers scales to some millimetres to over a centimetre per year in nature, which is well in line with tectonic displacements observed in nature (e.g. ArRajehi et al., 2010; Saria et al., 2014). Note that the deformation rate can be varied at will for brittle-only models due to the general strain-rate-independent behaviour of brittle model materials.

Table 1 Typical scaling parameters applied for analogue models of basin inversion.

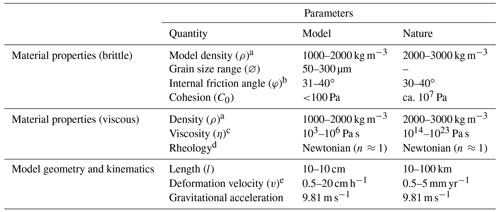
^a Bulk material density can vary between 1000 and 4000 kg m⁻³. The porosity of granular materials makes a big difference, as does the water content in clays and the model preparation method (e.g. materials are sieved, poured, scraped). ^b This includes internal friction angles at peak strength, dynamic-stable strength, and reactivation strength for most granular materials, excluding very well-rounded granular materials such as micro-beads, which have much lower internal friction values. Note that the often-used friction coefficient (μ) is defined as tan (φ). ^c May depend on strain rate if the material deviates from a (near-)Newtonian rheology. ^d Generally used analogue materials show (near-)Newtonian behaviour (silicone or PDMS), where n≈1. In nature, this represents the dislocation creep deformation mechanism, valid for gradual deformation over geological time periods (Rudolf et al., 2016, and references therein). ^e Most relevant for the scaling of viscous materials, as the rheology of granular materials is considered to be generally strain rate independent.

3.6 Model monitoring and analysis

A key part and the great strength of any analogue modelling study is the monitoring and quantification of model deformation over time. Since the dawn of analogue tectonic modelling, researchers have developed a variety of techniques, ranging from (time-lapse) photography, the generation of cross-sections, and topography analysis to advanced 2D and 3D digital image correlation techniques and X-ray CT scanning (e.g. Ranalli, 2001; Bonini et al., 2012; Ferrer et al., 2022b; Zwaan and Schreurs, 2022a, b). Most studies included a combination of these techniques.

3.6.1 Photography

Photography is a trusted method for analogue model monitoring, and time-lapse photography provides an especially excellent first-order insight into model deformation. Model monitoring through photography in basin inversion studies can be split into top-view and side-view approaches (Fig. 7a, b). Many modellers routinely apply top-view photography, where lighting is set to cast shadows that highlight surface structures and where a surface grid serves to trace deformation (Brun and Nalpas, 1996; Del Ventisette et al., 2005; Sani et al., 2007; Panien et al., 2005; Yagupsky et al., 2008; Wang et al., 2017) (Fig. 7a). Such top-view time-lapse imagery of the model surface allows for statistical fault orientation analysis (Jara et al., 2015) and fault length and displacement analysis (Keller and McClay, 1995).

In addition to top-view photography, model set-ups with transparent sidewalls enable direct monitoring of model deformation at the sides of the experiment (Koopman et al., 1987; McClay, 1989, 1995; Buchanan and McClay, 1992; McClay and Buchanan, 1992; Gomes et al., 2006, 2010; Jagger and McClay, 2016; Lebinson et al., 2020, Fig. 7b). In these cases, sidewall friction may cause boundary effects (e.g. Souloumiac et al., 2012), but this can be mitigated by using products like Rain-X spray (otherwise used for car windshield treatment, Krantz, 1991a; Herbert et al., 2015) or transparent Teflon foil (Cruz et al., 2010). In some models involving clay no transparent sidewalls were needed as the clay was stable enough to not deform under its own weight (Mitra, 1993; Mitra and Islam, 1994). By adding layers and other markers in section view, a first-order quantification of deformation becomes possible (Marques and Nogueira, 2008; Mitra, 1993; Mitra and Islam, 1994; McClay, 1995, Fig. 7b).

3.6.2 Model sectioning

Making cross-sections is another straightforward and popular method for analysing the final stages of internal model deformation (Eisenstadt and Withjack, 1995; Brun and Nalpas, 1996; Dubois et al., 2002; Amilibia et al., 2005; Del Ventisette et al., 2005, 2006; Konstantinovskaya et al., 2007; Munteanu et al., 2014; Dooley and Hudec, 2020, Fig. 7c). Prior to sectioning, models with sand layers are commonly stabilized by wetting these layers. If required, the wet sand can be frozen for extra stability (Cerca et al., 2010), which has the additional advantage that any viscous materials will be stiffer and thus more stable too. Alternatives are to impregnate the sand with additives (McClay and Buchanan, 1992), for instance with hot gelatine (Jara et al., 2015). Cutting sections can be done manually using knives, cardboard cutters or saws, or automatically with a dedicated slicing machine (Ferrer et al., 2016; Jagger and McClay, 2016; Dooley and Hudec, 2020). Differently coloured layers allow for an assessment of the model's internal deformation (Fig. 7c).

A drawback of making cross-sections is that the model will have to be destroyed, meaning that sectioning can only be done at the end of the model run. A clever workaround is presented by Burliga et al. (2012b), who sectioned only part of the model to obtain a continuous evolution, but this will only work in a model with no lateral variations in its set-up. Yamada and McClay (2003a, b, 2004) simply ran the same model set-up multiple times, cutting different sections with different orientations in these repeated models, including horizontal sections. Such horizontal sections were also made by Deng et al. (2019) and can be used to create isopach maps (Yamada and McClay, 2004). Further advanced model analysis through sectioning is presented by McClay (1996), Ferrer et al. (2016), Granado et al. (2017), Roma et al. (2018a, b), Dooley and Hudec (2020), and Ferrer et al. (2022a), who used fine-spaced cross-sections of constant thickness made with slicing machines to construct 3D voxel images and pseudo-seismic volumes (Fig. 7e). This method allows for a unique interpretation of 3D internal model structures in a very similar fashion to the analysis of 3D seismic surveys (Fig. 7e).

3.6.3 Topography analysis

Where top-view imagery gives a first impression of surface deformation, detailed topography analysis provides quantified insights into surface deformation (Fig. 7d). Various options are available, such as 3D digital image correlation (DIC) image analysis (Dooley and Hudec, 2020; Schmid et al., 2022, Sect. 3.6.4), photogrammetry on stereoscopic photographs (Maestrelli et al., 2020, 2021; Zwaan et al., 2020a, 2021, 2022), and fringe projection analysis (Barrientos et al., 2008; Martínez et al., 2016). The technique that has been generally used for topography analysis of basin inversion models is surface scanning through laser or white light methods (Bonini et al., 2012; Likerman et al., 2013; Jara et al., 2015, 2018; Granado et al., 2017; Deng et al., 2019, Fig. 7d). Such surface scanning generates digital elevation models that can be processed in GIS software, allowing, for example, the extraction of topographic profiles over time (Jara et al., 2015; Reitano et al., 2020, 2022).

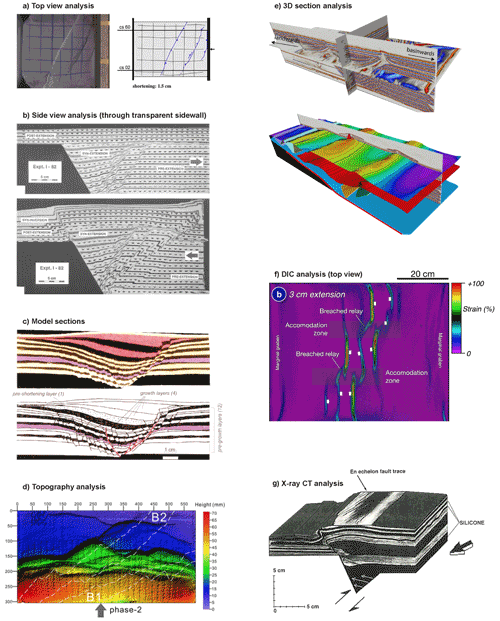
Figure 7 Examples of techniques used for the analysis of basin inversion models. (a) Top-view image from an inversion model by Panien et al. (2005), reproduced with permission from Elsevier. (b) Side-view imagery of an inversion model with a fixed rigid footwall block set-up after McClay (1995), reproduced with permission from the Geological Society, London. (c) Cross-section of an inversion model with a base plate set-up after Eisenstadt and Withjack (1995), reproduced with permission from the Geological Society, London. (d) Topography map of a basin inversion model by Deng et al. (2019), obtained via surface laser scanning. (e) Advanced analysis of model cross-sections in 3D seismic interpretation software by Roma et al. (2018b), reproduced with permission from the Geological Society, London. (f) Strain map of a basin inversion model by Dooley and Hudec (2020), obtained through digital image correlation (DIC) analysis. (g) X-ray CT analysis of an inversion model involving a mobile basement block after Letouzey et al. (1995) (AAPG © 1995, reprinted by permission of the AAPG, whose permission is required for further use).

3.6.4 Digital image correlation (DIC)

Time-lapse imagery of analogue models allows for the quantification of model surface deformation through digital image correlation (DIC) techniques (e.g. Adam et al., 2005; Boutelier et al., 2019). This method compares images from different moments in time to derive surface displacement in map view, or when multiple view angles are available, in three dimensions. The surface displacement field can subsequently be used to extract the amount of strain, and even the type of faulting (Broerse et al., 2021; Krstekanicì et al., 2021). Furthermore, the 3D displacement field provides an alternative method for topography analysis (Schmid et al., 2022). Even though DIC analysis has recently become a standard in the analogue modelling toolbox, it has only been sparsely used for basin inversion models. So far only Wang et al. (2017), as well as Guillaume et al. (2022) and Richetti et al. (2022), have applied 2D DIC on surface imagery of their inverted pull-apart basin experiments and in their perpendicular (or oblique) inversion experiments, respectively, whereas Dooley and Hudec (2020) have used 3D DIC analysis for their inversion models of salt-bearing systems (Fig. 7f). Furthermore, Jagger and McClay (2016) have gone beyond the tracing of markers on side view imagery (Sect. 3.6.1) by applying DIC analysis for monitoring deformation on such imagery.

3.6.5 X-ray CT scanning

Most model monitoring techniques (top-view imagery, DIC analysis, and surface laser scanning) can only provide insights into model surface deformation. Whereas cross-sections allow us to catch a glimpse of internal model structures, this commonly applies to the final stage of model deformation only, since the model has to be physically cut. Furthermore, side-view imagery through a transparent sidewall does allow direct observation of model deformation, yet these observations are only in 2D section view. So far, the only practical method to obtain concrete 3D insights into internal model evolution involves X-ray CT scanning (Richard, 1989; Colletta et al., 1991; Schreurs et al., 2003; Zwaan et al., 2018a; Schmid et al., 2022, Fig. 7g). Such CT scanning, which uses X-rays to image the internal structures of a model, has been used in a number of basin inversion studies (Sassi et al., 1993; Vially et al., 1994; Letouzey et al., 1995; Roure and Colletta, 1996; Panien et al., 2005, 2006a; Mattioni et al., 2007). Not only does CT imagery allow unique visualization of 3D model-internal structures, it can also be used to extract specific horizons from the models (Konstantinovskaya et al., 2007). These horizons can, similar to normal cross-sections, be highlighted by using layers with different densities that appear in different grey shades on the CT scans (Letouzey et al., 1995, Fig. 7g). Furthermore, in a similar way to the side-view imagery obtained through a transparent sidewall (Sect. 3.6.1), we can trace material pathways over time by following markers included in the models (e.g. iodine powder in Panien et al., 2005).

4 Overview of representative modelling results

In this section we present overviews of modelling results that are representative of the general structures obtained in analogue models of inversion tectonics (Figs. 8–16). The overviews are categorized in sub-sections that address the results obtained by each of the major types of model set-ups introduced in Sect. 3.2 (mobile or fixed basement blocks, base plate, distributed basal deformation, and pre-built basin or fault), with attention to the general influence of model layering and 3D factors such as oblique inversion. It is also important to emphasize that analogue modelling results can vary significantly due to variations in material properties and handling techniques (e.g. Schreurs et al., 2006, 2016, Sect. 3), different degrees of sedimentation, or different amounts and rates of extension and subsequent compression. Furthermore, analogue modellers always need to consider the specific limitations related to their model set-up, as well as the risk of related boundary effects that may influence the model results (e.g. Buchanan and McClay, 1991; McClay, 1995; Koyi, 1997; Souloumiac et al., 2012; Schreurs et al., 2006; Zwaan et al., 2019). Furthermore, the vast range of possible variations in set-ups and results cannot always be fully accounted for in our generalized overviews, and not all combinations of parameters have been tested so far, leading to gaps in the overviews. Hence, we urge the reader to use these overviews as a first-order guide only, and we refer the reader to the original research for more details.

4.1 Mobile basement set-ups

Mobile basement set-ups were among the first set-ups used for basin inversion (Lowell, 1974; Koopman et al., 1987; Mitra and Islam, 1994) and are normally used for orthogonal inversion experiments (Figs. 5a–c, 8). In the case of a full-graben set-up with a brittle cover (Fig. 8a), initial extension and downward motion of the central rift wedge block leads to the development of a symmetrical graben structure and the creation of accommodation space that can be filled with syn-rift sediments (Fig. 8b). When applying subsequent shortening, the central basement block moves upward again, and the rift boundary faults reactivate (Fig. 8c). However, new low-angle thrust faults, also known as “footwall shortcuts”, develop in the brittle cover so that only part of the inversion is accommodated by reactivation of the original rift boundary faults (Fig. 3c). A similar result is observed in half-graben models with a brittle cover (Burliga et al., 2012b, Fig. 8d–f).

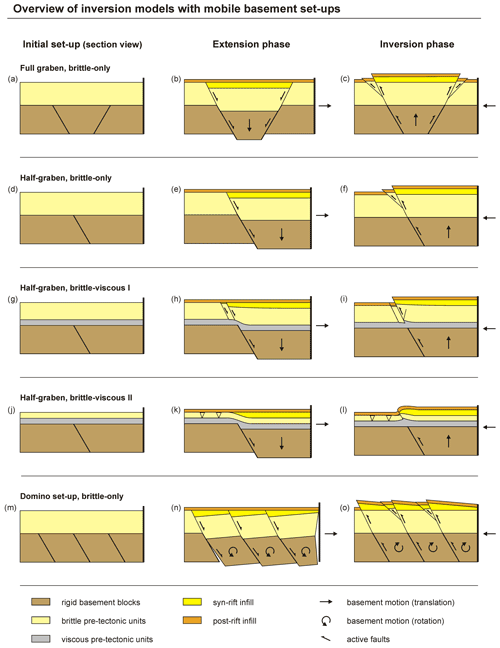
Figure 8 Section-view sketches of idealized results from basin inversion models involving a set-up with mobile basement blocks. (a–c) Full-graben set-up with brittle-only layering. (d–f) Half-graben set-up with brittle-only layering, with very similar inversion structures to those in the full-graben set-up. (g–i) Half-graben set-up I with brittle–viscous layering (high brittle-to-viscous thickness ratio). (j–l) Half-graben set-up II with brittle–viscous layering (low brittle-to-viscous thickness ratio). (m–o) Domino set-up with brittle-only layering. Images inspired by Koopman et al. (1987), Buchanan and McClay (1992), and Burliga et al. (2012b).

A viscous layer overlying the basement blocks detaches (decouples) the brittle overburden from the mobile basement and distributes the deformation induced by the basement fault (Fig. 8g–i). As a result, initial extension leads to the formation of multiple faults away from the basement fault (Fig. 8h), and subsequent inversion may only reactivate one of these faults (Fig. 8i) (Burliga et al., 2012b; Moragas et al., 2017). However, the (relative) thickness of the viscous layer and brittle cover has a strong influence on the coupling between cover and basement during extension, meaning that the structural evolution of such brittle–viscous inversion models can vary significantly (Withjack and Callaway, 2000). As also shown in previous modelling studies (Withjack and Callaway, 2000; Dooley et al., 2003; Moragas et al., 2017; Zwaan et al., 2020a), a relatively thin brittle cover may be subject to flexure during extension (Fig. 8j–l) (for more details see Burliga et al., 2012b). The impact of layer thickness on brittle-only systems should be much less important, as coupling is always high in such systems.

Finally, in models with domino set-ups as used by Buchanan and McClay (1992), McClay (1995), and Jagger and McClay (2016) a series of basement blocks is rotated (Fig. 8m–o), leading to the development of a series of half-grabens with growth strata during extension (Fig. 8n). Inversion of these half-grabens causes partial reactivation of initial normal faults, but also results in the development of footwall shortcuts akin to those in the (half-graben) models described above (Fig. 8c, f, o).

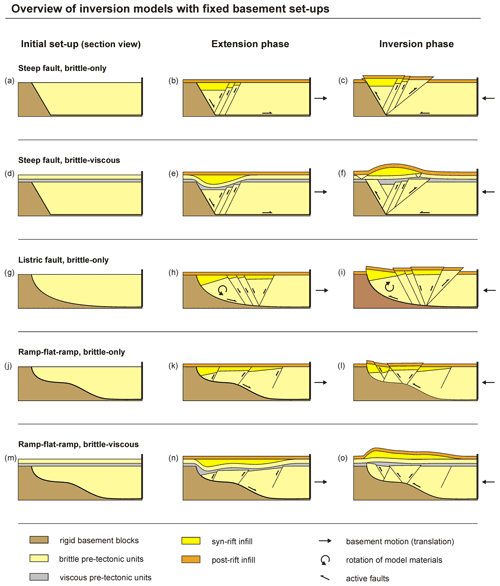
Figure 9 Section-view sketches of idealized results from basin inversion models involving a set-up with fixed basement blocks. (a–c) Inversion model with steep fault set-up and brittle-only model materials. (d–f) Inversion with steep fault set-up and a brittle–viscous layering. (g–i) Inversion model with a listric fault set-up and brittle-only model materials. Modellers have also included viscous layers in such a set-up, which has a similar impact as in the steep normal fault equivalent (Ferrer et al., 2016). (j–l) Inversion model with a ramp–flat–ramp fault set-up and brittle-only model materials. (m–o) Inversion with a variable fault dip set-up and a brittle–viscous layering. Image inspired by McClay (1989, 1995), Buchanan and McClay (1991), Gomes et al. (2006, 2010), and Ferrer et al. (2016).

Figure 10 A 3D drawing of inversion model results from Yamada and McClay (2004) (AAPG © 2004, image modified by permission of the AAPG, whose permission is required for further use).

4.2 Fixed basement set-ups

Similar to the mobile basement set-ups, fixed rigid basement (footwall) block set-ups have been used for some of the earliest basin inversion models (McClay, 1989, 1995; Mitra, 1993; Mitra and Islam, 1994; Buchanan and McClay, 1991). These set-ups primarily serve to study basin inversion as a 2D process with orthogonal extension followed by orthogonal compression (Figs. 5d–f, 9). The edge of the rigid basement block, representing a pre-existing basin boundary fault, can have various geometries (Figs. 5d–f, 9). It may be noted that the applied method of inversion (either by moving the backstop or moving the basement block relative to the model) can cause some variation in structural evolution. The description of these variations is beyond the scope of this review, and we refer the reader to the original publications for more details.

The most straightforward example is the steep normal fault set-up, with brittle-only materials (Buchanan and McClay, 1991; McClay, 1995; Ferrer et al., 2016, Fig. 9a). As extension is applied by either moving both the sidewall and the plastic sheet between the model materials and the rigid block away or by moving the rigid block itself away underneath from the model materials, normal faulting is induced (Fig. 9b). In this type of model, a series of normal faults dipping towards the basement block develops, as does a major normal fault along the basement block that accommodates most subsidence (Fig. 9b). Some minor tilting of layers towards the basement block may occur during extension. Inversion of this system slightly reactivates the normal faults from the initial extensional phase, but inversion is mostly accommodated by the major fault along the basement block, as well as by a major backthrust, effectively creating a general pop-up structure (Fig. 9c). The formation of such a pop-up structure is also observed in the models by Lebinson et al. (2020) with a similar basement block geometry, but which did not involve an initial extensional phase. Buchanan and McClay (1991) also show how, in the presence of a thick post-rift/syn-inversion sequence, the major fault along the basement block can change to a shallower angle when propagating into these shallower sequences (footwall cut-off).

As seen in the mobile basement models, adding a viscous layer into the pre-rift sequence can detach different parts of the model. Although no models with a basal viscous layer are known from literature, some researchers have included a viscous layer within the brittle materials of a fixed rigid basement model with a steep normal fault (Ferrer et al., 2016; Roma et al., 2018a, b, Fig. 9d–f). During rifting, the uppermost brittle units are detached from the lower faulted units and form a salt-detached ramp-syncline basin that is filled with syn-rift units (Fig. 9e). The continuity of the viscous layer that is deformed during the extensional phase becomes critical in the subsequent inversion phase. Contracting this system forms a pop-up structure in the units below the viscous layer and inverts the ramp syncline basin (Fig. 9f). However, the viscous layer acts as an efficient detachment during inversion so that part of the contractional deformation can be propagated above the footwall of the major fault (Ferrer et al., 2016). Importantly, the flow of the viscous layer causes welding (thinning) near the edge of the basement block and swelling (thickening) in other areas (Fig. 9f). The final structure is quite distinct from its counterpart without a viscous layer (compare Fig. 9c with Fig. 9f).

Another well-studied fixed rigid basement block set-up involves a listric fault geometry (McClay, 1989, 1995, 1996; Buchanan and McClay, 1991; McClay and Buchanan, 1992; Keller and McClay, 1995; Gomes et al., 2006, 2010; Ferrer et al., 2016, Fig. 9g–i). This set-up generally leads to the formation of a graben at some distance from the top edge of the basement block and results in strong tilting of layers near the block (Fig. 9h). During inversion, this tilting is reversed, and similar to its steep normal fault equivalent, a backthrust develops so that the overall final structure can again be described as a pop-up (Fig. 9i). Some of the other normal faults may be slightly reactivated as well (Fig. 9i). The listric fault results described here are typical of models involving a vertical backstop. Gomes et al. (2010) showed that different backstop geometries can also strongly affect reactivation (e.g. by promoting backthrusting). Furthermore, thin-skinned deformation, simulated by only having the upper part of the vertical backstop move inward (from either direction in section view) significantly alters the model results (Gomes et al., 2006), as is also known from thrust wedge experiments (Graveleau et al., 2012). Finally, adding a viscous layer to listric fault set-ups has a similar influence on structures as seen in the steep normal fault equivalent (Ferrer et al., 2016).

Various authors (McClay, 1989, 1995; Buchanan and McClay, 1992; Ferrer et al., 2016; Roma et al., 2018a, b) have tested the effects of more complex fault geometries, of which a version with a ramp–flat–ramp geometry has been most popular (Fig. 9j–l). Although the shallower parts of the main fault have a similar smooth shape to the main fault in the listric fault set-up, leading to similar tilting of layers near the basement block, the flat part in the middle causes a disturbance in the deformation field that can cause local reverse faulting during extension (Fig. 9k). When inverted, the tilted strata near the main fault are back-rotated, but typical of these (brittle-only) models is the development of a pop-up structure at the tip of the flat part (Fig. 9l). Similar to its steep fault equivalent (Fig. 9d–f), adding a viscous layer into the brittle layers of the variable fault set-up decouples the brittle materials above it from those below it, resulting in a sag-like syn-rift deposition pattern during extension (Ferrer et al., 2016; Fig. 9n). When considering the model parts below the viscous layer, inversion creates similar structures as in the brittle-only equivalent, but the flow of the viscous layer creates a smooth inverted basin in the cover units above the viscous layer (Fig. 9l, o). Similar to the steep fault model with a viscous layer, the viscous layer is locally thinned or thickened as well (Fig. 9f, o). For more insights into the complex interplay between basement fault geometry and brittle–viscous layering, see Ferrer et al. (2016) and Roma et al. (2018a, b).

Finally, even though most fixed basement set-up models were designed to investigate 2D inversion, Yamada and McClay (2003a, b, 2004) also explored the third dimension. In these 3D experiments, they applied sinusoidal along-strike variations of the fault surfaces, which induced complex structures in both the initial extension and the subsequent inversion phase. An example of their model results is shown in Fig. 10.

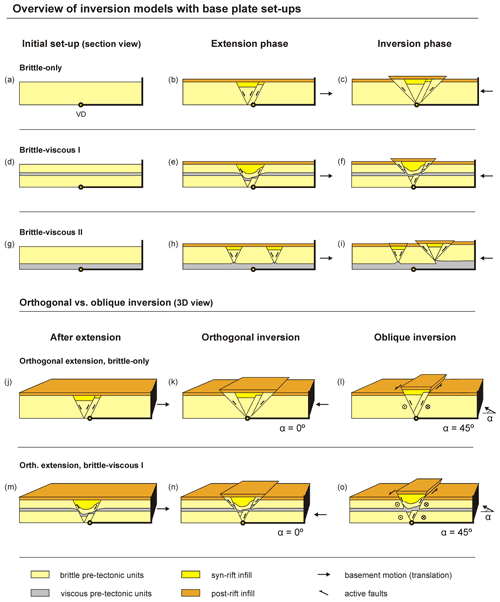
Figure 11 Sketches of representative results from basin inversion models involving a set-up with base plates. VD stands for velocity discontinuity. (a–c) Brittle-only inversion experiment. (d–f) Brittle–viscous set-up I with a viscous layer within the brittle layer. (g–i) Brittle–viscous set-up II with a viscous base layer. (j–o) The 3D effect of the inversion direction on reactivation of pre-existing faults. Oblique compression promotes oblique-slip reactivation of steep normal faults that are unlikely to be reactivated in an orthogonal compression situation. This effect is also observed in inversion models with a viscous basal detachment layer (Pinto et al., 2010; Muñoz-Sáez et al., 2014). Images inspired by Dubois et al. (2002), Nalpas et al. (1995), Brun and Nalpas (1996), and Mattioni et al. (2007).

4.3 Base plate set-ups

Base plate set-ups allow the localization of deformation along the edge of the base plate (velocity discontinuity, or VD) and have been regularly used for orthogonal (2D) as well as oblique (3D) inversion (Mitra and Islam, 1994; Eisenstadt and Withack, 1995; Nalpas et al., 1995; Brun and Nalpas, 1996; Bonini, 1998; Eisenstadt and Sims, 2005) (Fig. 11). Furthermore, some authors applied a base plate mechanism to induce a rift basin, which was subsequently inverted by moving a backstop into it (Panien et al., 2005; Del Ventisette et al., 2005, 2006; Sani et al., 2007; Yagupsky et al., 2008; Bonini et al., 2012; Likerman et al., 2013; Munteanu et al., 2014; Jara et al., 2015, 2018; Martínez et al., 2016, 2018; Granado et al., 2017). This latter type of model can be considered as deforming a pre-built basin by a backstop only and are therefore described in Sect. 4.5.

In base plate inversion models involving only brittle materials, the use of a VD leads to the development of a graben above the VD, which may become asymmetrical as extension progresses (Allemand and Brun, 1991; Ferrer et al., 2016) (Fig. 11a, b, j). Inverting this system in 2D causes reverse faulting starting from the VD and the formation of a pop-up structure, with only very limited reactivation of previously formed normal faults (Eisenstadt and Withjack, 1995; Eisenstadt and Sims, 2005) (Fig. 11c, k). Even so, some modelling studies (Nalpas et al., 1995; Brun and Nalpas, 1996) have shown that applying a high enough degree of oblique compression during inversion will (preferentially) reactivate the pre-existing normal faults in this type of experiment (Fig. 11j–l). However, Mitra and Islam (1994), who applied clay instead of granular materials, demonstrated that (2D) inversion could also be accommodated by large-scale folding, without reactivation of pre-existing faults or nucleation of new thrust faults. Such differences in model structures due to the use of either granular materials or clay (in this type of model) are excellently illustrated by the comparative modelling study by Eisenstadt and Sims (2005).

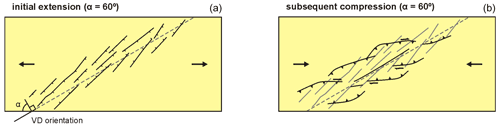
Figure 12 Top view of an inversion model involving a base plate set-up with brittle–viscous layering and (a) initial oblique extension leading to a series of en echelon normal faults, followed by (b) subsequent oblique inversion leading to (oblique) thrusting and strike-slip faulting. Inspired by Ustaszewski et al. (2005).

Nalpas et al. (1995) and Brun and Nalpas (1996) tested the influence of a viscous layer representing a salt interval in nature, embedded within the brittle model materials overlying a VD (Fig. 11d–f). The viscous layer partially decouples the brittle material above it from the brittle material below it during initial extension (Fig. 11e, m). During subsequent compression and inversion, the viscous material will advect along the active faults (Fig. 11f, n). Similar to the brittle-only base plate models (Fig. 11c, k), orthogonal inversion favours the development of new, lower-angle thrust faults (Fig. 11f, n), whereas oblique inversion preferentially reactivates the already existing basin boundary faults (Fig. 11l, o).

Adding a basal viscous layer to the base of the set-up will detach the VD (to a degree) from the cover (Dubois et al., 2002; Konstantinovskaya et al., 2007). Depending on various factors, such as layer thicknesses, extension velocity, viscosity of the detachment layer, and the presence of a single or double VD, a single or double-graben system or even a wide rift zone may develop during extension (compare the rift phases of, e.g. Dubois et al., 2002; Konstantinovskaya et al., 2007; Mattioni et al., 2007; see Zwaan et al., 2019; Zwaan et al., 2022, for a broader discussion on this topic). In Fig. 11h we show an example with a double-graben system developing above the VD, where some viscous material rises below the two grabens (Dubois et al., 2002; Mattioni et al., 2007). Note that such double grabens can also be formed when applying a narrow patch of viscous material above the VD (Pinto et al., 2010; Muñoz-Sáez et al., 2014). As this brittle–viscous system is inverted by orthogonal compression, basin boundary faults may slightly reactivate, but the bulk of the deformation is accounted for by new thrust faults rooting at the risen viscous material at the base of the graben, incorporating the original graben into a pop-up structure (Fig. 11i).

Dubois et al. (2002) show that, similar to the models without a viscous basal detachment (Fig. 11j–o), higher degrees of oblique compression during inversion will preferentially reactivate existing normal faults. Such ready reactivation due to oblique compression is also observed in Pinto et al. (2010) and Mattioni et al. (2007), even though the latter study involved a complex mechanical stratigraphy with multiple viscous layers. Still, it is not impossible for rift boundary faults to dominantly reactivate in brittle–viscous base plate models undergoing orthogonal inversion (Konstantinovskaya et al., 2007). Even more complex results are obtained by Ustaszewski et al. (2005), who applied a similar set-up involving initial oblique extension, followed by oblique compression (Fig. 12). Here the initial oblique extension phase developed en echelon normal fault structures typical of such a set-up (Tron and Brun, 1991; Brun and Tron, 1993; Bonini et al., 1997; Munteanu et al., 2014; Zwaan et al., 2021, 2022), which were partially reactivated during oblique compression (Fig. 12). The rate of compression and thus the degree of brittle–viscous coupling were both shown to have an effect on the resulting inversion structures (Ustaszewski et al., 2005).

As mentioned in Sect. 2.3, Wang et al. (2017) are to our knowledge the only authors to explore inversion of pull-apart basins (Fig. 6g–i). However, due to the rather specific set-up, including low degrees of transtension and transpression, and the sensitivity of such systems to slight deviations from pure strike-slip situations (Fedorik et al., 2019), a detailed discussion of the results in Wang et al. (2017) is beyond the general scope of this review.

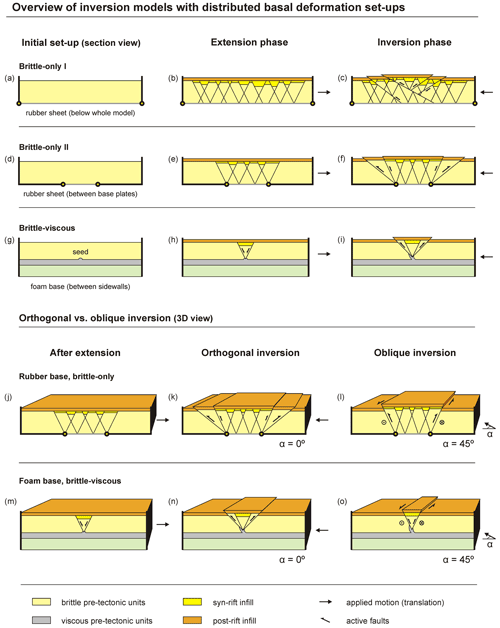
Figure 13 Sketches of representative results from brittle-only basin inversion models involving a set-up with distributed deformation at the base. (a–c) Brittle-only inversion experiment with a rubber base below the whole model. (d–f) Brittle-only inversion experiment with a rubber sheet spanned between two base plates. (g–i) Brittle–viscous inversion models with a foam base set-up. (j–o) The 3D effect of inversion direction on reactivation of pre-existing faults; oblique compression promotes oblique-slip reactivation of steep normal faults that are unlikely to be reactivated in an orthogonal compression situation. This effect is also observed in the brittle–viscous inversion models with a foam base. Images inspired by McClay (1989), Amilibia et al. (2005), and Richetti et al. (2022).

4.4 Distributed basal deformation set-ups

Although a rubber or foam base has been regularly used for the modelling of distributed rifting (Vendeville et al., 1987; McClay et al., 2002; Bahroudi et al., 2003; Bellahsen et al., 2003; Bellahsen and Daniel, 2005; Zwaan et al., 2019, 2020b; Zwaan and Schreurs, 2020; Osagiede et al., 2021), only a few authors have applied such a basal condition for inversion models (McClay et al., 1989; Amilibia et al., 2005; Dooley and Hudec, 2020; Guillaume et al., 2022; Richetti et al., 2022).

The inversion models by McClay et al. (1989) involved a rubber sheet covering the whole base of the model overlain by a brittle layer (Fig. 9a). During extension, the distributed deformation produced a pervasive pattern of normal faulting, similar to the structures seen in Vendeville et al. (1987) (Fig. 13b). Applying subsequent orthogonal inversion in such a model leads to the development of new thrust faults, crosscutting the previously established normal fault structure that remains inactive due to the unfavourable orientation of these faults for reactivation (Figs. 2, 3, 13c).

Amilibia et al. (2005) applied an oblique rubber sheet spanned between base plates in their inversion model (Fig. 13a). Even so, comparing cross-sections at the sidewalls of the model, where the system seems to have behaved in a more or less 2D fashion, with cross-sections from the centre of the model, where deformation was oblique, allows both a 2D and 3D interpretation of this type of model (Fig. 13d–f, j–l). Initial (orthogonal or oblique) extension creates pervasive normal faulting above the rubber sheet (Fig. 13d, e, j). Subsequent orthogonal compression favours the development of new thrusts rooting along the margins of the interface, whereas the pre-existing normal faults are only mildly inverted (Fig. 13f, k). By contrast, oblique compression preferentially reactivates the pre-existing (boundary) faults (Fig. 13l).

The study by Dooley and Hudec (2020) aimed at modelling a very specific setting and has a rather complex experimental set-up. The set-up involves offset patches of viscous material overlying a model-wide viscous layer, which itself sits on top of a rubber sheet between two base plates. The model also includes a syn-sedimentary sequence of viscous material representing salt, inserted between two phases of extension prior to inversion. As such, their 3D results are too intricate for our summarizing purposes in this review paper.

Guillaume et al. (2022) used foam as an alternative material for inducing basal distributed deformation in both brittle-only and brittle–viscous models. The authors apply extension-oblique compression, either during or after the extensional deformation phase. In these models a central seed serves to localize deformation in the brittle sand layer (Fig. 13g, h), the success of which depends on whether compression is synchronous to the extensional deformation, the relative extensional and compressional deformation velocities, the presence a viscous layer and the thickness of this layer. Under these circumstances, complex basin inversion structures emerge, including the reactivation of normal faults as strike-slip structures. Similar to the results by Dooley and Hudec (2020), the results from Guillaume et al. (2022) are too complex to efficiently summarize in this paper.

Finally, Richetti et al. (2022) also used a foam base to induce distributed deformation and a seed to localize extensional deformation, which generated a central graben structure in the sand layer of their brittle–viscous models during initial rifting (Fig. 13g–i). Inversion of this structure subsequently leads to the development of thrust faults rooting at the seed, creating a pop-up structure, whereas the initial normal faults remain mostly inactive (Fig. 13i). The authors studied various degrees of oblique extension and compression as well. These results (Fig. 13m–o) are very compatible with the insights derived from the models by Amibilia et al. (2005) (Fig. 13j–l): new thrusting is prevalent during orthogonal inversion, whereas oblique inversion favours reactivation of pre-existing normal faults.

4.5 Pre-built basin set-ups

Various authors have used pre-built basins or faults that were subsequently compressed by moving a backstop into the model for the simulation of basin inversion (Sassi et al., 1993; Panien et al., 2006a; Marques and Nogueira, 2008; Di Domenica et al., 2014; Martínez and Cristallini, 2017; Lebinson et al., 2020). McClay et al. (2000) instead used a first phase of differential sedimentary loading to create rift basins to be inverted by a moving backstop. Furthermore, the models by Panien et al. (2005), Del Ventisette et al. (2005, 2006), Sani et al. (2007), Yagupsky et al. (2008), Bonini et al. (2012), Likerman et al. (2013), Munteanu et al. (2014), Jara et al. (2015, 2018), Martínez et al. (2016, 2018), and Granado et al. (2017), are very similar in nature to set-ups with pre-built basins since these authors used a base plate to create the initial basin and applied a sidewall for compression and inversion. These models are therefore addressed in this section as well.

4.5.1 Inversion in section view

The simplest inversion pre-built basin model set-up involves a pre-cut normal fault in a brittle layer (Sassi et al., 1993; Marques and Nogueira, 2008) (Fig. 14a). Subsequently, the potential reactivation of this “fault” (usually a disturbed dilatant zone in granular materials) depends on how much the fault decreases the strength of the brittle layer. A strong fault (i.e. a poorly developed weakness) will not readily reactivate, meaning that a thrust wedge with newly formed thrust faults will have to accommodate the shortening imposed by the moving backstop (Fig. 14b), and such models are in fact very similar to common thrust wedge models (Colletta et al., 1991; Cotton and Koyi, 2000; Graveleau et al., 2012). By contrast, faults with a shallow dip or weakened with viscous material (Marques and Nogueira, 2008) may be reactivated, and a backthrust may develop to form a pop-up structure (Fig. 14c). Very similar effects are observed in models with a pre-built basin (Fig. 14d–f): a strong basin infill forces the development of new thrusts, whereas a weak basin infill favours reactivation of pre-existing faults and may even be folded and “squeezed-out” in a somewhat ductile fashion (Panien et al., 2006a; Martínez and Cristallini, 2017). Sassi et al. (1993) also showed that the spacing of pre-existing faults influences their reactivation, since not all pre-cut faults in their models with closely spaced faults were inverted.

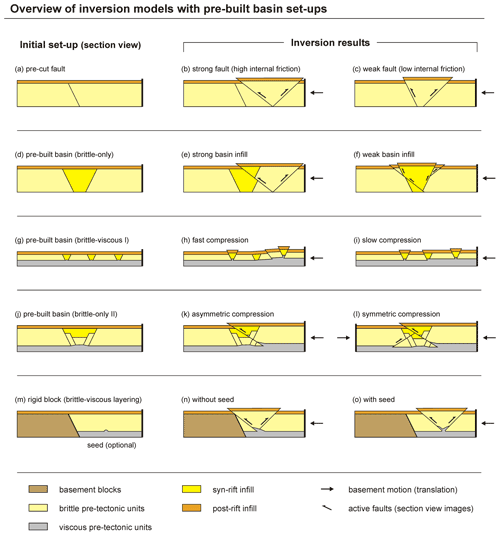
Figure 14 Section-view sketches of representative results from basin inversion models involving a set-up with pre-built basins and faults. (a–c) Inversion of a pre-built fault in a brittle-only layer, which is either relatively (b) strong or (c) weak. (d–f) Inversion of a pre-built basin, containing either a (e) strong brittle basin infill or a (f) weak brittle basin infill. (g–i) Inversion of a brittle–viscous system with thin brittle cover layer and dispersed grabens generated by initial extension with a base plate, during either (h) fast compression or (i) slow compression. (j–l) Inversion of a brittle viscous system with a thick brittle cover and a broad graben generated by initial extension using a base plate, either during (k) asymmetric compression or (l) symmetric compression. (m–o) Inversion of a basin with a viscous basal layer, adjacent to a fixed rigid footwall block: (n) model without seed and (o) with seed. Image inspired by Vially et al. (1994), Letouzey et al. (1995), Panien et al. (2005, 2006a), Marques and Nogueira (2008), Munteanu et al. (2014), and Schori et al. (2021).

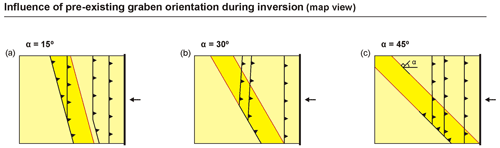
Figure 15 Effect of pre-existing graben orientation on fault reactivation during subsequent compression and inversion in brittle-only models, shown in map view. Grabens are indicated in yellow, and their orientation is defined as angle α, the angle between the normal to the graben strike and backstop motion direction. Image inspired by Yagupsky et al. (2008) and Deng et al. (2019).

The transfer of deformation onto the pre-existing structures away from the moving sidewall in these models is furthermore promoted by the insertion of a detachment layer consisting of micro-beads or viscous material (Panien et al., 2006a; Marques and Nogueira, 2008; Munteanu et al., 2014, Fig. 14g–i). Such a transfer of deformation away from the sidewall is well known from thrust wedge experiments involving a viscous detachment (Colletta et al., 1991; Cotton and Koyi, 2000; Borderie et al., 2018; Schori et al., 2021), and is in a way similar to the deformation transfer effect of a base plate during inversion (Fig. 11a–f). Brittle–viscous inversion models by Bonini et al. (2012) illustrate that this transfer of deformation through a viscous layer is affected by the inversion rate, where deformation during slow inversion is more distributed, whereas deformation during fast inversion is more concentrated towards the moving backstop (Fig. 14g–i). This concentration towards the backstop is evidently caused by the strengthening of the viscous material deforming under higher strain rates (e.g. Brun 1999). However, these structures reported by Bonini et al. (2012) are very different from the overthrusting focussed in the pre-existing basin seen in the models by Munteanu et al. (2014), potentially due to the thicker brittle cover layer in the latter study (compare Fig. 14g–i with Fig. 14j–k). Other variations observed in studies with similar model set-ups are likely due to different degrees of extension and compression, as well as the symmetry or asymmetry of compression (Likerman et al., 2013; Munteanu et al., 2014; Jara et al., 2015, 2018, see Sect. 4.5.2).

Vially et al. (1994) and Letouzey et al. (1995) have explored another pre-built basin set-up, involving a fixed rigid footwall block next to a pre-made basin containing a brittle infill on top of a viscous layer (Fig. 14m). The authors examined a set-up without a seed (Fig. 14n) and one with seeds to simulate the presence of salt diapirs (Fig. 14o). In the situation without a seed, deformation took a shortcut, and instead of reactivating the fault along the basement block, the shortening caused the development of a low-angle thrust, along with a backthrust, to form a pop-up structure (Fig. 14n). By contrast, the presence of a seed localizes shortening, meaning that a pop-up structure forms above the seed instead (Fig. 14o). Note that these drawings are simplified versions of the models, and we refer the reader to the original research papers for the detailed model depictions (Vially et al., 1994; Letouzey et al., 1995). It may furthermore be noted that Lebinson et al. (2020) have also performed a brittle-only model with a shallow-dipping fixed footwall block, which produced a simple pop-up structure reminiscent of the fixed rigid basement block equivalent but without the initial phase of deformation (Sect. 4.2, Fig. 9a–c).

4.5.2 Inversion in 3D

The 3D arrangement and location of pre-existing structures with respect to the shortening direction may strongly affect which of these structures will reactivate and how they reactivate, as observed in the brittle-only experiments by Panien et al. (2005), Yagupsky et al. (2008), Di Domenica et al. (2014), and Deng et al. (2019) (Fig. 15). These models show that oblique structures may be reactivated, and similar to (brittle–viscous) Jura Mountain models with oblique basement steps (Schori et al., 2021), the front of each new thrust sheet may partially follow the trend of the pre-existing structures before reorienting itself to become sub-perpendicular to the general direction of compression (Fig. 15). Further 3D complexities in models with a viscous basal detachment can be induced by having (partial) walls or backstops move inward from one or both sides of the model after creating an initial basin by means of base plates (Munteanu et al., 2014). As a result, different parts of these models have undergone different degrees of (asymmetric or symmetric) compression during inversion, leading to significant variations in structural style (Fig. 14k, l).

Figure 16 Rotational inversion model. (a) Extensional phase showing active subsidence at different extension percentages. (b) Compressional phase showing active topography increment at different shortening percentages. (c) The lines at I, II, and III are cross-sections at the end of initial extension by means of a base plate set-up. The lines are IV, V, and VI are cross-sections after homogeneous shortening by means of a backstop moving into the model. The original model thickness is 3.5 cm. Image adopted from Jara et al. (2015) and reproduced with permission from the Geological Society, London.

Another 3D factor is rotational tectonic deformation, as simulated by Jara et al. (2015, 2018), who applied a rotating base plate to generate along-strike basin width variations during extension, as well as rotational motion of a backstop for along-strike variations in compression during subsequent inversion. Figure 16 illustrates an example of initial rotational extension, followed by orthogonal compression in the brittle–viscous models from Jara et al. (2015). The rotational extension leads to the development of a V-shaped basin, with more stretching away from the rotation axis, together with increased tilting of fault blocks (Fig. 16a, c_I−III). The development of such V-shaped basins is typical of rotational extension systems (Souriot and Brun, 1992; Benes and Scott, 1996; Molnar et al., 2017; Zwaan et al., 2020b; Schmid et al., 2022), and the increased tilting of faults with increased amounts of extension is in line with observations from previous brittle–viscous models (e.g. Mandal and Chattopadhyay, 1995; Zwaan et al., 2016). When applying orthogonal inversion, the initial rift geometry has a clear effect on the final model structures (Fig. 16b, c_IV−VI). Closer to the original rotation axis, the model is relatively undeformed so that inversion has few weaknesses to reactivate. Therefore, deformation remains relatively close to the backstop (Fig. 16b, c_IV), similar to observations in other models (Panien et al., 2005; Bonini et al., 2012) (Fig. 14b, e, h). By contrast, farther away from the rotation axis, the more developed graben with its lower-angle normal faults represents a weakness that is readily reactivated (Fig. 16b, c_VI), meaning that deformation can be transferred farther from the backstop, as also observed by Bonini et al. (2012) and Munteanu et al. (2014) (Fig. 14g–l).

Figure 17 Influence of additional geological processes on basin inversion. (a–b) Effect of presence and absence of syn-rift sedimentation during rifting (inspired by Richetti et al., 2022). (c–d) Effect of magmatism and magma viscosity on inversion. Inspired by Martínez et al. (2018).

4.6 Influence of additional geological processes

Surface processes (i.e. erosion, transport, and sedimentation) are known to affect the development of both extensional and compressional tectonic systems (Koons, 1990; Burov and Cloetingh, 1997; Buiter et al., 2008; Graveleau et al., 2012; Moragas et al., 2017; Roma et al., 2018; Zwaan et al., 2018a; Borderie et al., 2019) and are thus of importance when considering basin inversion. However, modellers generally apply either “full sedimentation” (filling in the whole basin) or no sedimentation at all during model runs, with only a few studies testing the actual influence of sedimentation on the system. Richetti et al. (2022) show how the lack of syn-rift sedimentation causes the basin to be “squeezed” (Fig. 17b), whereas the presence of sediments fills the available accommodation space (i.e. the basin) and strengthens the system, obstructing such “squeezing” (Fig. 17a). Dubois et al. (2002) found that sedimentation prevents the reactivation of some faults in the system, and Pinto et al. (2010) provide similar results, highlighting that added sedimentation during both extension and subsequent compression reduces fault reactivation. These observations are very much in line with the results from inversion models involving pre-built basins with a strong or weak basin infill (Sect. 4.5.1, Fig. 14e, f): in the former case, the strong basin is poorly reactivated, whereas in the latter case, the reduced strength of the weak infill allows reactivation. Extrapolated, the total absence of basin infill makes the system weaker, increasing the likelihood of reactivation. Whereas the influence of sedimentation has thus received some attention in basin inversion models, the relative influence of erosional processes, despite being applied in a model by Strzerzynsky et al. (2021), has to our knowledge never been systematically tested.

Similar to sedimentary loading, tectonic loading can have an important influence on basin inversion tectonics. This is most relevant in models with moving sidewalls, which are indeed very similar to thrust wedge experiments (Graveleau et al., 2012, and references therein, Fig. 14). Granado et al. (2017) tested the influence of (differential) tectonic loading, revealing that high tectonic loading may prevent fault reactivation, whereas loading gradients may in fact promote reactivation of sub-thrust basins, i.e. basins below or near the tip of the thrust wedge. These authors have also applied tilting of the basin during inversion, which is known from critical taper theory and experiments to significantly affect the dynamics of thrust wedges (Buiter, 2012; Graveleau et al., 2012, and references therein). Since the results of Granado et al. (2017) are somewhat complex due to the incorporation of various parameters, we refer the reader the original article for more details.

Apart from the more general impact of (sedimentary) loading, some modellers have also included syn-tectonic deposition of viscous layering in their models to simulate the accumulation of evaporite (salt) or clay units (Del Ventisette et al., 2006, 2007; Sani et al., 2007; Mattioni et al., 2007; Dooley and Hudec, 2020). As also seen in models including pre-tectonic viscous layering (Brun and Nalpas, 1996; Ferrer et al., 2016, Figs. 9d–f, m–o, 11d–f, m–o), these viscous layers act as detachments and often cause very complex deformation (especially when multiple detachments are involved, Mattioni et al., 2007; Dooley and Hudec, 2020), as well as diapirism related to the activity of large faults (in a complex interaction with sedimentation patterns, Moregas et al., 2017). Simulated magmatism can have a similar effect, in that it detaches the overlying brittle units from the model base and can migrate along fault planes (Martínez et al., 2016, 2018). As such, enhanced magmatism during inversion may lubricate faults and promote the development of pop-up structures with magma accumulations near the surface, especially when the magma has a low viscosity (Fig. 17c, d).

Figure 18 Example of analogue–numerical model comparison (Panien et al., 2006a). Both set-ups aim to simulate orthogonal inversion of a pre-built basin. Pre-rift layer thickness is set to 3.5 cm. The numerical models are obtained with a finite element method. Reproduced with permission from the Geological Society, London.

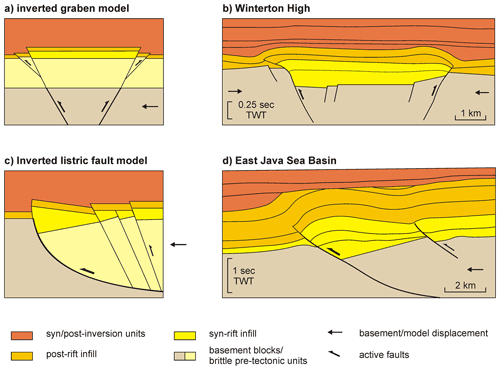
Figure 19 Comparison of schematic model results with natural examples. (a) Mobile basement graben set-up; see model details in Sect. 4.1 and Fig. 8c. (b) Winterton High in the southern North Sea (modified after Badley et al., 1989, with permission from the Geological Society, London). (c–d) Inversion of a listric fault basin in (c) an analogue model and (d) in nature (sketch of a seismic line from the East Java Sea Basin by Goudswaard and Jenyon, 1988). Modified after McClay (1995), with permission from the Geological Society, London. TWT stands for two-way travel time.

5 Comparison to numerical models and nature

5.1 Comparisons between analogue and numerical models

Whereas analogue modellers study tectonic processes by running scaled experiments in the laboratory, other researchers apply numerical modelling methods. These include techniques based on an assembly of particles (distinct element method, DEM) and continuum methods (finite element method, FEM). DEM methods may intuitively seem more appropriate for modelling granular materials, but it should be kept in mind that a DEM particle is generally of such size to include many scaled sand particles. Continuum methods generally do not produce discrete fault planes but have been shown to be well suited for simulating sand behaviour (Buiter et al., 2006, 2016; Crook et al., 2006). The numerical models allow for the inclusion of parameters that are highly challenging to implement in analogue models, such as thermal effects, isostasy, surface processes, parallel deformation mechanisms, and strain weakening. They also readily provide quantitative insights into internal deformation patterns and stress measures that are challenging, if not impossible, to obtain from analogue models. On the other hand, numerical models may lack sufficient resolution when studying tectonic processes in 3D (though this is rapidly improving), depend on their parameterization of especially brittle processes, and often require access to a high-performance computer cluster. As such, analogue and numerical modelling methods both have their strengths and weaknesses, and combining these methods for studying tectonic processes can provide more robust results (Ellis et al., 2004; Buiter et al., 2006, 2016; Burliga et al., 2012a; Zwaan et al., 2016; Brune et al., 2017).

Various authors have numerically modelled basin inversion (e.g. Hansen and Nielsen, 2003; Buiter and Pfiffner, 2003; Buiter et al., 2009; Dai et al., 2014; Caër et al., 2015; Granado and Ruh, 2019; Ruh and Vergés, 2018; Ruh, 2019), and a number of researchers have applied both analogue and numerical methods or compared analogue to numerical results. The study by Sassi et al. (1993) elegantly shows how shallow-dipping pre-existing faults are preferentially reactivated in both their analogue and numerical experiments. Buiter and Pfiffner (2003) compare their numerical models of inverted domino faulting to the analogue work by Buchanan and McClay (1992), finding a fair fit, which validates the results of both modelling studies. Panien et al. (2006a) also obtained a general good agreement between their analogue and numerical models of a pre-made basin deformed by sidewall compression (Fig. 18), with the models showing similar shear zone structures that highlight the difficulty of reverse-reactivating extensional shear zones during orthogonal shortening. Similarly, Yamada and McClay (2010) found that their numerical models of listric fault basin inversion fit well with their previous analogue modelling study (Yamada and McClay, 2004), even though the complex faulting in the analogue models is not reproduced in the numerical equivalent.

The limited number of studies that use a combination of analogue and numerical modelling techniques to investigate basin inversion may reflect the challenges involved in numerically simulating analogue set-ups (Buiter et al., 2016). Instead of direct comparisons aimed at achieving similarity in results, we would urge future studies to utilize the strengths of both methods to investigate complementary processes and factors in basin inversion. For example, analogue models could focus on 3D set-ups for known material properties, whereas numerical studies could add insights into thermal effects, rheological changes, or surface processes.

5.2 Comparison of analogue modelling results to natural cases

Here we present two examples published in previous basin inversion modelling studies (Fig. 19). The first comparison concerns a classic example of an inverted basin in the southern North Sea (the Winterton High, Bradley et al., 1989, Figs. 1a, 19b), as discussed by Panien et al. (2005). The inversion of the Triassic basin during a series of Cenozoic compression events affected large parts of northwestern Europe (Erratt et al., 1999; De Jager, 2003; Evans et al., 2003; Doornenbal and Stevenson, 2010, and references therein) and expelled the basin infill out of the original graben by reactivating the rift boundary faults. This is very similar to the inversion of the basin infill in the graben set-up used by Koopman et al. (1987) (Figs. 8a–c, 19a). Furthermore, where the faults in the basement forced reactivation of the boundary faults, the propagation of these faults in the weaker post-rift overburden has a shallower dip (Fig. 19b). This is also observed in analogue models (Fig. 19a), demonstrating the relevance of such analogue model results for our understanding of the dynamic evolution of the Winterton High and other similarly inverted basins.

A second example is provided by McClay (1995) and involves an inverted half graben controlled by a listric fault (Fig. 19c). Both the model and natural example in the East Java Sea (Goudswaard and Jenyon, 1988) show very similar structures: thickening of syn-rift sediments towards the listric fault that are subsequently uplifted as the basin is inverted due to reverse motion along the listric fault. Further similarities are the occurrences of (somewhat) inverted normal faults away from the main listric fault. Here the model also nicely fits the natural example, and by examining the model's development over time, we gain valuable insights into the dynamic evolution of its equivalent in nature.

Comparing model results with natural examples has indeed provided invaluable insights into basin inversion tectonics (e.g. McClay, 1995; Panien et al., 2005; Ferrer et al., 2022b, and references therein). However, one must always keep in mind the limitations of analogue modelling methods (e.g. Buchanan and McClay, 1991). For instance, most analogue models of basin inversion do not consider isostatic effects. Isostasy is an important factor in large-scale plate tectonic processes (Burov and Cloetingh, 1997) and is therefore included in lithospheric-scale analogue modelling studies of rifting (Vendeville et al., 1987; Nestola et al., 2013, 2015; Molnar et al., 2017; Beniest et al., 2018; Zwaan and Schreurs, 2022a, b), collisional and intra-plate tectonics (Willingshofer and Sokoutis, 2009; Luth et al., 2010; Sokoutis and Willingshofer, 2011; Willingshofer et al., 2013; Calignano et al., 2015, 2017; Santimano and Pysklywec, 2020), and basin inversion (Gartrell et al., 2005; Cerca et al., 2010). However, as basin inversion is generally studied in the context of basins that did not undergo continental break-up and that are to large degree filled by sediments, the effects of isostasy can be considered limited and the model results valid.

Similar arguments can be made for the influence of magmatism, thermal effects in general, and diagenesis. Even though modelling studies have shown that magmatism can significantly affect basin inversion tectonics (Martínez et al., 2016, 2018, Fig. 17c, d), it is not very common in rift basins prior to break-up or during subsequent inversion. The same is probably true for thermal effects and diagenesis; only when the system would go beyond the initial rifting phase can these effects be expected to gain an important influence on basin inversion tectonics.

Possibly more impactful limitations are the lack of pore fluid effects in analogue models, which are known to have a significant influence on inversion tectonics (Sibson, 1985, 1995, 2009). Another limitation is the past focus on 2D inversion, and although modelling efforts have more and more explored the third dimension, it is tempting to think of basin inversion as a 2D process (especially given the legacy of 2D seismic sections). Ongoing developments in the analogue modelling community, as well as in the world of seismic acquisition, are however making the analysis of 3D modelling results much more straightforward (see also Sect. 7).

Still, the comparisons presented above highlight the crucial use of analogue models for simulating the dynamic development of tectonic systems that take millions of years to unfold. This is especially true when combining these analogue models with numerical modelling techniques, as discussed in the preceding section.

6 Synopsis of main insights

The model results described above give insight into the processes and factors that result in successful basin inversion or may prevent a basin from being inverted.

The first requirement for successful (basin) inversion is the presence of a basin or fault structure that provides a relative weakness compared to the immediate surroundings to focus contractional deformation. Such weakening can originate from the infill of the basin, where weak sediments facilitate inversion (either by allowing fault reactivation, the nucleation of new faults near the basin edge, or upward folding of the infill). By contrast, a strong infill may prevent inversion (Fig. 14d–f). Similarly, normal faults that are either weakened or have a low dip angle are more likely to be reactivated (Fig. 14a–c), which is in line with fault theory, which predicts that new thrusts should form otherwise (Sect. 2). The preference for forming new thrust faults is particularly well known from the propagation of inverted normal faults into the post-rift overburden in models with (mobile) basement blocks (footwall shortcuts, Fig. 8c, f, o). Finally, the shape of pre-existing normal faults (e.g. straight, listric, or undulating) can strongly affect the resulting inversion structure as well (Figs. 9, 10).

A second requirement for inversion is the transfer of deformation into the basin or fault structure. Apart from the relative weakness of the modelled basin or fault, this depends on the boundary conditions, i.e. the model set-up, as well as the mechanical layering used in the model. Model set-ups involving deformation driven from the base are more likely to efficiently induce inversion. By contrast, inversion driven by a backstop generally needs a detachment layer of some sorts (either micro-beads or a layer of viscous material) that decouples the overburden from the model base. Otherwise, deformation will simply develop directly in front of the backstop, creating a thrust wedge (Fig. 14). In this context, a base plate set-up in fact acts as a sort of detachment as well, efficiently transferring deformation deep into the model (Fig. 11). Weak layers within the model materials can also act as detachments, leading to new levels of complexity (Figs. 8–17).

A third factor influencing basin inversion tectonics is the direction of shortening. Whereas high-angle normal faults may be often (partially) ignored in favour of newly formed thrust faults during orthogonal inversion, oblique inversion can readily reactivate these normal faults. Such reactivation of normal faults during oblique inversion is well documented in analogue models with a variety of different set-ups (Figs. 11j–o, 13j–o) and is explained by the reduced fault angle with respect to the orientation of the principal stresses (see fault theory specified in Sect. 2, Figs. 2, 3). Moreover, along-strike variations in the models due to variations in basement block or base plate geometries, differently oriented pre-existing structures and weak zones, or rotational extension or compression can cause highly complex distributions of structures (Figs. 10, 12, 15, 16). These complexities highlight the importance of considering the third dimension when studying tectonic processes.

Finally, additional geological processes such as sedimentation and magmatism can affect inversion processes as well. Sedimentation and erosion change the normal stress in the model layers, thus changing the frictional strength and affecting the likelihood of inversion. Magmatism can facilitate fault reactivation when intruding along fault planes, thus reducing fault strength (Fig. 17).

The insights from these analogue models are in line with the mechanisms of basin inversion summarized in Sect. 2 and concur to a high degree with results from numerical modelling studies, validating both modelling methods (Fig. 18). Furthermore, these insights have proven highly valuable to better understand the evolution of basin inversion tectonics in natural settings (Fig. 19).

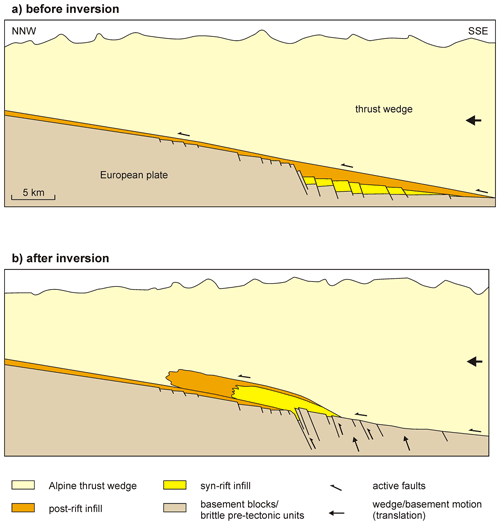
Figure 20 Inversion of the Doldenhorn Basin in the Swiss Alps, which was once a basin on the European passive margin of the Piemont–Ligurian Ocean, under a >10 km thick thrust wedge. The burial depth causes ductile rather than brittle behaviour during inversion. Modified after Musso Piantelli et al. (2022).

7 Perspectives for future analogue modelling studies of basin inversion

In this review we describe the current state of the art of analogue modelling of basin inversion. There are however many opportunities for improvements and future modelling studies, revolving around new modelling methods; the use of improved model analysis techniques; and the combination of analogue and numerical modelling methods, benchmarking studies, and establishing best practices in analogue modelling.

7.1 New modelling methods to tackle new questions

Improvements in experimental techniques can include the development and application of new model materials (e.g. Boutelier and Oncken, 2011; Boutelier et al., 2012; Abdelmalak et al., 2015; Zwaan et al., 2016, 2018a; Mayolle et al., 2021; Massaro et al., 2021). Such new materials allow the implementation of different degrees of viscosity in viscous materials (Zwaan et al., 2018b) or modifications to the cohesion of brittle materials (Abdalmalek et al., 2015; Montanari et al., 2017; Massaro et al., 2021). Further opportunities lie in the application of new materials with elastic–plastic behaviour such as gelatin for the study of inversion-related seismicity (Rosenau et al., 2009; Di Giuseppe et al., 2009), viscoplastic behaviour such as kinetic sand for better simulating the brittle–ductile transition in the crust (Mayolle et al., 2021), or temperature effects (e.g. Chemenda et al., 2002; Boutelier and Oncken, 2011; Boutelier et al., 2012; Katz et al., 2005; Krýza et al., 2019).

Other improvements are related to the development of new modelling apparatus that allow for improved simulation of tectonic processes and new model boundary conditions (e.g. Molnar et al., 2017; Zwaan et al., 2020b; Eisermann et al., 2021; Zwaan and Schreurs, 2022a, b). An interesting development is the application of force boundary conditions, rather than velocity boundary conditions (Gartrell et al., 2005; Konstantinovskaya et al., 2007). Constant force during rifting may explain rapid changes in tectonic deformation rates, for instance when the strength of the tectonic system is reduced due to necking of the lithosphere (Brune et al., 2016). Since increasing strain rates increases the degree of brittle–viscous coupling in tectonic systems (Brun, 1999; Bonini et al., 2012; Zwaan et al., 2021, 2022), such increases (and decreases) in strain rate can significantly change the style of deformation during basin inversion as well (Bonini et al., 2012). The influence of strain rates during basin inversion could be further explored, for instance using models in which deformation rates are programmed to be variable.

The majority of basin inversion models have been conducted on an (upper) crustal scale, motivated by the search for hydrocarbon reserves (e.g. in the North Sea) but can be built upon for new research aims. The insights gained from these models can for example be of use for CO₂ sequestration and mineral exploration. In addition, part of the future of basin inversion modelling may lie in the study of mantle exhumation as hyper-extended basins are inverted. The serpentinization of mantle rocks that were initially exhumed in hyper-extended rift basins, now incorporated in mountain belts, may be a source of future natural hydrogen production (Dumagin, 2019; Lefeuvre et al., 2021). The broad presence of mantle rocks in mountain belts, both in Europe (Faul et al., 2014; Frasca et al., 2016; Schmid et al., 2017) and elsewhere (Vaughan and Scarrow, 2003; Dilek and Furnes, 2011), indicates some highly interesting potential. Given the need for truly clean energy production in our efforts to realize a sustainable economy (Smith, 2002; Gaucher, 2020; Moretti and Webber, 2021; Scott, 2021), researching the tectonic processes causing and controlling basin inversion on a lithospheric scale through novel analogue modelling techniques is more relevant than ever.

Linked to such large-scale inversion processes is the influence of tectonic loading, which has not received much attention in analogue modelling studies. However, the presence of a thick orogenic wedge overthrusting a basin will have important consequences for inversion processes (Granado et al., 2017; Kiss et al., 2020; Musso Piantelli et al., 2022, Fig. 20). Another research topic to pursue is the effect of magma intrusion during inversion as pioneered by Martínez et al. (2016, 2018). Moreover, the healing of faults over the period between initial extension and subsequent compression could cause important differences in fault reactivation (Hunfeld et al., 2020; Rudolf et al., 2021). Further attention could be dedicated to the inclusion of the interactions between tectonics and surface processes (Graveleau and Dominguez, 2008; Graveleau et al., 2011, 2015; Reitano et al., 2020, 2022; Strzerzynsky et al., 2021), which may also significantly affect inversion processes (Sect. 4.6). In addition, the 3D aspects of inversion represent a fruitful avenue for further model studies, especially since basin inversion has traditionally been modelled from a pseudo-2D point of view. Various modellers have indeed started to study complex 3D inversion tectonics (e.g. Yamada and McClay 2004; Munteanu et al., 2014; Jara et al., 2015, 2018), but a whole new field of play, to our knowledge only explored by Wang et al. (2017), would be the inversion of pull-apart basins. Finally, changing (fluid) pressure has been simulated in analogue models using air flow systems (Cobbold et al., 2001; Mourgues and Cobbold, 2003), which could perhaps serve to reproduce changes in pore fluid pressure that are known to have important effects during inversion (Sibson, 1985, 1995, 2009).

7.2 Improved (applications of) model analysis techniques

In parallel with the ongoing development of modelling methods, techniques to analyse analogue models have significantly improved as well, following the general shift in the analogue modelling community from producing qualitative model results to quantification of these results. So far, several of the more advanced analysis techniques have only been sparsely applied to monitor and analyse basin inversion models. We propose that all tectonic modelling laboratories strive to develop the capabilities for combined use of DIC techniques, topography analysis, and systematic cross-sectioning.

DIC and topography analysis have indeed become standard techniques in the analogue modelling community over the past few years. New developments not only provide detailed insights into displacements and strain (Zwaan et al., 2021, 2022; Schmid et al., 2022) but also allow an analysis of the type of faulting (normal, reverse, or strike-slip, Broerse et al., 2021; Krstekanicì et al., 2021; Guillaume et al., 2022). However, DIC methods have so far only seen very limited use in basin inversion models (Wang et al., 2017; Dooley and Hudec, 2020; Guillaume et al., 2020; Richetti et al., 2022). Similarly, topography analysis, although routinely applied in tectonic laboratories (Sect. 3.6.3), has only sporadically featured in basin inversion studies, even though straightforward and affordable systems for 3D surface reconstruction are constantly being developed by the video gaming industry (e.g. Rincón et al., 2020, and references therein). Therefore, we urge (basin inversion) modellers to adopt these powerful analysis techniques in future studies.

Cross-sectioning has been widely used in inversion modelling works (Sect. 2.6.2). Wherever possible, these cross-sections could be used to create 3D representations of internal model structural architecture (Ferrer et al., 2016; Roma et al., 2018a, b; Dooley and Hudec, 2020, Fig. 7d). Perhaps even better is the use of CT scanning for analogue model analysis, which has been applied to a surprising degree in basin inversion studies. Next to the detailed 3D analysis of the evolution of model-internal structures (Konstantinovskaya et al., 2007; Chauvin et al., 2018; Fedorik et al., 2019), such CT data also allow for advanced 3D DIC analysis, or digital volume correlation (DVC), yielding unique quantified constraints on model-internal displacements in 3D (Adam et al., 2013; Zwaan et al., 2018a; Poppe et al., 2019; Schmid et al., 2022).

Another (novel) method that has been recently applied to the analysis of analogue models, and which would be highly interesting for basin inversion models as well, involves measuring local stresses in the model by means of stress-sensitive beads (Daniels et al., 2017; Ladd and Reber, 2020). It would also be possible to monitor stress through sensors on the model sides (Reber et al., 2014; Herbert et al., 2015; Ritter et al., 2018a, b) or even within the model (Nieuwland et al., 2000; Moulas et al., 2019). Finally, recent workers have pioneered how the reorientation of initially randomly distributed magnetic particles may reveal strain in models (Almqvist and Koyi, 2018; Schöfisch et al., 2021). As new analysis techniques are being developed in the analogue modelling community, these could be readily shared with colleagues and applied to basin inversion studies. Here, a powerful means to contact experts, set up collaborations, gain access to new methods, or share analogue modelling knowledge in general is the EU-funded EPOS multi-scale laboratories network (https://www.epos-eu.org/tcs/multi-scale-laboratories, last access: 22 October 2022).

Considerable improvements can be made by routinely integrating analogue modelling efforts with numerical studies and methods. Not only does the combined use of analogue and numerical modelling methods provide more robust results (Sect. 5.2), the scripts and algorithms used to process and quantify deformation in numerical models can also be used for the analysis of (quantified) data derived from analogue models. An intriguing opportunity would be the application of machine learning techniques (Corbi et al., 2019) for the semi-automatic analysis of analogue models. By doing so, modellers can truly bring together the best of both modelling worlds.

7.3 Benchmarking

Directly comparing the results from different analogue modelling studies is often challenging due to the many small and larger differences in model set-up, materials, and applied boundary conditions. Even if researchers aim to run the exact same model, some differences between the model results are to be expected due to variations in handling techniques or laboratory conditions (Krantz, 1991b; Lohrmann et al., 2003; Schreurs et al., 2006, 2016; Maillot, 2013; Klinkmüller et al., 2016; Rudolf et al., 2016; Schmid et al., 2020). The overviews presented in this review should therefore be taken as a guide, and the reader is referred to the specific studies for more details on the original model results.

Nevertheless, in order to distinctively determine the relative importance of set-ups, materials, and model parameters, systematic comparisons and benchmarking efforts, such as those done for thrust wedges and rifting (Souloumiac et al., 2012; Schreurs et al., 2006, 2016; Zwaan et al., 2019), are needed. Within the field of analogue modelling of basin inversion there is a great need for benchmarking, as virtually no such efforts have been published. Instead, most studies are focussed on the study of a specific set-up or aim to unravel the structural history of a natural example. The generalized overviews presented in this review may count as a first stimulus for such a benchmark but will need to be supported by systematic modelling efforts with standardized set-ups and methods.

Benchmarking efforts may also allow us to fill in the various knowledge gaps, as various combinations of model set-ups and materials have not been tested. Rerunning experiments in a systematic manner will also provide an opportunity for detailed analysis with state-of-the art methods (see Sect. 7.3). Such improved analysis will yield a wealth of data and new insights that would otherwise remain unnoticed (compare, e.g. the results from Zwaan et al., 2020a, with those from Schmid et al., 2022).

7.4 Best practices

Finally, we would like to point out the responsibility of researchers to describe their research efforts in as much detail as possible. This includes the description of the model set-up, experimental materials, and model preparation details, as well as an extensive and systematic description of the original model results (see Table A1 in the Appendix). Such detailed descriptions are crucial to ensure model reproducibility and to allow the reuse of established methods for future modelling studies. Indeed, differences in handling methods and lab conditions can considerably affect model results (see Sect. 7.3). Therefore, descriptions of methods and lab procedures should be as extensive and standardized as possible. Describing these details is part of the general shift in analogue modelling over the years, from a qualitative research method to a gradually more systematic, quantitative science as the techniques and methods steadily improved (Koyi, 1997; Ranalli, 2001; Bonini et al., 2012; Graveleau et al., 2012; Schellart and Strak, 2016; Di Giuseppe, 2018; Reber et al., 2020; Zwaan and Schreurs, 2022a). It is clear that not all details and results can always be included in the 20 or so pages of a scientific publication, but these can be published as supplementary materials, often in digital form, in parallel with the main scientific articles. Such supplementary material can consist of written descriptions, schematic representations, systematic overviews, and photos and videos of model results and may be stored on the publication web page or in independent repositories. These repositories should be organized according to the FAIR principles so that the data will be openly available to the community (e.g. GFZ Data Services, https://dataservices.gfz-potsdam.de, last access: 22 October 2022, which has been routinely used for the storage of modelling results by members of the EPOS Multi-scale laboratories network). This would ideally be accompanied by publishing the main article under an open-access licence, making all of the research publicly available.

8 Concluding remarks

Basin inversion is a great research topic for analogue modelling studies, and a thorough understanding of the processes involved is of great importance to both science and society. In this review we provide an up-to-date summary of the state of analogue modelling of basin inversion processes. In addition to reviewing the past modelling efforts, we also shed light on future modelling challenges and identify a number of opportunities for follow-up research. It follows that basin inversion modelling can continue to bring valuable new insights, providing a great incentive to continue our efforts in this field. We therefore hope that this review paper will form an inspiration for future analogue modelling studies of basin inversion.

Appendix A

Table A1 Checklist of parameters to report when describing analogue models of tectonic processes.