The 2022 M_W 6.0 Gölyaka–Düzce earthquake: an example of a medium-sized earthquake in a fault zone early in its seismic cycle

On 23 November 2022, a M_W 6.0 earthquake occurred in the direct vicinity of the M_W 7.1 Düzce earthquake that ruptured a portion of the North Anatolian Fault in 1999. The M_w 6.0 event was attributed to a small portion of the Karadere fault off the main North Anatolian Fault that did not rupture during the 1999 sequence. We analyze the spatiotemporal evolution of the M_W 6.0 Gölyaka–Düzce seismic sequence at various scales and resolve the source properties of the mainshock. Modeling the decade-long evolution of the background seismicity of the Karadere fault employing an Epistemic Type Aftershock Sequence model shows that this fault was almost seismically inactive before 1999, while a progressive increase in seismic activity is observed from 2000 onwards. A newly generated high-resolution seismicity catalog from 1 month before the mainshock until 6 d after was created using artificial-intelligence-aided techniques and shows only a few events occurring within the rupture area within the previous month, no spatiotemporal localization process and a lack of immediate foreshocks preceding the rupture. The aftershock hypocenter distribution suggests the activation of both the Karadere fault, which ruptured in this earthquake, and the Düzce fault that ruptured in 1999. First results on the source parameters and the duration of the first P-wave pulse from the mainshock suggest that the mainshock propagated eastwards, which is in agreement with predictions from a bimaterial interface model. The M_W 6.0 Gölyaka–Düzce event represents a good example of an earthquake rupture with damaging potential within a fault zone that is in a relatively early stage of the seismic cycle.

1 Introduction

Large strike–slip fault zones such as the San Andreas Fault in California, USA, or the North Anatolian Fault in Türkiye, among others, host some of the largest shallow earthquakes (typically up to M ∼ 8; see, e.g., Wesnousky, 1988; Stirling et al., 1996; Martínez-Garzón et al., 2015) worldwide. Some of these hazardous faults run near urban areas; hence, they have an associated risk. This is the case for the western portion of the North Anatolian Fault, which is a seismic threat for the Istanbul metropolitan area and nearby population centers. There, the return period of M > 7 earthquakes rupturing the main fault trace has been estimated to be approximately 250 years (Murru et al., 2016). The most recent large earthquakes along the North Anatolian Fault zone (NAFZ) were the 17 August 1999 M_W 7.4 İzmit event and the 11 November 1999 M_W 7.1 Düzce event (Fig. 1). Together, they ruptured approximately 180 km and connected the Marmara segment in the west to the 1944 rupture in the east (Bürgmann et al., 2002; Sengör, 2005; Bohnhoff et al., 2013). On 23 November 2022, a M_W 6.0 earthquake occurred around 6 and 10 km away from the cities of Gölyaka and Düzce, respectively, and about 200 km eastward of the Istanbul metropolitan area. In the following, we refer to this event as the Gölyaka–Düzce earthquake, as it was felt especially in the province of Düzce and its districts (Eyidoğan, 2022). Hypocenter locations provided by KOERI (Kandilli Observatory and Earthquake Research Institute; http://www.koeri.boun.edu.tr/new/en, last access: 18 October 2023) and AFAD (Disaster and Emergency Management Presidency; https://www.afad.gov.tr/, last access: 18 October 2023) reported that the Gölyaka–Düzce earthquake occurred close to the intersection of the ruptures of the 1999 M_W 7.4 İzmit and M_W 7.1 Düzce earthquake ruptures (Bouin et al., 2004; Konca et al., 2010; Fig. 1). Such M_W ∼ 6 earthquakes are relatively infrequent in the region (according to the ISC-GEM – International Seismological Centre Global Instrumental Earthquake Catalogue; http://www.isc.ac.uk/iscgem/, last access: 18 October 2023; similar-sized events could have occurred in 1926 and 1944), but they hold potential to damage key infrastructure and lead to casualties. Hence, analyzing this earthquake and its pre- and post-seismic deformation is important to illuminate the local fault architecture (e.g., Ross et al., 2020) and recover how moderate events nucleate in the region (e.g., Malin et al., 2018; Durand et al., 2020). In addition, analysis of the earthquake source properties can help us to decipher any preferential directions of seismic energy release, which is essential for seismic hazard estimation.

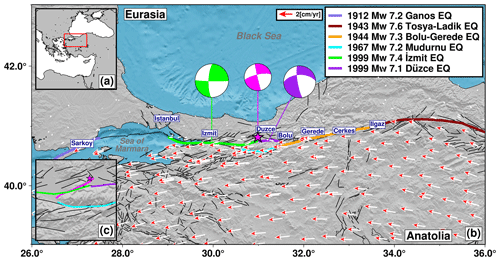
Figure 1 Seismotectonic setting. (a) Location map with a red rectangle indicating the area enlarged in panel (b). (b) Study area with the location of main population centers along the North Anatolian Fault zone (NAFZ). Colored lines denote rupture extents of historical earthquakes along NAFZ, with their respective magnitudes and dates indicated in the legend. Arrows are an updated GPS velocity field for Türkiye (Kurt et al., 2022), considering the Eurasia-fixed reference frame. The magenta star indicates the Gölyaka earthquake epicenter, along with its focal mechanism from KOERI, and the focal mechanisms of the İzmit (green) and Düzce (purple) earthquakes in 1999 (data from the global centroid moment tensor (CMT) catalog; Ekström et al., 2012; Dziewonski et al., 1981). (c) View of the region struck by the Gölyaka earthquake.

The Gölyaka–Düzce earthquake was the first M ∼ 6 in the area after the 1999 M > 7 earthquakes and their aftershock sequences. As such, it represents the occurrence of an earthquake with damaging potential in a fault zone that is broadly still in the early stage of the seismic cycle, which is when the accumulated elastic strain is relatively low. However, at this location, the geometry of the fault zone is highly complex, with slip partitioning along two main fault traces bounding the Almacık Block and numerous secondary faults being obliquely oriented (Fig. 1c). The moment tensor estimation by different agencies (Table S1 in the Supplement) consistently reported on a strike–slip mechanism with a small normal faulting component for this earthquake. The hypocenter location and fault plane appeared consistent with a portion of the Karadere fault (Fig. 1c). Different lines of evidence suggest that at least a few kilometers of the Karadere fault did not rupture during the 1999 İzmit–Düzce sequence and thus remained loaded and then ruptured in the Gölyaka–Düzce earthquake (Bohnhoff et al., 2016; Özalp and Kürcer, 2022). These include (i) the magnitude of the latest mainshock, (ii) the spatial extension of aftershocks and (iii) the previous surface mapping of local faults. First field surveys immediately after the M_W 6.0 Gölyaka–Düzce earthquake found no surface rupture, indicating that the slip did not extend to the surface (Özalp and Kürcer, 2022).

In this study, we analyze the spatiotemporal evolution of the Gölyaka–Düzce seismic sequence and the preceding seismicity in the area in detail, with a focus on the source mechanisms and in context of the local seismotectonic setting. Our primary goals are to determine how the earthquake initiated, what the ongoing deformation mechanisms in the region are and how the energy from this mainshock was radiated. Insights from this earthquake sequence are important for us to learn about the dynamics of potentially damaging earthquakes in complex transform fault settings and the rupture of highly stressed faults in the immediate vicinity of a major strike–slip transform with relatively low-stress conditions corresponding to the fault zone being early in its seismic cycle.

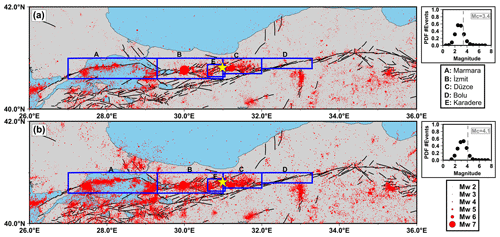
Figure 2 Regional seismicity. (a) AFAD catalog from 1990 to 30 November 2022. The yellow star denotes the M_W 6.0 Gölyaka–Düzce epicenter. Blue boxes indicate the target regions in which the seismicity is analyzed. The column on the right shows the catalog's probability distribution function of earthquake magnitude (PDF), where the vertical dashed line denotes the M^C. (b) Same as panel (a) but for the KOERI catalog. See Figs. S3 and S4 for the spatial distribution of seismicity inside each region.

2 Data and methodology applied

2.1 Background seismicity evolution

To put the Gölyaka–Düzce seismic sequence in a regional and long-term context, we established a consistent regional seismicity catalog between 1990 and 2022 from the two national seismic agencies. The AFAD catalog reported 31 081 events with magnitudes M (1.3–7.6) for such a period, whereas the KOERI catalog reported 42 050 events M (1.4–7.4). We analyzed the decade-long evolution of the AFAD and KOERI regional seismicity catalogs through a declustering process (Fig. 2). Both catalogs changed the reported magnitude type at the end of 2011 and beginning of 2012 from the duration magnitude M_d to local M_L. For consistency, we homogenized both catalogs, converting uniformly to moment magnitude, M_W, following the empirical relationships proposed for the study region by Kadirioğlu and Kartal (2016):

$$\begin{array}{}\text{(1)}& {\displaystyle }{M}_{\mathrm{W}}=\mathrm{0.7949}{M}_{\mathrm{d}}+\mathrm{1.3420},\text{(2)}& {\displaystyle }{M}_{\mathrm{W}}=\mathrm{0.8095}{M}_{\mathrm{L}}+\mathrm{1.303}.\end{array}$$

After both catalogs were homogenized to M_W, we estimated the magnitude of completeness M^C of each catalog, following a probabilistic approach to fit the frequency–magnitude curve (Ogata and Katsura, 1993; Daniel et al., 2008; Jara et al., 2017). In contrast to the maximum curvature method, this technique fits a function to explain the magnitude–frequency distribution, including all catalog events. The number of earthquakes is fit as a function of magnitude as follows:

$$\begin{array}{}\text{(3)}& N\left(m\right)=A\times {\mathrm{10}}^{-bm}\times q\left(m\right),\end{array}$$

where the b value represents the slope of the Gutenberg–Richter law, A is a normalization constant, and q(m) is the probability that one earthquake of magnitude m is listed in the catalog. Then, we modeled q as follows (Ogata and Katsura, 1993):

$$\begin{array}{}\text{(4)}& q\left(m\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{erf}\left({\displaystyle \frac{m-\widehat{\mathit{\mu }}}{\sqrt{\mathrm{2}}\widehat{\mathit{\sigma }}}}\right),\end{array}$$

where erf is the error function, and $\widehat{\mathit{\mu }}$ and $\widehat{\mathit{\sigma }}$ correspond to the mean and standard deviation of the probability distribution function, respectively. We optimized $\text{[}A,b,\widehat{\mathit{\mu }},\widehat{\mathit{\sigma }}\text{]}$ for each catalog, following a Bayesian approach to derive the parameters' posterior probability density function (PDF). We used the Markov chain Monte Carlo sampler of PyMC (Salvatier et al., 2016) to draw 500 000 samples from the posterior PDF. The inferred parameters and their associated uncertainties are given in Table S2. Then, the completeness magnitude M^C is computed as follows:

$$\begin{array}{}\text{(5)}& M^{\mathrm{C}}=\widehat{\mathit{\mu }}+\mathrm{2}\widehat{\mathit{\sigma }},\end{array}$$

i.e., with a 97.7 % probability threshold, which yielded a M^C=3.4 for the AFAD catalog, whereas, for the KOERI one, we obtained a M^C=4.1 (see the insets in Fig. 2 and the obtained fitting in Figs. S1 and S2). Once M^C was estimated for both catalogs, we declustered them using an epidemic-type aftershock sequence model (Marsan et al., 2017; Jara et al., 2017). Such an approach considers the total seismicity rates $\mathit{\lambda }(x,y,t)$ to be the following sum:

$$\begin{array}{}\text{(6)}& \mathit{\lambda }(x,y,t)=\mathit{\mu }(x,y,t)+\mathit{\nu }(x,y,t),\end{array}$$

where $\mathit{\nu }(x,y,t)$ accounts for the aftershock productivity, and $\mathit{\mu }(x,y,t)$ is the background seismicity rate for earthquakes occurring at a given location (x,y) and time t. The aftershock rate was estimated following the Omori–Utsu law modified by a power spatial density, as follows:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}{\mathit{\nu }}_i(x,y,t)& ={\sum }_{i\vee t_i<t}{\displaystyle \frac{\mathit{\kappa }\left(m_i\right)}{(t+c-t_i{)}^p}}\\ & \times {\displaystyle \frac{(\mathit{\gamma }-\mathrm{1})L(m_i{)}^{\mathit{\gamma }-\mathrm{1}}}{\mathrm{2}\mathit{\pi }{\left((x-x_i{)}^{\mathrm{2}}+(y-y_i{)}^{\mathrm{2}}+L_i^{\mathrm{2}}\right)}^{\frac{\mathit{\gamma }+\mathrm{1}}{\mathrm{2}}}}},\end{array}\end{array}$$

where c, γ and p are constants, and κ(m) is the productivity law with a constant α (Ogata, 1988). $L\left(m\right)=L_{\mathrm{0}}\times {\mathrm{10}}^{\mathrm{0.5}(m-M^{\mathrm{C}})}$ is the characteristic length in kilometers (Utsu and Seki, 1955; van der Elst and Shaw, 2015). Here, we imposed realistic values for the following parameters: α=2, p=1, $c={\mathrm{10}}^{-\mathrm{3}}\mathrm{d}$, γ=2, and L₀ = 1.78 km (Marsan et al., 2007; Jara et al., 2017; Karabulut et al., 2022). Parameters κ and $\mathit{\mu }(x,y,t)$ were inverted. The background seismicity was computed as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathit{\mu }(x,y,t)& ={\sum }_i{\displaystyle \frac{\mathit{\mu }(x_i,y_i,t_i)}{\mathit{\lambda }(x_i,y_i,t_i)}}{e}^{\frac{-\sqrt{(x-x_i{)}^{\mathrm{2}}+(y-y_i{)}^{\mathrm{2}}}}{l}}\\ & \times e^{-t-t_i\vee \mathit{\tau }}\times {\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }{l}^{\mathrm{2}}{a}_i}},\end{array}\end{array}$$

with l and τ as space and time and being smoothing parameters, and $a_i=\mathrm{2}\mathit{\tau }-\mathit{\tau }(e^{\frac{t_s-t_i}{\mathit{\tau }}}-e^{\frac{t_e-t_i}{\mathit{\tau }}})$, where t_s and t_e are the temporal beginning and end of the catalog, respectively. κ is inferred as

$$\begin{array}{}\text{(9)}& \mathit{\kappa }={\displaystyle \frac{{\sum }_i\mathrm{1}-\frac{\mathit{\mu }(x_i,y_i,t_i)}{\mathit{\lambda }(x_i,y_i,t_i)}}{{\sum }_i{e}^{\mathit{\alpha }{m}_i}\left(\text{ln}\right(t_e+c-t_i)-\text{ln}(c\left)\right)}}.\end{array}$$

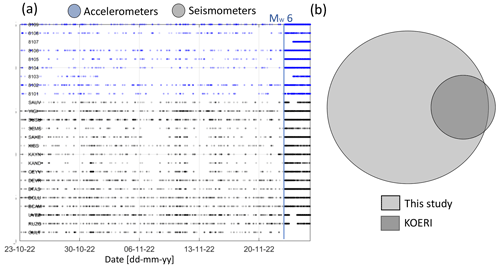
Figure 3 Picks and detections from the AI-derived catalog. (a) Associated picks as a function of time per station. The vertical blue line marks the M_W 6.0 Gölyaka–Düzce earthquake. (b) Venn diagram showing the earthquakes included in our catalog of detections vs. the events included in the KOERI catalog for the same spatiotemporal region.

Here, we used a smoothing length l = 100 km and a smoothing duration τ = 100 d. Such choices are able to preserve the potential accelerations or decelerations from the catalogs (Marsan et al., 2017; Jara et al., 2017). We declustered the catalogs using the obtained M^C for each catalog and the fault regions in Fig. 2. When doing so, we observed an apparent increase in the seismicity from the AFAD declustered catalog at around 2012 (Fig. S1). Around that time, AFAD changed the reported magnitudes from M_d to M_L. Although we converted the corresponding magnitudes to M_W, this change in the magnitude estimation might still produce spurious acceleration or deceleration in the background seismicity rate. We then tested higher M^C values, finding that such behavior disappears at around M^C = 4.1 (Fig. S1). Thus, we finally used M^C=4.1 for both catalogs (Fig. 3a and b). The final parameters utilized for each catalog are provided in Table S1.

2.2 Enhanced seismicity catalog framing the mainshock

To generate an optimized enhanced seismicity catalog with the lowest possible magnitude detection threshold around the M_W 6.0 Gölyaka–Düzce earthquake epicenter, we processed continuous waveform recordings from 16 local seismic stations and 9 local accelerometer stations. We covered a time period from 1 month before the mainshock up to almost 6 d after it (23 October 2022 at 00:00 LT up to 29 November 2022 at 00:00 LT). The employed stations belong to the AFAD and KOERI seismometer and strong motion networks.

We detected P- and S-wave onset times embedded in the continuous recordings by applying the supervised artificial intelligence (AI) method of PhaseNet (Zhu and Beroza, 2019) that is trained on the seismicity database from northern California. This method has proven to improve the detection process, especially for small earthquakes (e.g., Martinez-Garzon et al., 2023). With this method, 148 948 body wave onsets were detected, of which 78 410 were detections of P waves and 70 568 were detections of S waves.

The P and S picks were associated with seismic events using the unsupervised technique of Gaussian Mixture Model Association (GaMMA; Zhu et al., 2022). To classify an event to be an earthquake, a minimum of four necessary picks (either P and/or S) was set. The picks were spatiotemporally clustered using the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) method. About 19 % of the total number of picks were associated with earthquakes. In this way, we have obtained a catalog of detections containing 3361 possible seismic events (Fig. 3a).

As a comparison, KOERI reported a total of 505 events with magnitudes ≥ M_L 0.5 for the same region and time interval analyzed here (Fig. 3b). Out of these, 440 correspond to common events from both catalogs.

In the next step, the waveforms from all events corresponding to the period before the M_W 6.0 mainshock were visually inspected. About 343 detections from the time period before the mainshock were removed, as they showed signals in only one or two of the accelerometers, typically exhibiting $t_S-t_P>\mathrm{5}\mathrm{s}$, which is larger than what is expected for a small local event. Additionally, 35 events were identified as being regional events with locations outside the study region, and an additional 11 events were identified as being duplicates and removed. In the following, we refer to this catalog as the “catalog of detections”.

We calculated event locations by employing the probabilistic location software NonLinLoc (Non-Linear Location; Lomax et al., 2009). Here, only events with a minimum of six P and/or S picks were further processed, which implicitly removes possible false signal associations with fewer than six phases from the catalog of detections. The local 1-D velocity model from Bulut et al. (2007) was employed, assuming a constant $v_{\mathrm{p}}/v_{\mathrm{s}}$ ratio of 1.73. The search area encompassed a 400 km × 200 km region centered around the mainshock epicenter. In the following, we refer to this refined catalog as the “catalog of absolute locations”. Further details on the refining of the catalog of absolute locations are provided in Sect. S1 in the Supplement. In this way, we obtained a catalog of 1290 events with absolute locations that contain 8927 P-wave picks and 7822 S-wave picks for further processing (Fig. S5). In this catalog, the median errors in the x, y and z directions are 2.3, 3.1 and 3.4 km, respectively.

In the next step, a relative event relocation was performed using HypoDD (Waldhauser and Ellsworth, 2000; Waldhauser et al., 2004). We utilized both catalog differential travel times derived from the automatic PhaseNet P and S picks and the cross-correlation time differences derived from the event waveforms. To estimate the waveform cross-correlations, we employed time windows covering 1 and 2 s centered at the P and S onset, respectively. The waveforms were filtered with a third-order Butterworth bandpass filter between 2 and 10 Hz. The retrieved correlations with a normalized cross-correlation coefficient of at least 0.7 were kept, and the square of the cross-correlation coefficient was used as weight in the relocation procedure. To look at the spatiotemporal evolution of the seismicity, we demanded a minimum of eight catalog time differences (either P and/or S phases) for each event combination, resulting in a catalog of 918 relocated events. In the following, we refer to this further-refined subset as the “relocated catalog”. The median formal relative relocation errors in the x, y and z directions are 11, 13 and 12 m, respectively.

2.3 Earthquake source parameters and directivity

The estimation of point source parameters of the M_W 6.0 mainshock was performed using the spectral fitting method (Kwiatek et al., 2011, 2015). We used 249 high-gain seismometers of Kandilli Observatory (KO) and the National Seismic Network of Türkiye (TU). The combination of these networks offers a sufficient azimuthal coverage and signal-to-noise ratio for the analyzed catalog. From these networks, stations with epicentral distances of 200–800 km are used to derive source parameters of the mainshock.

Three-component ground velocity waveforms from stations with a signal-to-noise ratio of at least 4 dB were filtered using a second-order 0.02 Hz high-pass Butterworth filter and then integrated in the time domain. We utilized window lengths of 25 s from the P- and S-wave ground displacements, allowing for an additional 4 s before the P- or S-wave onsets. The selected window length of 25 s, in combination with the minimum station distance of 200 km, prevents contamination of the P-wave window by S-wave energy, as the S–P time difference is larger than 25 s and assumes average velocities and $v_{\mathrm{p}}/v_{\mathrm{s}}$ ratios along the travel path. The edges of the selected windows were smoothed using von Hann's taper. We utilized the three components from the far-field ground displacement spectra using the Fourier transform and then combined altogether. The observed ground displacement spectra were fit to Brune's point source model, which is expressed as

$$\begin{array}{}\text{(10)}& u^{\text{th}}\left(f\right)={\displaystyle \frac{\langle R_{\mathrm{c}}\rangle }{\mathrm{4}\mathit{\pi }\mathit{\rho }{V}_{\mathrm{c}}^{\mathrm{3}}R}}{\displaystyle \frac{M_{\mathrm{0}}}{\mathrm{1}+{\left(\frac{f}{f_{\mathrm{c}}}\right)}^{\mathrm{2}}}}\text{exp}\left({\displaystyle \frac{-\mathit{\pi }fR}{V_{\mathrm{c}}{Q}_{\mathrm{c}}}}\right),\end{array}$$

where R is the source–receiver distance; M₀ is the seismic moment; f_c is the corner frequency, Q_c is the quality factor, and 〈R_c〉 is the average radiation pattern correction coefficient, where c represents either the P or S wave. Following Boore and Boatwright (1984), we applied R_P=0.65 and R_S=0.7 for P and S waves, respectively, that are representative constants for the regional strike–slip faults. We used V_P = 5680 m s⁻¹ and V_S = 3280 m s⁻¹ (from Bulut et al., 2007; averaged at the depth interval where the earthquakes occurred), assuming $V_{\mathrm{P}}/V_{\mathrm{S}}$ = 1.73 and a density ρ = 2700 kg m⁻³. We inverted for (M₀, f_c; Q_c), optimizing the cost function

$$\begin{array}{}\text{(11)}& \mathrm{|}\mathrm{|}{\text{log}}_{\mathrm{10}}{u}^{\text{obs}}\left(f\right)-{\text{log}}_{\mathrm{10}}{u}^{\text{th}}\left(f\right)\mathrm{|}{\mathrm{|}}_{L\mathrm{1}}=\text{min},\end{array}$$

where u^th(f) and u^obs(f) are the theoretical and observed ground displacement amplitude spectrum for a given station and P or S wave. The starting model for M₀ and f_c was taken, using Snoke's integrals (Snoke, 1987), and we assumed initial values of Q=400 for both P- and S-wave trains. We utilized a grid search optimization (assuming a starting model), followed by simplex algorithms (starting from the best model of a grid search). Source parameters that deviated from the average by more than 3 standard deviations were eliminated from the calculation. The final source parameters (i.e., seismic moment, corner frequency and quality factor) were calculated as average values from all stations. An example of such calculated spectra for a station is provided in Fig. 4.

In the following, we calculated the static stress drop using the formula valid for a rectangular strike–slip fault (Shearer, 2019):

$$\begin{array}{}\text{(12)}& \mathrm{\Delta }\mathit{\sigma }={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}{\displaystyle \frac{M_{\mathrm{0}}}{W^{\mathrm{2}}L}},\end{array}$$

where W = 8 km represents the fault width, which is assumed from the depth extent of the aftershocks (see Sect. 3.2.2). The rupture length L is estimated to be double the source radius, using Brune's source model constants and, for comparison, Haskell's rectangular source, assuming V_R=0.9V_S (see Savage, 1972; Table 1 for details) and using

$$\begin{array}{}\text{(13)}& L={\displaystyle \frac{C_{\mathrm{C}}{V}_{\mathrm{c}}}{\mathrm{2}\mathit{\pi }{f}_{\mathrm{c}}}},\end{array}$$

in which C_C is the geometrical correction coefficient ($C_{\mathrm{P}}=C_{\mathrm{S}}=\mathrm{4.7}$ for Brune's model and C_P=1.2 and C_S=3.6 for Haskell's model; see Savage, 1972). f_c and V_c represent the corner frequency and seismic velocity of either P or S waves, respectively.

For the earthquakes comprising the absolute locations catalog, we estimated only moment magnitudes M_W using a simplified approach, following the Snoke (1987) integrals:

$$\begin{array}{}\text{(14)}& {\displaystyle }{J}_{\mathrm{S}}=\mathrm{2}\int \left[\dot{u}\right(f){]}^{\mathrm{2}}\mathrm{d}f,\text{(15)}& {\displaystyle }{K}_{\mathrm{S}}=\mathrm{2}\int \left[u\right(f){]}^{\mathrm{2}}\mathrm{d}f,\end{array}$$

where $\dot{u}\left(f\right)$ and u(f) are ground velocity and displacement S-wave spectra corrected for attenuation and prepared from S-wave waveforms processed in the same way as for the mainshock. The original seismograms were filtered with 1 Hz high-pass second-order Butterworth filter, and we used a shorter 5 s window framing the first S wave arrival to limit the influence of low-frequency noise for predominantly small earthquakes (M < 4). The integrals in Eqs. (14) and (15) were corrected for the finite frequency band, following Di Bona and Rovelli (1988). The seismic moment has been estimated with the following (Snoke, 1987):

$$\begin{array}{}\text{(16)}& M_{\mathrm{0}}=\mathrm{8}\mathit{\pi }\mathit{\rho }{V}_{\mathrm{S}}^{\mathrm{3}}R{\left({\displaystyle \frac{K_{\mathrm{S}}^{\mathrm{3}}}{J_{\mathrm{S}}}}\right)}^{\mathrm{0.25}},\end{array}$$

and the moment magnitude was calculated using the standard relation (Hanks and Kanamori, 1979).

$$\begin{array}{}\text{(17)}& M_{\mathrm{W}}={\displaystyle \frac{({\text{log}}_{\mathrm{10}}{M}_{\mathrm{0}}-\mathrm{9.1})}{\mathrm{1.5}}}\end{array}$$

Similar to the mainshock, for each event, the final seismic moment and moment magnitude were calculated as the average values from all stations containing S-wave arrivals. Due to the limited number of S waves with a sufficient signal-to-noise ratio for the smallest earthquakes, the uncertainties were estimated using the mean absolute deviation.

Large earthquake ruptures potentially involve a propagation process along a fault plane. The rupture propagation direction could be deduced from the azimuthal variations in the amplitude and frequency content of the apparent source time functions (ASTFs) providing important information for seismic risk assessment. For a unilateral rupture, ideally this would lead to shorter ASTFs displaying larger amplitudes in the direction of rupture propagation and longer-duration and smaller-amplitude ASTFs in the opposite direction. To obtain the ASTFs, we initially tested the application of empirical Green's function (EGF) technique and tried four EGF candidates (Table S3) to recover the directivity of the mainshock (see Sect. S2 for all details) that led to inconclusive results.

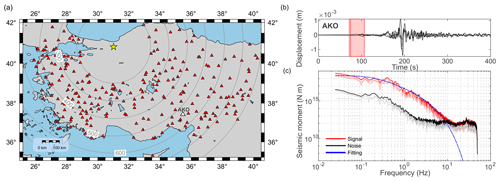
Figure 4 Source parameter analysis. (a) Station distribution employed for the source parameter estimation (upward-pointing red triangles). These stations lie within a source station distance between 200 and 800 km. The yellow star shows the 2022 M_W 6.0 Gölyaka–Düzce mainshock. (b) Three-component displacement waveforms for the mainshock recorded by station AKO (with epicentral distance ∼ 530 km; see the white triangle in panel a). The red rectangle highlights the employed P-wave window. (c) Ground displacement spectrum of the P-wave signal (red) and the noise before the signal (black). The thick blue line indicates the modeled spectrum yielding the source parameters of $M_{\mathrm{0}}=\mathrm{2.62}\times {\mathrm{10}}^{\mathrm{18}},f_{\mathrm{c}}=\mathrm{0.19}\mathrm{Hz},Q_P=\mathrm{308}$.

We therefore tested the azimuthal variations in the duration and frequency content of the initial P wave arrivals for seismometers located at epicentral distances of 50–100 km from the mainshock. For comparison, we additionally included integrated signals from accelerometers located at much closer distances. We only used the unclipped first P-wave pulses that were rotated into the radial direction from three-component seismograms to enhance the signal-to-noise ratio of the initial portions of the P wave. The first P-wave pulses contain a combination of information, including the source time function and effects related to the wave propagation. However, comparing P-wave pulse characteristics for stations located at similar distances from the mainshock epicenter allows us to suppress the propagation effects. Therefore, the initial portion of the seismogram can be taken as a proxy for the ASTFs. The variation in the rise time and duration of the P pulses can then be used to infer whether the earthquake displays rupture directivity.

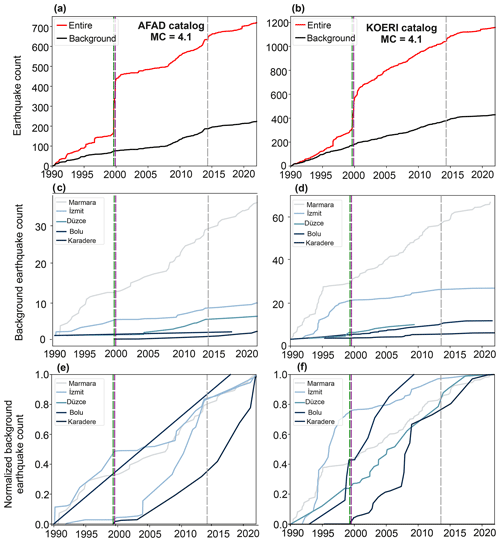
Figure 5 Temporal evolution of the background seismicity at different segments of the NAFZ. (a) Complete (red) and declustered (black) AFAD catalog using M^C=4.1. (b) Same as panel (a) but with KOERI catalog. (c) Cumulative background seismicity, color-coded by region. (d) Same as panel (c) but for the KOERI catalog. The vertical lines represent the time of occurrence of the M_W 7.4 İzmit, M_W 7.1 Düzce and M_W 6.9 Saros earthquakes. (e) Normalized cumulative background seismicity for the AFAD catalog. (d) Same as panel (c) but for the KOERI catalog.

3 Results

3.1 Long-term evolution of background seismicity in the Gölyaka–Düzce region

We analyzed the evolution of the background seismicity along defined segments of the NAFZ, including the Marmara, İzmit, Düzce, Bolu and Karadere segments (Fig. 2). Both of the national Turkish catalogs introduced above show that the Bolu segment displays a low background seismicity rate when compared to, for example, the İzmit or Marmara segments (Fig. 5). Aseismic slip (surface creep) has been reported to occur along this segment and has occurred for at least 70 years (Ambraseys, 1970; Cakir et al., 2005; Cetin et al., 2014; Bilham et al., 2016; Jolivet et al., 2023). This might be a possible explanation for the low seismicity rate. The Marmara, İzmit and Düzce segments appear to host a constant background seismicity rate with time, especially after the 1999 İzmit and Düzce sequence (Fig. 5). Both catalogs report a deceleration of background seismicity after the 2014 M_W 6.9 Saros earthquake (Bulut et al., 2018), supporting the idea that some significant deformation process not yet understood in detail was affecting the seismicity along the NAFZ (Karabulut et al., 2022).

The Karadere fault hosted a comparatively low background seismicity before the 1999 İzmit and Düzce earthquake sequence. A change in its seismic behavior is observed afterwards, which is when this segment experienced an increase in the seismic activity that included more than five events with M > M^C = 4.1. The shape of the background rates is different for the AFAD and KOERI catalogs. This difference might be due to the different number of seismic stations operated by the agencies in this area; hence, this affects the monitoring capabilities and detection thresholds. Therefore, it is likely that the region was tectonically activated by the earthquake sequence in 1999 and progressively loaded since then, leading to the M_W 6.0 Gölyaka–Düzce earthquake 23 years later. Interestingly, the region did not exhibit a lower background rate after the 2014 M_W 6.9 Saros earthquake, which is different to the other NAFZ segments in the area.

3.2 Spatiotemporal seismicity distribution before and after the 2022 Gölyaka–Düzce earthquake

We obtained an enhanced seismicity catalog with 1290 refined hypocenter locations, as described in Sect. 2.2, covering the area of latitude (40–42^∘ N) and longitude (30–32^∘ E) for the time period 23 October 2022 at 00:00 LT up to 29 November 2022 at 00:00 LT and including moment magnitudes as low as M_W 0.7. Out of these, a total of 222 and 1032 seismic events correspond to events preceding and following the 2022 Gölyaka–Düzce mainshock, respectively. For the same region and time interval, the seismicity catalog provided by the KOERI agency contained 529 events, out of which 23 and 506 corresponded to events preceding and following the mainshock, respectively (Fig. 3b).

Using a goodness-of-fit method (Wiemer and Wyss, 2000), the magnitude of completeness of the derived catalog within selected region is $M_{\mathrm{W}}^{\mathrm{C}}=\mathrm{1.5}$. Calculating the b value for events above M^C, from both the periods before and after the mainshock, we find a value of $b=\mathrm{0.95}\pm \mathrm{0.05}$ (Fig. S6). This could be related to the fact that we utilized M_W, while many other estimates use M_L, possibly leading to a larger b value (see, e.g., Raub et al., 2017). Alternatively, the relatively low b value may suggest that the fault did not yet release all of its accumulated strain (e.g., Gulia and Wiemer, 2019). Given the magnitude of the mainshock and the spatial extent of the rupture, we consider the latter option to be rather unlikely.

3.2.1 Seismic activity preceding the Gölyaka–Düzce earthquake

The M_W 6.0 Gölyaka–Düzce earthquake hypocenter is located at the northeastern portion of the Karadere fault that remained unbroken during the 1999 M_W 7.4 İzmit and 1999 M_W 7.1 Düzce events.

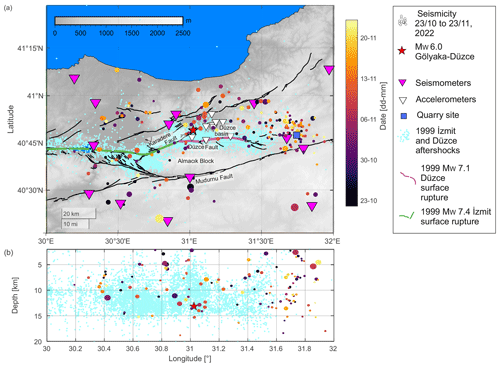
Figure 6 Seismicity located during the preceding month. Seismicity distribution included in the absolute location catalog (colored circles) during the month preceding the Gölyaka–Düzce earthquake (red star). Symbol size is encoded with magnitude. Surface ruptures of the 1999 M_W 7.4 İzmit and M_W 7.1 Düzce earthquakes are shown with dashed green and pink lines, respectively. For comparison, the seismic activity for three different time periods around the 1999 İzmit and Düzce mainshock is shown in cyan (from Bohnhoff et al., 2016; Bulut et al., 2007). Fault traces are from Emre et al. (2018).

The area that ruptured in the M_W 6.0 Gölyaka–Düzce earthquake and its surroundings only displayed a small number of seismic events during the 30 d preceding the mainshock. The catalog of absolute locations reported 222 seismic events during this time, out of which 55 could be successfully relocated. Most of the relocated seismic activity occurred away from the future M_W 6.0 earthquake rupture, extending up to 50 km to the east (Fig. 6). The locations of these seismic events show a good correspondence with the mapped local faults (Emre et al., 2018). A small cluster of events is visible at the eastern edge of the analyzed region, coinciding with the termination of a local fault, near a quarry area (see Fig. 6a for the location). The presence of a quarry in the area suggests that some of these events could be quarry blasts. However, these events appear to be regular seismic events based on the following: (i) these detections display regular P- and S-wave trains, (ii) their hypocentral depth is deeper than 8 km and (iii) these events occur randomly in time. Within a 25 km radius from the epicenter of the M_W 6.0 Gölyaka–Düzce earthquake, 23 events were included in the catalog of absolute locations. The most active time period was between 6 and 11 November, where a small spatially clustered seismic sequence with magnitudes up to M_W 2.2 occurred about 7.5 km to the north of the mainshock epicenter (Figs. 6 and S7). The location of this cluster coincides with the deepest part of the fault activated during the aftershock sequences.

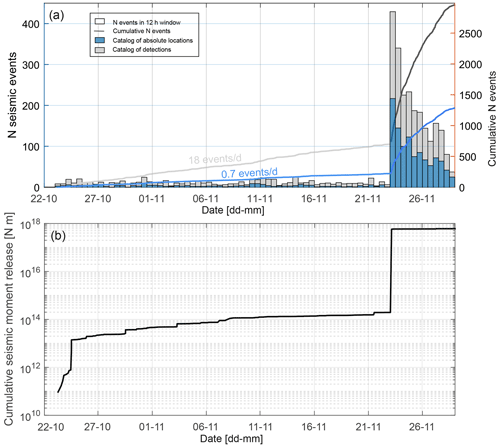
Figure 7 Temporal evolution of seismic activity and seismic moment. (a) Bars show the histogram of seismicity rates, where every bar represents a time period of 12 h. Gray and blue colors represent the seismicity included in the catalog of detections and absolute locations, respectively. Lines show the cumulative number of seismic events as a function of time. Lighter and darker colors represent the time periods before and after the mainshock. (b) Evolution of cumulative seismic moment release from the catalog of absolute locations.

Both the catalog of detections and the catalog of absolute locations show that seismicity rates were time-invariant, with a transient increase in seismic activity around 10 November, reflecting the transient cluster north of the future mainshock. This increase in the seismicity rates quickly decayed back to the level before the occurrence of the cluster and remained constant until the occurrence of the mainshock (Fig. 7). The regional seismicity did not display any significant acceleration at the scale of days to hours before the mainshock.

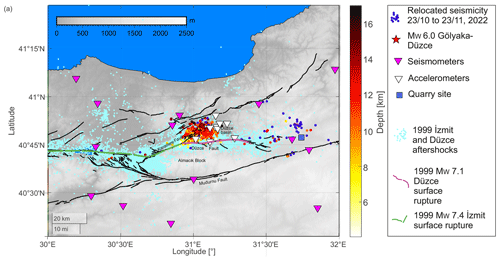
Figure 8 Seismicity distribution after the Gölyaka–Düzce earthquake (colored dots). Cyan dots in the background reflect 1999 İzmit and Düzce aftershocks (from Bohnhoff et al., 2016; Bulut et al., 2007).

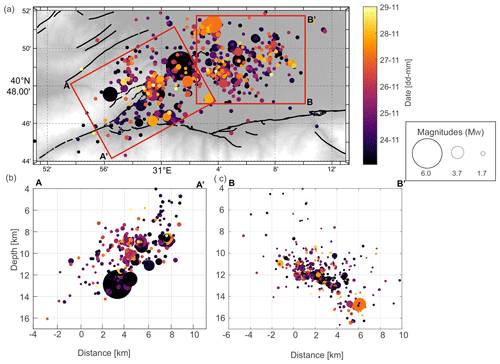
Figure 9 Magnification of the spatiotemporal distribution of the seismicity during 6 d following the Gölyaka–Düzce earthquake. (a) Map view. Depth profiles along (b) A-A' (approximately perpendicular to the Karadere fault strike), and (c) B-B' (approximately perpendicular to the strike of the Düzce fault). The symbol size and color are encoded with magnitude and date, respectively.

3.2.2 The aftershock sequence following Gölyaka–Düzce earthquake

After the M_W 6.0 Gölyaka–Düzce earthquake, vigorous seismic activity struck the region during the following days. Compared to the scattered seismicity in a much larger region, most of this early aftershock activity occurs within an area extending 15 km to the east and west, as well as 8 km to the north and south, of the mainshock epicenter, respectively (Figs. 8 and 9). Generally, aftershocks typically occur around the mainshock rupture area, and they may also activate nearby faults, due to stress changes induced by the mainshock. In a first-order approximation, the relocated aftershock activity delineates a planar structure trending SW–NE that is dipping towards the NNW, which is consistent with the geometry of the Karadere fault (Fig. 9). The plane best fitting to the seismicity (contained within 1 km distance) has a strike of $\mathit{\phi }=\mathrm{257}{}^{\circ }$ and a shallow dip of approximately $\mathit{\delta }=\mathrm{45}{}^{\circ }$ (Fig. 9). The strike of this plane is thus in good agreement with the moment tensor solutions for the M_W 6.0 mainshock (Table S2). However, the dip of our plane is shallower than the δ^fm = 72–82^∘ reported by the moment tensor solutions (Fig. 9c). The depth of the seismicity along the strike of the fault segment is not uniform, with the southwestern portion of the fault generally displaying shallower seismicity from 5 to 13 km depth and the northeastern portion of the activated fault between 9 and 16 km depth (Fig. 9b). Along the strike, the hypocentral location of the mainshock coincides with this depth change, suggesting the presence of a fault jog or a heterogeneity that could have promoted a stress concentration.

The mainshock triggered an aftershock sequence that within the first 6 d can be fitted with an Omori law of the shape $N\left(t\right)=k{t}^{-p}$, with p=0.90 and k=2.5 (see Fig. S8). Typical values observed for the p value representing the decay rate oscillate around 1.0, suggesting that the aftershock decay associated with this sequence is fairly standard, including three to four M_W > 4 earthquakes occurring within the analyzed time window.

3.3 Source parameters and directivity of the Gölyaka–Düzce mainshock

Earthquake source parameters for the 2022 M_W 6.0 Gölyaka–Düzce mainshock are provided in Table 1, with the average values and multiplicative error factors calculated in log10 domain (García-García et al., 2004). The averaged seismic moment is 8.80 × 10¹⁷, leading to a moment magnitude of M_W 5.9, which is equal to the moment magnitude given by AFAD. The average corner frequency f_c values obtained for P and S waves are 0.23 Hz and 0.24 Hz, respectively, with a ratio of $\frac{f_{\text{cP}}}{f_{\mathrm{cS}}}=\mathrm{0.96}$. The obtained ratio of corner frequencies from P and S waves is lower than the $\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}=\mathrm{1.73}$, which holds for a stationary source and can be decreased due to the rupture propagation effects (Sato and Hirasawa, 1973; Kwiatek and Ben-Zion, 2013). In general, the f_cP>f_cS arises for roughly equidimensional source models (length equal to width). For long and thin faults, lower $\frac{f_{\text{cP}}}{f_{\mathrm{cS}}}$ ratios are to be expected; for example, $\frac{f_{\text{cP}}}{f_{\mathrm{cS}}}=\mathrm{0.77}$, assuming rupture velocity V_R=0.9V_S (Savage, 1972). Nearly equal f_cP and f_cS values are given in a dislocation model with a unilateral rupture propagation (Haskell, 1964). The small $f_{\mathrm{cP}}/f_{\mathrm{cS}}$ ratio might imply that the fault width W could be overestimated from the aftershock distribution and could be smaller than 8 km, which is also supported by the narrower fault width estimated from the early aftershock distribution (Fig. 9).

Attenuation greatly affects the amplitude and frequencies included in the seismograms. Commonly, S waves tend to have larger attenuation than P waves. The ratio between the P and S quality factors is

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{Q_{\mathrm{P}}}{Q_{\mathrm{S}}}}={\displaystyle \frac{\mathrm{3}}{\mathrm{4}}}{\displaystyle \frac{V_{\mathrm{P}}^{\mathrm{2}}}{V_{\mathrm{S}}^{\mathrm{2}}}}.\end{array}$$

For a Poisson solid, $V_{\mathrm{P}}=\sqrt{\mathrm{3}}{V}_{\mathrm{S}}$, thus resulting in $\frac{Q_{\mathrm{P}}}{Q_{\mathrm{S}}}$ = 2.25. Our observations provide a considerably lower $\frac{Q_{\mathrm{P}}}{Q_{\mathrm{S}}}$ = 1.2. Such lower ratios are not uncommon and have been interpreted as being the attenuating effect of pore fluids (Olsen et al., 2003; Hauksson and Shearer, 2006; Kwiatek and Ben-Zion, 2013; Kwiatek et al., 2015).

Utilizing the average source size and seismic moment from both P and S waves, the static stress drop of the mainshock is estimated as 0.61 and 1.48 MPa, while using a Brune model (Eq. 12) and a Haskell model, respectively (Table 1). The estimated rupture length varies at around 14 and 6 km for the Brune and Haskell models, which yields a rectangular source with a small $L/W$ ratio. A relatively small aspect ratio was also observed for the M_W 7.1 in 1999 in the direct vicinity of this area (Bürgmann et al., 2002).

Table 1 Source parameters for the 2022 M_W 6.0 Gölyaka–Düzce earthquake. f_c is the corner frequency. M₀ is the seismic moment. L is the source rupture length. Q is the quality factor. Δσ is the stress drop.

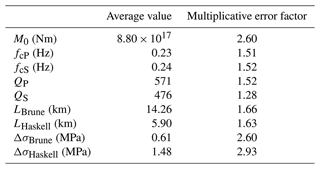
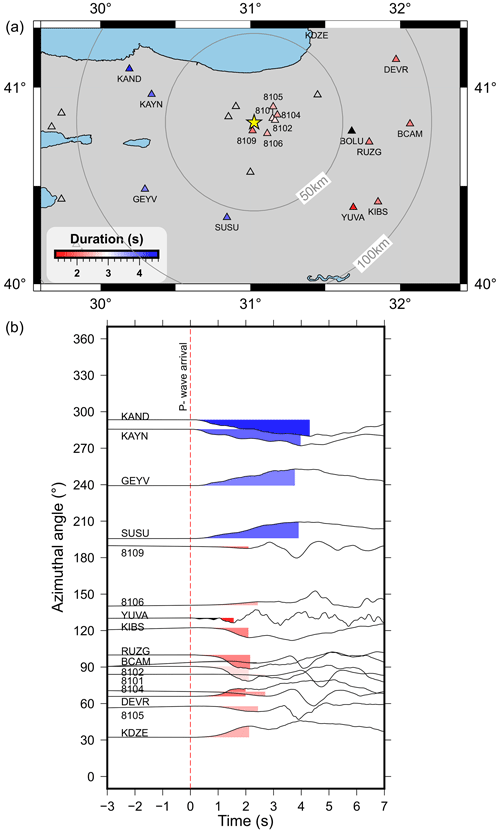
Figure 10 First-peak duration recorded at seismic stations between 50 and 100 km from the mainshock epicenter. (a) Station distribution near the epicenter (yellow star). Colored triangles highlight the stations used in panel (b). (b) Normalized ground displacement recordings on radial components. The waveforms are aligned relative to the P-wave arrival (0 s) in the time axis and are ordered according to the azimuthal angles relative to the mainshock. The time duration of the colored segments is shown color-coded for in the station symbols in panel (a).

Figure 10 shows P-wave arrivals highlighting the initial portion of the ground displacement record Δt. Longer Δt rise times and durations of first P-wave displacement pulses are observed for western stations with azimuth angles of 196–293^∘ (i.e., stations SUSU, GEYV, KAYN and KAND). At the same time, eastern stations at comparable distances and azimuth angles ranging from 32 to 130^∘ display shorter rise times and visibly higher-frequency content (see discussion in Douglas et al., 1988; Fig. 10b), especially for stations RUZG and BCAM near 90^∘ azimuth. These observations suggest an eastward rupture propagation, while assuming a unilateral rupture. However, in the case of a more complicated rupture process, the shorter rise time could also be promoted by a closer large local slip asperity in the easterly direction. We also estimated the azimuthal variations of f_c for the stations between 200 km and 800 km from the mainshock (Fig. S9). Larger f_c values are observed at approximately 100^∘, hence being roughly consistent with the eastward rupture propagation. However, we note that scattered large f_c values were also observed at other azimuths.

4 Discussion

The various spatiotemporal scales covered by the different methodologies applied in this study provide insights into the processes leading to and involved in the rupture of the M_W 6.0 Gölyaka–Düzce earthquake. In the following, we discuss the most important patterns that emerged from the obtained results and their relation with the rheology of the region, the development of previous large earthquakes (i.e., the M > 7 İzmit and Düzce earthquakes) and its stage in the seismic cycle.

4.1 The 1999 M > 7 İzmit and Düzce earthquakes promoted the seismic activation of the Karadere fault

The Karadere fault connects the Akyazı and Düzce basins, which are both pull-apart structures in response to the regional transtensional tectonic setting (Pucci et al., 2006; Ickrath et al., 2015; Bohnhoff et al., 2016). The spatiotemporal evolution of seismicity along different portions of the broader Marmara region since 1990 has shown that the Karadere fault was primarily quiet until the occurrence of the 1999 M > 7 İzmit and Düzce events (Fig. 5). Most of the Karadere fault was activated during the 17 August 1999 M_W 7.4 İzmit earthquake, while its northeastern portion likely hosted fewer aftershocks (Bohnhoff et al., 2016). The 1999 İzmit rupture was then extended further eastwards 87 d later, with the 11 November 1999 M_W 7.1 Düzce earthquake onto the east–west trending Düzce fault splaying off the Karadere fault, and also dipping towards the north, with a dip of around 55^∘ (Bürgmann et al., 2002).

The 23 November 2022 M_W 6.0 Gölyaka–Düzce rupture likely occurred on the northeastern portion of the Karadere fault that remained inactive in 1999, marking the western flank of the Düzce Basin as a topographic depression north of the Düzce fault as a releasing bend. The fact that the İzmit rupture stopped on the Karadere fault and redirected onto the Düzce fault indicates that the northeastern Karadere fault acted as a barrier in 1999. This is supported by the observation of a lower seismic velocity contrast in the Karadere fault with respect to the fault regions west of it (e.g., the Mudurnu fault; see Najdahmadi et al., 2016). Nevertheless, our results show increased background seismic activity from 1999 onwards in the Karadere segment, with a visible increase in 2004–2005. One hypothesis is that the stress redistribution from the 1999 İzmit and Düzce earthquake sequences brought the Karadere segment closer to failure by stress transfer, leading to a progressive activation of this segment over the years. In that way, after 23 years of additional continuous tectonic loading, it was finally activated with a M_W 6 event within a region of the fault zone that is still in a relatively early phase of the seismic cycle. Some support for this scenario comes from a reported change in stress regime, together with a rotation of the S_hmin orientation in the Karadere segment before and after the 1999 İzmit and Düzce sequences (Ickrath et al., 2015). Before the earthquakes, a predominantly normal faulting stress regime was observed, while the strike–slip regime was observed after the Düzce earthquake. As the magnitude of S_V at a certain depth is mostly given by the weight of the overburden, it is expected to remain approximately constant during the earthquake cycle. This suggests that the horizontal shear stresses on the fault increased after the 1999 sequence. We additionally note that the average recurrence period of M > 7 earthquakes in the area is around 250 years (Murru et al., 2016). Therefore, the recurrence time of a M > 6 earthquake should be about 25 years, which roughly fits with the occurrence of the last M > 7 earthquakes 23 years before the Gölyaka–Düzce event.

The observed changes in the background seismicity rates could also be related to a change in the seismic coupling of the region (e.g., Marsan et al., 2017; Jara et al., 2017). In particular, the occurrence of the 1999 M > 7 İzmit and Düzce earthquakes and their post-seismic deformation could have resulted in the promotion of the occurrence of an aseismic slip at depth, hence leading to a progressive decoupling of the fault. The buildup of stresses from the occurrence of enhanced aseismic slip can increase the background seismicity rates over the region with distributed deformation over a large area. Indeed, an additional proposed mechanism for the 1999 Düzce rupture was a viscoelastic post-seismic relaxation at depth, which affected a broad area from the 1999 İzmit rupture (e.g., Bürgmann et al., 2002; Ergintav et al., 2009). A detailed study on the microseismicity from this area also suggested that this possibility could account for the larger seismicity rates at depth (Beaucé et al., 2022).

4.2 How did the mainshock start?

Our catalog of absolute locations revealed at least 23 seismic events with an epicentral location less than 25 km from the M_W 6.0 Gölyaka–Düzce event during the month before its occurrence. Out of these, only two are located in the northeastern segment of the Karadere fault, as the main fault segment that ruptured in the Gölyaka–Düzce event. The spatiotemporal evolution of these events does not suggest clustering but rather a scattered activation of the area (Fig. S7).

Likewise, the foreshocks do not generally resemble a spatial or temporal localization of the seismicity prior to the mainshock. This is of relevance, since a number of moderate to large earthquakes in this region displayed systematic foreshock activity (Bouchon et al., 2011; Ellsworth and Bulut, 2018; Malin et al., 2018; Durand et al., 2020). A similar spatiotemporally scattered precursory activity pattern as seen for the mainshock was also found for the 1999 M_W 7.1 Düzce earthquake, where the largest event in the region of the earthquake rupture in the preceding 65 h was a M 2.6 event (Wu et al., 2013). Additional small events detected around the future Düzce 1999 rupture did not show any clear signatures of acceleration. The few seismic events preceding the 2022 M_W 6.0 event, together with their lack of spatiotemporal localization, suggest the existence of relatively homogenous local stress conditions along this fault segment or, alternatively, homogeneous fault strength that would allow a progressive fault loading without rupturing small heterogeneities in the medium reflecting foreshock activity. In this respect, laboratory rock deformation experiments have shown that seismic precursors are more frequent on rough fault surfaces, while seismic foreshocks are much less frequent on polished fault surfaces (Dresen et al., 2020). This is consistent with the linear and relatively simple geometry of the eastern portion of the Karadere segment. In fact, the decade-long seismicity along the Karadere fault shows that it is notoriously more localized within the fault trace than in other fault areas (see e.g., Wu et al., 2013).

The fault area that was activated in the 1999 M > 7 İzmit and Düzce earthquakes is documented to continue displaying post-seismic deformation almost 20 years after (Ergintav et al., 2009; Aslan et al., 2019), which is mainly related to afterslip and viscoelastic relaxation. In this respect, one possibility is that the initiation of the mainshock was also promoted by the occurrence of distributed aseismic slip in the region at depth over a broad area (e.g., Beaucé et al., 2022; Karabulut et al., 2022). This is supported by the observation of a small number of seismic events around 11 November, at the bottom of the Düzce fault, near the place where the 1999 Düzce earthquake nucleated (Fig. 6). Another hypothesis is that a regional or local stress perturbation could have destabilized the northeastern Karadere fault that was close to failure. Some examples for such a potential stress perturbation may include tidal effects or seasonal effects, such as the effect of precipitation (e.g., Hainzl et al., 2013) or barometric pressure changes (Martínez-Garzón et al., 2023). Regarding seasonal or semi-periodic stress perturbations, it is worth mentioning that the M_W 6.0 Gölyaka earthquake, a M_W 4.9 event in 2021, as the largest and most recent event in this area, and the 1999 M_W 7.1 occurred within the second-half of November. Further statistical analysis is not conducted in the frame of this study but may give a further indication with respect to whether earthquakes in this region show any significant temporal pattern.

4.3 Fault segments potentially activated during the mainshock and aftershock sequence

Based on the estimated rupture length from the mainshock source parameters, the event activated a ∼ 12 km long segment of the Karadere fault, terminating just east of the Düzce Basin (Fig. 9). Although we tested the application of EGF methods to recover the directivity more accurately, the analysis did not yield clear results (see Sect. S1 for details). The reasons for this are not clear. It may be that the events used for the EGF deconvolution did not fulfill all necessary criteria (e.g., occurring on the same location, with a similar focal mechanism and at least a unit of magnitude difference). Alternatively, it could be that the mainshock rupture did not activate a single fault segment, resulting in some complexities obscuring the directivity pattern.

The rupture complexity is also somewhat consistent with the spatial distribution of aftershock seismicity, which shows a heterogeneous event distribution, possibly also illuminating fault structures that were not directly involved in the mainshock rupture. On the western section, the spatial distribution of aftershock seismicity is oriented SW–NE, and part of the distribution suggests the activation of a NW-dipping fault plane of the mainshock, in accordance with fault–plane solutions of the event (Table S2) and with the size of the mainshock rupture estimated from the source parameters.

However, the eastern part of the aftershock distribution is also compatible with the fault geometry of the main Düzce fault activated in 1999. Indeed, the main cluster of events is located at approximately 10 km distance from the mapped surface trace of the Düzce fault. As the deepest aftershock seismicity is located at about 15 km depth, the distribution is also consistent with a fault dipping at about 55^∘, as we previously reported in Sect. 3.2.2 (Fig. 9). Indeed, this dip is more consistent with the fault geometry reported for the Düzce fault (Bürgmann et al., 2002) than with the dip of the Karadere fault extracted from the focal mechanism of the M_W 6.0 Gölyaka–Düzce earthquake.

Therefore, we suggest that the aftershock distribution that we obtained is likely reflecting the activation of both faults, with the Karadere segment displaying a steeper dip towards the northwest, as observed from the focal mechanisms, and the main Düzce fault at depth dipping more gently (around 55^∘) towards the north.

4.4 A proxy for rupture directivity suggests a larger radiation of energy towards the east

Higher-frequency P-wave pulses with shorter rise times were identified at seismic stations found eastward of the rupture, suggesting that the mainshock propagated towards the east. This is consistent with the rupture directivity derived for this earthquake from the analysis of ground motions (Türker et al., 2023). A statistically preferred rupture propagation towards the east was also resolved in the Karadere fault segment below 5 km depth, based on the analysis of fault zone head waves (FZHWs) and fault zone reflected waves (FZRWs; Najdahmadi et al., 2016). At depth, the authors identified the faster side as being the elevated crustal Almacık block to the SE. Together with models of bimaterial ruptures, these results suggest that earthquakes on the Karadere segment nucleating at > 5 km depth have a physically explainable preferred propagation direction to the east. However, at a shallower depth, the fault core was detected to host even slower material between both blocks to either side (Najdahmadi et al., 2016). This led the authors to decide on a narrow wedge-shaped structure of the fault rather than a simple first-order impedance contrast of the fault. A preferred rupture propagation towards the east was also resolved in the Mudurnu fault segment (about 70 km west of the mainshock epicenter; see Fig. 6) from detection of fault zone head waves (Bulut et al., 2012). From the moveout of the fault zone head waves, a velocity contrast of about 6 % was estimated, with a slower seismic velocity for the northern side of the fault. An eastward propagation of the rupture was also reported for the 1999 M_W 7.1 Düzce earthquake rupture from the joint analysis of geodetic, seismic and strong motion data (Konca et al., 2010). We conclude that based on our observations of an eastward-directed rupture during the M_W 6.0 Gölyaka–Düzce earthquake, the observations of fault zone head waves in the region and the existence of bimaterial faults in the area should be considered to be an important ingredient for refined seismic risk studies in the area, especially for the Istanbul metropolitan region further to the west. However, this only applies if earthquakes are located along the bimaterial interface. For earthquakes located on secondary splay faults or in the rock volume, their rupture directivities may be related to other factors. A future possible analysis of the source parameters from the smaller events of the sequence may reveal whether the eastward directivity is a persistent feature in the region.

5 Conclusions

We investigated the source parameters of the 2022 M_W 6.0 Gölyaka earthquake in NW Türkiye and the evolution of the seismicity framing this mainshock at various spatial and temporal scales. This earthquake mainly ruptured the Karadere fault, a small fault segment located in the direct vicinity of the 1999 M_W 7.1 Düzce earthquake. Hence, this case is an example of a medium-sized earthquake which ruptured a critically stressed fault embedded in a fault zone that is overall in a relatively early stage of the seismic cycle. Our primary goal was to determine how the earthquake initiated, what the ongoing deformation mechanisms in the region are and how the energy from this mainshock was radiated. The main conclusions extracted from our analysis are the following.

The decade-long evolution of background seismicity in the Karadere segment shows that the segment was mostly silent before the 1999 M > 7 İzmit and Düzce earthquakes. From the year 2000 to the present, the segment has been comparatively more seismically active, supporting the hypothesis of a progressive approach to critical stress level of the fault segment.

The high-resolution seismicity catalogs derived in this study report on 23 locatable events during the previous month within a 25 km radius from the 2022 Gölyaka–Düzce earthquake. Only few of them occurred close to the future earthquake rupture, suggesting relatively homogenous fault stress conditions, and no signatures of foreshock localization were observed.

The early aftershocks of the sequence (i.e., first 6 d) suggested the activation of the Karadere fault segment dipping steeply towards the NW, as reported by the moment tensor, and the Düzce fault in the southern part dipping shallower directly towards the north. This suggests that the mainshock rupture, located along the Karadere fault, was able to trigger abundant aftershocks in the neighboring fault segment.

An analysis of the mainshock rupture directivity patterns, including an attempt to employ empirical Green's function analysis, did not yield clear results. However, a shorter rise time and the higher-frequency content of the P-wave pulses is observed at seismic stations located east of the mainshock hypocenter. If the mainshock rupture did indeed show promoted directivity towards the east, then the observation is consistent with predictions from models of bimaterial interfaces and observations from fault zone head waves at this fault.