the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Influence of heterogeneous thermal conductivity on the long-term evolution of the lower-mantle thermochemical structure: implications for primordial reservoirs
Joshua Martin Guerrero
Frédéric Deschamps
Wen-Pin Hsieh
Paul James Tackley
The long-term evolution of the mantle is simulated using 2D spherical annulus geometry to examine the effect of heterogeneous thermal conductivity on the stability of reservoirs of primordial material. Often in numerical models, purely depth-dependent profiles emulate mantle conductivity (taking on values between 3 and 9 ). This approach synthesizes the mean conductivities of mantle materials at their respective conditions in situ. However, because conductivity also depends on temperature and composition, the effects of these dependencies on mantle conductivity are masked. This issue is significant because dynamically evolving temperature and composition introduce lateral variations in conductivity, especially in the deep mantle. Minimum and maximum variations in conductivity are due to the temperatures of plumes and slabs, respectively, and depth dependence directly controls the amplitude of conductivity (and its variations) across the mantle depth. Our simulations allow assessing the consequences of these variations on mantle dynamics, in combination with the reduction in thermochemical pile conductivity due to its expected high temperatures and enrichment in iron, which has so far not been well examined. The mean conductivity ratio from bottom to top indicates the relative competition between the decreasing effect with increasing temperature and the increasing effect with increasing depth. We find that, when depth dependence is stronger than temperature dependence, a mean conductivity ratio >2 will result in long-lived primordial reservoirs. Specifically, for the mean conductivity profile to be comparable to the conductivity often assumed in numerical models, the depth-dependent ratio must be at least 9. When conductivity is underestimated, the imparted thermal buoyancy (from heat-producing element enrichment) destabilizes the reservoirs and influences core–mantle boundary coverage configuration and the onset of dense material entrainment. The composition dependence of conductivity only plays a minor role that behaves similarly to a small conductivity reduction due to temperature. Nevertheless, this effect may be amplified when depth dependence is increased. For the cases we examine, when the lowermost mantle's mean conductivity is greater than twice the surface conductivity, reservoirs can remain stable for very long periods of time, comparable to the age of the Earth.
- Article
(8069 KB) - Full-text XML
-
Supplement
(12746 KB) - BibTeX
- EndNote
Tomographic studies of Earth's lower mantle reveal the presence of two large low-velocity provinces (LLVPs) that overlie the core–mantle boundary (CMB). Located below the Pacific Ocean and Africa, LLVPs have a combined coverage of up to 30 % of the CMB with vertical extents as high as 1200 km (Garnero et al., 2016). Detailed LLVP structure remains uncertain. In particular, spectral elements waveform tomographic models (e.g. French and Romanowicz, 2014), which achieve higher resolution, suggest a plume–bundle morphology with a potential dense basal layer (e.g. Davaille and Romanowicz, 2020), whereas models based on travel times only suggest tall dense dome-like piles (e.g. Houser et al., 2008). Independently of the exact geometry of LLVPs, authors define these anomalous regions either as purely thermal (Davies et al., 2012) or thermochemical (e.g. Trampert et al., 2004) in nature. However, several important observations, including the anti-correlation between shear and bulk-sound velocities, are better explained if they are not purely thermal in origin (Deschamps et al., 2015). LLVPs (or piles) may further affect plume generation (e.g. Tan et al., 2011; Heyn et al., 2020) and core-to-mantle heat flow (e.g. Deschamps and Hsieh, 2019). Furthermore, plumes sourced from deep-mantle reservoirs may provide a mechanism to explain the diverse chemistry observed in ocean island basalts (Deschamps et al., 2011). Two end-member views on the origin of piles (and their chemical composition) have been proposed: a primordial layer (composed of anomalously dense material) (e.g. Labrosse et al., 2007; Lee et al., 2010) and a growing layer (composed of mid-ocean ridge basalt sinking in the deep mantle and accumulating at the CMB) (e.g. Hirose et al., 1999; Nakagawa et al., 2009). However, mantle convection likely modifies the composition of piles over time and sources for the chemistry observed at the surface may be difficult to trace.
Piles' unique chemical composition determines physical properties, most importantly density, viscosity, and enrichment in heat-producing elements (HPEs), which affect their long-term stability. These property values remain uncertain, but numerical simulations that emulate Earth-like piles help constrain their ranges (e.g. Li et al., 2014, 2018, 2019; Gülcher et al., 2020; Citron et al., 2020). An important property, thermal conductivity, often radially parameterized, controls the heat flow between piles and the surrounding mantle and hence mean pile temperature (i.e. thermal buoyancy). Because thermal conductivity can vary significantly with temperature, pressure, and composition, heterogeneous heat transfer in the lowermost mantle can strongly affect the long-term stability of piles. The evolution and stability of piles will differ between radial and fully heterogeneous conductivity models.
Measured and estimated thermal conductivities of minerals are determined at variable temperature and pressure conditions relevant to regions of the mantle at shallow and great depths. In addition, aggregate compositions with variable fractions of mineral concentrations and elemental inclusions influence the mantle conductivities at depth. Thus, studies that investigate pressure effects (at fixed temperature) (e.g. Ohta et al., 2012; Dalton et al., 2013; Goncharov et al., 2015; Hsieh et al., 2017, 2018) or thermal effects (at fixed pressure) (e.g. Kanamori et al., 1968; Katsura, 1997; Hofmeister, 1999; Manthilake et al., 2011; Zhang et al., 2019) often include measurements on mineral samples with additional elemental impurities. Compared to pure magnesium end-members of mantle minerals, inclusion of other elements (e.g. iron or aluminium) in an aggregate sample can reduce thermal conductivity substantially (e.g. Ohta et al., 2012; Hsieh et al., 2017, 2018). Enrichment of a mantle aggregate in iron or aluminium-bearing minerals greatly reduces its total conductivity, as might be the case for LLVPs (Deschamps and Hsieh, 2019). In numerical models, this effect can be emulated by parametrizing a percentage reduction with the primordial composition field. Li et al. (2022) showed that composition dependence of conductivity can raise the topography of thermochemical piles.
Estimates of thermal conductivity at high temperature and high pressure are available, but Geballe et al. (2020) point out that calculations of thermal conductivity for bridgmanite, for example, can differ by a factor of 10 between different studies (Haigis et al., 2012; Dekura et al., 2013; Ammann et al., 2014; Tang et al., 2014; Stackhouse et al., 2015). In addition, laboratory measurements for pyrolite at both high temperature and pressure are still relatively unconstrained and coarsely sampled (e.g. at 124 GPa and 2000 to 3000 K (Geballe et al., 2020)).
In general, measurements from mantle minerals show that thermal conductivity increases with increasing pressure. At a fixed temperature (e.g. at room temperature ∼300 K), measurements of thermal conductivity increase with an approximately linear trend. At greater temperatures, conductivity decreases, but (even with temperature corrections for adiabaticity) the linear increase in conductivity with pressure is maintained. Enrichment of bridgmanite and ferropericlase (lower-mantle minerals) in iron significantly reduces the zero-pressure reference value and the slope of thermal conductivity (e.g. Deschamps and Hsieh, 2019). For iron-bearing bridgmanite and ferropericlase at room temperature and CMB pressures, thermal conductivities fall between 10 and 35 and between 35 and 60 , respectively (Deschamps and Hsieh, 2019). Considering thermal conductivities in this range for the lowermost mantle, we expect that heat exchange in that region will be more efficient. However, this effect will be curbed by temperature dependence.
The thermal conductivity decreases with increasing temperature and follows a relationship proportional to T−n. The mechanism controlling lattice heat transport determines the exponent n and the strength of temperature dependence. Experimental data (e.g. Klemens, 1960; Xu et al., 2004; Dalton et al., 2013) suggest that n is typically between 0.5 for (Fe, Al)-bearing minerals (three-phonon scattering at low phonon frequency) and 1.0 for MgSiO3 (anharmonic three-phonon scattering). Values below n=0.5 are possible, suggesting mantle minerals may be weakly temperature-dependent. Alternative thermal conductivity parameterization can lead to different n values. For instance, with additional temperature dependences, Hofmeister (1999) finds n=0.33 for silicates and 0.9 for MgO. Under upper-mantle conditions and density dependence, Manthilake et al. (2011) finds that n∼0.2 for Fe-bearing bridgmanite and periclase. For a typical temperature dependence (n=0.5) and a reference temperature of 300 K, a lowermost-mantle temperature of 3000 K results in a ∼70 % reduction in conductivity. Therefore, at lowermost mantle-pressures, a lowermost-mantle conductivity of 7.5 at 3000 K corresponds to a conductivity measurement of 25 at room temperature. Thus, the effect of temperature plays a significant role in making the lowermost mantle very poor at transferring heat.
Temperature and depth variations in conductivity had been considered previously for Boussinesq or extended Boussinesq fluid simulations. Using the Hofmeister (1999) lattice conductivity formulation in an isoviscous Boussinesq fluid, several effects were observed: temperature increases in the lower mantle (Dubuffet et al., 1999), a stabilizing effect on mantle flow, which manifests in thick and stable plumes (Dubuffet and Yuen, 2000), and the rapid thermal assimilation of cold downwelling slabs (Dubuffet et al., 2000). Yanagawa et al. (2005) examined the effects of a purely temperature-dependent conductivity in conjunction with a strongly temperature-dependent viscosity and observed a cooler and thinner upper thermal boundary layer when compared to a constant conductivity. More recently, Tosi et al. (2013) parameterized a temperature- and pressure-dependent thermal conductivity (and thermal expansivity) derived from mineral physics data. They observed a strong increase in bulk mantle temperature, which suppresses bottom thermal boundary layer instabilities and causes mantle flow to be driven by instabilities at the upper thermal boundary. Li et al. (2022) examined the effect of thermal conductivity in simulations featuring a compressible fluid and thermochemical piles, but conductivity changes with temperature were not included. In addition to lateral variations in temperature related to the flow, a compressible fluid introduces an adiabatic temperature increase with depth. For adiabatic temperature gradients in the lower mantle between 0.2 to 0.4 K km−1, temperature will increase by approximately 600 K from the 660 km transition to the core–mantle boundary (Katsura, 2022). Given the strength of thermal conductivity's dependence on temperature, such an adiabatic temperature increase in the lowermost mantle cannot be neglected in a primordial reservoir's total conductivity. Neglecting compressibility may result in an overestimation of thermal conductivity, thus changing the dynamics and evolution of primordial reservoirs.
In this study, we use compressible thermochemical mantle convection models to examine the effect of temperature-, depth-, and composition-dependent conductivity on the stability of thermochemical piles. By refining the conductivity parameters controlling the bottom-to-top conductivity ratio, we try to reproduce conductivity values comparable to lower-mantle measurements. Furthermore, we determine the longevity of systems evolving with Earth-like primordial reservoirs. First, we isolate the effect of purely depth-dependent thermal conductivity to understand the dynamics of primordial reservoirs under different lowermost-mantle conductivity conditions. Next, we introduce the effect of temperature and composition dependence to examine how the heating conditions in conjunction with depth dependence affect pile evolution. We conclude by examining the effect of a fully heterogeneous conductivity (featuring depth dependence based on mantle minerals) on the evolution of primordial reservoirs.
2.1 General physical properties
We model compressible thermochemical mantle convection using the finite-volume code StagYY (Tackley, 2008). Each calculation is performed in a 2D spherical annulus domain, which emulates convection in a variable-thickness slice of a spherical shell centred at the Equator (Hernlund and Tackley, 2008). The reference state characterizing compressible convection is based on the calculations presented in Tackley (1998). The parameters defining this reference state are listed in Table S1 and illustrated in Fig. S1 of the Supplement.
Thermochemical reservoirs are modelled with a dense primordial material origin. An initial dense layer occupies the bottom 160 km of the lower mantle, corresponding to a volume fraction of approximately 3 %. The buoyancy ratio, B, defines the density contrast between regular and primordial materials and depends on the radial profile of reference density (Sect. S2 and Eq. S4 in the Supplement). We fix its value to 0.23 in all simulations, which corresponds to a density contrast of 95 kg m−3 near the surface and 152 kg m−3 near the CMB. The mantle is basally heated and is also internally heated by HPEs and we prescribe a non-dimensional heating rate, H=20, which corresponds to a dimensional heating rate of W kg−1. We assume a primordial material is enriched in HPEs and has a heating rate up to 1 order of magnitude greater than regular mantle material. The initial temperature field is based on an adiabatic temperature profile of 2000 K with surface and core–mantle boundary layer thicknesses of approximately 30 km. Random temperature perturbations with an amplitude of 125 K are uniformly distributed throughout the domain. The surface and core–mantle boundary temperatures are defined at 300 and 3440 K, respectively. Mantle viscosity featuring depth-, temperature-, and composition dependence is modelled using an Arrhenius formulation. A factor of 30 viscosity contrast is imposed between lower-mantle material and thermochemical reservoirs because dense material enriched in iron oxide and in bridgmanite (Trampert et al., 2004; Mosca et al., 2012) may be more viscous than regular (pyrolitic) mantle aggregate (Yamazaki and Karato, 2001). A yield stress of 290 MPa is imposed at the surface to avoid the development of a stagnant lid. Viscosity is truncated so that non-dimensional viscosity varies between 10−3 and 105.
We model a phase change between upper- and lower-mantle materials but neglect the phase change from perovskite (Pv) to post-perovskite (pPv) at the bottom of the mantle. Li et al. (2015) show that weak pPv (i.e. low viscosity contrast between Pv and pPv) and a low TCMB (i.e. TCMB∼3350 K) can result in the entrainment of primordial reservoirs. Because of our model setup, including a Pv–pPv transition may result in the entrainment of a dense primordial reservoir and mask the effect of thermal conductivity, which is the main aim of this study.
2.2 Thermal conductivity
Heterogeneous conductivity is emulated using a non-dimensional parameterized model that characterizes its variations with non-dimensional depth (, where the depth, d, has a length scale defined by the mantle thickness, D), non-dimensional temperature (, where the temperature, T, is scaled by the super-adiabatic temperature difference, ΔTS), and composition, C, as separate functions. Thermal conductivity is non-dimensionalized with its surface value kS, which is here fixed to 3 . The total conductivity is a product of each individual functional dependence.
For depth dependence, we performed simulations with two different depth-dependence laws. First, we consider a linear depth dependence given by
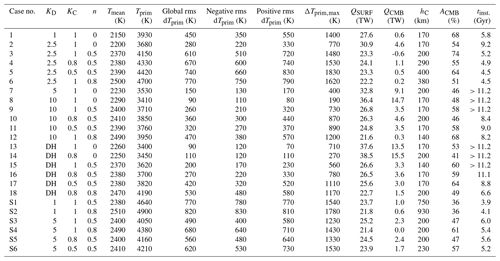
where KD specifies the bottom-to-top conductivity ratio. The non-dimensional depth-dependent conductivity thus takes on values between 1 and KD. Next, we consider depth dependence based on conductivity measurements of minerals in the upper and lower mantles. Conductivity values in the lower mantle were based on a parameterization of conductivity profiles (defined in Deschamps and Hsieh, 2019) for a 80 % bridgmanite (Bm) and 20 % ferropericlase (Fp) mixture. Measurements for bridgmanite were presented by Hsieh et al. (2017) and for ferropericlase by Hsieh et al. (2018). The conductivity profile in the upper mantle is defined by a quadratic curve that smoothly connects the surface conductivity to the conductivity profile of Bm–Fp at the 660 km transition. We find that there is good agreement between the modelled conductivity profile and the measurements of dry and wet olivine presented by Chang et al. (2017). The total conductivity profile is defined piecewise and continuous at the 660 km transition (; see Fig. 1) and is given by
The bottom-to-top conductivity ratio is 9.185, and this depth dependence is referred to as KDH in this study. Compared with the linear KD=10 depth profile, the quadratic depth dependence is slightly raised near the transition zone and slightly lowered near the CMB. Depth-dependent conductivity profiles are illustrated in Fig. 1.
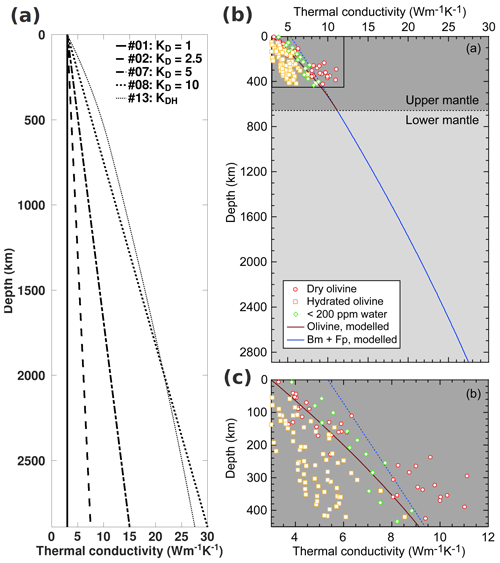
Figure 1(a) Radial profiles for different depth-dependent conductivity functions characterized by different KD values. (b) Conductivity measurements for upper- and lower-mantle materials. Olivine data points are from Chang et al. (2017), and the modelled Bm + Fp conductivity profile is based on data presented in Hsieh et al. (2017) and Hsieh et al. (2018). (c) Magnification of conductivity profile in the upper mantle.
The temperature dependence is given by
which always decreases thermal conductivity relative to the values defined in the depth-dependent profile when T>Tsurf. The super-adiabatic temperature difference, ΔTS, is set to 2500 K. Higher values of n indicate higher sensitivity to (and thus greater reduction with) increasing temperature. In this study, we consider n values of 0.5 and 0.8. The theoretical lower limit for n is 0.5 for materials that are enriched in iron, and a value of 0.8 is representative of oxides (e.g. Klemens, 1960; Xu et al., 2004). When n is 0.0, temperature dependence is switched off and only the remaining dependences are considered.
The composition dependence is given by
where KC is the reduction factor for composition dependence. For the primordial material considered in this study we consider 20 % and 50 % conductivity reduction (corresponding to KC=0.8 and 0.5, respectively), which encompasses a 26 % reduction in conductivity for LLVPs estimated by Deschamps and Hsieh (2019). When KC is 1.0, composition dependence is switched off. Finally, the total conductivity is given by
Figure 2Initial temperature profile (a) for all cases and sample initial conductivity profiles (b) for cases featuring KDH.
Figure 2 shows the initial temperature (panel a) and conductivity profiles (panel b) that correspond to models featuring a depth dependence (KDH) based on conductivity measurements of upper- and lower-mantle minerals. Different combinations of temperature and composition dependence are presented to show the degree of conductivity reduction resulting from these dependencies. The purely depth-dependent model (n=0) has a conductivity of 27.6 at the CMB. For the TCMB we consider (3440 K), the conductivity at the CMB will be reduced by approximately 70 % and 86 % for n=0.5 and 0.8 leading to conductivities of 8.1 and 3.9 , respectively. For primordial material at that depth, a 20 % reduction suggests conductivities of 22.0, 6.5, and 3.1 for and 0.8, respectively. Note that because the piles are enriched in HPEs, their conductivities will decrease as they heat up.
Because conductivity is allowed to vary throughout the system, the governing equation for conservation of energy is given by
The physical parameters in this equation include the reference density, ; the reference heat capacity, ; the reference thermal expansivity, ; the vertical velocity, vZ; the surface dissipation number, Disurf; the heat production, H; the reference Rayleigh number, Ra; and the viscous dissipation, Φ. The thermal conductivity, k, is included in the heat diffusion term ∇⋅(k∇T). One important consequence of heterogeneous conductivity is that the diffusion of heat through hot (piles or plumes) and cold (downwellings) regions is reduced and enhanced, respectively.
2.3 Model setup
Simulations are computed over a non-dimensional diffusion time of 0.0318, corresponding to 11.2 Gyr in dimensional units. Each simulation starts with a transient phase during which the basal layer of dense material heats up and whose duration depends on the input parameters. Note that because they do not include mantle initial conditions, which are not known, and time-decreasing radioactive heating, our simulations are not meant to model the mantle evolution, and therefore durations should not be used to interpret specific sequences of events. The longer simulation time is necessary to allow the simulations to achieve a quasi-steady state, during which the surface and CMB heat flows oscillate around nearly constant values. In addition, it is possible that shorter simulation times (i.e. 4.5 Gyr) may lead to a premature conclusion that primordial reservoirs have reached a metastable state. For systems with heterogeneous conductivity and constant heating conditions, significant changes in the evolution of thermochemical reservoirs may take longer to manifest. Using this setup, we run 24 simulations exploring the impact of conductivity variations (Table 1) with values of n, KD, and KC in the range of 0–0.8, 1–10, and 0.5–1.0, respectively. All observable and derived physical properties are averaged over a 2 Gyr window centred about t=4.5 Gyr (illustrated in Fig. 7) and are presented in Table 1. As the system evolves after t=4.5 Gyr, the pile volume diminishes and the core–mantle boundary surface is further exposed. The surface and core–mantle boundary heat flows oscillate between different values in a new quasi-steady state. However, pile statistics including mean temperature and average height differ when a system attains a new quasi-steady state. The averaged properties centred about t=9.0 Gyr and averaged from t=3 to 11.2 Gyr are presented in the Supplement (Tables S2 and S3, respectively). In general, while the ACMB values have decreased, the trends referred to in the figures still hold. Complete details of the methods are included in the Supplement.
To measure the evolution of the thermochemical structure, we examined our calculations once they became quasi-stationary, as defined by the mean core–mantle boundary heat flow, QCMB, and surface heat flow, QSURF. The stability of thermochemical reservoirs was assessed by their mean temperature, Tprim; average height, hC (defined in the Supplement); and coverage of the CMB, ACMB. The onset of instability, tinst., is calculated by examining time derivatives of average heights of primordial material (see the Supplement for details). We now examine the individual influences of conductivity changes with depth, temperature, and composition.
3.1 Effect of purely depth-dependent conductivity
First, we isolated the effect of purely depth-dependent conductivity. Relative temperature, primordial material, and conductivity fields are presented in Fig. 3. In Fig. 3 and all subsequent figures, the temperature fields are offset relative to the core–mantle boundary temperature () to help illustrate temperature excesses (or deficits) within the piles. When we increase KD from 1 to 10, we observe a decrease in the mean temperature of the piles (Tprim) (from 3930 down to 3410 K) and an increase in the mean mantle temperature (Tmean) (from 2150 up to 2290 K) because the piles transfer their heat to the ambient mantle more efficiently.
From the primordial material fields, we observe that a modest conductivity gradient (KD=2.5) is sufficient to stabilize the thermochemical reservoirs and stimulate a two-pile configuration (by t=4.5 Gyr) (compare Fig. 3e–h). This finding lends credence to pile configurations obtained by models that had adopted the canonical increase in conductivity by a factor of 2.5 from surface to core–mantle boundary. As KD is further increased, reservoirs progress toward an antipodal arrangement. In addition, the mantle flow becomes less vigorous since the increased thermal conductivity (and by extension thermal diffusivity) decreases the effective Rayleigh number.
Comparing between each KD case, for some arbitrary thermal gradient between piles and ambient mantle, a greater lowermost-mantle conductivity will result in more efficient heat extraction and thus a lower mean pile temperature. Furthermore, the heat flow at the core–mantle boundary is also increased (from 4.6 up to 14.7 TW, for KD between 2.5 and 10), which encompasses the lower and upper limits predicted for the Earth (Jaupart et al., 2007). Note that the greatest bottom-to-top conductivity ratio we consider, KD=10, implies a conductivity value of 30 at the CMB. However, the predicted thermal conductivities in the lowermost mantle do not exceed 10 . Therefore, temperature dependence, which reduces the thermal conductivity, must be considered.
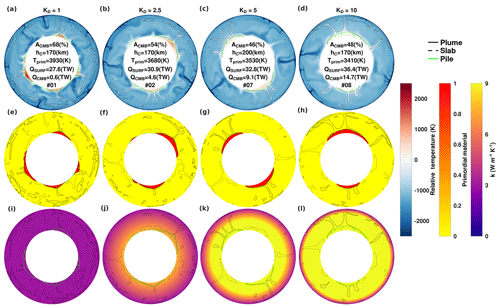
Figure 3Temperature (relative to the CMB temperature) (top row), primordial material (centre row), and conductivity (bottom row) fields at t=4.5 Gyr are shown as a function of KD. Contours are indicated in the legend and field values are indicated on the colour bars. The conductivity colour bar saturates at 9 so that the values in (k) and (l) may be larger. Averaged properties and case numbers are inset.
3.2 Effect of temperature- and depth-dependent conductivity
Next, we examine the combined effects of depth and temperature dependence. Figure 4 shows the relative temperature and thermal conductivity fields for end-member cases featuring KD=2.5 and 10 (a similar plot for KD=5 is shown in Supplement Fig. S5), and Supplement Figs. S3 and S4 plot the corresponding radial profiles. The effect of temperature clearly appears on the conductivity fields. Compared to the purely depth-dependent cases, thermal conductivity is strongly reduced throughout the mantle, and the depth dependence is strongly attenuated. By contrast, lateral variations in conductivity can be observed between hot (less conductive) piles and cold (more conductive) downwellings.
For KD=2.5, the lowest non-zero n value tested (i.e. 0.5) results in a 70 % reduction in conductivity (from 7.5 down to approximately 2.2 (see conductivity profiles in Fig. S3)) at the core–mantle boundary, and a mean bottom-to-top conductivity ratio is <1. This reduction is further amplified with greater n values. The piles evolving under these conductivity conditions move towards a more asymmetric configuration and may take on a columnar morphology (Fig. 4c). Overall, temperature dependence of conductivity results in a lower conductivity at the bottom of the mantle, with mean bottom-to-top conductivity ratio <1, which promotes thermochemical pile instability, as poorly conducting piles retain more heat and become more thermally buoyant.
For KD=10, the thermal effect on conductivity as n increased is compensated for by the strong increase in conductivity with depth, and a mean bottom-to-top conductivity ratio larger than 1 is established (e.g. Fig. 4 plots k and l, resulting in a two-pile arrangement). For instance, a mean conductivity ratio ≥2 is produced for KD=10 and n=0.5. The horizontally averaged conductivities near the CMB are brought closer to predicted values for the Earth's lower mantle (∼8 (case no. 9)) and are much lower compared to the purely depth-dependent cases (30 (case no. 8), for KD=10; Fig. S4).
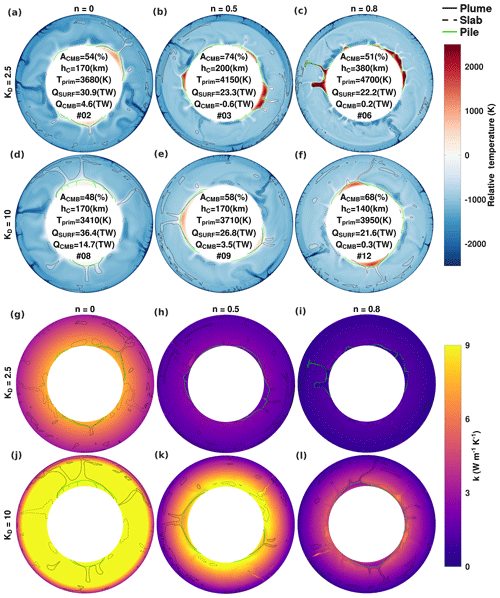
Figure 4Temperature fields (relative to the CMB temperature) and conductivity fields at t=4.5 Gyr are shown for cases as a function of KD and n. Contours are indicated in the legend and field values are indicated on the colour bars. The conductivity colour bar saturates at 9 so that the values in (j) and (k) may be larger. Averaged properties and case number are inset. (Primordial material fields are illustrated in Fig. S2.)
For cases featuring KD=5 (see Fig. S5), increasing pile temperature with temperature dependence is also observed. Because the resulting mean bottom-to-top conductivity ratio is >1, pile morphology tends to be more dome-like and evolution is similar to cases with KD=10. Trade-offs between the temperature and depth effects on the lowermost-mantle conductivity (and the mean bottom-to-top conductivity ratio) can be observed. For instance, case no. 12 in Fig. 4l and case no. S3 in Fig. S5h (and case no. 3 in Fig. 4h and case no. S4 in Fig. S5i) demonstrate that equivalent conductivity fields may be obtained by systems characterized by greater combined depth and temperature dependence or lesser combined depth and temperature dependences.
The pile configuration and downwelling planform influence one another and evolve in parallel. Specifically, within the first 2 Gyr, the initial downwelling currents determine the initial subdivision of the primordial reservoir that further determine the upwelling currents. As the system evolves further, the impact of returning downwelling flow depends on the relative density of the primordial material. The latter depends on the thermal evolution and hence on the conductivity of the piles. When conductivity of piles is greater (i.e. mean bottom-to-top conductivity ratio >1), the piles remain cooler and more dense compared to downwelling currents. Thus, the bulk accumulation of primordial material remains approximately fixed in place and the thinner margins get pushed laterally by downwelling currents. We find that long-lived degree-2 thermochemical structure and downwelling planforms are found for bottom-to-top conductivity ratios >2. Given the trade-offs between depth and temperature dependences, a set of KD and n that produce a bottom-to-top conductivity ratio of 2 can be computed using Eq. (5) for any particular TCMB.
We observed that Tprim increased with greater temperature dependence (columns viewed left to right in Fig. 4). Because piles' conductivity is reduced with increasing n, piles become less prone to losing their heat to the mantle and piles' temperature increases. However, temperature still decreased with an increased depth-dependent gradient, KD (e.g. cases no. 4 and no. 10 and cases no. 5 and no. 11 in Fig. 4) but to a lower extent than in the purely depth-dependent cases. For cases with a mean conductivity ratio <1, pile temperature increases significantly so that a Tprim in excess of 500 K of the TCMB (e.g. cases no. 1, no. 3 and no. 6 and cases no. S1, no. S2, and no. S4) is obtained. Because the temperature excess causes a negative temperature gradient between the piles and the CMB, a locally negative bottom heat flux within piles is obtained. The evolution of the piles in these cases tends to eventual entrainment. In those systems, entrainment is typically preceded by columnar pile morphologies that become too thermally buoyant and eject blobs of primordial material. When piles retain more heat, temporal variations in the mean height of the piles due to thermal buoyancy are more rapid than the deformation by downwelling currents. The timing for the onset of instability, tinst., is listed for each case in Table 1. A pile's stability depends on how efficiently it can rid itself of heat. We find that greater heat extraction can be achieved for conductivity models characterized by KD=10 and that temperature dependence can emulate conductivities relevant to Earth's lowermost mantle. Because composition (i.e. iron enrichment) also attenuates piles' conductivity, this effect must be examined in conjunction with temperature and depth's influence on the mantle's mean conductivity ratio.
3.3 Including the effect of composition-dependent conductivity
The effect of composition dependence is highlighted in Fig. 5 for the cases featuring KD=2.5 and 10 with n=0.5. For the cases featuring KD=2.5, composition dependence further reduces the conductivity of piles below the conductivity of the ambient mantle at lowermost-mantle depths (Fig. 5h and i). Although small, the reduction in pile conductivity due to composition dependence amplifies the behaviour observed for temperature-dependent cases with similar depth dependence (i.e. a decrease in the piles' stability) and results in earlier instability (see Fig. S11).
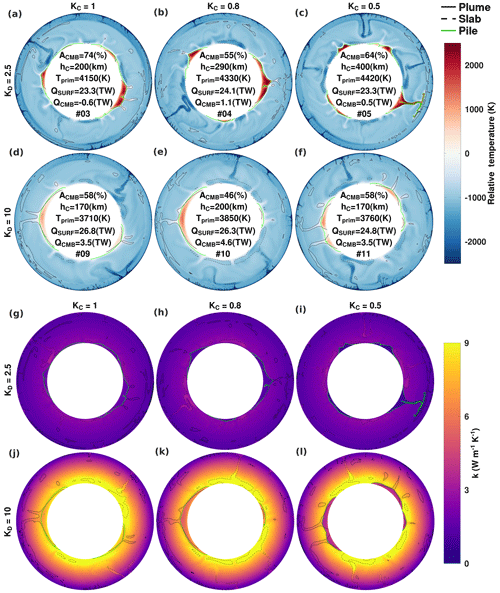
Figure 5Temperature (relative to the CMB temperature) and conductivity fields at t=4.5 Gyr are shown as a function of KD and KC when n=0.5. KC is increased from right to left. Contours and inset values are defined similarly as in Fig. 4. The conductivity colour bar saturates at 9 so that the values in (j), (k), and (l) may be larger. (Primordial material fields are illustrated in Fig. S6.)
Similarly, for the KD=10 case, accounting for composition dependence of conductivity amplifies the effects induced by temperature dependence. In addition, the magnitude of the reduction in conductivity is also amplified. The percentage conductivity difference at a depth of 2500 km (i.e. at a depth adjacent to the bulk of the piles) is ∼40 % when KC=0.8 and ∼60 % when KC=0.5. This conductivity difference between piles and the ambient mantle induces a minor increase in pile temperature that grows over time. When KC=0.8, this increase in temperature leads to a slowly manifesting thermal instability that results in a bulk ejection of primordial material by t=8.4 Gyr. However, the entrainment of the piles does not occur shortly after this episode of ejection (see Fig. S12).
For the intermediate depth-dependent case KD=5 (Fig. S9), the mean lowermost-mantle conductivity is greater than the surface conductivity and does not vary significantly when the conductivity of primordial material is reduced (i.e. <1 in the lowermost mantle; Fig. S10). The maximum conductivity, characterized by the remnant downwelling material localized within the bottom 300 km, is approximately 2 higher than the mean conductivity profile. The minimum conductivity, characterized by the hottest regions of the reservoirs, is approximately 2 lower than the mean and is localized near the tops of the piles, where the hottest and most buoyant primordial material accumulates (approximately 500–800 km above the CMB). Pile temperature marginally increased when KC was reduced. The additional thermal buoyancy imparted into the piles quickened the onset of instability. For this KD value, the erosion of piles is initiated approximately 0.4 and 0.8 Gyr earlier from t=6 Gyr when KC=0.8 and KC=0.5, respectively. Furthermore, pile configuration may change. When KC<1, single pile configuration can be attained as early as t=8 Gyr (Fig. S13). At all depth dependences tested, we found that the effect of composition dependence was small compared the dominant temperature-dependent effect. Nevertheless, at greater depth dependences, the compounded conductivity reduction is amplified, and thermal instability within piles is inevitable. Comparing cases when composition dependence is neglected or is considered, the difference in tinst. is greater when depth dependence is greater.
3.4 Long-term stability of thermochemical reservoirs featuring mineral-physics-derived conductivities
Finally, we examine the effect of depth dependence, based on measured conductivities of upper- and lower-mantle minerals (Hsieh et al., 2017, 2018), on the long-term stability of thermochemical reservoirs. First, we isolate the effects of temperature (n=0.5) and composition (KC=0.8) in conjunction with mineral conductivities. Second, we construct the fully heterogeneous thermal conductivity model (n=0.5 and KC=0.8; case no. 16), which we use as a reference case. We find that the resulting lower-mantle conductivities for this reference case are comparable to current estimates (e.g. Geballe et al., 2020). Figure 6 indicates that for given values of n and KC, models obtained with the mineral physics depth dependence are very similar to those obtained with linear depth dependence with KD=10 (see Figs. 4 and 5 for comparison). Heat flows for our models reached a quasi-steady state by approximately t=4 Gyr (Fig. 7). We found that temperature-dependent conductivity greatly reduced both CMB and surface heat flows (by approximately 73 % and 30 %, respectively), as less heat can be extracted from the base. Furthermore, we find that composition dependence is of secondary importance, in agreement with the Li et al. (2022) findings. Despite a 20 % reduction in the conductivity of primordial material (green), QCMB is marginally greater (by 2 TW). Similarly, QCMB is marginally greater when temperature-dependent conductivity included composition dependence (by 0.3 TW). This behaviour is likely owing to less CMB coverage in composition-dependent cases. Differing conductivity conditions can result in many thermochemical reservoir evolution and cooling histories. For the cases examined in Fig. 6, we found that the mean height of piles and CMB coverage approached a quasi-steady value. However, Tprim greatly increased when temperature dependence was considered. For systems with a temperature-dependent conductivity (i.e. red or black curves), piles slowly heat up during their long-standing CMB coverage. Piles' gained thermal buoyancy increased their height (thus exposing the core–mantle boundary surface to the cooler ambient mantle) and allowed more heat to be extracted from the core. Determining the mechanisms that trigger different outcomes will provide constraints for plausible mantle conductivity models.
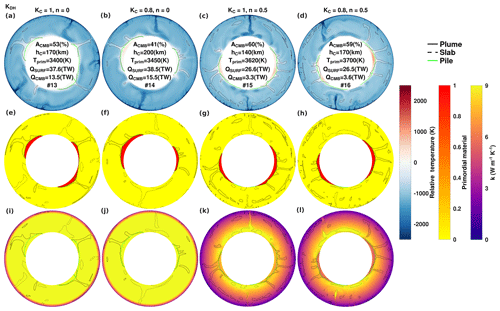
Figure 6Temperature (relative to the CMB temperature) (top row), primordial material (middle row), and conductivity (bottom row) fields at t=4.5 Gyr are shown for cases featuring KDH. Contours and inset values are defined similarly as in Fig. 4. The conductivity colour bar saturates at 9 so that the values in (i)–(l) may be larger.
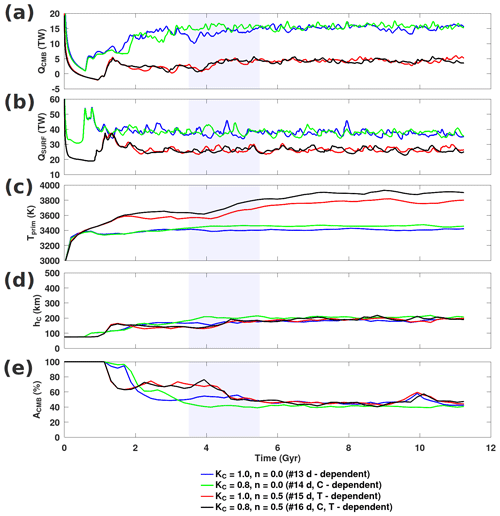
Figure 7Evolution of cases featuring KDH corresponding to those presented in Fig. 6. The quasi-stationary period centred about t=4.5 Gyr is shaded in grey.
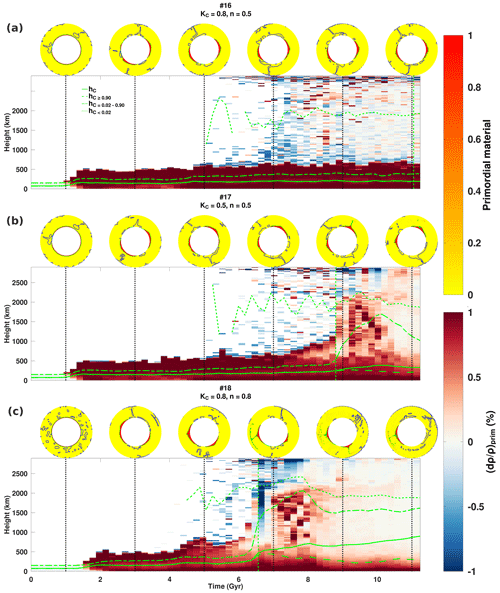
Figure 8Evolution of the horizontally averaged primordial material density anomalies is illustrated for cases featuring KDH. Primordial field snapshots are sampled at 2 Gyr intervals starting at t=1 Gyr above the time series (dashed black vertical line indicates the time). Mean heights of primordial material are plotted on top of the density anomaly time series. The dashed green vertical line indicates the onset of instability in thermochemical reservoirs. In the snapshots, downwelling structures are indicated by solid blue contours and piles are indicated by solid green contours.
Figure 8, plotting the heights of primordial material (for different ranges of C) in conjunction with the horizontally averaged density anomalies as a function of time, illustrates the evolution of the thermochemical structure for cases with different n and KC. Because the horizontally averaged profiles mask the spatial distribution, primordial field snapshots with 2 Gyr intervals are also indicated for reference. The average heights and vertical variations in the density anomaly profiles evolve synchronously, correspond to the same measure of instability, tinst., and can capture changes in individual pile behaviour (with confirmation in the primordial field snapshots). Figure 8 may be used to examine departures from the reference moderate temperature dependence (n=0.5) and composition dependence (KC=0.8) (case no. 16). The variations in average height do not discriminate between “intrinsic” (i.e. thermal buoyancy) or “extrinsic” (i.e. downwellings) deformation. However, the influence of downwellings can be observed following the transient period (on the density anomaly time series, the initial transient period is characterized by the flat average height curves overlying the white layer below 200 km). For cases no. 16 and no. 17, the transient period lasts approximately 1 Gyr and for case no. 18 approximately 1.5 Gyr. The first downwellings impinge on the initial dense layer but do not result in a rapid uplift of material (sufficient to eject blobs of dense material). Once the initial dense layer has organized into piles, downwellings tend to move dense material laterally over the CMB but do not increase the pile height rapidly. Nevertheless, we find that it is easier for downwelling currents to push primordial material that has been made lighter due to their retained heat.
Different initial conditions altering the thermal histories of case no. 17 are examined to check the robustness of our findings. We consider lower and higher initial mantle temperatures, Tinit, of 1750 and 2250 K, and temperature perturbations, dT, of 375 K are added to cases with Tinit=2000 and 2250 K (see Fig. S15 for the radial profiles and Table S4 for model averages). Overall, initial conditions on temperature control the duration of the initial transient phase but do not substantially alter the subsequent evolution of the system. In particular, greater dT does not significantly alter the influence of initial downwellings or the evolution of piles and tinst. is approximately 0.2 Gyr later (Fig. S16a, b). In addition, tinst. is approximately 2 Gyr earlier (1 Gyr later) for systems with hotter (cooler) Tinit (Fig. S17). A greater dT further decreases tinst. when Tinit=2250 K (Fig. S16c). The different histories (with similar downwelling planforms) show that the onset of instability within piles is an intrinsic thermal effect and hotter thermal conditions are also consistent with this finding.
In the reference case, thermochemical convection exhibits a stable two-pile configuration during the entire simulation. The total pile height can be roughly read from the density anomaly plot (i.e. the initial sharp contrast in colour between red and white). For stable piles, the average heights of the pile (hC) will then be roughly less than half of their maximum pile height. (Average height is calculated based on volumetric weighting in a spherical geometry (see Supplement Sect. S3.3)). These primordial reservoirs remain highly concentrated with a thin veneer of less concentrated material (from mixing with the ambient mantle) covering the piles. Thus, the average height of the veneer () is slightly greater than the average height of the piles because it is localized at the top and sides of the reservoirs. In Fig. 8, is indicated in the time series by dot–dashed green curves and on the primordial field snapshots by the solid green contours. The average heights are weighted with respect to the primordial material field C; when buoyant primordial structures (i.e. columnar plumes or ejected blobs) are present, their average heights cannot be distinguished compared to the lower-lying piles if only material with C>0.90 is considered. Because the volume of material in the veneer is much lower compared to piles, its average height can be differentiated from the piles and the onset of thermal instability is easier to analyse using this metric. For the reference case, the slow erosion of the least concentrated primordial material (C<0.02) from this veneer occurs after t=5 Gyr. From the temporal variations in average heights, we find that thermal instability appears to manifest very late in the simulation run time (after approximately 11 Gyr), which is consistent with the gradual accumulation of heat within the piles (observed in the slowly increasing mean pile temperature (see Fig. 9c)).
When only KC is reduced, from 0.8 to 0.5 (case no. 17), a two-pile configuration is also maintained throughout the simulation, but episodes of bulk erosion in thin plume conduits are possible (e.g. around t=9 Gyr). Following the erosion of light material, the long-term build-up of heat in the thermochemical pile (from t=7 to 9 Gyr) manifests a less dense region localized towards the top of the pile. By t=9 Gyr, the density anomaly plot is dominated by an upwelling that extends to the base of the upper mantle. Following the impingement of the plume (from t=9 to 11 Gyr), a fallout of dense blobs of primordial material are circulated about the mid-part of the lower mantle. Compared with cases with lesser depth dependence, the effect of composition dependence appears to have a greater influence on thermal instability (see cases no. 4 and no. 5 in Fig. S11 compared with cases no. 16 and no. 17 in Fig. 8). A lesser depth dependence implicitly makes temperature dependence the dominant factor in heat exchange. Thus, the effect of composition will easily be overshadowed.
When only n is increased from 0.5 to 0.8 (case no. 18), the onset of instability occurs ∼5 Gyr sooner compared to the reference case. Because it is more temperature-dependent, thermal conductivity is reduced, which makes the heat transfer between the piles and the ambient mantle poorer. From t=5 to 7 Gyr, similarly to case no. 17, the piles' retention of heat results in a reduced density anomaly (relative to the bulk pile). The ejection of primordial material from the largest of the two reservoirs occurs at t=6.6 Gyr. The fallout blobs of primordial material are circulated in the lower mantle but are mainly localized above the pile. After t=9 Gyr, the smaller pile is pushed by downwelling currents, and by t=11 Gyr the piles coalesce.
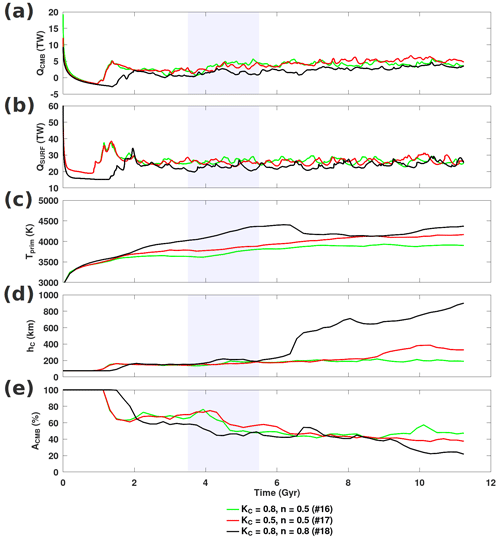
Figure 9Evolution of cases corresponding to Fig. 8. The quasi-stationary period centred about t=4.5 Gyr is shaded in grey.
Examining the time series for the cases presented, Tprim increased marginally due to composition dependence and increased significantly with temperature dependence (see Fig. 9). In general, Tprim increases when thermochemical reservoir conductivity is reduced; i.e. temperature dependence (and, to a lesser extent, composition dependence) is strong. Only until hC had increased (indicating that piles became unstable and started eroding) did Tprim decrease (i.e. case no. 18). Temperature dependence greatly amplifies Tprim and is the dominant effect over composition. The long-term evolution of reservoirs characterized by a marginal temperature increase may result in a stable arrangement of piles with increased topography with respect to the initial layering (see Fig. 6, case no. 16), whereas a substantial increase in temperature (i.e. exceeding approximately 500 K) may lead to the entrainment of piles (see Fig. 8, case no. 18). Between these two cases, the onset of instability differs by approximately 4.5 Gyr. The differences in system's conductivity fields (profiles and bottom-to-top conductivity ratios) clarify these observations.
The distribution of light material (C<0.02) is scattered about the lower mantle and may be ejected in small amounts into the upper mantle. An initial negative density anomaly is established compared with the mean mantle density (which is dominated by cold downwelling structures). When the thermochemical reservoirs finally become unstable, material with C between 0.02 and 0.90 is rapidly lifted away from the piles. This material dominates the mean density profile and produces a positive anomaly. The onset of light erosion precedes the onset of instability and the period between light and heavy erosion is reduced when the mean conductivity gradient is reduced (e.g. dotted and dot–dashed curves in Figs. 8, and S14. Interestingly, the radial conductivity profile obtained by models no. 16 and no. 17 lead to average CMB conductivity (and lower-mantle conductivities) within values estimated from mineral physics (i.e. between 3 and 10 ) (Hsieh et al., 2018; Deschamps and Hsieh, 2019; Geballe et al., 2020) (see Fig. S14). However, the mean conductivity values in the lower mantle obtained by case no. 18 span the lower end of current estimates.
The evolution of thermochemical reservoirs depends on their temperature and the mean bottom conductivity. The value of bottom conductivity results mainly from the competing thermal and pressure effects. Considering purely depth-dependent conductivity models, a greater lower-mantle conductivity stabilizes thermochemical reservoirs by mitigating any (additional) thermal buoyancy imparted by internal heat sources. When temperature dependence (and, to a lesser extent, composition dependence) is considered, the conductivity of reservoirs is reduced with respect to the surrounding mantle. If depth dependence is insufficient to compensate for this conductivity reduction, a positive feedback loop forms whereby a poorly conducting pile cannot evacuate heat, becomes hotter, and further reduces its conductivity. The imparted thermal buoyancy destabilizes the reservoirs and influences CMB coverage configuration, erosion rate, and the onset of entrainment. The effect of composition dependence is secondary to the thermal effect and quickens the onset of instability (e.g. by approximately 2 Gyr, comparing cases no. 16 and no. 17; Fig. 8). Moreover, the positive feedback loop persists over a prolonged period for conductivity models with greater depth dependence (e.g. by approximately 4 Gyr, comparing cases no. S6 and no. 17).
Our models are consistent with the two-pile configuration found in lower-resolution tomographic models. Of our simulations that attain a two-pile configuration at approximately t=4.5 Gyr, when n=0.5 (lower temperature-dependent conductivity), we find that the conductivity fields suggest a pyrolytic lower-mantle conductivity between 8 and 10 and pile conductivity between 2 and 8 . When n=0.8 (greater temperature-dependent conductivity), we find that the conductivity fields suggest a pyrolytic lower-mantle conductivity approximately 5 and pile conductivity between 2 and 4 . These simulations suggest that a conductivity ratio greater than 1.5 and not much greater than 2 can match estimates of lowermost-mantle conductivity. Furthermore, we find that in combination with temperature dependence, the depth dependence we propose KDH, as well as linear profiles with KD=5 and 10, produce conductivity values between the upper and lower bounds of measurements made by Geballe et al. (2020). The values of hC and ACMB are overall consistent with observations pointing to mostly continuous LLVPs (as seen, for instance, in the Houser et al., 2008 seismic tomography models) but somehow disagree with the bundle models proposed by Davaille and Romanowicz (2020) on the basis of full waveform tomography (French and Romanowicz, 2014). For instance, the maximum height of our piles is approximately 500 km, which is 300 km larger than the estimates of dense basal layer in high-resolution tomographic models (Davaille and Romanowicz, 2020), and the CMB coverage we find is greater than 30 %. From our findings, we suggest that increasing the temperature dependence to an intermediate value between 0.5 and 0.8 could allow piles to attain less CMB coverage and more height, which may help piles attain plume-like morphologies in addition to dense layering. Alternatively, a lower buoyancy ratio and/or viscosity parameters may also lead to bundle-like structures (Deschamps et al., 2018).
Variations in the physical properties of thermochemical reservoirs, most notably the buoyancy ratio and enrichment in HPEs, have a strong influence on the long-term evolution of these reservoirs. Constraints on these properties are still being determined and subjects of ongoing research. Given the scope of this study, the effect of heterogeneous thermal conductivity on pile stability is difficult to differentiate from variable conditions that affect piles' chemical and thermal buoyancy. For example, greater composition dependence for conductivity is related to pile's enrichment in iron and thus implies density increase requiring an increase in buoyancy ratio. In contrast, amount of enrichment in HPEs will directly influence the thermal buoyancy and destabilize piles in the long term. Furthermore, we do not consider a decaying rate of internal heating. Assuming a mean 3 Gyr half-life, internal heating rate should be reduced by almost an order of magnitude by the end of the simulation period we consider. It may be possible that the stronger influence of thermal buoyancy is limited to earlier periods of maximum heat input. The influence of these parameters in conjunction with the moderate heterogeneous conductivity profile we propose (i.e. case no. 16) should be examined in further detail.
The core–mantle boundary temperature may also be an important factor in the stability and evolution of thermochemical reservoirs when a heterogeneous conductivity is considered. In our study, the reference state imposes a CMB temperature (TCMB=3440 K) that is on the lower end of current estimates (for a recent review see Frost et al., 2022). Several studies, including Boehler (2000); Price et al. (2004) and Kawai and Tsuchiya (2009), suggest greater temperatures, in excess of 3750 and up to 4000 K, are possible. For the constant system heating conditions we consider, a greater CMB temperature implies that the mean temperatures in the lowermost mantle will also be increased, resulting in a lower thermal conductivity in that region and within the piles. In addition, higher thermal gradients at the base of the mantle will result in an increase in mean CMB heat flow. Thus, at very high CMB temperatures piles may become unstable. However, stable piles (under hotter conditions) can be accommodated by considering a lower n or a greater depth-dependent conductivity or by other physical parameters (e.g. temperature dependence of viscosity or the buoyancy ratio). Therefore, conclusions drawn from our results should be unchanged. Because a cooling bottom boundary is not considered, it is possible that piles evolving with our CMB temperature (or in hotter systems) could become more stable as the mantle cools and the mean lowermost-mantle conductivity (and potentially the CMB heat flow) rises. However, examining evolving system heating conditions is beyond the scope of our study.
Alternative formulations of the lattice conductivity exist in the literature featuring temperature and density dependences (e.g. Manthilake et al., 2011; Okuda et al., 2017). Furthermore, measurements of the temperature-dependent exponent for lower-mantle materials may take on values that are less than 0.5 (i.e. between 0.2 and 0.47). For the lattice conductivity we consider, a lower exponent (lesser temperature dependence) will promote stability in piles. In addition, the radiative component of conductivity is much less than the lattice component for temperatures lower than the CMB temperature (e.g. Dubuffet et al., 1999). It may be possible that the piles' temperature increases we observe could curb the conductivity reduction due to the lattice component. We do not rule out these possibilities but propose that different conductivity formulations are subjects for future studies.
In this study, we investigate the influence of variations in thermal conductivity on thermochemical convection and find that a heterogeneous conductivity strongly influences the long-term evolution of thermochemical reservoirs. The combined influences of temperature and depth variations determine the mean conductivity ratio from bottom to top. In the calculations we present, for the mean conductivity profile to be comparable to the conductivity often assumed in numerical models, the depth-dependent ratio must be at least 9 times the surface conductivity. The composition dependence for conductivity only plays a minor role that augments and behaves similarly to a small conductivity reduction due to temperature. Nevertheless, this effect may be amplified when depth dependence is increased. For the cases we examine, when the mean conductivity in the lowermost mantle is much greater than the surface conductivity, large reservoirs can be maintained until the end of the simulation.
The numerical code is available by reasonable request to Paul James Tackley. A detailed description of the code can be found in Tackley (2008). The data corresponding to the numerical simulations are too large to be stored online, but they can be requested from the corresponding authors as can the input files used to run the simulations.
The supplement related to this article is available online at: https://doi.org/10.5194/se-14-119-2023-supplement.
JMG: contributed to the study design, formal analysis, visualization, and writing – original draft preparation. FD: contributed to the study design, investigation, visualization, writing – review and editing. YL: contributed to writing – review and editing. WPH: contributed to consultation on the thermal conductivity model and writing – review and editing. PJT: contributed to software by designing the 3D thermochemical convection code and writing – review and editing. All authors collaborated and contributed intellectually to this paper.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This study was funded by the National Science and Technology Council grants NSTC 110-2116-M-001-025 and 111-2116-M-001-025. The authors would like to thank the topical editor Juliane Dannberg and executive editor Susanne Buiter for handling our paper. Joshua Martin Guerrero would like to thank the three anonymous referees for helping improve the clarity of the paper.
This research has been supported by the National Science and Technology Council (NSTC) of Taiwan, Republic of China (grant nos. NTSC 110-2116-M-001-025 and 111-2116-M-001-025).
This paper was edited by Juliane Dannberg and reviewed by three anonymous referees.
Ammann, M. W., Walker, A. M., Stackhouse, S., Wookey, J., Forte, A. M., Brodholt, J. P., and Dobson, D. P.: Variation of thermal conductivity and heat flux at the Earth's core mantle boundary, Earth Planet. Sc. Lett., 390, 175–185, 2014. a
Boehler, R.: High-pressure experiments and the phase diagram of lower mantle and core materials, Rev. Geophys., 38, 221–245, 2000. a
Chang, Y. Y., Hsieh, W. P., Tan, E., and Chen, J.; Hydration-reduced lattice thermal conductivity of olivine in Earth’s upper mantle, P. Natl. Acad. Sci. USA, 114, 4078–4081, 2017. a, b
Citron, R. I., Lourenço, D. L., Wilson, A. J., Grima, A. G., Wipperfurth, S. A., Rudolph, M. L., Cottaar, S., and Montési, L. G.: Effects of Heat‐Producing Elements on the Stability of Deep Mantle Thermochemical Piles, Geochem. Geophy. Geosy., 21, e2019GC008895, https://doi.org/10.1029/2019GC008895, 2020. a
Dalton, D. A., Hsieh, W. P., Hohensee, G. T., Cahill, D. G., and Goncharov, A. F.: Effect of mass disorder on the lattice thermal conductivity of MgO periclase under pressure, Scientific Reports, 3, 2400, https://doi.org/10.1038/srep02400, 2013. a, b
Davaille, A. and Romanowicz, B.: Deflating the LLSVPs: bundles of mantle thermochemical plumes rather than thick stagnant “piles”, Tectonics, 39, e2020TC006265, https://doi.org/10.1029/2020TC006265, 2020. a, b, c
Davies, D. R., Goes, S., Davies, J. H., Schuberth, B. S. A., Bunge, H. P., and Ritsema, J.: Reconciling dynamic and seismic models of Earth's lower mantle: The dominant role of thermal heterogeneity, Earth Planet. Sc. Lett., 353, 253–269, 2012. a
Dekura, H., Tsuchiya, T., and Tsuchiya, J.: Ab initio lattice thermal conductivity of MgSiO3 perovskite as found in Earth’s lower mantle, Phys. Rev. Lett., 110, 025904, https://doi.org/10.1103/PhysRevLett.110.025904, 2013. a
Deschamps, F. and Hsieh, W. P.: Lowermost mantle thermal conductivity constrained from experimental data and tomographic models, Geophys. J. Int., 219, S115–S136, 2019. a, b, c, d, e, f, g
Deschamps, F., Kaminski, E., and Tackley, P. J.: A deep mantle origin for the primitive signature of ocean island basalt, Nat. Geosci., 4, 879–882, 2011. a
Deschamps, F., Li, Y., and Tackley, P. J.: Large-scale thermo-chemical structure of the deep mantle: observations and models, in: The Earth's heterogeneous mantle, Springer, Cham, 479–515, https://doi.org/10.1007/978-3-319-15627-9_15, 2015. a
Deschamps, F., Rogister, Y., and Tackley, P. J.: Constraints on core-mantle boundary topography from models of thermal and thermochemical convection, Geophys. J. Int., 212, 164–188, 2018. a
Dubuffet, F., and Yuen, D. A.: A thick pipe-like heat‐transfer mechanism in the mantle: Nonlinear coupling between 3‐D convection and variable thermal conductivity, Geophys. Res. Lett., 27, 17–20, 2000. a
Dubuffet, F., Yuen, D. A., and Rabinowicz, M.: Effects of a realistic mantle thermal conductivity on the patterns of 3-D convection, Earth Planet. Sc. Lett., 171, 401–409, 1999. a, b
Dubuffet, F., Yuen, D. A., and Yanagawa, T.: Feedback effects of variable thermal conductivity on the cold downwellings in high Rayleigh number convection, Geophys. Res. Lett., 27, 2981–2984, 2000. a
French, S. W., and Romanowicz, B. A.: Whole-mantle radially anisotropic shear velocity structure from spectral-element waveform tomography, Geophys. J. Int., 199, 1303–1327, 2014. a, b
Frost, D. A., Avery, M. S., Buffett, B. A., Chidester, B. A., Deng, J., Dorfman, S. M., Li, Z., Liu, L., Lv, M., and Martin, J. F.: Multidisciplinary Constraints on the Thermal-Chemical Boundary Between Earth's Core and Mantle, Geochem. Geophy. Geosy., 23, e2021GC009764, https://doi.org/10.1029/2021GC009764, 2022. a
Garnero, E. J., McNamara, A. K., and Shim, S. H.: Continent-sized anomalous zones with low seismic velocity at the base of Earth's mantle, Nat. Geosci., 9, 481–489, 2016. a
Geballe, Z. M., Sime, N., Badro, J., van Keken, P. E., and Goncharov, A. F., Thermal conductivity near the bottom of the Earth's lower mantle: Measurements of pyrolite up to 120 GPa and 2500 K, Earth Planet. Sc. Lett., 536, 116161, https://doi.org/10.1016/j.epsl.2020.116161, 2020. a, b, c, d, e
Goncharov, A. F., Lobanov, S. S., Tan, X., Hohensee, G. T., Cahill, D. G., Lin, J. F., Thomas, S.-M., Okuchi, T., and Tomioka, N.: Experimental study of thermal conductivity at high pressures: Implications for the deep Earth’s interior, Phys. Earth Planet. In., 247, 11–16, 2015. a
Gülcher, A. J., Gebhardt, D. J., Ballmer, M. D., and Tackley, P. J.: Variable dynamic styles of primordial heterogeneity preservation in the Earth's lower mantle, Earth Planet. Sc. Lett., 536, 116160, https://doi.org/10.1016/j.epsl.2020.116160, 2020. a
Haigis, V., Salanne, M., and Jahn, S.: Thermal conductivity of MgO, MgSiO3 perovskite and post-perovskite in the Earth's deep mantle, Earth Planet. Sc. Lett., 355, 102–108, 2012. a
Hernlund, J. W. and Tackley, P. J.: Modeling mantle convection in the spherical annulus, Phys. Earth Planet. In., 171, 48–54, 2008. a
Heyn, B. H., Conrad, C. P., and Trønnes, R. G.: How thermochemical piles can (periodically) generate plumes at their edges, J. Geophys. Res.-Sol. Ea., 125, e2019JB018726, https://doi.org/10.1029/2019JB018726, 2020. a
Hirose, K., Fei, Y., Ma, Y., and Mao, H. K.: The fate of subducted basaltic crust in the Earth's lower mantle, Nature, 397, 53–56, 1999. a
Hofmeister, A. M.: Mantle values of thermal conductivity and the geotherm from phonon lifetimes, Science, 283, 1699–1706, 1999. a, b, c
Houser, C., Masters, G., Shearer, P., and Laske, G.: Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms, Geophys. J. Int., 174, 195–212, 2008. a, b
Hsieh, W. P., Deschamps, F., Okuchi, T., and Lin, J. F.: Reduced lattice thermal conductivity of Fe‐bearing bridgmanite in Earth's deep mantle, J. Geophys. Res.-Sol. Ea., 122, 4900–4917, 2017. a, b, c, d, e
Hsieh, W. P., Deschamps, F., Okuchi, T., and Lin, J. F.: Effects of iron on the lattice thermal conductivity of Earth's deep mantle and implications for mantle dynamics, P. Natl. Acad. Sci. USA, 115, 4099–4104, 2018. a, b, c, d, e, f
Jaupart, C., Labrosse, S., and Mareschal, J.: Temperatures, Heat and Energy in the Mantle of the Earth, in: Treatise on Geophysics, volume 7, 1st edn., edited by: Bercovici, D., Elsevier, 2007, 253–303, https://doi.org/10.1016/B978-044452748-6.00114-0, 2007. a
Kanamori, H., Fujii, N., and Mizutani, H.: Thermal diffusivity measurement of rock‐forming minerals from 300 to 1100 K, J. Geophys. Res., 73, 595–605, 1968. a
Katsura, T.: Thermal diffusivity of periclase at high temperatures and high pressures, Phys. Earth Planet. In., 101, 73–77, 1997. a
Katsura, T.: A revised adiabatic temperature profile for the mantle, J. Geophys. Res.-Sol. Ea., 127, e2021JB023562, https://doi.org/10.1029/2021JB023562, 2022. a
Kawai, K. and Tsuchiya, T.: Temperature profile in the lowermost mantle from seismological and mineral physics joint modeling, P. Natl. Acad. Sci. USA, 106, 22119–22123, 2009. a
Klemens, P. G.: Thermal resistance due to point defects at high temperatures, Phys. Rev., 119, 507–509, https://doi.org/10.1103/PhysRev.119.507, 1960. a, b
Labrosse, S., Hernlund, J. W., and Coltice, N.: A crystallizing dense magma ocean at the base of the Earth's mantle, Nature, 450, 866–869, 2007. a
Lee, C. T. A., Luffi, P., Höink, T., Li, J., Dasgupta, R., and Hernlund, J.: Upside-down differentiation and generation of a “primordial” lower mantle, Nature, 463, 930–933, 2010. a
Li, Y., Deschamps, F., and Tackley, P. J.: The stability and structure of primordial reservoirs in the lower mantle: insights from models of thermochemical convection in three-dimensional spherical geometry, Geophys. J. Int., 199, 914–930, 2014. a
Li, Y., Deschamps, F., and Tackley, P. J.: Effects of the post-perovskite phase transition properties on the stability and structure of primordial reservoirs in the lower mantle of the Earth, Earth Planet. Sc. Lett., 432, 1–12, https://doi.org/10.1016/j.epsl.2015.09.040, 2015. a
Li, Y., Vilella, K., Deschamps, F., Zhao, L., and J. Tackley, P.: Effects of iron spin transition on the structure and stability of large primordial reservoirs in Earth's lower mantle, Geophys. Res. Lett., 45, 5918–5928, 2018. a
Li, Y., Deschamps, F., Yang, J., Chen, L., Zhao, L., and Tackley, P. J.: Effects of the Compositional Viscosity Ratio on the Long‐Term Evolution of Thermochemical Reservoirs in the Deep Mantle, Geophys. Res. Lett., 46, 9591–9601, 2019. a
Li, Y., Deschamps, F., Shi, Z., Guerrero J. M., Hsieh, W. P., and Tackley, P. J.: Influence of composition-dependent thermal conductivity on the long-term evolution of primordial reservoirs in Earth's lower mantle, Earth Planets Space, 74, 46, https://doi.org/10.1186/s40623-022-01608-3, 2022. a, b, c
Manthilake, G. M., de Koker, N., Frost, D. J., and McCammon, C. A.: Lattice thermal conductivity of lower mantle minerals and heat flux from Earth’s core, P. Natl. Acad. Sci. USA, 108, 17901–17904, https://doi.org/10.1073/pnas.1110594108, 2011. a, b, c
Mosca, I., Cobden, L., Deuss, A., Ritsema, J., and Trampert, J.: Seismic and mineralogical structures of the lower mantle from probabilistic tomography, J. Geophys. Res.-Sol. Ea., 117, B06304, https://doi.org/10.1029/2011JB008851, 2012. a
Nakagawa, T., Tackley, P. J., Deschamps, F., and Connolly, J. A.: Incorporating self‐consistently calculated mineral physics into thermochemical mantle convection simulations in a 3‐D spherical shell and its influence on seismic anomalies in Earth's mantle, Geochem. Geophy. Geosy., 10, Q03004, https://doi.org/10.1029/2008GC002280, 2009. a
Ohta, K., Yagi, T., Taketoshi, N., Hirose, K., Komabayashi, T., Baba, T., Ohishi, Y., and Hernlund, J.: Lattice thermal conductivity of MgSiO3 perovskite and post-perovskite at the core-mantle boundary, Earth Planet. Sc. Lett., 349, 109–115, 2012. a, b
Okuda, Y., Ohta, K., Yagi, T., Sinmyo, R., Wakamatsu, T., Hirose, K., and Ohishi, Y.: The effect of iron and aluminum incorporation on lattice thermal conductivity of bridgmanite at the Earth's lower mantle, Earth Planet. Sc. Lett., 474, 25–31, 2017. a
Price, G. D., Alfè, D., Vočadlo, L., and Gillan, M. J.: The Earth’s core: an approach from first principles, in: The State of the Planet: Frontiers and Challenges in Geophysics, Geophys. Monogr. Ser., vol. 150, edited by: Sparks, R. S. J. and Hawkesworth, C. J., AGU, Washington, D. C., 1–12, https://doi.org/10.1029/150GM02, 2004. a
Stackhouse, S., Stixrude, L., and Karki, B. B.: First-principles calculations of the lattice thermal conductivity of the lower mantle, Earth Planet. Sc. Lett., 427, 11–17, 2015. a
Tackley, P. J.: Three-dimensional simulations of mantle convection with a thermo-chemical basal boundary layer: D. The Core-Mantle Boundary Region, Geodyn. Ser., 28, 231–253, 1998. a
Tackley, P. J.: Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid, Phys. Earth Planet. In., 171, 7–18, https://doi.org/10.1016/j.pepi.2008.08.005, 2008. a, b
Tan, E., Leng, W., Zhong, S., and Gurnis, M.: On the location of plumes and lateral movement of thermochemical structures with high bulk modulus in the 3‐D compressible mantle, Geochem. Geophy. Geosy., 12, Q07005, https://doi.org/10.1029/2011GC003665, 2011. a
Tang, X., Ntam, M. C., Dong, J., Rainey, E. S., and Kavner, A.: The thermal conductivity of Earth's lower mantle, Geophys. Res. Lett., 41, 2746–2752, 2014. a
Tosi, N., Yuen, D. A., de Koker, N., and Wentzcovitch, R. M.: Mantle dynamics with pressure-and temperature-dependent thermal expansivity and conductivity, Phys. Earth Planet. In., 217, 48–58, 2013. a
Trampert, J., Deschamps, F., Resovsky, J., and Yuen, D.: Probabilistic tomography maps chemical heterogeneities throughout the lower mantle, Science, 306, 853–856, 2004. a, b
Xu, Y., Shankland, T. J., Linhardt, S., Rubie, D. C., Langenhorst, F., and Klasinski, K.: Thermal diffusivity and conductivity of olivine, wadsleyite and ringwoodite to 20 GPa and 1373 K, Phys. Earth Planet. In., 143, 321–336, 2004. a, b
Yamazaki, D. and Karato, S. I.: Some mineral physics constraints on the rheology and geothermal structure of Earth's lower mantle, Am. Mineral., 86, 385–391, 2001. a
Yanagawa, T. K., Nakada, M., and Yuen, D. A.: Influence of lattice thermal conductivity on thermal convection with strongly temperature-dependent viscosity, Earth, Planets and Space, 57, 15–28, 2005. a
Zhang, Y., Yoshino, T., Yoneda, A., and Osako, M.: Effect of iron content on thermal conductivity of olivine with implications for cooling history of rocky planets, Earth Planet. Sc. Lett., 519, 109–119, 2019. a