the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Time-dependent frictional properties of granular materials used in analogue modelling: implications for mimicking fault healing during reactivation and inversion
Michael Rudolf
Matthias Rosenau
Onno Oncken
Analogue models are often used to model long-term geological processes such as mountain building or basin inversion. Most of these models use granular materials such as sand or glass beads to simulate the brittle behaviour of the crust. In granular material, deformation is localised in shear bands, which act as an analogue to natural fault zones and detachments. Shear bands, also known as faults, are permanent anomalies in the granular package and are often reactivated during a test run. This is due to their lower strength compared to the undeformed material. When the fault movement stops, time-dependent healing immediately begins to increase the strength of the fault. Faults that have been inactive for a long time therefore have a higher strength than younger faults. This time-dependent healing, also called time consolidation, can therefore affect the structure of an analogue model as the strength of the fault changes over time. Time consolidation is a well-known mechanism in granular mechanics, but it is poorly described for analogue materials and on the timescales of typical analogue models. In this study, we estimate the healing rate of different analogue materials and evaluate the impact on the reactivation potential of analogue faults. We find that healing rates are generally less than 3 % per 10-fold increase in holding time, which is comparable to natural fault zones. We qualitatively compare the frictional properties of the materials with grain characteristics and find a weak correlation of healing rates with sphericity and friction with an average quality score. Accordingly, in models where there are predefined faults or reactivation is forced by blocks, the stability range of the fault angles that can be reactivated can decrease by up to 7∘ over the duration of 12 h. The stress required to reactivate an existing fault can double in the same time, which can favour the development of new faults. In a basin inversion scenario, normal faults cannot be inverted because of the strong misorientation, so time consolidation plays little additional role for such models.
- Article
(4108 KB) - Full-text XML
- BibTeX
- EndNote
Crustal tectonics involves fault localisation and reactivation, as well as changes in fault slip rates (transients) and slip directions (inversion), over timescales from hundreds of years (seismic cycle) to tens of millions of years (Wilson cycle). For example, the inversion of sedimentary basins is governed by a change from extensional to compressional tectonics, which leads to the shortening of basin structures (Turner and Williams, 2004). In such a scenario, shortening can be accommodated by either the reactivation of pre-existing structures or the formation of new faults. Structural inhomogeneities that localise deformation during inversion are mainly the normal faults formed under extension and stratigraphic layers of the basin sediments. In many cases, newly formed structures link with existing ones, forming shortcuts to create the most energetically favourable fault configuration. This interplay of extensional and compressional tectonics, as well as inherited and newly formed structures, creates a complex structural inventory that is inherent to many sedimentary basins worldwide, which are regions that are of high societal and economic importance hosting earthquakes, ore deposits and hydrocarbon resources (Buchanan et al., 1995; Turner and Williams, 2004).
Many experimental studies show that the localisation of brittle deformation into narrow bands is governed by the strain-weakening characteristics of rocks. As a result, faults are mechanically weaker than the undeformed host rock and thus are reactivated when subjected to stress (Sibson, 1980). However, other factors influence the reactivation characteristics of a fault, most notably the orientation of stresses with respect to the fault. Additionally, fluid pressure, the exact mechanical properties of the fault zone and interaction with other faults can prevent or promote fault reactivation (Niemeijer et al., 2008). There is a multitude of numerical, mechanical and analogue modelling studies that address the influence of these parameters on fault reactivation (e.g. Jara et al., 2018; Yagupsky et al., 2008; Panien et al., 2006, and references in Table 2). Especially in analogue models, the reactivation of normal faults is largely dependent on the orientation, as the other factors are rarely incorporated into the model (Bonini et al., 2012).
Analogue modelling is a widely used technique for tectonic modelling in general and for basin inversion models in particular because it is inherently three-dimensional and can handle discontinuities with large displacements, which is a challenge for most numerical approaches. Analogue models are built around the principle of similitude (Hubbert, 1937), which states that a system can be modelled by a geometrically smaller model if the governing dimensionless properties are the same. This is frequently used for geological modelling of complex tectonic processes and in other disciplines where numerical approaches are still not entirely feasible, such as hydraulic engineering. While numerical models are easy to quantify and there is a large amount of freedom in defining material properties, analogue modellers have access to only a small range of suitable materials for specific problems. In the past this has been limited to various natural (e.g. sands) and artificial granular materials (e.g. glass beads) as frictional components (Klinkmüller et al., 2016; Ritter et al., 2016a, 2018; Montanari et al., 2017), sometimes mixed with more fine-grained (powder) materials, like flour and plaster, to increase the cohesion according to scaling laws (Poppe et al., 2021; Galland et al., 2006). Models involving viscous layers (e.g. lower crust, salt) typically use silicone oils (PDMS) (Rudolf et al., 2016; Weijermars, 1986) and other visco-elastic materials. Recently, there has been a surge in new materials to fine-tune specific properties of the brittle or ductile layer (see Reber et al., 2020, for a detailed review). However, all analogue models rely on accurate and suitable material characterisation to be able to quantify the similarity of stresses and ultimately the similitude of the model (ten Grotenhuis et al., 2002).
A property that has received little to no attention is the time dependency of frictional material properties, in particular healing (i.e. static strengthening). In this context we identify two major implications for the analysis of reactivated structures with analogue models. The first is that due to the consolidation of granular materials over time, the reactivation strength increases. This could lead to problems with repeatability when there are differences in the timing of extensional and compressional phases between model runs. In the engineering community this effect is known as time consolidation and is usually considered to be minor in typical analogue materials (Schulze, 2008). However, most studies on time consolidation focus on large piles or silos with several metres of overburden material and not the few centimetres present in analogue models. Due to the increase in shear resistance over time, reactivation angles and structures could differ between a model that has, for example, a 1 min static phase between extension and compression in comparison to a model that has a several hours stop between extension and compression. Models with erosion and sedimentation are especially prone to this effect because they usually require the model to be stopped for some time to add or remove material. The same applies to models that have to be measured using time-consuming procedures, such as laser scanners or CT scanners. Secondly, natural faults also show time-dependent healing due to pressure solution, Ostwald ripening and fracture sealing by hydrothermal minerals (Karner et al., 1997; Niemeijer et al., 2008). At short timescales of the seismic cycle, this behaviour is described by the dimensionless healing rate b in the rate-and-state framework (Dieterich, 2007), while for longer tectonic timescales the quantification is more challenging (Yasuhara et al., 2005). To accurately mimic this natural healing in analogue models, it is required that the analogue materials show quantitatively similar characteristics to rocks, e.g. the same healing rate b.
Consequently, the aim of this study is (1) to quantify the healing properties of analogue materials from different laboratories and to relate them to first-order observable grain characteristics, (2) to analyse the impact on the reactivation angles during typical analogue models of basin inversion, and (3) to examine the possible use of certain materials as analogues for naturally healing faults. The material properties of 36 samples were characterised by standardised ring shear tests and slide–hold–slide tests. Furthermore, we used image analysis to gather more detailed information on grain size distributions, grain shapes and grain surface features for each material. The results are then used to review typical analogue modelling schemes and to probe possible scenarios under which the materials may or may not be suitable for modelling.
2.1 Materials
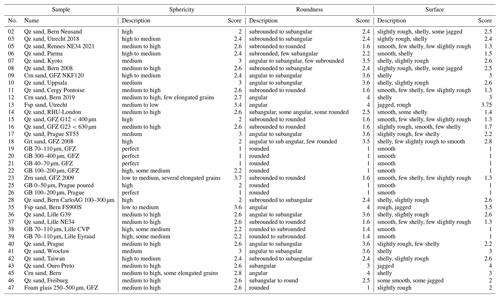
For this study we use a selection of samples that were archived from collaborative material property studies (e.g. Klinkmüller et al., 2016) in our laboratory and newly acquired samples from 14 laboratories worldwide that sent materials that are currently used for their analogue models. Some of these materials were characterised in terms of time-independent frictional properties in the original GeoMod benchmark study by Klinkmüller et al. (2016), while others have been characterised in the framework of EPOS transnational-access activities (Table 1, Wessels et al., 2022; Elger et al., 2022). Most of them have been subjected to standard ring shear tests to determine their time-independent friction parameters (friction coefficient and cohesion) and rate-dependent (velocity strengthening or weakening) friction parameters. To have consistent evaluation parameters, we re-picked and re-analysed the existing datasets with the newest software RST-Evaluation (Rudolf and Warsitzka, 2021), which is the current standard for ring shear tests in our laboratory. New materials that were not in our test database were tested with the standard ring shear test outlined in Sect. 2.2. For this study, we tested all samples with the slide–hold–slide procedure developed in Rudolf et al. (2021), which is outlined in Sect. 2.4.
Schmid et al. (2020b); Zwaan et al. (2018)Klinkmüller et al. (2016)Schmid et al. (2020b); Zwaan et al. (2018)Willingshofer et al. (2018)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016); Rosenau et al. (2018a); Ritter et al. (2016b)Klinkmüller et al. (2016); Rosenau et al. (2018b); Ritter et al. (2016b)Warsitzka et al. (2019b)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Aschauer and Kenkmann (2017)Schmid et al. (2020a)Klinkmüller et al. (2016)Klinkmüller et al. (2016)Willingshofer et al. (2018)Zwaan et al. (2022)Klinkmüller et al. (2016)Pohlenz et al. (2020a)Pohlenz et al. (2020b)Klinkmüller et al. (2016)Klinkmüller et al. (2016); Pohlenz et al. (2020c)Rudolf et al. (2022)Rosenau et al. (2022)Klinkmüller et al. (2016)Warsitzka et al. (2019a)Table 1Samples included in this study and references showing where standard ring shear tester data can be found. Materials that were included in Klinkmüller et al. (2016) are highlighted with “∗”. Some materials have not been published previously and are marked with “new”. These have been tested for friction and healing properties. All other samples have only been tested for their healing properties. Sample numbers refer to the numbering scheme of the slide–hold–slide tests found in the data publication.
2.2 Ring shear tester setup
We use a RST-01.pc (Schulze, 1994) ring shear tester to measure the frictional properties of the dry granular materials. The method is well established for analogue materials (Lohrmann et al., 2003; Panien et al., 2006; Klinkmüller et al., 2016; Montanari et al., 2017) and follows international standards for powder and bulk material testing (ASTM, 2016). The machine consists of a rotating, ring-shaped shear cell onto which normal stress is applied using a stationary lid. The shear stress required to hold the lid in place is measured using two tie rods that are each attached in series to force transducers. To improve the contact of the cell and lid with the material, the surface of the lid and the bottom of the shear cell are structured with slats and grooves. Normal stress is applied through a cantilever system with a moving mass and is therefore instantly adjusted by gravity, in contrast to other mechanical tests where the stresses are adjusted with a servo-hydraulic or electronic system. During each measurement, the shear velocity, shear stress, normal stress and lid position are monitored. Further information on the setup and device is available in Schulze (1994), Lohrmann et al. (2003) and Ritter et al. (2016a).
The testing procedure follows standardised procedures for sample preparation (Lohrmann et al., 2003; Klinkmüller et al., 2016), testing procedure (Lohrmann et al., 2003; Ritter et al., 2016a) and data analysis (Rosenau et al., 2018a; Rudolf et al., 2021). All samples are first oven dried to remove excess humidity and then stored in the air-conditioned laboratory for several days to equilibrate with ambient laboratory conditions of T=25 ∘C and ≈50 % humidity. The samples are sieved using the SM sieve into the cell from a height of ca. 30 cm and above, ensuring a similar package density for each test (Lohrmann et al., 2003). We do not use the same sieve as Klinkmüller et al. (2016), called a “GeoMod” sieve, because for our measurements the samples are pre-sheared and the package density after sieving is not a primary concern. Excess material is scraped off, and the weight of the material is determined. After inserting the cell into the tester, the normal stress is applied and the shear procedure is started. Each property has a specific shear procedure, which is outlined in the respective subsections (Sect. 2.3 for friction μ and cohesion C and Sect. 2.4 for the healing rate b).
2.3 Mohr–Coulomb friction
Most tectonic analogue models use dry granular materials as analogues for crustal rocks in the brittle regime (Klinkmüller et al., 2016), with only a few exceptions using wet clay or other non-granular material (Bonini et al., 2012). The greatest advantage of granular materials is that they obey the empirical Mohr–Coulomb criterion (Eq. 1):
Granular analogue materials show friction coefficients μ and cohesion values C that are comparable (in case of C when scaled) to typical crustal rocks: specifically, sands with μ=0.6 to 0.7 and C in the order of tens of pascals (scaling to few MPa) or glass beads with μ=0.4 to 0.5 and C in the order of few pascals. Moreover, the granular materials show stress–strain relationships similar to crustal rocks involving strain weakening and static healing (Lohrmann et al., 2003; Ritter et al., 2016a). This gives rise to three different coefficients of friction μ and cohesion C attributed to different stages of fault evolution (Lohrmann et al., 2003). The highest strength μpeak is reached during initial shearing of undisturbed granular material and therefore is analogous to the strength of undeformed rock (static friction). With continued shearing the materials loses strength (strain weakening) and reaches a lower strength during stable sliding μstable corresponding to the sliding resistance of a fault zone (sliding, dynamic or kinetic friction). If a material has been sheared, the granular fault zone is persistent and leaves a heterogeneity with lower density in the bulk material. If re-sheared, a new peak strength μreactivation occurs that reflects the strength of a pre-existing fault zone. Usually, it is higher than the stable sliding strength but lower than the initial peak strength. Consequently, models with granular materials localise deformation into narrow shear bands because of their lower sliding resistance and reactivate these structures under favourable circumstances due to the lower reactivation strength. From now on, we will refer to these three friction coefficients by their shortened versions, i.e. μp, μs and μr, throughout this study. Note that corresponding cohesion values exist, i.e. Cp, Cs and Cr.
2.4 Time consolidation (healing) and rate-and-state friction
In addition to the dependence on effective normal stress σ, sliding and reactivation friction coefficients μs and μr show a measurable dependence on slip rate and hold time th, respectively. This is highly non-linear and described using the rate-and-state framework (Dieterich, 1978). This formulation is widely accepted as a good heuristic approximation of laboratory shear tests and natural phenomena (Marone, 1998; Scholz, 2002; Dieterich, 2007) where a time and strain rate dependence is observed. In general, there are two additional contributions to shear resistance: the rate effect and the state effect . Both are defined by a ratio with respect to reference constants (denoted by asterisks) and added to the reference friction μ0:
The direct effect a, healing rate b and μ0 are derived empirically from experimental measurements. The evolution of state θ can take several forms as a function of time (ageing law, Dieterich, 1978), slip (slip law, Ruina, 1983), time-dependent healing (Kato law, Kato and Tullis, 2001) or stressing rate (Nagata law, Nagata et al., 2012), which has to be assessed from experiments.
The change in strength over time in granular materials is known as time consolidation and can be very large depending on the material (Schulze, 2008). For this study we assume purely time-dependent healing (ageing law) and use the healing rate b to calculate the time consolidation for each sample. We use slide–hold–slide tests to measure the healing rate following the procedure outlined in Rudolf et al. (2021), and references therein. After sample preparation (Sect. 2.2) and loading with σN=1 kPa the sample is sheared by 10 mm at a loading velocity vL=0.5 mm s−1, leading to a fully developed shear zone. The sample is then subjected to several slide–hold–slide intervals (Fig. 1a). The hold intervals are increased exponentially from th=101 to 104 s at increments of half a 10-fold increase in time and repeated three times per interval. An additional single hold interval of th=36 000 s = 10 h ≈104.55 s gives a long term data point to each series. The full test duration is approximately 23 h.
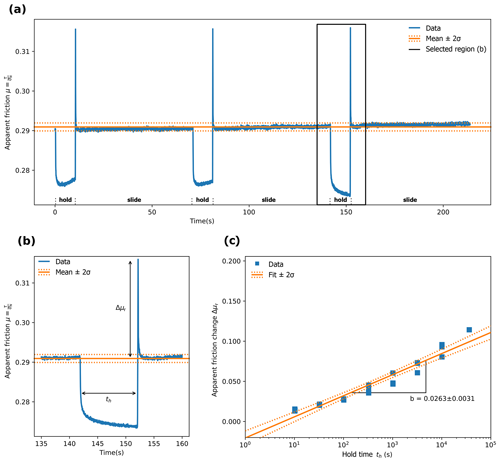
Figure 1Time series of one slide–hold–slide sequence and picked values. (a) Slide–hold–slide sequence of GFZ 70–110 µm glass beads for th=10 s. Slide and hold phases are marked along the time axis. (b) Detailed time series showing a single hold phase and the picked value for Δμr. (c) Fit of all picked reloading friction values versus hold time. The error ranges are the 95 % confidence bands for the fit.
We pick the shear stress needed to reactivate the shear zone after each hold time th and normalise it to the mean stress during stable sliding: (Fig. 1b). This results in an effective stress measure assuming no cohesion. The healing rate is then the change in Δμ in comparison to the natural logarithm of hold time th (Beeler et al., 1994; Bhattacharya et al., 2017) and is obtained from the slope of Δμ versus ln th (Fig. 1c):
We calculate the compaction rate in the same manner by using the difference in lid position between the start and end of the hold phase. The same power law relation is found with strong compaction for short hold phases. Values for the compaction rate are negative because higher compaction results in smaller sample heights. All data are automatically picked and evaluated using a dedicated Python code published as part of the open-source software “RST-Stick-Slipy” (Rudolf, 2021).
2.5 Grain characteristics
Ultimately, the frictional response of a bulk material is the result of granular interactions and therefore depends primarily on the geometric characteristics of the grains. The shear zones forming in the ring shear tester usually span 11 to 16 times the mean grain size (Panien et al., 2006). The grains react to stress by creating force chains that frequently change their orientation (Cates et al., 1998; Daniels and Hayman, 2008). As a result, frictional resistance between individual grains and material elasticity has major implications on the bulk behaviour.
However, it is technically very challenging to measure friction between the individual grains, and therefore we assess the tendency of each material to create locked states by using a qualitative index for several key features. We categorise the materials with three different parameters: sphericity, roundness and surface roughness. The definition of the shape parameters follows that of clastic sediments. Sphericity is defined as the closeness to a perfect sphere. Roundness is given by the shape of the edges of a grain. Surface roughness is a measure of the small-scale surface properties (not of the grain shape itself). Each parameter is assigned a score from 1 to 4 that expresses the materials proneness to locking with 4 being “low impact” and 1 being “high impact”. Some materials have grains with different characteristics: for example, sands that are crushed are usually mixtures of rounded and angular grains. Therefore, depending on the degree of mixing, they are given an intermediate quality score. Grain size distribution was not taken into account because comparable measurements do not exist for all materials. A heterogeneous grain size distribution changes the bulk density of the material, which can influence the frictional characteristics (Lohrmann et al., 2003). However, the effect is minor (Mair et al., 2002). Table 2 shows an overview of the parameters, criteria and associated literature.
Table 2Categorisation scheme for granular materials with a simple “quality score”. A lower score indicates a tendency for higher internal friction and time consolidation.
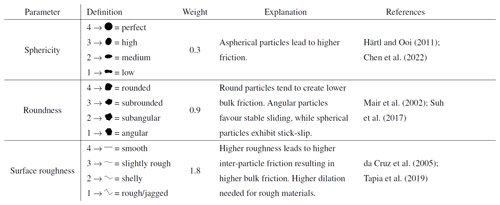
The quality score is a qualitative measure that only gives a general tendency of material behaviour and follows an arbitrary scale. We use this scale to turn a qualitative observation into a quantity. Here, the purely subjective observation of the grains, without capturing a truly measurable quantity, represents a major source of error. The quality score is therefore only a theoretical support to find possible correlations between the parameters. In no way should the score be seen as an objective quantity. It could serve as a preliminary stage for future measurable variables and give a rough direction.
However, the relative importance of the grain parameters sphericity, roundness and surface roughness can be estimated by comparing studies that systematically varied them as part of either numerical or experimental studies (references in Table 2). To account for the impact of each parameter, we take a weight average that uses the estimated effect on bulk friction from the references. We assume that this weighted average tends to reflect the amount of inter-particle locking during a hold phase and therefore also is a proxy to healing rate b. The weights are estimated by comparing the influence of each parameter on the value of friction in the respective studies. Härtl and Ooi (2011) report an increase in sliding friction from μd=0.56 for spherical particles to μd=0.59, which is a 10 % increase in friction. Particle roundness has been shown by Mair et al. (2002) to increase friction from μ=0.45 for round particles to μd=0.6, which is an increase of 30 %. Tapia et al. (2019) show an increase from μd=0.23 for slightly roughened particles to μd=0.37 for highly roughened particles, reflecting a 60 % increase. This is the strongest influence of all examined parameters. As a result, the relative weighting of the parameters is given as the ratio between the three percentages to each other summed up to three. Coincidentally, all three percentages sum up to one, and therefore the percentages given previously also reflect their relative proportion for the weighted average (10 %, 30 % and 60 % or 0.3, 0.9 and 1.8 given as weights, respectively).
2.6 Reactivation of faults
The reactivation of pre-existing faults in nature and in analogue models is primarily governed by (i) fault geometry, (ii) the surrounding stress field and (iii)the fault's frictional properties (Bonini et al., 2012). For natural fault systems, an additional mechanism is fluid overpressure, e.g. in basin sediments. However, fluids and fluid pressures cannot be accurately modelled in a scaled fashion and are thus rarely implemented in tectonic analogue models. We therefore focus on the aforementioned three factors (i) to (iii) to estimate the tendency to reactivate a pre-existing fault instead of forming a new fault. We do this in a typical basin inversion scenario and use a simplified Amonton wedge model to estimate the stresses needed to push a sidewall with a reactivated pre-existing fault and compare it to the stress needed to form a new fault (Collettini and Sibson, 2001; Mulugeta and Sokoutis, 2003).
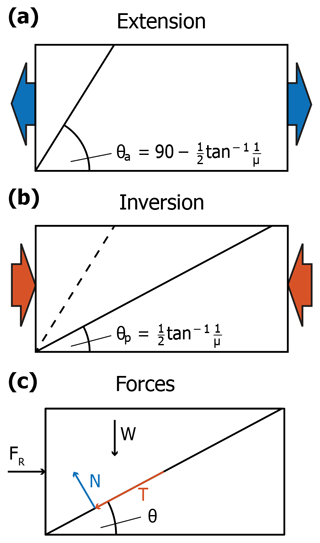
Figure 2Definition of fault angles during (a) extension and (b) compression. In (b) the pre-existing fault is shown as a dashed line, showing the difference in orientation. (c) Force balance and definition of the force FR required to move a block of weight W along a fault with an angle of θ (modified after Mulugeta and Sokoutis, 2003).
The first step is to calculate the optimal fault dip angle θa with respect to the horizontal at which the fault forms during extension to approximate the preferred fault geometry in the first phase of the basin inversion scenario (Eq. 4, Fig. 2a, after Collettini and Sibson, 2001). This fault angle is defined by the friction μ of the material so that higher friction leads to steeper faults in the model.
After the extensional phase, the basin switches to compression, and the optimal angle for a new fault θp with respect to the horizontal is as follows (Fig. 2b):
To calculate what is energetically more favourable, reactivation of an inherited fault versus formation of a new fault, we calculate the horizontal force FR required to move the wedge of material formed by the side wall, surface and fault angle θ (Fig. 2c). This force additionally incorporates the weight W=ρgh of the material (Mulugeta and Sokoutis, 2003). For the calculations we assume a normal stress of σN=1000 Pa, analogous to the slide–hold–slide tests corresponding to a height h=3.5 to 5.5 cm for materials with a bulk density of ρ=1800 to 3000 kg m−3, respectively:
A fault is considered severely misoriented when its angle is twice as large as the optimal fault angle. In this case, the term leading to extremely large values for FR. In the locking region, and therefore FR<0, which is unrealistic.
To account for healing, the friction for a reactivated fault is time dependent (i.e. increases with hold time) with the healing rate b as the power law coefficient:
This methodology neglects possible edge effects, such as shear stresses along the sidewall, because we assume a continuous granular layer that is cross-cut by several normal faults, which are going to be inverted. Additionally, we do not incorporate changes in the stress field due to differences in elasticity of the material after healing and the formation of lower-density shear bands that could lead to stress concentrations. Another important constraint of this simple model is that it is not suitable for materials with higher cohesion because these tend to form surface cracks during extension, leading to a change in fault angle with depth.
All calculations incorporate full uncertainty propagation through the Python module “uncertainties” assuming normally distributed variables. For the frictional parameters μ, C and b the error given is 2 standard deviations calculated from the covariance of the fit and averaged per material (quartz sand, feldspar sand, glass beads, etc.). For density ρ the value is the arithmetic mean and error is 2 standard deviations of density for each material.
3.1 Grain characteristics
The materials are well sorted and very homogeneous because they are standardised industrial products for specific purposes. As a consequence, they contain few to no impurities, such as clay or pebbles, and are mostly monomineralic. Therefore, the properties presented here should apply to all batches from the same manufacturer. See Table A1 for a more detailed description of each sample and Fig. 7 for a comparison of the quality index with the frictional properties.

Figure 3Quality scores and some exemplary materials that show specific characteristics. (a)–(d) Stacked and sorted quality score for the individual properties and weighted average according to Table 2. (e) Glass beads with high sphericity, high roundness and low surface roughness. (f) Glass beads with some low-sphericity grains. (g) Typical quartz sand with medium sphericity, good roundness and low surface roughness (aeolian sand). (h) Feldspar sand with low sphericity, low roundness and high surface roughness. (i) Foam glass with medium sphericity, good roundness and medium surface roughness. (j) Sand with high surface roughness due to shelly and jagged surfaces (crushed sand). (k) Corundum sand with some elongated grains leading to a higher sphericity score. (l) Zircon sand with many elongated and elliptical grains but good roundness. (m) Garnet sand with spherical, subangular grains and high surface roughness due to broken grains.
3.1.1 Quartz sands
Quartz sands are the most frequently used analogue material and therefore represent the majority of samples. The colour of most sands is yellowish to white with clear to translucent grains. Some sands are very homogeneous, consisting of more than 99 % quartz, while others contain considerable (>5 %) traces of feldspars, mica and other minerals. The sphericity is medium to high across all samples and differences are only minor. Roundness shows a larger spread with some rounded samples, such as the GFZ sands (Fig. 3g), and some very angular sands, e.g. those from Wrocław. Roundness is mostly derived from the origin of the sands. Some sands are unprocessed aeolian or fluvial sands that are (sub)round, while others have been processed and therefore have high angularity due to crushing (Fig. 3j). This division is also evident in the large spread of surface roughness. The sands that are rounded to subrounded generally have smoother surfaces. The angular sands often have shelly or jagged surfaces leading to high surface roughness. Some sands are seemingly mixtures of rounded and angular sands and therefore receive a lower score.
3.1.2 Glass beads
Most glass beads show a very high sphericity, are perfectly rounded and have very smooth surfaces. Depending on the manufacturer, they are very well sorted and have only very few impurities (Fig. 3e), e.g. glass beads from GFZ and Prague that are both supplied from the same manufacturer. Some samples either contain non-spherical grains (Fig. 3f), fragments, or a significant amount of beads that are stuck together or have small protrusions. This leads to a slightly lower score for sphericity and roundness. Usually, the glass beads are perfectly clear with a few whitish dots on the surface that probably stem from impacts of other beads during manufacture and transport.
3.1.3 Corundum sands
The corundum sands, which are exclusively processed (crushed) material, have medium sphericity with some elongated grains, leading to a devaluation to a lower score in comparison to quartz sands. The colour is yellowish brown but transparent for the brown corundum sands and clear for white corundum sands. In general, they are very angular with sharp and pointy edges (Fig. 3k). This also leads to a high surface roughness, although the faces between the edges are generally flat and smooth. Some surfaces are shelly, adding even more surface roughness. As a result, the average quality score is very low.
3.1.4 Feldspar sands
The feldspar sands feature milky to translucent white grains with low sphericity due to their elongated and triangular shape (Fig. 3h). They are very angular, and some seem to be aggregates of smaller grains. The surfaces are very rough, with many sharp edges and surfaces, possibly due to cleavages. Most grains are internally fractured, which contributes to the milky and translucent appearance. Therefore, the feldspar sands have the lowest average quality score.
3.1.5 Zircon sands
The zircon sand, which is crushed like corundum sand, is poorly sorted and contains a large variety of grain sizes and grain shapes (Fig. 3l). Many grains are elongated and show the characteristic habit of zircon crystals, and some seem to be fragments of these larger crystals. The colour is reddish brown to off-white and the grains are translucent to clear. The grains are angular to rounded depending on the grain size. Large grains tend to be well rounded and almost spherical, while smaller ones are angular to subangular. The more or less intact crystals have subrounded crystal faces and edges. Due to the heterogeneous composition, the surface roughness also has a strong variation. The majority of the grains have a smooth surface; however, there are a few that show shelly or slightly rough surfaces.
3.1.6 Garnet sands
On average, the garnet sands have spherical grains with a small proportion of elongated grains (Fig. 3m). They are mostly transparent with a reddish tint, and about 10 % of the grains are dark and opaque. The transparent grains are angular to subangular and have a shelly surface. The darker grains are subrounded and have a slightly rough surface. Additionally, larger grains seem to be more rounded than smaller ones.
3.1.7 Foam glass
Similar to the glass beads, the foam glasses are an industrially manufactured product and are therefore very homogeneous. No impurities could be found, and the grain size distribution is very narrow and corresponds to the given specifications. They have a medium sphericity and a ellipsoidal to random shape similar to asteroids (Fig. 3i). The colour is grey, and the grains are opaque. The grains are well rounded with no visible edges or faces. They have a very fine surface, similar to sandpaper, resulting in a slightly rough surface. Due to their surface roughness they rank just below the glass beads but still above the quartz sands.
3.2 Healing and compaction rates
We find that most materials exhibit healing rates in the range of b≤0.03 (Fig. 4), i.e. an increase in strength of less than 3 % per 10-fold increase in hold time (e.g. 10 s versus 100 s). Only two samples show healing rates that are not significantly different from zero, “Freiburg” and “Bern, CarloAG (100–300 µm)”, and these are therefore not considered to show healing over experimental timescales. Most quartz sands show lower than average healing rates of roughly 1 % per 10-fold increase in hold time. Foam glass shows healing rates generally lower than those of quartz sands. Glass beads exhibit higher healing rates and show considerable spread between b=0.015 and 0.025. Corundum sands are distributed over the full range of healing rates, and feldspar sands overlap with glass beads. However, the number of samples for materials other than quartz sands and glass beads is too small to generalise.
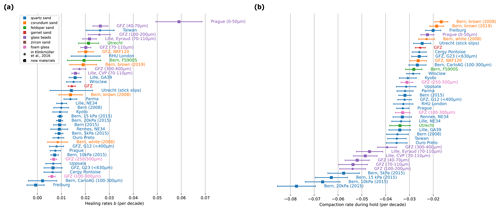
Figure 4Stacked and sorted plot of (a) healing rates and (b) compaction rates for all tested materials. The numbers either indicate grain size range (e.g. Prague 0–50 µm), type (e.g. G23) or year of acquisition (e.g. Bern, brown 2019). Similar materials often plot in the same range of healing or compaction rate. Notable exceptions are the healing rate for very fine glass beads (Prague, 0–50 µm) and the compaction rates for higher normal stresses (Bern, 5–20 kPa).
Compaction rates are more diverse and show a clearer separation between the materials (Fig. 4b). Glass beads show the strongest compaction rates of to −0.04 at the reference normal stress of σN=1 kPa. This means that sample thickness decreases by 4 % to 5.5 % per 10-fold increase in hold time. The only exception are the very fine glass beads (Prague, 0–50 µm), which show a very low compaction in comparison to the other glass bead samples. Quartz sands show small compaction rates between and −0.02, with the majority of quartz sands having . Feldspar sands and foam glass compaction rates are again comparable with quartz sands. In general, corundum sands exhibit the lowest compaction rates.
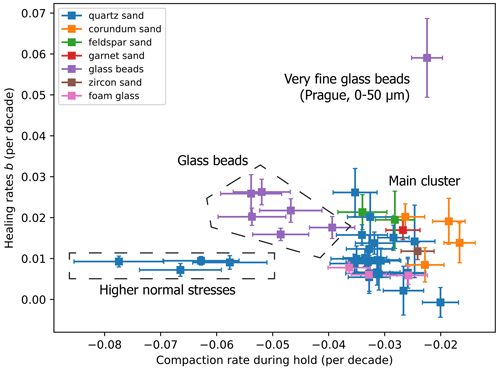
Figure 5Comparison of healing rate and compaction rate. Materials that behave similarly are grouped in clusters.
There is a strong influence of normal stresses on compaction, which leads to much stronger compaction during hold intervals. However, the healing rate is not significantly correlated with higher compaction, and therefore the measurements with higher normal stresses form a distinct cluster when plotting compaction rate versus healing rate (Fig. 5). Most samples do not show a clear distinction between sample material, compaction and healing rate. They all plot in a single cluster, with no significant correlation of compaction rate and healing rate. The glass beads are exceptional because they show high healing rates and high compaction rates and therefore form a separate cluster. Using the main cluster and glass bead cluster, a weak negative correlation of healing rate and compaction rate is visible. An increase in healing with stronger compaction might be recognisable, but this is not statistically significant. The most notable exception is again the very fine glass beads (Prague, 0–50 µm). These show a significantly stronger healing at small compaction rates.
3.3 Reactivation properties
For the reactivation properties we summarised the samples into seven groups by taking the average and the standard deviation 2σ of all properties (friction coefficients μ, healing rate b and density ρ). As material height we choose h=0.05 m, which is comparable to a normal stress of σN=1000 Pa for most materials and lies in the range of typical analogue model setups.
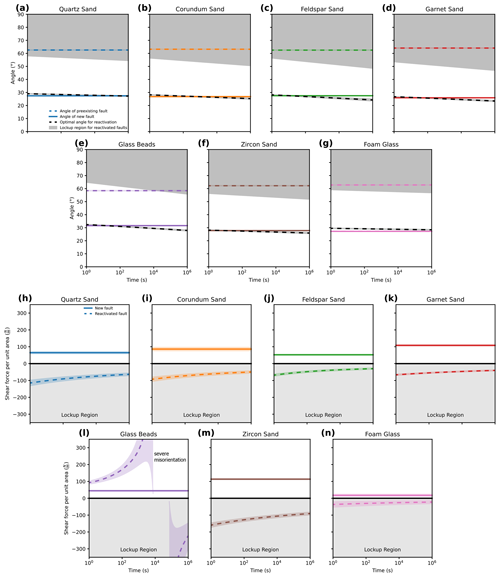
Figure 6Optimal angles and shear forces for new and reactivated faults. (a)–(g) Optimal angles of faults for each material. (h)–(n) Shear forces required to move a wedge of material along a new and reactivated fault. Errors are derived from the uncertainties of the parameters and represent 2σ.
For the first phase of a typical basin inversion model, the material is subjected to extensional stresses (σ1∥Sv, Eq. 4), while fault angles are defined by the materials peak friction of μp=0.50 to 0.75, which results in θa=58 to 64∘ (dashed coloured lines in Fig. 6a–g). During compression the stress field changes (σ1∥Shmax) and so does the angle of newly generated faults (Eq. 5). The friction coefficient is the same because new faults mainly cross cut undisturbed material and angles are in the range of θp=26 to 32∘, which leads to flatter faults in the model (solid coloured lines in Fig. 6a–g).
The locking regions of all materials become increasingly larger as reactivation friction μr increases over time. We find that for all materials, with the exception of glass beads, the angles of the pre-existing faults fall within the locking region. As a result, none of the faults that were created during extension should reactivate because they are severely misoriented. The optimal angle for reactivation using the time-dependent μr is similar to the optimal angle of a new fault with μp. This means that the difference in friction due to healing is not large enough to facilitate sliding along the inherited normal faults.
We find the same for the force required to move a wedge of material along the pre-existing fault or the creation of a new fault (Fig. 6h–n). For new faults the shear force per unit area ranges between FR=50 and 150 N m−1, which means that for a triangular wedge of 5 cm height and 100 cm length in the direction of σ2 between 50 and 150 N is required to initiate a new fault. While the height of the wedge has an influence on the absolute values of forces, the ratio between the forces is independent of height. For reactivated faults most materials show negative values, and therefore reactivation is not possible.
The only exception is glass beads, which are still in the field of possible reactivation up to th=104 s after shear. However, the stress required to reactivate these faults is roughly twice as high as for creating a new fault and reaches extremely high values already after th=103 s (Fig. 6l). A close inspection of the individual glass bead samples shows that glass beads with low grain sizes (e.g. GFZ, GB 70–110 µm) are fully outside the locking region. The stresses to reactivate these faults are only 1.5 to 2 times higher than the stress for new faults. The fault orientation is still more than 20∘ away from the optimal value, but under certain conditions a reactivation is possible for this sample. In general, reactivation is very unlikely despite the small difference between optimal and inherited angles.
4.1 Impact of time consolidation
4.1.1 Reactivation of faults in basin inversion models
Our results show that for the tested materials the reactivation of inherited normal faults generated during extension as reverse faults should generally not be possible. This means that the difference between peak and reactivation friction of 5 % to 15 % is too small to create faults outside the locking region (Sibson, 1980). Additionally, extensional faults in typical analogue models show higher angles than what is inferred from friction measurements with ring shear testers (Panien et al., 2006). This is in accordance with the results of other studies that show only weak to no reactivation of pre-existing structures in purely frictional sandbox models (Jara et al., 2018; Marques and Nogueira, 2008; Almilibia et al., 2005; Yagupsky et al., 2008; Molnar and Buiter, 2022). Due to their relatively low friction coefficient, glass beads are a certain exception. Reactivation is, however, still unlikely due to the high stresses required. As a consequence, many modellers use strong boundary conditions, such as heterogeneities or blocks, to force fault reactivation along specific normal faults (Bonini et al., 2000).
For setups that aim to reactivate extensional structures that are generated in situ, a possible solution could be to increase the amount of extension. On average the misorientation between the locking region and fault orientation is less than 10∘. During extension the blocks rotate in a bookshelf-like motion, thereby creating flatter fault angles. The stresses to reactivate faults close to the locking regions are still quite high, and therefore a rotation of or more is required to lead to structures that can be reactivated. In analogue models the fault orientations usually show a larger spread than what is calculated in our theoretical model. The graben systems that form during extension usually contain several fault angles with flatter and steeper segments. Therefore, some faults could already be well within the reactivation field due to the heterogeneity in the analogue model, e.g. due to variation in bulk density.
Our model has limitations in quantifying the effect of cohesion on the reactivation of faults. The ring shear tests suggest that the reactivation cohesion is up to twice as high as peak cohesion for most materials, which hinders fault reactivation even more. This effect is amplified for models with small thicknesses because for these the ratio of cohesive to gravitational stress is larger (Ritter et al., 2016a). To decrease the effect of cohesion the only option is to increase the normal stress by increasing the layer thickness. We note, however, that cohesion is not directly measured here but is inferred from extrapolation. Because cohesion in granular materials used in analogue modelling is typically very small (few tens of Pa) or even zero, differences in cohesion might not be quantitatively sound.
4.1.2 Implications of healing rates on basin inversion models
Regardless of the mechanism creating the faults, most materials show a measurable amount of healing. The healing rates in the tested materials are low to moderate and lead to an increasingly larger locking region over time. For materials that have high healing rates, e.g. glass beads, this increase is up to 1.5∘ per 10-fold increase in hold time. This means that granular faults that are about 12 h old require a 7∘ lower angle to remain in the activity field. Depending on the type of setup this can change the number of active faults, especially in graben systems consisting of several similarly oriented faults. Healing can lead to a smaller amount of active faults when the time between fault creation and fault motion is increasing. In theory this should also apply to precut faults because they alter the grain packaging in a similar way. This could even lead to the creation of new faults instead of localisation at the predefined locations. However, with our methodology this is not verifiable and other mechanisms, such as the formation of shear fabrics in the granular material, could play a role.
Due to the exponential nature of Eq. (7), healing is very strong immediately after a fault comes to rest. Changing stress distribution in a running model commonly leads to constant simultaneous activity on many faults. Therefore, only when a model is stopped, i.e. the model settles under the influence of gravity, can healing have a visible effect. Healing rates are low for most materials, meaning that no effect on reactivation angles can be expected for several hours, despite healing being strongest in the first few hours. In comparison with other processes, such as sieving techniques or boundary conditions, fault healing only has a small secondary influence on fault behaviour like the velocity dependence of friction during shear (Rosenau and Oncken, 2009). Consequently, if a model is continuously run without longer interruptions (th<1 h), the effect of healing is indistinguishable from other instantaneous mechanisms that influence an analogue fault's strength.
4.1.3 General impact of time consolidation on analogue models
In the general context of analogue models, time-dependent change in fault strength has further effects whose influence is small but should nevertheless be taken into account. There is a class of analogue models, also common in basin inversion, where frequent interrupts are inevitable. Typical examples are models with concurrent sedimentation or erosion where material is added or removed during a hold phase (e.g. Bonnet et al., 2007; Graveleau and Dominguez, 2008; Molnar and Buiter, 2022). With the increased use of computer tomography or laser-based topography scanning to screen experiments comes another type of model that must be interrupted at regular intervals. As mentioned in Sect. 4.1.2, interruptions that are shorter than 1 h should not have a great effect. The change in normal stress due to the addition or removal of overburden should have a much stronger effect than the restrengthening due to time consolidation. During the addition of material and the associated preparation of the model surface, a hardening of the fault zone could occur. For example, smoothing the surface with a spatula or ruler could exert additional stress on the fault zone and thus promote compaction. However, this effect is already commonly known for such models and has a much greater impact than the healing.
Repeatability of models can become an issue when the timing of the individual model runs is not the same. In recent years, more attention has been paid to the repeatability of analogue experiments. For example, Santimano et al. (2015) were able to demonstrate that various parameters such as fault length and activity are intrinsically variable. Experiments where fault activity is monitored with or without erosion therefore could be influenced and even altered by repeated interruption (Hoth et al., 2006, 2007). Likewise, in many studies a repetition of simple experiments is carried out to quantify the influence of preparation, setup and climatic conditions. Time strengthening brings another factor into play here. For example, models that have the same setup but run for different lengths of time due to the duration could have differences in fault activity or fault orientation. An experiment that is left overnight or for a longer period of time tends to have a higher strength than a model that is deformed within a short period of time. There is anecdotal evidence of analogue models that have failed to reach the expected results when the material has been sitting in the box for too long. For example, a typical sandbox experiment is performed more frequently at GFZ Potsdam's analogue laboratory (HelTec) for demonstration purposes. It was found that the time difference between preparation and execution should not exceed 1 d for a representative result. Therefore, especially in experiments with heterogeneities, for example due to faults or precut surfaces, care should be taken that the duration of inactivity of the faults is approximately the same in repeated experiments.
4.2 Relation of frictional properties with grain characteristics
We compare the quality score of each material with all frictional parameters to recognise possible influences. To quantify correlations we calculate Pearson r and Spearman ρ correlation coefficients. The Pearson correlation coefficient assumes a linear correlation between two variables, but this is not always the case. Therefore, we also use the Spearman correlation coefficient that is independent of the underlying distribution. For both parameters the p value is determined, which gives an indication of the significance of correlation. Generally, if p<0.05 one assumes that the found correlation is not possible through random permutation of the original data and therefore statistically significant. It should be noted, however, that in this paper the quantification of the quality score is subjective, while the friction parameters (including their errors) are based on real measured values. Thus, the use of correlation coefficients is only an aid to identify trends more easily in the set of measurements and samples.
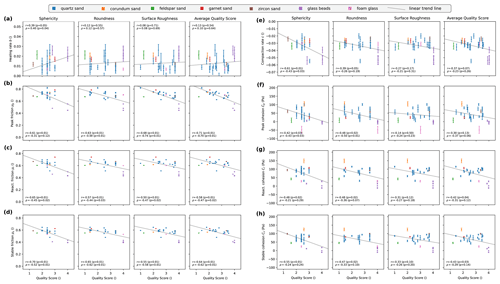
Figure 7Correlation of frictional properties with quality score: (a) healing rate, (b)–(d) friction coefficient, (e) compaction rate, and (f)–(h) cohesion. The grey lines are simple linear fits of the data to highlight the trends in the datasets. They are not necessarily of statistical significance.
We find that the healing rate b does show a weak positive correlation with sphericity (r=0.39, p=0.05; ρ=0.40, p=0.04; Fig. 7a) and is otherwise not correlated with any other quality measure. This means that with higher sphericity the materials tend to have higher healing rates. This is probably related to the compaction rate, which shows a similar negative correlation with sphericity. Spherical grains compact more than aspherical beads, as indicated by the higher compaction rates of glass beads (Figs. 5 and 7e). This is consistent with a tendency of glass beads to compact more easily during cyclic axial loading tests reported by Klinkmüller et al. (2016). Higher sphericity is associated with lower void ratios before and after shearing (Härtl and Ooi, 2011), and therefore the individual grains are compacted more during a hold phase. As a consequence, the stress required to mobilise these materials is higher because a larger amount of dilation is needed.
All three friction types (peak, reactivation and static; see Fig. 7b-d) show a moderate negative correlation with all quality scores (, p<0.05). As a result, there is a tendency to get lower frictional coefficients for materials that have high sphericity, higher roundness and smoother surfaces. The negative correlation of quality index with cohesion is very weak and has a much higher p value, leading to a higher uncertainty in the correlation (Fig. 7f–h). These results are in accordance with previous studies on granular characteristics (Klinkmüller et al., 2016; Panien et al., 2006, and references in Table 2). We find a high correlation of peak friction with average quality score (, , p=0.01) mostly influenced by the correlation of peak friction with roundness and surface quality.
The exceptionally high healing rate for very fine glass beads (Prague, 0–50 µm) is probably the result of a strong increase in cohesion. In contrast to the other glass bead samples, they only show a small compaction rate, i.e. only a small reduction in density. Because of the wide particle size distribution and large amount of fine materials, the void space is largely filled with finer glass powder. Additionally, very fine granular materials are susceptible to electrostatic effects that increase the attractive forces between particles.
Another outlier is the sand from Utrecht that shows stick–slip behaviour. Due this behaviour, we assume an increased healing rate, as in this case there can theoretically be several effects. The higher the healing rate b, the greater the difference a−b, with the direct effect a being constant. In theory, this makes the material more velocity weakening and thus more unstable (Dieterich, 2007). Additionally, with higher b the critical stiffness increases. Therefore, a system that was previously stable, such as the ring shear tester, now needs to have a higher stiffness to sustain stable sliding. As a result the system shows a higher tendency for stick–slip behaviour. However, due this behaviour it is not possible to measure the healing rates adequately. This would require a much higher apparatus stiffness, which was not possible to change for our ring shear tester.
4.3 Suitability for modelling natural faults
Geodetic studies on post-seismic surface motion demonstrate that faults quickly relock after a large earthquake (Bedford et al., 2016). A similarly high post-slip healing rate is required to explain the observations in analogue models of subduction zone kinematics using sticky rice as a fault zone analogue (Rosenau et al., 2009; Kosari et al., 2022). We observe the same strong healing in the first few hold intervals caused by the power law relation of strength and hold time (Eq. 7), which is also observed for laboratory experiments on synthetic and natural fault rocks (Karner et al., 1997; Carpenter et al., 2016; Scuderi et al., 2014). Healing rates for dry synthetic and natural fault gouges range between 0.001 and 0.01 at room temperature (Ikari et al., 2016). Under wet conditions this healing rate can increase by an order of magnitude at temperatures >300 ∘C (Niemeijer et al., 2008, and references therein). The rates are even higher for gouges containing salt or salt–muscovite layers. A general correlation between the healing properties and the behaviour of fault zones thus seems plausible.
Quartz sands and foam glass show healing rates that are generally low and closer to dry gouges, while the glass beads, especially the very fine glass beads, have values that are closer to hydrothermal healing rates. However, the frictional strength is too low to use glass beads as well-scaled analogues of self-healing faults in a model. A possibility might be the addition of a small percentage of fine material to sands, which would thus achieve cohesion-driven healing while retaining the overall higher bulk strength of sand. Such material mixes were not part of this study but can easily be tested with the methodology outlined here.
Healing rates and grain characteristics of a set of commonly used analogue materials from different laboratories were acquired through slide–hold–slide tests and by qualitative description. Furthermore, the reactivation potential of inherited normal faults in these materials was calculated using additional information from previous ring shear tests. These experiments provide a better understanding of transient, time-dependent changes in analogue models and their potential impacts on the suitability of these materials for certain types of analogue models, such as basin inversion models. The experiments allow us to make the following conclusions.
-
There is a measurable time dependency in brittle analogue models in the form of fault strengthening over the experimental timescale.
-
The time consolidation is small in comparison to other factors that influence the strength of analogue materials, such as preparation technique or climatic conditions, i.e. air humidity. However, there is a possible negative impact on repeatability and model outcome for long-running experiments or experiments with substantial downtime between the deformation phases.
-
Healing rates are generally low but comparable to natural faults and gouges. The use of the tested analogue materials as analogues of healing faults might be possible. Glass beads show the highest amount of healing due to their spherical shape and smooth surface, which leads to increased compaction during hold intervals.
-
Reactivation of pre-existing faults in the tested granular materials is very unlikely if the faults are not manually predefined. Fault orientations generated by extension are too steep and always lie in the locking region. Only overextending with associated block rotation could lead to faults that are in the reactivation region. However, the generation of new faults is almost always energetically more favourable.
-
The frictional properties of most materials only show a weak correlation with grain characteristics. The strongest correlation was found for healing rates with sphericity and friction with an average quality score. A general trend is that a low quality score roughly correlates with higher friction.
All data used in this study are available in the form of a data publication (https://doi.org/10.5880/fidgeo.2023.009, Rudolf et al., 2023) together with Python scripts to generate all figures in the form of the Python module “granularhealing” (https://doi.org/10.5880/fidgeo.2023.010, Rudolf, 2023).
A video showing the experimental procedure of the ring shear test is available on the EPOS-MSL channel on YouTube: https://youtu.be/erEXPj8xaSM (Rudolf and Hecht, 2023).
Conceptualisation of this project was done by MRu and MRo. Measurements were done by MRu and MRo. Data analysis and programming were done by MRu. The manuscript was written by MRu with the help of MRo and OO. All authors read and approved the final manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “Analogue modelling of basin inversion”. It is not associated with a conference.
We thank all participants from the laboratories who sent their samples to be tested for this study. The authors thank the technical staff at the Helmholtz Laboratory for Tectonic Modelling for running some of the long-term tests (Frank Neumann) and for setting up the monitoring devices (Thomas Ziegenhagen). We kindly thank Jens Mingram (GFZ Potsdam) and Laura Stutenbecker (TU Darmstadt) for providing support and access to the microscopes at their institutes. In addition, we thank Hanna Elston and an anonymous reviewer for their helpful comments and ideas that have been instrumental in moving this paper forward. Heinrich Hecht is thanked for shooting and producing the video.
This research has been supported by the Deutsche Forschungsgemeinschaft (grant no. 235221301).
This paper was edited by Federico Rossetti and reviewed by Hanna Elston and one anonymous referee.
Almilibia, A., Mc Clay, K., i Montserrat, F. S., Muñoz, J., and Roca, E.: Analogue modelling of inverted oblique rift systems, Geol. Acta, 2, 251–251, https://doi.org/10.1344/105.000001395, 2005. a
Aschauer, J. and Kenkmann, T.: Impact cratering on slopes, Icarus, 290, 89–95, https://doi.org/10.1016/j.icarus.2017.02.021, 2017. a
ASTM, D.: Test Method for Bulk Solids Using Schulze Ring Shear Tester, https://doi.org/10.1520/d6773-16, 2016. a
Bedford, J., Moreno, M., Li, S., Oncken, O., Baez, J. C., Bevis, M., Heidbach, O., and Lange, D.: Separating rapid relocking, afterslip, and viscoelastic relaxation: An application of the postseismic straightening method to the Maule 2010 cGPS, J. Geophys. Res.-Sol. Ea., 121, 7618–7638, https://doi.org/10.1002/2016jb013093, 2016. a
Beeler, N., Tullis, T., and Weeks, J.: The roles of time and displacement in the evolution effect in rock friction, Geophys. Res. Lett., 21, 1987–1990, https://doi.org/10.1029/94gl01599, 1994. a
Bhattacharya, P., Rubin, A. M., and Beeler, N. M.: Does fault strengthening in laboratory rock friction experiments really depend primarily upon time and not slip?, J. Geophys. Res.-Sol. Ea., 122, 6389–6430, https://doi.org/10.1002/2017JB013936, 2017. a
Bonini, M., Sokoutis, D., Mulugeta, G., and Katrivanos, E.: Modelling hanging wall accommodation above rigid thrust ramps, J. Struct. Geol., 22, 1165–1179, https://doi.org/10.1016/s0191-8141(00)00033-x, 2000. a
Bonini, M., Sani, F., and Antonielli, B.: Basin inversion and contractional reactivation of inherited normal faults: A review based on previous and new experimental models, Tectonophysics, 522–523, 55–88, https://doi.org/10.1016/j.tecto.2011.11.014, 2012. a, b, c
Bonnet, C., Malavieille, J., and Mosar, J.: Interactions between tectonics, erosion, and sedimentation during the recent evolution of the Alpine orogen: Analogue modeling insights, Tectonics, 26, TC6016, https://doi.org/10.1029/2006tc002048, 2007. a
Buchanan, J. G., Buchanan, P. G., and Ziegler, P.: Basin inversion, vol. 88, Geological Society London, https://doi.org/10.1144/GSL.SP.1995.088.01.30, 1995. a
Carpenter, B. M., Ikari, M. J., and Marone, C.: Laboratory observations of time-dependent frictional strengthening and stress relaxation in natural and synthetic fault gouges, J. Geophys. Res.-Sol. Ea., 121, 1183–1201, https://doi.org/10.1002/2015JB012136, 2016. a
Cates, M., Wittmer, J., Bouchaud, J.-P., and Claudin, P.: Jamming, force chains, and fragile matter, Phys. Rev. Lett., 81, 1841–1844, https://doi.org/10.1103/physrevlett.81.1841, 1998. a
Chen, C., Gu, J., Peng, Z., Dai, X., Liu, Q., and Zhu, G.-Q.: Discrete element modeling of particles sphericity effect on sand direct shear performance, Scientific Reports, 12, 5490, https://doi.org/10.1038/s41598-022-09543-9, 2022.
Collettini, C. and Sibson, R. H.: Normal faults, normal friction?, Geology, 29, 927–930, https://doi.org/10.1130/0091-7613(2001)029<0927:nfnf>2.0.co;2, 2001. a, b
da Cruz, F., Emam, S., Prochnow, M., Roux, J.-N., and Chevoir, F.: Rheophysics of dense granular materials: Discrete simulation of plane shear flows, Phys. Rev. E, 72, 021309, https://doi.org/10.1103/physreve.72.021309, 2005.
Daniels, K. E. and Hayman, N. W.: Force chains in seismogenic faults visualized with photoelastic granular shear experiments, J. Geophys. Res., 113, B11411, https://doi.org/10.1029/2008jb005781, 2008. a
Dieterich, J. H.: Time-Dependent Friction and the Mechanics of Stick-Slip, Pageoph, 116, 790–806, https://doi.org/10.1007/BF00876539, 1978. a, b
Dieterich, J. H.: Applications of rate-and state-dependent friction to models of fault slip and earthquake occurrence, Treatise on Geophysics, 4, 107–129, https://doi.org/10.1016/b978-044452748-6.00065-1, 2007. a, b, c
Elger, K., ter Maat, G., Caldeira, R., Cimarelli, C., Corbi, F., Dominguez, S., Drury, M., Funiciello, F., Lange, O., Ougier-Simonin, A., Rosenau, M., Wessels, R., Willingshofer, E., and Winkler, A.: The EPOS Multi-Scale Laboratories: A FAIR Framework for stimulating Open Science practice across European Earth Sciences Laboratories, Ann. Geophys., 65, DM318, https://doi.org/10.4401/ag-8790, 2022. a
Galland, O., Cobbold, P. R., Hallot, E., de Bremond d'Ars, J., and Delavaud, G.: Use of vegetable oil and silica powder for scale modelling of magmatic intrusion in a deforming brittle crust, Earth Planet. Sc. Lett., 243, 786–804, https://doi.org/10.1016/j.epsl.2006.01.014, 2006. a
Graveleau, F. and Dominguez, S.: Analogue modelling of the interaction between tectonics, erosion and sedimentation in foreland thrust belts, C. R. Geosci., 340, 324–333, https://doi.org/10.1016/j.crte.2008.01.005, 2008. a
Härtl, J. and Ooi, J. Y.: Numerical investigation of particle shape and particle friction on limiting bulk friction in direct shear tests and comparison with experiments, Powder Technol., 212, 231–239, https://doi.org/10.1016/j.powtec.2011.05.022, 2011. a, b
Hoth, S., Adam, J., Kukowski, N., and Oncken, O.: Influence of erosion on the kinematics of bivergent orogens: Results from scaled sandbox simulations, in: Tectonics, Climate, and Landscape Evolution, Geological Society of America, https://doi.org/10.1130/2006.2398(12), 2006. a
Hoth, S., Hoffmann-Rothe, A., and Kukowski, N.: Frontal accretion: An internal clock for bivergent wedge deformation and surface uplift, J. Geophys. Res., 112, B06408, https://doi.org/10.1029/2006jb004357, 2007. a
Hubbert, M. K.: Theory of scale models as applied to the study of geologic structures, Geol. Soc. Am. Bull., 48, 1459–1520, https://doi.org/10.1130/GSAB-48-1459, 1937. a
Ikari, M. J., Carpenter, B. M., and Marone, C.: A microphysical interpretation of rate- and state-dependent friction for fault gouge, Geochem. Geophy. Geosy., 17, 1660–1677, https://doi.org/10.1002/2016gc006286, 2016. a
Jara, P., Likerman, J., Charrier, R., Herrera, S., Pinto, L., Villarroel, M., and Winocur, D.: Closure type effects on the structural pattern of an inverted extensional basin of variable width: Results from analogue models, J. S. Am. Earth Sci., 87, 157–173, https://doi.org/10.1016/j.jsames.2017.10.018, 2018. a, b
Karner, S. L., Marone, C., and Evans, B.: Laboratory study of fault healing and lithification in simulated fault gouge under hydrothermal conditions, Tectonophysics, 277, 41–55, https://doi.org/10.1016/s0040-1951(97)00077-2, 1997. a, b
Kato, N. and Tullis, T. E.: A composite rate-and state-dependent law for rock friction, Geophys. Res. Lett., 28, 1103–1106, https://doi.org/10.1029/2000GL012060, 2001. a
Klinkmüller, M., Schreurs, G., Rosenau, M., and Kemnitz, H.: Properties of granular analogue model materials: A community wide survey, Tectonophysics, 684, 23–38, https://doi.org/10.1016/j.tecto.2016.01.017, 2016. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac
Kosari, E., Rosenau, M., and Oncken, O.: Strain Signals Governed by Frictional-Elastoplastic Interaction of the Upper Plate and Shallow Subduction Megathrust Interface Over Seismic Cycles, Tectonics, 41, e2021TC007099, https://doi.org/10.1029/2021tc007099, 2022. a
Lohrmann, J., Kukowski, N., Adam, J., and Oncken, O.: The impact of analogue material properties on the geometry, kinematics, and dynamics of convergent sand wedges, J. Struct. Geol., 25, 1691–1711, https://doi.org/10.1016/s0191-8141(03)00005-1, 2003. a, b, c, d, e, f, g, h
Mair, K., Frye, K. M., and Marone, C.: Influence of grain characteristics on the friction of granular shear zones, J. Geophys. Res.-Sol. Ea., 107, ECV 4-1–ECV 4-9, https://doi.org/10.1029/2001jb000516, 2002. a, b
Marone, C.: Laboratory-derived friction laws and their application to seismic faulting, Annu. Rev. Earth Pl. Sc., 26, 643–696, https://doi.org/10.1146/annurev.earth.26.1.643, 1998. a
Marques, F. and Nogueira, C.: Normal fault inversion by orthogonal compression: Sandbox experiments with weak faults, J. Struct. Geol., 30, 761–766, https://doi.org/10.1016/j.jsg.2008.02.015, 2008. a
Molnar, N. and Buiter, S.: Analogue modelling of the inversion of multiple extensional basins in foreland fold-and-thrust belts, EGUsphere [preprint], https://doi.org/10.5194/egusphere-2022-1014, 2022. a, b
Montanari, D., Agostini, A., Bonini, M., Corti, G., and Ventisette, C.: The Use of Empirical Methods for Testing Granular Materials in Analogue Modelling, Materials, 10, 635, https://doi.org/10.3390/ma10060635, 2017. a, b
Mulugeta, G. and Sokoutis, D.: Hanging wall accommodation styles in ramp-flat thrust models, Geological Society, London, Special Publications, 212, 197–207, https://doi.org/10.1144/gsl.sp.2003.212.01.13, 2003. a, b, c
Nagata, K., Nakatani, M., and Yoshida, S.: A revised rate-and state-dependent friction law obtained by constraining constitutive and evolution laws separately with laboratory data, J. Geophys. Res.-Sol. Ea., 117, B02314, https://doi.org/10.1029/2011JB008818, 2012. a
Niemeijer, A., Marone, C., and Elsworth, D.: Healing of simulated fault gouges aided by pressure solution: Results from rock analogue experiments, J. Geophys. Res., 113, B04204, https://doi.org/10.1029/2007jb005376, 2008. a, b, c
Panien, M., Schreurs, G., and Pfiffner, A.: Mechanical behaviour of granular materials used in analogue modelling: insights from grain characterisation, ring-shear tests and analogue experiments, J. Struct. Geol., 28, 1710–1724, https://doi.org/10.1016/j.jsg.2006.05.004, 2006. a, b, c, d, e
Pohlenz, A., Rudolf, M., Kemnitz, H., and Rosenau, M.: Ring shear test data of glass beads 40–70 µm used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2020.006, 2020a. a
Pohlenz, A., Rudolf, M., Kemnitz, H., and Rosenau, M.: Ring shear test data of glass beads 70–110 µm used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2020.007, 2020b. a
Pohlenz, A., Rudolf, M., Kemnitz, H., and Rosenau, M.: Ring shear test data of glass beads 300–400 µm used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2020.008, 2020c. a
Poppe, S., Holohan, E. P., Rudolf, M., Rosenau, M., Galland, O., Delcamp, A., and Kervyn, M.: Mechanical properties of quartz sand and gypsum powder (plaster) mixtures: Implications for laboratory model analogues for the Earth's upper crust, Tectonophysics, 814, 228976, https://doi.org/10.1016/j.tecto.2021.228976, 2021. a
Reber, J. E., Cooke, M. L., and Dooley, T. P.: What model material to use? A Review on rock analogs for structural geology and tectonics, Earth-Sci. Rev., 202, 103107, https://doi.org/10.1016/j.earscirev.2020.103107, 2020. a
Ritter, M. C., Leever, K., Rosenau, M., and Oncken, O.: Scaling the Sand Box – Mechanical (Dis-) Similarities of Granular Materials and Brittle Rock, J. Geophys. Res.-Sol. Ea., 121, 6863–6879, https://doi.org/10.1002/2016jb012915, 2016a. a, b, c, d, e
Ritter, M. C., Leever, K., Rosenau, M., and Oncken, O.: Supplement to: Scaling the Sand Box – Mechanical (Dis-) Similarities of Granular Materials and Brittle Rock, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2016.005, 2016b. a, b
Ritter, M. C., Rosenau, M., and Oncken, O.: Growing Faults in the Lab: Insights Into the Scale Dependence of the Fault Zone Evolution Process, Tectonics, 37, 140–153, https://doi.org/10.1002/2017tc004787, 2018. a
Rosenau, M. and Oncken, O.: Fore-arc deformation controls frequency-size distribution of megathrust earthquakes in subduction zones, J. Geophys. Res.-Sol. Ea., 114, B10311, https://doi.org/10.1029/2009jb006359, 2009. a
Rosenau, M., Lohrmann, J., and Oncken, O.: Shocks in a box: An analogue model of subduction earthquake cycles with application to seismotectonic forearc evolution, J. Geophys. Res.-Sol. Ea., 114, B01409, https://doi.org/10.1029/2008jb005665, 2009. a
Rosenau, M., Pohlenz, A., Kemnitz, H., and Warsitzka, M.: Ring-shear test data of quartz sand G12 used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2019.003, 2018a. a, b
Rosenau, M., Pohlenz, A., Kemnitz, H., and Warsitzka, M.: Ring-shear test data of quartz sand G23 used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2019.004, 2018b. a
Rosenau, M., Kemnitz, H., Pohlenz, A., Warsitzka, M., and Zavada, P.: Ring-shear test data of glass beads 100–200 µm used for analogue experiments in the tectonic modelling labs at GFZ Potsdam and the Institute of Geophysics of the Czech Academy of Sciences, Prague, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2022.001, 2022. a
Rudolf, M.: RST-Stick-Slipy, GFZ Data Services [software], https://doi.org/10.5880/GFZ.4.1.2021.007, 2021. a
Rudolf, M.: Granular Healing – Python module associated to the 2022 GeoMod material benchmark, GFZ Data Services [software], https://doi.org/10.5880/fidgeo.2023.010, 2023. a
Rudolf, M. and Hecht, H.: Setup of the Ring Shear Tester for Measuring Time Dependent Healing of Granular Materials, uploaded by EPOS Multi-scale Laboratories, YouTube [video], https://youtu.be/erEXPj8xaSM (last access: 6 March 2023), 2023. a
Rudolf, M. and Warsitzka, M.: RST Evaluation – Scripts for analysing shear experiments from the Schulze RST.pc01 ring shear tester, GFZ Data Services [software], https://doi.org/10.5880/GFZ.4.1.2021.001, 2021. a
Rudolf, M., Boutelier, D., Rosenau, M., Schreurs, G., and Oncken, O.: Rheological benchmark of silicone oils used for analog modeling of short-and long-term lithospheric deformation, Tectonophysics, 684, 12–22, https://doi.org/10.1016/j.tecto.2015.11.028, 2016. a
Rudolf, M., Rosenau, M., and Oncken, O.: The spectrum of slip behaviours of a granular fault gouge analogue governed by rate and state friction, Geochem. Geophy. Geosy., 22, e2021GC009825, https://doi.org/10.1029/2021GC009825, 2021. a, b, c
Rudolf, M., Rosenau, M., Warsitzka, M., and Zavada, P.: Ring-shear test data of glass beads <50 µm used for analogue experiments in the tectonic modelling labs at GFZ Potsdam and the Institute of Geophysics of the Czech Academy of Sciences, Prague, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2022.003, 2022. a
Rudolf, M., Rosenau, M., and Oncken, O.: Slide-Hold-Slide Data of Granular Materials Used In Analogue Modelling, GFZ Data Services [data set], https://doi.org/10.5880/fidgeo.2023.009, 2023. a
Ruina, A.: Slip instability and state variable friction laws, J. Geophys. Res.-Sol. Ea., 88, 10359–10370, https://doi.org/10.1029/jb088ib12p10359, 1983. a
Santimano, T., Rosenau, M., and Oncken, O.: Intrinsic versus extrinsic variability of analogue sand-box experiments – Insights from statistical analysis of repeated accretionary sand wedge experiments, J. Struct. Geol., 75, 80–100, https://doi.org/10.1016/j.jsg.2015.03.008, 2015. a
Schmid, T., Schreurs, G., Warsitzka, M., and Rosenau, M.: Effect of sieving height on density and friction of brittle analogue material: Ring-shear test data of corundum sand used for analogue experiments in the Tectonic Modelling Lab of the University of Bern (CH), GFZ Data Services [data set], https://doi.org/10.5880/FIDGEO.2020.005, 2020a. a
Schmid, T., Schreurs, G., Warsitzka, M., and Rosenau, M.: Effect of sieving height on density and friction of brittle analogue material: Ring-shear test data of quarz sand used for analogue experiments in the Tectonic Modelling Lab of the University of Bern, GFZ Data Services [data set], https://doi.org/10.5880/FIDGEO.2020.006, 2020b. a, b
Scholz, C. H.: The mechanics of earthquakes and faulting, Cambridge University Press, 2nd Edition, ISBN 0521655404, 2002. a
Schulze, D.: Development and application of a novel ring shear tester, Aufbereitungs Technik, 35, 524–535, 1994. a, b
Schulze, D.: Powders and bulk solids, Springer, https://doi.org/10.1007/978-3-540-73768-1, 2008. a, b
Scuderi, M. M., Carpenter, B. M., and Marone, C.: Physicochemical processes of frictional healing: Effects of water on stick-slip stress drop and friction of granular fault gouge, J. Geophys. Res.-Sol. Ea., 119, 4090–4105, https://doi.org/10.1002/2013jb010641, 2014. a
Sibson, R. H.: Power dissipation and stress levels on faults in the upper crust, J. Geophys. Res.-Sol. Ea., 85, 6239–6247, https://doi.org/10.1029/JB085iB11p06239, 1980. a, b
Suh, H. S., Kim, K. Y., Lee, J., and Yun, T. S.: Quantification of bulk form and angularity of particle with correlation of shear strength and packing density in sands, Eng. Geol., 220, 256–265, https://doi.org/10.1016/j.enggeo.2017.02.015, 2017.
Tapia, F., Pouliquen, O., and Guazzelli, É.: Influence of surface roughness on the rheology of immersed and dry frictional spheres, Physical Review Fluids, 4, 104302, https://doi.org/10.1103/physrevfluids.4.104302, 2019. a
ten Grotenhuis, S. M., Piazolo, S., Pakula, T., Passchier, C. W., and Bons, P. D.: Are polymers suitable rock analogs?, Tectonophysics, 350, 35–47, https://doi.org/10.1016/s0040-1951(02)00080-x, 2002. a
Turner, J. P. and Williams, G. A.: Sedimentary basin inversion and intra-plate shortening, Earth-Sci. Rev., 65, 277–304, https://doi.org/10.1016/j.earscirev.2003.10.002, 2004. a, b
Warsitzka, M., Ge, Z., Schönebeck, J.-M., Pohlenz, A., and Kukowski, N.: Ring-shear test data of foam glass beads used for analogue experiments in the Helmholtz Laboratory for Tectonic Modelling (HelTec) at the GFZ German Research Centre for Geosciences in Potsdam and the Institute of Geosciences, Friedrich Schiller University Jena, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2019.002, 2019a. a
Warsitzka, M., Závada, P., Pohlenz, A., and Rosenau, M.: Ring-shear test data of quartz sand used for analogue experiments in the laboratory of the Institute of Geophysics of the Czech Academy of Science, Prague, GFZ Data Services [data set], https://doi.org/10.5880/GFZ.4.1.2019.008, 2019b. a
Weijermars, R.: Flow behaviour and physical chemistry of bouncing putties and related polymers in view of tectonic laboratory applications, Tectonophysics, 124, 325–358, https://doi.org/10.1016/0040-1951(86)90208-8, 1986. a
Wessels, R., ter Maat, G., Bello, E. D., Cacciola, L., Corbi, F., Festa, G., Funiciello, F., Kaviris, G., Lange, O., Lauterjung, J., Pijnenburg, R., Puglisi, G., Reitano, D., Ronnevik, C., Scarlato, P., and Spampinato, L.: Transnational Access to Research Facilities: an EPOS service to promote multi-domain Solid Earth Sciences in Europe, Ann. Geophys., 65, DM214, https://doi.org/10.4401/ag-8768, 2022. a
Willingshofer, E., Sokoutis, D., Beekman, F., Schönebeck, J.-M., Warsitzka, M., and Rosenau, M.: Ring shear test data of feldspar sand and quartz sand used in the Tectonic Laboratory (TecLab) at Utrecht University for experimental Earth Science applications, GFZ Data Services [data set], https://doi.org/10.5880/FIDGEO.2018.072, 2018. a, b
Yagupsky, D. L., Cristallini, E. O., Fantín, J., Valcarce, G. Z., Bottesi, G., and Varadé, R.: Oblique half-graben inversion of the Mesozoic Neuquén Rift in the Malargüe Fold and Thrust Belt, Mendoza, Argentina: New insights from analogue models, J. Struct. Geol., 30, 839–853, https://doi.org/10.1016/j.jsg.2008.03.007, 2008. a, b
Yasuhara, H., Marone, C., and Elsworth, D.: Fault zone restrengthening and frictional healing: The role of pressure solution, J. Geophys. Res.-Sol. Ea., 110, B06310, https://doi.org/10.1029/2004JB003327, 2005. a
Zwaan, F., Schreurs, G., Gentzmann, R., Warsitzka, M., and Rosenau, M.: Ring-shear test data of quartz sand from the Tectonic Modelling Lab of the University of Bern (CH), GFZ Data Services [data set], https://doi.org/10.5880/FIDGEO.2018.028, 2018. a, b
Zwaan, F., Schreurs, G., Rudolf, M., and Rosenau, M.: Ring-shear test data of feldspar sand FS900S used in the Tectonic Modelling Laboratory at the University of Bern (Switzerland), GFZ Data Services [data set], https://doi.org/10.5880/FIDGEO.2022.008, 2022. a