Importance of forearc topography for the triggering of aftershocks of megathrust earthquakes: insights from mechanical models and the Tohoku-Oki and Maule earthquakes

Aftershocks of megathrust earthquakes at subduction zones may be driven by stresses arising from the topography of the forearc. However, the effect of topographic stresses on aftershock triggering is quantitatively not well understood and has been neglected in Coulomb failure stress models that assess whether the stress change caused by an earthquake promotes or inhibits failure on nearby faults. Here we use analytical and numerical models to examine the importance of topographic stresses on Coulomb failure stress changes caused by megathrust earthquakes. We show that topographic stresses are a prerequisite for widespread aftershock seismicity in the forearc and that their superposition with tectonic stresses leads to a dependence of the forearc stability on the stress state before and after the earthquake. The dependence can be taken into account by determining the Coulomb failure stress change between optimal failure planes before and after the earthquake, which requires constraining the total stresses in the forearc. Applying our modelling approach to the 2011 M_w 9.0 Tohoku-Oki and 2010 M_w 8.8 Maule megathrust earthquakes yields coseismic Coulomb failure stress changes of up to ∼40 MPa, which promoted the majority of aftershocks in the Japanese and Chilean forearcs. The model results further reveal that the spatial distribution of aftershocks was not only influenced by the megathrust stress drop and the proximity of faults to failure but also by local differences in forearc topography and pre-earthquake stress state. Our analysis highlights the significance of total stresses in Coulomb failure stress calculations, enabling a better estimation of seismic hazard at subduction zones.

1 Introduction

The concept of Coulomb failure stress change (ΔCFS) finds broad application to investigate earthquake-induced stress changes and the triggering of aftershocks in various tectonic settings, including continental interiors and active margins (e.g. Bagge et al., 2018; Farías et al., 2011; King et al., 1994; Lin and Stein, 2004; Oppenheimer et al., 1988; Pace et al., 2014; Ryder et al., 2012; Saltogianni et al., 2021; Stein, 1999; Terakawa et al., 2013; Toda et al., 2011a). The Coulomb failure stress change describes the relative change in shear and normal stresses imparted by an earthquake on nearby faults and indicates whether it promotes (positive ΔCFS) or inhibits (negative ΔCFS) failure (e.g. King et al., 1994; Harris, 1998).

Over the past decades, the development of Coulomb failure stress (CFS) models addressed various factors, including the effects of the tectonic regime and regional stress field on Coulomb failure stress changes, as well as the mechanisms influencing stress changes in the post-seismic and interseismic periods, such as viscoelastic relaxation, poroelasticity, and pore pressure changes (e.g. Bagge and Hampel, 2016, 2017; Cocco and Rice, 2002; Freed and Lin, 1998; Hainzl, 2004; Hardebeck, 2014; Hardebeck et al., 1998; Peikert et al., 2024; Peña et al., 2022; Segou and Parsons, 2020). One aspect that has found no consideration in Coulomb failure stress models is the dependence of the regional stress field on topographic and tectonic stresses. It is the purpose of the present paper to show how the superposition of topographic and tectonic stresses at active margins influences the Coulomb failure stress change caused by megathrust earthquakes in the forearc.

Topographic stresses result from the gradient in potential energy that arises in the gravitational field of the Earth between areas of lower and higher elevation (e.g. Molnar and Lyon-Caen, 1988). Topographic stresses are particularly relevant at active continental margins, where the gradient in potential energy imposed by the continental margin relief (i.e. the difference in elevation between the oceanic trench and the mountains and volcanoes in the upper plate) induces margin-normal tension in the forearc (e.g. Lamb, 2006; Wang and He, 1999). The margin-normal tension is counteracted by the shear stress on the megathrust, which causes margin-normal compression (Fig. 1a). To a first approximation, the superposition of margin-normal tension and margin-normal compression determines the stress field in the forearc. During subduction earthquakes, the shear stress on the megathrust decreases, which reduces the compression of the forearc and alters the superposition of stresses (e.g. Dielforder et al., 2023, 2020; Herman and Govers, 2020; Wang et al., 2019; Wang and Hu, 2006).

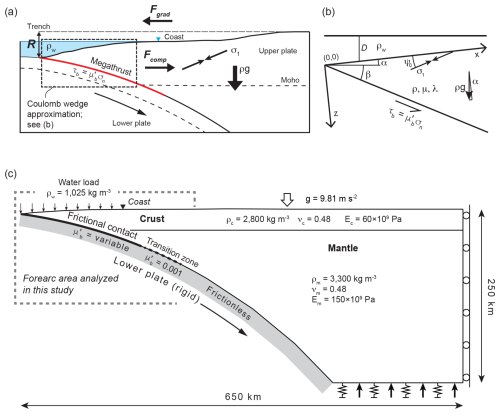
Figure 1 Conceptual and mechanical models discussed in this study. (a) Main forces determining the stress state in a forearc. Here, ρ is the rock density, ρ_w is the seawater density, g is the gravitational acceleration, σ₁ is the greatest compressive stress, ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is the effective coefficient of megathrust friction, and τ_b and σ_n are the shear and normal stresses on the megathrust. The continental margin relief, R, imposes a gradient in potential energy that is proportional to the density contrasts between the forearc, seawater, and air, and it stretches the forearc seawards (force F_grad). The force F_grad is counteracted by the shear stress on the megathrust, which compresses the upper plate (force F_comp). (b) The Coulomb wedge model discussed in Sect. 2 showing the local coordinate system (x,z). Here, D is the water depth; μ is the coefficient of friction of the wedge material; ψ₀ is the angle between the axis of σ₁ and the wedge surface; and λ is the pore fluid pressure ratio within the wedge, defined by Eq. (1). (c) Setup and boundary conditions of the finite-element model discussed in Sect. 3. Here, ν is Poisson's ratio, and E is Young's modulus. Indices c, m, and w indicate crust, mantle, and water, respectively.

The decrease in megathrust shear stress (stress drop) and resulting stress changes may trigger aftershock seismicity in the forearc, as indicated by upper-plate normal-faulting sequences after large megathrust earthquakes (e.g. Asano et al., 2011; Dewey et al., 2007; Farías et al., 2011; Hardebeck, 2012, Hasegawa et al., 2012; Ryder et al., 2012; Yoshida et al., 2012). Normal faulting after the 2011 M_w 9.0 Tohoku-Oki earthquake, Japan, occurred in forearc areas that failed by thrust faulting before the earthquake (e.g. Hasegawa et al., 2012; Yoshida et al., 2012). The change in fault kinematics indicates that the Tohoku-Oki earthquake locally reversed the stress state in the forearc, which has been mechanically explained by the stress changes resulting from the stress drop on the megathrust (e.g. Cubas et al., 2013; Dielforder et al., 2023; Wang et al., 2019).

The details of stress changes caused by megathrust earthquakes and their potential to trigger aftershocks are, however, still not fully understood. In particular, assessing total stresses and stress changes at subduction zones requires accounting for the superposition of topographic and tectonic stresses and hence including gravity, forearc topography, and megathrust shear stresses in models. The parameters are not included in common Coulomb failure stress models based on dislocation solutions for a fault embedded in an elastic half-space (e.g. King et al., 1994; Lin and Stein, 2004). Therefore, in this study, we use mechanical models that allow the calculation of total stresses in consideration of gravity, forearc topography, and megathrust shear stress. We firstly use analytical stress solutions of the dynamic Coulomb wedge theory (Wang and Hu, 2006) to describe the main effects of topographic and tectonic stresses on Coulomb failure stress changes in a uniform subduction zone prism representing the frontal part of a forearc (Fig. 1b). We then use plane-strain finite-element models (Fig. 1c) to investigate Coulomb failure stress changes caused by the 2011 M_w 9.0 Tohoku-Oki and the 2010 M_w 8.8 Maule earthquakes in the Japanese and Chilean forearcs, respectively. The finite-element models allow us to investigate the stress changes in consideration of a more complex upper-plate structure and earthquake stress change.

Our analysis uses a two-dimensional (2D) simplification of a three-dimensional system; i.e. we investigate stresses in the vertical plane of cross-section normal to the plate margin and do not address aspects of oblique plate convergence. We further assume in the finite-element models a linear elastic rheology for the forearc and restrict our analysis to the immediate coseismic stress change induced by the earthquake. In the following, we use the rock mechanics convention of defining compressive stresses as positive.

2 Coulomb failure stress changes in an idealized Coulomb wedge

2.1 Application and implications of the dynamic Coulomb wedge theory

The dynamic Coulomb wedge theory describes the first-order mechanics of subduction zone prisms in megathrust earthquake cycles by considering temporal variations in megathrust shear stress (Wang and Hu, 2006). The theory builds on the classical critical taper model (Dahlen, 1984; Zhao et al., 1986) and approximates the outermost part of the forearc as a uniform wedge of density ρ overlying the megathrust (Fig. 1b). The wedge geometry is defined by the surface slope angle α and the basal dip angle β. The wedge has an elastic-perfectly Coulomb plastic rheology; i.e. it can be in a stable elastic state and in critical state at Coulomb failure. The Coulomb plastic rheology is defined by the coefficient of friction μ and the pore fluid pressure ratio

$$\begin{array}{}\text{(1)}& \mathit{\lambda }=(P-{\mathit{\rho }}_{\mathrm{w}}gD)/({\mathit{\sigma }}_z-{\mathit{\rho }}_{\mathrm{w}}gD),\end{array}$$

where P is pore fluid pressure within the wedge, ρ_w is water density, D is water depth, σ_z is stress in z direction (see Fig. 1b for local coordinates), and g is gravitational acceleration (Dahlen, 1984; Wang and Hu, 2006). The megathrust shear stress can be written in terms of effective normal stress ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\mathrm{n}}={\mathit{\sigma }}_{\mathrm{n}}(\mathrm{1}-\mathit{\lambda })$ as

$$\begin{array}{}\text{(2)}& {\mathit{\tau }}_{\mathrm{b}}={\displaystyle \frac{{\mathit{\mu }}_{\mathrm{b}}^{\prime }{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\mathrm{n}}}{(\mathrm{1}-\mathit{\lambda })}}={\mathit{\mu }}_{\mathrm{b}}^{\prime }{\mathit{\sigma }}_{\mathrm{n}},\end{array}$$

where ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is the effective coefficient of megathrust friction and depends on both the intrinsic friction coefficient μ_b and the effect of pore fluid pressure ratio λ_b in the fault zone, i.e. ${\mathit{\mu }}_{\mathrm{b}}^{\prime }={\mathit{\mu }}_{\mathrm{b}}(\mathrm{1}-{\mathit{\lambda }}_{\mathrm{b}})$. For this study, it suffices to consider only values of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ without defining μ_b and λ_b separately. Note that parameter ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ was termed ${\mathit{\mu }}_{\mathrm{b}}^{\prime \prime }$ in Wang and Hu (2006) and that Dahlen (1984) and Wang and Hu (2006) used the term “effective coefficient of friction” to refer to parameter ${\mathit{\mu }}_{\mathrm{b}}^{\prime }/(\mathrm{1}-\mathit{\lambda })$ instead of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ as is common in Earth science (cf. Hu and Wang, 2008; Wang et al., 2019).

The pore fluid pressure ratio in the wedge and the effective coefficient of megathrust friction determine the mechanical state of an elastic-perfectly Coulomb plastic wedge as qualitatively illustrated in Fig. 2a. The wedge may be in a critical state and fail by thrust faulting and normal faulting if ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is sufficiently high and low, respectively. For intermediate values of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$, the wedge may be in a stable state, where the range of stability decreases with increasing λ. The stable state can be further distinguished into a compressively stable state in which the wedge experiences deviatoric compression, a neutrally stable state (dashed horizontal line in Fig. 2a), and an extensionally stable state in which the wedge experiences deviatoric tension. The possible mechanical states are illustrated in Fig. 2c. Note that, for high values of λ and low values of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$, the wedge may attain a critical state at which both thrust faulting and normal faulting can occur (dashed part of the failure envelope in Fig. 2a).

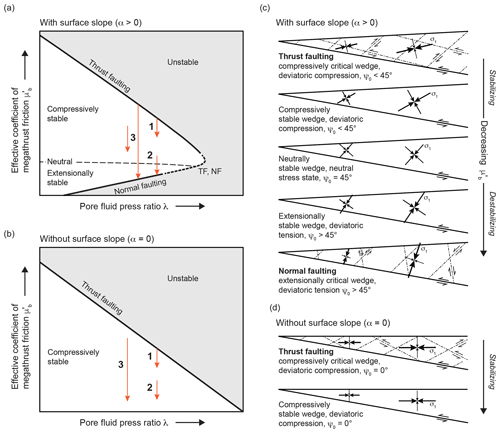
Figure 2 Mechanical states of an elastic-perfectly Coulomb plastic wedge. (a, c) Mechanical states for surface slope angle α>0; (b, d) mechanical states for α=0. (a, b) Wedge stability as controlled by megathrust friction ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ and pore fluid pressure ratio λ in the wedge. The white area indicates the range of λ–${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ pairs, for which the wedge is compressively, neutrally, or extensionally stable. The thick black line indicates the critical states that promote thrust faulting (TF) or normal faulting (NF). The thick dashed part of the critical-state line indicates the range of λ–${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ pairs that allow TF and NF. The orange arrows indicate exemplary changes in the mechanical state of the wedge due to a megathrust earthquake modelled by a decrease in ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$. (c, d) Different mechanical states of an elastic-perfectly Coulomb plastic wedge. For critical states, dashed–dotted lines are potential failure planes (at optimal orientation to σ₁) with sense of shear indicated. Angle ψ_o is the plunge of σ₁ (Fig. 1b). Note that a stress drop tends to stabilize the wedge if the state changes from a compressively stable/critical state toward neutral and tends to destabilize the wedge if the state changes from toward extensionally stable/critical.

The λ–${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ space allows us to investigate the mechanical states a wedge may achieve at different stages of an earthquake cycle (Wang and Hu, 2006). Over the interseismic period, the shear stress on the seismogenic megathrust increases progressively such that the maximum compression of the wedge occurs toward the end of the earthquake cycle. During megathrust earthquakes, the shear stress on the plate interface decreases abruptly due to coseismic weakening processes (e.g. Kanamori and Brodsky, 2004; Scholz, 1998; Wang and Hu, 2006). The average stress drop on the megathrust can be modelled as a change in the effective coefficient of megathrust friction $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }={\mathit{\mu }}_{\text{b-pre}}^{\prime }-{\mathit{\mu }}_{\text{b-post}}^{\prime }$, where ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ and ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ are the ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values that describe the megathrust shear stress just before and after the earthquake, respectively (Wang and Hu, 2006).

The effect of the stress drop on the mechanical stability of the wedge is illustrated for different scenarios in the λ–${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ space (Fig. 2a) by orange arrows. In the first scenario (1 in Fig. 2a), the wedge is in a compressively critical state and fails by thrust faulting before the earthquake, and it is in a compressively stable state after the earthquake. The stress drop on the megathrust stabilizes the wedge. In the second scenario, the stress drop pushes the wedge from a compressively stable state into an extensionally critical state, causing normal faulting. The stress drop destabilizes the wedge, although the relative change in ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is the same as in scenario 1: only the value of ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ differs. Scenario 3 shows a stress drop that has no effect on the wedge stability. The large stress drop (larger arrow) pushes the wedge from a compressively critical state into an extensionally critical state. The wedge is just as close to failure after the earthquake as it was before the earthquake. The same applies for the smaller stress drop, with the only difference being that the wedge is compressively stable before and after the earthquake and not critical.

The above scenarios only apply if the surface slope angle α>0; i.e. the described effect of the stress drop on the wedge stability depends on topographic stresses resulting from the gradient in potential energy. When α=0, there is no gradient in potential energy, and the Coulomb wedge can only attain a compressively critical state and fail by thrust faulting or a compressively stable state. In that case, the megathrust stress drop always stabilizes the wedge (scenarios 1–3 in Fig. 2c and d)

2.2 Total stress and Coulomb failure stress changes in a Coulomb wedge

The tendency of a megathrust stress drop to stabilize or destabilize the Coulomb wedge does not depend on whether or not the wedge attains a critical state and can be described in terms of Coulomb failure stresses without determining λ. For this, we start by considering the total stresses in a Coulomb wedge. The analysis is based on the analytical expressions of the dynamic Coulomb wedge theory summarized in Appendix A.

Figure 3a illustrates the stress in a Coulomb wedge as a function of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ in terms of stresses σ_x and σ_z. The stress solutions are obtained for a non-cohesive, stable reference wedge model with α=3°, β=10°, μ=0.7, and λ=0. The dependence of stress on ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is the same everywhere in the uniform wedge (Dahlen, 1984; Wang and Hu, 2006) and is described in terms of normalized stress values. To allow an estimation of total stresses, we provide stress values at 10 km depth in the wedge on the secondary ordinate (right vertical axis) in Fig. 3a.

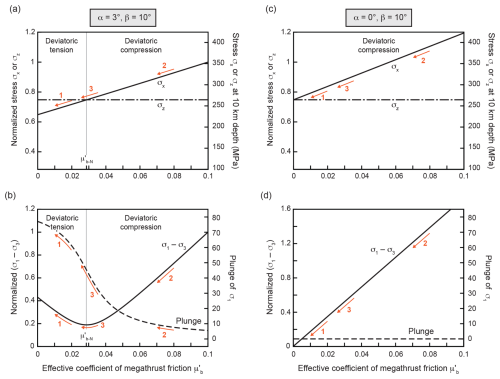
Figure 3 Analytical stress solutions for a stable dynamic Coulomb wedge. (a, b) Solutions for the reference wedge model discussed in the text. (a) Superposition of stresses σ_x and σ_z as a function of the effective coefficient of megathrust friction ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$. Parameter ${\mathit{\mu }}_{\text{b-N}}^{\prime }$ denotes the ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ value, for which the stress state is neutral (σ_x=σ_z). The left ordinate shows stress values normalized to the maximum value of σ_x. The right ordinate shows total stresses at 10 km depth. (b) Differential stress (σ₁−σ₃) and plunge of σ₁ as a function of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$. The differential stress is normalized to the maximum value of (σ₁−σ₃). (c, d) Similar to panels (a) and (b) but for α=0. Orange arrows indicate stress changes discussed in Sect. 2.2.

For low values of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$, σ_x is smaller than σ_z and the wedge is under deviatoric tension (Fig. 3a). The stress state results from the margin-normal tension induced by the topographic relief, which reduces σ_x relative to σ_z. The magnitude of σ_z results from the weight of the overburden. Increasing ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ increases the margin-normal compression and decreases the difference between σ_x and σ_z until both stresses are equal. At that point, the compression caused by the megathrust shear stress equals the tension induced by the topographic relief and the wedge is in a neutral state. The value of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ at the neutral stress state is denoted ${\mathit{\mu }}_{\text{b-N}}^{\prime }$ (dashed horizontal line in Fig. 2a) (Wang and Hu, 2006). If ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is larger than ${\mathit{\mu }}_{\text{b-N}}^{\prime }$, σ_x is larger than σ_z and the wedge is under deviatoric compression (Fig. 3a).

Figure 3b illustrates the same stress dependence in terms of differential stress (σ₁−σ₃), where σ₁ and σ₃ are the greatest and least compressive principal stresses, respectively. The differential stress is a convex function of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ and is minimal if the stress state is neutral, i.e. if ${\mathit{\mu }}_{\mathrm{b}}^{\prime }={\mathit{\mu }}_{\text{b-N}}^{\prime }$. The second ordinate in Fig. 3b shows the plunge of stress axis σ₁. The plunge decreases with increasing ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ from ∼78 to ∼6° and is 45° at the neutral stress state.

The dependence of the stress on ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ is similar for every wedge geometry, but the value of ${\mathit{\mu }}_{\text{b-N}}^{\prime }$ decreases with the surface slope angle α (Fig. S1 in the Supplement). In the absence of surface slope (α=0), the wedge experiences no deviatoric tension and is always under deviatoric compression (Fig. 3c and d). The stress within the wedge also depends on the basal dip angle but to a lesser extent than on the surface slope angle (Fig. S1).

The stress drop in a megathrust earthquake reduces the horizontal compression of the wedge; i.e. it decreases the stress σ_x (orange arrows in Fig. 3a). In the presence of surface slope, the corresponding change in differential stress varies with the effective coefficient of megathrust friction before the earthquake. The dependence is illustrated by orange arrows in Fig. 3b for a stress drop of $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }=\mathrm{0.01}$. The $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ value of 0.01 corresponds to an average stress drop of ∼5 MPa at 10–30 km depth, which is compatible with estimates of rupture-zone-averaged stress drops of <10 MPa (e.g. Allmann and Shearer, 2009; Brown et al., 2015; Lee et al., 2011; Luttrell et al., 2011; Kubota et al., 2022; Wang et al., 2020). When ${\mathit{\mu }}_{\text{b-pre}}^{\prime }\le {\mathit{\mu }}_{\text{b-N}}^{\prime }$, the wedge is under deviatoric tension before and after the earthquake and the stress drop on the megathrust increases the differential stress because the difference between σ_x and σ_z increases (arrow 1 in Fig. 3a and b). When ${\mathit{\mu }}_{\text{b-pre}}^{\prime }\gg {\mathit{\mu }}_{\text{b-N}}^{\prime }$, the wedge is under deviatoric compression before and after the earthquake and stress drop decreases the differential stress because σ_x converges to σ_z (arrow 2 in Fig. 3a and b). When ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ is only slightly larger than ${\mathit{\mu }}_{\text{b-N}}^{\prime }$, the megathrust stress drop may increase or decrease the differential stress within the wedge, while the stress state may switch from deviatoric compression to deviatoric tension (arrow 3 in Fig. 3a and b). In the absence of surface slope, ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ is always greater than ${\mathit{\mu }}_{\text{b-N}}^{\prime }$ and the stress drop always decreases the differential stress in the wedge (Fig. 3c and d).

The stress change caused by the megathrust stress drop can be expressed in terms of Coulomb failure stress change to indicate whether it promotes or inhibits failure on faults within the wedge. The Coulomb failure stress on a fault plane is defined as

$$\begin{array}{}\text{(3)}& \text{CFS}=\left|\mathit{\tau }\right|-\mathit{\mu }{\mathit{\sigma }}_{\mathrm{n}}\end{array}$$

(e.g. Reasenberg and Simpson, 1992). The shear stress and normal stress on the fault plane are given by

$$\begin{array}{}\text{(4a)}& {\displaystyle }\mathit{\tau }=\mathrm{0.5}({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})\sin \mathrm{2}\mathit{\omega },\text{(4b)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{n}}=\mathrm{0.5}({\mathit{\sigma }}_{\mathrm{1}}+{\mathit{\sigma }}_{\mathrm{3}})-\mathrm{0.5}({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})\cos \mathrm{2}\mathit{\omega },\end{array}$$

where ω is the angle from the fault plane to the axis of σ₁. Note that the CFS considers the magnitude of the shear stress $\left|\mathit{\tau }\right|$, while the shear stress on a fault may be positive or negative depending on its sense of shear (e.g. King et al., 1994; Reasenberg and Simpson, 1992). In most studies, the Coulomb failure stress change is determined on faults of specified orientation, for example, on faults known from field observations, on the nodal planes of focal mechanism solutions, or on generic faults (e.g. Farias et al., 2011; Ishibe et al., 2017; Jara-Muñoz et al., 2022; Nakamura et al., 2016; Toda et al., 2011a, b). The change in Coulomb failure stress is then defined as

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }{\text{CFS}}_{\text{sf}}=\mathrm{\Delta }\mathit{\tau }-\mathit{\mu }\mathrm{\Delta }{\mathit{\sigma }}_{\mathrm{n}},\end{array}$$

where Δτ is the change in shear stress (positive if slip in the direction of mainshock is promoted) and Δσ_n is the change in normal stress (positive for increased compression) on the fault (e.g. Oppenheimer et al., 1988; Reasenberg and Simpson, 1992). The subscript “sf” stands for specified fault.

Figure 4a shows the Coulomb failure stress change resolved on a normal fault dipping at 60° toward the tip of the wedge for the reference wedge model and for $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }=\mathrm{0.01}$. The ΔCFS_sf value is always positive on the normal fault, irrespective of the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ value. In the absence of surface slope (α=0), the Coulomb failure stress change is larger, but the trend is similar. Note that the ΔCFS_sf values show a weak dependence on ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ because σ_x depends on the factor ${\mathit{\mu }}_{\mathrm{b}}^{\prime }/(\mathrm{1}-{\mathit{\mu }}_{\mathrm{b}}^{\prime })$ in a dynamic Coulomb wedge (Appendix A).

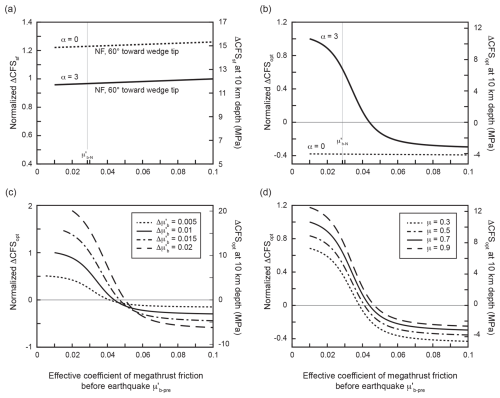
Figure 4 Coulomb failure stress change as function of effective coefficient of megathrust friction before the earthquake, ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$, and for a change in megathrust friction of $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }=\mathrm{0.01}$. Solid lines indicate solutions for the reference wedge model discussed in the text. Dashed and dotted lines indicate solutions for adjusted model parameters. (a) Coulomb failure stress change on a normal fault (NF) dipping at 60° toward the wedge tip. (b) Difference in Coulomb failure stress on optimal failure planes before and after the earthquake, ΔCFS_opt. (c, d) Dependence of ΔCFS_opt on $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ and coefficient of friction μ. Left ordinates show ΔCFS values normalized to the maximum ΔCFS value obtained for the reference wedge model. Right ordinates indicate ΔCFS values at 10 km depth. All ΔCFS values in panels (a–c) are calculated for μ=0.7.

The ΔCFS_sf values, although mathematically correct, do not reflect that a stress drop can be stabilizing or destabilizing depending on the mechanical state of the wedge (Fig. 2a) because it only depends on the relative change in σ_x. The sign of the ΔCFS_sf value may be correct when the investigated type of faulting agrees with the mechanical state of the wedge, but the values may be misleading when the investigated type of faulting and mechanical state do not agree. For example, normal faulting is not promoted when the wedge is under deviatoric compression, and the fault plane, if activated, would fail as a steep backthrust but not as a normal fault.

To take the mechanical state of the wedge into account, we determine the Coulomb failure stress change between the potential failure planes with an optimal orientation to σ₁ before the earthquake and after the earthquake. The Coulomb failure stress change can then be defined as

$$\begin{array}{}\text{(6)}& \mathrm{\Delta }{\text{CFS}}_{\text{opt}}=\mathrm{\Delta }\left|\mathit{\tau }\right|-\mathit{\mu }\mathrm{\Delta }{\mathit{\sigma }}_{\mathrm{n}}.\end{array}$$

The shear and normal stresses on the optimal failure planes are given by solving Eq. (4) for ${\mathit{\omega }}_{\text{opt}}=\mathrm{0.5}{\tan }^{-\mathrm{1}}(\mathrm{1}/\mathit{\mu })$ (e.g. Sibson, 1998). Our determination of the Coulomb failure stress change builds on the calculations of King et al. (1994) for optimally oriented faults, with the main difference being that we account for the change in the plunge in σ₁ by distinguishing between optimal failure planes after the earthquake and before the earthquake. The ΔCFS_opt values therefore reflect the same tendency as a change in ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ in the λ–${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ space (Fig. 2a).

Figure 4b illustrates the Coulomb failure stress change between optimal failure planes for the same setting as in Fig. 4a. The Coulomb failure stress change decreases with increasing ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$, with its magnitude and sign being mainly controlled by the stress state in the wedge. The Coulomb failure stress change is positive if the wedge is under deviatoric tension before and after the earthquake (i.e. if ${\mathit{\mu }}_{\text{b-pre}}^{\prime }\le {\mathit{\mu }}_{\text{b-N}}^{\prime }$), in which case the decrease in σ_x and the increase in (σ₁−σ₃) promote normal faulting. Conversely, the Coulomb failure stress change is negative if the wedge is under deviatoric compression before and after the earthquake (i.e. if ${\mathit{\mu }}_{\text{b-pre}}^{\prime }\gg {\mathit{\mu }}_{\text{b-N}}^{\prime }$), in which case the decreases in σ_x and (σ₁−σ₃) inhibit thrust faulting. Note that ΔCFS_opt can be positive if ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ is only slightly larger than ${\mathit{\mu }}_{\text{b-N}}^{\prime }$. In that case, the plunge in σ₁ is close to 45° after the earthquake, and the Coulomb failure stress change promotes thrust faulting on one of the failure planes (the steeper one) and normal faulting on the other (see also Fig. 2a). In the absence of surface slope (α=0), ΔCFS is always negative because the wedge cannot attain a state of deviatoric tension and normal faulting is never promoted (Figs. 2b and 4b). The Coulomb failure stress change further increases with the magnitude of the stress drop (Fig. 4c) and with the coefficient of friction μ (Fig. 4d).

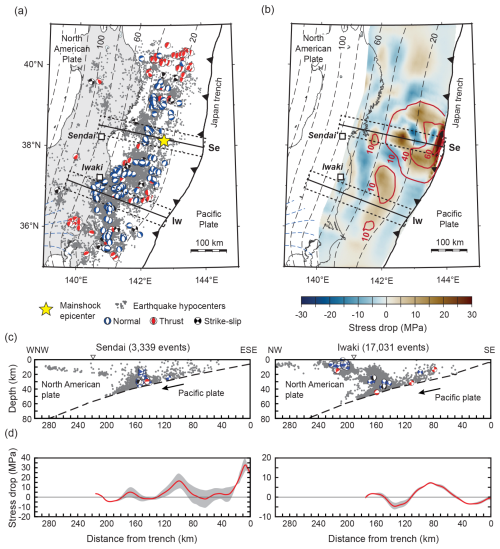
Figure 5 Seismotectonic setting of northeastern Japan. (a) Seismicity in the upper (North American) plate after the 2011 M_w 9.0 Tohoku-Oki earthquake (yellow star). Grey dots are aftershock hypocentres from the Japan Meteorological Agency (JMA). All events have a magnitude ≥ magnitude of completeness of 1.5 (determined with the maximum curvature method of Wiemer and Katsumata, 1999). Beach balls denote JMA focal mechanism solutions. (b) Earthquake slip contours in metres (pink lines and numbers) and coseismic megathrust stress drop (blue to red colour bar signal). Slip contours and stress drop from Iinuma et al. (2012) and Brown et al. (2015), respectively. (a, b) Black lines indicate the locations of cross-sections shown in panels (c) and (d). Dashed rectangles indicate the width of swaths (50 km) used to evaluate the seismicity distribution and fault kinematics (c) and the average stress drop on the megathrust (d) along the Sendai (Se) and Iwaki (Iw) cross-sections.

It should be noted that Fig. 4 illustrates the Coulomb failure stress changes due to a “positive” stress drop on the megathrust, i.e. a decrease in megathrust shear stress. A negative stress drop, i.e. an increase in megathrust shear stress, has the opposite effect on the total stresses in the wedge and the corresponding Coulomb failure stress changes (see Fig. S2 in the Supplement). An increase in megathrust shear stress tends to inhibit normal faulting if the wedge is under deviatoric tension and tends to promote thrust faulting if the wedge is under deviatoric compression. In nature, negative stress drops contribute to arresting the earthquake rupture and may occur downdip and updip of the main rupture area or along velocity-strengthening patches enclosed in the main rupture area (e.g. Bilek and Lay, 2002; Brown et al., 2015; Luttrell et al., 2011; Wang and Hu, 2006; Wang et al., 2020).

3 Assessment of Coulomb failure stress changes caused by the Tohoku-Oki and Maule megathrust earthquakes

We showed in Sect. 2 that the tendency of a megathrust earthquake to promote or inhibit failure in the wedge depends on the mechanical state of the wedge. Failure is promoted if the wedge is close to a neutral state or under deviatoric tension after the earthquake. Whether the earthquake results in such a stress state depends on the magnitude of the stress drop and on the stress state before the earthquake and requires the presence of topographic relief. The mechanical state, the megathrust stress drop, and the forearc topography all vary along strike and across the plate margin. The Coulomb failure stress change therefore differs with the location in the forearc, which needs to be taken into account when assessing ΔCFS_opt for megathrust earthquakes.

In the following, we determine the Coulomb failure stress changes caused by the 2011 M_w 9.0 Tohoku-Oki earthquake, Japan, and the 2010 M_w 8.8 Maule earthquake, Chile, using plane-strain finite-element models of force balance. The models consider the interaction of topographic and tectonic stresses, such as the Coulomb wedge model, but allow us to take into account spatial variability in stress state, stress drop, and topography across the plate margin. We construct for each megathrust earthquake individual finite-element models for two sections across the forearc. The cross-sections are oriented perpendicular to the plate margin and cover the area of the megathrust earthquake hypocentre and the area of most intense aftershock seismicity in the forearc (Sendai and Iwaki cross-sections in Fig. 5; and Pichilemu and Concepción cross-sections in Fig. 6).

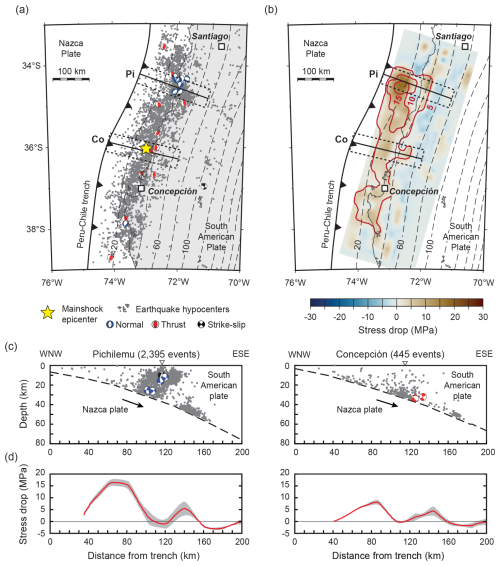
Figure 6 Seismotectonic setting of southern central Chile. (a) Seismicity in the upper (South American) plate after the 2010 M_w 8.8 Maule earthquake (yellow star). Grey dots are aftershock hypocentres from Lange et al. (2012). All events have a magnitude ≥ magnitude of completeness of 2.0 (determined with the maximum curvature method of Wiemer and Katsumata, 1999). Beach balls denote focal mechanism solutions from Şen et al. (2015). (b) Earthquake slip contours in metres (pink lines and numbers) and coseismic megathrust stress drop (blue to red colour bar signal). Slip contours and stress drop from Luttrell et al. (2011). (a, b) Black lines indicate the locations of cross-sections shown in panels (c) and (d). Dashed rectangles indicate the width of swaths (50 km) used to evaluate the seismicity distribution and fault kinematics (c) and the average stress drop on the megathrust (d) along the Pichilemu (Pi) and Concepción (Co) cross-sections.

3.1 Model setup

The finite-element models are based on the modelling approaches of Wang et al. (2019) and Dielforder et al. (2023) and yield the total stresses in a forearc resulting from gravity, forearc topography, and the shear stress on the megathrust (Fig. 1c). The models are created with the commercial finite-element software ABAQUS (version 2018) and comprise a rigid lower plate in frictional contact with an elastic upper plate that is subdivided into continental crust and mantle. Following previous studies (Dielforder et al., 2023; Dielforder and Hampel, 2021; Wang et al., 2019; Wang and He, 1999), we adopt a nearly incompressible material for the upper plate (Poisson's ratio ν=0.48) and densities of 1025, 2800, and 3300 kg m⁻³ for water, crust, and mantle, respectively. We note that using a different Poisson's ratio (e.g. ν=0.3) makes little difference to the model results (cf. Dielforder and Hampel, 2021). The Young's moduli for crust and mantle are 60 and 150 GPa, respectively. A lithostatic pressure and an elastic foundation are applied to the bottom of the model to implement isostasy (arrows and springs in Fig. 1c). The right-hand side of the model (back side of the upper plate) is free to move vertically but is fixed in the horizontal direction. All models are meshed with linear tetrahedral elements with an average element edge length of ∼1 km. The margin topography is approximated by the mean elevation, which we calculate from the ETOPO1 global relief model using TopoToolbox for MATLAB (Amante and Eakins, 2009; Schwanghart and Scherler, 2014). The slab geometry is approximated by fitting an arc with constant curvature through the upper 80 km of the Slab2 model (Hayes et al., 2018).

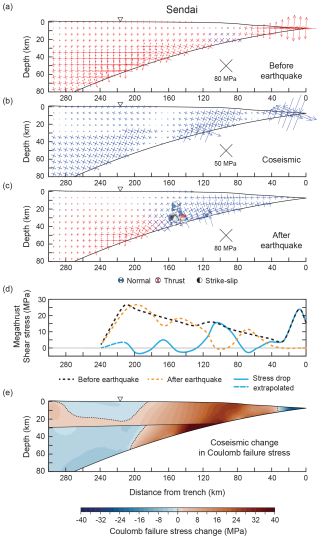
Figure 7 Preferred model of forearc stress change due to the Tohoku-Oki earthquake along the Sendai cross-section. See Fig. 5a for the location of the cross-section. Red and blue stress crosses in panels (a)–(c) indicate that the plunge in σ₁ is less than 40° (deviatoric compression) and more than 50° (deviatoric tension), respectively; purple crosses indicate a plunge in σ₁ between 40 and 50°. The size of the stress crosses scales with the differential stress. (a) Deviatoric stress before the earthquake. (b) Incremental change in deviatoric stress caused by the earthquake. (c) Deviatoric stress after the earthquake. Beach balls indicate focal mechanism solutions of aftershocks (cf. Fig. 5). (d) Modelled megathrust shear stress before (black) and after (orange) the earthquake and the megathrust stress drop (blue). (e) Coseismic change in Coulomb failure stress calculated for μ=0.7.

The megathrust is implemented as a frictional contact between the upper and lower plates and extends from the trench down to a depth of 60 km. The shear stress on the megathrust obeys the friction law for a cohesionless fault and is generated by displacing the lower plate in downdip direction tangential to the plate interface. The displacement ensures that the entire plate interface is at a state of failure (cf. Wang and He, 1999). The stress and strain in the upper plate are independent of the total displacement of the lower plate. The coefficient of megathrust friction can vary along the megathrust, which allows a detailed control on stress magnitudes. In nature, the megathrust transitions into a viscous shear zone downdip of the seismogenic zone, with the shear stress decreasing towards zero with depth (Lamb, 2006; Wada and Wang, 2009). We implement the transition zone in the models as frictional contact between the downdip limit of the megathrust and 80 km depth (cf. Dielforder and Hampel, 2021). The ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ value of the transition zone is set to 0.001, which results in a low shear stress of 2–3 MPa. Below a depth of 80 km, the contact between the lower and upper plates is frictionless; i.e. the shear stress on the contact is zero.

Each model run includes three analysis steps. In the first step, a lithostatic pre-stress is assigned, gravity is applied, and isostatic equilibrium is established. The pre-stress facilitates the computation of the total stresses resulting from the boundary conditions. The second and third analysis steps are used to calculate the total stresses in the forearc just before and after the earthquake, similarly to the pre-earthquake and post-earthquake steps in the dynamic Coulomb wedge model. In the second analysis step, the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values are assigned to the megathrust and the lower plate is displaced. At that stage, ABAQUS yields the total stresses in the upper plate for the pre-earthquake configuration. In the third analysis step, the ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ values are assigned to the megathrust, the lower plate is displaced, and ABAQUS yields the total stresses in the upper plate for the post-earthquake configuration.

3.2 Estimation of forearc stress states and megathrust stress drop

The calculation of ΔCFS_opt requires an estimation of the forearc stress state before and after the earthquake. If the megathrust stress drop is given, one of the stress states can be estimated from the other. Here, we estimate the stress states using the following procedure (cf. Wang et al., 2019). We first calculate the mean stress drop along the cross-sections using published stress-drop models and determine the corresponding $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values. For the Tohoku-Oki earthquake, we use the stress-drop model of Brown et al. (2015) for the coseismic-slip model of Iinuma et al. (2012) (Fig. 5b and d). For the Maule earthquake, we use the stress-drop model of Luttrell et al. (2011) for the coseismic-slip model of the same authors (Fig. 6b and d). We then use ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values derived from heat dissipation models (Gao and Wang, 2014) and force-balance models (Dielforder, 2017; Lamb, 2006) as an initial estimate of ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ (applied in model step 2). The ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values estimate the apparent strength of the megathrust, i.e. the level of shear stress that the fault can sustain before great earthquakes (heat dissipation models) and that is required to prevent the continental margin relief from gravitational collapse (force-balance models). Both modelling approaches yield comparable ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values of about 0.03 ± 0.01 for the Japanese and Chilean megathrusts (Dielforder, 2017; Gao and Wang, 2014; Lamb, 2006). Subtracting the $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values obtained from the megathrust stress drop from the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values yields an estimation of the ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ values (applied in model step 3).

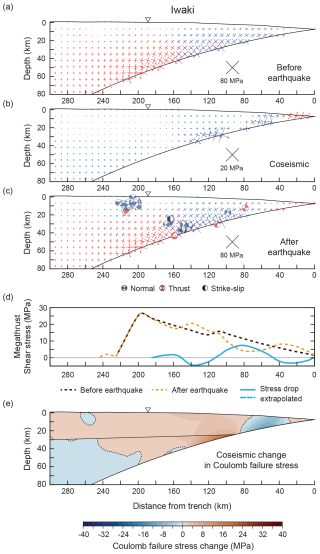
Figure 8 Preferred model of forearc stress change due to the Tohoku-Oki earthquake along the Iwaki cross-section. See Fig. 5a for the location of the cross-section. The meaning of panels (a)–(e) is the same as in Fig. 7. The coseismic change in Coulomb failure stress in panel (e) is calculated for μ=0.7.

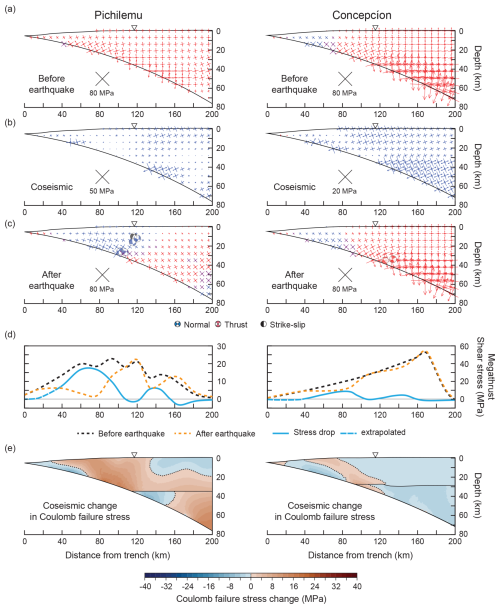
Figure 9 Preferred model of forearc stress change due to the Maule earthquake along the Pichilemu (left) and Concepción (right) cross-sections. See Fig. 6a for the location of the cross-sections. The meaning of panels (a)–(e) is the same as in Fig. 7. The coseismic change in Coulomb failure stress in panel (e) is calculated for μ=0.7.

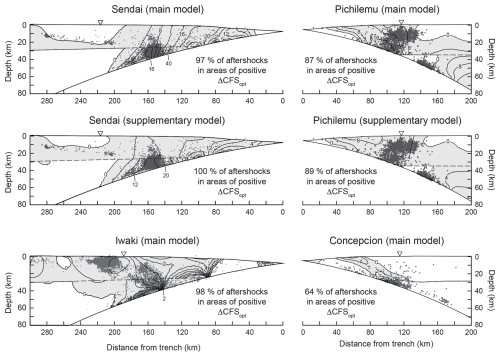
Figure 10 Earthquake hypocentres (grey dots) within 50 km wide swath profiles projected onto the plane cross-section. See Figs. 5a and 6a for locations of swath profiles. Grey areas indicate areas of positive Coulomb failure stress increase as in Figs. 7e–9e and 11e. Black contour lines in steps of 4 MPa (Sendai, Pichilemu), 2 MPa (Concepción), and 0.5 MPa (Iwaki). Main model results for the stress-drop models of Brown et al. (2015) for Japan (Sendai, Iwaki) and Luttrell et al. (2011) for Chile (Pichilemu, Concepción). Supplementary model results for the stress-drop models of Kubota et al. (2022) for Sendai and Wang et al. (2020) for Pichilemu.

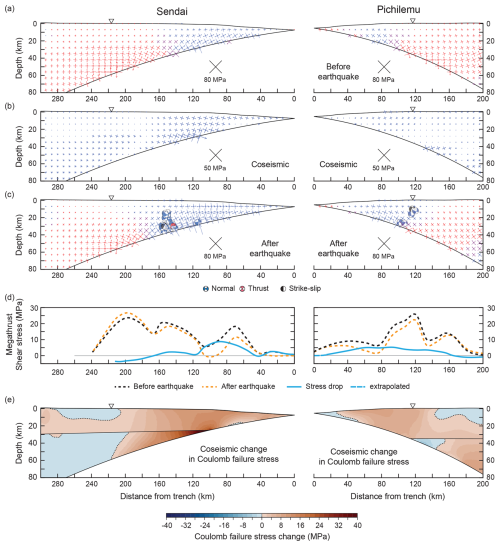
Figure 11 Supplementary Coulomb failure stress models for the Sendai cross-section, Japan, using the stress-drop model of Kubota et al. (2022) (left) and the Pichilemu cross-section, Chile, using the stress-drop model of Wang et al. (2020) (right). The meaning of panels (a)–(e) is the same as in Fig. 7. The coseismic change in Coulomb failure stress in panel (e) is calculated for μ=0.7.

We then solve the finite-element model and evaluate whether the post-earthquake stress state is compatible with focal mechanisms of upper-plate earthquakes that occurred within the 50 km wide swath profiles in the first year after the megathrust earthquake (Figs. 5c and 6c). The focal mechanisms are from the Japan Meteorological Agency and from the earthquake catalogue of Şen et al. (2015) for Japan and Chile, respectively. We assume that the modelled stress state is compatible with focal mechanism solutions, if thrust-faulting and normal-faulting events occur in areas of deviatoric compression and deviatoric tension, respectively. A near-neutral stress state (plunge in σ₁ between 40–50°) is considered to be consistent with both thrust faulting and normal faulting. If the stress state and focal mechanism are not compatible, we adjust the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values, determine the corresponding ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ values, and solve the model again.

We repeat the procedure until the stress state after the earthquake agrees with the majority of the focal mechanisms. We thereby obtain an estimation of the total stresses in the forearc and corresponding megathrust shear stresses shortly before and after the megathrust earthquakes that is consistent with the stress-drop models and the post-mainshock fault kinematics in the forearc. The forearc stress states in the interseismic periods before and after the mainshock are not determined and do not influence the calculation of the coseismic Coulomb failure stress change. However, it should be noted that most of the post-mainshock focal mechanisms indicate normal faulting, some of which may have been caused by afterslip and aftershocks on the megathrust in the post-seismic period (e.g. Bedford et al., 2016; Nakamura et al., 2016; Sun et al., 2014). Such events may record stress release on the megathrust in addition to the coseismic stress drop and influence our assessment of the post-seismic stress state. We expect this potential effect to be small on our calculations because the normal faulting started soon after the mainshocks (e.g. Farías et al., 2011; Lange et al., 2012; Yoshida et al., 2012; Japan Meteorological Agency) and always affected the same forearc areas in the first post-seismic year (Figs. S3 and S4 in the Supplement).

The procedure of estimating the pre-earthquake and post-earthquake stress states is similar for all models, except for the Concepción model crossing the hypocentre location of the Maule earthquake, for which the fault kinematics in the forearc are poorly constrained by focal mechanisms (Fig. 6c). We therefore calculate the Coulomb failure stress change for the Concepción model for the initial estimate of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ of 0.03 derived from heat dissipation models (Gao and Wang, 2014).

4 Results of the finite-element models

The main modelling results are presented in Figs. 7–10. Supplementary modelling results for alternative stress-drop models and model parameters are shown in Figs. 11 and S5–S14 and are discussed in Sect. 5. The forearc stresses before and after the earthquake and the incremental stress change caused by the earthquake are illustrated in terms of 2D deviatoric stress; i.e. the hydrostatic stress $({\mathit{\sigma }}_x+{\mathit{\sigma }}_z)/\mathrm{2}$ is subtracted from the stress tensor (cf. Wang et al., 2019). The Coulomb failure stress changes reported in Figs. 7–10 are computed from the total stresses following Eq. (6) and for μ=0.7.

4.1 Results for the 2011 M_w 9.0 Tohoku-Oki earthquake

4.1.1 Sendai cross-section

Figure 7 shows the preferred model of forearc stress change due to the Tohoku-Oki earthquake for the Sendai cross-section. The forearc experiences deviatoric compression almost everywhere before the earthquake (red crosses in Fig. 7a). The stress drop on the megathrust reduces the compression in the entire forearc (blue crosses in Fig. 7b). After the earthquake, the stress state is more heterogeneous and the forearc experiences deviatoric tension between 0 and ∼220 km and at ∼280–300 km from the trench (blue crosses in Fig. 7c). The extent of deviatoric tension in the model is compatible with the normal-faulting focal mechanisms between ∼110–160 km from the trench (Figs. 5c and 7c) but not with the thrust-faulting focal mechanism at ∼140 km from the trench. This event has a potential failure plane parallel to the plate interface, and we interpret it as an event on the megathrust (cf. Nakamura et al., 2016). Alternatively, the event may indicate a local stress heterogeneity that we cannot reproduce in our models.

The modelled megathrust shear stresses before and after the Tohoku-Oki earthquake and the modelled megathrust stress drop are shown in Fig. 7d. Before the earthquake, the megathrust shear stress tends to increase with distance from the trench (i.e. depth along the fault), except near the trench, where the shear stress is comparatively high. The shear stress values relate to ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values of 0.015 to 0.022, except for the shallowest portion of the megathrust within 10 km from the trench, for which ${\mathit{\mu }}_{\mathrm{b}}^{\prime }=\mathrm{0.2}$. The elevated ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ value near the trench is required to allow a large stress drop on the shallowest part of the megathrust related to the large fault slip of ≥60 m near the trench (Fig. 5a) and causes the strong compression near the trench before the earthquake (large stress crosses in Fig. 7a and b). Note that high stress drop near the trench may be an artefact inherited from the rupture model of Iinuma et al. (2012), a point we will revisit in Sect. 5.2.

After the earthquake, the megathrust shear stress is more heterogeneous and reaches zero at ∼0–40 km and ∼100 km from the trench, indicating locally complete stress drops (e.g. Brodsky et al., 2020; Chiba et al., 2013; Hasegawa et al., 2011). The corresponding ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ values vary between 0 and 0.025 along the megathrust. The $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values vary between −0.005 and 0.022, except for the shallowest portion of the megathrust, for which $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }=\mathrm{0.2}$. The stress change in the forearc causes large changes in Coulomb failure stress of −20 to +40 MPa (Fig. 7e). Areas of positive ΔCFS include most of the submarine forearc within 200 km from the trench and parts of the continental crust of inland Japan. Areas of negative ΔCFS include the mantle wedge at >200 km from the trench and the upper crust between ∼200 and 280 km from the trench. The areas of Coulomb failure stress increase contain ∼97 % of the forearc seismicity along the Sendai cross-section (Fig. 10).

4.1.2 Iwaki cross-section

The stress state in the forearc along the Iwaki cross-section is heterogenous before the earthquake (Fig. 8a). Most of the submarine forearc is in a neutral stress state (plunge in σ₁ of 40–50°) or under deviatoric tension, which is compatible with mixed reverse and thrust faulting reported for the years before the Tohoku-Oki earthquake (e.g. Hasegawa et al., 2012; Nakamura et al., 2016; Yoshida et al., 2012). At greater distance to the trench, larger forearc areas are under deviatoric compression. The megathrust stress drop decreases the horizontal compression in the forearc except near the trench, where the compression increases (Fig. 8b).

The modelled extent of deviatoric tension after the earthquake is compatible with the majority of the normal-faulting focal mechanisms between ∼100 and ∼230 km from the trench (Figs. 5c and 8c). There is one normal-faulting focal mechanism at ∼170 km from the trench occurring in an area of deviatoric compression. Thrust-faulting events at ∼80 and ∼110 km from the trench have potential failure planes parallel to the plate interface and are interpreted as megathrust events. In contrast, the thrust-faulting events at ∼160 and ∼215 km from the trench have potential failure planes oblique to the plate interface and are likely upper-plate events. In particular, the thrust faulting at ∼215 km from the trench, directly beneath the normal-faulting events in the upper crust, has been constrained by detailed moment tensor inversion (Yoshida et al., 2015). Both the thrust faulting near the plate interface at 160 km from the trench and in the lower crust at ∼215 km from the trench are compatible with the modelling results (Fig. 8c).

The modelled megathrust shear stress increases with depth along the fault before the megathrust earthquake (Fig. 8d). The corresponding ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values vary between 0.02 and 0.023. There is no local peak in megathrust shear stress near the trench as there is for the Sendai cross-section. After the megathrust earthquake, the shear stress is more heterogenous due to the stress drop, which is nowhere complete and is smaller than for the Sendai cross-section (Fig. 5b and d). The ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ and $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values vary between 0.008–0.036 and −0.015–0.013, respectively. The stress drop on the megathrust causes changes in Coulomb failure stress of −10 and +12 MPa (Fig. 8e). Areas of positive ΔCFS include most of the forearc crust at >80 km from the trench and much of the mantle wedge between 100 and 240 km from the trench. The Coulomb failure stress mainly decreases in the submarine forearc at 40–80 km from the trench and in the mantle wedge at >240 km. The areas of Coulomb failure stress increase contain ∼98 % of the forearc seismicity along the Iwaki cross-section (Fig. 10).

4.2 Results for the 2010 M_w 8.8 Maule earthquake

4.2.1 Pichilemu cross-section

The forearc along the Pichilemu transect experiences mainly deviatoric compression before the Maule earthquake (Fig. 9a). The stress drop on the megathrust decreases the horizontal compression in the entire forearc (Fig. 9b) and reverses the stress state from deviatoric compression to deviatoric tension within ∼20 to 130 km from the trench (Fig. 9c). The extent of deviatoric tension in the model is compatible with the normal-faulting focal mechanisms between ∼100 and 130 km from the trench (Figs. 6c and 9c). The modelled megathrust shear stress before the earthquake increases along the fault to about ∼20 MPa and then fluctuates by a few megapascals before decreasing toward zero at >120 km from the trench, i.e. at a depth >40 km (Fig. 9d). The corresponding ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values vary between 0.043 and 0.02 at 5–40 km depth and between 0.02 and 0.005 at 40–60 km depth (i.e. the coefficient of megathrust friction tends to decrease with depth). The stress drop on the megathrust is near complete at ∼60–80 km from the trench, where the shear stress on the megathrust approaches zero after the earthquake. The ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ and $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values vary between 0.006–0.04 and −0.002–0.036, respectively. It should be noted that the stress drop within 40 km from the trench is not well constrained (Fig. 5b) due to the lack of seafloor geodetic observations and is assumed here to decrease to zero toward the trench (dashed part in Fig. 9d).

The stress change in the forearc causes changes in Coulomb failure stress of −10 and +18 MPa (Fig. 9e). The Coulomb failure stress increases almost everywhere in the forearc except for some areas along the megathrust and in the upper forearc crust between ∼130 and 200 km from the trench. The areas of Coulomb failure stress increase contain ∼87 % of the forearc seismicity along the Pichilemu transect (Fig. 10).

4.2.2 Concepción cross-section

The forearc along the Concepción cross-section experiences mainly deviatoric compression before the Maule earthquake, except between ∼20 and 50 km from the trench (Fig. 9a). The stress drop on the megathrust decreases the horizontal compression in the entire forearc except near the trench, where the compression slightly increases (Fig. 9b). After the earthquake, deviatoric tension occurs up to ∼70 km from the trench (Fig. 9c). Further landward, the forearc remains under deviatoric compression, which agrees with two thrust-faulting focal mechanisms at about 120–130 km from the trench (Figs. 6c and 9c). Both events have potential failure planes oblique to the plate interface and are interpreted as events in the mantle wedge above the megathrust.

The shear stress on the megathrust before the earthquake increases with distance from the trench to about 50 MPa at the downdip limit of the megathrust (∼170 km from the trench) (Fig. 9d). The steady increase in megathrust shear stress reflects the constant ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ value of 0.03. The largest stress drop of ∼8 MPa occurs at about 80 km from the trench, close to the hypocentre of the Maule earthquake (Figs. 6a and 9d). The stress drop is smaller than for the Pichilemu cross-section and is nowhere complete. The ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ and $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values vary between 0.016–0.035 and −0.005–0.014, respectively.

The stress drop causes changes in Coulomb failure stress from −6 to +6 MPa (Fig. 9e). The areas of Coulomb failure stress increase contain ∼64 % of the forearc seismicity along the Concepción cross-section (Fig. 10).

5 Discussion

5.1 Main factors controlling failure after large megathrust earthquakes

We use analytical stress solutions of the dynamic Coulomb wedge theory (Wang and Hu, 2006) and numerical finite-element models of force balance (Dielforder et al., 2023; Wang et al., 2019) to investigate coseismic Coulomb failure stress changes caused by a megathrust earthquake in the forearc. The Coulomb failure stress change is determined as the difference in Coulomb failure stress on the pre-earthquake and post-earthquake optimal failure planes and takes into account the total stresses in the forearc and the resulting mechanical state.

The mechanical state of a forearc is crucial for understanding the conditions under which the stress drop in megathrust earthquakes may trigger failure in the forearc. Widespread failure is only promoted if the megathrust shear stress before the earthquake is so low that the compression of the forearc is not much higher than the deviatoric tension due to topographic relief. Under these conditions, the forearc is close to a neutral state and the megathrust stress drop can increase the deviatoric tension in the forearc, which promotes failure. If the forearc compression is much higher than the deviatoric tension due to topographic relief, the megathrust stress drop only decreases the compression, which inhibits failure.

The near-neutral stress conditions required for failure agree with independent estimates of forearc stresses. Force-balance analyses of global subduction zones indicate that near-neutral stress conditions are given for effective coefficients of megathrust friction of ∼0.03 ± 0.02 (Dielforder et al., 2020; Lamb, 2006; Matthies et al., 2024; Seno, 2009). The ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ values from force-balance models are consistent with estimates of ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ derived from other methods, including heat dissipation models (e.g. Bird, 1978; Gao and Wang, 2014; van den Beukel and Wortel, 1987, 1988; Wada and Wang, 2009), constraints on pore fluid overpressures and effective stresses based on the analysis of seismic velocity ratios of P waves to S waves (e.g. Moreno et al., 2014; Tsuji et al., 2014), field observations from exhumed megathrust faults (e.g. Angiboust et al., 2015; Cerchiari et al., 2020; Oncken et al., 2021), and analysis of the energy budget of megathrust earthquakes (e.g. Lambert et al., 2021). We therefore expect that near-neutral stress conditions as inferred for Japan and Chile are common along subduction zones worldwide, which implies that most forearcs are prone to failure.

Another factor that controls failure in the forearc is the strength of faults. Coulomb failure stress models usually only describe whether a stress change promotes or inhibits failure, but they do not determine the conditions that eventually allow failure, such as the critical pore fluid pressure. Likewise, our models do not describe the conditions for failure, but the total stresses in our models indicate that faults at failure must be almost as weak as the megathrust (cf. Dielforder et al., 2023; Wang et al., 2019; Wang and Hu, 2006; Yang et al., 2013). The low strength may be explained by high pore fluid overpressures (λ>0.9) reducing the effective stresses in the forearc or a low intrinsic strength of the fault zone. The latter may be caused by the presence of sheet silicates and the development of shear fabrics in the fault zone, which can reduce the coefficient of friction to values as low as ∼0.2 (Ikari and Kopf, 2017; Moore and Lockner, 2004; Tesei et al., 2012).

The requirement of weak faults for failure also implies that their absence may cause tectonic quiescence even though the Coulomb failure stress increases. High pore fluid overpressures may be difficult to sustain through time and over large areas such that only small fractions of the forearc lithosphere may be close to failure. Stress changes caused by megathrust earthquakes may therefore preferentially drive small earthquakes (Wang et al., 2019). Consistently, the vast majority of the earthquakes investigated in this study have low magnitudes of about 2.5–3.5 and record local failure on small faults. However, the aftershock seismicity of both mainshocks also included damaging earthquakes with magnitudes of 6.6–7.0 inland Japan near Iwaki (Fig. 5a) and in the coastal region near Pichilemu, Chile (Fig. 6a). The large magnitude aftershocks occurred in earthquake clusters affecting the entire crust down to 20 km (Iwaki) and 35 km (Pichilemu) depth, which shows that megathrust earthquakes can cause pervasive failure in the interior of forearcs.

5.2 Robustness of the modelled Coulomb failure stress changes

The modelling results are subject to uncertainties in model parameters such as the choice of slip model and coefficient of friction (e.g. Ishibe et al., 2017; Reasenberg and Simpson, 1992; Toda et al., 2011b). Uncertainties in megathrust stress drop may be large if the earthquake slip model used for the stress-drop calculation is constrained by onshore geodetic observations only as for the Maule earthquake (Luttrell et al., 2011; Stressler and Barnhart, 2017). There are also a large number of competing slip models for the Tohoku-Oki and Maule earthquakes and models that average different slip models (e.g. Benavente and Cummins, 2013; Delouis et al., 2010; Hooper et al., 2013; Kubota et al., 2022; Minson et al., 2014; Moreno et al., 2012; Sun et al., 2017; Wang et al., 2019, 2020; Wei et al., 2012). We therefore conducted supplementary finite-element models for the Sendai and Pichilemu cross-sections using different stress-drop models (Fig. 11). For Sendai, we used the stress-drop model of Kubota et al. (2022) for the slip model of the same authors. The slip model of Kubota et al. (2022) includes a lower slip (∼53 m) near the trench than the slip model of Iinuma et al. (2012) (∼80 m) and is similar to the model of Sun et al. (2017) that quantifies the slip near the trench from high-resolution bathymetry differences before and after the Tohoku-Oki earthquake. For the Pichilemu cross-section, we used the stress-drop model of Wang et al. (2020) for the average slip model of the same authors, averaging 12 published slip models.

The stress-drop models of Kubota et al. (2022) and Wang et al. (2020) yield smaller stress drops than the models of Brown et al. (2015) and Luttrell et al. (2011) (Fig. 11d). The absolute Coulomb failure stress changes are therefore up to 10 MPa smaller than in the main model results (Figs. 7e and 8e). However, the general patterns of Coulomb failure stress change are similar, while the proportions of aftershocks in areas of positive ΔCFS increase slightly (Figs. 10 and 11; Table 1).

Table 1 Percentages of aftershocks in areas of positive Coulomb failure stress change.

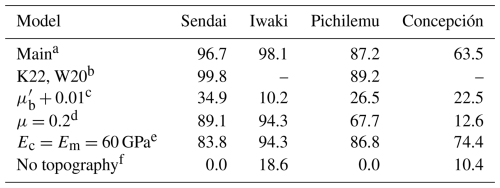
^a Main results for the stress-drop models of Brown et al. (2015) for Japan and Luttrell et al. (2011) for Chile as presented in Figs. 7–9.
^b Supplementary model results for the stress-drop models of Kubota et al. (2022) for Sendai and Wang et al. (2020) for Pichilemu as presented in Fig. 11.
^c As ^a but for effective coefficients of megathrust friction ${\mathit{\mu }}_{\mathrm{b}}^{\prime }$ increased by 0.01. See Figs. S5–S7 for details.
^d As ^a but using a coefficient of friction μ of 0.2 instead of 0.7 for the calculation of the Coulomb failure stress change. See Fig. S8 for details.
^e As ^a but using the same Young's modulus of 60 GPa for the crust (E_c) and mantle (E_m). See Figs. S9–S11 for details.
^f As ^a but without topography and water loads. See Figs. S12–S14 for details.

The effect of the stress-drop model on the spatial distribution of positive and negative Coulomb failure stress changes is comparatively small, mainly because our modelling approach requires that the post-earthquake stress state is consistent with the fault kinematics of upper-plate aftershocks. The post-earthquake stress state is therefore the same for the different slip models, while the pre-earthquake stress state differs. In detail, the lower stress drops in the models of Kubota et al. (2022) and Wang et al. (2020) would necessitate that the pre-earthquake stress states are less compressive so that larger forearc areas experience deviatoric tension. The pre-earthquake stress states obtained for the alternative stress-drop models may underestimate the compression of the forearc, at least for Sendai, where there is evidence for thrust faulting in the forearc 100–150 km from the trench before the Tohoku-Oki earthquake (e.g. Nakamura et al., 2016). The mismatch could be removed by increasing the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ values of the megathrust above the Moho intersection by ∼0.006, which translates to an increase in stress drop of about 2 MPa on the shallow megathrust.

For comparison, if the post-earthquake stress state is not constrained to be consistent with the upper-plate fault kinematics, the Coulomb failure stress change differs significantly. For example, increasing the ${\mathit{\mu }}_{\text{b-pre}}^{\prime }$ and ${\mathit{\mu }}_{\text{b-post}}^{\prime }$ values in the models by 0.01 causes the post-earthquake stress states to become partially incompatible with the fault kinematics so that normal faulting occurs in areas of deviatoric compression (Figs. S5–S7). In that case, the areas of positive ΔCFS_opt become significantly smaller and include only 10 %–35 % of the aftershocks (Table 1).

We further evaluated the effect of the coefficient of friction μ, the rigidity contrast between the crust and mantle, and topographic stresses on the modelling results. Using a μ value of 0.2 instead of 0.7 slightly reduces the proportions of aftershocks in areas of positive ΔCFS_opt (Table 1) but does not change the general pattern of the Coulomb failure stress change (Fig. S8). Removing the rigidity contrast between the crust and the mantle by applying the same Young's modulus of 60 GPa to both reduces the contrast in total stresses and Coulomb failure stresses at the crust–mantle transition (Figs. S9–S11). The areas of positive ΔCFS_opt change slightly and are less impacted by the aftershocks (Table 1). To test the effect of topographic tresses, we constructed additional models without water loads and a flat surface such that there is no gradient in potential energy and no topographic stresses (Figs. S12–S14). Without topographic stresses, the Coulomb failure stress change decreases almost everywhere in the forearc, except for some smaller areas, in which the compression of the forearc increases. The areas of ΔCFS_opt contain 0 %–20 % of the aftershocks (Table 1).

Taken together, we find that the model results vary with the stress-drop model, the coefficient of friction, and Young's modulus but are most sensitive to the forearc topography and the forearc stress state after the earthquake. Thus, a robust estimate of the Coulomb failure stress change requires that the topography and stress state are constrained in addition to the megathrust stress drop, as in our models for Japan and Pichilemu, Chile. For comparison, the stress state along the Concepción cross-section is less well constrained and the model results are less robust.

5.3 Significance of the modelled stress changes as triggers of aftershock seismicity

The finite-element models indicate that the megathrust stress drop during the Tohoku-Oki and Maule earthquakes caused a broad increase in Coulomb failure stress in the forearc so that the majority of all the forearc seismicity occurred in areas of Coulomb failure stress increase (Fig. 10). For Japan, there is a continuous record of forearc seismicity covering the time before and after the Tohoku-Oki earthquake (Japan Meteorological Agency). The forearc seismicity along the investigated cross-sections occurred immediately after the earthquake and throughout the forearc (Figs. S3 and S4) (e.g. Dielforder et al., 2023; Hasegawa et al., 2012; Toda et al., 2011a; Yoshida et al., 2012). Seismicity rates were highest in the month following the Tohoku earthquake and decayed at a power-law-like rate afterwards. For Chile, a detailed record is available only for about 2 weeks after the Maule earthquake (Lange et al., 2012), but the record also shows a decrease in seismicity rates (Fig. S3). Overall, the records for Japan and Chile indicate that the forearc seismicity is related to the mainshock, and our modelling results indicate that most of the seismicity was promoted and likely triggered by the stress drop on the megathrust.

We further showed that the investigated Coulomb failure stress change depends on the superposition of topographic and tectonic stresses and that increases in ΔCFS_opt require a prevalence of topographic stresses after the earthquake. The dataset shows different characteristics that corroborate the influence of topography on aftershock triggering. The aftershock seismicity is dominated by normal faulting, which requires deviatoric tension. The tension resulting from forearc topography agrees well with the spatial extent of normal faulting but also allows deviatoric compression in areas of thrust faulting such as inland Japan. The modelling results further indicate that all of the aftershock seismicity was coupled to a rotation of σ₁ toward the vertical and partially involved an increase in differential stress (∼84 % and ∼11 % of the aftershocks in Japan and Chile, respectively). For Coulomb failure, the strength of faults, i.e. the stress at failure, decreases with an increasing plunge in σ₁, while increases in differential stress generally promote failure. Both the modelled stress rotation and the increases in differential stress result from the effect of topography and explain the triggering of aftershocks.

The modelled Coulomb failure stress changes also reveal some details resulting from topography that appear to influence the distribution of seismicity. The Sendai models show seaward-inclined isolines of ΔCFS_opt (Fig. 10), which is primarily due to the submarine margin relief. The landward extent of seismicity in the lower crust and mantle at about 160–200 km from the trench follows these isolines (Fig. 7e). The Sendai models further show an increase in Coulomb failure stress in 200–280 km distance only in the lower crust, while the Iwaki model also shows an increase in the upper crust. The difference is partially due to a local topographic high along the coast of Iwaki (the Abukuma Plateau), which is missing near Sendai. For Pichilemu, isolines of ΔCFS_opt at a distance of 80–130 km form landward-inclined lobes that encompass the main cluster of seismicity that is landward-inclined too (Fig. 9e). The landward inclination is due to the topography of the Chilean Central Valley, which forms a gentle depression between the Coastal Range and the high Andes. Likewise, the decrease in Coulomb failure stress in the crust at a distance of 130–200 km results from the valley.

However, the consistency in the aftershock ΔCFS patterns does not imply that there is a general, simple dependence of the seismicity distribution on the earthquake stress changes. For example, the largest earthquake slip and the largest stress changes in Japan occurred near the Tohoku-Oki hypocentre along the Sendai cross-section, but most of the aftershocks occurred ∼140 km to the southwest in the coastal area near Iwaki, where the earthquake slip and stress changes were comparatively low (Figs. 5, 7, and 8). For comparison, in Chile, the largest earthquake slip and stress changes occurred near Pichilemu, ∼200 km north of the mainshock hypocentre, where most of the aftershock seismicity also occurred (Figs. 6 and 9).

The differences in the aftershock occurrence likely reflect spatial heterogeneities in fault strength and proximity to failure. For Japan, our model results indicate that tectonically active forearc areas along the Iwaki cross-section were already in a near-neutral stress state before the Tohoku-Oki earthquake (Fig. 8a), which is consistent with mixed upper-plate fault kinematics near Iwaki in the years before the Tohoku-Oki earthquake (Hasegawa et al., 2012; Nakamura et al., 2016). Thus, normal faults along the Iwaki transect were closer to failure than normal faults along the Sendai transect, which experienced deviatoric compression before the mainshock (Fig. 7a) (Wang et al., 2019). The comparatively small stress changes near Iwaki may thus have been enough to trigger normal faulting.

For comparison, the outer forearc along the Sendai transect <140 km from the trench shows comparatively little seismicity despite large increases in Coulomb failure stress (Fig. 7). The outer forearc experienced strong coseismic dilation due to the large slip near the trench causing seaward surface displacements ≥20 m (Kido et al., 2011; Sato et al., 2011), which may have caused dilatant hardening (e.g. Brace, 1978), i.e. a drop in pore fluid pressure and respective increase in fault strength.

The aftershock seismicity of the Tohoku-Oki and Maule earthquakes may have been further affected by processes not captured in our models. For example, aftershocks can be triggered by dynamic stress changes resulting from the passage of seismic waves emitted by the mainshock (e.g. Gomberg et al., 2004; Kato et al., 2013; Miyazawa, 2011). Coulomb failure stress changes caused by seismic waves can reach a few megapascals near the earthquake hypocentre (e.g. Kilb et al., 2000; Miyazawa, 2011), which is comparable to the Coulomb failure stress change caused by the stress drop on the megathrust. Dynamic triggering in the nearfield of the earthquake should be quasi-instantaneous with the mainshock (e.g. Belardinelli et al., 2003; Harris, 1998) and may have affected the immediate seismic response to the Tohoku-Oki and Maule earthquakes. The longer-term aftershock seismicity may have been influenced by poroelastic effects and pore pressure changes (e.g. Cocco and Rice, 2002; Hainzl, 2004; Peikert et al., 2024; Peña et al., 2022; Terakawa et al., 2013; Yoshida et al., 2017), viscoelastic stress relaxation in the mantle wedge and lower crust (Bagge and Hampel, 2017; Becker et al., 2018; Diao et al., 2014; Sun et al., 2014), and stress changes induced by larger aftershocks (M_w≥5), as they occurred, for example, near Iwaki and Pichilemu (e.g. Calle-Gardella et al., 2021; Fukushima et al., 2013, 2018; Lange et al., 2012; Ryder et al., 2012; Wimpenny et al., 2023).

5.4 Comparison with previous Coulomb failure stress models

The results of the finite-element models indicate that the majority of the aftershock seismicity along the studied forearc cross-sections occurred in areas of Coulomb failure stress increase (∼97 %–98 % for Japan; ∼87 % and ∼64 % for Pichilemu and Concepción, respectively) (Table 1). The proportions of positively stressed aftershocks (i.e. aftershocks in areas of positive ΔCFS) are higher than in previous Coulomb failure stress models based on dislocation solutions for a fault embedded in an elastic half-space. Toda et al. (2011b) investigated normal-faulting events in the Japanese forearc after the Tohoku-Oki earthquake and found that ∼71 % of them were positively stressed. Ishibe et al. (2017) found that ∼ 60 % and ∼43 % of the aftershocks of the Tohoku-Oki earthquake and Maule earthquake, respectively, were positively stressed. Miao and Zhu (2012) concluded that less than 50 % of the aftershock seismicity of the Tohoku-Oki and Maule earthquake was positively stressed. It is important to note that the above studies used different approaches and datasets, which makes a direct comparison of model results difficult. For example, the studies investigate larger areas than we do and partially include lower-plate and interplate events in the analysis.

Toda et al. (2011b) and Ishibe et al. (2017) resolved the Coulomb failure stress on nodal planes of earthquake focal mechanisms; i.e. the authors determined the Coulomb failure stress change on specified failure planes (Eq. 5). The analytical stress solutions presented in Sect. 2 show that the sign of ΔCFS_sf and ΔCFS_opt values should match if the investigated type of faulting agrees with the mechanical state (e.g. normal faulting under deviatoric tension) (Fig. 4). Consistently, the results of Toda et al. (2011b), Ishibe et al. (2017), and our study indicate an increase in Coulomb failure stress in forearc areas experiencing normal faulting, for example, near Iwaki, Japan, and Pichilemu, Chile. However, there are also significant differences in the modelling result. For example, Ishibe et al. (2017) find that the slip model of Luttrell et al. (2011) for the Maule earthquake yields a mean decrease in Coulomb failure stress, while we find that the model causes broad increases in Coulomb failure stress that explain the aftershock seismicity well. Toda et al. (2011a) resolved the Coulomb failure stress change on the nodal planes of earthquakes from before the Tohoku-Oki earthquake and compared it with changes in seismicity rate. If the regional stress field does not change much during the mainshock, the earthquake stress change may trigger faults that have been active before the mainshock. However, the approach may be misleading if the regional stress field changes. The authors therefore exclude the area near Iwaki from their analysis, even though the area records the most intense change in seismicity rate and the most severe aftershocks. For comparison, our approach takes into account changes in the regional stress, and the ΔCFS_opt can be directly compared with seismicity rate changes without resolving the stress change on pre-mainshock nodal planes. The Coulomb failure stress model of Terakawa et al. (2013) yields a decrease in Coulomb failure stress inland Japan and offshore Sendai, such that large portions of the aftershock seismicity are negatively stressed. The authors argue that the negatively stressed aftershocks may record a triggering of misoriented faults due to increases in pore fluid pressure. For comparison, our models indicate that the seismicity offshore Sendai and near the volcanic arc inland Japan was positively stressed and does not require a complex triggering mechanism.

Finally, the analytical stress solutions and the finite-element models yield ΔCFS values that can reach tens of megapascals (MPa), which is similar to the magnitude of the modelled differential stress and changes in differential stress (Figs. 3 and 7–9) and distinctly higher than previous estimates of ΔCFS on the order of 0.01–1 MPa (e.g. Farías et al., 2011; Ishibe et al., 2017; Jara-Munoz et al., 2022; Nakamura et al., 2016; Ryder et al., 2012; Stressler and Barnhart, 2017; Terakawa et al., 2013; Toda et al., 2011a, b; Qiu and Chan, 2019). The ΔCFS values increase with the megathrust stress drop and are particularly high if the stress state switches from deviatoric compression to deviatoric tension, especially in the proximity of steep margin topography. Accordingly, we find that the largest Coulomb failure stress changes occur along the Sendai transect, Japan, and the Pichilemu transect, Chile, close to the shelf break at about 100 km distance from the trench (Figs. 7 and 9). In comparison, the Coulomb failure stress changes are lower along the Iwaki transect, Japan, and the Concepción transect, Chile, where the megathrust stress drop and the stress changes in the forearc are smaller (Figs. 8 and 9).

6 Conclusions

Our analysis illustrates that topographic stresses allow the stress state in a forearc to switch from deviatoric compression to deviatoric tension if the shear stress on the megathrust is sufficiently low. The switch in stress state is the main factor that promotes widespread aftershock seismicity at the scale of the forearc. Without the stress reversal, megathrust earthquakes have the tendency to stabilize the forearc and inhibit aftershock seismicity. A switch in stress state is supported if the megathrust is very weak and the forearc is close to a neutral state (margin normal compression ≈ margin normal tension) before the earthquake. Near-neutral stress conditions have been inferred for most global subduction zones (Dielforder et al., 2020; Heuret et al., 2011; Lamb, 2006). Thus, the mechanisms evaluated here are crucial for assessing the geohazard at convergent margins.

The dependence of the forearc stability on the stress state can be taken into account by calculating the Coulomb failure stress change as the difference in Coulomb failure stress between the optimal failure planes before and after the earthquake, ΔCFS_opt, but this requires the constraint of the total stresses in the forearc. We show that the total stresses may be constrained within reasonable uncertainties by moment tensor solutions of upper-plate earthquakes and estimates of the megathrust stress drop in the mainshock. Thus, the availability of earthquake moment tensor solutions and stress-drop estimates is crucial for evaluating seismic hazards at active margins. This underlines the importance of installing high-quality geophysical networks, such as those in Japan. If detailed geophysical observations are not available, ΔCFS_opt may still be estimated, for example, by using for the stress calculations an effective coefficient of friction for the megathrust determined by other means. However, this approach can introduce uncertainties and lead to less accurate models, as likely reflected in our model for the Concepción cross-section in Chile.

The benefit of constraining the total stresses before and after the earthquake is that it allows a better estimate of Coulomb failure stress changes and provides insights into the factors promoting aftershock seismicity. Our models for Japan reveal differences in the preseismic stress conditions along the Sendai and Iwaki cross-sections, which may explain why the comparatively small stress changes near Iwaki could trigger intense aftershock seismicity. In contrast, the intense aftershock seismicity near Pichilemu (Chile) was dependent on the large stress changes that resulted from large slip and stress drop on the megathrust ∼200 km north of the mainshock hypocentre. We further find that the aftershock occurrence, including the large-magnitude events near Iwaki, Japan, and Pichilemu, Chile, was influenced by the local forearc topography. Our findings therefore reveal that topography is not only a prerequisite for widespread aftershock seismicity but also influences its details.

Finally, our models illustrate the importance of forearc mechanics for understanding Coulomb failure stress changes and aftershock triggering, but they are currently limited in their application to two-dimensional cross-sections normal to the plate margin. Future work will therefore include the development of three-dimensional models, which will account for differences in continental margin relief and total stresses along strike of the margin.

Appendix A

The stress solutions for an elastic-perfectly Coulomb plastic wedge can be written in terms of effective stresses as (Wang and Hu, 2006)

$$\begin{array}{}\text{(A1a)}& {\displaystyle }{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_x=m(\mathrm{1}-\mathit{\lambda })\mathit{\rho }gz\cos \mathit{\alpha },\text{(A1b)}& {\displaystyle }{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_z=(\mathrm{1}-\mathit{\lambda })\mathit{\rho }gz\cos \mathit{\alpha },\text{(A1c)}& {\displaystyle }{\mathit{\tau }}_{xz}=(\mathrm{1}-{\mathit{\rho }}^{\prime })\mathit{\rho }gz\sin \mathit{\alpha },\end{array}$$

where

$$\begin{array}{}\text{(A2)}& m=\mathrm{1}+{\displaystyle \frac{\mathrm{2}\left[\tan {\mathit{\alpha }}^{\prime }+{\mathit{\mu }}_{\mathrm{b}}^{\prime }/(\mathrm{1}-\mathit{\lambda })\right]}{\sin \mathrm{2}\mathit{\theta }\left[\mathrm{1}-{\mathit{\mu }}_{\mathrm{b}}^{\prime }/(\mathrm{1}-\mathit{\lambda })\tan \mathit{\theta }\right]}}-{\displaystyle \frac{\mathrm{2}\tan {\mathit{\alpha }}^{\prime }}{\tan \mathit{\theta }}}\end{array}$$

and

$$\begin{array}{}\text{(A3)}& \tan {\mathit{\alpha }}^{\prime }={\displaystyle \frac{\mathrm{1}-{\mathit{\rho }}^{\prime }}{\mathrm{1}-\mathit{\lambda }}}\tan \mathit{\alpha },\end{array}$$

where $\mathit{\theta }=\mathit{\alpha }+\mathit{\beta }$ and ${\mathit{\rho }}^{\prime }={\mathit{\rho }}_{\mathrm{w}}/\mathit{\rho }$. The total stresses σ_x and σ_z can be obtained by solving Eq. (A1) for λ=0.

The principal stresses can be written as

$$\begin{array}{}\text{(A4a)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{1}}={\mathit{\sigma }}_x{\cos }^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{0}}+{\mathit{\sigma }}_z{\sin }^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{0}}+\mathrm{2}{\mathit{\tau }}_{xy}\sin {\mathit{\psi }}_{\mathrm{0}}\cos {\mathit{\psi }}_{\mathrm{0}},\text{(A4b)}& {\displaystyle }{\mathit{\sigma }}_{\mathrm{3}}={\mathit{\sigma }}_x{\sin }^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{0}}+{\mathit{\sigma }}_z{\cos }^{\mathrm{2}}{\mathit{\psi }}_{\mathrm{0}}-\mathrm{2}{\mathit{\tau }}_{xy}\sin {\mathit{\psi }}_{\mathrm{0}}\cos {\mathit{\psi }}_{\mathrm{0}},\end{array}$$

where ψ₀ is the angle between the surface of the wedge and the axis of σ₁ (Fig. 1b). Angle ψ₀ is determined from the following equation (Wang and Hu, 2006):

$$\begin{array}{}\text{(A5)}& {\displaystyle \frac{\tan \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}}{\cos {\mathit{\phi }}^{\mathrm{p}}\sec \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}-\mathrm{1}}}={\displaystyle \frac{\tan {\mathit{\alpha }}^{\prime }}{\mathrm{1}+\mathit{\eta }}},\end{array}$$

where

$$\begin{array}{}\text{(A6)}& {\mathit{\phi }}^{\mathrm{p}}=\arcsin \sqrt{{\displaystyle \frac{(m-\mathrm{1}{)}^{\mathrm{2}}+\mathrm{4}{\tan }^{\mathrm{2}}{\mathit{\alpha }}^{\prime }}{(\mathrm{2}\mathit{\eta }+m+\mathrm{1}{)}^{\mathrm{2}}}}}.\end{array}$$

The cohesion gradient η is a dimensionless constant that allows us to account for wedge cohesion (Zhao et al., 1986). Equation (A5) may be rewritten in explicit forms as

$$\begin{array}{}\text{(A7a)}& {\displaystyle }{\mathit{\psi }}_{\mathrm{0}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\arcsin \left({\displaystyle \frac{\sin {\mathit{\alpha }}^{\prime \prime }}{\sin {\mathit{\phi }}^{\mathrm{p}}}}\right)-{\mathit{\alpha }}^{\prime \prime }\right),{\mathit{\psi }}_{\mathrm{0}}\le \mathit{\pi }/\mathrm{4}-{\mathit{\alpha }}^{\prime \prime }/\mathrm{2},\text{(A7b)}& {\displaystyle }{\mathit{\psi }}_{\mathrm{0}}={\displaystyle \frac{\mathit{\pi }}{\mathrm{2}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\arcsin \left({\displaystyle \frac{\sin {\mathit{\alpha }}^{\prime \prime }}{-\sin {\mathit{\phi }}^{\mathrm{p}}}}\right)-{\mathit{\alpha }}^{\prime \prime }\right),{\mathit{\psi }}_{\mathrm{0}}>\mathit{\pi }/\mathrm{4}-{\mathit{\alpha }}^{\prime \prime }/\mathrm{2},\end{array}$$

where

$$\begin{array}{}\text{(A8)}& {\mathit{\alpha }}^{\prime \prime }=\arctan \left({\displaystyle \frac{\tan {\mathit{\alpha }}^{\prime }}{\mathrm{1}+\mathit{\eta }}}\right).\end{array}$$

The wedge enters a critical state if

$$\begin{array}{}\text{(A9)}& m=m^{\mathrm{c}}=\mathrm{1}+{\displaystyle \frac{\mathrm{2}(\mathrm{1}+\mathit{\eta })}{\csc \mathit{\phi }\sec \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}^{\mathrm{c}}-\mathrm{1}}},\end{array}$$

where φ=arctan μ and ${\mathit{\psi }}_{\mathrm{0}}^{\mathrm{c}}$ is the angle between the axis of σ₁ and the surface slope at critical state (Wang and Hu, 2006; Zhao et al., 1986). Angle ${\mathit{\psi }}_{\mathrm{0}}^{\mathrm{c}}$ is determined from the following equation, which is similar to Eq. (A5):

$$\begin{array}{}\text{(A10)}& {\displaystyle \frac{\tan \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}^{\mathrm{c}}}{\cos \mathit{\phi }\sec \mathrm{2}{\mathit{\psi }}_{\mathrm{0}}^{\mathrm{c}}-\mathrm{1}}}={\displaystyle \frac{\tan {\mathit{\alpha }}^{\prime }}{\mathrm{1}+\mathit{\eta }}}.\end{array}$$

The effective coefficient of megathrust friction at neutral stress state can be calculated as (Wang and Hu, 2006)

$$\begin{array}{}\text{(A11)}& {\mathit{\mu }}_{\text{b-N}}^{\prime }={\displaystyle \frac{(\mathrm{1}-\mathit{\lambda })\cos \mathrm{2}\mathit{\theta }}{\cot {\mathit{\alpha }}^{\prime }+\sin \mathit{\theta }}}.\end{array}$$