Impact of terrestrial reference frame realizations on altimetry satellite orbit quality and global and regional sea level trends: a switch from ITRF2008 to ITRF2014

A terrestrial reference frame (TRF) is a basis for precise orbit determination of Earth-orbiting satellites, since it defines positions and velocities of stations, the tracking data of which are used to derive satellite positions. In this paper, we investigate the impact of the International Terrestrial Reference Frame realization ITRF2014, as compared to its predecessor ITRF2008, on the quality of orbits, namely, on root-mean-square (rms) fits of observations and orbital arc overlaps of three altimetry satellites (TOPEX/Poseidon, Jason-1, and Jason-2) in the time interval from August 1992 to April 2015 and on altimetry products computed using these orbits, such as single-satellite altimeter crossover differences, radial and geographically correlated mean sea surface height (SSH) errors and regional and global mean sea level trends. The satellite orbits are computed using satellite laser ranging (SLR) and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) observations of a global network of stations.

We have found that using ITRF2014 generally improves the orbit quality as compared to using ITRF2008. Thus, the mean values of the rms fits of SLR observations decreased (improved) by 2.4 % and 8.8 % for Jason-1 and Jason-2, respectively, but are almost not impacted for TOPEX/Poseidon when using ITRF2014 instead of ITRF2008. The internal orbit consistency in the radial direction (as derived from arc overlaps) is reduced (improved) by 6.6 %, 2.3 %, and 5.9 % for TOPEX/Poseidon, Jason-1, and Jason-2, respectively.

Single-satellite altimetry crossover analyses indicate reduction (improvement) in the absolute mean crossover differences by 0.2 mm (8.1 %) for TOPEX, 0.4 mm (17.7 %) for Jason-1, and 0.6 mm (30.9 %) for Jason-2 with ITRF2014 instead of ITRF2008. The major improvement of the mean values of the rms of crossover differences (0.13 mm; 0.3 %) has been found for Jason-2.

Multi-mission crossover analysis shows slight improvements in the standard deviations of radial errors: 0.1 %, 0.2 %, and 1.6 % for TOPEX, Jason-1, and Jason-2, respectively. The standard deviations of geographically correlated mean SSH errors improved by 1.1 % for Jason-1 and 5.4 % for Jason-2 and degraded by 1.3 % for TOPEX.

The change from ITRF2008 to ITRF2014 orbits only has minor effects on the estimation of regional and global sea level trends over the 22-year time series from 1993 to 2015. However, on interannual timescales (3–8 years) large-scale coherent trend patterns are observed that seem to be connected to drifts between the origins of the tracking station networks. This leads to the changes in interannual global mean sea level of up to 0.06 mm yr⁻¹ for TOPEX, 0.05 mm yr⁻¹ for Jason-1, and up to 0.12 mm yr⁻¹ for Jason-2, i.e., up to 4 % of the corresponding sea level signal based on altimetry for timescales of 3 to 8 years. The respective changes in the regional sea level trend on these timescales are up to 0.4 mm yr⁻¹ in the time span from April 1993 to July 2008 and up to 1.0 mm yr⁻¹ in the time span from July 2008 to April 2015.

1 Introduction

Precise information on positions and the motion of points located on the Earth's surface is important for practical applications, such as positioning and navigation, and scientific investigations, such as Earth's rotation, plate tectonics, seismological deformations, and precise orbit determination (POD). Precise positions and velocities of geodetic stations are provided by International Terrestrial Reference System (ITRS) realizations created by ITRS Combination Centres based on solutions provided by International DORIS Service (IDS), International GNSS (Global Navigation Satellite System) Service (IGS), International Laser Ranging Service (ILRS), and International VLBI Service for Geodesy and Astrometry (IVS). These solutions are derived from the analysis of Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS), Global Positioning System (GPS), satellite laser ranging (SLR), and very long-baseline interferometry (VLBI) observations. Three new recently released ITRS realizations are ITRF2014 (Altamimi et al., 2016), DTRF2014 (Seitz et al., 2016), and JTRF2014 (Abbondanza et al., 2017).

A precise and stable terrestrial reference frame (TRF) is important for the long-term consistency of altimetry measurements, since it provides the basis for mapping sea level change to an accurate and stable coordinate system for calibration and validation and improved long-term monitoring of sea level changes (Fu and Haines, 2013; Wöppelmann and Marcos, 2016). The realization of a terrestrial reference system has been shown (Beckley et al., 2007) to have a detectable impact on the regional and global mean sea levels trends derived from altimetry. Thus, they found changes of up to ±1.5 mm yr⁻¹ in the regional sea level rates related to the change from ITRF2000 to ITRF2005. Morel and Willis (2005) showed that a 10 mm error in the T_Z realization of a terrestrial reference frame can cause a systematic error of −1.2 mm in the derived mean sea level. Using TOPEX/Poseidon altimetry data, they estimated a precision of 3.0 mm in sea level and 0.37 mm yr⁻¹ in sea level trend in the case of ITRF97. From the analysis of Jason-1 and Jason-2 orbits derived using GPS and SLR and DORIS observations in 2002–2014 in ITRF2008 instead of ITRF2005, Couhert et al. (2015) estimated a sea level trend error caused by these ITRF realizations of 0.05 mm yr⁻¹ (globally) and 0.3 mm yr⁻¹ (regionally) at the decadal timescale. From their study, the sea level trend error caused by these ITRF realizations can reach 0.03 mm yr⁻¹ (globally) and 1 mm yr⁻¹ (regionally) at the interannual timescale. More recently, from the analysis of TOPEX altimetry observations for the period 1993 to 2004, Esselborn et al. (2018) have estimated a sea level trend error caused by ITRF2008 realization, as compared to ITRF2014 of 0.01 mm yr⁻¹ (globally) and 0.2 mm yr⁻¹ (regionally) at the decadal timescale and 0.03 mm yr⁻¹ (globally) and 0.2 mm yr⁻¹ (regionally) at the interannual timescale. Recently, Zelensky et al. (2018) investigated the impact of ITRF2014, DTRF2014, and JTRF2014 on orbits of altimetry satellites TOPEX/Poseidon, Jason-1, Jason-2, and Jason-3 derived using SLR and DORIS measurements over 1992–2016. They found that the replacement of ITRF2008 by ITRF2014 impacts the regional sea level trend within ±0.2 mm yr⁻¹.

The most widely used ITRS realizations are derived by the International Earth Rotation and Reference Systems Service (IERS) ITRS Product Center at Institut National de l'Information Géographique et Forestière, France. Therefore, in this paper we assess the impact of the new (ITRF2014) realization, as compared to its predecessor, ITRF2008 (Altamimi et al., 2011), on the orbits of three altimetry satellites, namely, TOPEX/Poseidon (from 23 September 1992 to 9 October 2005), Jason-1 (from 13 January 2002 to 5 July 2013), and Jason-2 (from 5 July 2008 to 6 April 2015), since these are the reference missions for sea level investigation (Quartly et al., 2017). We have computed orbits of these satellites (called GFZ VER13; Rudenko et al., 2018b) using the ITRF2014 reference frame. We analyze these orbits, as compared to the GFZ VER11 orbits (Rudenko et al., 2017) of the same satellites derived within the second phase of the Sea Level project of the European Space Agency (ESA) Climate Change Initiative (CCI) program (Legeais et al., 2018) using the ITRF2008 reference frame. For both sets of orbits, all other background models for precise orbit determination and estimated parameters are the same. Both VER11 and VER13 orbits are derived using SLR and DORIS observations available from ILRS (Pearlman et al., 2002) and IDS (Willis et al., 2010), respectively. We investigate the impact of ITRF2014, as compared to ITRF2008, on the root-mean-square (rms) of residuals of SLR and DORIS observations used for orbit determination; on the rms and mean of single-satellite altimetry crossover differences and radial errors; and on the global and regional mean sea level trends (between 66^∘ S and 66^∘ N in latitude). We performed similar investigations for studying the impact of geopotential models (Rudenko et al., 2014) and ocean and atmospheric de-aliasing products (Rudenko et al., 2016). By contrast with the paper of Zelensky et al. (2018), we investigate the impact of the replacement of ITRF2008 by ITRF2014 also on 2-day arc overlaps in radial, cross-track, and along-track directions and the geographically correlated mean sea surface height (SSH) errors. Moreover, we use 3.7- and 5-year longer time intervals for TOPEX/Poseidon and Jason-1, respectively, than those used by Zelensky et al. (2018). Additionally, we use another software and models for orbit computation and altimetry analysis. All this leads to slightly different results than those obtained by Zelensky et al. (2018).

The rest of the paper is organized as follows. A short description of the ITRF2014 and its differences with respect to ITRF2008 is given in Sect. 2. A description of the models used for POD of altimetry satellites and the impact of the ITRF2014, as compared to ITRF2008, on the rms fits of SLR and DORIS observations used for orbit determination as well as on the 2-day arc overlaps in the radial, cross-track, and along-track directions is discussed in Sect. 3. The impact of ITRF realizations on the rms and mean of single-satellite altimetry crossover differences for the three satellites is presented in Sect. 4. The influence of the change from ITRF2008 to ITRF2014 on the radial orbit errors and geographically correlated mean sea surface height errors as well as on the global and regional mean sea level trends is presented in Sects. 5 and 6, respectively. The main results of our study are summarized in Sect. 7.

2 ITRF realizations used for precise orbit determination

The detailed description of ITRF2008 and ITRF2014 is given in Altamimi et al. (2011) and Altamimi et al. (2016), respectively. The main differences in ITRF2014 with respect to ITRF2008 consist of

• 6-year longer time span (2009.0–2015.0) used for the generation of the reference frame and, therefore, an increased number of stations and their occupations,

• using information from 36 new surveys performed since the release of ITRF2008, which resulted in employing 139 local ties for ITRF2014 instead of 104 for ITRF2008,

• enhanced modeling of nonlinear station motions, provided by annual and semiannual variations in station positions that were excluded prior to the determination of station positions and velocities and by post-seismic deformations made available for stations affected by major earthquakes.

Since only observations from DORIS and SLR stations are used in our study, the following description concerns only these stations. Since an additional time span was used in ITRF2014 for SLR and DORIS stations, ITRF2014 contains 30 additional DOMES (Directory Of MERIT (Monitoring Earth Rotation and Intercomparison of Techniques) Sites) numbers for DORIS stations and 12 for SLR stations as compared to ITRF2008 (Table 1). ITRF2014 includes 22 additional discontinuities for DORIS stations and 17 for SLR stations as compared to ITRF2008. Moreover, ITRF2014 provides post-seismic deformation models for 13 DORIS and 10 SLR stations that have been used by us for this reference frame. No annual and semiannual signals were applied by us for ITRF2008 or for ITRF2014, since they are not a part of these realizations and were estimated internally for ITRF2014 by its authors for enhancing the velocity field estimation of the secular frame.

Table 1 The number of DOMES numbers and discontinuities and data span for DORIS and SLR stations in the ITRF2008 and ITRF2014.

3 Impact of ITRF2008 and ITRF2014 realizations on the orbit quality

To perform our study, we have derived orbits of TOPEX/Poseidon (from 23 September 1992 to 9 October 2005), Jason-1 (from 13 January 2002 to 5 July 2013), and Jason-2 (from 5 July 2008 to 6 April 2015) at 12-day arcs with 2-day arc overlaps. Orbit computations were performed using the “Earth Parameter and Orbit System – Orbit Computation (EPOS-OC)” software (Zhu et al., 2004) developed at GeoForschungsZentrum (GFZ) Potsdam. We use SLR and DORIS observations for all three satellites. To derive the satellite orbits, we use the same models, procedures, and parameterization as described in Rudenko et al. (2017) but use two different ITRF realizations – ITRF2008 and ITRF2014. The main models used for orbit determination are given in Table 2. For the details on the models and procedures used for the POD, the reader is referred to Rudenko et al. (2014) and Rudenko et al. (2017). The orbits of these satellites derived using ITRF2008 and ITRF2014 are called VER11 (version 11) and VER13 (version 13) orbits, respectively. Some of the models used by us for POD correspond to Geophysical Data Records (GDR)-E POD standards; some of them, like ITRF2014, correspond to Precise Orbit Ephemeris (POE)-F standards. At the same time, some of the models used by us, e.g., the EOT11a ocean tide model, the EIGEN-6S4 Earth gravity field model, and the GFZ AOD1B RL05 nontidal atmospheric and oceanic gravity model, differ from those defined in GDR-E and POE-F POD standards, details on which can be found at ftp://ftp.ids-doris.org/pub/ids/data/POD_configuration_POEF.pdf (last access: 23 January 2019).

Table 2 The main models used for orbit determination (for the details and references for the models, see Rudenko et al., 2014, 2017).

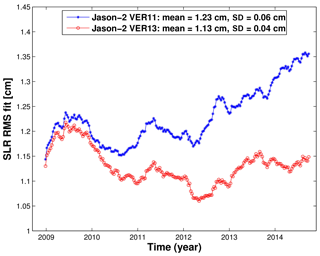
The rms fits of observations are an indicator of the accuracy of observations, models, reference frame realizations, and parameterization used for POD. Since we use the same observations, models, and parameterization to compute the VER11 and VER13 orbits and replace only ITRF realizations, the changes in rms fits of observations indicate the impact of the change in ITRF realizations on the rms fits of observations. We have found that a switch from ITRF2008 to ITRF2014 did not change the rms fits of SLR observations of TOPEX/Poseidon significantly. Their mean value slightly increased from 1.96 to 1.97 cm, i.e., by 0.3 %. However, the mean values of SLR rms fits decreased (improved) from 1.19 to 1.16 cm, i.e., by about 2.4 %, for Jason-1 and from 1.23 to 1.13 cm, i.e., by 8.1 %, for Jason-2 when using ITRF2014 instead of ITRF2008. The major reduction in the SLR rms fits is obtained in 2009–2015 (Figs. 1–2), since ITRF2014 was derived using additional observations for this time span allowing a more precise determination of station positions for this time span and station velocity over the whole time interval. In these figures, we use a 52-week running mean in order to get rid of short-periodic variations in the rms fits.

The mean values of DORIS rms fits are reduced (improved) for Jason-2 from 0.3490 to 0.3484 mm s⁻¹, i.e., by about 0.2 % when using ITRF2014 instead of ITRF2008. A larger improvement of 0.3 %–1.0 % is observed in 2012–2015. A rather small impact on DORIS rms fits of Jason-1 is found. Thus, a small improvement (about 0.2 %) of DORIS rms fits is observed in 2010–2011 and a small degradation (about 0.3 %) of DORIS rms fits is observed in 2012–2013 for this satellite. The mean values of DORIS rms fits are almost unchanged for TOPEX/Poseidon when using ITRF2014 instead of ITRF2008. However, an improvement of DORIS rms fits of 1 %–3 % is observed at about 20 arcs in 1993–1998 when using ITRF2014 instead of ITRF2008. The number of accepted DORIS observations at these arcs is 1.2–2.5 times larger when using ITRF2014 due to a better fitting of observations.

Satellite orbit and adjusted parameters are computed at different arcs using a different observations and, in some cases, using different parameterization depending on the amount of available observations. Therefore, though the background models used for orbit computations at orbit overlaps are the same, non-zero differences in satellite coordinates at overlaps are obtained. We call the differences in satellite coordinates of overlaps internal consistency, since the orbits are computed using the same software and the same background models. We have found from our analysis that the internal consistency of satellite orbits derived using ITRF2014 has improved, as compared to that obtained using ITRF2008 (Table 3). The most significant reduction (improvement) is found for the along-track arc overlap.

Table 3 Mean values of the rms fits of SLR and DORIS measurements, 2-day arc overlaps, and the number of arcs used to compute these values for TOPEX/Poseidon (from 23 September 1992 to 9 October 2005), Jason-1 (from 13 January 2002 to 5 July 2013), and Jason-2 (from 5 July 2008 to 6 April 2015) orbits derived at the time intervals specified using ITRF2008 and ITRF2014. The percentage of the parameter change by switching from ITRF2008 to ITRF2014 is given in parentheses (positive value indicates an improvement).

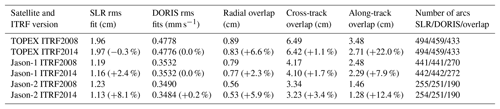
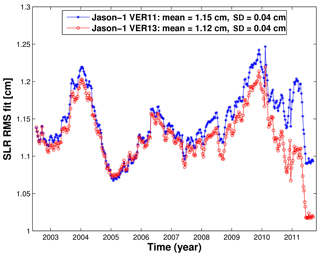
Figure 1 Fifty-two-week running mean of the rms fits of Jason-1 SLR observations obtained using ITRF2014 (VER13 orbit) and ITRF2008 (VER11 orbit) from 13 January 2002 to 16 February 2012. SD denotes standard deviation.

Figure 2 Fifty-two-week running mean of the rms fits of Jason-2 SLR observations obtained using ITRF2014 (VER13 orbit) and ITRF2008 (VER11 orbit) from 5 July 2008 to 6 April 2015. SD denotes standard deviation.

4 Impact of the change from ITRF2008 to ITRF2014 on the single-satellite altimetry crossover differences

Single crossover analyses for all three missions have been performed based on ESA CCI Sea Level v2 ECV data (Legeais et al., 2018). The data are available with a 1 Hz sampling rate, and all corrections for instrumental and geophysical effects by the state-of-the-art models are provided with the data. For consistency reasons, we replaced some internal correction models, in particular, the ocean tide and loading correction with the EOT11a tide model (Savcenko and Bosch, 2012) and the solid Earth tides following the IERS Conventions 2003 (McCarthy and Petit, 2004). The altimeter crossover differences (ascending pass minus descending pass) are calculated at a 10-day step with GFZ's Altimeter Database and Processing System (ADS; Schöne et al., 2010) for each test orbit (VER11 and VER13) separately. The global mean crossover difference and the associated rms values are calculated after applying a 3σ test. On average, about 5000 valid crossover points are found with some annual changes due to hemispheric change in sea ice coverage. To find valid crossover points, all internal quality criteria, which are part of the GDRs, are checked. In addition, we use only those points which meet the following criteria: deep water (with depth deeper than 200 m), wind speed less than 15 m s⁻¹, significant wave height less than 12 m, and crossover difference less than 1.5 m. The latter is especially valid in areas with sea ice occurrence. For all three missions, the rms of the crossover differences is around 5 cm. The non-zero mean of the crossover differences which indicates a constant offset in sea level heights between ascending and descending tracks is also notable. Comparing VER11 and VER13 results, the mean of the crossover differences becomes smaller for VER13, indicating smaller discrepancies between ascending and descending tracks. Also, a slight improvement of 0.01–0.13 mm in the rms of crossover differences is observed (Table 4) when replacing the VER11 orbit by the VER13 orbit. The quality of Jason-2 crossovers improves noticeably, indicating a better performance of the ITRF2014-based VER13 orbit.

Table 4 Statistics of crossover differences for orbits derived using ITRF2008 and ITRF2014. For Jason-1 the geodetic phase is not considered due to the change in crossover point distribution. The values are means over all 10-day analyses in millimeters.

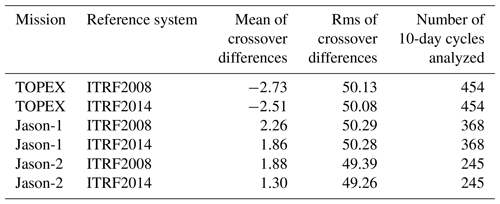
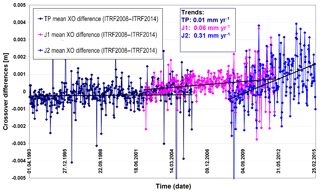
The evolution of the difference in the mean crossover difference per 10-day periods of VER11 minus VER13 orbits (Fig. 3), which emphasizes the changes in discrepancies between the ascending and descending tracks, is also of interest. The differences for TOPEX are stable over the full mission period with only minor variations. They can be attributed to very small changes in the radial orbit component. For Jason-1 a small, negligible drift of 0.06 mm yr⁻¹ can be observed. This (positive) drift indicates that for the VER13 orbits, the discrepancy between ascending and descending tracks becomes smaller with time. The drift in the difference for Jason-2 is much larger and reaches 0.31 mm yr⁻¹. It is also notable that starting around the middle of 2009, the differences for Jason-1 and Jason-2 show a sinusoidal signal with a period of about 120 days (the period is fixed to 10 days as per the analyses period) with amplitudes of around 4 mm. The larger scatter of crossover differences for the periods after the middle of 2009 shown in Fig. 3 are due to the fact that station positions used for the computation of satellite positions are computed in the case of using ITRF2008 by the extrapolation of station velocities derived by 2009.0 beyond this instant, while station velocities in the case of using ITRF2014 are derived by 2015.0. This is an indication of an error, introduced by an older ITRF realization used beyond the time span at which it was derived.

Figure 3 Differences of the crossover (XO) differences for the TOPEX (TP), Jason-1 (J1), and Jason-2 (J2) missions between VER11 and VER13 orbits. Values are in meters. The x axis shows time from 1 April 1993 to 25 February 2015.

5 Impact of the change from ITRF2008 to ITRF2014 on the radial orbit errors and geographically correlated mean sea surface height errors

In order to investigate the influence of using satellite orbits based on different realizations of the reference system on the precision and consistency of altimetry-derived sea level products, SSH crossover differences with a maximum time limit of 2 days are analyzed. For this purpose, a global multi-mission crossover analysis (MMXO) as described by Bosch et al. (2014) is applied to derive radial errors as well as geographically correlated error patterns for all three missions and for both orbit solutions. The comparison of the results obtained using ITRF2008 and ITRF2014 reveals valuable information on the product quality and consistency for different periods.

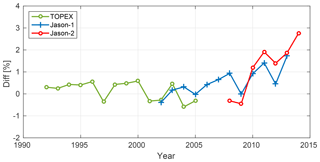
Figure 4 Relative difference (VER11-VER13) in the standard deviation of radial errors per year for three missions: TOPEX (green), Jason-1 (blue), and Jason-2 (red). Positive values indicate improvements for orbits based on ITRF2014.

For all three missions, slight improvements in the standard deviations of radial errors are obtained through the use of ITRF2014 orbits as can be seen in Table 5. The choice of the reference system only has a small impact on the overall scatter of the radial errors and changes the standard deviations by less than 1 mm for all missions. However, whereas for TOPEX and Jason-1, the improvement is less than 1 %, for Jason-2 an improvement of 1.6 % is visible. This larger relative improvement is partly related to the smaller scatter of radial errors. However, it is expected that the different behavior is also related to the measurement period of the missions. Thus, in order to access the temporal evolution of these values, standard deviations for each calendar year are computed. These values are plotted in Fig. 4 and reveal clear trends for Jason-1 and Jason-2. After 2010, observable improvements for all missions are visible reaching a maximum of nearly 3 % for Jason-2 in 2014.

Table 5 Standard deviations of the radial errors obtained using orbits of three satellites based on ITRF2008 and ITRF20014 and their differences (positive values indicate improvements for orbits computed using ITRF2014).

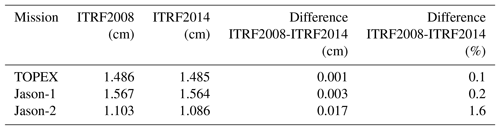
For many sea level applications, the most harmful errors are those with a fixed geographical pattern. Following the theory of Rosborough (1986), the MMXO provides geographically correlated mean SSH errors (GCEs) for all missions involved (Dettmering and Bosch, 2010; Dettmering et al., 2015). The change from ITRF2008 to ITRF2014 for orbit computation also influences the GCE. Figure 5 displays the GCE for VER13 orbits (based on ITRF2014) as well as the GCE differences to VER11 orbit solutions. One can see that for all three missions, the GCEs remain below about 1 cm and the change in ITRF accounts for less than 2 mm differences (positive as well as negative). Over the entire globe, the improvement yields 1.1 % for Jason-1 and 5.4 % for Jason-2 and a degradation by 1.3 % for TOPEX (in terms of reduction in standard deviation as can be seen from Table 6).

Table 6 Standard deviations of geographically correlated mean SSH errors obtained using orbits of three satellites based on ITRF2008 and ITRF20014 and their differences (positive values indicate improvements obtained for the orbits computed using ITRF2014).

Figure 5 Geographically correlated mean SSH errors for three missions based on ITRF2014 orbits (a, c, e) and VER11-VER13 differences (b, d, f) for TOPEX (a, b), Jason-1 (c, d), and Jason-2 (e, f); wrt.: with respect to, diff.: difference.

6 Impact of the change from ITRF2008 to ITRF2014 on regional and global mean sea level

We investigate the interannual signals and long-term trends of the regional and global mean sea level from altimetry related to the change from the ITRF2008 to ITRF2014. Since the radial orbit component maps directly onto the sea level measurement, it is possible to study the effect of the improved ITRF on global and regional sea level from altimetry by analyzing orbit data only. The main focus of this analysis is on timescales of more than 1 year.

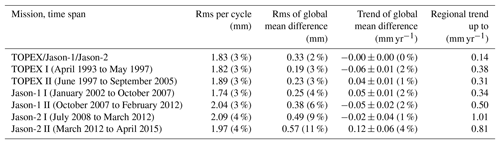
Table 7 Rms per cycle, rms, and trend of the global mean over the ocean and maximum regional (absolute) trend values from VER11 minus VER13 radial orbit differences for the combined TOPEX, Jason-1, and Jason-2 series and for subseries. The percentage of the ITRF-related changes relative to the total signal measured by altimetry is given in brackets for comparison.

We evaluate the VER11 minus VER13 radial orbit differences sampled over the oceans. The orbits calculated in ITRF2014 are converted to the ITRF2008 system by a Helmert transformation by applying the transformation parameters from Altamimi et al. (2016). Jason-1 data from the geodetic phase (starting in May 2012) are excluded from the analysis. The orbit differences are mapped cycle by cycle along-track and are interpolated on a $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ grid. From these data a global mean time series over the ocean is inferred. From the global mean and the $\mathrm{1}{}^{\circ }\times \mathrm{1}{}^{\circ }$ mapped time series, rms and trend values are estimated, as described by Esselborn et al. (2018).

A measure of the amount by which the radial components of the two orbits differ is the rms value per cycle (Fig. 6). Its mean value is 1.8 mm for the combined TOPEX, Jason-1, and Jason-2 VER11 minus VER13 series which corresponds to 3 % of the rms value per cycle of the corresponding sea level data from altimetry (Table 7). While the values for most of the TOPEX time series and also for the first few years of the Jason-1 series are below the mean, they are increased for the interleaved orbits of the TOPEX series (after the middle of 2002) and after the middle of 2006 for the Jason-1 and also the Jason-2 series.

The impact of the change in the ITRF solution on the estimated global mean sea level is minor. The rms of the global mean radial differences over the ocean is 0.3 mm, which corresponds to 2 % of the rms of the global mean sea level from altimetry over the corresponding period (Table 7). The rms of the global mean radial orbit differences over the ocean is slightly higher for Jason-2 than for the TOPEX and Jason-1 missions. The global mean radial orbit differences are of the order of 0.5 mm for TOPEX and of 0.3 mm for Jason-1 and Jason-2. This offset between the two ITRFs is consistent with a slight shift (a few mm) in the VER13 origin from the South Pacific in the direction of Eurasia relative to the origin of the VER11 orbits. Such a shift is, most probably, related to slight changes in the positions of the tracking station network.

The spectral analysis of the global mean radial orbit differences over the ocean shows that most of the energy can be found for periods of less than 110 days; however, this analysis focuses on the interannual to decadal timescales. The low-pass filtered time series of the global mean VER11 minus VER13 radial orbit differences over the ocean is shown in Fig. 7. The global mean sea level trend over the oceans is not affected by the switch from the ITRF2008 to the ITRF2014 realization for POD (Table 7). However, the global mean of the VER11 minus VER13 series (Fig. 7) exhibits interannual- to decadal-scale variability. In order to study these effects in detail we define the following four periods, which are covered by the denoted missions from the inflection points of the time series:

1. April 1993 to May 1997 (TOPEX I),

2. June 1997 to October 2007 (TOPEX II, Jason-1 I),

3. October 2007 to March 2012 (Jason-1 II, Jason-2 I),

4. March 2012 to April 2015 (Jason-2 II).

For these periods, the trends of the global mean radial orbit differences range between −0.06 and 0.12 mm yr⁻¹, which corresponds to up to 4 % of the sea level trend from altimetry over the corresponding periods (Table 7). The geographical patterns of the trends for these four periods are given in Fig. 8. Note that the trend patterns for Jason-1 I and Jason-2 I (not shown) resemble closely the patterns for TOPEX II and Jason-1 II (shown). The changes in the global and regional trends strongly depend on the analyzed period of time (see Table 7 and Fig. 7). For the first two periods (up to 2007), the trend patterns are consistent with relative drifts of the Z components of the origins with a change in direction in 1997. The regional trends in this period reach maximum values of 0.3 to 0.4 mm yr⁻¹. For the last two periods, relative drifts of the origin in the horizontal plane are dominant. The regional trends after 2007 reach maximum values of 0.5 to 1 mm yr⁻¹. The changes in the regional sea level trend (up to 0.14 mm yr⁻¹) found by us from the analysis of TOPEX, Jason-1, and Jason-2 for the period 1993 to 2015 agree with those (up to 0.2 mm yr⁻¹) obtained by Zelensky et al. (2018) by using the same altimetry missions for the period 1992 to 2016.

The uncertainties in global mean sea level trends due to the TRF realization have decreased considerably during the last decades. Beckley et al. (2007) reported global mean sea level changes of 0.44 mm yr⁻¹ related to the change from ITRF2000 to ITRF2005. The change from ITRF2005 to ITRF2008 still led to apparent global sea level drifts of 0.05 mm yr⁻¹ (Couhert et al., 2015) at the decadal timescale. For the change from ITRF2008 to 2014, Zelensky et al. (2018) – based on five GSFC orbits - estimated an uncertainty in the global mean sea level of 0.03 mm yr⁻¹. According to our studies the global mean sea level trend for the 22-year series is hardly impacted at all. This is a major improvement with respect to the previous TRF realizations. The uncertainties in the global mean sea level trends have been dominated by uncertainties in the z coordinate of the origin (Beckley et al., 2007). From our analyses we observe corresponding patterns until 2008, even though the amplitudes decreased by a factor of 4. After 2008 the uncertainties in the horizontal coordinates of the origin increasingly impact regional sea level drifts.

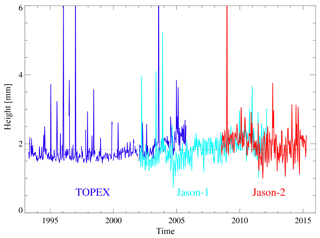
Figure 6 Global mean rms per cycle of gridded radial orbit differences (VER11-VER13) for TOPEX (blue), Jason-1 (cyan), and Jason-2 (red). The mean value is marked by the dashed line.

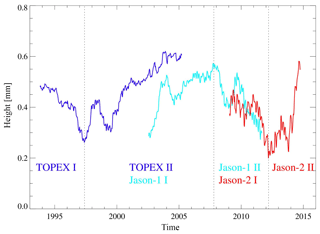
Figure 7 Mean radial height differences (VER11-VER13) over the global ocean low pass filtered by 1-year boxcar filter for TOPEX (blue), Jason-1 (cyan), and Jason-2 (red). The sub-periods used for the calculation of trends are marked by dashed lines.

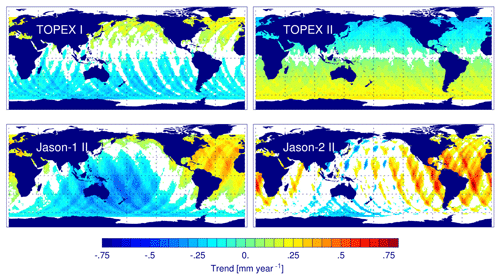
Figure 8 Trend differences in radial orbit components for VER11-VER13 for four periods. TOPEX I: April 1993–May 1997; TOPEX II: June 1997–September 2005; Jason-1 II: October 2007–February 2012; Jason-2 II: March 2012–April 2015. Regions with formal errors larger than the fitted value are masked out (white). The global mean trend difference is given in Table 7.

7 Conclusions

From the analysis of TOPEX/Poseidon (September 1992 to October 2005), Jason-1 (January 2002 to July 2013), and Jason-2 (July 2008 to April 2015) orbits computed by us using the ITRF2008 and ITRF2014 realizations, we have found that using ITRF2014 generally improves the orbit quality as compared to using ITRF2008. Thus, the mean values of the rms fits of SLR observations are reduced (improved) by 2.4 % and 8.8 % for Jason-1 and Jason-2, respectively, and are almost not impacted for TOPEX/Poseidon when using ITRF2014 instead of ITRF2008. At the same time, the replacement of ITRF2008 by ITRF2014 has a minor impact (less than 0.1 %) on the rms fits of DORIS observations of TOPEX/Poseidon and Jason-1. A slightly larger impact has been found for Jason-2, for which the mean values of DORIS rms fits are reduced (improved) by about 0.2 % over the whole time span (2008–2015) and a larger improvement of 0.3–1.0 % is observed in 2012–2015.

The internal orbit consistency in the radial direction being important for altimetric applications and being characterized by the satellite position differences in this direction at 2-day arc overlaps is reduced (improved) by 7.1 %, 2.4 %, and 5.1 % for TOPEX/Poseidon, Jason-1, and Jason-2, respectively. The internal orbit consistency in the cross-track direction improved by 1.1 % for TOPEX/Poseidon, 1.7 % for Jason-1, and 3.4 % for Jason-2 in the time spans analyzed when using ITRF2014 instead of ITRF2008. Even more significant improvement of the internal orbit consistency has been obtained in the along-track direction: by 22.0 % for TOPEX/Poseidon, 7.9 % for Jason-1, and 12.4 % for Jason-2.

Single-satellite altimetry crossover analyses indicate a reduction (improvement) in the absolute mean crossover differences by 0.2 mm (8.1 %) for TOPEX, 0.4 mm (17.7 %) for Jason-1, and 0.6 mm (30.9 %) for Jason-2 with ITRF2014 instead of ITRF2008. The reduction in the mean of crossover differences indicates reduction in the discrepancies between ascending and descending tracks when using ITRF2014 instead of ITRF2008. The mean values of the rms of crossover differences also show a reduction (improvement) when using ITRF2014 instead of ITRF2008 but to a lesser extent: by 0.05 mm (0.1 %) for TOPEX, 0.01 mm (0.02 %) for Jason-1, and 0.13 mm (0.3 %) for Jason-2.

Multi-mission crossover analysis shows slight improvements in the standard deviations of radial errors through the switch from ITRF2008 to ITRF2014 for POD: 0.1 % for TOPEX, 0.2 % for Jason-1, and 1.6 % for Jason-2. The standard deviations of geographically correlated mean SSH errors improved by 1.1 % for Jason-1 and 5.4 % for Jason-2 but degraded by 1.3 % for TOPEX.

The change from ITRF2008 to ITRF2014 orbits only has minor effects on the estimation of regional and global sea level trends over the 22-year time series from 1993 to 2015. However, on interannual timescales (3–8 years) large-scale coherent trend patterns are observed that seem to be connected to drifts between the origins of the tracking station networks. This leads to changes in the global interannual trends of up to 0.06 mm yr⁻¹ for TOPEX, 0.05 mm yr⁻¹ for Jason-1, and up to 0.12 mm yr⁻¹ for Jason-2, which corresponds to changes of up to 4 % in the actual sea level trends from altimetry. The respective changes in the regional sea level trend reach maximum values of 0.4 mm yr⁻¹ for TOPEX, of 0.5 mm yr⁻¹ for Jason-1, and of 1.0 mm yr⁻¹ for Jason-2. While until 2008 regional sea level drifts are mainly related to uncertainties in the z coordinate of the origin, recently uncertainties in the horizontal coordinates have become increasingly important. This shows the effects of the increasing uncertainties in the tracking station positions and velocities in ITRF2008 after 2009.0 on the estimated regional sea level trends. For this period the user requirements for the error of the regional mean sea level (Ablain et al., 2015) cannot be met everywhere when using ITRF2008 orbits.

Our analyses show that the use of ITRF2014 instead of ITRF2008 slightly improves the satellite orbits as well as the derived sea level values since 1993. The analyses and statistics for TOPEX/Poseidon show the differences between the two ITRF realizations until 2005. More evident improvements are found from 2009.0 for Jason-1 and, in particular, for Jason-2. This is in agreement with the results obtained by Rudenko et al. (2018a) and Zelensky et al. (2018). To minimize errors caused by the extrapolation of station velocities beyond the time span at which they had been derived, ITRS realizations should be regularly (at least every 5–6 years) updated. Therefore, it is strongly recommended to use the new ITRS realization for precise orbit determination for the time span beyond the time instant of the end of the time interval used for the generation of a previous ITRS realization. This also stresses a need for the periodical reprocessing of altimetry satellite orbits using a new ITRS realization to get reliable and high-accuracy altimetry products.