The physics of fault friction: insights from experiments on simulated gouges at low shearing velocities

The strength properties of fault rocks at shearing rates spanning the transition from crystal–plastic flow to frictional slip play a central role in determining the distribution of crustal stress, strain, and seismicity in tectonically active regions. We review experimental and microphysical modelling work, which is aimed at elucidating the processes that control the transition from pervasive ductile flow of fault rock to rate-and-state-dependent frictional (RSF) slip and to runaway rupture, carried out at Utrecht University in the past 2 decades or so. We address shear experiments on simulated gouges composed of calcite, halite–phyllosilicate mixtures, and phyllosilicate–quartz mixtures performed under laboratory conditions spanning the brittle–ductile transition. With increasing shear rate (or decreasing temperature), the results consistently show transitions from (1) stable velocity-strengthening (v-strengthening) behaviour, to potentially unstable v-weakening behaviour, and (2) back to v strengthening. Sample microstructures show that the first transition seen at low shear rates and/or high temperatures represents a switch from pervasive, fully ductile deformation to frictional sliding involving dilatant granular flow in localized shear bands where intergranular slip is incompletely accommodated by creep of individual mineral grains. A recent microphysical model, which treats fault rock deformation as controlled by competition between rate-sensitive (diffusional or crystal–plastic) deformation of individual grains and rate-insensitive sliding interactions between grains (granular flow), predicts both transitions well. Unlike classical RSF approaches, this model quantitatively reproduces a wide range of (transient) frictional behaviours using input parameters with direct physical meaning, with the latest progress focusing on incorporation of dynamic weakening processes characterizing co-seismic fault rupture. When implemented in numerical codes for crustal fault slip, the model offers a single unified framework for understanding slip patch nucleation and growth to critical (seismogenic) dimensions, as well as for simulating the entire seismic cycle.

1 Introduction

Earthquakes are the result of a sudden release of energy during rapid slip (> 1 m s⁻¹) along geologic fault zones in the Earth's crust or upper mantle, which generates seismic waves that can be highly destructive at the Earth's surface. Throughout history, earthquakes and associated tsunamis have claimed countless lives and caused severe material and economic damage (Guha-Sapir et al., 2016), with their impact increasing today as urban populations in tectonically active regions continue to increase. It is therefore of utmost importance to improve prognoses on the frequency, location, and magnitude of future seismic events. This demands sophisticated modelling of earthquake nucleation and dynamic rupture propagation, which in turn requires a fundamental understanding of fault sliding, or more specifically the internal fault rock shearing mechanisms that are active under in situ conditions in the Earth.

Tectonically loaded faults can exhibit aseismic slip transients (“creep”) without producing earthquakes, or else sporadic unstable slip, resulting in slow-slip events or catastrophic failure as is the case for earthquakes (Scholz et al., 1969; Peng and Gomberg, 2010). Unstable or seismic fault motion can occur at the lithosphere scale, such as along subduction zone megathrusts (Simons et al., 2011; Nishikawa et al., 2019), at the reservoir scale as in the case of human-induced seismicity (Elsworth et al., 2016; Grigoli et al., 2018), and also within millimetre- to metre-scale samples in the laboratory (Passelègue et al., 2013; Yamashita et al., 2015; Ikari, 2019). The fault zones involved typically show a multi-scale, self-affine structure characterized by shear strain localization into narrow principal slip zones (PSZs) (Tchalenko, 1970; King, 1983; Sibson, 2003), suggesting that the rheology of the comminuted fault rock or “gouge” within PSZs controls macroscopic fault behaviour. From a mechanistic point of view, improvement of seismic hazard assessments and forecasting requires rationalization of the physics of the earthquake source as controlled by the material properties of, and deformation processes active within, sheared fault rock.

Laboratory investigations of fault slip performed under conditions relevant to Earth's upper crust are key to probing the physics of fault behaviour and seismogenesis. The mechanical data serve as direct input for empirically based numerical simulations of fault rupture (e.g. Tse and Rice, 1986; Noda and Lapusta, 2013), while post-mortem observations of recovered deformed specimens can be used to infer the underlying physical processes controlling deformation (e.g. Gu and Wong, 1994; Heilbronner and Keulen, 2006; Peč et al., 2016). In general, we can distinguish two types of laboratory fault-slip experiments. Firstly, low-velocity friction (LVF) tests are used to investigate both stable fault creep and the early (nucleation) stages of earthquake rupture. These LVF experiments are typically conducted at imposed shearing velocities (v) of nanometres to micrometres or millimetres per second under fixed conditions of normal stress (σ_n) and temperature (T). Secondly, high-velocity friction (HVF) tests are used to investigate dynamic earthquake slip processes that occur during unstable, runaway slip at slip velocities of 1 to 10 m s⁻¹(see Heaton, 1990). In HVF tests, frictional heating at the slipping fault interface triggers thermally activated processes such as pore fluid pressurization, phase changes, and melting, which come to dominate the evolution of fault strength (Rice, 2006; Di Toro et al., 2011; Yao et al., 2016; Rattez and Veveakis, 2020). In recent years, technological improvements in both LVF and HVF apparatuses, as well as electron beam and other instruments used to perform post-mortem micro- and nanostructural analyses, have enabled major advances in the understanding of fault rock material properties and crustal fault rheology (for reviews see De Winter et al., 2009; Viti, 2011; Niemeijer et al., 2012; Rowe and Griffith, 2015; Chen et al., 2015a).

In this paper we integrate findings from experimental, microstructural, microphysical, and numerical modelling studies of the frictional behaviour of gouge-filled faults in the low-velocity or nucleation regime conducted at Utrecht University (UU) in the past 2 decades or so. Our aim is to provide a unified view of the physics of fault friction behaviour at low velocities. We begin with a summary of key concepts and definitions, followed by a summary of the LVF experimental techniques used at UU. We go on to present key results from experiments on simulated faults composed of halite–phyllosilicate and phyllosilicate–quartz mixtures, as well as of calcite. Data from these experiments consistently suggest that low velocity frictional deformation of fault gouge is controlled by competition between rate-sensitive (diffusional or crystal–plastic) deformation and rate-insensitive sliding interactions (dilatant granular flow) – competition which was already suggested on the basis of theoretical considerations by Rutter and Mainprice (1979). This forms the foundation for a unified microphysical modelling approach for low-velocity sliding and static healing of gouge-filled faults, described in progressive detail by Niemeijer and Spiers (2007) and by Chen and Spiers (2016), for example, and referred to here for convenience as the Chen–Niemeijer–Spiers (CNS) model. We outline the principles of this model and present some applications and implications for reproducing laboratory data and numerical simulations of earthquake nucleation and the full earthquake cycle.

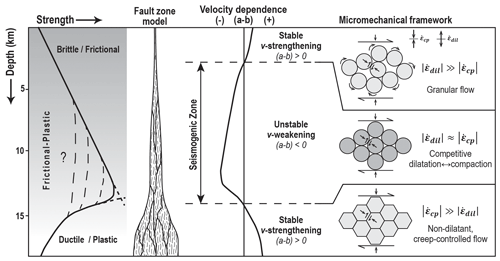
Figure 1 Conceptual model for an upper-crustal fault zone, highlighting the frictional-to-viscous transition and the seismogenic zone, which is characterized by v-weakening friction (i.e. (a−b) < 0); after Sibson (1982, 1983) and Scholz (1988, 2019). On the far right we summarize implications from the CNS model for shear of gouge-filled faults involving competition between creep-controlled compaction and dilatation by granular flow (occurring at rates of ${\dot{\mathit{\epsilon }}}_{\mathrm{cp}}$ and ${\dot{\mathit{\epsilon }}}_{\mathrm{gr}}$, respectively). For model details see Bos and Spiers (2002a), Niemeijer and Spiers (2006, 2007), and Chen and Spiers (2016).

2 Crustal fault strength and fault-slip models

The strength of the Earth's crust is classically approximated using a Coulomb-type, brittle–frictional failure law representing the upper part, which abruptly gives way to ductile deformation (here used synonymously with “plastic” deformation to indicate non-dilatant permanent deformation) below ∼ 10 to 20 km of depth depending on the geothermal gradient (Fig. 1) (Byerlee, 1978; Brace and Kohlstedt, 1980; Kohlstedt et al., 1995). A brittle-to-ductile transition within this depth range is consistent with geological and seismological observations of a depth interval in the crust where the majority of earthquakes nucleate, known as the “seismogenic zone” (Sibson, 1982, 1983; Meissner and Strehlau, 1982; Scholz, 1988, 2019). In the fully ductile regime, stress build-up and associated rupture nucleation are inhibited by plastic flow in shear zones, which is achieved by solid-state diffusive mass transfer and/or dislocation-mediated deformation mechanisms active at the grain scale (e.g. Karato, 2008). Within the seismogenic zone and shallower, field and laboratory observations on a wide range of fault rock types point to the concurrent operation of brittle–frictional (cataclastic) processes that depend linearly on effective normal stress and rate-sensitive plastic deformation (e.g. pressure solution, dislocation- or diffusion-mediated creep) (Wintsch et al., 1995; Holdsworth et al., 2001; Imber et al., 2008; Collettini et al., 2011; Siman-Tov et al., 2013; Fagereng et al., 2014; Delle-Piane et al., 2018; Verberne et al., 2019). The relation between this “frictional–plastic” deformation of fault rock and seismogenesis, including the competing effects between time-sensitive and -insensitive deformation processes on failure, creep, compaction, and healing, as well as how these control the depth range of the seismogenic zone, remains the subject of intensive study in fault mechanics and fault geology (e.g. Fagereng and Den Hartog, 2016; Gao and Wang, 2017; Reber and Peč, 2018; Aharonov and Scholz, 2018, 2019; Collettini et al., 2019; Masuda et al., 2019; Hirauchi et al., 2020).

In a strictly phenomenological sense, earthquakes are analogous to the recurring frictional instability that is frequently observed in laboratory rock friction experiments known as “stick-slip” (Brace and Byerlee, 1966). Byerlee (1970) proposed that a frictional instability may arise from sudden weakening of the fault interface combined with a sufficiently low shear stiffness of the surrounding medium (experimental apparatus or host rock). However, this “slip-weakening” model does not include a mechanism for the intrinsic fault restrengthening or “healing” which is required to account for long-term, repetitive slip events (Dieterich, 1979a). To capture the time- and sliding-velocity-dependent effects of fault friction in an empirical way, Dieterich (1979a, b) proposed a rate- and “age”-dependent friction model that was later recast by Ruina (1983) in terms of the rate-and-state-dependent friction equations (RSFs), given by

$$\begin{array}{}\text{(1)}& \mathit{\mu }={\mathit{\mu }}_{\mathrm{ss}}^{\ast }+a\ln \left({\displaystyle \frac{v}{v^{\ast }}}\right)+b\ln \left({\displaystyle \frac{v_{\mathrm{0}}\mathit{\theta }}{d_{\mathrm{c}}}}\right),\end{array}$$

$$\begin{array}{}\text{(2a)}& {\displaystyle }\dot{\mathit{\theta }}=\mathrm{1}-{\displaystyle \frac{v\mathit{\theta }}{d_{\mathrm{c}}}},\text{(2b)}& {\displaystyle }\dot{\mathit{\theta }}=-{\displaystyle \frac{v\mathit{\theta }}{d_{\mathrm{c}}}}\ln \left({\displaystyle \frac{v\mathit{\theta }}{d_{\mathrm{c}}}}\right),\end{array}$$

where μ is the coefficient of friction defined as shear stress over effective normal stress (ignoring cohesion), ${\mathit{\mu }}_{\mathrm{ss}}^{\ast }$ is the steady-state coefficient of friction at a reference sliding velocity v^∗, v is the instantaneous slip velocity, a is a parameter that quantifies the “direct effect”, b is the parameter that describes the “evolution effect”, and d_c is a characteristic or critical slip distance over which the state variable, θ, evolves (for reviews see Marone, 1998; Scholz, 1998, 2019). The state variable θ has units of time and is thought to represent the average lifetime of grain-scale asperity contacts (at steady state). The conceptual interpretation of RSF finds its origin in two observations, namely that the true area of contact of any interface is always smaller than the nominal contact area and that this area of contact changes with time (Bowden and Tabor, 1950, 1964; Rabinowicz, 1956, 1958; Dieterich and Kilgore, 1994). The equations for the state variable time derivative ($\dot{\mathit{\theta }}$; Eqs. 2a and 2b) embody two views of how a population of contacts may evolve during slip. Equation (2a) is sometimes called the “slowness” or “ageing” (Dieterich) law because in this formulation, the frictional contact area continues to evolve in the absence of slip, whereas in Eq. (2b), slip is needed for the state variable to evolve. Accordingly, the latter equation is called the “slip” (Ruina) law.

In the case of steady-state sliding ($\mathit{\mu }={\mathit{\mu }}_{\mathrm{ss}};\dot{\mathit{\theta }}=\mathrm{0}$) both the slowness and slip laws reduce to

$$\begin{array}{}\text{(3)}& {\mathit{\mu }}_{\mathrm{ss}}={\mathit{\mu }}_{\mathrm{ss}}^{\ast }+\left(a-b\right)\ln \left({\displaystyle \frac{v}{v^{\ast }}}\right),\end{array}$$

where (a−b) represents a dimensionless quantity that characterizes the velocity (v) dependence of the sliding surface. Ruina (1983) showed that for an instability to nucleate spontaneously and repeatedly (i.e. the case of stick-slip), the sliding surface must decrease in strength with increasing velocity and hence be v weakening, characterized by (a−b) < 0. In the opposite case v strengthening occurs, characterized by (a−b) > 0, which leads to a state of stable sliding (Ruina, 1983; Rice and Ruina, 1983). Linear stability analysis of a single-degree-of-freedom spring–slider model demonstrated a critical stiffness K_c below which sliding is unstable (Ruina, 1983).

$$\begin{array}{}\text{(4)}& K_{\mathrm{c}}={\displaystyle \frac{\left(b-a\right)\cdot {\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}}{d_{\mathrm{c}}}}\end{array}$$

Thus, an instability may occur when the stiffness of the deforming medium falls below K_c and (a−b) < 0. Importantly, when applied to natural faults, the (a−b) value or v dependence of the sliding medium is a material property of deforming rock in the fault core, and its constitutive properties are strongly affected by coupled thermo–hydro–mechanical–chemical processes in the general sense. With reference to the Earth's crust and Fig. 1, the seismogenic zone is believed to represent the depth interval where shear deformation of fault rock leads to v-weakening behaviour, as opposed to v strengthening above and below.

The RSF approach has enabled a simple and highly successful description of laboratory rock friction behaviour over a wide range of conditions (Marone, 1998; Scholz, 1998, 2019) and is widely used in numerical simulations of the earthquake cycle (e.g. Dieterich, 1994; Lapusta and Rice, 2003; Ampuero and Rubin, 2008; Matsuzawa et al., 2010; Noda and Lapusta, 2013; Ohtani et al., 2014). However, laboratory observations and microphysical modelling show that the empirically fitted parameters appearing in the RSF equations, notably the values of (a−b) and d_c, are not fundamental independently measurable material constants (Ikari et al., 2016; Aharonov and Scholz, 2018). The implication is that extrapolation to natural conditions not attainable in the laboratory presents a significant source of uncertainty in numerical modelling (for a discussion see Ide, 2014; Van den Ende et al., 2018). To address this, a (micro)physically based interpretation and description of the processes controlling fault deformation is needed. Based on data from friction experiments on simulated quartz gouges at room temperature, Marone et al. (1990) hypothesized that dilatation and shear strain localization play a key role in controlling gouge shear strength and velocity dependence. Despite the key importance and application of their experimental findings and conceptual explanation (see e.g. Segall and Rice, 1995; Beeler et al., 1996), friction models derived from this pioneering work and fitted to experimental data lack a rigorous microphysical basis. An example of a mechanistically based and microstructurally founded model developed to explain v-dependence effects of fault rock friction, proposed by Bos, Niemeijer, and Spiers (Bos et al., 2002a; Niemeijer and Spiers, 2006, 2007), is based on the accommodation of shear deformation by a combination of frictional and plastic deformation processes. It was demonstrated that if the rates of intergranular compaction (${\dot{\mathit{\epsilon }}}_{\mathrm{cp}}$) and dilatation (${\dot{\mathit{\epsilon }}}_{\mathrm{dil}}$) are of comparable magnitude, or $\left|{\dot{\mathit{\epsilon }}}_{\mathrm{dil}}\right|\approx \left|{\dot{\mathit{\epsilon }}}_{\mathrm{cp}}\right|$, this leads to v-weakening behaviour, whereas under conditions in which either process dominates, stable v strengthening occurs. In other words, in this framework the seismogenic zone corresponds to a depth interval where shear deformation of gouge-filled faults is characterized by $\left|{\dot{\mathit{\epsilon }}}_{\mathrm{dil}}\right|\approx \left|{\dot{\mathit{\epsilon }}}_{\mathrm{cp}}\right|$ (Fig. 1).

3 Low-velocity friction (LVF) testing methods

Research on low-velocity rock friction at UU includes fault-slip experiments under pressure–temperature conditions that range from ambient surface conditions to those relevant throughout the upper ∼ 20–30 km of the Earth's crust. To achieve this, the ring- and direct-shear testing methods developed at UU, which are summarized below, play a critical role. For more details on the testing procedures and data analysis methods employed we refer to the various papers cited.

Figure 2 Apparatuses and testing assemblies used for low-velocity, ring- and direct-shear friction experiments at UU. (a, b) The room-temperature ring-shear set-up. (b, e) The hydrothermal ring-shear set-up. (c, f) The direct-shear set-up using a triaxial pressure cell (in this case the “shuttle vessel”). Photo (a) courtesy of Miki Takahashi (Geological Survey of Japan). Photo (d) taken with publishers' permission from Van den Ende and Niemeijer (2019).

Ring-shear LVF experiments at UU are conducted using two distinct set-ups that are interchangeable within a single rotary shear deformation apparatus consisting of an Instron loading frame with electrically actuated ram for axial loading (application of normal stress) plus a rotation drive for imposing shear displacement onto the sample (Fig. 2a, b). The earliest ring-shear assembly, developed in the late 1990s (Bos et al., 2000a), enables simulated fault sliding tests at room temperature and at elevated normal stresses and pore fluid pressures (up to ∼ 10 MPa), achieving in principle unlimited rotational displacements. The simulated fault sliding rates that can be achieved depend on the arrangement of gear boxes used and range from 3 nm s⁻¹ to up to 1 cm s⁻¹. The assembly consists of two grooved piston rings (inner diameter 80 mm, outer diameter 100 mm) that grip a ∼ 1–2 mm thick, annular sample layer upon the application of normal stress, with radial confinement facilitated by tightly fitting inner and outer rings (Fig. 2a, d). This room-temperature ring-shear set-up has played an important role in investigations of shear deformation of monomineralic halite and halite–phyllosilicate mixtures (e.g. Takahashi et al., 2017; Van den Ende and Niemeijer, 2019), as well as of granular system dynamics using synthetic polymer and glass beads (Kumar et al., 2020).

A later “hydrothermal” ring-shear assembly was designed and commissioned in 2002–2005 (Fig. 2b, e) with the aim of enabling high-shear-strain rotary shear tests under pressures, temperatures, and displacement rates representative for the seismogenic reaches of crustal-scale faults and subduction megathrusts (Niemeijer et al., 2008; Van Diggelen et al., 2010; Den Hartog et al., 2012a, b). In this set-up, the piston–sample assembly is located in a pressure vessel with an internal furnace, which in turn is emplaced within the Instron frame with a rotation drive (Fig. 2b). A ∼ 1 mm thick sample layer is sandwiched between a set of grooved pistons and prevented from extruding by an inner confining ring with a diameter of 22 mm and an outer confining ring with a diameter of 28 mm (Fig. 2e). The vessel is pressurized with water, which has direct access to the sample, thus providing the pore fluid pressure. Experiments in this set-up can be conducted at effective normal (axial) stresses up to 300 MPa (provided by the Instron frame), temperatures up to 700 ^∘C, and pore fluid pressures up to 300 MPa. The rotary drive system provides simulated fault zone displacement rates ranging from around 1 nm s⁻¹ to several millimetres per second. The maximum rotation or shear displacement that can be achieved is limited by the connections of the water cooling and pore fluid systems to their respective external reservoirs, but it is in practice very large (> 100 mm). The hydrothermal ring-shear machine has been used extensively in investigations of the shear behaviour of rock compositions believed to be widespread along subduction megathrust faults (e.g. Hirauchi et al., 2013; Ikari et al., 2013; Sawai et al., 2016, 2017; Kurzawski et al., 2016, 2018; Boulton et al., 2019; Okamoto et al., 2019, 2020) and in the upper and middle continental crust (Niemeijer and Collettini, 2014; Niemeijer and Vissers, 2014; Niemeijer et al., 2016; Hellebrekers et al., 2019).

Direct-shear tests are carried out using a “conventional”, externally or internally heated, oil-medium, triaxial deformation apparatus, such as that shown in Fig. 2c. Following the design of Logan et al. (1992), the direct-shear or “69” assembly comprises two L-shaped pistons in a jacketed face-to-face (⌊⌉) arrangement that sandwiches a cuboid sample (Fig. 2f). A soft, near-Newtonian viscous material (such as silicone putty) or soft elastomer fills the voids at the top and bottom of the assembly (Samuelson and Spiers, 2012; Sánchez-Roa et al., 2016). In the set-up used at UU, the sample measures 35 mm wide by 49 mm long with a thickness of typically ∼ 1 mm. Direct-shear experiments can be carried out at confining pressures (normal stress) and pore pressures up to 100 MPa and temperatures up to 150 ^∘C, reaching shear displacements up to ∼ 6 mm. The direct-shear assembly has proven especially useful for tests employing corrosive pore fluid compositions such as reservoir brine or CO₂ (e.g. Pluymakers et al., 2014; Pluymakers and Niemeijer, 2015; Bakker et al., 2016; Hunfeld et al., 2017, 2019).

4 Low-velocity friction experiments on simulated gouges – some case studies

4.1 Halite–phyllosilicate mixtures

Bos et al. (2000a, b) and Bos and Spiers (2000, 2001, 2002a, b) employed the room-temperature ring-shear assembly (Fig. 2a, d) to investigate the shear behaviour of brine-saturated, simulated fault gouge composed of (mixtures of) halite and kaolinite. The Bos et al. experiments were carried out under conditions favouring rapid pressure solution in the halite–brine system, which is well-constrained from compaction tests and microphysical modelling (Spiers et al., 1990; Spiers and Schutjens, 1990). Kaolinite was added in varying proportions to investigate the effect on shear behaviour while simulating the presence of phyllosilicates that are observed to be widespread in natural fault zones (Wintsch et al., 1995; Holdsworth, 2004; Takeshita and El-Fakharani, 2013). The aim was to elucidate the combined role of pressure solution creep and foliation development in controlling the strength of faults in the upper crust, viewing the halite–kaolinite mixtures as a mid-crustal rock analogue (see e.g. Shimamoto, 1986; Hiraga and Shimamoto, 1987; Chester and Logan, 1990). Velocity (v) and normal stress (σ_n) stepping experiments (Fig. 3a), as well as post-mortem microstructural analyses which revealed a classical foliated mylonitic (i.e. phyllonitic) microstructure (Fig. 3b), pointed to frictional–viscous flow in the case of halite–kaolinite mixtures but to purely frictional behaviour in the case of the monomineralic endmember gouges (Fig. 3a). Based on these results, Bos and Spiers (2001, 2002a) proposed a micromechanical model for the combined effect of frictional sliding on phyllosilicate folia, pressure solution of halite clasts, and dilatation on the foliation (Fig. 3c). This model offered the first microstructurally based interpretation for v-strengthening frictional–viscous flow of gouge-filled faults.

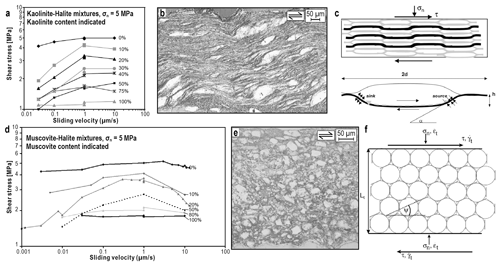
Figure 3 Data from ring-shear experiments on halite–phyllosilicate mixtures conducted at room temperature. (a, b) Halite–kaolinite mixtures deformed in the v-strengthening frictional–viscous regime (adapted from Bos et al., 2000b – license no. 4656341028661). (c) Model microstructure for v-strengthening frictional–viscous flow (taken with publisher's permission from Bos and Spiers, 2002a). σ_n: normal stress; τ: shear stress; α: the angle between the leading edge of the halite grain and the horizontal; h: amplitude of the foliation; d: grain size (long axis). (d) Velocity dependence effects in halite–muscovite gouges (adapted from Niemeijer and Spiers, 2006 – license no. 4656330624652), with (e) a sample deformed in the v-weakening regime (taken with publisher's permission from Niemeijer and Spiers, 2005). (f) Model microstructure for v-weakening granular flow (taken with publisher's permission from Niemeijer and Spiers, 2007). ${\dot{\mathit{\epsilon }}}_{\mathrm{t}}$: macroscopic normal strain rate; ${\dot{\mathit{\gamma }}}_{\mathrm{t}}$: macroscopic shear strain rate; ψ: dilatation angle; L_t: thickness of the deforming zone; other symbols are the same as in (c).

Niemeijer and Spiers (2005) refined the Bos and Spiers model by incorporating effects of plasticity of phyllosilicate folia and a distributed grain size. Moreover, their experiments used muscovite instead of kaolinite and covered a wider range of sliding velocities. Their experiments revealed a v-weakening regime beyond v=1 µm s⁻¹ (Fig. 3d), characterized by a strong increase in porosity with increasing v (Niemeijer and Spiers, 2005, 2006). Compared with v-strengthening samples, those deformed under v-weakening conditions showed a chaotic, cataclastic microstructure (Fig. 3e). On this basis it was hypothesized that v weakening results from competition between dilatation by granular flow and intergranular compaction by pressure solution (Niemeijer and Spiers, 2006). This microphysical model concept was further developed and quantified to enable calculation of steady-state shear strength in the v-weakening regime based on physically meaningful input parameters such as the kinetics parameters for pressure solution, porosity, and dilation angle for granular flow (Niemeijer and Spiers, 2007) (Fig. 3f). By combining the model for frictional–viscous flow with that for v-weakening frictional sliding, the lab-observed transition from v strengthening to weakening with increasing shear displacement rate in halite–phyllosilicate mixtures could be accurately reproduced.

4.2 Phyllosilicate–quartz mixtures

The experiments using halite–phyllosilicate mixtures as a fault rock analogue system trigger the inevitable question of whether the same processes and mechanical behaviour really occur within crustal faults. Specifically, the microphysical models developed for v dependence of gouge-filled faults required testing for real crustal fault rock types under conditions relevant for the seismogenic zone. With this in mind, Den Hartog et al. (2012a, b, 2013, 2014) investigated the frictional behaviour of phyllosilicate–quartz gouge mixtures using the hydrothermal ring-shear apparatus (Fig. 2b, d) under P–T conditions broadly representative for the seismogenic reaches of a subduction zone megathrust. The samples consisted mainly of 465:35 illite–quartz gouge mixtures, but muscovite–quartz gouge mixtures and clay-rich samples derived from the Nankai Oceanic Drilling Project (Leg 190) were also tested. Experiments were carried out at effective normal stresses (${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}$) ranging from 25 to 200 MPa, at pore fluid pressures (P_f) of 0 (dry) to 200 MPa, and temperatures (T) of 100 to 600 ^∘C. The data consistently showed v-strengthening behaviour at relatively low temperatures (up to ∼ 250–350 ^∘C, Regime 1), v weakening at intermediate temperatures (∼ 250–500 ^∘C, Regime 2), and again v strengthening at the highest temperatures investigated (> 500 ^∘C, Regime 3) (Fig. 4a). Such “three-regime” v dependence with increasing temperature has been observed for granite (Blanpied et al., 1991, 1995) and gabbro (He et al., 2007) gouges, but Den Hartog and co-workers were the first to report this for a realistic megathrust fault rock composition. The temperature range in which v weakening was reported is broadly consistent with the temperature–depth range of the subduction seismogenic zone such as in Nankai (Hyndman et al., 1997; Yoshioka et al., 2013; Okamoto et al., 2019).

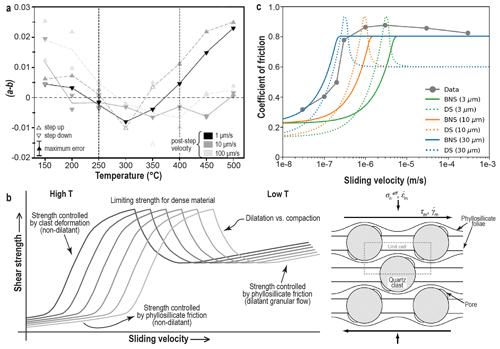
Figure 4 Data from hydrothermal ring-shear experiments on quartz–phyllosilicate mixtures. (a) Three regimes of v dependence seen in experiments on illite–quartz mixtures (taken with publisher's permission from Den Hartog and Spiers, 2014). (b) Conceptual interpretation of quartz–phyllosilicate strength evolution with sliding velocity and temperature (left) (taken with publisher's permission from Den Hartog and Spiers, 2013) and the model microstructure envisioned by Den Hartog and Spiers (2014) (DS model, right). (c) Coefficient of friction at steady state against sliding velocity including data from constant-v experiments by Niemeijer (2018) in grey. The coloured curves are generated using the model for frictional–viscous deformation (BNS, solid lines) (Bos and Spiers, 2002a; Niemeijer and Spiers, 2005) and using the DS model (dashed lines) for different nominal grain sizes as indicated. The peaks mark a transition from v strengthening to v weakening (taken with publisher's permission from Niemeijer, 2018).

The above observations on illite–quartz and muscovite–quartz gouges were explained first qualitatively and later using a quantitative model based on the Niemeijer and Spiers (2007) approach, but employing a phyllosilicate-dominated model microstructure (Fig. 4b) (Den Hartog and Spiers, 2013, 2014; see also Noda, 2016). The change in the sign of (a−b) with increasing temperature was proposed to occur due to changes in the role of thermally activated deformation of the quartz clast phase (by stress corrosion cracking and/or pressure solution) versus that of athermal granular flow of the mixture accompanied by dilatation (Fig. 4b). On the basis of widespread experimental observations (Ikari et al., 2011), expected v-strengthening effects of frictional slip within the phyllosilicate matrix and foliation were taken into account. Assuming pressure solution as the controlling thermally activated process, the experimentally observed three-regime v dependence could be reproduced. On the other hand, Niemeijer (2018) recently showed a good match between data from constant-v shear experiments using 80:20 quartz–muscovite gouges and predictions of the Bos–Spiers–Niemeijer model for frictional–viscous flow (Bos and Spiers, 2002a; Niemeijer and Spiers, 2005) (Fig. 4c). Regardless of the details of the model used, the results of Den Hartog and co-workers, and those of Niemeijer (2018), imply that shear strain accommodation involving competition between rate-sensitive (thermally activated creep of clast phases) and rate-insensitive processes (dilatant intergranular sliding) plays a key role in controlling v-dependent frictional and frictional–viscous flow of phyllosilicate–quartz mixtures.

4.3 Calcite

Motivated by the frequency of destructive earthquakes in tectonically active carbonate-bearing terranes such as the Apennines (Italy) and the Longmen Shan (China), Verberne et al. (2013, 2014a, b, 2015) and Chen et al. (2015b, c) investigated the frictional behaviour of simulated calcite(-rich) fault gouge. Initial experiments employing the direct-shear assembly (Fig. 2c, f) were conducted at T=20–150 ^∘C, ${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}=\mathrm{50}$ MPa, and a pore water pressure P_f=10 MPa or else under room-dry conditions. Dry and wet velocity stepping (v=0.1, 1, 10 µm s⁻¹) experiments consistently showed a thermally activated transition from v strengthening to weakening at 80–100 ^∘C (Fig. 5a, b). Furthermore, results from fault healing (“slide–hold–slide” or SHS) tests pointed to an important role for the presence of (pressurized) pore water. Dry samples exhibited classical “Dieterich-type” healing behaviour (Dieterich, 1978), characterized by a transient peak in shear resistance after each hold period with no effects on steady-state frictional strength. By contrast, wet experiments showed (i) an increase in apparent steady-state friction upon re-sliding after a hold period (note Δμ_r in Fig. 5a, inset), and (ii) a pronounced increase in (a−b) after the SHS stage (Chen et al., 2015b, c). Verberne et al. (2015) extended the temperature range of shear tests on simulated calcite gouge to 600 ^∘C using the hydrothermal ring-shear apparatus and employing a constant effective normal stress of 50 MPa. The results showed a three-regime trend in (a−b) values with increasing temperature, reminiscent of that predicted by the Den Hartog and Spiers model (i.e. the derivative of the curves in Fig. 4b, sketched in the inset to Fig. 5b) (Den Hartog and Spiers, 2013, 2014; Verberne et al., 2015).

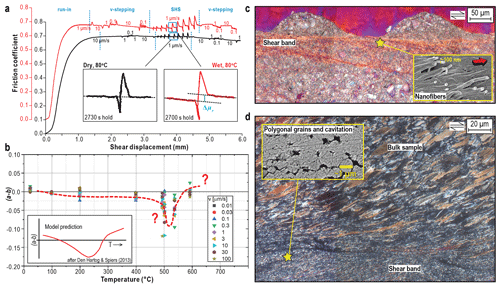
Figure 5 Data from shear experiments on simulated calcite fault gouge. (a) Direct-shear tests conducted at an effective normal stress (${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}$) of 50 MPa, at 80 ^∘C, under lab-dry conditions (black curve), and using a pore fluid pressure of 10 MPa (red curve). The test includes velocity stepping (VS) and slide–hold–slide (SHS) sequences; Δμ_r indicates residual healing after a hold period (adapted from Chen et al., 2015b – license no. 4658610579860). (b) Velocity dependence (a−b) against temperature for experiments conducted up to 600 ^∘C at ${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}$ = 50 MPa using the hydrothermal ring-shear set-up (data from Verberne et al., 2015). (c, d) Cross-polarized, transmitted light micrographs of samples sheared in v-stepping experiments conducted nominally dry at room temperature (c) and wet at 500 ^∘C (d). Inset in (c) shows nanofibres observed on split sample fragments after an experiment. Inset in (d) highlights cavitated arrays of polygonal grains.

Regardless of the large changes in (a−b) observed in LVF experiments on simulated calcite gouge, the microstructures formed at temperatures up to 550 ^∘C consistently showed localization into at least one narrow (< 100 µm) boundary-parallel shear band. At low temperatures (< 150 ^∘C), boundary shears represent a porous, sheet-like volume of calcite nanocrystallites (grain size down to 5 nm) that are locally arranged in dense patches composed of ∼ 100 nm wide spherical grains and fibres (Fig. 5c, inset) (Verberne et al., 2014a, b, 2019). Towards higher temperatures (400–550 ^∘C) the shear band is composed of linear, cavitated arrays of polygonal grains (∼ 0.3–1 µm in size), suggestive of incomplete grain boundary sliding and (possible post-test) grain growth (Fig. 5d) (Verberne et al., 2017). The nano- and microcrystalline boundary shears developed in experiments carried out at ≤550 ^∘C showed a strong crystallographic preferred orientation (Verberne et al., 2013, 2017). Somewhat surprisingly, the post-mortem calcite gouge microstructures resemble those formed in HVF experiments using simulated gouge material of similar compositions (Smith et al., 2013; De Paola et al., 2015; Rempe et al., 2017; Pozzi et al., 2019). Above 550 ^∘C, a more homogeneous (non-localized), plastically deformed, and recrystallized microstructure is observed, consistent with flow controlled by dislocation and possibly diffusional deformation mechanisms (Verberne et al., 2015, 2017; Chen et al., 2020b).

5 The Chen–Niemeijer–Spiers microphysical model for the shear of gouge-filled faults

Inspired by the modelling work of Bos, Niemeijer, Den Hartog, and Spiers (Figs. 3, 4), as well as the observations on monomineralic calcite gouge (Fig. 5), Chen and Spiers (2016) developed a more general microphysical model for (localized) shear deformation of gouge-filled faults. This model employs rate-strengthening grain boundary friction plus standard equations for pressure solution creep and covers both steady-state and transient gouge shearing behaviour. It is capable of reproducing results from v stepping and SHS tests using physically based, independently measured input parameters. In the following, we describe the main features of this Chen–Niemeijer–Spiers (CNS) model.

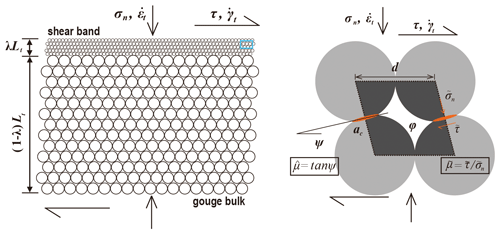
Figure 6 Gouge layer geometry assumed in the Chen–Niemeijer–Spiers (CNS) model. After Chen and Spiers (2016).

5.1 Model outline

The CNS model assumes an idealized geometry for fault gouge that consists of a densely packed, two-dimensional array of cylinders or spheres while allowing for localized deformation in a boundary-parallel shear band located at the margin of a bulk gouge zone (Fig. 6). The shear band and the bulk are represented by the same grain packing geometry but with different nominal grain diameters internally. Deformation of the gouge layer is controlled by parallel processes active within each zone: that is, dilatant granular flow plus a creep process such as intergranular pressure solution (IPS). The model considers frictional energy dissipation for a constant grain size and shear band thickness, ignoring (de-)localization, grain rolling, and comminution (cataclasis, microcracking). The governing constitutive equations are derived from kinematic, energy, and entropy considerations (Chen and Spiers, 2016);

$$\begin{array}{}\text{(5a)}& {\displaystyle }\mathit{\tau }={\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}{\displaystyle \frac{\stackrel{\mathrm{̃}}{\mathit{\mu }}+\tan \left(\mathit{\psi }\right)}{\mathrm{1}-\stackrel{\mathrm{̃}}{\mathit{\mu }}\tan \left(\mathit{\psi }\right)}},\text{(5b)}& {\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\mu }}={\stackrel{\mathrm{̃}}{\mathit{\mu }}}^{\ast }+a_{\stackrel{\mathrm{̃}}{\mathit{\mu }}}\ln \left({\displaystyle \frac{{\dot{\mathit{\gamma }}}_{\mathrm{gr}}}{{\dot{\mathit{\gamma }}}_{\mathrm{gr}}^{\ast }}}\right),\text{(5c)}& {\displaystyle \frac{\dot{\mathit{\phi }}}{\left(\mathrm{1}-\mathit{\phi }\right)}}=-{\dot{\mathit{\epsilon }}}_{\mathrm{pl}}+{\dot{\mathit{\gamma }}}_{\mathrm{gr}}tan\mathit{\psi },\end{array}$$

where τ is shear stress, ${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}$ is the effective normal stress, and φ is the shear band porosity. Further, $\dot{\mathit{\gamma }}$ and $\dot{\mathit{\epsilon }}$ are respectively the shear and normal strain rates, where the subscript “pl” indicates time-dependent plastic creep and “gr” indicates granular flow. Equation (5a) represents a “friction law”, in which shear resistance is expressed in terms of grain boundary friction $\stackrel{\mathrm{̃}}{\mathit{\mu }}$ and the resistance due to intergranular dilatation, tan(ψ). Here, ψ is the mean dilatancy angle of the shearing grain pack (Fig. 6). An intrinsically v-strengthening, cohesionless grain boundary slip criterion is adopted (Eq. 5b), where $a_{\stackrel{\mathrm{̃}}{\mathit{\mu }}}$ is a strain-rate-dependent coefficient and ${\stackrel{\mathrm{̃}}{\mathit{\mu }}}^{\ast }$ is the grain boundary friction coefficient at a reference shear strain rate ${\dot{\mathit{\gamma }}}_{\mathrm{gr}}^{\ast }$. Equation (5c) captures the evolution of porosity and deformation in the fault-normal direction (i.e. volumetric strains). Granular flow implies dilatation, or ${\dot{\mathit{\epsilon }}}_{\mathrm{gr}}=-{\dot{\mathit{\gamma }}}_{\mathrm{gr}}\tan (\mathit{\psi }$) (Paterson, 1995; Gudehus, 2011). The evolving “state” variable in the CNS model is porosity (Eq. 5c), which is clearly physically measurable and microstructurally quantifiable, as opposed to that characterizing the classical RSF equations (Eqs. 1, 2). To capture transient frictional behaviours such as those occurring upon a perturbation in displacement rate, the deforming gouge plus elastic surrounding (testing apparatus or host rock) is modelled as a spring–slider system assuming zero inertia. Recently, Chen et al. (2019) extended the CNS model to seismic slip rates (∼ 1 m s⁻¹) by incorporating superplastic flow activated by frictional heating (De Paola et al., 2015). This refined model is capable of predicting not only low-velocity frictional behaviour but also (the transition to) rapid dynamic weakening effects frequently seen in high-velocity friction experiments (see Di Toro et al., 2011).

5.2 Comparison with lab data and model predictions

The CNS model has been strikingly successful in reproducing mechanical behaviours observed in laboratory fault-slip experiments (Figs. 7a, b) (Chen and Spiers, 2016; Chen and Niemeijer, 2017; Chen et al., 2017, 2019, 2020; Hunfeld et al., 2019, 2020a, b). In order to reproduce experimental data, the parameters appearing in Eqs. (5a)–(5c) are implicit from the testing configuration used, experimentally derived values, or values derived from post-mortem microstructural analysis. The model shows favourable consistency with laboratory observations, predicting a dependence of the steady-state friction coefficient on sliding velocity, including a transition from v weakening to strengthening with increasing v (Fig. 7a). Transient strength data upon steps in displacement rate and decaying strength oscillations are also reproduced well (Fig. 7b – see the step from 1 to 0.1 µm s⁻¹). When applied over a wide range of sliding velocities, the CNS model output for the steady-state friction coefficient essentially represents a flow-to-friction profile (Fig. 7c), characterized by transitions with increasing v from v strengthening, to weakening, back to v strengthening, and finally v weakening associated with dynamic thermal weakening at high velocities (Chen and Niemeijer, 2017; Chen et al., 2019). These v-dependence transitions are accompanied by marked changes in mean porosity (bottom Fig. 7c). In the intermediate velocity weakening regime, the mean porosity increases with increasing v to relatively high values; however, this decreases to much lower levels when creep becomes the dominant deformation mechanism. Since decreasing shear strain rate in the model is, to some extent, equivalent to an increase in temperature (Bos and Spiers, 2002a; Tenthorey and Cox, 2006; Den Hartog and Spiers, 2013), the model can also be used to predict v-dependence transitions with increasing temperature.

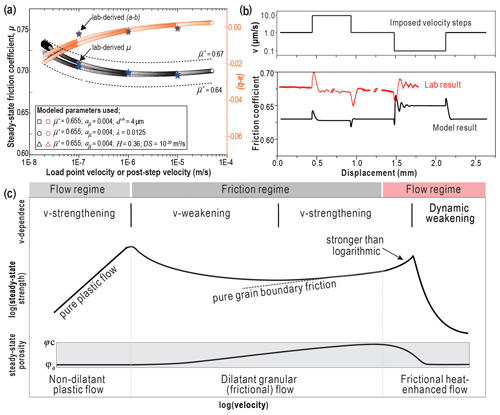
Figure 7 Reproduction of experimental data using the CNS model. (a) Steady-state frictional strength and (a−b) values, as well as (b) v-stepping tests. Data from experiments on calcite gouge performed at T = 80 ^∘C and ${\mathit{\sigma }}_{\mathrm{n}}^{\mathrm{eff}}$ = 50 MPa (see Fig. 5a). (c) Model output for a wide range of fault sliding rates.

Using the CNS model, the above “critical” sliding velocities or temperatures marking transitions in fault gouge v dependence can be derived theoretically. Furthermore, the model can be used to derive analytical solutions for the RSF parameters a, b, and d_c as functions of gouge material properties (solid solubility, activation volume), microstructural parameters (grain size, porosity, shear band thickness), and experimental conditions (temperature, effective normal stress, imposed slip rate) (Chen et al., 2017). This shows that d_c scales with shear band thickness (consistent with Marone and Kilgore, 1993), while varying only slightly with slip velocity, and that the equivalent slip distance in response to large perturbations, d₀, increases with the size of the velocity perturbation (Fig. 8a). Furthermore, Van den Ende et al. (2018) showed that the process zone size (h_cr) for a propagating rupture can be expressed as $h_{\mathrm{cr}}=d_{\mathrm{c}}G/b{\mathit{\sigma }}_{\mathrm{n}}$, where G is the shear modulus of the elastic medium. This result is consistent with the process zone size or “nucleation length” L_b derived from RSF analyses (Rubin and Ampuero, 2005). Similarities between the RSF and CNS models are also apparent when applying classical fault stability theory (see Eq. 4) (Ruina, 1983; Gu et al., 1984). Specifically, varying the stiffness K enables simulation of a wide range of transient frictional behaviours frequently seen in laboratory experiments (Chen and Niemeijer, 2017), including stable sliding, healing, attenuating or self-sustained (quasi-static) oscillations, and stick-slip (Fig. 8b) (see Baumberger et al., 1994; Leeman et al., 2016). The transition from stable to unstable behaviour occurs at the critical stiffness K=K_c. The model similarly implies that the transition at low shearing rates, from fully ductile v-strengthening behaviour to dilatant v weakening (first peak in Fig. 7c), marks the point at which v weakening causes acceleration and, ultimately, a dynamic instability (second peak in Fig. 7c).

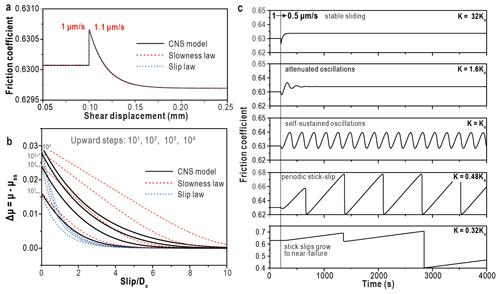
Figure 8 Comparison between CNS- and RSF-based models. (a) Small (1→1.1 µm s⁻¹) and large (up to 4 orders of magnitude) perturbations in sliding velocity (the upper and lower diagrams, respectively). The RSF parameter values used are the equivalent values calculated from the CNS model (see Chen et al., 2017). (b) CNS modelling of a velocity step 1→0.5 µm s⁻¹ for different stiffnesses K (see Chen and Niemeijer, 2017).

Significantly, stick-slip oscillations generated using the CNS model can also be reproduced using numerical discrete element modelling (DEM) of gouges subject to direct shear, accommodated by concurrent granular flow and intergranular pressure solution (IPS) (Van den Ende and Niemeijer, 2018). Even though the detailed mechanics and assumptions used in DEM are dramatically different from those underlying the CNS model, the concept of shear strain accommodation involving competition between dilatant granular flow and IPS is sufficiently robust to reproduce a wide range of frictional sliding modes.

6 Earthquake cycle simulations using the CNS model

6.1 Empirical and physically based earthquake cycle simulations

Laboratory observations of fault rock deformation can be thought of as measurements of a point along a fault characterized by a certain state of stress and thermodynamic conditions. Analytical models such as the CNS model offer a quantitative description of the mechanical behaviour of the fault at that point. Numerical simulations are indispensable for upscaling these “point measurements” to the scale of the Earth's crust. In simulations of earthquake rupture nucleation and dynamic propagation, a section of crust or fault is usually discretized such that the continuum is represented by a collection of points, the behaviour of each of which is described with a constitutive relation. Over the last few decades, the rate-and-state friction model has been the preferred choice for numerical simulations of fault slip, which has led to important insights into the spectrum of fault-slip behaviour (Shibazaki and Iio, 2003; Hawthorne and Rubin, 2013), earthquake rupture propagation and arrest (Tinti et al., 2005; Noda and Lapusta, 2013; Lui and Lapusta, 2016), and the relation between the earthquake source and seismological and geodetic observations (Kaneko et al, 2010; Thomas et al., 2017; Barbot, 2019; Ulrich et al., 2019). However, a major challenge that remains is relating laboratory data on RSF parameters to fault rheology at depth in the Earth's crust.

Physics-based models for fault slip such as the CNS model provide a transparent origin of the constitutive parameters used, so when employed in numerical simulations a substantial portion of epistemic uncertainty is eliminated. Conveniently, in the case of the CNS model, its numerical implementation into a seismic cycle simulator (QDYN in the study of Van den Ende et al., 2018; see Luo et al., 2017) is similar to that of the RSF equations, implying that it is compatible with existing codes for seismic cycle and dynamic rupture simulations. Furthermore, the modular nature of the CNS model enables specific microscale deformation mechanisms to be incorporated based on microstructural observations of lab-deformed and natural samples, offering a framework for studying the interaction between time-sensitive and -insensitive deformation mechanisms (i.e. creep and granular flow). That said, more work is needed to learn about and quantitatively capture the microphysical processes controlling deformation across the entire fault-slip velocity spectrum, covering quasi-static deformation in interseismic periods and dynamic rupture.

6.2 Insights into the physics of fault behaviour from CNS-based simulations

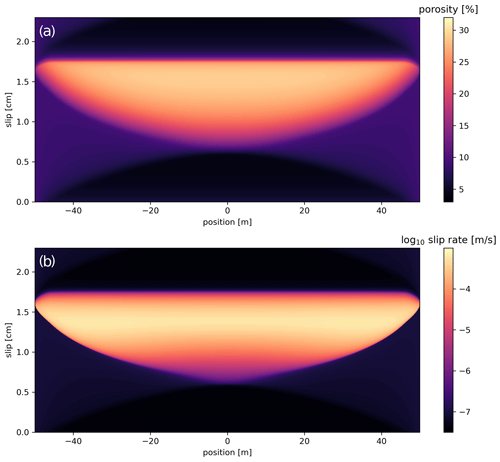
Because the dynamics of the CNS model are different from rate-and-state friction (RSF), CNS-based numerical simulations of fault slip may lead to new insights into the physics of fault deformation. In a comparison between RSF- and CNS-based simulations, Van den Ende et al. (2018) found that fault strength evolution near steady state is practically identical but that the behaviour far from steady state differs; hence, there are differences between seismic cycle predictions. Specifically, in the absence of high-velocity dynamic weakening mechanisms, instead of producing seismic events with large co-seismic slip as expected from RSF-based simulations, CNS-based simulations produce earthquakes with limited co-seismic displacement (Fig. 9). The latter can be explained by the transition from v weakening to strengthening with increasing slip rate implicit in the CNS model (see Fig. 7c), which effectively slows down dynamic rupture. In other words, the transition with increasing v (or decreasing T) from v weakening to strengthening constitutes a potential mechanism for the generation of slow earthquakes (as previously speculated upon by Rubin, 2011; see also Bürgmann, 2018).

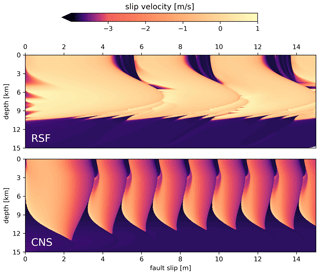
Figure 9 Numerical simulation of the spatio-temporal evolution of slip rates on a simulated strike-slip fault based on rate-and-state friction (RSF; top) and on the CNS model (bottom). Brighter colours indicate higher slip rates, and dark purple indicates slow creep. While the RSF-based simulation exhibits large and fast earthquakes, the CNS-based simulation exhibits mostly small slow-slip events. After Van den Ende et al. (2018).

The emergence of slow ruptures in numerical simulations is closely related to the nucleation of a frictional instability, which, in the CNS model, occurs near the transition from the ductile creep regime (v strengthening) to the dilatant granular flow regime (v weakening) (Fig. 7c). In numerical simulations that employ classical RSF and an ageing law (Eqs. 1 and 2a), a rupture becomes dynamic when it exceeds a length scale that is proportional to the nucleation length L_b (Ampuero and Rubin, 2008; Rubin, 2008). When L_b approaches the size of the fault, the rupture is unable to fully accelerate to co-seismic slip rates, causing a slow-slip event or slow earthquake (Rubin, 2008). For the CNS model, equivalent expressions for L_b can be obtained that apply to rupture nucleation near the ductile–frictional transition. However, in the case of a transition from v weakening to v strengthening, the transition from slow slip to fast slip is no longer accurately described by traditional estimates of the nucleation length using constant rate-independent coefficients. Rather, a more detailed fracture mechanics approach (as adopted by Hawthorne and Rubin, 2013, for a modified RSF framework) may shed new light on the parameters controlling earthquake and slow-slip nucleation, as well as of the thermodynamic and rheological conditions that control the spectrum of slip modes observed in nature.

Another example that highlights the major benefits of using a physically based constitutive relation in numerical simulations involves studies of fluid pressure stimulation of faults (see Van den Ende et al., 2020, this volume). In the case of fluid injection or extraction, the change in hydrological properties with time is crucial for modelling thermo–hydro–mechanical coupling in the system. For the RSF framework, empirical formulae have been proposed that describe the relation between volumetric deformation and evolution of the state variable, $\dot{\mathit{\theta }}$ (Segall and Rice, 1995; Shibazaki, 2005; Sleep, 2005; Samuelson et al., 2009). However, such a relation is not evident from the classical physical interpretation of θ as an asperity contact lifetime. In the CNS model, gouge porosity assumes the role of the state parameter, implying that its evolution can be directly related to changes in fluid pressure, effective normal stress, and/or hydrological properties within the fault (Van den Ende et al., 2020). To illustrate this, we simulate the evolution of porosity during nucleation, propagation, and arrest of a slow earthquake rupturing a one-dimensional fault with uniform frictional properties (Fig. 10) for the regime in which dynamic high-velocity slip is not yet triggered. During the nucleation stage, the fault dilates and weakens simultaneously with accelerated slip. As the rupture reaches its peak slip rates, the gouge attains maximum dilatancy and minimum strength, after which the gouge compacts upon deceleration and rupture arrest. During this cycle of nucleation, propagation, and arrest, the hydrological properties (i.e. hydraulic conductivity) can be computed based on the local porosity. In turn, and informed by laboratory experiments, this enables investigation of the dynamic coupling between fluid flow and fault slip (e.g. Cappa et al., 2019).

Figure 10 Spatio-temporal evolution of fault gouge porosity (a) and slip rate (b) during nucleation, propagation, and arrest of a rupture on a fault with uniform frictional properties. The rupture nucleates in the centre and propagates outwards.

7 Remaining challenges

To date, the microphysical and earthquake cycle modelling work described above has mainly focused on the inter-seismic and nucleation stages of the seismic cycle. For a complete and self-consistent description of fault deformation, co-seismic slip rates must be considered as well. However, the present model assumptions are reasonable for gouge shear deformation at low slip rates, but they break down when frictional heating and associated dynamic fault rupture processes come into play. Specifically, the model requires adaption to include heat production during deformation at the ultra-high shear strain rates (≫ 100 s⁻¹) capable of triggering weakening processes such as thermal pressurization, decomposition, or melting (Rice, 2006; Di Toro et al., 2006, 2011; Platt et al., 2015). As described earlier in this paper, a first step in this direction has been made by Chen et al. (2019), who take into account slip-rate-dependent heat production coupled with temperature and grain size sensitivity of creep processes (see Fig. 7c) (see De Paola et al., 2015; Pozzi et al., 2019).

Another major challenge yet to be addressed in fault deformation models lies in capturing the dynamics of micro- and nanostructure formation in sheared fault rock. The CNS model adopts a constant granular structure (Fig. 6), implying that the thickness of the deforming zone and the grain size within must be defined a priori. This is problematic, for example, under conditions close to the transition with increasing strain rate or decreasing temperature from v strengthening to v weakening (ref. Fig. 7c). Microstructures from experiments on simulated calcite gouge at high temperatures (500–600 ^∘C) point to the role of grain growth in addition to grain size reduction, suggestive of trade-offs between grain size, temperature, slip velocity, and localization (Verberne et al., 2015, 2017). Moreover, there is the additional complexity that the deformation properties of individual mineral particles can change with changing particle size. Constraining this is especially important in the case of nanometric gouges (grain size < 100 nm), which, along with (partly) amorphized host rocks, are widespread in natural and experimentally sheared fault gouges (Power and Tullis, 1989; Yund et al., 1990; for a recent review see Verberne et al., 2019). Individual nanoparticles and nanocrystalline aggregates frequently exhibit dramatically different physical properties compared with their bulk counterparts (e.g. Meyers et al., 2006; Hochella et al., 2019) – the room-temperature ductile nanofibres encountered in calcite gouge being an example of this (Fig. 5c, inset) (Verberne et al., 2014b, 2019). The implication is that extrapolation of data from compaction experiments using micron-sized crystals or larger, which are used to constrain parameter values appearing in the CNS model, may lead to large errors when applied to nanogranular or (partly) amorphous fault rock.

Even when coarser-grained fault rocks are considered, frictional sliding on the contact between two grains is ultimately governed by nanometre-scale processes. This can be envisioned as lattice-scale solid–solid interactions for “dry” contacts or contacts with incomplete coatings of adsorbed species, such as water (used in the CNS model; Chen and Spiers, 2016), or as interactions arising from the unique properties of fully developed, adsorbed water or hydration layers (Leng and Cummings, 2006; Sakuma et al., 2018). Since the nanometric realm is inaccessible by standard observation techniques, directly probing the processes leading to grain-scale friction remains challenging, in particular for the LVF tests described in Sect. 3. Instead, atomic force microscopy (AFM) experiments, also known as friction force microscopy (FFM; see Bennewitz, 2005 for a review), may provide critical observations of the sample response to variations in sliding rate, normal stress, and chemical environment (Diao and Espinosa-Marzal, 2018, 2019). These observations will inform nanophysical models in a similar way as grain- and aggregate-scale observations have informed the CNS model.

Finally, we note that the capability of the CNS model to fully describe the frictional behaviour of strongly heterogeneous gouge compositions, including transients, remains to be investigated. To date this has only been demonstrated for monomineralic calcite (Chen and Spiers, 2016; Chen et al., 2017, 2020a, b). In the case that phyllosilicates constitute large portions of the fault gouge, the overall constitutive behaviour can no longer be represented by taking bulk mean values of rheological properties (pressure solution kinetics, grain size, etc.). Instead, the interactions between the various phases within the gouge need to be considered more closely in the assumed microphysical model geometry (e.g. Fig. 4b) or using numerical simulations that enable aggregate heterogeneity (using discrete or finite-element models; see Wang et al., 2019; Beall et al., 2019). While microphysical modelling of heterogeneous systems poses some challenges, its potential outcomes likely offer new insights on natural fault deformation, including on the problem of upscaling to more realistic fault geometries.

8 Conclusions

We reviewed experimental and microphysical modelling work on the physics of low-velocity fault friction processes carried out at Utrecht University (UU) since the early 2000s. Data from shear deformation experiments on simulated fault rocks composed of halite–phyllosilicate and phyllosilicate–quartz mixtures, as well as of monomineralic calcite, consistently show that fault gouge strength and stability is controlled by competition between rate-sensitive creep and rate-insensitive granular flow processes. Under conditions in which ductile deformation occurs in the Earth's crust, fault shear deformation is non-dilatant and controlled purely by creep, which is intrinsically stable. However, towards shallower depths, frictional(–viscous) deformation occurs, which is controlled by creep of individual mineral grains operating alongside dilatant granular flow. The seismogenic zone represents a depth interval in the crust where these processes operate at comparable rates, $\left|{\dot{\mathit{\epsilon }}}_{\mathrm{dil}}\right|\approx \left|{\dot{\mathit{\epsilon }}}_{\mathrm{cp}}\right|$, which leads to velocity weakening and hence seismogenic fault-slip behaviour. This conceptual model framework is quantitatively described by the Chen–Niemeijer–Spiers (CNS) model for shear of gouge-filled faults, which constitutes a physically based microphysical model that is capable of reproducing a wide range of (transient) frictional behaviours. Despite numerous challenges ahead on capturing deformation process active in slipping gouge-filled faults, including at co-seismic slip rates, the CNS model offers new microstructurally and physically founded input for earthquake cycle simulators and therewith new scope for the interpretation of earthquake source processes.