The role of edge-driven convection in the generation of volcanism – Part 1: A 2D systematic study

The origin of intraplate volcanism is not explained by plate tectonic theory, and several models have been put forward for explanation. One of these models involves edge-driven convection (EDC), in which cold and thick continental lithosphere is juxtaposed with warm and thin oceanic lithosphere to trigger convective instability. To test whether EDC can produce long-lived high-volume magmatism, we run numerical models of EDC for a wide range of mantle properties and edge (i.e., the oceanic–continental transition) geometries. We find that the most important parameters that govern EDC are the rheological parameters mantle viscosity η₀ and activation energy E_a. However, even the maximum melting volumes predicted by our most extreme cases are insufficient to account for island-building volcanism on old seafloor, such as at the Canary Islands and Cabo Verde. Also, beneath old seafloor, localized EDC-related melting commonly transitions into widespread melting due to small-scale sublithospheric convection, inconsistent with the distribution of volcanism at these volcano chains. In turn, EDC is a good candidate to sustain the formation of small seamounts on young seafloor, as it is a highly transient phenomenon that occurs in all our models soon after initiation. In a companion paper, we investigate the implications of interaction of EDC with mantle plume activity (Manjón-Cabeza Córdoba and Ballmer, 2021).

1 Introduction

Understanding the origin of volcanism improves our understanding of Earth's deep interior processes, structure and composition. In this context, intraplate volcanism deserves particular attention because it is not readily explained by plate tectonics processes. One of the leading theories to explain intraplate magmatism involves mantle plume theory. In this theory, a magmatic hotspot is sustained by a fixed and columnar mantle upwelling, or “plume”, forming a volcano chain on a steadily moving plate (Wilson, 1963; Morgan, 1971).

Plume theory makes specific testable predictions, such as the distribution of volcanism, the age–distance relationship along the volcanic chain, and anomalies in heat flux and topography (hotspot swells). These predictions have been successfully compared to observations at several locations (e.g., Hawaii, Louisville), however, comparisons fail at other locations (see Courtillot et al., 2003). For example, the age–distance relationship measured along the Pukapuka Ridge does not agree with the overriding plate motion (Sandwell et al., 1995; Ballmer et al., 2013), and at Madeira, there is no apparent swell (Anderson, 2005; Ballmer et al., 2013; King and Adam, 2014). Accordingly, alternative or complementary models have been proposed for sustaining intraplate volcanism (Foulger and Anderson, 2005; Hirano, 2011; Ballmer et al., 2015; Green, 2015).

One of these models involves edge-driven convection (EDC; King and Anderson, 1995, 1998). EDC is a variant of small-scale convection (SSC; Richter, 1973; Parsons and McKenzie, 1978; Huang et al., 2003; Dumoulin et al., 2005), i.e.,  a thermal boundary-layer instability that is largely driven by cooling of the lithosphere and the related density inversion (Ballmer et al., 2009; Ballmer, 2017). EDC is triggered by the presence of lithospheric steps (or lateral heterogeneity): the related lateral density difference promotes the instability (which is ultimately driven by the density inversion), setting up a convection cell (Fig. 1). But apart from this, it has all the characteristics of SSC. According to King and Anderson (1995, 1998), the associated upwelling(s) may be sufficient to sustain mantle melting without the need of a plume. This magmatism is predicted to occur at a distance from the step in lithospheric thickness (e.g., nearby a cratonic margin) of a few hundred kilometers.

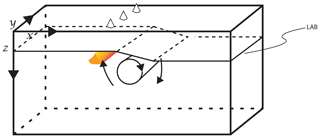
Figure 1 Schematic of edge-driven convection. A downwelling is promoted on the thick continental side of the lithospheric edge, triggering a passive upwelling that sustains mantle decompression melting (orange) and related volcanism parallel to the continent–ocean transition (cones). The lithosphere–asthenosphere boundary (LAB) is labeled.

In the Atlantic Ocean basin, several volcanic chains occur near the margin of the continental platform (e.g., the Canary Islands, Cabo Verde or the Cameroon Volcanic Line). For many (or all) of these chains, several predictions of classic plume theory are not fulfilled. For example, the Canary Islands do not display a strictly linear age progression, with coeval volcanism occurring over hundreds of kilometers and sustained volcanism at a single island or seamount for >20 Ma (Abdel-Monem et al., 1971, 1972; Carracedo, 1999; Geldmacher et al., 2005). Given these complexities, several alternative hypotheses have been proposed. For instance, some authors have invoked the extraction of magmas along elongated shear zones of preexisting melt (Araña and Ortiz, 1991; Doblas et al., 2007; Martinez-Arevalo et al., 2013), possibly associated with a thermal anomaly (Anguita and Hernan, 2000). Alternatively, the “passive” upwelling of “mantle blobs” (Hoernle and Schmincke, 1993; Thirlwall et al., 2000) or EDC with or without a contribution from a nearby plume (King and Ritsema, 2000; Geldmacher et al., 2005) may sustain Canary volcanism. EDC has also been proposed as an underlying mechanism for other Atlantic hotspots such as Bermuda or Cabo Verde (Vogt, 1991; King and Ritsema, 2000).

Despite the long-lasting debate on the origin of near-continental intraplate volcanism, there is no published comprehensive geodynamic study of EDC and related magmatism in a continental–oceanic setting. Some authors (King and Ritsema, 2000; Sacek, 2017) have explored the dynamics of this mechanism and applied their results to the eastern Atlantic but have not explicitly and consistently modeled mantle melting. Others have studied EDC in great detail but for a purely continental setting (van Wijk et al., 2008, 2010; Till et al., 2010; Kaislaniemi and Van Hunen, 2014; Ballmer et al., 2015; Currie and van Wijk, 2016).

In this contribution, we study EDC-related flow and melting in the upper mantle using numerical models in order to understand the origin of intraplate volcanism in the eastern Atlantic. EDC can be approximated as a purely two-dimensional (2D) mode of convection, with convection roll(s) infinitely extending along the continental margin (King and Anderson, 1995; Kaislaniemi and Van Hunen, 2014). Therefore, we have chosen to investigate 2D models, which allows us to explore a wide parameter space, and to test the potential of EDC to systematically sustain intraplate volcanism. Finally, we compare model predictions with observations at the Canaries and Cabo Verde and evaluate the limitations of our results in the limit of our model assumptions.

We find that melt generation by EDC alone is too restrictive and transient to be a suitable explanation for the occurrence of large volcano chains such as the Canary Islands or Cabo Verde. Our models predict that EDC sensu stricto generates volcanism only for a small subset of the parameter space, and if it does so, only with small amounts of very enriched volcanism and only below young and thin oceanic lithosphere. EDC remains a suitable explanation for small seamounts in the area (e.g., Van Den Bogaard, 2013). A complementary paper (Manjón-Cabeza Córdoba and Ballmer, 2021, to be submitted) explores the dynamics of plume-EDC interaction, showing that a contribution from at least a weak plume is required to sustain island-building volcanism.

2 Methods

We run 2D numerical models using the mantle convection code CITCOM (Moresi and Solomatov, 1995; Moresi and Gurnis, 1996; Zhong et al., 2000) with the additions described in Ballmer (2009). We use the code to solve the equations of conservation of mass, momentum, and energy according to the “extended Boussinesq approximation” (Christensen and Yuen, 1985), which includes shear heating, latent heat of melt, adiabatic heating, and internal heating due to radioactive nuclides. The code solves these equations in a Cartesian frame of reference. Non-diffusive fields (e.g., composition or melt depletion) are advected by passive tracers. King and Ritsema (2000) demonstrate that EDC is confined to the upper mantle whenever the phase change at 660 km is present, so all our experiments are regional models with a vertical extent of 660 km. We do not include the phase change at 410 km depth, since it is not expected to effect EDC strongly (King and Ritsema, 2000). The Cartesian model box of dimensions 2640 km × 660 km is resolved by 384 × 96 elements without grid refinement. Resolution tests confirm that results converge well at this resolution.

Kinematic boundary conditions involve no slip at the top and bottom boundaries. In some models, a non-zero plate velocity (v_plate) is imposed. When v_plate is 0, both side boundaries are free slip. Otherwise, we impose a self-consistent (Couette-like) velocity profile in the inflow (left) boundary and open the opposite outflow boundary.

In terms of thermal boundary conditions, we impose temperatures of T_surf=0 ^∘C and T_ref=1350 ^∘C at the top and bottom, respectively. These temperatures are potential in nature and therefore do not take into account any possible adiabatic gradient. We then approximate the initial adiabatic gradient as a linear temperature increase with depth of 0.3 K km⁻¹. This addition is necessary for the consistent calculations of viscosity and melting. According to this approximation, the bottom temperature corresponds to $\mathrm{1350}+\mathrm{0.3}\times \mathrm{660}=\mathrm{1548}$ ^∘C. Lateral boundaries are reflective (zero heat flow) except when inflow happens because of finite-plate motion, in which case the thermal boundary condition is fixed at the initial profile. The models also include internal (i.e., radioactive) heating with a reference value of $H=\mathrm{7.75}\times {\mathrm{10}}^{-\mathrm{12}}$ W kg⁻¹, but we also run models with higher values of H. In addition, we discuss models with increased radiogenic heating that occurs only in the continental crust.

The initial thermal profiles of the oceanic (left) and continental (right side of the box) lithosphere are calculated according to the half-space cooling model (e.g., Fig. 2a; Turcotte and Schubert, 2014) plus a small random thermal noise to simulate small-scale heterogeneity and advance the solution of the initial time steps. Both the thermal age of the continental lithosphere and the age of the oceanic lithosphere are free model parameters (τ_c, τ_o). The edge (i.e., the transition in lithospheric thickness) is imposed as a linear interpolation between the oceanic and continental lithospheric thermal profiles. We choose this setting because it allows us to freely vary the geometry of the transition between oceanic and continental lithosphere.

The geometry of the edge is an unconstrained parameter, the effects of which on EDC have not yet been studied systematically. The edge is defined by the initial lithospheric thickness on either side, and the width of the linear transition between the two (w). Hence, we systematically explore the parameters age of the oceanic lithosphere (τ_o) and age of the continental lithosphere (τ_c). To study how much the dynamics change due to a change in the aspect ratio of the transition between ocean and continent, we also changed the width of the wedge between the two lithospheres (w).

The modeled mantle consists of a fine-scale mixture of peridotite (97 %) and recycled basaltic eclogite (3 %, from now on, pyroxenite; Hirschmann and Stolper, 1996). Peridotite itself consists of a depleted peridotitic component (DC) and an enriched peridotitic component (EC). Mantle depletion of both lithologies increase with increasing degrees of melting, which affects mantle density ρ:

$$\begin{array}{}\text{(1)}& \mathit{\rho }={\mathit{\rho }}_{\text{ref}}-\mathit{\alpha }\cdot {\mathit{\rho }}_{\text{ref}}\cdot (T-T_{\text{ref}})+F\cdot \mathrm{\Delta }{\mathit{\rho }}_F+\mathit{\varphi }\cdot \mathrm{\Delta }{\mathit{\rho }}_{\mathit{\varphi }},\end{array}$$

where ρ_ref is the mantle density at T_ref, α the thermal expansivity, T the temperature, F the melt depletion extent, ϕ the mantle porosity, and Δρ_F and Δρ_ϕ the density differences related to melt depletion and melt retention (Schutt and Lesher, 2006; Ballmer et al., 2009). The depleted lithosphere is, therefore, more buoyant than the underlying mantle. To calculate the initial depletion profile of the oceanic lithosphere for our EDC models, we run 2D simulations of flow and melting of a simplified mid-ocean ridge using the same parameters as in the corresponding EDC models. An example of one of these ridge models, with an extended explanation, can be found in Appendix A.

As for the initial depletion profile at the base of the continental lithosphere, we have chosen to impose the same ridge depletion as in the oceanic side on the continental part, adding a depleted lid (with F=1) on the top (Fig. 2b). This depleted lid mimics the excess buoyancy of continental crust, although it may overestimate the actual density values of the upper crust. The initial thickness of this lid is arbitrarily defined as 40 km for the reference case, but it is adjusted for models with different continental thicknesses to follow the same change in depth as the 0.9 T_ref isotherm on the continental side (according to the half-space cooling model). The edge itself consists of a wedge of crustal depletion (F=1) of width w that thins toward the oceanic lithosphere (Fig. 2). Indeed, it has been suggested that the subcontinental lithospheric mantle is harzburgitic in nature (Bodinier and Godard, 2013), but the specific profile remains unconstrained.

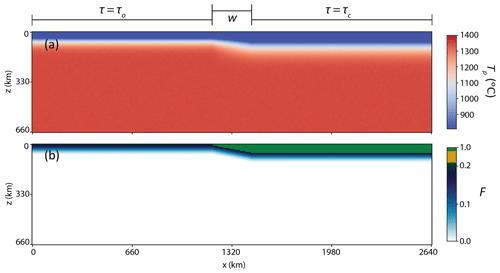
Figure 2 Initial conditions for the reference model. (a) Initial field of potential temperature T_p (i.e., with the adiabatic gradient removed). (b) Initial compositional field of depletion (F) for the hydrous peridotite component. The areas where τ=τ_o and τ=τ_c, as well as w, are labeled for clarity. A comparison of the fields for different lithologies can be found in Appendix A (Fig. A2).

We consider melting explicitly in our models following Ballmer et al. (2009), assuming (see above) that the lithological assemblage consists of 82 % depleted peridotite (DC), 15 % enriched peridotite (EC, for the aforementioned sum of 97 %), and 3 % pyroxenite. Peridotite melting is calculated using the parameterization of Katz et al. (2003). We assume an H₂O content of 100 ppm for the background depleted peridotitic component, and 300 ppm for the enriched peridotitic component (H₂O is a placeholder for any kind of enrichment). The pyroxenite (PX) melting law is taken from Pertermann and Hirschmann (2003). Melt flow and extraction occurs on timescales much shorter than convective flow. We therefore assume instantaneous extraction (outside the model box) of any melt fractions that exceed the critical porosity (ϕ_c).

We use a simplified rheology with a dependence of viscosity on temperature T and pressure P:

$$\begin{array}{}\text{(2)}& \log \mathit{\eta }=\log {\mathit{\eta }}_{\mathrm{0}}+{\displaystyle \frac{E_{\text{a}}+P\cdot V_{\text{a}}}{R\cdot T}}-{\displaystyle \frac{E_{\text{a}}}{R\cdot T_{\text{ref}}}},\end{array}$$

where η is the viscosity, E_a and V_a the activation energy and volume, respectively, T and P are the temperature and pressure, R the ideal gas constant, and T_ref is the reference (potential) temperature. In this formulation, η₀ is the reference viscosity defined at T=T_ref and zero pressure, and hence it does not represent the viscosity of the asthenosphere. Our reference activation energy is 200 kJ mol⁻¹, i.e., lower than the lower limit constrained by deformation experiments (Karato and Wu, 1993; Hirth and Kohlstedt, 1996). We use such reduced values for E_a to account for the effects of stress-dependent viscosity (e.g., due to dislocation creep) in a simplified Newtonian rheology description (Christensen, 1984; van Hunen et al., 2005). While such a simplified approach cannot model the local effects and potential feedbacks of stress-dependent rheology, it correctly replicates the major features of convection, including the thickness of the thermal boundary layer, which is critical for the vigor of EDC and related melting. We do not systematically explore the effects of compositional (e.g., pyroxenite vs. peridotite, water-dependent) rheology in this work. Nonetheless, we run some test cases with a simplified depletion stiffening rheology (Appendix B). These tests confirm that EDC sensu stricto remains a transient phenomenon even with a stabilized lithosphere, and our results (and the subsequent conclusions) are robust, even though the edge remains more stable with than without depletion stiffening rheology.

Our choice of rheology parameterization causes the depth dependency of viscosity to be due to both, E_a and V_a (Eq. 2). This dependency is problematic because, due to the simplified parameterization and our decreased E_a, the effect of the physical parameters on the viscosity along the adiabat is unrealistic. Instead, we chose to keep the viscosity along the adiabat the same between cases and chose to focus on the effect of E_a on the stability of the lithosphere–asthenosphere boundary, which is crucial for any kind of SSC (including EDC). To make sure that the slope of the viscosity profile along the adiabat remains the same in all cases, we slightly adjust V_a as parameter E_a is varied. Any variations in V_a (see Table 1) are only due to this adjustment. For an example of a viscosity profile with depth, see Appendix B (Fig. B1).

Table 1 Relevant reference parameters for the models described in this chapter. Values in parentheses represent the explored parameter space, with the exception of V_a (see Sect. 2 for explanation).

3 Results

3.1 Reference case

To characterize flow and melting of EDC, we first describe a reference case. Figure 3 shows a typical example of EDC as a series of snapshots for the reference case. The convective pattern initially resembles (Fig. 3a) the pattern of the idealized case in Fig. 1, as well as the cases reported by King and Anderson (1998): there is one major convection cell with a dominant downwelling on the continental side of the edge and upwelling return flow on the oceanic side. The downwelling is mainly sustained by lateral inflow of sublithospheric material from the oceanic side due to the asymmetry in viscosity structure, but some material from the continental side is also entrained. As a response to this entrainment, a secondary return-flow upwelling is soon generated on the continental side (Fig. 3b). The flow patterns promptly change to more complex configurations, with several upwellings and downwellings adjacent to the initial convection cell. Soon thereafter (at 35–40 Ma), the oceanic lithosphere as a whole becomes thermally unstable triggering widespread small-scale convection (SSC; Fig. 3d). At this point, EDC becomes almost undistinguishable from SSC (in our 2D models).

From this point, we do not characterize EDC further, as it is not possible to distinguish which properties are due to EDC and which ones are due to SSC. We therefore define this onset of SSC as the maximum of the first time derivative of the second peak of the v_z,rms (the first peak corresponds to EDC).

Ultimately, SSC also develops beneath the continental lithosphere (∼45 Ma, not shown).

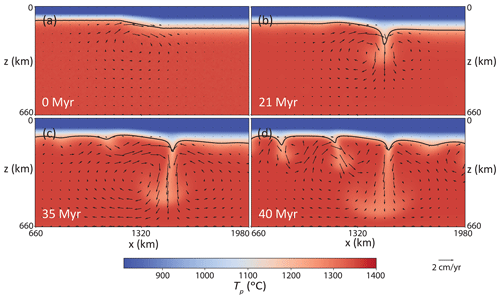
Figure 3 Series of snapshots of potential temperature for the reference case (for parameters, see Table 1). In black, the 1215 ^∘C isotherm (0.9 T_ref) is shown as a proxy for the base of the lithosphere. Arrows reflect the instantaneous velocity field. No melting is predicted by this model at any time step.

An important consequence of EDC (and subsequent SSC) is the erosion of the base of the lithosphere (represented by the black contour in Fig. 3). At 21 Ma (Fig. 3b), a clear “bump” (or small cavity;  Conrad et al., 2010) appears at the base of the lithosphere due to the upwelling pushing the material, as well as material entrainment by the major downwelling, hence promoting local extension of the lithosphere. Not only is this thermal erosion partly responsible for triggering secondary downwellings and transmitting SSC toward the oceanic side (Fig. 3c, d) (e.g., Dumoulin et al., 2005), but it is also a requirement for melting. Displacement of at least the base of the depleted lid is necessary for melting because the temperatures are below the melting point of the lithosphere at time step zero. Nonetheless, in this reference model, erosion of the depleted lid remains insufficient to allow mantle melting to occur throughout model evolution.

3.2 Effects of physical properties of the mantle

To understand the optimal conditions for melting generated by edge-driven convection, we systematically explore several physical properties of the models. We focus on the effects of reference viscosity (η₀), activation energy (E_a), and initial potential temperature (T_ref).

Increasing the reference viscosity (according to Eq. 2) tends to delay the onset of convective instability and hamper melting (Figs. 4a, b; 5a). Thereby, the duration of EDC (which starts immediately at t=0, albeit with a smaller vigor compared to the reference case) vs. SSC is enhanced (we would like to point out at this point that the ages in Fig. 5 are counted starting from time step = 0 and therefore must be added to the age of 40 Ma of the initial oceanic lithosphere age). Figure 4b shows a snapshot of a case with ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{1.95}\times {\mathrm{10}}^{\mathrm{19}}$ Pa s, which displays a similar pattern of convection as the reference case with ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{8.61}\times {\mathrm{10}}^{\mathrm{18}}$ Pa s (Fig. 3c) but at a much later model time of 82 Ma. Accordingly, the onset of SSC is much later than estimated for a typical ocean basin on Earth (Stein and Stein, 1994; Doin and Fleitout, 1996), and the lithospheric thickness on the oceanic side of the model is far too thick to potentially allow the asthenosphere to melt. In turn, cases with ${\mathit{\eta }}_{\mathrm{0}}\le \mathrm{3.83}\times {\mathrm{10}}^{\mathrm{18}}$ Pa s (Figs. 4a, 5a) display melting during a limited period of time (i.e., over a few million years) but based on the (late) timing and (widespread) distribution of melting, most of this melting is associated with SSC rather than with EDC.

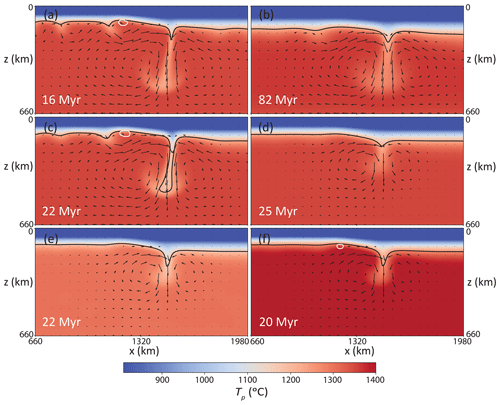
Figure 4 Effects of rheological parameters and reference temperature on edge-driven convection, shown by snapshots of potential temperature of various cases. (a) ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{3.83}\times {\mathrm{10}}^{\mathrm{18}}$. (b) ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{1.96}\times {\mathrm{10}}^{\mathrm{19}}$. (c) E_a=120 kJ mol⁻¹. (d) E_a=300 kJ mol⁻¹. (e) T_ref=1300 ^∘C. (f) T_ref=1400 ^∘C. White contours outline areas with active melting. Black contour refers to the isotherm of T=1215 ^∘C = 0.9 T_ref. Note that snapshots are chosen such that they show a similar stage of model evolution as in Fig. 3b (i.e., mature EDC major downwelling), while model times differ due to the effects of rheological parameters on onset and vigor of EDC or SSC. Also note that the reference case (Fig. 3b, c) corresponds to an intermediate case for the trends shown in any of the rows: ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{8.61}\times {\mathrm{10}}^{\mathrm{18}}$; E_a=200 kJ mol⁻¹; T_ref=1350 ^∘C.

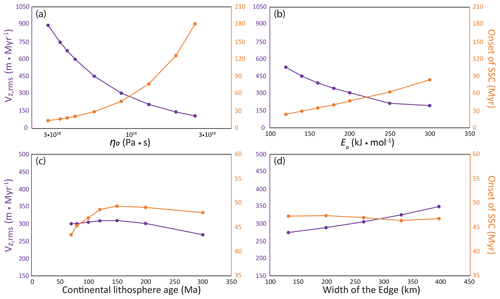
Figure 5 Diagrams showing the sensitivities of v_z,rms (root mean square of vertical velocities) and of the onset age of small-scale convection (starting from an oceanic crust of age 40 Ma, which needs to be added to the values in the figure) to selected parameters. (a) Reference viscosity (η₀). (b) Activation energy (E_a). (c) Age (or thickness) of the continental lithosphere (τ_c). (d) Width in the horizontal direction of the edge (w). Note that the vertical axes of (c) and (d) are exaggerated with respect to those of (a) and (b).

Decreasing activation energy (Figs. 4c, 5b) tends to advance and increase the vigor of EDC and SSC. For low E_a, the viscosity of the base of the lithosphere is decreased, and hence the lithosphere becomes more mobile. For E_a≤140 kJ mol⁻¹, the related erosion of the base of the lithosphere is sufficient to permit early and localized EDC-related melting. However, in these cases, more vigorous melting ultimately occurs across the entire oceanic domain due to SSC. Also, the onset of SSC and related seafloor flattening is < 70 Ma, i.e., earlier than is realistic for the Atlantic (Stein and Stein, 1994), although we can compensate for this by choosing a different reference viscosity. In turn, cases with high E_a≥250 kJ mol⁻¹ display a late onset of SSC and a stable lithosphere with ultimate thicknesses greater than are realistic (Figs. 4d, 5b).

Regarding convection patterns, the entrainment of sublithospheric material by the dominant downwelling near the edge tends to be more symmetric for low E_a. This prediction implies that the activation energy will have an important effect on the final geometry of the oceanic–continental transition. Finally, cooling of the mantle is more efficient for low E_a than for high E_a, since the base of the lithosphere is more mobile. This effect also occurs for decreasing η₀ but is more pronounced for decreasing E_a (see isotherms in Fig. 4a vs. Fig. 4c).

Increasing T_ref tends to advance convective instability and boost magmatism. An increment of potential temperature from 1350 to 1400 ^∘C (Fig. 4e) induces minor melting in the area of maximum erosion of the lithosphere during a limited period of time. This effect is smaller than expected because it is largely compensated for by an increase in the thickness of the pre-calculated depleted lithosphere (see Sect. 2) and because the lithosphere still cools via conduction. Increasing the temperature even more may further increase melting but would also lead to unrealistic crustal thicknesses in the corresponding pre-calculated models. Also note that the peridotite melting parameterization used in this study (Katz et al., 2003) is on the lower end in terms of solidus temperatures (e.g., McKenzie and Bickle, 1989; Iwamori et al., 1995; Hirschmann, 2000; Lambart et al., 2016).

Figure 6 presents a summary of the joint effect of η₀ and E_a on EDC-related mantle melting. We also label the viscosity at 206 km depth as a representative of the viscosity of the asthenosphere. The melting rate characteristic for EDC (Fig. 6a) is determined at the first local maximum of root mean square vertical velocity v_z,rms, which corresponds to the development of the first major downwelling from near the edge. Determining the exact volume of EDC-related melting remains difficult because melting occurs before and/or after this maximum and commonly transitions into persistent SSC-related melting. For example, the model with E_a=140 kJ mol⁻¹ (and with reference values of η₀) displays some EDC-related melting just before the onset of SSC, but this melting episode is extremely short-lived and would likely be insufficient to sustain any significant volcanism. Nonetheless, there is a systematic trend between melt volume fluxes that are measured as described above with both parameters. This result suggests that the stability and final thickness of the lithosphere ultimately control melting due to EDC and, probably, due to SSC. This final thickness (i.e., beneath old ocean basins) is constrained by seismic observations and seafloor topography (Stein and Stein, 1994; Doin and Fleitout, 1996; van Hunen et al., 2005).

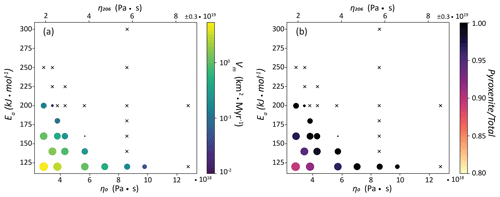
Figure 6 Scatterplots showing the melt property variation with respect to the reference viscosity (η₀) and activation energy (E_a). The upper axis η₂₀₆ refers to the viscosity in the asthenosphere measured at z=206 km depth on the oceanic side for all cases with E_a=200 kJ mol⁻¹. For all other cases, this value slightly varies according to (very small) temperature changes related to the half-space cooling model (see Eq. 2) but by less than 5 %. (a) Melt volume flux due to EDC (colored circles), measured at the point of maximum EDC-related vertical velocities (i.e., v_z,rms). Crosses mark cases in which no melting is detected. The size of the circles also scale with melt volume fluxes. Melt volume fluxes are reported in km² Myr⁻¹ due to the 2D character of the model (i.e.,  corresponding to km³ Myr⁻¹ per km of plate in the out-of-plane direction). (b) Scatterplot showing the origin of the melting products (i.e., proportion of melt derived from pyroxenite vs. total melt; colored circles). Notation of crosses and size of circles as in (a). Note that the color scale is set between 0.8 and 1.

Figure 6b shows the compositional origin of the melts from Fig. 6a. In many of the models, only the pyroxenite component melts, if melting occurs at all. This prediction implies the formation of magmas that are extremely enriched. The enrichment tends to slightly decrease with increasing melt flux. The least enriched case is consistent with the highest volume in Fig. 6a and corresponds to a model with E_a=120 kJ mol⁻¹ and ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$ Pa s. Even in this extreme case, the melts are mostly pyroxenite-derived. Although the absolute numbers in Fig. 6b depend on the choices of our melting parameterizations and lithological assemblage (see Sect. 2), the general trends will be similar as shown in Fig. 6b unless the pyroxenite component melts at a higher temperature than peridotite (Yaxley and Green, 1998; Shorttle et al., 2014; Lambart et al., 2016).

3.3 Effects of lithospheric-edge geometry

Modification of τ_o within the small range explored here controls the convection patterns of EDC. We explore τ_o only in a small range ($\mathrm{30}\le {\mathit{\tau }}_{\mathrm{o}}\le \mathrm{50}$ Ma) because any smaller τ_o yields melting at time t = 0 and any larger τ_o yields a metastable base of the lithosphere (i.e., due to τ_o close to or larger than the onset age of SSC for η₀ in the reference case). With τ_o=30 Ma, melting appears during the early stages of EDC but quickly ceases (at t<10 Ma), consistent with the results of the reference case (τ_o=40 Ma). Reducing or increasing τ_o changes the convection patterns of EDC: decreasing the age (and hence initial thickness) of the oceanic lithosphere tends to promote more asymmetric downwellings. For η₀ as in the reference case, significant EDC-related melting requires τ_o≤30 Ma. Widespread SSC (and related melting) is largely independent of τ_o.

Changing the continental thicknesses also modifies the patterns of convection. Figure 7a, b show that thicker continental lithospheres tend to increase the vigor of EDC, therefore augmenting the volume of related melting. However, this increase only occurs up to some point: for τ_c>150 Ma (Figs. 5c and 7b) the pattern of convection changes such that the maximum vertical velocity occurs at significantly greater depths than in the reference case (Fig. 3). As a result, the characteristic velocities of EDC slow down because the viscosity increases with depth (see Eq. 2). The onset of SSC also decreases for τ_c>150 Ma. Similar to the effects of decreasing τ_o, increasing τ_c enhances the asymmetry of the EDC cell. This asymmetry, in turn, implies that less material from the base of the continental lithosphere and more material from the base of the oceanic lithosphere is entrained by the EDC downwelling for higher τ_c.

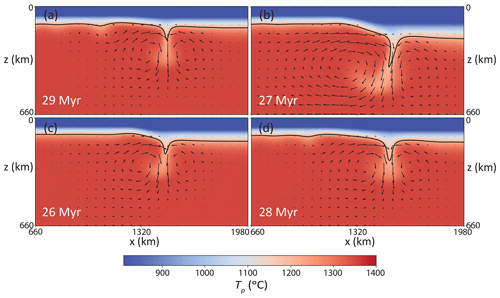
Figure 7 Effects of edge geometry on edge-driven convection, shown by snapshots of potential temperature. (a) τ_c=70 Ma. (b) τ_c=150 Ma. (c) w=132 km. (d) w=396 km. All other parameters as in the reference case. Note that no melting occurs in any of the models. For clarity, note that the values of the reference case are τ_c=100 Ma and w=64 km.

Increasing w increases the v_z,rms of EDC, probably due to more material from the lithosphere (thermal boundary layer) entrained in the downwelling(s) (Fig. 7d). Contrary to the previous cases, changing w does not noticeably affect the onset of SSC, which remains largely constant (Fig. 5d). These differences between changing τ_o and τ_c and changing w suggest that the geometrical effects cannot be simplified to an aspect-ratio-dependent parameter and that all geometrical parameters have a distinct effect.

Finally, we devise a model for the Canary Islands with τ_o=40 Ma, w=528 km, and a continental thermal age τ_c=350 Ma (corresponding to a depth of 275 km for the 1215 ^∘C isotherm), consistent with the lithospheric thickness maps presented by Jessell et al. (2016, and references therein). The Canary Islands are located on an oceanic crust much older than 40 Ma; however, it is not possible within the limitations of our models to initiate a case with an oceanic crust of 100 to 150 Ma. Thus we decide to keep τ_o as in the reference case. Results from this model conform with the combined predictions of our cases with a very wide edge and with a very thick continental lithosphere ($v_{z,\text{rms}}=\mathrm{287}$ m Myr⁻¹, and onset of SSC = 48 Ma), suggesting that extrapolations from the trends in Fig. 5c, d are viable for settings outside the range of parameters systematically explored here. Also note that no melting was detected in this case.

3.4 Effects of internal heating

We also explore the effects of internal heating on model results. In principle, radioactive heating in the mantle should be much lower than that in the crust, but chemical heterogeneity may locally increase internal heating. We explore cases with increased internal heating everywhere and others with increased internal heating just in the continental “crust” (i.e., yellow area in Fig. 2 with F=1; as defined in Sect. 2). We find that tripling the radiogenic heat production compared to the reference case everywhere has little influence on the vigor and geometry of EDC. However, it has an important influence on mantle melting and also advances the onset of SSC which, then, becomes more vigorous than in the reference case (i.e., with increased v_z,rms).

Increasing internal heating can induce melting and boost the degrees and rates of melting, by limiting asthenospheric cooling. For example, as the mantle internal heating rate is unrealistically tripled in a model with activation energy E_a=160 kJ mol⁻¹, there is an increase in volcanism equivalent to reducing the E_a from 160 to 140 kJ mol⁻¹ or to reducing η₀ from 8.61×10¹⁸ to 5.68×10¹⁸ Pa s.

In nature, heat-producing elements tend to be concentrated in the continental crust due to their incompatible nature with respect to the mantle. We run an additional set of models with increased internal heating only in the continental crust H_c. Increasing the internal heating to $H_{\mathrm{c}}=\mathrm{5}\times H$ does not have any apparent effects on melting nor it does affect the convection patters or v_z,rms. For $H_{\mathrm{c}}=\mathrm{10}\times H$, the average v_z,rms is increased but no substantial changes in terms of convection patterns are detected. Only for $H_{\mathrm{c}}\ge \mathrm{50}\times H$, significant changes occur compared to the reference case, with progressive lithospheric thinning on the continental side due to the effects of radioactive heating on the viscosity. At $H_{\mathrm{c}}=\mathrm{100}\times H$, melting occurs in the lower crust (followed by melting in the eroded continental lithosphere). In any case, $H_{\mathrm{c}}\ge \mathrm{50}\times H=\mathrm{3.875}\times {\mathrm{10}}^{-\mathrm{10}}$ W kg are unrealistic as an average value for the whole crustal thickness (Turcotte and Schubert, 2014).

3.5 Effects of volatile contents

Fluids released from the transition zone or other volatility-rich heterogeneities entrained by upper-mantle convection may also play an important role for intraplate volcanism because they can greatly decrease melting temperatures. Unfortunately, dealing with amounts of water in a rock greater than the ones presented above remains a challenge for modeling (Green, 2015). We increase the water content in the enriched peridotitic component (EC) to 1000 ppm (0.1 %) in some models. In others, we also increase the abundance of EC (from 15 % to 25 %). However, we emphasize that we are limited by the melting parameterization applied here (Katz et al., 2003) and hence are unable to explicitly model compositions that bear hydrous phases or other volatiles such as CO₂. In other words, H₂O concentrations in these additional models are a qualitative proxy for bulk volatiles in terms of their effects on melting behavior.

We find that for sufficiently large contents of H₂O in EC, EC melting starts to occur for the reference setting. The solidus of hydrous peridotite for 1000 ppm H₂O is below that of pyroxenite. In previous cases, pyroxenite was the main source (or even the sole one) of mantle melting. In this case the composition of magmas or melts is different than in previous cases and mostly peridotite-derived. In cases with high water contents in EC, melting is usually widespread, occurring due to EDC and SSC. Nonetheless, the amount of melting is very limited because of the low productivity of melting at low F in hydrous peridotite (Hirschmann et al., 1999; Katz et al., 2003; Asimow et al., 2004); note that this productivity is much lower than that of the pyroxenite used here (Pertermann and Hirschmann, 2003). For example, the peak melt production in a case with 1000 ppm H₂O in EC and a content of 25 % EC in the mantle assemblage is 2 orders of magnitude lower than that of the case with activation energy E_a=120 kJ mol⁻¹ and ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$ (i.e., the case with maximum melt flux in Fig. 6).

3.6 Effects of plate motion

Another potentially important effect involves upper-mantle shear imposed by plate motion. All models presented above are stationary, i.e., with v_plate=0 cm yr⁻¹, but on Earth plates move at finite speeds. Hence, we run additional models with an imposed plate velocity of 2, 4, and 6 cm yr⁻¹ in both directions perpendicular to the edge. Related shearing of the asthenosphere may contribute to melt production near the continent–ocean transition for plate motions in the direction of the continent (and hence opposite directions of mantle shear) due to shear-driven upwelling (King and Anderson, 1995, 1998; Conrad et al., 2010; Till et al., 2010). We find, however, that no melting is generated for plate velocities ≤6 cm yr⁻¹, in models with a setting that otherwise conforms to the reference case.

4 Discussion

To explore the potential of EDC in terms of sustaining mantle melting and intraplate oceanic volcanism, we run a series of 2D convection models in a systematic parameter study. One robust result of our models involves the transient nature of EDC, with an evolving flow pattern and vigor. In all cases, EDC is followed by SSC and EDC alone (i.e., before the onset of widespread SSC) is never associated with high degrees or large volumes of mantle melting. In most models, EDC-related melting does not occur at all and, when it does, it is often short-lived and almost invariably followed by widespread melting due to SSC (except for the cases of T_ref=1400 ^∘C and τ_o=30 Ma).

In all models in which melting due to EDC occurs, it happens soon after the beginning of the model and for only a short time span. Keep in mind that EDC occurs mostly because the initial conditions of our models are metastable and in reality should have started significantly earlier than time t = 0 Ma in our models, e.g., immediately following rifting (van Wijk et al., 2010). Thus, any significant magmatism due to EDC beneath mature oceanic lithosphere is not realistic. On old lithosphere, if any melting occurs, it should occur in a widespread (due to SSC) and not localized (due to EDC) manner. Pushing mantle properties to values that are more favorable for EDC-related melting invariably advances the onset of SSC (Fig. 5), therefore constraining even more the timing of purely EDC-related melting.

Although overall consistent (compare Fig. 6a with Fig. 6a of Kaislaniemi and Van Hunen, 2014), many of our results may strike one as surprising when compared to previous work. In particular, our main conclusion of little to no melting due to EDC is in contrast to King and Anderson (1995, 1998), Till et al. (2010), and, to a smaller extent, Kaislaniemi and Van Hunen (2014). To our knowledge, no other work has self-consistently calculated the initial oceanic lithosphere depletion profile, and the initial condition has a big influence on melting in these models, mostly due to the very transient nature of EDC. Indeed, a step-like edge can promote at least short-lived vigorous EDC and melting but may not be realistic. This is not necessarily a criticism of previous work – for example, Kaislaniemi and Van Hunen (2014) deal with a tecton–craton transition in a continental setting – but this is rather a cautionary tale for future work regarding melting in the oceanic domain.

Kaislaniemi and Van Hunen (2014) also used higher than realistic values for radiogenic heating to compensate for the potential lack of basal heating due to whole-mantle convection in regional-scale models. This increased heating may maintain otherwise transient EDC-related melting and cause hotter temperatures beneath the continents. Our results suggest that higher-than-realistic internal heating can have a significant effect on melting by elevating mantle temperatures such that they exceed those for which the initial mid-ocean ridge depletion profile was calculated on the oceanic side (but note that in this case, the relevant origin of melting is not EDC anymore). Furthermore, the lack of basal heating is not necessarily unrealistic because, for realistic rheologies, sub-adiabatic lower mantles have been inferred (e.g., Christensen and Yuen, 1985; Ulvrova et al., 2019). Indeed, EDC is a transient process and will be affected by re-heating of the upper mantle, but re-heating is achieved by other processes than those studied here (e.g., mantle wind or mantle plumes).

To stabilize the continental lithosphere, some authors have applied composition-dependent rheology (e.g King and Anderson, 1995; Kaislaniemi and Van Hunen, 2014). Such an approach has the advantage of keeping the edge geometry mostly constant and being more suitable to studying long-term processes. Unfortunately, there is no obvious and self-consistent way to calculate the lithological and rheological profile at the base of the continental lithosphere (see “Methods” section) and any proper analysis would hence require an extended parameter search. The models explored in Appendix B confirm that the results of our models predict upper bounds in terms of amounts of melting. Moreover, the total amount of mantle melting due to EDC is smaller with rheological stabilization than without (for details, see Appendix B).

Another effect that emerges in models with rheological stabilization and radiogenic heating is a blanketing effect that may cause melting by processes other than EDC (see Appendix B). In reality, although a local enrichment of radiogenic elements or a blanketing effect by a continent is possible, Jain et al. (2019) showed recently that there is an inverse relation between increased radiogenic heating and the ability of continents to “heat” the underlying mantle by isolation.

As demonstrated by our high-temperature models, EDC may (temporarily) sustain higher-volume fluxes of melting if hot materials are brought to the oceanic–continental transition for any reason. Such hot materials may be transported to the base of the lithosphere mainly by two processes: flow related to whole-mantle convection (e.g., Behn et al., 2004; Conrad et al., 2011) or mantle plumes (for detailed investigation, see companion paper). Alternatively, the entrainment of hydrous or enriched materials by EDC may sustain moderate volcanism locally. For example, hydrous upwellings from the transition zone may be conveyed by EDC or SSC to the base of the lithosphere (Long et al., 2019). In this case, the underlying origin of mantle melting in the first place are the hydrous upwellings, and not EDC, even though the latter may ultimately control the geographic distribution of volcanism.

In any case, degrees of melting and related volume fluxes predicted by our models are unable to account for the high eruptions rates of the Canary Islands or Cabo Verde (Hoernle and Schmincke, 1993; Carracedo et al., 1998; Plesner et al., 2003), even for a slow moving plate. We consider the case with the greatest melt fluxes in Fig. 6a (E_a=120 kJ mol⁻¹; ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$): all magma produced in the mantle before the onset of SSC-related melting will result in a 2D edifice of only 2.55 km height, assuming the most favorable conditions (no melt retention in the mantle and complete extrusion to the surface) and an edifice slope of 18^∘ (Smith, 1988). This height is insufficient to explain emerged islands in the Canary archipelago, since the seafloor is >3 km below sea level. If we assume that 3D effects will focus melts into conical edifices with a spacing in the third dimension of 50 km (consistent with the separation of the islands La Palma and El Hierro), the height of the edifices would be 4.66 km above the sea floor, compatible with the height of small islands, such as El Hierro, but inadequate to explain the height of islands such as La Palma or Tenerife. These calculations demonstrate that not even this extreme case, with parameters that are marginally realistic for the Earth’s mantle (E_a=120 kJ mol⁻¹; ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$) and considering favorable assumptions, can reproduce the volumes of major (subaerial) volcano chains such as the Canary Islands (or Cabo Verde).

In addition, the short lifespan of EDC-related melting in models with low τ_o suggests that any related volcanism should occur on seafloor much younger than that underlying the Canaries or Cabo Verde. Besides, no widespread magmatism such as that due to SSC is observed in the vicinity of any of these archipelagos. Also, strictly speaking, EDC melting is expected to sustain volcanism in an elongated zone that is parallel to the cratonic margin and not localized like a hotspot. On the basis of the results of the models here presented, we draw the conclusion that edge-driven convection alone is insufficient to sustain island-building volcanism near the African margin.

Furthermore, our models predict that EDC-related lavas invariably originate from mantle melting of enriched lithologies such as pyroxenite (Fig. 6b). While volcanic compositions in the shield building stage of the Canaries are slightly more enriched than their Hawaiian counterparts (Abdel-Monem et al., 1971, 1972; Carracedo, 1999), they are not consistent with mostly pyroxenite-derived primary magmas. The models in which hydrous peridotite melts first – i.e., the hydrous models – present even lower productivities and melting volumes. Geochemically speaking, we cannot favor an EDC origin for the main shield building stage of the Canary or Cabo Verde archipelagos either.

Nonetheless, there are some enriched volcanic compositions in the eastern Atlantic, for example, the outcrops of carbonatites in the two archipelagos mentioned above (Allegre et al., 1971; Hoernle et al., 2002; Doucelance et al., 2010). Moreover, data about fluid inclusions in recent work suggest that current eruptions are among the most CO₂-rich for ocean islands (Taracsák et al., 2019, Esteban Gazel, Cornell University, personal communication, 2018). Although it has been suggested that a high amount of CO₂ in the source is not required to explain the magmatic signatures of these islands (Schmidt and Weidendorfer, 2018), the influence of CO₂ on melting should not be ignored. Unfortunately, no parameterization which we could implement with our numerical scheme includes the effects of CO₂ on melting in the mantle, which remain poorly constrained. And the high water models of Sect. 3.5 are only a proxy for what could happen.

While an alternative origin (such as a thermal anomaly) is required for the volcanic archipelagos, this does not imply that EDC does not happen near the western African margin. EDC occurs in all of our models and must occur along every continental margin on Earth. Patriat and Labails (2006) found a “bulge” in the basement of the ocean–continent transition between the Canary Islands and Cabo Verde. The location of this topographic anomaly coincides with the position of the main upwelling in our models (i.e., at similar distances from the margin as predicted here). In turn, this “bulge” does not coincide with the inferred position of the Canary or Cabo Verde hotspots.

In addition, Van Den Bogaard (2013) describes the formation of seamounts near the current position of, but significantly preceding, the Canary hotspot (Geldmacher et al., 2005). The timing and location of these seamounts is consistent with EDC-related melting beneath oceanic seafloor younger than 60 Ma, such as predicted by our models (for example, the Bisabuelas seamount erupted 142 Myr ago in a much younger African Plate). Given our model results, the geochemical signatures of these seamounts can be used as a test for their origin. We demonstrate that any EDC-related melting robustly implies strong geochemical enrichment.

One of the main conclusions of this study is the occurrence of EDC in absolutely all models run here, at least for a short duration. This is an intuitive result, as mantle convection is driven by lateral density differences. Even for a lithosphere that is intrinsically buoyant due to chemical anomalies, the thermal boundary layer will grow to the point where EDC starts (Lee et al., 2005). It is very likely that EDC starts as soon as rifting indents the lithosphere, resulting in an increased magmatism and erosion (King and Anderson, 1995; Sleep, 2007). Furthermore, although we have shown that EDC (by itself) is not a suitable mechanism for creating voluminous volcanic archipelagos, it could be responsible for smaller seamount provinces on young oceanic crust, such as the Canary Islands seamount province of Van Den Bogaard (2013).

Gerya et al. (2015) suggested that several processes during the history of the lithosphere may weaken it sufficiently to overcome the resistance to subduction initiation. In this sense, EDC-related low-degree magmatism, although insufficient to generate archipelagos, may help to decrease the strength of the lithosphere in the continental–oceanic transition. This weakening could help to localize subduction zones along continental margins. The stresses related to EDC and SSC may further contribute to breaking plates (Solomatov, 2004; Mulyukova and Bercovici, 2018). We show that EDC can thermally erode and indent the lithosphere locally and that melting will occur just below this indentation. Future work should focus on the role of EDC in subduction initiation.

Concerning limitations, our models are intentionally simplified because we attempt to explore the systematic effects of rheological and geometrical parameters on edge-driven convection and melting. As the depleted and dehydrated lithosphere is expected to be more viscous than modeled here, our predicted velocities of EDC can be understood as upper bounds (see Appendix B). Moreover, we show that erosion of the lithosphere is a prerequisite for EDC-related melting, and considering the effect of depletion stiffening will only reduce the degrees of melting and related volumes discussed in Sect. 3. Lee et al. (2005) showed the importance of composition-dependent rheology for stabilizing cratons, and the influence of these variables on EDC needs to be better constrained. On the other hand, Currie and van Wijk (2016) showed that EDC and craton stability are intimately associated and that the influence of EDC on craton formation and stability is poorly understood.

Finally, 3D models of EDC may present small differences with their 2D counterparts (Kaislaniemi and Van Hunen, 2014). We expect these discrepancies to be small, however, in particular for models with small plate velocities. For large plate velocities, the preferred geometry of SSC (longitudinal rolls; Richter and Parsons, 1975) is different than that prescribed in 2D models, and hence the onset age of SSC may be further advanced. In this sense, again, our model setup is conservative. Test models indeed confirm that key model predictions remain robust in 3D geometry.

5 Conclusions

In this paper, we study the formation of mantle melting and oceanic intraplate volcanism due to edge-driven convection (EDC). As a complex, transient phenomenon, EDC is strongly affected by mantle rheological properties and the geometry of the base of the lithosphere. The following points summarize the key findings of this paper:

• Although EDC melting is not very vigorous, mantle flow due to EDC occurs for any combination of physical parameters realistic for the Earth, although it remains a transient phenomenon. We predict that EDC should occur everywhere on Earth where lateral density variations exist in the lithosphere, but if melting occurs, it will soon transition to melting due to widespread SSC.

• For a wide range of parameters, EDC is insufficient to sustain mantle melting at all. Only for a subset of the parameter space (e.g., for low E_a and/or low η₀) can EDC sustain magmatism. However, even for these models, EDC-related magmatism is rather weak and can only sustain the formation of small seamounts with very enriched geochemistry on young oceanic crust (e.g the Cretaceous to Paleogene Canary Islands seamount province).

• In turn, EDC is by far insufficient to sustain voluminous island-building volcanism, particularly on old seafloor (such as the Canaries or Cabo Verde). On old seafloor, volcanism is predicted by our models to occur in a widespread manner due to SSC and not in a localized way due to EDC (if it occurs at all).

• Increased mantle temperatures or water contents can modify the vigor of convection and the amount of melting, but future work is needed to quantify the conditions under which such thermal or compositional anomalies can be sustained continuously in order to reproduce the large volumes of volcanism observed at the eastern Atlantic archipelagos.

A comprehensive paper (in preparation) will investigate the interaction between mantle plumes and edge-driven convection.

Appendix A: Additional figures and explanations for the “Methods” section

The following figures complement those presented in Sect. 2. Figure A1 shows a snapshot of a corner flow model simulating flow and melting at a mid-ocean ridge. These models are run to calculate the initial melt depletion profiles for the oceanic (and continental) lithosphere of the EDC models presented in the main text. Boundary conditions are different than those in the main text, with an open bottom and right boundary to simulate a corner flow (with lithosphere cooling) in the top-left corner. Plate velocity (2 cm yr⁻¹) is imposed at the surface. We evaluate the models when a statistical steady state is reached. The depletion profile is extracted from these models at a location sufficiently far away from the ridge axis (i.e., once melting ceases in a determinate column moving away from the ridge axis) at the steady state.

Figure A2 shows the different compositional fields for a snapshot of the reference case. The most important feature of this figure is that the most enriched lithologies (EC and PX) are depleted also at the very base of the lithosphere. Erosion and removal of these enriched lithologies are crucial for melting in any models without significant thermal anomalies in the mantle (including our EDC models) and for which the depletion at the base of the lithosphere is self-consistently calculated.

Figure A1 Temperature field and melting for an example mid-ocean ridge model (for description, see “Methods” section). For reference to contour lines, see captions of Figs. 3 and 4.

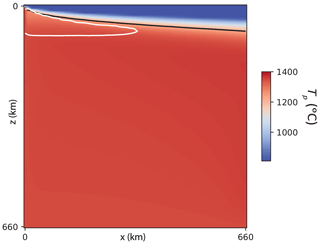
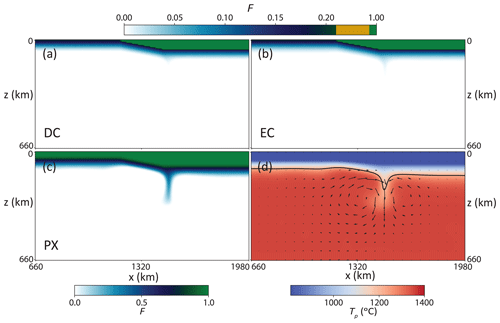
Figure A2 Snapshots of composition and temperature of the same time step of the reference model as shown in Fig. 3b. Panels (a) and (b) show melt depletion of the peridotitic compositions: DC and EC, respectively. Panel (c) shows the same field for the pyroxenitic (PX) component. Panel (d) is identical to Fig. 3b. Note that while the depleted lithospheres of peridotitic components are barely eroded and entrained by EDC (with EC being slightly more affected), this is not true for the depleted part of the PX component, which is more efficiently removed by the mantle flow. Also note that the scale for (c) is different than that of (a) and (b).

Appendix B: Extended discussion on rheological stabilization of continents and EDC

To explore the effects of rheological stiffening and stabilization of the continental lithosphere, we run additional models of flow and melting with composition-dependent viscosity. A priori, there is no indication that accounting for compositional rheology should strongly affect our results: a stiffer lithosphere is expected to promote less entrainment and erosion of the base of the lithosphere, which in turn should result in less melting. On the other hand composition-dependent rheology may help to maintain the edge, hence extending EDC-related flow.

We follow the rheological stiffening method of Ballmer et al. (2009), which calculates the increase in viscosity due to water loss in the main lithology (with increasing depletion of DC). We use a depletion stiffening coefficient ξ (for definition of this coefficient, see Eq. 10 of Ballmer et al., 2009) with a value of 274.8, which corresponds to a viscosity contrast of a factor of 100 between a fully hydrated mantle (with water contents in DC and EC as defined in Sect. 2) and a dry mantle. This method relates stiffening to depletion as DC loses water during melting. Since the upper part of the continental lithosphere is simulated as an extremely depleted lid, this method leads to a greatly increased viscosity (i.e., a factor of 100) of the lithosphere on the continental side of the model. Consistently, significant stiffening also happens on the oceanic side, as the oceanic lithosphere is fully dehydrated at the top. For a comparison of viscosity profiles between the reference case of Fig. 3 and an equivalent case with rheological stiffening, see Fig. B1

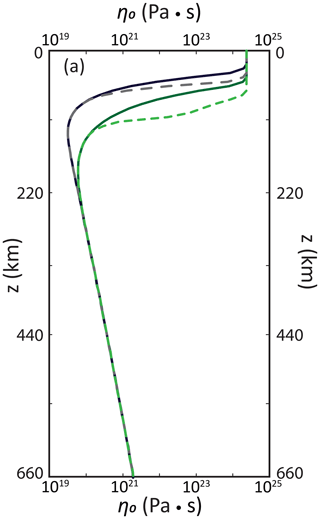
Figure B1 Viscosity profiles for cases with and without rheological stiffening. Solid lines correspond to cases without rheological stiffening, while dashed lines correspond to cases which include rheological stiffening. In black and gray, profile at the oceanic side of the model; in dark and light green, profile at the continental side of the model. All the remaining properties as in the reference case.

Figure B2a shows a comparison of a model with rheological stabilization and one without. Indeed, they show similar characteristics, but the case with composition-dependent rheology shows less removal of the base of the lithosphere (Fig. B2b). Due to this less extensive removal, models with lithological stabilization produce lower melting volumes. For example, the models shown in Fig. B2 feature the same η₀ and E_a as the case with maximum melting in Fig. 6, but the case with compositional stiffening displays lower volumes of melting than its counterpart without viscosity adjustment (i.e.,  2.49 vs. 5.32 km² Myr⁻¹).

The effect of lithological stiffening also emerges when analyzing the vigor of convection. Figure B3 shows different v_z,rms for equivalent cases with and without composition-dependent rheology. As can be seen, the cases with compositional rheology display systematically lower v_z,rms than cases without. This result suggests that the melt volumes and vigor of EDC predicted by our models without compositional rheology (as presented in the main text) can be taken as upper bounds, therefore corroborating our conclusions.

Finally, our models do not predict that the duration of EDC and EDC-related melting would be significantly extended for cases with compositional rheology and with stable continent and edge geometries (as suggested by Kaislaniemi and Van Hunen, 2014).

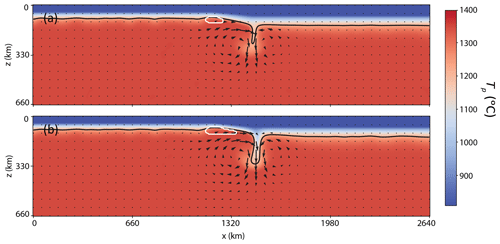
Figure B2 Model snapshots of mantle flow and melting for a case with composition-dependent rheology (a) and a case without composition-dependent rheology (b). Physical properties as in the case with maximum melting in Fig. 6 (${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$ Pa s; E_a=120 kJ mol⁻¹). Note that although the velocity fields are very similar, the case with rheological stabilization (a) shows less erosion at the base of the lithosphere than the case without (b), resulting in less vigorous upwellings and downwellings. Consequently, melting rates are also lower for the cases with composition-dependent rheology (compare the white contour of panel of a with that of b).

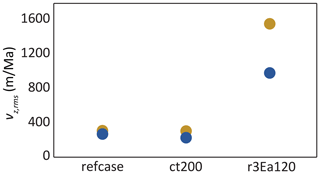
Figure B3 Diagram showing v_z,rms for equivalent cases with (blue) and without (light brown) composition-dependent rheology. refcase corresponds to the reference case (see Fig. 3); ct200 corresponds to a case with τ_c=200 Ma; and r3E120 corresponds to a case with ${\mathit{\eta }}_{\mathrm{0}}=\mathrm{2.87}\times {\mathrm{10}}^{\mathrm{18}}$ Pa s and E_a=120 kJ mol⁻¹ (i.e., the case with maximum melting in Fig. 6). All other parameters as in the reference case (Fig. 3).