Benchmark study using a multi-scale, multi-methodological approach for the petrophysical characterization of reservoir sandstones

This paper presents a detailed description and evaluation of a multi-methodological petrophysical approach for the comprehensive multi-scale characterization of reservoir sandstones. The suggested methodology enables the identification of links between Darcy-scale permeability and an extensive set of geometrical, textural and topological rock descriptors quantified at the pore scale. This approach is applied to the study of samples from three consecutive sandstone layers of Lower Cretaceous age in northern Israel. These layers differ in features observed at the outcrop, hand specimen, petrographic microscope and micro-CT scales. Specifically, laboratory porosity and permeability measurements of several centimetre-sized samples show low variability in the quartz arenite (top and bottom) layers but high variability in the quartz wacke (middle) layer. The magnitudes of this variability are also confirmed by representative volume sizes and by anisotropy evaluations conducted on micro-CT-imaged 3-D pore geometries. Two scales of directional porosity variability are revealed in quartz arenite sandstone of the top layer: the pore size scale of ∼0.1 mm in all directions and ∼3.5 mm scale related to the occurrence of high- and low-porosity horizontal bands occluded by Fe oxide cementation. This millimetre-scale variability controls the laboratory-measured macroscopic rock permeability. More heterogeneous pore structures were revealed in the quartz wacke sandstone of the intermediate layer, which shows high inverse correlation between porosity and clay matrix in the vertical direction attributed to depositional processes and comprises an internal spatial irregularity. Quartz arenite sandstone of the bottom layer is homogenous and isotropic in the investigated domain, revealing porosity variability at a ∼0.1 mm scale, which is associated with the average pore size. Good agreement between the permeability upscaled from the pore-scale modelling and the estimates based on laboratory measurements is shown for the quartz arenite layers. The proposed multi-methodological approach leads to an accurate petrophysical characterization of reservoir sandstones with broad ranges of textural, topological and mineralogical characteristics and is particularly applicable for describing anisotropy and heterogeneity of sandstones on various rock scales. The results of this study also contribute to the geological interpretation of the studied stratigraphic units.

1 Introduction

Permeability is an effective property of a reservoir rock that varies enormously over a wide range of rock length scales, attributed to a hierarchy of dominant sedimentary depositional features (Norris and Lewis, 1991; Nordahl and Ringrose, 2008; Ringrose and Bentley, 2015). Permeability should thus be properly upscaled through the following sequence of scales (Nordahl and Ringrose, 2008; Ringrose and Bentley, 2015 and references therein): (1) from the pore scale (the microscale, typically micrometres to millimetres) to the representative elementary volume of a single lamina (the macroscale, typically millimetres to centimetres, e.g. Wildenschild and Sheppard, 2013; Andrä et al., 2013b; Bogdanov et al., 2011; Narsilio et al., 2009); (2) to the scale of geological heterogeneity, e.g. the scale of a stratigraphic unit (decimetres to decametres, e.g. Jackson et al., 2003; Nordahl et al., 2005); and (3) to the field scale or the scale of an entire reservoir or aquifer (hundreds of metres to kilometres) (Haldorsen and Lake 1984; Rustad et al., 2008). Pore-scale imaging and modelling enable us to relate macroscopic permeability to basic microscopic rock descriptors (Kalaydjian, 1990; Whitaker, 1986; Cerepi et al., 2002; Wei et al., 2014; Nelson, 2009). Therefore, the first stage in the above sequence is crucial for successful upscaling to the overall reservoir scale permeability.

Over the past few decades, 3-D pore-scale imaging and flow simulations (Bogdanov et al., 2012; Blunt et al., 2013; Cnudde and Boone, 2013; Wildenschild and Sheppard, 2013; Halisch, 2013a) have started to serve as a reliable method for rock characterization. The advantages of these techniques are their non-destructive character and their capability to provide reliable information about the real pore-space structure and topology of rocks that is impossible to obtain using the conventional experimental methods (e.g. Arns et al., 2007; Knackstedt et al., 2010; Blunt et al., 2013). However, despite its importance, the upscaling from the pore scale is sometimes omitted; as a result, effective petrophysical rock characteristics (e.g. porosity, surface area and permeability) are often evaluated at the macroscale through only conventional laboratory experiments, which often suffer from errors due to local heterogeneities, anisotropy or an insufficient number of samples (e.g. Meyer, 2002; Halisch, 2013a).

Digital 3-D microscale core analysis should also become a necessary technique for rocks that are difficult to characterize due to various reasons (e.g. for tight sandstones, Liu et al., 2017; Du et al., 2018; Munawar et al., 2018; Zhang et al., 2019) or for those with inhomogeneous or anisotropic pore space (e.g. Meyer, 2002; Farrel et al., 2014). Preferential fluid flow pathways are inherently connected to rock microstructure, formed by depositional sedimentary structures such as pore shapes and their preferential orientation (Sato et al., 2019) or lamination (Lewis, 1988). Those can be modified with time by dissolution of grains, by grain rearrangement and pore collapse (Halisch et al., 2009; Clavaud et al., 2008), by cementation (Louis et al., 2005) or by deformation structures (fractures). The later may drastically alter the host rock depositional porosity pattern and create new permeability pathways (Zhu et al., 2002; Farrel et al., 2014).

The present paper provides a detailed description and evaluation of a multi-methodological petrophysical approach for the comprehensive multi-scale characterization of reservoir sandstones. The proposed approach includes petrography, gas porosimetry and permeametry, mercury intrusion porosimetry, 3-D imaging and image analysis, and flow modelling at the pore scale. The suggested computational workflow enables the identification of Darcy-scale permeability links to an extensive set of geometrical, textural and topological rock descriptors, quantified at the pore scale by deterministic methods. The approach presented herein is important for the identification of anisotropy and inhomogeneity. Ultimately, this approach is applied to the study of three different consecutive sandstone layers of Lower Cretaceous age in northern Israel.

The multi-methodological validation procedure is significant for properly upscaling permeability from the microscale to the macroscale (Ringrose and Bentley, 2015). This validation, thereby, allows an accurate petrophysical analysis of reservoir sandstones with broad ranges of textural and topological characteristics. The findings contribute also to the current geological knowledge regarding non-marine sandstones of Lower Cretaceous age (e.g. Akinlotan, 2016, 2017, 2018; Li et al., 2016; Ferreira et al., 2016) and specifically regarding the studied stratigraphic unit.

2 Geological setting

The study is based on samples collected from a steep outcrop at Wadi E'Shatr near Ein Qiniyye on the southern slopes of Mt. Hermon (Fig. 1). The outcrop consists of sandstones from the Lower Cretaceous Hatira Formation (Sneh and Weinberger, 2003). This formation (Fm.) acts as a reservoir rock for hydrocarbons in Israel (Fig. 1a), both onshore, namely, Heletz (Grader and Reiss, 1958; Grader, 1959; Shenhav, 1971, Calvo, 1992; Calvo et al., 2011), and offshore, namely, Yam Yafo (Gardosh and Tannenbaum, 2014; Cohen, 1971; Cohen and Boehm, 1983).

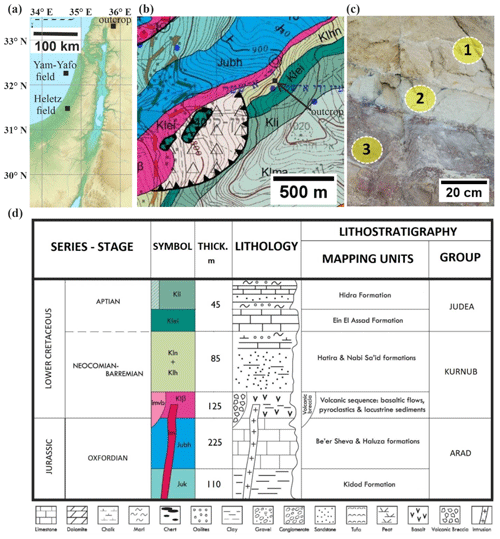
Figure 1 Geographical and geological settings. (a) Schematic relief map of Israel (modified from https://www.mapsland.com/asia/israel/large-relief-map-of-israel, last access: March 2021). (b) Geological map of Ein Qiniyye. The Hatira Fm. sandstone and the overlying limestone and marl of the Nabi Said Fm. are marked as Klhn (map is adopted from Sneh and Weinberger, 2014). (c) Outcrop of the Lower Cretaceous Hatira Fm. sandstones (Klhn) at Ein Qiniyye. The studied sandstone layers have distinct colours: yellow–brown (1), grey–green (2) and red–purple (3). (d) Stratigraphic table of the geological map (modified from Sneh and Weinberger, 2014).

The Hatira Fm. is the lower part of the Kurnub Group (Fig. 1d) of Lower Cretaceous (Neocomian–Barremian) age. The Hatira Fm. nomenclature used in Israel and Jordan is equivalent to Grès de Base in Lebanon (Massaad, 1976). This formation occurs in Israel in outcrops from the Eilat area along the rift valley, in the central Negev and in the northernmost outcrops on Mt. Hermon; it forms part of a large Palaeozoic–Mesozoic platform and continental margin deposits in northeastern Africa and the Arabian Peninsula. The Hatira Fm. consists of siliciclastic units, typically dominated by quartz-rich sandstones (Kolodner et al., 2009 and references therein). The underlying Palaeozoic sandstones cover large areas in north Africa and the Arabian Peninsula from Morocco to Oman; these sandstones overlie a Precambrian basement affected by Neoproterozoic (pan-African) orogenesis (Garfunkel, 1988, 1999; Avigad et al., 2003, 2005). The lower Palaeozoic sandstones in Israel and Jordan originated from the erosion of that Neoproterozoic basement, the Arabian–Nubian Shield, with contributions from older sources. These lower Palaeozoic sandstones (Cambrian and Ordovician) are described as first-cycle sediments (Weissbrod and Nachmias, 1986; Amireh, 1997; Avigad et al., 2005). Exposures of the Hatira Fm. in the central Negev, the Arava Valley, Eilat and Sinai were originally defined as the Wadi (Kurnub) Hatira sandstone (Shaw, 1947). The largely siliciclastic section of the Hatira Fm. is intercalated with carbonates and shales representing marine ingressions that increase towards the north (Weissbrod, 2002).

The Lower Cretaceous sandstones of the Kurnub Group are described as super-mature, cross-bedded, medium- to fine-grained, moderately sorted to well-sorted quartz arenites with a high zircon–tourmaline–rutile (ZTR) index (for more details, see Kolodner et al., 2009). Earlier observations indicated the relatively scarce occurrence of siltstones and claystones compared to sandstones (Massaad, 1976; Abed, 1982; Amireh, 1997). These Lower Cretaceous sandstones are mainly the recycled products of older siliciclastic rocks throughout the Phanerozoic; the sand was first eroded from the surface of the pan-African orogeny approximately 400 Myr prior to its deposition in the Lower Cretaceous sediments (Kolodner et al., 2009).

The Mt. Hermon block was located at the southern border of the Tethys Ocean during the Early Cretaceous (Bachman and Hirsch, 2006). A palaeogeographical reconstruction indicates that the sandy Hatira Fm. (Fig. 1) was deposited in a large basin, which included both terrestrial and coastal environments such as swamps and lagoons (Sneh and Weinberger, 2003). The Hermon block, located next to the Dead Sea transform, was rapidly uplifted during the Neogene (Shimron, 1998). The area is marked by intense erosion, which resulted in extensive outcrops such as those near Ein Qiniyye on the southeastern side of Wadi E'Shatr (Fig. 1).

The Kurnub Group in the study area (Fig. 1b and d) consists of a volcanic sequence at its base that is overlain with an angular uncomformity by sandstone and clay layers of the Hatira Fm.; the upper unit consists of limestone, marl and chalk – the Nabi Said Fm. (Sneh and Weinberger, 2003). At the section investigated by Saltzman (1968), which is approximately 100 m SW of the sampling area of the present study, the 58 m thick variegated sandstone is interbedded with layers of clay and clay marl. The sandy component is white–yellow–brown or red and consists of largely angular, poorly sorted, fine- to coarse-grained quartz sand. Individual sandstone layers are cemented by Fe oxide (FeOx). The outcrops show lenticular benches 0.2–1.0 m thick. The clay-rich interlayers are grey and normally silty and brittle. Locally, these layers contain lignite. The outcrop investigated and the specific beds sampled in the present study are shown in Fig. 1c.

3 Methods

3.1 Sample description

Samples were extracted from three consecutive layers of different colours from a stratigraphic sequence (Fig. 1c and d). The lower layer (3) is ∼1.5 m thick and consists of sandstone that is light (pale) red–purple in colour with undulating bedding planes between the sublayers. The middle layer (2) is composed of grey–green shaly sandstone that is 20 cm thick with dark horizons at the bottom and top. The upper layer (1) comprises 1.5 m thick homogenous brown–yellow sandstone. Large sample blocks of ∼10–20 cm size were collected from these three layers, and the directions perpendicular to the bedding planes (defined as the z directions in our study) were noted. Subsequently, in the laboratory, smaller subsamples (described below) were prepared from these large samples for textural observations and various analytical measurements and computations. In total, seven subsamples from the top layer, eight subsamples from the middle layer and four subsamples from the bottom layer were investigated in the laboratory (Table 2).

3.2 Laboratory and computational methods for rock characterization

The integrated analytical programme designed for this study includes the following laboratory measurements and computations conducted at different scales (from the microscale reflecting the scale of individual pores and grains to the core scale reflecting the scale of the laminas at the outcrop) (Table 1). Specimens ∼5–7 cm in size were investigated by petrographic and petrophysical lab methods. Subsamples ∼1 cm in size were retrieved from the aforementioned plugs for investigation by 3-D imaging, digital image analysis and simulation techniques (described in detail below).

Petrographic and petrophysical analysis (nos. 1–7 in Table 1) were conducted following the RP40 guidelines (Recommended Practices for Core Analysis, API, 1998), giving detailed information on theory, advantages and drawbacks of each method. An extended computational workflow (no. 8 in Table 1) combines several methods that may contain some variability in their application for the rock characterization. Those are described in more detail below.

Table 1 Laboratory methods employed and petrophysical characteristics determined from these methods.

Petrographic descriptions of rock compositions and textures at the microscale, notably those of the fine fraction, were performed using scanning electron microscopy (JCM-6000 Bench Top SEM device; e.g. Krinsley et al., 2005) using both backscatter and secondary electron modes.

Thin-section optical microscopy (Olympus BX53 device; e.g. MacKenzie et al., 2017) was used to estimate the mineral abundance and surface features of the grains and the mineralogical and textural features of matrix and cement. Grain size distributions were determined by a laser diffraction particle size analyser (LS 13 320; e.g. Wang et al., 2013). X-ray diffraction (Miniflex 600 device by Rigaku; e.g. Asakawa et al., 2020) was applied to powdered samples to determine their mineralogical composition.

Effective porosity and permeability were evaluated on dried cylindrical samples (2.5 cm in diameter and 5–7 cm in length). Effective porosity (ϕ) was measured using a steady-state nitrogen gas porosimeter produced by Vinci Technologies (HEP-E, Vinci Technologies; e.g. Viswanathan et al., 2018). Absolute permeability (κ) was measured by using a steady-state nitrogen gas permeameter (GPE, Vinci Technologies; e.g. Tidwell and Wilson, 1999).

Mercury intrusion porosimetry (Micromeritics AutoPore IV 9505, which considers pore throats larger than 0.006 µm; e.g. Giesche, 2006), was applied to dried cylindrical samples ∼1 cm³ in size to evaluate the following parameters (Table 1):

• pore throat size distribution (PTSD) (Lenormand, 2003);

• specific surface area (SSA): the pore surface to bulk sample volume (Rootare and Prenzlow, 1967; Giesche, 2006);

• characteristic length (l_c): the largest pore throat width (obtained from the increasing intrusion pressure) at which mercury forms a connected cluster (Katz and Thompson, 1987);

• pore throat length of maximal conductance (l_max): defines a threshold for the pore throat size l at which all connected paths composed of l≥l_max contribute significantly to the hydraulic conductance, whereas those with l<l_max may completely be ignored (Katz and Thompson, 1987);

• permeability (Katz and Thompson, 1987):

  $$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathit{\kappa }={\displaystyle \frac{\mathrm{1}}{\mathrm{89}}}{l}_{\text{max}}^{\mathrm{2}}{\displaystyle \frac{l_{\text{max}}}{l_{\mathrm{c}}}}\mathit{\varphi }S\left(l_{\text{max}}\right),\end{array}$$

where S(l_max) is the fraction of connected pore space that is composed of pore throat widths of size l_max and larger. This model (Katz and Thompson, 1987), which was derived from percolation theory (Ambegaokar et al., 1971), is applicable for sandstones with a broad distribution of local conductances with short-range correlations only.

An extended computational workflow (similar to the procedure presented by Boek and Venturoli, 2010; Andrä et al., 2013a, b) (Fig. 2) serves as one of the main methodologies in our study to upscale to permeability and derive microscopic rock descriptors. It includes 3-D micro-CT imaging of porous samples, digital image processing and segmentation, analyses for the determination of representative elementary volumes and pore-scale flow modelling through the 3-D pore geometry of the rock. First, cylindrical subsamples 4–8 mm in diameter and 5–10 mm in length were retrieved from the larger samples studied in the laboratory (Fig. 2a) and were scanned non-destructively (Fig. 2b) by using a Nanotom 180 S micro-CT device (GE Sensing & Inspection Technologies, Phoenix X-ray product line; Brunke et al., 2008). The achieved voxel size of the data sets was 2.5 or 5 µm (isotropic), suitable for imaging pore throats that effectively contribute to the flow in the studied type of sandstone (e.g. Nelson, 2009). Afterwards, all data sets were filtered for denoising, X-ray artefact removal and edge enhancement (Fig. 2c). The post-processed images scanned with 2.5 µm resolution had an edge length of 1180 voxels or 2950 µm. Image artefacts were processed as described by Wildenschild and Sheppard (2013). Beam hardening artefacts were removed by applying the best-fit quadratic surface algorithm (Khan et al., 2016) to each reconstructed 2-D slice of the image. Ring artefact reduction and image smoothing (with preservation of sharp edge contrasts) were performed using a non-local means filter (Schlüter et al., 2014). Segmentation was performed to convert the grey-scale images obtained after image filtering into binary images to distinguish between voids and solid phases (Fig. 2c). The local segmentation approach, which considers the spatial dependence of the intensity for the determination of a voxel phase, was used in addition to a histogram-based approach (Iassonov et al., 2009; Schlüter et al., 2014). Segmentation was performed by the converging active contour algorithm (Sheppard et al., 2004), a combination of a watershed (Vincent and Soille, 1991) with an active contour algorithm (Kass et al., 1988).

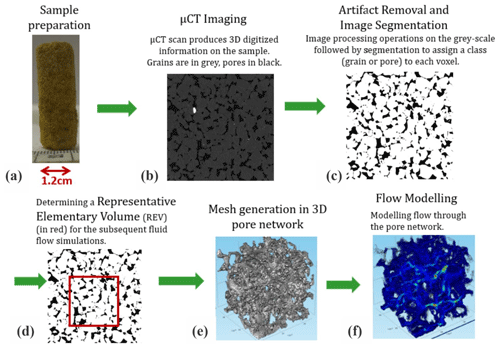
Figure 2 Extended computational workflow. See text for more details. Images in panels (e) and (f) are adopted from Bogdanov et al. (2012).

Simulations involving the real geometry of an imaged rock are computationally power and time consuming. Therefore, the determination of a representative elementary volume (REV) is required (Fig. 2d), assuming that porous media are homogeneous at REV dimensions (Bear, 2013), to perform fluid flow simulations. Porosity, a basic macroscopic structural property of porous media, is used here for the estimation of an REV (Bear, 2013; Halisch, 2013a; Tatomir et al., 2016) based on its correlation with permeability (Kozeny, 1927; Carman, 1937) (refer to the Discussion section).

A “classic” REV approach was used that claims that the REV is attained when porosity fluctuations in the subvolumes that grow isotropically in three orthogonal directions become sufficiently small (Bear, 2013; Halisch, 2013a, b). Practically, a large number of randomly distributed cubes were analysed through the entire 3-D sample for their image porosity (IP). The chosen initial cube size (with an edge length of 10 pixels in our case) was increased by 10–100 voxels. The REV size was specified when agreements between the mean and median IP values as well as saturation in the IP fluctuations were attained.

Further, the representative binary 3-D image (REV) of the pore space was spatially discretized by tetrahedrals with Materialize software (Belgium) (Fig. 2e). This step is required for importing the REV into the finite element method (FEM)-based modelling software (Comsol Multiphysics simulation environment, v5.2a). Stokes flow (Re≪1) is simulated (Table 1) in the pore network (Fig. 2f) by the following equations (e.g. Narsilio et al., 2009; Bogdanov et al., 2011):

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }\text{Stokes equation:}-\mathrm{\nabla }p+\mathit{\mu }{\mathrm{\nabla }}^{\mathrm{2}}\stackrel{\mathrm{‾}}{u}=\mathrm{0}\text{(3)}& {\displaystyle }& {\displaystyle }\text{continuity equation:}\mathrm{\nabla }\cdot \stackrel{\mathrm{‾}}{u}=\mathrm{0},\end{array}$$

where ∇p is the local pressure gradient, $\stackrel{\mathrm{‾}}{u}$ is the local velocity vector in the pore space, and μ is the dynamic fluid viscosity. Fixed pressures (p=const) were specified at the inlet and outlet boundaries of the fluid domain with a constant pressure gradient of 2.424 Pa mm⁻¹ over the domain, prescribed in all the simulations for consistency. At the internal pore walls and at the lateral domain boundaries, no-slip boundary conditions ($\stackrel{\mathrm{‾}}{u}=\mathrm{0})$ were imposed (e.g. Guibert et al., 2016). These boundary conditions are also used to simulate the flow setup in a steady-state experimental permeameter (e.g. Renard et al., 2001). The macroscopic fluid velocity $\langle \stackrel{\mathrm{‾}}{v}\rangle$ was evaluated by volumetrically averaging the local microscopic velocity field (e.g. Narsilio et al., 2009; Guibert et al., 2016). Then, from the average macroscopic velocity vectors ${\mathit{v}}_i^j$ in three orthogonal i directions corresponding to the pressure gradients ∇p_j imposed in the j direction, the full 3-D second-rank upscaled permeability tensor κ can be found:

$$\begin{array}{ll}{\displaystyle }\left(\begin{array}{ccc}{v}_x^x& v_x^y& v_x^z\\ v_y^x& v_y^y& v_y^z\\ v_z^x& v_z^y& v_z^z\end{array}\right)=& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{\mathit{\mu }\mathit{\varphi }}}\left(\begin{array}{ccc}{\mathit{\kappa }}_{xx}& {\mathit{\kappa }}_{xy}& {\mathit{\kappa }}_{xz}\\ {\mathit{\kappa }}_{yx}& {\mathit{\kappa }}_{yy}& {\mathit{\kappa }}_{yz}\\ {\mathit{\kappa }}_{zx}& {\mathit{\kappa }}_{zy}& {\mathit{\kappa }}_{zz}\end{array}\right)\\ \text{(4)}& {\displaystyle }& {\displaystyle }\times \left(\begin{array}{ccc}\mathrm{\nabla }{p}_x& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{\nabla }{p}_y& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& \mathrm{\nabla }{p}_z\end{array}\right),\end{array}$$

where z direction of the CT specimen used in this analysis is perpendicular to the natural layering of the sandstone identified in the outcrop and in the petrographic observations. x and y orthogonal directions lie in the horizontal plane, with an azimuth chosen randomly. The permeability tensor is symmetrized by

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{\mathit{\kappa }}_{\text{sym}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathit{\kappa }+{\mathit{\kappa }}^T\right).\end{array}$$

Additional permeability tensor simulations in the multiple REV subvolumes of one of the investigated samples have been performed by using the FlowDict module (Linden et al., 2015, 2018) of the GeoDict toolbox (Wiegmann, 2019). Pre-processing as well as boundary conditions are identical to those used in Comsol setup.

Tortuosity (τ; Bear, 2013; Boudreau, 1996) was calculated separately in the x, y and z directions in the meshed domain using the particle tracing tool of Comsol Multiphysics software (an additional method for deriving τ is presented later in this section).

3-D image analysis (Table 1) was conducted on a high-quality, fully segmented micro-CT image (edge length of 2950 µm scanned at a 2.5 µm voxel size). Non-connected void clusters in the binary specimen were labelled and then separated into objects (single pores and grains) by using a distance map followed by the application of a watershed algorithm (e.g. Brabant et al., 2011; Dullien, 2012). Image analysis operations were assisted by Fiji-ImageJ software (Schindelin et al., 2012) and by the MorphoLibJ plug-in (Legland et al., 2016). The following geometrical descriptors were derived from the segmented image limited by the image resolution of 2.5 µm (Table 1):

• micro-CT image porosity (IP);

• pore-specific surface area (PSA) (surface to pore volume);

• Tortuosity: evaluated in the x, y and z directions by finding the average of multiple shortest paths through the main pore network using the fast marching method (Sethian, 1996) implemented using an accurate fast marching plug-in for MATLAB;

• pore size distribution (PSD): obtained by a Feret maximum calliper (Schmitt et al., 2016);

• Euler characteristic (χ) – a topological invariant (Wildenschild and Sheppard, 2013; Vogel, 2002) that describes the structure of a topological space (see the Supplement for more details). Since the number of pore connections depends on the number of grains (N), it is essential to normalize χ (Scholz et al., 2012) to compare the connectivity among three samples that have the same dimensions but different grain sizes. Thus, a connectivity index (CI) parameter, $\text{CI}=\left|\mathit{\chi }\right|/N$ was defined, where χ and N were computed using image analysis.

Table 1 allows conducting a comparison between the characteristics derived by the different methods at the different scales of investigation (similarly to Table 1 in Tatomir et al., 2016, which focuses on the similar rock).

Additionally, we propose a new simple method to estimate the image porosity at a given resolution. Multiplication of the mercury effective saturation at the capillary pressure corresponding to the micro-CT resolution (e.g. 2.5 µm) by the porosity of the same sample measured by a gas porosimeter yields the micro-CT-predicted image porosity from MIP at the given resolution limit (Table 1).

4 Results

4.1 Petrographic and petrophysical rock characteristics

Three types of sandstone rocks were characterized by techniques 1–8 listed in Table 1. The results are presented in Figs. 3–8 and summarized in Table 2.

Sandstone S1

The top unit layer with a thickness of ∼1.5 m (Fig. 1c) consists of yellow–brown sandstone (Fig. 3a), which is moderately consolidated. The sandstone is a mature quartz arenite (following Pettijohn et al., 1987) with minor FeOx, feldspar and heavy minerals (e.g. rutile and zirconium). The grain size distribution has a mean of ∼325 µm (Fig. 6a, Table 2). The grains are moderately sorted (according to the classification of Folk and Ward, 1957) and subrounded to well-rounded with local thick (millimetre scale), relatively dark envelopes (Fig. 3b). The sandstone consists of alternating millimetre-scale layers of large and small sand grains. Secondary silt (∼45 µm) and clay (∼0.95 µm) populations are detected in the grain size distribution (Fig. 6). X-ray diffraction detected a small amount of kaolinite. The FeOx grain-coating and meniscus-bridging cement is composed of overgrown flakes aggregated into structures ∼10 µm in size (Fig. 3c–f). Mn oxide is also evident but is scarce (Fig. 3e).

Figure 3 Representative images of sandstone S1. (a) Darker laminae in the x–y plane at the millimetre scale are observed. (b) Thin-section image of S1, P refers to open pores, Q to quartz, Ox to oxide. (c) FeOx flakes (yellow) on quartz grains (pale grey). (d) SEM image of S1: grain-coating, meniscus-bridging cement and overgrowth of FeOx flakes. (e, f) Magnified images at different scales.

Figure 4 Representative images of sandstone S2. (a) Dark stains in the rock are mud streaks; yellowish zones are due to increased FeOx cement. (b) The dark laminae are richer in clays and FeOx. P refers to open pores, Q to quartz, and C to clay. (c) Clay and silt accumulated as meniscus and as a clay matrix. (d) Pore clogged by clay and FeOx. (e) Rock texture. The clay matrix is white, and quartz grains are pale grey.

The pore network is dominated by primary intergranular well-interconnected macroporosity (Fig. 3b). However, sealed and unsealed cracks in grains are also observed. Higher FeOx cementation at the millimetre scale on horizontal planes is recognized (Fig. 3a). In addition, smaller voids between FeOx aggregates and flakes occur at the micrometre scale and smaller (Fig. 3d–f).

The pore throat size analysis conducted with MIP shows that 82 % of the pore volume is composed of macropores (>10 µm) following a log-normal distribution with a peak at 44 µm (Fig. 7a). The characteristic length, i.e. the largest pore throat length at which mercury forms a connected cluster, is l_c=42.9 µm (Fig. 7b), and the pore throat length of maximal conductance is l_max=34.7 µm (Fig. A1 in Appendix A). The porosity evaluated by laboratory gas porosimetry varies in the range of 26 %–29 % for seven different samples of S1 (Fig. 8). Multiplying the mercury effective saturation (85.8 %) at the micro-CT resolution (2.5 µm) (Fig. 7a, dashed red line) by the porosity of the same sample measured by gas porosimetry (27.3 %) yields a micro-CT-predicted image porosity of 23.5 % at a resolution limit of 2.5 µm (Table 2).

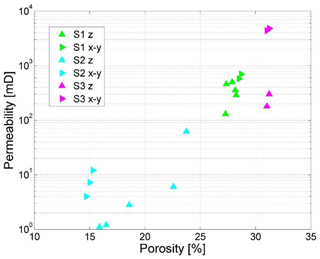
The permeability evaluated by a laboratory gas permeameter has averages of 350 mD (range of 130–500 mD) for five samples measured perpendicular to the depositional plane (z direction) and 640 mD for two samples measured parallel to the depositional plane (x and y directions) (Fig. 8). MIP measurement (Katz and Thompson, 1987) (see Sect. 3.2) yields a permeability of 330 mD (Table 2).

Table 2 Petrophysical characteristics of the three studied sandstone layers.

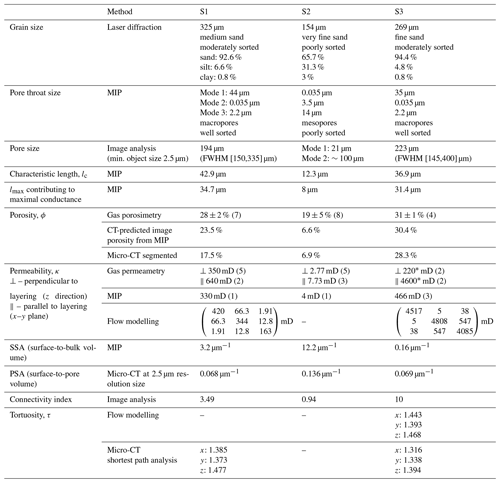
Numbers in parentheses related to gas porosity, gas permeability and MIP permeability indicate the number of plugs for the measurements. Other measurements and calculations were conducted on single plugs. FWHM – full width at half maximum, log-normal distribution.

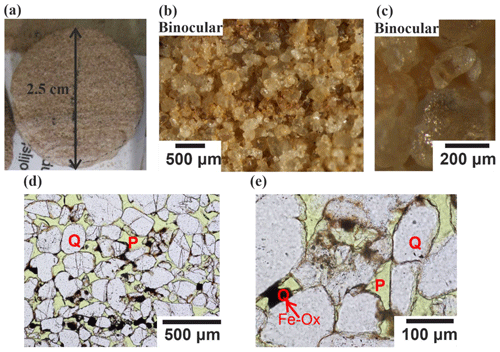
Figure 5 Representative images of sandstone S3. (a) Laminae are recognized by their slightly dark and red colour. (b) General view reveals red laminae ∼300 µm thick. (c) High-resolution observation of a clear grain. (d) A millimetre-scale lamina is indicated by enhanced meniscus-type FeOx cementation and partly by intergranular fill. Grain surfaces are coated by thin FeOx. Black and orange cements represent crystallized and non-crystallized FeOx, respectively. Some cracked grains are observed, sporadically cemented by FeOx. P refers to open pores, Q to quartz. (e) Partially dissolved grains are coated by cement.

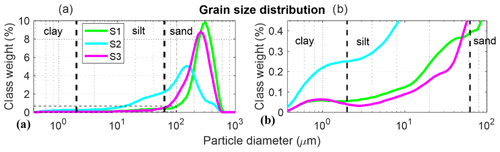
Figure 6 (a) Grain size distribution. (b) Magnified grain size distribution in the fine-grain size region plotted for sandstones S1 (green), S2 (blue) and S3 (purple). S1 and S3 have a unimodal distribution and are moderately sorted with a small skewness tail. Sample S2 has a multi-modal distribution and is poorly sorted.

Sandstone S2

The intermediate unit layer with a thickness of ∼20 cm consists of grey–green moderately consolidated sandstone (Figs. 1c and 4) composed of subrounded to rounded, very fine sand grains (∼154 µm); the sandstone is poorly sorted with 35 % of the particles being silt and clay (Fig. 6, Table 2). Secondary silt (∼40 µm), sand (∼400 µm) and clay (∼1.5 µm) populations are also detected. The grains are composed of quartz with minor FeOx coating the grains and minor quantities of heavy minerals (e.g. rutile and zirconium) (Fig. 4c). Clay filling the pore space was identified by XRD as a kaolinite mineral. It appears as a grain-coating, meniscus-bridging and pore-filling matrix (Fig. 4b and c). Therefore, the unit layer (Fig. 1c) is classified as a quartz wacke sandstone (Pettijohn et al., 1987).

The pore space is reduced by clays deposited on coarser grains, identified mostly in laminae (Fig. 4a, d). However, the intergranular connectivity of macropores can still be recognized (Fig. 4b and c). The effective pore network consists of intergranular macropores distributed between the laminae or zones richer in clay and FeOx. Integrating the grain size and pore throat size analysis results (Figs. 6 and 7) confirms that the reduction in the intergranular pore space in S2 is due to the clay matrix, which is reflected in the poor grain sorting and large variance in pore size. In the pore throat size analysis (Fig. 7), only 15 % of the pore volume is composed of macropores that are larger than 10 µm. The prominent submicrometer pore mode is ∼35 nm, with a population containing ∼45 % of the pore volume (Fig. 7a). This population of pores occurs inside the clay matrix. The secondary pore volume population is poorly distributed within the range of 0.8–30 µm. The characteristic length (Sect. 3.2), l_c=12.3 µm (Fig. 7b), and the pore throat length of maximal conductance, l_max=8 µm (Fig. A1 in Appendix A) (both lengths have large analytical uncertainties resulting from uncertainty in the threshold pressure, cyan colour in Fig. 7b), suggest a connectivity of macropores regardless of their small fraction within the total pore space. The porosity of S2 evaluated for eight different samples varies in the range of 14.5 %–23.5 % (Fig. 8). From the PTSD (Table 1) and gas porosimetry results (for a sample with a porosity of 18.6 %), micro-CT predicts an image porosity of 6.6 % at a resolution limit of 2.5 µm (Table 2). The gas permeability in the z direction was measured in five samples (Fig. 8): in four of them, the permeability ranges within 1–12 mD and increases with porosity. However, one sample had an exceptionally large porosity and permeability of 23 % and 62 mD, respectively. The permeability measured for three samples in the x–y plane ranges within 4–12 mD, also showing ∼15 % porosity (Fig. 8). In addition, samples with ∼15 % porosity have permeability values larger in the x–y plane (parallel to the layering) than in the z direction (perpendicular to the layering). The permeability derived from MIP reaches 4 mD, which agrees with an average of 2.77 and 7.73 mD (Table 2) measured in the z direction with a gas permeameter (excluding one exceptionally high value; Fig. 8).

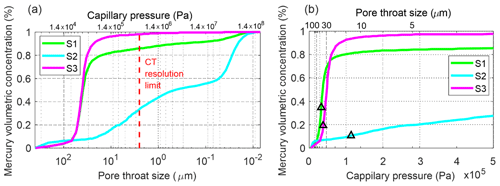
Figure 7 Cumulative pore throat sizes of the studied sandstones. (a) Capillary pressure on a logarithmic scale. The resolution limit of the micro-CT imaging indicates the fraction of the pore space that could be resolved. (b) Capillary pressure on a linear scale. The triangles indicate the characteristic length, l_c.

Figure 8 Results of porosity–permeability lab measurements. The permeability of the samples was measured in directions perpendicular to the bedding (z direction) and parallel to the bedding (x–y plane).

Sandstone S3

The bottom unit layer with a thickness of ∼1.5 m consists of (pale) red–purple poorly consolidated sandstone (Fig. 1c) with grains covered by a secondary red patina (Fig. 5). The sandstone is composed of friable to semi-consolidated, fine (∼269 µm), moderately sorted sand (Table 2), where only 5.6 % of particles are silt and clay (Fig. 6). Secondary silt (∼50 µm) and clay (∼0.96 µm) populations were also detected. The sandstone consists of subrounded to rounded grains showing a laminated sedimentary texture consisting of the cyclic alternation of relatively dark and light red bands of millimetre-scale thickness (Fig. 5a). The dark laminae contain slightly more FeOx meniscus-bridging and pore-filling cementation (Fig. 5b and d). Overall, this bed consists of a ferruginous quartz arenite. The grains are dominated by quartz with very minor feldspar and black opaque mineral grains, perhaps FeOx (Fig. 5d). X-ray diffraction indicated quartz only. The FeOx coating of grains is less extensive than in other samples (Fig. 5c). The pore interconnectivity in this sandstone is high (Fig. 5d). Heavier cementation is rarely observed (Fig. 5d) and is organized in horizontal laminae (Fig. 5a). Features including grain cracks, grain-to-grain interpenetration and pressure solution are also recognized (Fig. 5e). The PTSD showed that 95 % of the pore volume is presented by macropores (Fig. 7a), which agrees with the scarcity of fine particles. The characteristic length and pore throat length of maximal conductance are l_c=36.9 µm (Fig. 7b) and l_max=31.4 µm (Fig. A1 in Appendix A), respectively.

The porosity measured by a gas porosimeter in the laboratory varies in the range of 30 %–32 % for four different samples (Fig. 8). From PTSD and gas porosimetry (Figs. 7 and 8), the micro-CT-predicted image porosity at a resolution limit of 2.5 µm is 30.4 % (Table 2). The permeability measured by a laboratory gas permeameter averages 220 mD for two samples measured in the z direction and 4600 mD for two samples measured in the x–y plane (Fig. 8), showing a 10-fold difference (discussed in Sect. 5). The permeability derived from MIP reaches 466 mD (Table 2). Overall, the relative decrease in l_max with respect to l_c is greater for the layers containing more fines (Table 2).

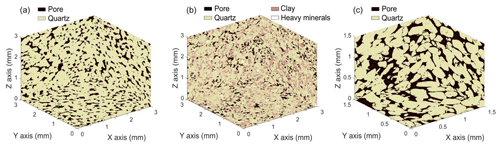
Figure 9 Visualized subvolumes of segmented CT samples of (a) S1, (b) S2 and (c) S3. S1 and S2 in this visualization have volumes of 3³ mm³ scanned with 5 µm voxel size resolution; S3 has a volume of 1.5³ mm³ scanned with 2.5 µm voxel size.

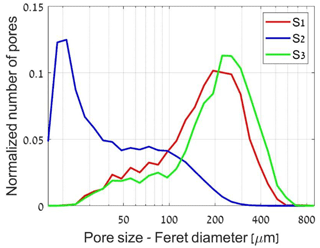
Figure 10 Statistics of the pore sizes calculated by image analysis for three sandstone samples: S1, S2 and S3. Number of pores analysed: S1 – 3500, S2 – 45 000, S3 – 3500. The CT data sets used for this analysis had 2.5 µm voxel size resolution to capture grain and pore shapes better compared to those at a resolution of 5 µm.

Additionally, pore surface roughness may be evaluated from the SSA measured by MIP (Table 2). A larger SSA implies a rougher surface (e.g. Tatomir et al., 2016). The SSAs for S1 and S2 (3.2 and 12.2 µm⁻¹, respectively) are similar to those given in the literature for sandstones of similar properties (e.g. Cerepi et al., 2002). The SSA of S2 is higher because of its high silt and clay content of 34.3 %, which is only 7.4 % for S1 (Fig. 6a). The SSA of S3 (where silt and clay constitute only 5.6 %, including the FeOx rim coating) is only 0.16 µm⁻¹, which is 20 times smaller than that of S1 (Table 2). The difference in SSAs between S1 and S3, which are similar in their grain and pore throat size distributions (Figs. 6 and 7), is a result of S1 having a higher FeOx grain coating than S3 (compare Figs. 3d and 5c).

In summary, although the S1 pore network has larger pore throats, it also has greater grain roughness and lower connectivity than S3. These two properties dominate and generate a smaller permeability for S1 than for S3 (Table 2).

4.2 Image analysis

Visualized segmented subvolumes of samples S1, S2 and S3, depicting quartz, pores, clay and heavy minerals, are presented in Fig. 9. The main pore size population in PSD of S1 is at ∼100–500 µm range with majority at ∼194 µm (Fig. 10). A smaller population of pores of ∼30–100 µm was identified as well, which may refer to (Mode 1) pore throat size derived from the MIP experiment (Table 2). Image resolution of 2.5 µm limited the analysis. The PSA calculated from micro-CT images is 0.068 µm⁻¹. The tortuosity, measured from the whole CT image, indicates similar values in the x and y directions of 1.37 and 1.38, respectively, whereas in the z direction, the tortuosity is 1.48 (Table 2). As many paths were considered, this difference indicates the textural features that appear in horizontal plane (Fig. 3a).

For S2 (Fig. 9), the main pore size population is in the ∼15–50 µm range (Fig. 10), with majority at ∼21 µm. This may refer to the pore throat size derived from MIP. However, smaller pore throat sizes which were derived from the MIP (mode peak is at ∼3.5 µm) could not be visualized due to the limited resolution of the image (2.5 µm) and because of high uncertainty associated with size of pores smaller than 10 µm (four voxels). Accordingly, they were excluded from the PSD evaluation (Fig. 10). A large pore population is also recognized at ∼100 µm (Fig. 10), which corresponds to the pore size scale recognized from the petrography (Fig. 4), MIP (Fig. 7) and CT image (Fig. 9). The PSA calculated from micro-CT images is 0.136 µm⁻¹ (Table 2), which is twice as large as the PSA of S1.

For S3 (Fig. 9), the main pore size population is in the ∼ 100–500 µm range (Fig. 10), with majority at ∼223 µm. The geometry-based tortuosity values measured from the whole CT image with multiple paths is 1.32, 1.34 and 1.39 in the x, y and z directions, respectively. The tortuosity is lower for S3 than for S1 in all directions, which is a direct result of the smaller amount of cement in the pore throats. The PSA of S3 is 0.069 µm⁻¹, which is similar to that of S1.

4.3 REV analysis

4.3.1 Quartz arenite sandstones (S1 and S3)

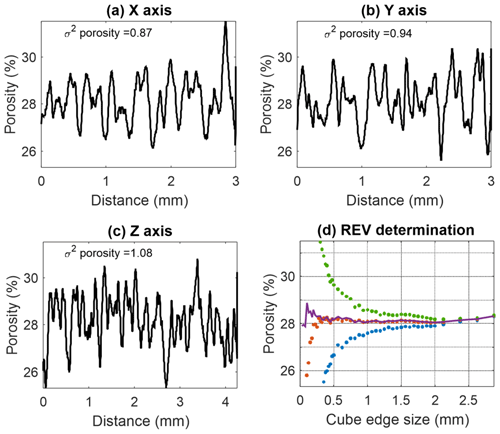
One-dimensional profiles of porosity of S1 (Fig. 11a–c) were evaluated by averaging the pore voxels over each slice in sequential slices in three orthogonal directions (hereafter referred as slice-by-slice porosity). The investigated domain had a volume of $\mathrm{6.8}\times \mathrm{6.9}\times \mathrm{9.2}$ mm³ scanned with a voxel size of 5 µm (suitable for imaging pore throats that effectively contribute to the flow in S1; Table 2). The slice-by-slice porosity distinguishes the z direction as having an exceptional behaviour, with variance in porosity fluctuations being 4 times larger than that in the x and y directions (i.e. 0.98 in the z direction, compared to 0.17 and 0.16 in the x and y directions, respectively). Porosity fluctuates with a peak-to-trough length of ∼0.1 mm in the x and y directions that could refer to an average pore cross section over the slice and thus being attributed to grain packing. In the z direction, an additional larger-scale wavelength of ∼3.5 mm is observed, where peaks and troughs could refer to higher and lower porosity layers, respectively, thus being attributed to depositional processes.

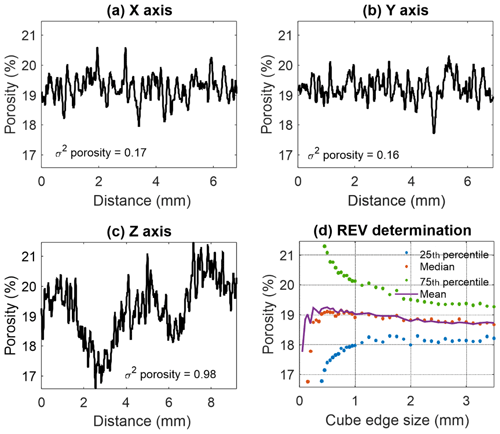
Figure 11 Determination of REV in S1. One-dimensional porosity profile of S1 slices evaluated in the (a) x direction, (b) y direction and (c) z direction. (d) Classic REV analysis. Investigated volume size is $\mathrm{6.8}\times \mathrm{6.9}\times \mathrm{9.2}$ mm³.

Alternatively, the REV size was estimated as ∼2.5 mm (Fig. 11d) by classic REV analysis, where the mean, median, 25th and 75th percentile porosity changes decline. Considering these results (Fig. 11), we decided to use a segmented specimen cube with a maximal available edge length of 2950 µm, scanned with a higher resolution of 2.5 µm (to preserve the grain surface geometry and a consistency between S1 and S3 samples) for flow simulations.

One-dimensional profiles of slice-by-slice porosity were evaluated in sequential slices in the orthogonal directions of S3 with a maximal segmented volume of $\mathrm{3}\times \mathrm{3}\times \mathrm{4.2}$ mm³ scanned with a voxel size of 2.5 µm (Fig. 12a–c). Porosity fluctuates in all directions with a peak-to-trough distance of ∼0.1 mm that could refer to an average pore cross section over the slice, as clarified for S1. The variance is similar in all directions (0.87, 0.94 and 1.08, respectively), which implies a homogenous sample. REV with an edge length of 875 µm was estimated by classic analysis (Fig. 12d), which was used for the flow simulation in S3.

Figure 12 Determination of REV in S3. One-dimensional porosity profile of S3 slices evaluated in the (a) x direction, (b) y direction and (c) z direction. (d) Classic REV analysis. Investigated volume size is $\mathrm{3}\times \mathrm{3}\times \mathrm{4.2}$ mm³.

4.3.2 Quartz wacke sandstone (S2)

Sample S2 is more heterogeneous than S1 and S3 because of the deposition of clay in a patchy distribution. The sample is visualized in Fig. 9b with quartz grains (yellow), pore volume (black), clay matrix (brown) and heavy minerals (white). In Fig. 13a–c, the porosity of sequential slices in the orthogonal directions is shown together with clay matrix content, evaluated in segmented volume of $\mathrm{7.9}\times \mathrm{6.8}\times \mathrm{9.2}$ mm³ size scanned with a voxel size of 5 µm. In the z direction, a clear trend in porosity is observed, which has a negative correlation with the clay content (Fig. 13f), whereas in the horizontal (x–y) plane there is no clear correlation (Fig. 13d and e). This correlation in the z direction implies that the porosity is controlled by depositional processes. However, the similar large-scale wavy structures of the clay content in the x and y directions (Fig. 13a and b) may refer to errors originated from the scanning and inversion in the CT acquisition, as x and y coordinates are associated with the side boundaries of the cylindrical sample.

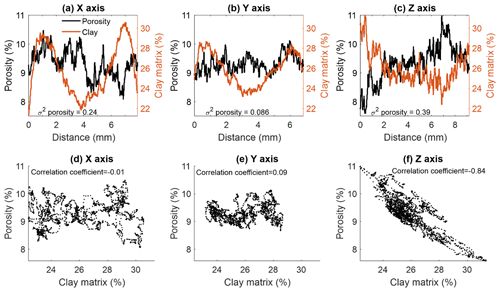
Figure 13 Correlation between porosity and clay in S2. Porosity and clay profiles (left and right y axes, respectively) in slices of S2 evaluated in the (a) x direction, (b) y direction and (c) z direction. Scatterplots of clay content and porosity in S2 in the (d) x direction, (e) y direction and (f) z direction. Investigated maximal segmented volume size is $\mathrm{7.9}\times \mathrm{6.8}\times \mathrm{9.2}$ mm³ (see text for more details).

Figure 14 Classic REV analysis of S2. Investigated volume size is $\mathrm{7.9}\times \mathrm{6.8}\times \mathrm{9.2}$ mm³.

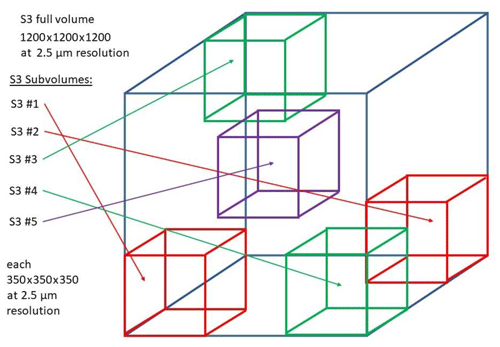
Figure 15 Selection of the subvolumes in the S3 CT data set for additional permeability tensor simulations. Each subvolume has a size of 350 voxels cubed, while the full volume has a size of 1200 voxels cubed.

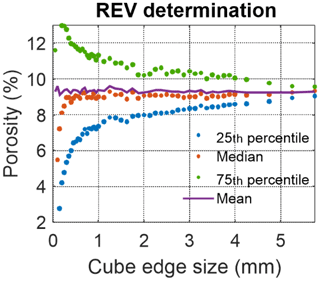
Classic REV evaluation (Fig. 14) may indicate a cube edge size of ∼3 mm. However, the porosity trend in the z direction (Fig. 13c) in the volume under investigation implies that no REV can be found in S2 sample. As a result, flow modelling could not be conducted in sample S2.

4.4 Flow modelling at the pore scale

Fluid flow was modelled at the pore scale in two different micro-CT-scanned geometries: (1) a full cube of sample S1 and (2) sample S3 within its REV dimensions (Table 3), imaged with 2.5 µm voxel size. Modelling of the 3-D geometry of sample S2 was not performed due to its non-stationarity, which did not allow for finding the REV in the investigated domain.

Table 3 Porosity losses in S1 and S3 over the course of applying the extended computational workflow (Fig. 2).

The porosity of the meshed domain of sample S1 is 13.6 % (in contrast to 17.5 % in the segmented image; Table 3), and the mesh edge length is 14 µm along the pore walls. The observed porosity loss results from disconnecting narrow pore throats from the connected cluster imaged with a 2.5 µm voxel size due to the use of a 14 µm mesh size (the lowest possible for our computational needs). A maximum Reynolds number of Re=0.084 was used to guarantee the simulation in a creeping flow regime.

Figure 16 Permeability tensor simulation results and evaluated 3-D image porosity data for the subvolumes and full sample of S3 specified in Fig. 15.

The symmetrized permeability tensor, κ (Eq. 5), was obtained as follows (Table 2):

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{\mathit{\kappa }}_{\text{sym}}=\left(\begin{array}{ccc}\mathrm{420}& \mathrm{66.3}& \mathrm{1.91}\\ \mathrm{66.3}& \mathrm{344}& \mathrm{12.8}\\ \mathrm{1.91}& \mathrm{12.8}& \mathrm{163}\end{array}\right).\end{array}$$

The permeability tensor is anisotropic, with κ_zz being more than twice as small as κ_xx and κ_yy. This result is in agreement with the appearance of horizontal banding with higher cementation (Fig. 3a).

The porosity of the meshed domain of sample S3 is 25.9 % (in contrast to 28.3 % in the segmented image; Table 3), and the mesh edge length is 5 µm along the pore walls. A maximum Reynolds number of Re=0.22 was used to guarantee the simulation in a creeping flow regime. The symmetrized permeability tensor is close to isotropic (Table 2):

$$\begin{array}{}\text{(7)}& {\displaystyle }{\mathit{\kappa }}_{\text{sym}}=\left(\begin{array}{ccc}\mathrm{4517}& \mathrm{5}& \mathrm{38}\\ \mathrm{5}& \mathrm{4808}& \mathrm{547}\\ \mathrm{38}& \mathrm{547}& \mathrm{4085}\end{array}\right).\end{array}$$

Additional permeability tensor simulations on equivalently REV-sized segmented subvolumes of S3 and on the full S3 (Fig. 15, cube volume of $\mathrm{3}\times \mathrm{3}\times \mathrm{3}{\mathrm{mm}}^{\mathrm{3}}$) have been performed with GeoDict toolbox to ensure consistency of the estimated REV size. Subvolume locations are presented. Symmetrized permeability tensors simulated in these domains (Fig. 16) are close to the former one (Eq. 7), being also nearly isotropic.

The tortuosity of S3 computed from particle tracing in the x, y and z directions is 1.44, 1.39 and 1.47, respectively (Table 2). The largest value is observed in the z direction, which is in agreement with the lowest permeability in the z direction.

5 Discussion

5.1 Validation of permeability by micro- and macroscale rock descriptors

Each of the evaluated micro- and macroscale rock descriptors supplies a qualitative information about the sample permeability (Tables 2 and 3), which is used to validate the multi-methodological approach presented in this paper. Specifically, the increasing mercury effective saturation with increasing pressure shows a similar pore throat size distribution curve slope for sandstone samples S1 and S3 in the macropore throat range (Fig. 7), suggesting that these samples have similar structural connectivity. However, S1 has a smaller imaged volume fraction of pore space available for fluid flow that is controlled by macropore throats (i.e. 81 % in S1 vs. 93 % in S3; Fig. 7) due to its higher contents of silt, clay and FeOx cement. The intermediate layer (S2) with 19 % porosity comprises more fines, which form a clay matrix (Table 2) due to poor grain sorting and smaller mechanical resistance of clay to pressure under the burial conditions. Only ∼15 % of the pore volume fraction in S2 is controlled by bottle-neck macropore throats (Fig. 7). However, the characteristic length of S2, 12.3 µm (Table 2), indicates that macropore connectivity is still possible even when the pore space consists mainly of sub-macroscale porosity. This 0.15 volume fraction is in agreement with Harter (2005), who estimated a volume fraction threshold of 0.13 for correlated yet random 3-D fields required for full interconnectivity.

The value of the connectivity index of S3 (10) evaluated from CT data is approximately 3 times higher than that of S1 (3.49), while both rocks are defined as moderately sorted sandstones (Table 2). This difference is due to S1 having a smaller number of inequivalent loops within the imaged pore network than S3, leading to smaller Euler characteristics (see the Supplement for more details). Inequivalent loops are positively correlated with pore throats; their number is affected by the resolution of the CT image and by the partial volume effect at grain surfaces (Cnudde and Boone, 2013; Kerckhofs et al., 2008), where some voxels could be identified as grains and thus “clog” the small pore throats. Artefact porosity loss is apparent for S1, where the IP is 17.5 % (in contrast to the CT porosity of 23.5 % predicted from MIP; Table 2). The connectivity index of S2 (0.94; Table 2) is lower than those of both S1 and S3 because of the clay matrix, which clogs pores with sizes below the image resolution. The effect of the partial volume effect on the image connectivity and on the preservation of small features was reviewed by Schlüter et al. (2014).

A correlation was found between the grain size and the amount of FeOx cement in S1 evaluated at each slice along the z direction (from the image analysis; Fig. 17). Exceptionally large grains are detected (indicated by the red rectangle) near the cemented region at ∼750 µm. Large grains and a relatively high amount of cement can also be observed in the S1 thin section (Fig. 3b). Large grains cause large pores and generate relatively permeable horizons through which water flow and solute transport can become focused (McKay et al., 1995; Clavaud et al., 2008), supplying iron solutes. We suggest that a vadose zone was formed after flooding events, where the water flow mechanism could have changed from gravity dominated to capillary dominated. Water then flowed due to capillary forces along grain surfaces towards regions with larger surface areas, and iron solutes precipitated in a reaction with oxygen available in the partly saturated zone. We suggest that with time, this cementation mechanism caused a decrease in the pore throat size near the preferential path, while the preferential path with a low surface area remained open, eventually generating the observed anisotropic flow pattern.

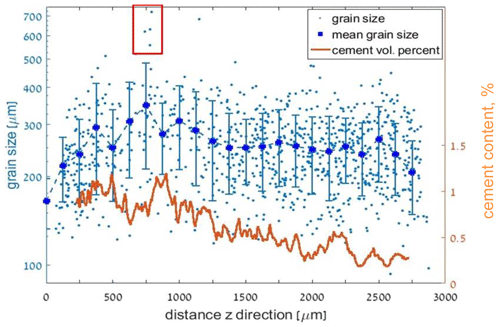
Figure 17 Grain size scattering and FeOx cement content in sandstone S1 in slices along the z direction. The red rectangle emphasizes very large grains that were detected.

In this respect, permeability anisotropy in sandstones at a small scale is usually attributed to the shape or preferential orientation of grains and pores (e.g. Sato et al., 2019) and to a heterogeneous distribution of cementing material at grain contacts (Louis et al., 2005). Clay-free and cement-free layers in S1 thus constitute the main avenues for flow in the parallel direction, shown by variation in porosity in the z direction (Fig. 11c) that is correlated with anisotropic permeability tensor (Eq. 6). At a larger scale, a higher degree of permeability anisotropy is usually associated with the presence of localized beds, foliation and compaction bands that constitute barriers to flow in the perpendicular direction (see Halisch et al., 2009; Clavaud et al., 2008, and references therein).

Flow modelling in the specified REV of S1 shows anisotropy (Table 2) and an average permeability value of 310 mD that is close to that derived from MIP (330 mD). However, the average permeability is lower than the average experimental gas permeability (∼543 mD); this difference should be related to the loss of porosity due to limitations on the CT resolution, image processing and meshing (Table 3; see Sect. 5.2 for more details).

In contrast, flow modelling and upscaling to the macroscale indicate an isotropic S3 sample (Eq. 7). However, the modelled permeability (∼4500 mD) is 10 times higher than the MIP-derived permeability (∼466 mD; Table 2). Gas permeability measurements indicate anisotropy, yielding permeabilities of ∼4600 mD in the x–y plane and ∼220 mD in the z direction (with an anisotropy ratio of ∼20, defined here as ${\mathit{\kappa }}_{\parallel }/{\mathit{\kappa }}_{\perp }$, e.g. Tiab and Donaldson, 2004). For comparison, the values of this ratio obtained from experimental permeability measurements were ∼1.2 for Bentheim sandstone (Louis et al., 2005), ∼1.7–2.5 for a sandstone within the Cretaceous Virgelle Member, Alberta, Canada (Meyer and Krause, 2001), and ∼8.5 for Berea sandstone (Sato et al., 2019). However, in our laboratory measurements conducted parallel to the layering (in the x–y plane), poorly cemented grains in S3 could dislocate from the weakly consolidated sample due to the application of a pressure gradient. This could have resulted in a higher measured gas flux and thus a higher permeability parallel to the layering, yielding a high anisotropy.

Alternatively, the disagreement between the laboratory-determined permeability perpendicular to the layering, κ_⊥, and the isotropic permeability obtained from the flow modelling (Table 2, Eq. 7) may also stem from the small dimension of the modelled REV domain (cube edge length of ∼0.875 mm), which may not have included the additional textural features (e.g. Fig. 5d) that constrain fluid flow on a larger scale of the lab sample of S3 (2.5 cm in diameter and 5–7 cm in length).

However, the consistency of the REV size in S3 by the additional permeability simulations on equivalently REV-sized segmented subvolumes and on the entire sample (Figs. 15 and 16) is confirmed by yielding nearly isotropic permeability tensors that are also in good agreement with previously simulated permeability tensor in the REV (Eq. 7). The average permeability derived from all REV-sized subvolumes is ∼4381 mD, compared to the average permeability of ∼ 4500 mD simulated over the entire S3 geometry. This, again, is in good accordance with the gas permeability of S3 measured parallel to the layering (∼4600 mD, Table 2). These additional simulation results (Fig. 16) strengthen our conclusion that those may not have included the textural features that constrain fluid flow on a larger scale of the sample S3 tested by the laboratory experiments. Similarly, the differences with the permeability estimated by MIP seem to originate from the same reason.

For sample S2, REV and slice-by-slice porosity analysis indicated an REV size larger than the investigated sample size (Figs. 13c and 14). For this reason, the analytical programme formulated in our study cannot entirely be applied to S2 due to the impossibility of determining a reliable REV and hence conducting pore-scale flow modelling. As a result, although sample S2 represents a common sandstone, it is very heterogeneous in nature, and a sample larger than at least 9 mm (which is a maximal length in the z direction of the tested domain; Fig. 13c) is required to capture its REV. The MIP-derived permeability is 4 mD; this low permeability is due to a clay-rich matrix that encloses substantial void space (Hurst and Nadeau, 1995; Neuzil, 2019). The gas permeability of the quartz wacke layer (S2, ∼4.6 mD on average) is approximately 2 orders of magnitude lower than that of the quartz arenite layers (S1 and S3; Table 2). The permeability anisotropy ratio of S2 is $\sim \mathrm{2.8}.$ The high inverse correlation between the porosity and clay matrix content enhanced in the z direction (Fig. 13c and f) suggests that the clay matrix pattern appears as horizontal layering, thus generating the observed anisotropy.

Finally, non-marine sandstones of Lower Cretaceous age (as well as sandstones in general) feature big complexity and variability in their characteristics, as immediately seen even from a comparison of our samples S1, S2 and S3 from the same outcrop (Table 2). For instance, low porosity of Wealden quartz arenite sandstones from the Weald Basin within the Ashdown and Wadhurst Clay formations in southeast England ranges between 6.3 % and 13.2 %, while permeability ranges between 0.4 and 11.9 mD (Akinlotan, 2016), suggested to be controlled mainly by grain sizes, grain shapes and sorting that are directly linked to their depositional environment. Average porosities of 3.06 % and 0.19 % were evaluated in medium- and fine-grained tight gas sandstones, respectively, from the Lower Cretaceous Denglouku Fm. in the Songliao Basin, China (Zhang et al., 2019). Alternatively, a secondary porosity of 4 % to 22 % was generated by acidic fluids acting in the compactional regime, destructing a high primary porosity in sandstone of Lower Cretaceous Shurijeh Fm. in the eastern Kopet Dagh Basin in NE Iran (Moussavi-Harami and Brenner, 1993). Significant average porosity and permeability of 20 % and 3700 mD, respectively, were quantified in the Masila Block, Upper Qishn Fm. of the Lower Cretaceous Age, Republic of Yemen (Harding et al., 2002). The multi-methodological approach suggested in this study is applicable to all those sandstones with broad ranges of their textural, topological and mineralogical characteristics and should lead to their accurate petrophysical characterization.

5.2 Upscaling permeability: accuracy of the extended computational workflow

The extended computational workflow (Fig. 2) serves as the main tool in this study for upscaling permeability from the pore-scale velocity field. The accuracy of each step in the workflow affects the ultimate result.

Following the steps of the workflow, a micro-CT image resolution of 2.5 µm limits the reliability of the representation of the porous medium and defines the lower pore identification limit using this method. As an example of this limitation, the bulk SSA calculated by MIP is larger than the PSA calculated by micro-CT image analysis in all the samples (Table 2), although the pore volume is always smaller than the bulk volume. The PSA from micro-CT is limited by the image resolution and therefore does not consider relatively small pores with large surfaces. The PSAs of S1 and S3 are similar, but the SSA (from MIP) of S1 is 20 times larger than that of S3 because S1 has a larger surface area at small pores created mainly by FeOx cement (compare Fig. 3c–f for S1 to Fig. 5c for S3). In contrast to SSA, PSA in S2 is only twice as large as that of S1 due to the presence of clay and clay matrix with large surface areas.

Image processing and segmentation were applied in this study to recover the image geometry, which was blurred by noise or affected by the partial volume effect (see Sect. 3). Then, the loss of pore space due to the resolution limits was estimated in this study from the amount of mercury filling the pores with diameters equal to the resolution limit (Fig. 7a). After segmentation, sample S1 had a segmented image porosity of 17.5 % and a CT-predicted porosity of 23.5 % from MIP (Tables 2 and 3). Therefore, the difference in porosities generated by the partial volume effect in the image processing scheme (e.g. Cnudde and Boone, 2013) is a significant component of error, especially for small structures, such as pores with a large surface area-to-volume ratio. In contrast, the image porosity of S3 after segmentation was 28.3 %, which is close to the porosity of 30.4 % estimated from MIP (Tables 2 and 3). This is a result of the very small degree of cementation and the absence of FeOx flakes in the majority of the sample pores, leading to the small contribution of the partial volume effect. In comparison, a fine-grained and well-sorted Lower Cretaceous Fm. sandstone from the Heletz field (e.g. Fig. 1a) (Tatomir et al., 2016) comprising clay and calcite had MIP and micro-CT porosities of 26.7 % and 20.9 %, respectively.

An additional source of inaccuracy is the use of a porosity-based REV for permeability approximations. Mostaghimi et al. (2012) showed that for CT images of sandpacks (homogenous samples), the porosity-based REV had an edge length of 0.5 mm, whereas the permeability-based REV was twice as large. Moreover, the porosity- and permeability-based REVs in images of crushed bead packs derived by Zhang et al. (2000) had edge lengths of 1.71 and 2.57 mm, respectively. According to Mostaghimi et al. (2012), larger REV values for permeability rely on contributions from the tortuosity and connectivity of pore spaces, whereas the larger REV values of Zhang et al. (2000) might be related to the heterogeneity of the sample.

This discrepancy indicates a larger REV for a rock property evaluated using physics-based simulations than for those estimated using morphology-based methods (Saxena et al., 2018, and references therein). Furthermore, implementing the classic REV determination methodology (e.g. Callow et al., 2020) using very small search subvolumes is not in agreement with capturing a sufficient structural complexity (Saxena et al., 2018).

Flow simulations performed in subvolumes and full sample of S3 (Figs. 15 and 16) support this conclusion. Small dimensions of the evaluated REV (∼0.875 mm) of homogeneous S3 ensure efficient calculations. Both porosity and permeability demonstrate good agreement (Table 2, Fig. 16), thus confirming a representativeness of the estimated REV and a continuity of these characteristics over the chosen sample. However, the differences in porosity between the subsamples and the full sample are smaller than the corresponding differences in permeability (Fig. 16), as anticipated from the porosity-based REV derivation discussed above.

An additional verification of the REV size for flow simulations in S3 follows the approach given by Saxena et al. (2018). They demonstrated that for homogeneous sandstones, the smallest pore throats can be accurately resolved at N_I>10, where $N_I=D_D/\mathrm{\Delta }x$ is a ratio of the pore throat size corresponding to mercury entry pressure, D_D, to the voxel size, Δx. N_I controls the lower bound on permeability that can be reliably calculated using a digital rock image, to capture sufficient structural complexity of rock microstructure which affects flow, attributed to D_D visualized using Δx. For our subvolumes of sample S3 imaged with Δx=2.5 µm resolution and D_D=35 µm (Table 2), $N_I=\mathrm{14}>\mathrm{10}$. In addition, there is a requirement for the minimal REV size for representativeness for permeability calculation, $N_{\text{REV}}=L/D_{\text{eff}}>\mathrm{5}$ (Saxena et al., 2018), where L is a digital rock (i.e. domain) length and D_eff is the effective grain diameter (e.g. Říha et al., 2018). For S3 subvolumes with L=875 µm REV size and D_eff=58.6 µm (computed from laboratory grain size data which includes both sand and fines, Fig. 6), this requirement is achieved as well: $N_{\text{REV}}=\mathrm{15}>\mathrm{5}$, which also proves the reliability of the subvolume permeability modelling with the presented approach. The calculations in subvolume performed with Comsol (Eq. 7, Table 2) demonstrate the smallest deviation in mean permeability compared to that in the full sample (0.85 %). In comparison, other subvolumes modelled with GeoDict (Fig. 16) have larger mean permeability deviations from the full sample (ranging between 5 % and 17 %), still demonstrating a very good agreement with those conducted on the full-scale S3 domain.

Further, according to Saxena et al. (2018), REV size supported by N_REV for flow simulations should also be insensitive to the choice of boundary conditions, whose effect on tensorial flow properties diminishes with an increasing sample size (e.g. Guibert et al., 2016; Gerke et al., 2019). No-slip boundary conditions applied in our study at four lateral faces of the modelling domains correspond to those in the experimental permeability measurements and are also the most commonly used boundary conditions for the pore-scale flow simulations (Guibert et al., 2016 and references therein). However, they were recently shown to suppress the transversal flow through the simulation domain to some extent, resulting in deviation in alignment of the permeability tensor and in underestimation of its magnitude (Gerke et al., 2019) even at REV dimensions. Thus, the difference in the mean permeability derived from all REV-sized subvolumes (∼4381 mD) and that simulated over the entire S3 geometry (∼4500 mD) (Fig. 16) can also be attributed to this effect. For future studies, we suggest that determining REV size for the flow simulation from porosity is justified by acknowledging the typical ratio of 2 between those for permeability and porosity.

To upscale to permeability reliably, the REV domain should be sufficiently large such that it is bounded from below by the scale of the textural bedding but should not be larger than necessary to optimize the computational efficiency (while remaining within the same scale of heterogeneity, i.e. at the macroscale). As a result, a REV with an edge length of ∼2950 µm was chosen in the current study in sample S1, based on slice-by-slice porosity profiles that reveal millimetre-scale layering in the z direction (Fig. 11c) rather than on the classic isotropic REV approach. For comparison, in other studies, the edge lengths of REVs in sandstones were 0.68 mm (Ovaysi and Piri, 2010), 0.8 mm (Mostaghimi et al., 2012) and 1.2 mm (Okabe and Oseto, 2006; Tatomir et al., 2016) derived by the classic approach. In contrast to the classic REV estimation, where porosity analysis does not consider directionality, 1-D profiles from slice-by-slice porosity provide additional information on anisotropy and inhomogeneity of the sample which have implications on the ultimate determination of the REV. In the future studies, the 1-D profiles can be used to calculate spatial correlation length (e.g. using variogram analyses) of geological structures that include layering, as in S1 in the current study.

Another source of inaccuracy is the geometry used for the flow model. The geometry considered in this study included only the pore network connecting six faces of the REV cube. Other pore spaces in the REV disconnected from the main network were deleted (because all paths smaller than the resolution were prescribed as grain pixels due to the partial volume effect), thus resulting in the smaller effective size of the simulation domain. The image porosity of sample S1 was 17.5 %, whereas its connected porosity was estimated as 15.6 % (Table 3), while those of sample S3 were 28.3 % and 27.9 %, respectively.

Furthermore, the mesh was generated by taking a trade-off between the size of the mesh elements (four elements in the smallest pore throat) and computational limits into account, while coarsening the mesh elements towards the pore centre. The connectivity between pores with very fine pore throats that could not be replaced by mesh elements could be lost, resulting in the loss of those pores in the calculations. In sample S1, the porosity used in the simulation was approximately 50 % smaller than the porosity estimated by gas porosimetry (Tables 2 and 3). In contrast, the porosity used in the simulations in S3 was mostly preserved, comprising ∼84 % of that estimated in the laboratory.

For comparison, in the fine-grained sample of the Lower Cretaceous sandstone from Heletz field in Israel (Fig. 1a), which has grain size characteristics similar to those of S1 but with higher clay and additional calcite contents (Tatomir et al., 2016), the permeability upscaled from micro-CT flow modelling (conducted by the same simulation method as that in the current study) exceeded the gas permeability by a factor of $\sim \mathrm{7}.$ This could be related to the reduction in the specific surface area by image processing and meshing (Mostaghimi et al., 2012) conducted for the flow modelling.

Finally, the upscaling process from the flow modelling successfully predicted the permeability anisotropy ratio of ∼2.3 in S1, as discussed above. For comparison, the permeability anisotropy ratio evaluated using micro-CT flow monitoring in clay-free sandstones (Clavaud et al., 2008) had a mean value of ∼2.5 (ranging from ∼1.7 to ∼5.2), related to the presence of less permeable silty layers. This is consistent with the ratio estimated at the pore scale in Rothbach sandstone (∼5) (Louis et al., 2005), attributed to lamination due to differences both in the characteristics of the solid phase (grain size and packing) and in the content of the FeOx.

6 Conclusions

This paper presents a detailed description and evaluation of a multi-methodological petrophysical approach for the comprehensive multi-scale characterization of reservoir sandstones. The validation was performed on samples from three different consecutive layers of Lower Cretaceous sandstone in northern Israel. The following conclusions can be drawn:

1. The suggested methodology enables the identification of links between Darcy-scale permeability and an extensive set of geometrical, textural and topological rock descriptors. Specifically, microscale geometrical rock descriptors (grain and pore size distributions, pore throat size, characteristic length, pore throat length of maximal conductance, specific surface area and connectivity index) and macroscale petrophysical properties (porosity and tortuosity), along with anisotropy and inhomogeneity, are used to predict the permeability of the studied layers.

2. Laboratory porosity and permeability measurements conducted on centimetre-scale samples show less variability for the quartz arenite (top and bottom) layers and more variability for the quartz wacke (intermediate) layer. The magnitudes of this variability in the samples are correlated with the dimensions of their representative volumes and anisotropy, both of which are evaluated within the micro-CT-imaged 3-D pore geometry. This variability is associated with clay and cementation patterns in the layers.

3. Two different porosity variation patterns are revealed in the top quartz arenite layer: fluctuations at ∼100 µm half wavelength in all directions, associated with an average pore cross section, and those at ∼3.5 mm wavelength in the vertical direction only, associated with the occurrence of high- and low-porosity horizontal bands occluded by FeOx cementation. The latter millimetre-scale variability is found to control the macroscopic rock permeability measured in the laboratory. Bands of lower porosity could be generated by FeOx cementation in regions with higher surface areas adjacent to preferential fluid flow paths.

4. More heterogeneous pore structures were revealed in the quartz wacke sandstone of the intermediate layer. This heterogeneity resulted mainly from the presence of patchy clay deposition structure.

5. Quartz arenite sandstone of the bottom layer shows stationarity in the investigated domain and lower anisotropy characteristics than that of the top layer, due to less horizontal cement bands.

6. The macroscopic permeability upscaled from the pore-scale velocity field simulated by flow modelling in the micro-CT-scanned geometry of millimetre-scale sample shows agreement with laboratory petrophysical estimates obtained for centimetre-scale samples for the quartz arenite layers. Comparison of permeability tensors evaluated in multiple REV subvolumes and in the full segmented sample of the bottom layer shows a particular agreement attributed to the homogeneity of this sample.

7. The multi-methodological petrophysical approach detailed and evaluated in this study allows the accurate petrophysical characterization of reservoir sandstones with broad ranges of textural and topological features.

Appendix A: Maximum hydraulic conductance

Figure A1 The pore throat length of the maximal hydraulic conductance, l_max, is defined from the maximal (normalized) hydraulic conductance (Katz and Thompson, 1987), specified at the vertical axis of the chart. The corresponding pore throat diameters (x axis) marked by black arrows define the pore throat diameters (or pore throat lengths of maximal conductance), l_max, where all connected paths composed of l≥l_max contribute significantly to the hydraulic conductance (see Sect. 3.2).