The analysis of slip tendency of major tectonic faults in Germany

Seismic hazard during subsurface operations is often related to the reactivation of pre-existing tectonic faults. The analysis of the slip tendency, i.e., the ratio of shear to normal stress acting on the fault plane, allows an assessment of the reactivation potential of faults. We use the total stresses that result from a large-scale 3D geomechanical–numerical model of Germany and adjacent areas to calculate the slip tendency for three 3D fault geometry sets with increasing complexity. This allows us to draw general conclusions about the influence of the fault geometry on the reactivation potential.

In general, the fault reactivation potential is higher in Germany for faults that strike NW–SE and NNE–SSW. Due to the prevailing normal stress regime in the geomechanical–numerical model results, faults dipping at an angle of about 60^∘ generally show higher slip tendencies in comparison to steeper or shallower dipping faults. Faults implemented with a straight geometry show higher slip tendencies than those represented with a more complex, uneven geometry. Pore pressure has been assumed to be hydrostatic and has been shown to have a major influence on the calculated slip tendencies. Compared to slip tendency values calculated without pore pressure, the consideration of pore pressure leads to an increase in slip tendency of up to 50 %. The qualitative comparison of the slip tendency with the occurrence of seismic events with moment magnitudes M_w>3.5 shows areas with an overall good spatial correlation between elevated slip tendencies and seismic activity but also highlights areas where more detailed and diverse fault sets would be beneficial.

1 Introduction

Seismic activity is a crucial aspect for many subsurface constructions and activities such as the production of oil and gas, coal mining, geothermal energy production, the storage of gas, or the construction and safe long-term operation of a nuclear waste repository. The occurrence of seismic activity is closely linked to the presence of pre-existing tectonic faults and their reactivation (Sibson, 1985). To estimate the potential to trigger seismic events, knowledge about the reactivation potential of tectonic faults is essential (Moeck et al., 2009; Worum et al., 2004). Slip on a fault occurs when the resolved shear stress τ is larger than the frictional resistance τ_f (Sibson, 1974; Jaeger et al., 2011):

$$\begin{array}{}\text{(1)}& \mathit{\tau }\ge {\mathit{\tau }}_{\mathrm{f}}=C+\mathit{\mu }\cdot {\mathit{\sigma }}_{\mathrm{neff}},\end{array}$$

where C is the fault cohesion, μ is the coefficient of static friction and σ_neff the effective normal stress on the fault. The relevant parameters for the assessment of the fault reactivation potential are therefore the following: (1) the stress tensor to estimate τ and the absolute normal stress σ_n; (2) the pore pressure required for the calculation of σ_neff; (3) the fault orientation that influences the magnitudes of σ_n and τ; (4) the frictional fault properties C and μ that describe the fault's mechanical behavior.

The stress tensor in previous works has mainly been estimated utilizing stress inversion (McFarland et al., 2012; Yukutake et al., 2015; Ferrill et al., 2020), point-wise stress data from field observations (Neves et al., 2009; Lee and Chang, 2009; Moeck et al., 2009; Morris et al., 2021) or Monte Carlo simulation (Healy and Hicks, 2022) for 2D lineaments and in some cases 3D fault geometries. Worum et al. (2004) calculated the 3D stress tensor with an analytical model and used it for the estimation of the fault reactivation potential of 3D faults of the Roer Valley Graben. Stress tensor estimates from 3D geomechanical–numerical models have been used to determine fault reactivation potential on regional scales, e.g., for the Upper Rhine Graben (Peters, 2007) or the Val d'Agri (Italy) (Vadacca et al., 2021), but this has not been achieved for all of Germany. In this study, we focus on the whole of Germany.

Here, we use the first 3D geomechanical–numerical model of Germany by Ahlers et al. (2021b) that provides an estimate of the 3D stress tensor that is variable with depth and lateral extent (Cornet and Röckel, 2012) due to inhomogeneous density and elastic rock properties. Furthermore, we compile three sets of 3D fault geometries with increasing complexity and use the stress tensor from the Germany model to predict the fault reactivation potential. The fault sets can be used not only to derive a first-order estimation of the fault reactivation potential but also to highlight the effect of fault geometry on the fault reactivation potential. We also investigate the impact of hydrostatic pore pressure as well as assumed overpressure on the reactivation potential estimates and compare our results with the spatial distribution of seismic events with moment magnitudes M_w≥3.5.

2 Data and method

2.1 Study area

This study focuses on Germany and some adjacent areas. It is subdivided into the three crustal units of the East European Craton, Avalonia and the Amorican Terrane Assemblage (Meschede and Warr, 2019; Ahlers et al., 2021a) (Fig. 1a). Most parts of the European basement have a Variscan overprint and can be subdivided into the roughly SW–NE-striking regions defined by Kossmat: the Rhenohercynican, the Saxothuringian, including the Mid-German Crystalline Zone, and the Moldanubian Zone (Walter, 2007). North Germany is characterized by the North German Basin as part of the Southern Permian Basin (van Wees et al., 2000) and almost N–S-striking graben structures such as the Glückstadt Graben and SW–SE-striking basins (Walter, 2007). Central and south Germany are characterized by several low mountain ranges such as the Black Forest, the Harz, the Ore Mountains or the Rhenish Massif and sedimentary basins such as the Upper Rhine Graben and the Molasse Basin. The southernmost part of Germany is dominated by the roughly E–W-striking Alps.

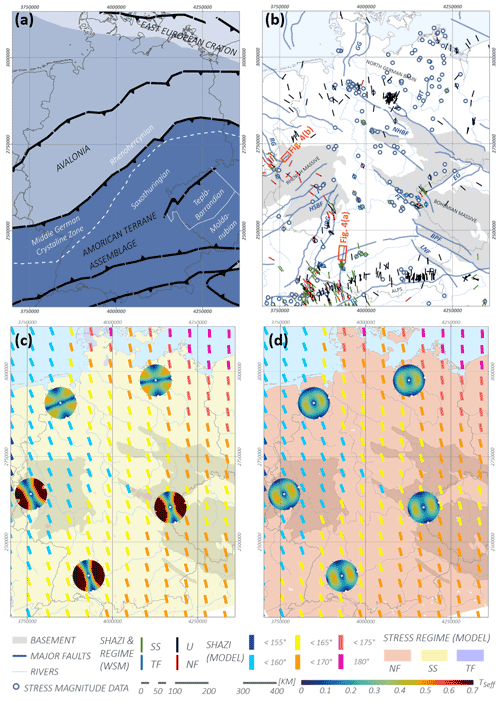
Figure 1 (a) Crustal units in Germany are indicated by different shades of blue and labeled with dark gray, capital text. White text labels Variscan units. Modified after Meschede and Warr (2019) and Ahlers et al. (2021a). (b) Stress data available in Germany: the rotated line markers represent data on the orientation of the maximum horizontal stress (S_Hazi) available in the World Stress Map (Heidbach et al., 2016) and are colored by the stress regime associated with the data points (normal faulting (NF), strike-slip faulting (SS), thrust faulting (TF) and unknown regime (U)). Plotted alongside are the locations of stress magnitude data (Morawietz and Reiter, 2020) and major tectonic faults in Germany as blue lines with (outcropping) basement structures indicated by gray areas The location of Fig. 4a and b is indicated by orange squares. BPF: Bavarian Pfahl Fault; EG: Eger Graben; FL: Franconian Line; GG: Glückstadt Graben; HSBF: Hunsrück Southern Border Fault; LNF: Landshut–Neuötting Fault; NHBF: Northern Harz Boundary fault; RG: Roer Valley Graben: RT: Rheinsberg Trough; URG: Upper Rhine Graben (modified after Kley and Voigt, 2008 and Ahlers et al., 2021a). Panels (c) and (d): the stress regime calculated by the Germany model at 1 and 8 km depth, respectively, is indicated by the background color; S_Hazi calculated by the Germany model has been averaged along a regular grid. The mean S_Hazi of each grid point is indicated by the orientation and color of the marker. For five areas within the model area, fault reactivation stereo plots are shown, displaying what fault orientations and dips are most favorable for reactivation under the given stress conditions. ©EuroGeographics for the administrative boundaries.

Seismicity is mainly observed in the Rhine area, the Swabian Jura and eastern Thuringia as well as western Saxony (German Research Centre For Geosciences, 2022). Induced seismicity has mainly been documented in the context of gas production (Müller et al., 2020), geothermal energy production (Bönnemann et al., 2010; Stober and Bucher, 2020) and especially mining activities, which have caused induced seismic events with local magnitudes of up to 5.6 (Grünthal and Minkley, 2005). Poro-elastic stress changes should be considered for significant pore pressure changes, as shown for production-induced earthquakes (Müller et al., 2020). In the case of geothermal sites, fluid injections into the sedimentary rocks have been suggested to not be as seismogenic as injections into crystalline rocks. In general, the presence of faults close to the injection well as fluid pathways increases the risk of seismic events (Evans et al., 2012)

2.2 Stress state

Stress data are not evenly distributed throughout Germany (Fig. 1b) and vary between different regions of Germany both in terms of orientation and the stress magnitudes, i.e., the stress regime. For the North German Basin, Röckel and Lempp (2003) describe a normal faulting regime and mostly N–S-striking S_Hmax orientations (S_Hazi) with a NNW–SSE influence towards the Dutch border and an NNE–SSW influence towards Poland. For the Upper Rhine Graben (URG) area in southwest Germany, Homuth et al. (2014) calculate a transtensional regime with a strong strike-slip influence with S_Hazi around 135^∘, while modeling results of Buchmann and Connolly (2007) suggest a present-day strike-slip reactivation of the URG. For the Molasse Basin in south Germany, S_Hazi rotates from striking N–S in southeast Germany to striking NNW–SSE in the southwest (Reinecker et al., 2010), and the stress regime most likely varies between normal faulting and strike slip (Drews et al., 2019; Seithel et al., 2015)

Since these stress data are available only point-wise, we use the stress tensor derived from the 3D geomechanical–numerical model of Germany by Ahlers et al. (2021b) for the assessment of the fault reactivation potential. The model covers Germany and adjacent areas and provides a continuum-mechanics-based prediction of the stress tensor. The purely elastic finite-element (FE) model comprises seven mechanical units, i.e., sediments, four upper crustal units, the lower crust and parts of the lithospheric mantle. The four crustal units represent the crustal framework of Germany as shown in Fig. 1a and the Alps–Carpathian–Pannonia. The lateral grid resolution is 6 × 6 km² and the vertical resolution decreases from 800 m within the sediments to 7500 m at the model base. Each unit is characterized by its respective density, Young's modulus and Poisson's ratio (Ahlers et al., 2021a).

The model is calibrated with stress magnitude data from the magnitude database by Morawietz et al. (2020) and compared with stress orientations from the World Stress Map database (Heidbach et al., 2016); both data sets are shown in Fig. 1b. The resulting best-fit model provides the 3D absolute stress tensor σ_ij within the model domain (Ahlers et al., 2021a), i.e., for Germany and adjacent areas. In order to consider effective stresses, we assume a hydrostatic pore pressure. Even though overpressure is well documented for the Molasse Basin (Drews et al., 2018; Müller et al., 1988), there is not enough spatial information on pore pressure available to justify the use of different pore pressure gradients in our analysis.

Figure 1c and d show the stress regime in the Germany model and S_Hazi at 1 and 8 km depth, respectively. In the uppermost kilometer of the model, thrust faulting (TF) and strike-slip (SS) regimes are present. Below 1 km depth, the model is dominated by an SS regime with some areas showing normal faulting (NF) regimes. With increasing depth, the NF regime becomes increasingly dominant as can be seen in Fig. 1d. In contrast, the stress orientations are almost constant with depth but change noticeably laterally. While S_Hazi is almost purely N–S in the northeastern part of the model, the orientation switches more towards a NNE–SSW orientation in the western part of the model. Additionally, the figure shows fault reactivation stereo plots for five regions in Germany. The plots are based on data provided by the model at the respective locations and illustrate the reactivation potential of faults striking between 0 and 360^∘ and dipping between 0 and 90^∘ represented by their normal vectors. They indicate high reactivation potentials in the upper 1 km of the model in south Germany for shallow to moderately dipping and NNE–SSW- to SSE–NNW-striking faults. The reactivation potential for faults in north Germany is noticeably lower. In 8 km depth, the reactivation potential is predicted as relatively low for all areas and fault orientations. The highest reactivation potential at this depth is predicted for moderately dipping faults striking roughly in a NE–SW direction.

2.3 Fault data sets

A spatially comprehensive collection of 2D fault lineaments in Germany has been compiled by Schulz et al. (2013). Three-dimensional fault geometries are available on a regional scale for some regions in Germany, such as the North German Basin (BGR et al., 2021), the Molasse Basin (GeoMol Team, 2015) in south Germany or in the model of Saxony (Geißler et al., 2014). However, there are no comprehensive 3D fault geometry compilations available for Germany. We created a total of three fault sets of increasing complexity. The first fault set is based on the 2D fault collection by Schulz et al. (2013), which comprises the 2D lineaments of 900 faults in Germany. The faults used in the second fault set have been chosen according to selection criteria. The selection criteria comprise the length of the fault (≥ 250 km), the horizontal displacement (≥ 10 km), the vertical displacement (≥ 2.5 km) and the seismic activity of the fault (since 800 CE or later). Furthermore, the general spatial pattern of fault orientations should be reproduced. In areas, where no faults met the criteria, we selected some additional faults to reproduce the general spatial distribution of faults. This approach lead to a final compilation of 55 faults. For these faults the fault type, namely strike-slip, normal fault or thrust fault, was known from a data collection (Suchi et al., 2014; Agemar et al., 2016) or relevant literature (such as Aleksandrowski et al., 1997; Badura et al., 2007; Grzempowski et al., 2012; Kachlík, 1993; Konon, 2007; Porpaczy, 2011; Schwarz and Henk, 2005; Valenta et al., 2008; van Hoorn, 1987). For the third fault set, we used geological and seismic cross sections in the depth domain to compile data on the 3D geometry of the selected faults. For 23 faults, cross sections with sufficient vertical extent were available. Based on the three described fault sets we generated three different 3D geometry sets of increasing complexity for slip tendency calculation:

1. Vertical fault set. All 900 faults of the fault catalogue (Agemar et al., 2016) were implemented as 90^∘-dipping faults extending to the base of the lower crust. The assumption of a vertical dip is an oversimplification due to the lack of data on most faults and introduces significant errors to the calculated reactivation potentials of faults that dip differently in reality. However, it allows the consideration of a large quantity of faults and therefore a more diverse representation in terms of location and strike than the other two sets with more realistic dips.

2. Andersonian fault set. The 55 selected faults have been implemented depending on their Andersonian fault type as normal faults, thrust faults or strike-slip faults. For normal faults a dip angle of 60^∘ was assigned, for thrust faults an angle of 30^∘ and for strike-slip faults and angle of 90^∘. The faults reach the base of the lower crust. Table S1 in the Supplement lists the implemented faults with a corresponding ID.

3. Semi-realistic fault set. For 23 faults, a more complex geometry on the basis of seismic and geological cross sections is used. The depth of the faults is not constant as in the Vertical and Andersonian fault sets but is chosen in accordance with the depths given in the sections used. The vertical cross sections used for the generation of the Semi-realistic fault set are compiled in Table 1. The quantity of available cross sections per fault varied considerably. For many faults, only one cross section was available leading to a uniform geometry over the entire length of the fault.

Table 1 Sources with suitable geological and seismic cross sections for the generation of semi-realistic fault geometries and the specific faults they were used for.

2.4 Three-dimensional slip tendency analysis

To estimate the fault reactivation potential we use definitions and terms of Morris et al. (1996). Assuming that cohesion can be neglected, they defined the parameter slip tendency as the ratio between τ and σ_n. We use this definition as a first slip tendency type:

$$\begin{array}{}\text{(2)}& T_{\mathrm{S}}={\displaystyle \frac{\mathit{\tau }}{{\mathit{\sigma }}_{\mathrm{n}}}}.\end{array}$$

We further use three additional slip tendency parameters for our analysis. T_Seff considers σ_neff, which takes the influence of pore pressure on σ_n (Jaeger et al., 2011) into account.

$$\begin{array}{}\text{(3)}& T_{\mathrm{Seff}}={\displaystyle \frac{\mathit{\tau }}{{\mathit{\sigma }}_{\mathrm{neff}}}}\end{array}$$

A normalization to μ has been used for example by Peters (2007) and is additionally calculated as T_Snorm and T_Snormeff. We choose μ as 0.57, which is in the middle of the range reported by Jaeger et al. (2011). For T_Snorm and T_Snormeff slip is likely to occur if they approach values around 1 or larger.

$$\begin{array}{}\text{(4)}& T_{\mathrm{Snorm}}={\displaystyle \frac{\frac{\mathit{\tau }}{{\mathit{\sigma }}_{\mathrm{n}}}}{\mathit{\mu }}}\end{array}$$

$$\begin{array}{}\text{(5)}& T_{\mathrm{Snormeff}}={\displaystyle \frac{\frac{\mathit{\tau }}{{\mathit{\sigma }}_{\mathrm{neff}}}}{\mathit{\mu }}}\end{array}$$

The pore pressure P_p for the calculation of σ_neff is computed from the depth z [m] (which is the true vertical depth below the topographic surface of the German stress model), gravity g [9.81 m s⁻²] and the fluid density ρ [1000 kg m⁻²]:

$$\begin{array}{}\text{(6)}& P_{\mathrm{p}}=\mathit{\rho }\cdot g\cdot z.\end{array}$$

To estimate the slip tendencies, the fault geometries are discretized as surfaces with triangles with a side length of 800 m. Then the 3D stress tensor components from the geomechanical–numerical model of Ahlers et al. (2021b) are mapped onto the corner nodes of the triangles using Tecplot 360 EX v2019 and the Add-on Geostress (Heidbach et al., 2020). The mean stress tensor of the three nodes is multiplied with the normal vector of each triangle to estimate τ and σ_n. With the hydrostatic pore pressure, the four slip tendency parameters are calculated.

3 Results

3.1 Vertical fault set

The results for the Vertical fault set are shown for all four slip tendency parameters in Fig. 2. As the faults are vertical, the top view only shows the values along the fault top. T_S of the Vertical fault set ranges mainly between 0 and 0.5 (histograms are shown in Fig. S2 in the Supplement). Higher T_S values are reached for the uppermost parts of some faults as can be seen in Fig. 2a. With increasing depth T_S decreases rapidly to nearly 0 for all faults. Faults striking NNE–SSW and NW–SE show elevated T_S values in the uppermost parts of the faults when compared to faults of other strike directions.

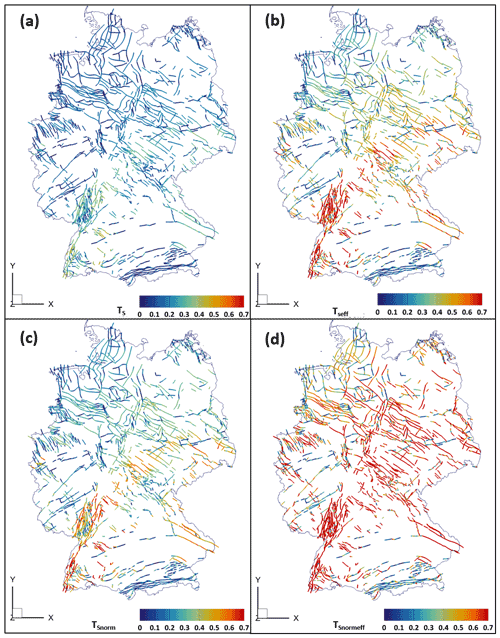
Figure 2 Top view of the slip tendency of the Vertical fault set calculated for four cases. Due to the vertical nature of the faults only the uppermost parts of the faults are visible. (a) T_S; (b) T_Seff (with effective normal stresses); (c) T_Snorm (normalized to a coefficient of friction of 0.57); (d) T_Snormeff (with effective normal stresses and normalized to a coefficient of friction of 0.57). ©EuroGeographics for the administrative boundaries.

T_Seff is higher than T_S and ranges mainly between 0 and 0.7. T_Seff is highest in the uppermost fault parts and decreases rapidly with increasing depth as well. NW–SE- and especially NNE–SSW-striking faults show higher T_Seff than faults of other strike directions. T_Snorm values mainly range between 0 and 0.7, and T_Snormeff ranges mostly between 0 and 1. The same trends for depth and fault strike apply as for T_S and T_Seff. T_Snorm and T_Snormeff are however higher in the uppermost parts of the faults than T_Seff.

3.2 Andersonian fault set

The resulting slip tendencies of the Andersonian fault set are shown for all four slip tendency types in Fig. 3 (additional histograms are given in Fig. S3). T_S ranges mainly between 0 and 0.2. Only the uppermost parts of some NNW–SSE- and NE–SW-striking faults such as the URG, the Albstadt Shear Zone and the Landshut–Neuötting Fault show slightly higher values.

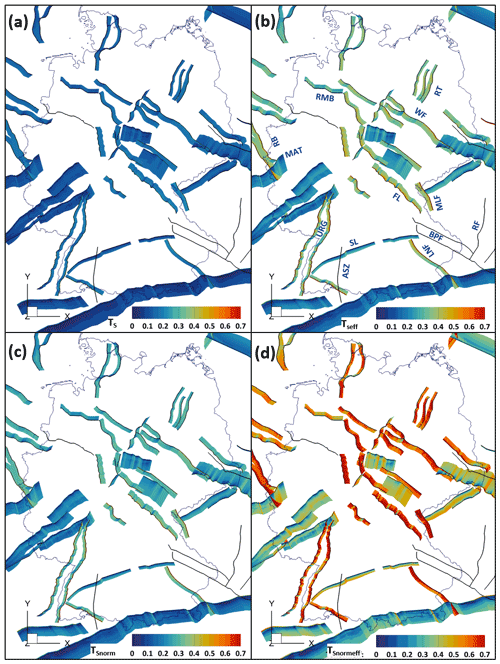
Figure 3 Top view of the slip tendency of the Andersonian fault set calculated for four slip tendency types. (a) T_S; (b) T_Seff (with effective normal stresses); (c) T_Snorm (normalized to a coefficient of friction of 0.57); (d) T_Snormeff (with effective normal stresses and normalized to a coefficient of friction of 0.57). ASZ: Albstadt Shear Zone; BPF: Bavarian Pfahl Fault; FL: Franconian Line; LNF: Landshut–Neuötting Fault; MAT: Midi-Aachen Thrust; MLF: Mariánské Lázne Fault; URG: Upper Rhine Graben; RB: Roer Basin; RT: Rheinsberg Trough; RF: Rodl Fault; RMB: Rheder Moor–Blenhorst Fault; SL: Swabian Lineament; WF: Wittenberg Fault. ©EuroGeographics for the administrative boundaries.

T_Seff mostly ranges between 0 and 0.4. Only 5 % of the values are higher than 0.4. T_Seff is generally elevated for faults and fault segments striking in a NNE–SSW and NW–SE direction such as the URG, the Franconian Line, the Albstadt Shear Zone, the Wittenberg Fault, the Rheinsberg Trough, the Landshut–Neuötting Fault and the Roer Valley Graben. The influence of fault strike direction is especially prominent for faults with segments of varying orientation. The NW–SE-striking parts of the Rheder Moor–Blenhorst Fault show elevated T_Seff values when compared to the more WNW–ESE-striking segments of the fault. For strike-slip faults, T_Seff strongly decreases within the uppermost fault parts and keeps decreasing with increasing depth as shown for parts of the Albstadt Shear Zone in Fig. 4a. T_Seff slightly increases with depth after the initial strong decrease for some normal and thrust faults. This is shown for the Midi-Aachen Thrust in Fig. 4b. T_Snorm ranges mainly between 0 and 0.3 and shows an overall similar behavior to T_Seff. While the high T_Snormeff values reach up to 1.0, areas with low T_Snormeff show values in the same range as for the other three slip tendency parameters. The spatial distribution of areas of low and high T_Snormeff values is similar to T_Snorm and T_Seff.

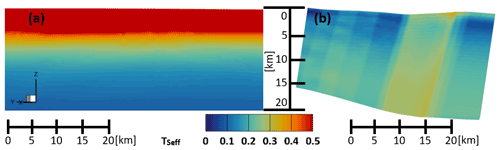
Figure 4 Vertical section of T_Seff along faults. (a) T_Seff of a northern part of the Albstadt Shear Zone decreases over the entire depth; (b) T_Seff of an eastern part of the Midi-Aachen Thrust slightly increases again (after an initial strong decrease) as indicated by the shift from blue to greenish colors at greater depths. Color bar applies to both (a) and (b).

3.3 Semi-realistic fault set

Figure 5 shows the results of the slip tendency calculations for the Semi-realistic fault set; additional histograms are shown in Fig. S4. T_S ranges mainly between 0 and 0.2. For the Semi-realistic fault set, the NNE–SSW- and NW–SE-striking faults show elevated T_S compared to faults of other orientations. The highest T_S can be observed at the uppermost steeply dipping sections of the URG, the Franconian Line, the Albstadt Shear Zone, the Wittenberg Fault and the Roer Valley Graben. For most faults, T_S decreases with increasing depth. However, most faults are significantly less deep than in the Andersonian fault set.

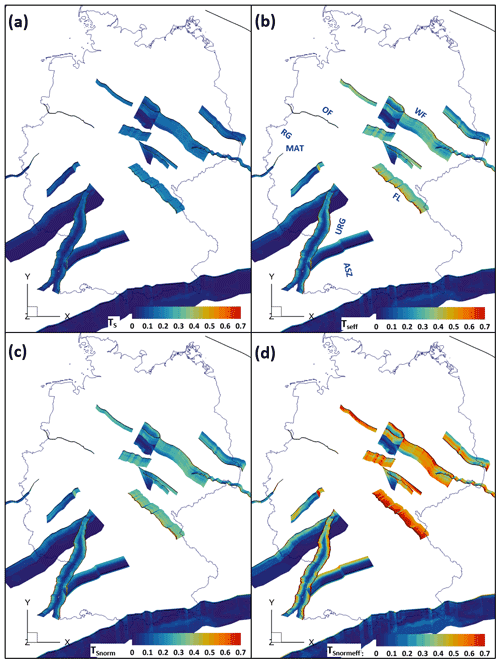
Figure 5 The semi-realistic fault geometries are color-coded by their slip tendency for four cases. (a) T_S; (b) T_Seff (with effective normal stresses); (c) T_Snorm (normalized to a coefficient of friction of 0.57); (d) T_Snormeff (with effective normal stresses and normalized to a coefficient of friction of 0.57). ASZ: Albstadt Shear Zone; FL: Franconian Line; MAT: Midi-Aachen Thrust; OF: Osning Fault; URG: Upper Rhine Graben; RG: Roer Valley Graben; WF: Wittenberg Fault. ©EuroGeographics for the administrative boundaries.

T_Seff ranges mainly between 0 and 0.4 with 5 % of values 0.5 or higher. Faults striking in a NNW–SSE and NE–SW direction such as the URG, the Franconian Line, the Albstadt Shear Zone, the Wittenberg Fault and the Roer Valley Graben show elevated T_Seff as compared to faults of other strike directions. This influence is especially noticeable for the Franconian Line where the WNW–ESE-striking segments of the fault show lower T_Seff than the NNW–SSE-striking ones. For sections of the uppermost parts of the URG and the Roer Valley Graben T_Seff exceeds values of 1. The decrease in T_Seff with increasing depth is especially prominent for faults that have been implemented with a listric geometry (such as the URG or the Hunsrück Southern Border Fault). While the listric URG geometry shows some of the highest T_Seff values for the Semi-realistic fault set in its uppermost parts, T_Seff decreases drastically with depth. The same decrease can be observed for the listric Hunsrück Southern Border Fault. In contrast, T_Seff increases drastically in the lowermost part of the Swabian Lineament after a steady decrease in T_Seff with increasing depth for the most part of the fault.

T_Snorm mainly ranges between 0 and 0.4 The T_Snorm distribution is almost identical to the one of T_Seff. T_Snormeff mainly ranges between 0 and 0.8. The high T_Snormeff values mainly occur on the NW–SE- and NNE–SSE-striking faults, while the areas with low T_Snormeff show values similar to the other slip tendency types in the respective areas.

4 Discussion

4.1 Influence of fault strike on slip tendency

To investigate the influence of the spatial orientation of the faults on the slip tendency, we prepared scatterplots of T_Seff as a function of fault strike for all faults of each of the three fault sets (Fig. 6). The normal faults, thrust faults and strike-slip faults of the Andersonian set are displayed in separate subfigures (Fig. 6b, c and d, respectively).

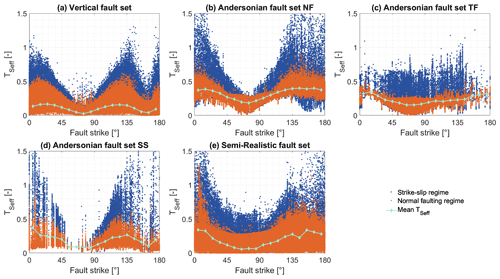
Figure 6 Scatterplots showing T_Seff and the fault strike of each node of the fault mesh. Additionally, the stress regime the data points are subjects to is indicated by its color (blue for strike-slip regime, orange for normal faulting regime). The mean T_Seff in 10^∘ fault strike steps is plotted as a mint-colored line. (a) Vertical fault set; (b) normal faults of the Andersonian fault set; (c) thrust faults of the Andersonian fault set; (d) strike-slip faults of the Andersonian fault set; (e) Semi-realistic fault set.

Overall, the minimum T_Seff values occur consistently at strikes of 75^∘ for all fault types, i.e., the reactivation potential is generally the lowest for ENE–WSW-striking faults, as could be expected in the context of the stress orientation shown in Fig. 1c and d. Vertical faults also show a low reactivation potential on NNW–SSE-striking segments (corresponding to strikes of 165^∘). The maximum T_Seff occurs for strikes of 5–25^∘ for all fault types, i.e., the reactivation potential is generally highest for N–S to NNE–SSW-striking faults; these faults strike at an angle of 25^∘ to S_Hazi with an orientation between 160 and 175^∘. The vertical faults also have a high reactivation potential for NW–SE strikes, the Andersonian normal faults for NNW–SSE-striking segments. Due to the uniform dip of the Vertical fault set, dip is not a variable of influence for this fault set and only the location in the stress field and the strike of the fault lead to differences in slip tendency.

4.2 Influence of depth and shear stress on slip tendency

For all three fault sets, a strong decrease in the slip tendencies can be observed from the surface to a depth of 5–10 km as shown in Figs. 7 and 8 for the Vertical and Andersonian fault sets, respectively. At greater depths, the slip tendency gradient is low. This is the case for all four slip tendency types. For the Vertical fault set (Fig. 7), slip tendency decreases steadily for all four slip tendency types with the exception of a dent between 32 and 38 km. However, since only very few fault segments reach this depth, the influence of fault strike strongly superimposes the depth dependency for these depths. For the Andersonian fault set (Fig. 8), the same trends apply in general as for the Vertical fault set. However, for the thrust and normal faults the initial strong decrease in slip tendency occurs within the uppermost 3–4 km. At this depth, the stress regime switches from a strike-slip regime to a normal faulting regime in most parts of the model. The slip tendencies of the strike-slip faults are generally higher than the ones of the thrust and normal faults in the upper 5–10 km but generally lower at greater depths. In contrast to the strike-slip faults, both normal and thrust faults show a slight increase in the mean slip tendency with increasing depth below 5 km depth. The mean slip tendency increase with depth is higher for the thrust faults than for the normal faults.

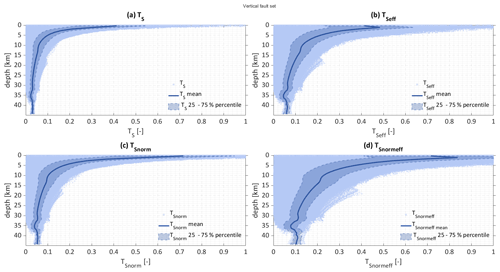
Figure 7 All slip tendency data are plotted vs. depth for the Vertical fault set. The mean slip tendency is plotted as a solid line; the 25 %–75 % percentile is shown as a shaded area.

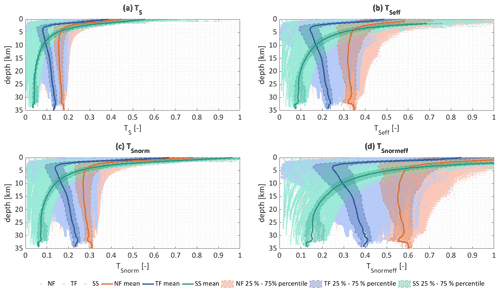
Figure 8 All four slip tendency types at each data point of the Andersonian fault set are plotted vs. their depth. The mean slip tendency is plotted as a solid line; the 25 %–75 % percentile is shown as a shaded area. Due to the different behavior of normal, thrust and strike-slip faults, the three fault types are colored individually. Data corresponding to the normal faults are shown in orange, data corresponding to thrust faults are shown in blue, and data corresponding to strike-slip faults are shown in mint color.

For normal, thrust and strike-slip faults σ_n increases at a similar rate with increasing depth. On the other hand, τ on strike-slip faults and the faults of the Vertical fault set increases less strongly. Since slip tendency has been defined as $\mathit{\tau }/{\mathit{\sigma }}_{\mathrm{n}}$, low τ leads to low slip tendencies for the strike-slip faults and the faults of the Vertical fault set. Figure 9 shows τ for the Vertical fault set. Additionally, σ_neff, τ and the resulting T_Seff of the Landshut–Neuötting Fault are shown exemplarily. While σ_neff increases to over 250 MPa, τ only increases to around 20 MPa at a depth of 30 km (note that the range of the color bar of σ_neff is 10 times the range of the τ). This results in T_Seff strongly decreasing with increasing depth for all faults regardless of their strike direction in the Vertical fault set.

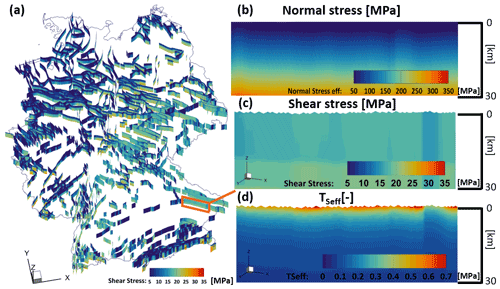
Figure 9 (a) Shear stress τ in MPa of the Vertical fault set with the color map ranging from 5 to 35 MPa (oblique view). (b)–(d) Zoomed in view of the Landshut–Neuötting Fault normal to the strike reaching to a depth of around 30 km; (b) effective normal stress σ_neff with the color map ranging from 50 to 350 MPa; (c) shear stress τ with the color map ranging from 5 to 35 MPa; (d) T_Seff of the Landshut–Neuötting Fault is shown with the color map ranging between 0 and 0.7. ©EuroGeographics for the administrative boundaries.

4.3 Influence of fault dip

In order to investigate the influence of the 3D fault geometry, we compare the slip tendency histograms of the Vertical (blue), Andersonian (orange) and Semi-realistic (mint) fault set (Fig. 10). For all four slip tendency types, the Vertical fault set shows a right-skewed bell shape, the Semi-realistic fault set displays as J shape, and the Andersonian fault set shows a bimodal distribution. The bimodal character of the Andersonian fault set is more distinct for T_Seff and T_Snormeff. The slip tendency values of the first peak are mainly concentrated on the thrust faults, whereas the slip tendency values of the second peak are mainly present on normal faults.

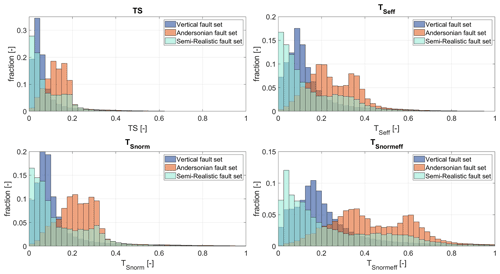
Figure 10 Comparison of the slip tendency histograms of the Vertical (blue), Andersonian (orange) and Semi-realistic (mint) fault set for the four slip tendency types. Slip tendency values greater than 1 are not shown. The slip tendency values have been calculated on the nodes of the fault mesh; mesh resolution is 800 m for all three fault sets. Bin size is 0.025.

As the normal faulting regime is predominant in most parts of the Germany model (especially at depths greater than 4 km) in general σ_n is lower for normal faults than for thrust faults, which have been implemented with a dip of 60 and 30^∘, respectively, in the Andersonian fault set, leading to the bimodal distribution of T_S.

The more prominent bimodal distribution of T_Seff and T_Snormeff in the Andersonian fault set results from the influence of the calculation of the pore pressure as a function of depth. In combination with the normal faulting regime in most parts of the Germany model, this leads to a stronger relative reduction in σ_neff for normal faults than for thrust faults.

The listric geometry of the URG in the Semi-realistic fault set is based on DEKORP 9N (Brun et al., 1992). The URG shows high T_Seff values in the uppermost parts for both the Andersonian and the Semi-realistic fault set. With increasing depth, the dip of the Semi-realistic URG faults decreases until it becomes sub-horizontal. This decrease in dip coincides with a significant T_Seff decrease. In contrast, T_Seff for the Andersonian fault geometries decreases at a significantly lower rate. This results from the fact that while σ_neff increases at a similar rate for both fault types, τ of the Semi-realistic URG increases at a much lower rate than it does for the Andersonian URG (also shown in Fig. S5). Results from the Hunsrück Southern Border Fault, another listric fault, (derived from DEKORP 9N and 1C, Henk, 1993) show a similar behavior.

The overall low slip tendency values of the Vertical fault set were to be expected due to the prevailing normal faulting regime in most parts of the model and the uniform 90^∘ dip of the Vertical fault set. The low values do not properly reflect the actual fault reactivation potential of faults with different dips in reality. The reactivation potential for faults with other dips in reality is underestimated in areas with normal and thrust faulting regimes and overestimated in a strike-slip regime.

4.4 Influence of pore pressure

The use of a hydrostatic pore pressure is a major simplification since the pore pressure is not hydrostatic everywhere in Germany. Considerable overpressures have been shown for example in the Molasse Basin (Drews et al., 2018; Müller et al., 1988). Müller et al. (1988) describes pore pressure gradients of up to 24 MPa km⁻¹ in the vicinity of the lineament of the Alpine Thrust. Figure 11 shows T_Seff for the Alpine Thrust for pore pressure gradients of (a) 10 MPa km⁻¹ (hydrostatic) (b) 16 MPa km⁻¹ and (c) 22 MPa km⁻¹. T_Seff increases drastically with increasing pore pressure. For the gradient of 16 MPa km⁻¹ T_Seff reaches values of up to 0.7 for favorably oriented segments of the fault. For a pore pressure gradient of 22 MPa km⁻¹ T_Seff increases to over 0.7 for almost all parts of the fault and reaches values well in excess of 1 over large areas. Even though these pore pressure gradients are unlikely to occur over large areas of the fault, this highlights the crucial impact of the pore pressure on the fault reactivation potential.

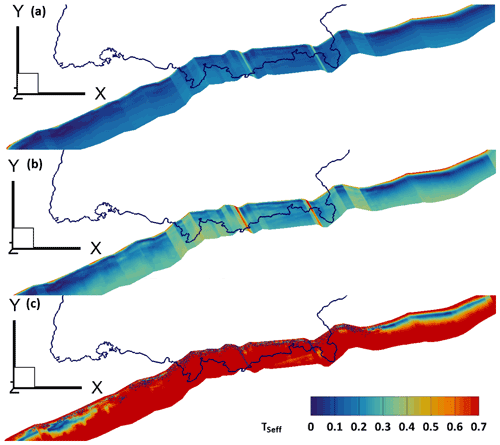
Figure 11 T_Seff of the Alpine Thrust for different pore pressures. (a) T_Seff with hydrostatic pore pressure corresponding to a gradient of 10 MPa km⁻¹; (b) T_Seff for an overpressured pore pressure with a gradient of 16 MPa km⁻¹; (c) T_Seff for an overpressured pore pressure with a gradient of 22 MPa km⁻¹. The color bar applies to all three cases. ©EuroGeographics for the administrative boundaries.

4.5 Comparison between slip tendency and seismicity

In order to evaluate our slip tendency results, we test them qualitatively against the distribution of tectonic earthquakes. The earthquakes are taken from the EMEC seismic event catalogue of Grünthal and Wahlström (2012) that covers the period between 1000 to 2006 CE in the investigation area and provides earthquakes with magnitudes M_w≥ 3.5. We added events to this compilation with M_w≥ 3.5 for the years 2007–2021 from the GEOFON data center at the GFZ German Research Centre (Quinteros et al., 2021). For the events with a given hypocentral depth, the majority occur at 8 km (refer to Fig. S6), and the largest moment magnitudes are observed at 8 to 10 km depth. Therefore, we use the slip tendency values at a cross section at 8 km depth for the comparison with seismic events.

Figure 12a shows the location of the seismic events with M_w≥ 3.5 color-coded by their moment magnitude alongside a horizontal cross section through the Vertical fault set at a depth of 8 km. The faults are color-coded by their T_Seff values. The overall T_Seff at this depth is very low with values of only up to 0.3 as the 90^∘ dip is unfavorable for reactivation in the normal faulting regime at this depth. However, the NNE–SSW-striking faults of the seismically active Upper Rhine area show slightly higher T_Seff values than other areas with low seismicity. While several seismic events in east Germany are localized close to faults with elevated T_Seff, there are several faults with similar or higher values where no seismicity is documented. The seismicity in the Roer Valley Graben area and its SE-trending elongation is localized along faults where only some segments show slightly elevated T_Seff values or where no faults at all have been mapped. While the Vertical fault set is based on a very comprehensive fault selection it is apparent from the distribution of seismic events that some relevant structures are likely still missing.

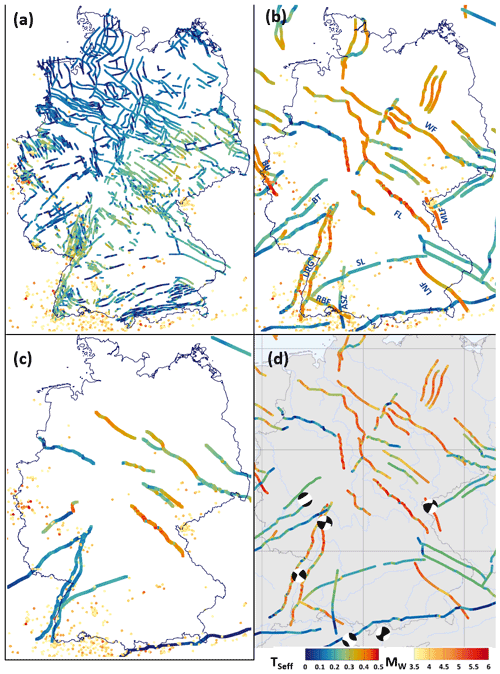
Figure 12 Seismic events with M_w>3.5 color-coded by their moment magnitude (yellow to red) displayed on horizontal cross sections through the fault sets color-coded by T_Seff (hydrostatic pore pressure) at 8 km depth. (a) Vertical fault set; (b) Andersonian fault set; (c) Semi-realistic fault set. The color bars of T_seff and M_w apply to (a)–(d); (d) Andersonian fault set with fault plane solutions from the GFZ GEOFON catalogue (Quinteros et al., 2021) visualized using the focalmech script (Conder, 2022). ASZ: Albstadt Shear Zone; BT: Boppard Thrust; LNF: Landshut–Neuötting Fault; MLF: Mariánské Lázne Fault; RBF: Randen–Bonndorf Fault; RB: Roer Basin; SL: Swabian Lineament; URG: Upper Rhine Graben. ©EuroGeographics for the administrative boundaries.

This is not surprising when considering the results of fault detection using photo-lineations derived from high-resolution data of satellite missions such as the European Remote Sensing Satellite (ERS) 1/2. For example, Franzke and Wetzel (2001) present in their work for southern Germany that there are numerous additional fault networks on a smaller scale that could potentially serve as faults for the catalogued seismicity with small magnitudes. However, if we only used large events with M_w>6 instead that, according to empirical relations, have a rupture length of >10 km (Wells and Coppersmith, 1994), these would fit our resolution better, but in a low-strain area these magnitudes do not occur very often and even the largest recorded event in Germany from the year 1911 with M_w 5.8 in the Albstadt Shear Zone would not be usable; only the historical events where the epicenter estimation based on intensity reports is highly uncertain could be used.

A cross section through the Andersonian fault set at a depth of 8 km is shown in Fig. 12b; the same color codes as for Fig. 12a apply. The occurrence of seismic events is in good accordance with the elevated T_Seff of the URG, the Roer Valley Graben, the Mariánské Lázne Fault and the Randen–Bonndorf Fault. However, especially in east Germany and in the SE-trending elongation of the Roer Valley Graben there are areas without faults despite numerous seismic events. Furthermore, T_Seff is rather low along the Albstadt Shear Zone, one of the seismically most active areas in Germany due to the implementation as a 90^∘-dipping strike-slip fault. In contrast, there are also areas with T_Seff in the same range as the URG with no or only very little seismicity, especially in northern Germany. Here, T_Seff is either overestimated in comparison to seismically active areas or stress relief is achieved by other processes.

Since only a subset of the Andersonian fault set could be implemented in the Semi-realistic fault set, there are many areas where earthquakes occur but no fault geometry is considered (Fig. 12c). While the shallow sections of the URG and the Albstadt Shear Zone show T_Seff of 0.6 and higher, T_Seff is relatively low at a depth of 8 km. In general, T_Seff is lower at the 8 km depth cross section for the Semi-realistic fault set than for the Andersonian fault set.

While some of the seismogenic areas show elevated T_Seff values, the absolute values are rather low, especially at 8 km depth and deeper, where most of the considered seismic events take place. If μ is low enough, seismicity can still occur even with T_Seff in the range below 0.4. The range of μ of faults can vary greatly and even reach values below 0.4 for faults with fault gouge (Numelin et al., 2007; Haines et al., 2014) as a compilation by Ferrill et al. (2017) shows. For higher μ, as they have been shown for different locations (Zoback and Healy, 1992, 1985; Brudy et al., 1997) and collected by Peters (2007), T_Seff would need to reach higher values in order to explain seismic events. This could be achieved through higher τ or lower σ_n. In order to achieve these, either significant changes regarding the stress tensor from the geomechanical model of Germany or changes in the fault geometry would be required. The changes to the stress tensor required would not be warranted by the calibration data used for the model of Germany. In order to elevate T_Seff of the Franconian Line to values of 0.7 and higher, an additional 30 MPa of τ would be required at 8 km depth. The required stress changes however would not fit the data from the kontinentale Tiefbohrung (German Continental Deep Drilling Program) (KTB) nearby that has been used for the model calibration. On the other hand, the fault geometries are subject to major uncertainties due to the sparse data available on the geometries at greater depths. As shown above, both fault strike and fault dip drastically impact the resulting slip tendency, and the uncertainties regarding the 3D fault geometries could therefore at least partly explain the overall low values.

A comparison of the faults of the Andersonian fault set with three fault plane solutions (Quinteros et al., 2021) (Fig. 12d) shows that one of the nodal planes' strike is (sub-) parallel to the URG, even though the corresponding dips are steeper at around 75^∘ than they were assumed for the URG in the Andersonian fault set. For the Alpine Thrust, one fault plane solution in the fault's proximity shows a parallel strike of 78^∘ but a much steeper dip of 71^∘ than the 30^∘ dip that had been assumed for the Alpine Thrust, with another fault plane solution indicating reactivation along a fault that is not present in the fault set. A fault plane solution close to the NNW–SSE-striking Mariánské Lázne Fault indicates seismicity linked to a NNE–SSW-striking fault. Reactivation along a fault striking in a NNW–SSE direction rather than NE–SW direction is indicated by a fault plane solution in the area of the NE–SW-striking Boppard Thrust. Such faults are present in the Vertical fault set, even though their slip tendencies are rather low due to the 90^∘ dip in the normal faulting regime. Even though the Andersonian fault set roughly replicates the general fault pattern documented for Germany, a more diverse fault set in terms of strike, location and dip is required for a more comprehensive comparison with the seismic events.

4.6 Data limitations

The relevant data for this slip tendency analysis are the stress tensor, pore pressure, frictional fault properties and fault geometry. The model by Ahlers et al. (2021b), which provides the 3D absolute stress tensor for our study, has a coarse resolution and only implements a single sediment layer as well as only four upper crustal units. Tectonic faults are not implemented and thus local stress variations due to their presence are not considered in the model. Ahlers et al. (2021a) describe a good fit to the stress magnitude data that are used for the model calibration. However, these are located in the uppermost kilometers of the model where we predict the overall highest slip tendencies. At greater depths, where our slip tendency results are visibly lower, no calibration data were available for the geomechanical model.

Wide regions and depth intervals of the numerical model indicate a prevailing normal faulting stress regime. However, focal mechanisms of seismic events (Heidbach et al., 2016) indicate a possible strike-slip regime also at greater depths. In such a regime, an overestimation of the minimum horizontal stress S_hmin reduces the slip tendencies. Similarly, the underestimation of the maximum stress (either the vertical stress S_v in normal faulting stress regime or the maximum horizontal stress S_Hmax in a strike-slip stress regime) might explain the low slip tendencies.

A second major source of uncertainty results from the limited data available regarding the 3D fault geometries of the selected faults with sufficient depth extension (mostly >5 km). Only few seismic sections and geological cross sections could be used for the 3D fault geometry generation. Due to the sparse data available for most faults the 3D geometry has been deduced from only one section. The resulting geometries are therefore unlikely to properly represent the real 3D fault geometries (dip, strike, depth extent) over the entire fault lengths. As shown above, strike and dip have major influences on the resulting slip tendency.

Pore pressure data are too sparse to justify the discrimination of areas of distinct pore pressure gradients and thus only a hydrostatic pore pressure could be assumed for the estimation of T_Seff and T_Snormeff with the abovementioned effects. Since data on the frictional fault properties were not available, we assumed the faults to be cohesionless. If the considered faults have cohesion greater than 0, the resulting slip tendencies would be further reduced.

4.7 Comparison with earlier studies

Peters (2007) analyzed the slip tendency of the URG with the help of a numerical model. Using a dip of 60^∘ for faults with a known dip direction and assuming hydrostatic pore pressure calculated slip tendencies reached values of up to 0.8 at a depth of 2.5 km and with a normalization to a coefficient of friction of 0.4. Even though the slip tendency in this study has been normalized to a higher coefficient of friction of 0.6 the overall slip tendency values in this study are around 0.2 higher than the results in Peters (2007). However, the URG boundary faults show elevated values for similar segments to the ones in the study by Peters (2007). The study of Worum et al. (2004) calculates T_Seff values between 0.2 and 0.4 for the Roer Valley Graben using an analytical model for faults reaching depths of around 2–3 km for comparable $S_{\mathrm{hmin}}/S_{\mathrm{Hmax}}$ ratios and the strike-slip regime that is present in the Germany model at the before mentioned depths. T_Seff of the Roer Valley Graben boundary faults in this study ranges between 0.6 for the southernmost parts of the faults and 0.2 in the northern parts, which is in contrast to the trends displayed in Worum et al. (2004), where the southern parts of the faults show the lowest T_Seff values. However, the high T_Seff values appear on short segments with ideal orientation for reactivation under the given strike-slip regime with S_Hazi around 155^∘. Slightly less well-oriented segments show values that are in better agreement with the results by Worum et al. (2004).

5 Main outcome and recommendations

The slip tendency analysis on basis of the 3D absolute stress tensor from the geomechanical–numerical model of Germany (Ahlers et al., 2021b) allowed the identification of regions with a higher reactivation potential and regions where faults are more stable. Elevated slip tendencies have been found especially for NNE–SSW- and NW–SE-striking faults such as the URG, the Franconian Line, the Albstadt Shear Zone, the Wittenberg Fault, the Rheinsberg Trough, the Landshut–Neuötting Fault and the Roer Valley Graben. However, a comparison with focal mechanisms points towards reactivation of a more diverse set of faults, which should be subject to further studies.

The major influence of fault geometry on the calculated slip tendency has been shown by the comparison of three fault sets. High-quality information on fault geometry can be provided for example by interpreted seismic sections for large-scale faults. To improve this kind of analysis, faults should be characterized by multiple seismic cross sections. The analysis has also shown the crucial influence of the pore pressure on slip tendencies for the fault sets considered. However, no spatially comprehensive pore pressure data for the entire area of Germany are available. The same applies for the frictional properties of faults, which are only poorly restrained. Lastly, further and more information on the stress state in Germany is crucial for a more reliable slip tendency analysis.