the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An efficient partial-differential-equation-based method to compute pressure boundary conditions in regional geodynamic models
Dave A. May
Modelling the pressure in the Earth's interior is a common problem in Earth sciences. In this study we propose a method based on the conservation of the momentum of a fluid by using a hydrostatic scenario or a uniformly moving fluid to approximate the pressure. This results in a partial differential equation (PDE) that can be solved using classical numerical methods. In hydrostatic cases, the computed pressure is the lithostatic pressure. In non-hydrostatic cases, we show that this PDE-based approach better approximates the total pressure than the classical 1D depth-integrated approach. To illustrate the performance of this PDE-based formulation we present several hydrostatic and non-hydrostatic 2D models in which we compute the lithostatic pressure or an approximation of the total pressure, respectively. Moreover, we also present a 3D rift model that uses that approximated pressure as a time-dependent boundary condition to simulate far-field normal stresses. This model shows a high degree of non-cylindrical deformation, resulting from the stress boundary condition, that is accommodated by strike-slip shear zones. We compare the result of this numerical model with a traditional rift model employing free-slip boundary conditions to demonstrate the first-order implications of considering “open” boundary conditions in 3D thermo-mechanical rift models.
- Article
(10162 KB) - Full-text XML
-
Supplement
(4280 KB) - BibTeX
- EndNote
In Earth sciences and geodynamic modelling, computing the pressure can be essential. Specifically, numerous regional thermo-mechanical studies use the lithostatic pressure or a reference pressure based on some density structure as a normal stress boundary condition (e.g. Baes et al., 2018; Brune, 2014; Brune et al., 2012, 2014, 2017; Chertova et al., 2012, 2014; Glerum et al., 2018; Ismail-Zadeh et al., 2013; Popov and Sobolev, 2008; Quinteros et al., 2010; Yamato et al., 2008). By imposing only the normal stress, material is permitted to flow in and out of the domain in response to the other boundary conditions and or deformation in the domain interior. This is inherently closer to the reality of the dynamics within a regional segment of the Earth,compared to a regional domain that is closed and in which neither inflow nor outflow is permitted. Hence, the ultimate intent of imposing the normal stress is to provide dynamical behaviour that is similar to that which would occur if the models were performed in a much larger domain. Moreover, the reference pressure can also be used as an initial guess for the pressure when solving linear or non-linear system flow problems with iterative methods.
The common approach to compute a reference pressure P is to define a set of depth columns and integrate the rock density ρ(x) over each column to obtain the pressure at depth. Thus, to compute the pressure P at some point of x′, we evaluate the 1D integral as follows:
where is the projection of x′ onto the surface of the Earth in the direction opposite to the gravity vector g and Ps is the reference pressure at the surface . For the case of a constant density and gravity, this expression reduces to , where D is the distance (depth) given by and . When the density is a function of space and gravity is constant, the 1D integral is decomposed into different segments Di and a suitable quadrature rule is applied over each segment. For example using a one-point Gauss quadrature rule we have
where ρi is the density at the centroid of the segment Di. For the case of a uniform mesh with cell edges aligned with the gravity vector, all the cell edges and vertices are located along straight lines that are parallel to the direction of gravity. Hence, Eq. (2) can be simply evaluated by traversing along a column associated with a set of cells (or vertices). In this special case, the sub-division of the integral is naturally defined by mesh cells. If the column sweep is performed from the surface to depth, then only a single pass over each cell in a column is required to compute the pressure at any depth within that column by accumulating values from cells at shallower depths. Therefore, if we traverse from segments i = 0, 1, 2, …, N, where the segments are ordered such that Di+1 is located at greater depth than Di, then we have the following sequence , , …, .
Although evaluating Eq. (2) may appear simple, its implementation may be inefficient or too algorithmically complex for general use. Below we outline some common use cases that render the column-wise integration difficult (or expensive):
-
a mesh with cell edges (2D) or faces (3D) that are not aligned with the gravity vector (Fig. 1a),
-
an unstructured mesh (Fig. 1b),
-
a density structure (or gravity vector) that is spatially varying,
-
a parallel decomposition of the mesh (Fig. 1c),
-
time dependence in the density or mesh coordinates that requires continual re-evaluation of the reference pressure.
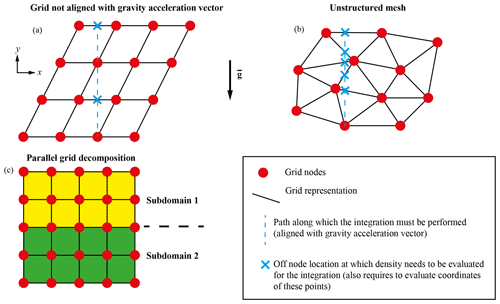
Figure 1Schematic representation of meshes for which computing an integral in the vertical direction can be challenging: (a) mesh with a grid not aligned with the gravity vector, (b) unstructured mesh, and (c) parallel distribution of a mesh. The dashed blue lines represent the direction along which the integral must be performed. The blue crosses represent the points that have to be evaluated during the integration.
To compute P(x′) we first have to define the location . In general this is non-trivial for use cases (1) and (2). If both the density and gravity are constant, then the only complexity associated with meshes identified in points (1) and (2) relate to computing . Due to the fact that the path of the integral (i.e. the “column”) does not coincide in general with a set of mesh cells or vertices, the line integral must be performed for each point x′ in the mesh, meaning that the single pass approach used in the gravity-aligned mesh is not possible. If the density (or gravity) vary in space throughout the domain, the integral must be approximated via a suitable sub-division in space and/or a quadrature rule. Assuming that the density is a piecewise constant over each cell, the simplest approximation would be to determine the intersection between the line segment and each cell and apply a one-point quadrature rule over the intersecting segment times. In Fig. 1a and b we depict the complexity of this procedure for a non-coordinate-aligned and unstructured mesh. When performing simulations in parallel where the mesh is distributed across multiple Message Passing Interface (MPI) ranks, even for the case of a uniform mesh aligned with the gravity vector, the column-wise integration approach is somewhat complicated. Individual MPI ranks may compute their local contribution to the sum of accumulated pressures; however, the final pressure requires a partial sum to be performed over mesh sub-domains that intersect the 1D line integral. The global reduction (with the chosen MPI ranks overlapping with each 1D line integral) is complicated to define for mesh types identified in points (1) and (2). Lastly, if the reference pressure associated with some density structure is to be used as a boundary condition in a mechanical model, time dependence of that density structure (or mesh) will require one to re-compute the reference pressure at each time step. Hence, the efficiency of the implementation used to compute the pressure is important.
Moreover, when the density structure evolves with time as deformation occurs, the pressure gradients may no longer be aligned with the gravitational acceleration vector. In these non-hydrostatic cases, this pressure is not lithostatic. However, to be able to provide an approximation for the total pressure or to use stress boundary conditions, it is still important to approximate the total pressure in the best possible way.
For these reasons, we propose an efficient mesh and numerical method (finite elements, finite differences, finite volumes, etc.) to compute a reference pressure associated with the density structure of a domain in hydrostatic cases or an approximation of the total pressure for non-hydrostatic cases for all scenarios given above by solving a partial differential equation (PDE) derived from the conservation of the non-inertial momentum equation for an incompressible fluid. We also present thermo-mechanical numerical models and static numerical models applied to Earth sciences and geodynamics to show the usefulness of this approach.
For an incompressible fluid in a domain Ω, the non-inertial form of the conservation of momentum is given by the Stokes equation
where v is the velocity of the fluid, P is the total pressure, is the deviatoric stress tensor with η the viscosity, is the strain rate tensor, is the density, is the gravity vector, and x and t denote the space and time, respectively. The incompressibility constraint is given as follows:
In the context of our problems we will decompose the boundary of the domain into two non-overlapping segments: ∂Ωsurf that we will regard as the free surface and prescribe that tangential and normal stresses are zero, i.e. , and ∂Ωi, which denotes the interior parts of the boundary along which we may impose any valid combination of velocity or stress in the normal and tangential directions. Furthermore, and . The outward-pointing unit normal vector to ∂Ω will be denoted via .
To define the pressure associated with the density structure we make the “ansatz” that v=0; hence, Eq. (4) is trivially satisfied, and Eq. (3) reduces to the usual hydrostatic equilibrium problem
For spatial dimensions , Eq. (5) is over-determined as there are more equations (nd) than unknowns:
As such, there is no unique solution to Eq. (5). To obtain a unique solution to Eq. (5), we require a single equation for P. This can be achieved by taking the divergence of Eq. (5):
Eq. (7) will be referred to as the pressure Poisson equation (PPE).
Equation (7) can be obtained in an alternative manner with less restrictive assumptions. First, we assume that we have a solution ((v),p) for Eqs. (3), (4). Then we take the divergence of the momentum equation (as before) and integrate over Ω
Then, applying the divergence theorem to the first term we obtain
If we assume the boundary term on the left-hand side is small, we have
which must be true for any arbitrary domain, thus resulting in Eq. (7).
Assuming that is constant or slowly varying and that τ is symmetric yields
Hence, dropping the first term in Eq. (9) is equivalent to saying that for all . Alternatively, the term is zero if for all . This condition is satisfied if the fluid experiences either rigid body translations or rigid body rotation along ∂Ω.
2.1 Boundary conditions
A unique solution to Eq. (7) requires boundary conditions to be specified on P. Our choice of boundary conditions for Eq. (7) is motivated by Earth-like bodies. The boundary conditions will be specified in the usual manner, i.e. in terms of a Dirichlet constraint in which we impose P and Neumann constraints in which we impose the behaviour of .
Along the surface of the domain, which represents the free surface of the Earth, we impose
Equation (12) is a Dirichlet constraint and specifies that the reference (or datum) pressure should be zero on the surface of our geological body. This is consistent with the observation that the mean pressure on all points on the surface (above sea level) are approximately equal. This Dirichlet boundary condition is a natural extension of the free surface boundary condition used for the flow problem in Eqs. (3), (4), namely , which reduces to and with a tangent unit vector to the boundary such that . Equation (12) is consistent with a fluid at rest since τ=0. In the non-hydrostatic case, we require to arrive at Eq. (12). We also note that is proportional to the mean curvature κ of the boundary ∂Ω (Barth and Carey, 2007). Hence, if there is zero topography, κ=0 and P=0 on ∂Ωsurf, and if the change in topography is small, then κ≈0 and P≈0.
Two different boundary conditions are introduced to constrain . These are defined as a direct extension of the 1D hydrostatic assumptions to 2D and 3D domains. We first introduce some additional quantities that will aid the definition of the Neumann boundary condition. First, we split ∂Ωi into two parts, such that . Next, we define the gravity unit vector such that
and the unit vector , which is perpendicular to , i.e.
The first constraint states that P should increase only in the direction of gravity. Hence, from Eq. (5) we have
The second constraint states that P should not change along directions perpendicular to the gravity; hence,
Since the unit vector normal to the boundary ∂Ω can be decomposed according to
we have
Hence, the two Neumann boundary conditions may be stated as
and
Equations (19) and (20) may appear peculiar since both the left-hand side and right-hand side involve the gradient of pressure. In principle, to obtain a unique solution to Eq. (7) one can constrain the gradient in any direction, independent of the boundary normal , and our 1D inspired gradients do exactly that.
We note for domains with boundaries parallel to either or that the Neumann conditions (19) and (20) simplify (and in some cases do not provide any) the information to constrain . For example, consider a 2D Cartesian domain's right and left boundaries Γr,l with normal and a bottom boundary Γb with normal and . Invoking Eq. (19), we obtain
Invoking Eq. (20) we obtain
Clearly conditions (21a) and (22b) are redundant. As such, the usage of Eqs. (19) and (20) cannot be used arbitrarily.
One may also consider employing both Eqs. (19) and (20) simultaneously. In this way we would obtain
which is identical to the result obtained by computing the dot product of Eq. (5) with . Equations (23) certainly avoids the potential issue of using Eqs. (19) and (20). If we again consider the 2D Cartesian domain example, imposing Eq. (23) on all of ∂Ωi is equivalent to imposing Eqs. (21b) and (22a).
Nevertheless, for an arbitrarily shaped domain, using boundary conditions (15), (16) or (23) does not yield the same result (see Sect. 3.3). For general use (i.e. when considering arbitrarily shaped domains), we suggest employing Eqs. (15) and (16) as they are a direct extension of the 1D hydrostatic assumptions to 2D and 3D domains.
2.2 Weak formulation
To define the weak formulation of the PPE we will use functions that are square integrable in the sense of Lebesgue, i.e.
and functions from the H1(Ω) Sobolev space
Finally we will require the space of functions in H1(Ω) that vanish on the Dirichlet boundary ∂Ωsurf:
Given a test function , the weak form of the PPE is obtained by multiplying Eq. (7) by q and integrating both sides over Ω
Applying integration by parts to the left- and right-hand sides yields
Note that the boundary ∂Ωsurf does not appear in Eq. (25) since the test function q vanishes along the Dirichlet boundary. We also note that Eq. (25) only requires ρg∈L2(Ω), and thus the formulation is valid for cases when the density ρ is discontinuous.
Splitting the surface integrals over the two segments and using Eqs. (19), (20) we have
Noting that the second term of the left-hand side and part of the last term on the right-hand side exactly cancel each other yields the following
From Eq. (25), the weak formulation obtained if using Eq. (23) applied over all of ∂Ωi is simply
2.3 Implementation
The strong (Eq. 7) and weak (Eq. 25) formulations of the pressure Poisson problem can be solved using the standard spatial discretization techniques, e.g. finite differences or finite elements. Moreover, since the equation is of Poisson type, it is readily amenable to being solved using standard iterative multigrid and/or direct solvers. Lastly, because the formulation is expressed in terms of a PDE, it is also straightforward to compute the pressure on parallel computing architecture as we can re-use existing discretization implementations that support domain decomposition.
In this section we provide several numerical models to show the following items:
-
the accuracy and consistency of the method for hydrostatic cases,
-
the accuracy of the approximation of the total pressure in non-hydrostatic cases,
-
the effect of using the depth-integrated approach and the pressure Poisson problem approach to impose boundary conditions on the momentum equation,
-
the usefulness of the method for 3D geodynamic thermo-mechanical modelling.
3.1 Hydrostatic pressure
To compare the numerical solution of Eq. (7) with the analytical solution obtained with Eq. (2), we designed four hydrostatic models (in 1D and 2D) for which the analytical solution is easily obtained (Figs. 2 and 3).
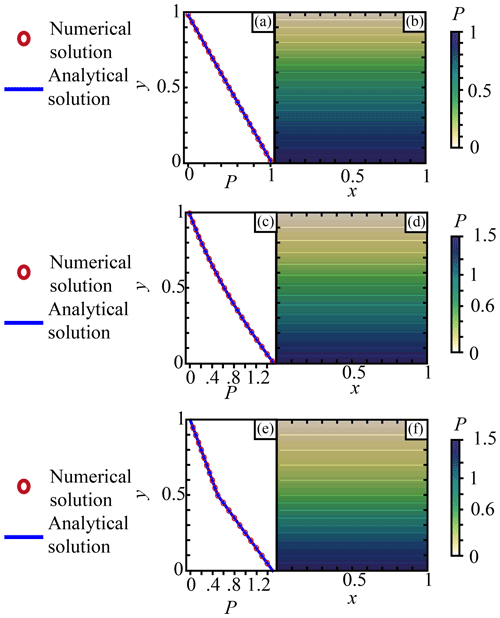
Figure 2Pressure for non-dimensioned hydrostatic cases. Panels (a, c, e) show the 1D pressure for (a) a constant density ρ=1, (c) a continuous y-dependent density , and (e) a discontinuous density. The blue line is the analytical solution computed with Eq. (2), and the red circles represent the numerical solution computed with Eq. (7). Panels (b, d, f) show the 2D numerical solution for (b) a constant density ρ=1, (d) a continuous y-dependent density , and (f) a discontinuous density.
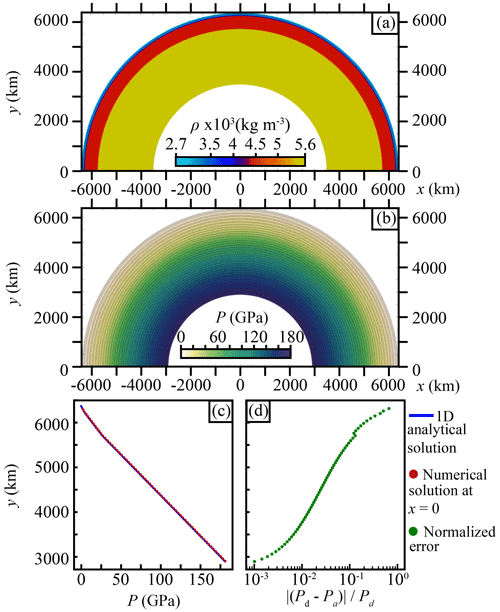
Figure 3Pressure for a hydrostatic case in a half annulus approximating a simplified and idealized layered Earth. (a) Density structure for the half-annulus model. (b) Numerical solution of the 2D half-annulus model. (c) The blue line shows the 1D analytical solution for the density structure shown in (a) along a line parallel to the gravity vector. The red circles show the numerical solution extracted from (b) at coordinate x=0 along a line parallel to the gravity vector. (d) Green dots show the normalized error between the analytical solution and the numerical solution at x=0 as .
3.1.1 Box domain
We define the domain and assume that . We consider three depth-dependent density structures ρ=ρ(y) that thus admit a hydrostatic pressure solution, i.e. satisfy , .
- Case 1.
-
This case assumes a constant density, ρ(y)=1 (Fig. 2a, b). The analytic pressure solution is given by
- Case 2.
-
This case assumes a continuous depth-varying density (Fig. 2c, d). The analytic pressure solution is given by
- Case 3.
-
This case assumes a discontinuous density such that ρ(y)=1 for and ρ(y)=2 for (Fig. 2e, f). The analytic pressure solution is given by
with D the distance between the surface and the y coordinate at which the pressure is computed.
A finite-element (FE) method employing an unstructured triangular mesh with a P2 function space was used to obtain the numerical solution for each case. The FE method was applied to Eq. (27) using boundary conditions described by Eq. (15) at the base and Eq. (16) on the lateral sides. Along the upper surface we impose the Dirichlet constraint P=0. Unless otherwise stated, when solving the PPE with FEs the Dirichlet constraints are imposed strongly (i.e. point-wise), whereas Neumann constraints are imposed weakly via surface integrals defined on facets of the FE cells that live on the boundary of the domain. Accordingly, all points living on ∂Ωsurf (including corner points) will be associated with the Dirichlet constraint. Figure 2a–f shows the 1D and 2D solution of these three models. On the 1D models both the numerical and analytical solutions of Eqs. (7) and (2) are shown, whereas on the 2D models only the numerical solution is provided. Since the P2 FE approximation contains the monomials 1, y, and y2, the FE solution exactly reproduces the analytic solution for case 1 and case 2 independent of the number of finite elements used in the domain (e.g. sub-dividing the box into two triangles would be sufficient to obtain an exact solution). For case 3, the analytic pressure solution is piecewise linear, and provided that the density discontinuity is exactly resolved by the faces of the triangular FE mesh (which was the case here), the FE method exactly reproduces the analytic solution.
3.1.2 Half-annulus domain
The 2D half-annulus model aims to show the efficiency of the method when computing the lithostatic pressure in a body with a radial gravity vector and concentric density structure (Fig. 3a). This model represents a domain extending from
where θ is the polar angle, r is the radius in polar coordinates, RE is the approximative Earth radius (6371 km), and RE−2891 km is the approximative core-mantle boundary. Mapped into Cartesian coordinates this gives x=rsin (θ) and y=rcos (θ). The gravity vector pointing to the centre () is defined as m s−2, and the density is defined as five concentric layers with a constant density in each (Fig. 3a). The pressure was computed by solving Eq. (27) with the boundary condition of Eq. (15) on the core–mantle boundary and the conditions of Eq. (16) on the sides parallel to . At the surface of the domain we impose the Dirichlet constraint P=0. As in Sect. 3.1 we use a finite-element discretization employing an unstructured mesh of triangles employing a P2 function space. Pressure values vary from 0 to 180 GPa with a concentric distribution following the density distribution and the gravity vector orientation (Fig. 3b).
The numerical solution extracted at x=0 along a line parallel to the gravity vector field reproduces the analytical solution computed for a 1D profile using Eq. (2) for the density distribution displayed in the half-annulus model (Fig. 3c). The difference between the pressure obtained using the depth-integrated approach and the PPE is very small (Fig. 3d). Unlike the analytic solution for the box models, the analytic solution for P here is non-polynomial (in Cartesian coordinates); hence, the FE solution (which was discretized in Cartesian coordinates) cannot exactly reproduce the analytic solution.
The four hydrostatic models clearly illustrate that the solutions obtained using the depth-integrated approach and the pressure Poisson equation (with one set of boundary constraints) are equivalent for scenarios that admit a hydrostatic solution.
3.2 Non-hydrostatic pressure
Here, we show the differences and accuracy of the depth-integrated equation (Eq. 2) and the pressure Poisson equation (Eq. 7) approaches to approximate the total pressure. First, we compute and compare the pressure from the different methods in a large domain (referred to as the “global” model) containing a topographic perturbation (Fig. 4). Following this, we compute the pressure in a smaller domain (referred to as the “regional” model) and show the accuracy of the different methods to approximate the total pressure from the large domain (Figs. 5a, c and 6). Finally, we show the velocity field resulting from applying these approximated pressures as boundary conditions to solve the conservation of momentum in the small domain (Fig. 5b, d). The pressure Poisson problem was discretized and solved using the same FE method described in Sect. 3.1. The flow field was computed using the same underlying FE mesh and a mixed P2-P1 function space for velocity and pressure, respectively.
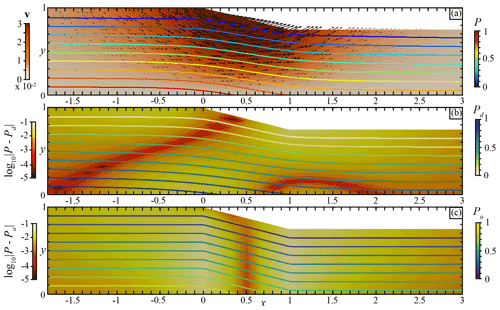
Figure 4Non-dimensional “global” model for a large domain with a topographic perturbation. (a) The background colour shows the velocity field computed with the Eq. (3). The coloured curves show the total pressure P iso-values every 0.1 computed with Eq. (3). (b) Comparison between the total pressure from Eq. (3) and the pressure Pd computed from Eq. (7). The coloured background shows the difference . The coloured curves show the pressure Pd iso-values every 0.1 computed with Eq. (7). (c) Comparison between the total pressure from Eq. (3) and the pressure Pa computed from Eq. (2). The coloured background shows the difference . The coloured curves show the pressure Pa iso-values every 0.1 computed with Eq. (2).
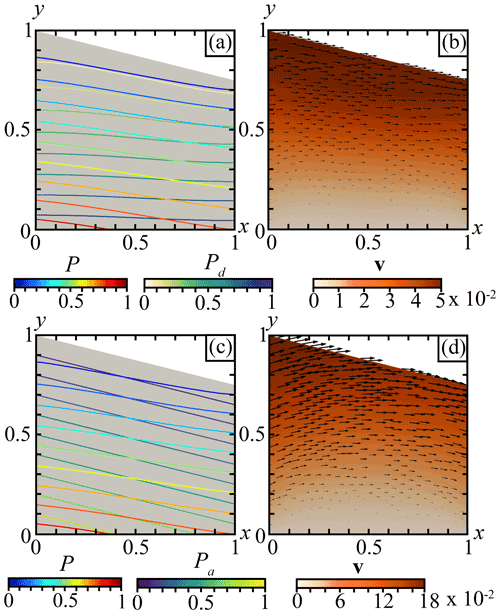
Figure 5Non-dimensional “regional” model for a small domain with a varying topography. (a) The coloured curves show the total pressure P iso-values computed with Eq. (3) in the global model every 0.1 and the pressure Pd computed with Eq. (7) in the regional model every 0.1. (b) The coloured background shows the velocity field computed with Eq. (3) with stress boundary conditions described by Eq. (33) using Pd computed with Eq. (7). The black arrows show the velocity vectors. (c) The coloured curves show the total pressure P iso-values computed with Eq. (3) in the global model every 0.1 and the pressure Pa computed with Eq. (2) in the regional model every 0.1. (d) The coloured background shows the velocity field computed with Eq. (3) with stress boundary conditions described by Eq. (33) using Pa computed with Eq. (2). The black arrows show the velocity vectors.
3.2.1 “Global” model
We define a large domain representing a global model, i.e. 20 times larger than the domain of interest, in order to avoid boundary condition influence (Fig. 4). In this domain, we introduce a topographic perturbation through a slope defined as , where ys is the surface between x=0 and x=1. For demonstration purposes this topography is highly exaggerated with respect to the depth of the domain compared with the actual regional geodynamic models. Moreover, we use a constant density ρ=1 and a vertical gravity vector .
We solve the flow problem described by Eqs. (3), (4) using a constant viscosity and density, along with the following boundary conditions: no-slip at base, free-slip on the right and left faces, and a free surface along the top of the model domain. Due to the topography, a non-vertical pressure gradient that will drive flow is generated below that perturbation (Fig. 4a). The generated flow shows a velocity field characteristic of a gravitational collapse. Figure 4b shows the difference between the total pressure solution from Eq. (3) with the pressure Pd obtained by solving Eq. (7) using the boundary conditions described by Eq. (16) on the vertical sides, Eq. (15) on the bottom boundary, and Pd=0 on the upper surface. Figure 4c shows the difference with the pressure Pa obtained with Eq. (2).
The difference between the total pressure and the approximated pressure Pd is negligible in the non-perturbed domain and increases with the topography perturbation. It shows that as the system tends towards a hydrostatic state the total pressure and the approximated pressure Pd tends to the same value, i.e. the hydrostatic pressure. However, in the vicinity of the topographic perturbation the differences between the total pressure and the approximated pressure can be extremely small (Fig. 4b). In contrast, the difference between the total pressure and depth-integrated approximated pressure Pa is larger below the topographic slope, particularly below the points at which the slope begins and ends (Fig. 4c). In general, the pressure Pa obtained by applying the 1D solution is less accurate than Pd within both the interior and along the left, right, and bottom boundaries.
3.2.2 “Regional” model
Nevertheless, modelling a domain 20 times larger than the domain of interest can hardly be achieved in practice, mainly due to the numerical cost it represents. Thus, the boundary conditions are a first-order component of regional models in order to best capture the global behaviour and interactions in a region without having to model the whole Earth. Therefore, we define a smaller domain representing a regional model (Fig. 5). This domain represents the portion of the large domain in which the topographic slope is defined.
In this case we aim to apply a normal stress on the boundaries of our regional model that will generate a flow similar (or close) to the flow generated in the global model. To achieve this we present two models using Eqs. (7) and (2), respectively, to compute an approximated pressure that is then used as a boundary condition for the momentum equation (Eq. 3) on vertical boundaries as follows:
where denote the pressure computed using the pressure Poisson equation and the 1D depth-integrated approach, respectively. The viscous flow problem for the regional domain setting employs the following additional boundary conditions: a free surface on the top boundary and a no-slip condition at the base. To solve for the pressure Pd using Eq. (7), we impose the following boundary conditions: Pd=0 on the surface, on vertical sides, and at the bottom.
Figure 5a shows the pressure field Pd computed on the regional domain and the total pressure P extracted from the global model. The approximated pressure Pd highlights differences with the total pressure from the global model, especially those regarding depth along the boundaries (blue lines in Fig. 6b, d). These differences are mainly due to the size of the domain that defines only the perturbed region without providing information about the domain in which it is enclosed. The boundary condition described by Eq. (16) used to solve Eq. (7) enforces the idea that the pressure gradient must be co-linear with the gravity vector on the boundary. Therefore, given the definition of g, ∇P is enforced to be vertical on the vertical sides, whereas the deflection of the pressure field due to the topographic perturbation should occur in spatial offset from the topographic perturbation, as shown by the total pressure in the global model (Fig. 4a).
In Fig. 5b we show the velocity field resulting from solving the Stokes equation (Eqs. 3, 4) using Pd in Eq. (33). The flow field highlights velocities of around (velocity unit) at the surface pointing toward the right side of the domain, i.e. the bottom of the slope. Velocities progressively decrease at depth. While the orientation of the velocity field is more laminar than in the global model, its magnitude is very close, with the highest velocities being only 1.5× higher than in the global model.
Figure 5c displays the pressure field Pa computed from the depth-integrated approach (Eq. 2) within the regional domain and the total pressure P extracted from the global model. Because of the 1D behaviour of that method, the differences between the approximated pressure Pa and the total pressure P (red lines in Figs. 5c and 6b, d) are independent of the domain size and boundary conditions, and thus they are exactly the same as in the global model (Fig. 4c). The velocity field (Fig. 5d) resulting from using these approximated pressure values as a boundary condition to solve the momentum equation is approximatively 4 times higher than velocities obtained while using the pressure Pd (Fig. 5b) and approximatively 6 times higher than in the global model (Fig. 4a). As for the velocity field orientation, the vectors at the top of the slope show that the material uplifts, whereas in the global model velocities at the same location show a gravitational sliding. This orientation results from a stress value that is too high being imposed in the boundary conditions by the value of the pressure Pa at the boundaries (Fig. 6).
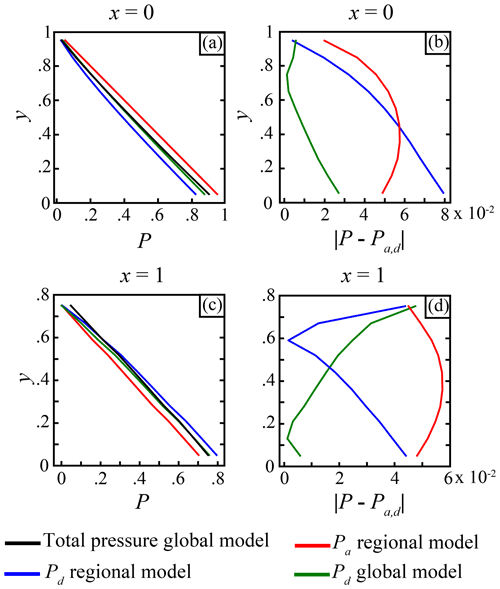
Figure 6Curves showing the pressure from the regional and global models along the profiles (a) x=0 and (c) x=1. Absolute value of the difference between the total pressure P in the global model and the different pressures in the global and regional models along the profiles (b) x=0 and (d) x=1.
These simple tests demonstrate that the approximated pressure Pd computed from the Eq. (7) is more accurate for approximating the total pressure P than the pressure Pa computed from the Eq. (2). The only area where this is not true is located in the bottom-left corner of the regional model, and this is again due to the boundary condition not capturing the deflection of the pressure due to the size of the domain. Thus, the pressure computed with the pressure Poisson problem should be preferred for use as a boundary condition for the momentum equation. Moreover, as the domain size increases the error with the total pressure decreases, which is not the case with the depth-integrated approach due to its 1D nature.
3.3 Influence of the boundary condition type
The boundary conditions used to solve the pressure Poisson problem are stated in Eqs. (15), (16), and (23). To show the influence of the boundary conditions choices on the resulting pressure field, we define an irregular quadrilateral domain with the same topographic perturbation as the one described in Sect. 3.2, with a constant density ρ=1, a gravity vector , and a Dirichlet boundary condition Pd=0 at the top surface (Γs). The irregular domain (shown in Fig. 7) is constructed such that none of the three boundary segments defining are parallel or perpendicular to g. The PPE was solved using the same FE method described in Sect. 3.1.
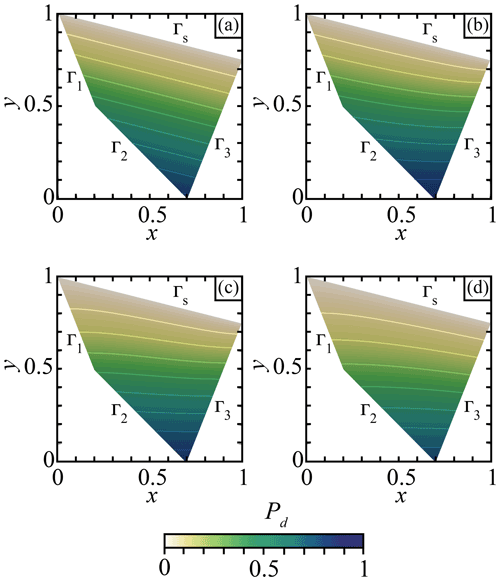
Figure 7Pressure field Pd computed using Eq. (7) for different boundary conditions applied to the individual boundary segments . The boundary conditions were defined according to (a) Eq. (15) on Γ1, Γ2, and Γ3; (b) Eq. (15) on Γ1 and Γ2 and Eq. (16) on Γ3; (c) Eq. (15) on Γ2 and Eq. (16) on Γ1 and Γ3; and (d) Eq. (15) on Γ3 and Eq. (16) on Γ1 and Γ2.
In Fig. 7 we show different pressure fields Pd obtained using several different boundary condition configurations. These results show that the boundary conditions described by Eq. (16) (or Eq. 20) force the pressure gradient to be parallel to g, i.e. (Fig. 7b segment Γ3, Fig. 7c segments Γ1,3, and Fig. 7d segments Γ1,2). We also confirm that boundary conditions described by Eq. (15) (or Eq. 19) constrain ∇Pd to be equivalent to the 1D solution of Eq. (2) on the boundary (Fig. 7a segments , Fig. 7b segments Γ1,2, Fig. 7c segment Γ2, and Fig. 7d segment Γ3). Figure 7a highlights that the solution of the PPE can be identical to that obtained using the depth-integrated approach with a specific choice of boundary conditions.
Moreover, Fig. 8a shows the pressure field Pd obtained using the boundary condition described by Eq. (23). The pressure solution is relatively similar to the solution obtained in Fig. 7c. However, as shown in Fig. 8b, the solution along the boundary (and therefore also in the interior) differs since Eq. (23) does not enforce the pressure gradient to be vertical on the boundary compared with the condition (16).
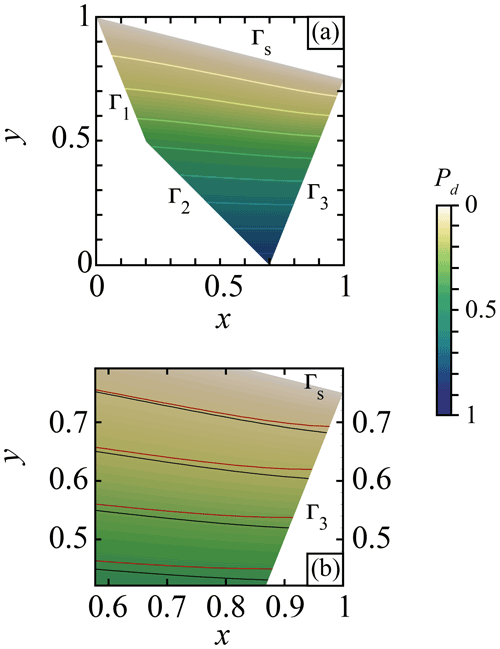
Figure 8Pressure field Pd computed using Eq. (7) with the boundary conditions described by Eq. (23) for (a) Pd over the entire model with boundary conditions defined by Eq. (23) applied on Γ1, Γ2, and Γ3. (b) Closer view of the right-hand boundary region. The black curves show the iso-values of the pressure computed with boundary conditions using Eq. (23). The red curves show the iso-values of the pressure computed using the boundary conditions used in Fig. 7c.
As previously noted, discretizations employing the weak form with Eq. (23) are certainly simpler to implement than imposing the Eqs. (19) and (20) as all the surface integrals cancel (see Eq. 28), and thus no surface integrals appear in either the linear form or bilinear form. We also reiterate that when the domain has boundaries that are aligned with g, using the boundary conditions (15) on the boundaries orthogonal to g and the condition (16) on the boundaries that are parallel to g results in an identical formulation.
3.4 Thermo-mechanical model
3.4.1 Physical model
To simulate the long-term evolution of the deformation of the lithosphere, we solve the stationary, non-inertial form of the conservation of momentum described by Eq. (3) with the incompressible constraint (Eq. 4). Moreover, to consider the temperature variations in the domain, the following time-dependent conservation of energy is solved:
where T is the temperature, t is the time, k is the thermal conductivity, H is the heat source, ρ0 is the reference density, and Cp the thermal heat capacity.
The numerical solution of Eqs. (3) and (4) is obtained using a mixed finite-element method that independently discretizes the velocity and pressure fields. Hence, the numerical velocity and pressure obtained are solutions of the weak form of the Stokes problem given by
where w∈H1(Ω) and q∈L2(Ω) are test functions for the velocity and pressure, respectively, ΓN denotes the Neumann boundary, T denotes the traction vector given by , and is the outward pointing normal vector from the boundary. The bilinear forms for the Stokes problem are given by (Elman et al., 2014):
Both the Stokes and thermal problems were solved using the parallel finite-element code pTatin3D (May et al., 2014, 2015),
which employs a mixed Q2-P1 discretization for velocity and pressure.
3.4.2 Initial conditions and rheology
To model the strain localization we use non-linear visco-plastic rheologies expressed in term of viscosity. The ductile parts of the domain are simulated using an Arrhenius flow law for dislocation creep
where A, Q, and n are material-defined parameters (see Table 1); R is the universal gas constant; V is the activation volume; and is the square root of the strain rate second invariant, computed as
The brittle parts of the domain are simulated using a Drucker–Prager yield criterion adapted to continuum mechanics, which is given by
where C is the cohesion of the material and ϕ is the friction angle.
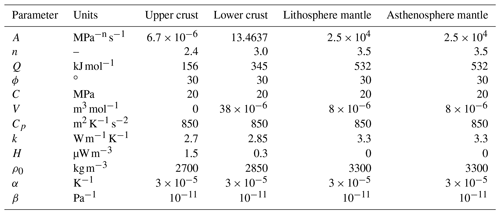
The modelled domain contains four initial flat layers representing the upper continental crust, the lower continental crust, the lithosphere mantle, and the asthenosphere mantle, respectively (Fig. 9a). The upper crust extends from the surface of the domain (y=0 km) to km and is modelled with a dislocation creep quartz rheology (Ranalli, 1997). The lower crust extends from km to km and is modelled with a dislocation creep anorthite rheology (Rybacki and Dresen, 2000). The lithosphere mantle extends from km to km, whereas the asthenosphere mantle extends from km to km. They are both modelled using a dislocation creep olivine flow law (Hirth and Kohlstedt, 2003).
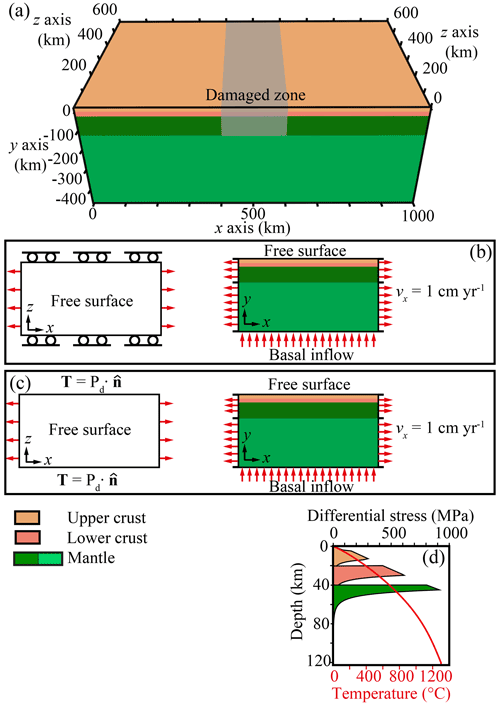
Figure 9(a) A 3D view of the modelled domain. An initial plastic strain with a Gaussian repartition is applied in the central part of the domain in the lithosphere. (b) Map and cross section of the boundary conditions for the model with free-slip boundary conditions. (c) Map and cross section of the boundary conditions for the model with normal stress boundary conditions. (d) Yield–stress envelope and initial temperature of the first 120 km.
The initial density distribution follows the lithologies and is reported in Table 1. In addition, the density varies with pressure and temperature following the Boussinesq approximation
where ρ0 is the reference density at T0 and P0, P is the total pressure computed from the conservation of momentum (Eq. 3) and continuity equation (Eq. 4), α is the thermal expansion and β the compressibility. The Boussinesq approximation states that perturbations of density, if sufficiently small, can only be considered in the buoyancy term and neglected elsewhere regardless of the origin of the perturbation.
Moreover, the initial temperature field is computed as a steady-state solution of the heat equation
using a surface temperature of T=0 ∘C at y=0 km and T=1450 ∘C at km. Moreover, to simulate an adiabatic thermal gradient in the asthenosphere due to thermal convection, the initial temperature field is solved with a conductivity of k=70 W m−1 K−1 in the asthenospheric mantle. However, for the actual model run we used a more realistic conductivity of k=3.3 W m−1 K−1 to solve Eq. (34). Other thermal parameters are reported in Table 1.
3.4.3 Boundary conditions
To show the influence of the normal stress boundary condition, we compare two rift models. In the reference model, an extension velocity of vx=1 cm yr−1 is applied on the whole faces of normal x, whereas on faces of normal z a free-slip boundary condition is applied (Fig. 9c). To ensure mass conservation we impose an inflow velocity on the bottom face of normal y to balance any outflow that occurs due to the imposed extension. Along the surface of the model we use a free surface (zero normal stress, zero tangential stress) boundary condition.
The second rift model (Fig. 9b) uses the same Dirichlet boundary conditions on faces of normal x. On the faces of normal z we impose a Neumann boundary condition as
where Pd is the pressure computed with Eq. (7) and is the normal vector pointing outward from the domain.
To account for the density evolution through time due to the deformation and material advection, Eq. (7) is solved at every non-linear iteration for each time step, and the Neumann boundary condition described by Eq. (40) is evaluated at every non-linear iteration. Using ρ(P,T) computed from Eq. (38) to evaluate the pressure Pd going into the boundary condition described by Eq. (40) adds a new non-linearity to the system.
The bottom of the domain is prescribed as an inflow condition balancing the outflow, and the surface of the domain is a free surface where the mesh deforms according to the computed velocity field. These Neumann boundary conditions allow material to flow both in and out through the boundary depending only on the Dirichlet boundary conditions and deformation that occurs inside the modelled domain.
3.4.4 Pressure Poisson problem in the 3D geodynamic model
In the context of our finite-element forward model, we also solve the pressure Poisson problem using finite elements. As such, to compute Pd we employ the weak formulation given by Eq. (27) using boundary conditions from Eqs. (15) and (16) on bottom boundary and vertical boundaries, respectively. In our particular implementation, we employ Q1 for Pd, and these Q1 elements overlap the Q2 elements used to approximate the velocity.
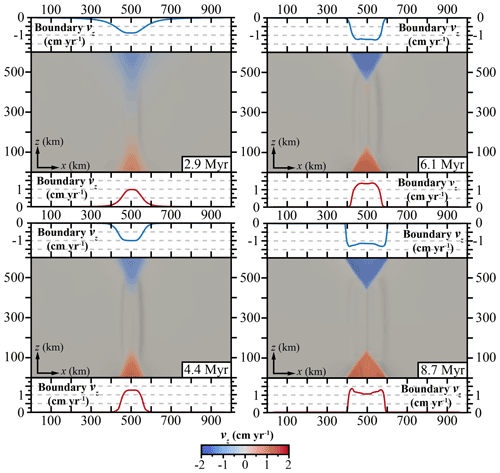
As a demonstration of the computed Pd using this approach, in Fig. 10c and d we show the approximated pressure in our rift model at 8.7 Myr after large deformations that led to mantle exhumation and differential thinning of the continental crust, causing a variable topography. In this model, Pd was evaluated on a mesh consisting of finite elements on 1024 MPI ranks. The discrete pressure Poisson system was solved using geometric multigrid. As a rough estimate, solving for Pd required ∼0.2 % of the time required to solve the non-linear viscous flow problem. Obviously this value is strongly dependent on both the physical model (linear viscous versus non-linear viscous) and the implementation details, as well as the efficiency of how the discrete flow problem is solved. However, when considering even the simplest flow problem imaginable (i.e. linear iso-viscous flow laws), it remains true that solving the Poisson problem will be far less expensive than solving either the linear or non-linear viscous flow problem.
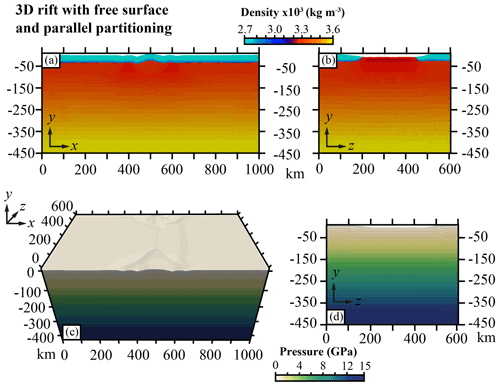
Figure 10(a) Cross section showing the density of the 3D rift model with normal stress boundary conditions in the x–y plane at z=0. (b) Cross section showing the density of the z–y plane at x=500 km. (c) 3D view of the pressure computed with Eq. (7). (d) Cross section of the z–y plane at x=500 km for the reference pressure. The contour lines are plotted every 0.25 GPa.
3.4.5 Tectonics evolution
The model using free-slip boundary conditions displays a cylindrical deformation pattern that could be reduced to a two-dimensional model. As shown by the shear zone orientation and strain regime, the deformation is only extensional and perpendicular to the extension direction (Figs. 11a–d and 12). This strain localization is directly due to the free-slip boundary condition stating that any flow perpendicular to the boundary is prohibited.
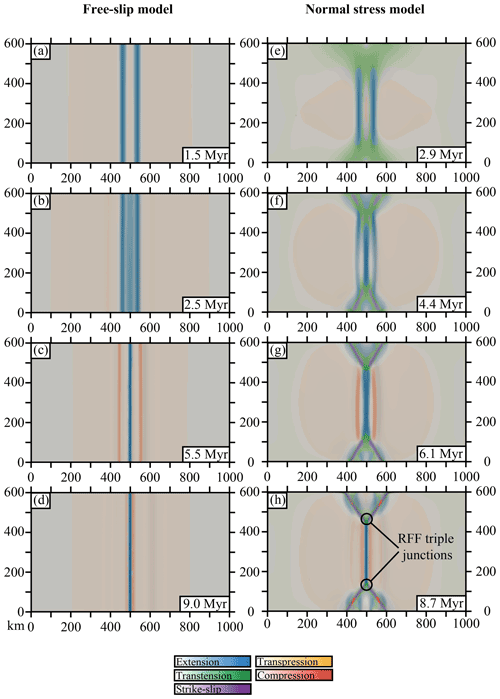
Figure 11Map view of the strain regime evolution in time and space of the model with (a–d) free-slip boundary conditions and (e–h) normal stress boundary conditions.
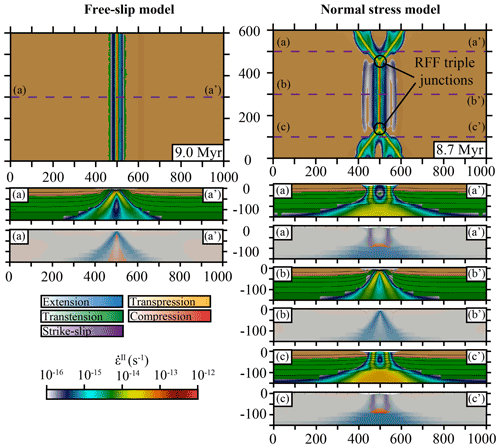
Figure 12Map view of the models with free-slip (left) and normal stress (right) boundary conditions. The dashed lines in the upper panels indicated by (a–a′, b–b′, c–c′) correspond to the cross sections displayed in the lower panels with the same labelling. The cross sections show the numerical lithologies with the second invariant of the strain rate (Eq. 36) and the strain regime.
In contrast, the model using the Pd pressure as a boundary condition displays a non-cylindrical deformation. While extensional shear zones perpendicular to the extension direction develop in the central part of the domain, the edges of the rift experience oblique and strike-slip deformation (Fig. 11e to h). As the extension goes on, the extensional deformation localizes along a spreading centre, causing an increasing inflow on the boundaries of the domain with the normal stress boundary condition (Fig. 13c). As a result, near these boundaries the velocity field introduces non-cylindrical features that are accommodated by strike-slip faults (Fig. 11g, h). These strike-slip faults delimit a triangular region terminating on a triple junction between two strike-slip faults and a ridge (ridge–fault–fault, RFF, triple junction). Along these strike-slip faults, the deformation is partitioned between purely vertical strike-slip shear zones and shallow-dipping normal shear zones rooting into the strike-slip shear zones (Fig. 12).
4.1 Alternative PDE-based approaches
Recall that the starting point of defining the PPE was purely algebraic, with the sole intention of removing the non-uniqueness associated with Eq. (5). Here we discuss two alternative PDE-based approaches constructed with a similar rationale.
Rather than enforcing Eq. (15) only along the boundary, suppose we wished to enforce it everywhere throughout the domain,
This constraint can be interpreted as the steady-state solution of the following scalar hyperbolic PDE:
where τ plays the role of a time-like parameter having units of length and plays the role of a velocity-like quantity. Along the “inflow segments” we will impose P=01. On the outflow segments Γout = ∂Ω \ Γin; due to the hyperbolic nature of the PDE, no boundary constraint are required. Since we seek the steady-state solution of Eq. (42), no initial condition is required, but for completeness we chose . Hence, the solution of Eq. (42) is equivalent to solving
along the family of characteristics given by
with and .
Compared to the PPE, the hyperbolic formulation has several disadvantages.
-
We have less freedom to specify how ∇P varies along the boundary. The choice of boundary conditions (BCs) is largely dictated by the “inflow” and “outflow” segments. Along outflow segments, the only constraint available is Eq. (41) evaluated on ∂Ω. If inflow occurs on any part of ∂Ω not contained in ∂Ωsurf, we have to choose a flux BC, as using P=0 does not make physical sense. Consistency may require the use of a constraint that is independent of the PDE, e.g. Eq. (16).
-
The formulation may place restrictions on the shape of ∂Ω. If we wish to avoid the definition of new flux BCs (described above), the domain must be defined such that for every there exists a characteristic that intersects both xb and ∂Ωsurf.
-
The lack of flexibility in controlling the boundary behaviour of ∇P will in general result in solutions of Eq. (42) being identical to a family of 1D solutions to Eq. (2) applied in directions parallel to the direction of gravity; see Fig. 14b, d.
-
The spatial discretization required for the accurate solution of Eq. (42) is arguably more complicated to implement (on unstructured meshes) compared with discretizations for the Poisson equation. Scalable multi-level solvers for the steady-state hyperbolic problem are much more challenging to develop in comparison to the Poisson problem.
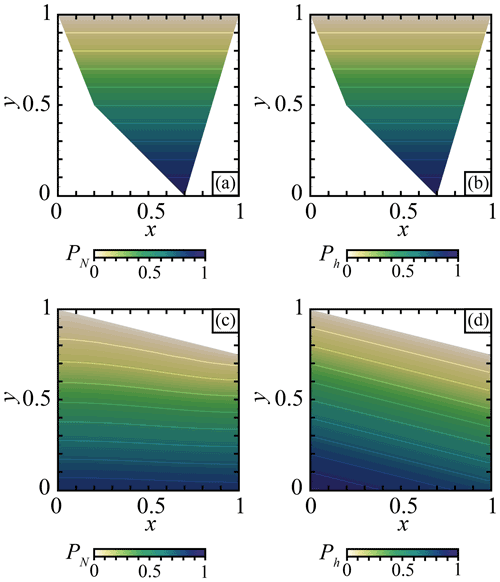
Figure 14Pressure in non-dimensional models with constant density ρ=1. Pressure computed for a hydrostatic case in an irregularly shaped domain using (a) the normal equations (Eq. 45) and (b) the hyperbolic equation (Eq. 42). Pressure computed for a non-hydrostatic case due to topography using (c) the normal equation (Eq. 45) and (d) the hyperbolic equation (Eq. 42). The contour lines show contours of iso-pressure values every 0.1.
From a linear algebra perspective, the non-uniqueness of Eq. (5) can alternatively be addressed by (i) discretizing Eq. (5) in space, yielding Gp=F, and then (ii) solving the normal equations
This approach obtains a unique solution that minimizes the following objective function:
In some senses, this approach is like the discrete counterpart of the PPE, in so much as GTG are the discrete Laplacian defined on the approximation space used to represent pressure. The similarity between the pressure solution from the PPE and are shown in Fig. 14a, c. Similar to the hyperbolic formulation, obtaining the pressure via the normal equations is restrictive from a modelling perspective as the formulation does not allow for control of the behaviour of ∇P on the boundary, and as such only the Dirichlet data on ∂Ωsurf can be specified. In Fig. 14a, c we provide snapshots of the pressure obtained from solving Eq. (45) in two different domains. Interestingly, the solutions indicate that appears to be approximately zero along the boundary despite the lack of a constraint enforcing this.
4.2 Flexibility of the PPE with respect to boundary conditions
Since the PPE is a second-order PDE, the formulation permits a range of possible boundary constraints on ∇P to be imposed. Specific choices allow one to define whether (i) the equivalent of 1D pressure profiles as would be obtained by applying Eq. (2) along a boundary face or (ii) an approximation of the pressure field on the boundary would be obtained if a complete flow field was computed in a much larger global domain.
Experiments showed that the PPE approach better approximates the total pressure computed from the momentum equation. Therefore, its use as a boundary condition (or as an initial guess) for the pressure field to solve the momentum equation is preferred over hydrostatic solutions associated with Eq. (2). Moreover, as the domain size increases, the PPE formulation gives a more accurate approximation of the total pressure than the 1D depth-integrated approach.
4.3 Implications for lithosphere deformation
In the geodynamic rift model, using the pressure computed with Eq. (7) as a boundary condition produces a velocity field perpendicular to the extension direction in the rift axis (Fig. 13). This velocity field introduces non-cylindrical deformation accommodated for by oblique and strike-slip structures (Fig. 11). The results of this study are very similar to previous studies directly applying an inflow perpendicular to the extension direction (Le Pourhiet et al., 2018; Jourdon et al., 2020). At the tip of the rift, a triangular region delimited by strike-slip faults or very oblique rift develops to accommodate the oblique velocity field. The similarity of these results shows that using open boundary conditions instead of kinematic boundary conditions in 3D may reveal first-order implications for the lithosphere strain localization. In the case of geodynamic systems presenting the characteristics of a propagating rift (or ridge) with oblique and strike-slip deformation at its tip, considering the forces applied by the surrounding material weight could be the first-order process at the origin of non-cylindrical deformation.
4.4 Linear and non-linear density
Two approaches can be considered to compute the pressure using Eq. (7). The first approach (also the simplest) is to consider that the density ρ is defined as a reference density ρ0 that only depends on rock type for a reference state, e.g. T0 and P0. In that case, Eq. (7) is linear and only depends on the reference density structure. The second approach is to consider that the density ρ can vary with respect to other parameters. In our geodynamic example, we considered that the density can vary with pressure and temperature according to Eq. (38). In that case the Eq. (7) becomes non-linear. This kind of non-linearity is not rare in geodynamics, and the formulation of Eq. (38) may appear in the pressure computation when solving for an incompressible Boussinesq approximation or a compressible Stokes problem (e.g. Dannberg and Heister, 2016; King et al., 2010; Tackley, 2008).
In this study we presented a method to compute a reference pressure associated with the density structure of a domain in which we cast the problem in terms of a partial differential equation (PDE). From a practical standpoint, the PDE approach is generic (it is applicable to all spatial discretization and on any type of computational grid), efficient, and applicable in parallel computing environments. From the modelling perspective, the PDE approach has specific advantages, for example in models with a variable density structure (stationary or time-dependent) and models that employ a reference pressure as a boundary condition of the flow problem (stationary or time-dependent problems). Re-evaluating that pressure in time-dependent problems is not problematic (even if the mesh deforms) since solving the Poisson problem can be performed using optimal preconditioners (e.g. geometric or algebraic multigrid preconditioners). Importantly, the time to solve the pressure Poisson problem is a small fraction of the time required to solve the linear (or non-linear) incompressible viscous flow problem. Moreover, we also demonstrate that the PDE formulation results in a better approximation of the total pressure than the 1D depth-integrated approach in non-hydrostatic cases.
Lastly, we showed in the context of 3D geodynamic models of continental rifting that using a reference pressure as a boundary condition within the flow problem resulted in non-cylindrical velocity fields. These 3D velocity fields produced strain localization in the lithosphere along large-scale strike-slip shear zones and the formation and evolution of triple junctions.
The code pTatin3D used in this study to produce the 3D thermo-mechanical models is an open-source free software licensed under GPL3. The Supplement contains the version of the code used to produce the models presented in this study. To run the same models, users should use the driver named test_driver_checkpoint_fv.app and the options files (.opts) provided in the Supplement.
We also provide Firedrake code (Firedrake team, 2022; Balay et al., 2019, 1997; Dalcin et al., 2011; Rathgeber et al., 2016) to compute the pressure Poisson problem in a half-annulus domain, in a deformed domain, and in the large and small domains with a topography perturbation used in this study. The version of Firedrake used is 0.13.0+4944.g22178416 and is freely available.
We also provide FEniCS code (FEniCS team, 2022; Alnaes et al., 2015; Logg et al., 2012b; Logg and Wells, 2010; Logg et al., 2012a) to reproduce the models solving for the normal and hyperbolic equations. The version of FEniCS used is 2016.1.0 and is freely available.
The supplement related to this article is available online at: https://doi.org/10.5194/se-13-1107-2022-supplement.
AJ and DAM conceptualized the project and made the mathematical and software development. AJ and DAM conceived, designed, and performed the experiments. AJ analysed the results. AJ and DAM drafted and corrected the manuscript. DAM procured funding and supervised the project.
The contact author has declared that neither they nor their co-author has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (https://www.gauss-centre.eu, last access: 27 June 2022) for providing computing time on the GCS Supercomputer SuperMUC-NG at the Leibniz Supercomputing Centre (https://www.lrz.de, last access: 27 June 2022) through project pr63qo. The authors also thank Cedric Thieulot and Rene Gassmoeller for their constructive reviews.
This project was supported by NSF Award EAR-2121666. Anthony Jourdon has been supported by the European Union's Horizon 2020 research and innovation programme (TEAR ERC Starting, grant no. 852992).
This paper was edited by Taras Gerya and reviewed by Rene Gassmoeller and Cedric Thieulot.
Alnaes, M. S., Blechta, J., Hake, J., Johansson, A., Kehlet, B., Logg, A., Richardson, C., Ring, J., Rognes, M. E., and Wells, G. N.: The FEniCS Project Version 1.5, Archive of Numerical Software, 3, 9–23, https://doi.org/10.11588/ans.2015.100.20553, 2015. a
Baes, M., Sobolev, S. V., and Quinteros, J.: Subduction initiation in mid-ocean induced by mantle suction flow, Geophys. J. Int., 215, 1515–1522, https://doi.org/10.1093/gji/ggy335, 2018. a
Balay, S., Gropp, W. D., McInnes, L. C., and Smith, B. F.: Efficient Management of Parallelism in Object Oriented Numerical Software Libraries, in: Modern Software Tools in Scientific Computing, edited by: Arge, E., Bruaset, A. M., and Langtangen, H. P., 163–202, Birkhäuser Press, https://doi.org/10.1007/978-1-4612-1986-6_8, 1997. a
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Dalcin, L., Eijkhout, V., Gropp, W. D., Karpeyev, D., Kaushik, D., Knepley, M. G., May, D. A., McInnes, L. C., Mills, R. T., Munson, T., Rupp, K., Sanan, P., Smith, B. F., Zampini, S., Zhang, H., and Zhang, H.: PETSc Users Manual, Tech. Rep. ANL-95/11 – Revision 3.11, Argonne National Laboratory, 2019. a
Barth, W. L. and Carey, G. F.: On a boundary condition for pressure-driven laminar flow of incompressible fluids, Int. J. Numer. Meth. Fl., 54, 1313–1325, 2007. a
Brune, S.: Evolution of stress and fault patterns in oblique rift systems: 3-D numerical lithospheric-scale experiments from rift to breakup, Geochem. Geophy. Geosy., 15, 3392–3415, https://doi.org/10.1002/2014GC005446, 2014. a
Brune, S., Popov, A. A., and Sobolev, S. V.: Modeling suggests that oblique extension facilitates rifting and continental break-up, J. Geophys. Res., 117, 1–16, https://doi.org/10.1029/2011JB008860, 2012. a
Brune, S., Heine, C., Pérez-Gussinyé, M., and Sobolev, S. V.: Rift migration explains continental margin asymmetry and crustal hyper-extension, Nat. Commun., 5, 1–9, https://doi.org/10.1038/ncomms5014, 2014. a
Brune, S., Heine, C., Clift, P. D., and Pérez-Gussinyé, M.: Rifted margin architecture and crustal rheology: Reviewing Iberia-Newfoundland, Central South Atlantic, and South China Sea, Mar. Petrol. Geol., 79, 257–281, https://doi.org/10.1016/j.marpetgeo.2016.10.018, 2017. a
Chertova, M. V., Geenen, T., van den Berg, A., and Spakman, W.: Using open sidewalls for modelling self-consistent lithosphere subduction dynamics, Solid Earth, 3, 313–326, https://doi.org/10.5194/se-3-313-2012, 2012. a
Chertova, M. V., Spakman, W., Geenen, T., Van Den Berg, A., and van Hinsbergen, D. J. J.: Underpinning tectonic reconstructions of the western Mediterranean region with dynamic slab evolution from 3-D numerical modeling, J. Geophys. Res.-Sol. Ea., 119, 5876–5902, https://doi.org/10.1002/2014JB011150, 2014. a
Dalcin, L. D., Paz, R. R., Kler, P. A., and Cosimo, A.: Parallel distributed computing using Python, new Computational Methods and Software Tools, Adv. Water Resour., 34, 1124–1139, https://doi.org/10.1016/j.advwatres.2011.04.013, 2011. a
Dannberg, J. and Heister, T.: Compressible magma/mantle dynamics: 3D, adaptive simulations in ASPECT, Geophys. J. Int., 207, 1343–1366, https://doi.org/10.1093/gji/ggw329, 2016. a
Elman, H. C., Silvester, D. J., and Wathen, A. J.: Finite elements and fast iterative solvers: with applications in incompressible fluid dynamics, Numer. Math. Sci. Comp., Oxford Scholarship Online, https://doi.org/10.1093/acprof:oso/9780199678792.001.0001, 2014. a
FEniCS team: FEniCS, https://fenicsproject.org/download/, last access: 27 June 2022. a
Firedrake team: Firedrake, https://www.firedrakeproject.org/download.html, last access: 27 June 2022. a
Glerum, A., Thieulot, C., Fraters, M., Blom, C., and Spakman, W.: Nonlinear viscoplasticity in ASPECT: benchmarking and applications to subduction, Solid Earth, 9, 267–294, https://doi.org/10.5194/se-9-267-2018, 2018. a
Hirth, G. and Kohlstedt, D. L.: Rheology of the Upper Mantle and the Mantle Wedge: A View from the Experimentalists, Geophys. Monogr., 138, 83–105, 2003. a
Ismail-Zadeh, A., Honda, S., and Tsepelev, I.: Linking mantle upwelling with the lithosphere decent and the Japan Sea evolution: A hypothesis, Sci. Rep.-UK, 3, 1–7, https://doi.org/10.1038/srep01137, 2013. a
Jourdon, A., Le Pourhiet, L., Mouthereau, F., and May, D.: Modes of Propagation of Continental Breakup and Associated Oblique Rift Structures, J. Geophys. Res.-Sol. Ea., 125, 1–27, https://doi.org/10.1029/2020JB019906, 2020. a
King, S. D., Lee, C., Van Keken, P. E., Leng, W., Zhong, S., Tan, E., Tosi, N., and Kameyama, M. C.: A community benchmark for 2-D Cartesian compressible convection in the Earth's mantle, Geophys. J. Int., 180, 73–87, https://doi.org/10.1111/j.1365-246X.2009.04413.x, 2010. a
Le Pourhiet, L., Chamot-Rooke, N., Delescluse, M., May, D. A., Watremez, L., and Pubellier, M.: Continental break-up of the South China Sea stalled by far-field compression, Nat. Geosci., 11, 605–609 https://doi.org/10.1038/s41561-018-0178-5, 2018. a
Logg, A. and Wells, G. N.: DOLFIN: Automated Finite Element Computing, ACM T. Math. Software, 37, 1–8, https://doi.org/10.1145/1731022.1731030, 2010. a
Logg, A., Mardal, K., and Wells, G. N. (Eds.): Automated Solution of Differential Equations by the Finite Element Method, Springer, https://doi.org/10.1007/978-3-642-23099-8, 2012a. a
Logg, A., Wells, G. N., and Hake, J.: DOLFIN: a C++/Python Finite Element Library, in: Automated Solution of Differential Equations by the Finite Element Method, edited by: Logg, A., Mardal, K., and Wells, G. N., Vol. 84 of Lecture Notes in Computational Science and Engineering, chap. 10, Springer, https://doi.org/10.1007/978-3-642-23099-8, 2012b. a
May, D. A., Brown, J., and Le Pourhiet, L.: pTatin3D : High-Performance Methods for Long-Term Lithospheric Dynamics, Proceeding SC′14 Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, IEEE (Institute of Electrical and Electronics Engineers, 274–284, https://doi.org/10.1109/SC.2014.28, 2014. a
May, D. A., Brown, J., and Le Pourhiet, L.: A scalable, matrix-free multigrid preconditioner for finite element discretizations of heterogeneous Stokes flow, Comput. Method. Appl. M., 290, 496–523, https://doi.org/10.1016/j.cma.2015.03.014, 2015. a
Popov, A. A. and Sobolev, S. V.: SLIM3D: A tool for three-dimensional thermomechanical modeling of lithospheric deformation with elasto-visco-plastic rheology, Phys. Earth Planet. In., 171, 55–75, https://doi.org/10.1016/j.pepi.2008.03.007, 2008. a
Quinteros, J., Sobolev, S. V., and Popov, A. A.: Viscosity in transition zone and lower mantle: Implications for slab penetration, Geophys. Res. Lett., 37, L09307, https://doi.org/10.1029/2010gl043140, 2010. a
Ranalli, G.: Rheology of the lithosphere in space and time, Geol. Soc. Lond. Spec. Publ., 121, 19–37, https://doi.org/10.1144/GSL.SP.1997.121.01.02, 1997. a
Rathgeber, F., Ham, D. A., Mitchell, L., Lange, M., Luporini, F., McRae, A. T. T., Bercea, G.-T., Markall, G. R., and Kelly, P. H. J.: Firedrake: automating the finite element method by composing abstractions, ACM T. Math. Softw., 43, 24:1–24:27, https://doi.org/10.1145/2998441, 2016. a
Rybacki, E. and Dresen, G.: Dislocation and diffusion creep of synthetic anorthite aggregates, J. Geophys. Res.-Sol. Ea., 105, 26017–26036, https://doi.org/10.1029/2000JB900223, 2000. a
Tackley, P. J.: Modelling compressible mantle convection with large viscosity contrasts in a three-dimensional spherical shell using the yin-yang grid, Phys. Earth Planet. In., 171, 7–18, https://doi.org/10.1016/j.pepi.2008.08.005, 2008. a
Yamato, P., Burov, E., Agard, P., Le Pourhiet, L., and Jolivet, L.: HP-UHP exhumation during slow continental subduction: Self-consistent thermodynamically and thermomechanically coupled model with application to the Western Alps, Earth Planet. Sc. Lett., 271, 63–74, https://doi.org/10.1016/j.epsl.2008.03.049, 2008. a