the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of continental lithospheric thermal structure in the evolution of orogenic systems: application to the Himalayan–Tibetan collision zone
Mengxue Liu
Dinghui Yang
Rui Qi
Continental collision is a crucial process in plate tectonics. However, in terms of the evolution and the controlling parameters of its lateral heterogeneity, our understanding of the tectonic complexities at such a convergent plate boundary remains largely unclear. In this study, we conducted a series of two-dimensional numerical experiments to investigate how continental lithospheric thermal structure influences the development of lateral heterogeneity along the continental collision zone. The following two end-members were achieved. First, continuous subduction mode, which prevails when the model has a cold procontinental Moho temperature (≤450 ∘C). In this case, a narrow collision orogen develops, and the subducting angle steepens with the increasing retrocontinental Moho temperature. Second, continental subduction with a slab break-off, which generates a relative wide collision orogen and dominates when the model has a relatively hot procontinental Moho temperature (≥500 ∘C), especially when the Moho temperature ≥ 550 ∘C. Radioactive heat production is the second-order controlling parameter in varying the continental collision mode, while it prefers to enhance strain localization in the upper part of the continental lithosphere and promote the growth of shear zones there. By comparing the model results with geological observations, we suggest that the discrepant evolutionary paths from the continuous subduction underlying the Hindu Kush to the continental subduction after slab break-off beneath eastern Tibet may originate from the inherited lateral inhomogeneity of the Indian lithospheric thermal structure. Besides, the high content of crustal radioactive elements may be one of the most important factors that controls the formation of large thrust fault zones in the Himalayas.
- Article
(8706 KB) - Full-text XML
-
Supplement
(2289 KB) - BibTeX
- EndNote
The collision between the Indian and Asian continents, following the closure of the Neo-Tethys Ocean, is regarded as one of the key geodynamical processes of plate tectonics (Toussaint et al., 2004), which creates the world's largest orogen (the Alpine–Himalaya orogen) and highest plateau (the Tibetan Plateau). It would be really hard to maintain a homogeneous plate morphology and the crustal–mantle deformation features during such a large-scale collision stretching thousands of kilometers. Many of the previous observations have already provided insights into the significant lateral heterogeneity of Himalayan–Tibetan orogen (Zhou and Murphy, 2005; Li et al., 2008; Chen et al., 2015). Specifically, the horizontal underthrusting distance of the Indian lithosphere decreases, and the subducting angle increases laterally from west to east. Despite various mechanisms that have been invoked, including the geometry of the subducting plate (Nettesheim et al., 2018; Koptev et al., 2019), inhomogeneous inherit lithospheric structure, variations in rock composition, characters of terrane assembly, and the complex tectonic settings (Beaumont et al., 1994; Chen et al., 2016, 2019; Vogt et al., 2018; Liu and Yang, 2022), the development of the collision zone's lateral heterogeneity remains ambiguous and requires further investigation.
Many of the laboratory (Willingshofer and Sokoutis, 2009; Luth et al., 2010) and numerical modeling experiments (Beaumont et al., 1994; Pysklywec, 2001; Toussaint et al., 2004; Huangfu et al., 2017; Liao and Gerya, 2017; Vogt et al., 2018; S. Liu et al., 2022) have suggested that the lithospheric thermal structure is one of the important controlling parameters contributing to the regulation the evolution of continental collision (Pysklywec, 2001; Faccenda et al., 2008; Ueda et al., 2012; Tang et al., 2020; M. Liu et al., 2022). Pysklywec (2001) once used a series of thermomechanical models that focused on the evolutionary modes of the continental lithospheric mantle during collision. The experiments suggested that an increase in the lithospheric geotherm resulted in a transition of the lithospheric mantle from an asymmetric, subduction-like mode to ablative subduction. Similarly, on the basis of two-dimensional mechanical models, Toussaint et al. (2004) investigated the potential scenarios for the evolution of continental collision. They concluded that models with a relatively low (<550 ∘C) Moho temperature and a fast convergence rate (>5 cm yr−1) are more likely to maintain stable subduction. On the contrary, among warmer and slower convergent models, lithospheric folding, pure-shear thickening, and Rayleigh–Taylor (RT) instabilities prevailed. Ghazian and Buiter (2013) used 2D numerical models to discuss the sensitivity of various collision modes to velocity, crust–mantle temperature structure, lithospheric rheology, and the density difference between the lithospheric mantle and asthenosphere. They recognized that velocity, lithospheric rheology, and temperature have important controls. More precisely, stable continental subduction evolves over a large range of values for convergent velocity and lithospheric temperature. Fast and cold models tend to fold, while slow and warm ones can generate RT-type dripping. Heron and Pysklywec (2016) subsequently presented dynamic thermomechanical experiments to explore the role of lithospheric inherited weakness in the orogenic process. According to their model results, lithospheric temperature exerts a strong control on lithospheric strength; it may influence the brittle–ductile transition depth to help determine which layer (upper crust, lower crust, or lithospheric mantle) dominantly controls the lithospheric deformation style in a collision system. Recently, Huangfu et al. (2019) employed systematic numerical simulations to study the dynamics of the lithospheric-scale subduction and crustal-scale underthrusting of the continental collision zone. They found that models with low convergence velocity and a cold upper plate are inclined to lithospheric-scale subduction, whereas models with high velocity and a hot overriding plate contribute to crustal-scale underthrusting. Though numerous numerical simulations are employed to qualify the effects of lithospheric thermal structure, it is noteworthy, however, that earlier studies consistently and mainly focused on the influences of the overriding lithospheric thermal structure. A fairly large number of them neglected oceanic subduction prior to the continental collision for simplicity. Thus, our understanding of tectonic complexities that may emerge during progressive crust–mantle deformation at the convergent plate boundary remains largely unclear.
Here we present a series of high-resolution numerical experiments to gain new insights to how continental lithospheric thermal structure influences the evolutionary path of the continental collision system. Temperature heterogeneities are incorporated by altering the continental Moho temperature (Tmoho) and crustal radioactive heat production (Hr), respectively. In the end, the results of our models are used to draw comparisons with some first-order characters of the Indian–Asian collision zone.
2.1 Governing equation
We use the parallel code Advanced Solver for Problems in Earth's ConvecTion (ASPECT; Kronbichler et al., 2012), an extensible code of the C program library deal.ii (Differential Equations Analysis Library; https://www.dealii.org/, last access: 24 June 2023), which is targeted at the computational solution of partial differential equations, using adaptive finite elements (Arndt et al., 2021), to solve three conservation equations. The methodology is similar to our recent work (Liu and Yang, 2022; M. Liu et al., 2022). The models are calculated by solving the following equations of conservation of mass, momentum, and internal energy for an incompressible medium and adopting the extended Boussinesq approximation (van Zelst et al., 2022).
On the right-hand side of Eq. (3), the three terms represent the internal heat production that includes radioactive decay, frictional heating, and adiabatic compression of material. η is the viscosity, is the deviator of the strain rate tensor, u is the velocity, p is the pressure, g is the gravitational acceleration, Ω is the interesting domain, Cp is the heat capacity, k is the heat conductivity, H is the intrinsic specific heat production, α is the thermal expansion coefficient, and ρ0 is the adiabatic reference density. ci is named compositional fields here (e.g., upper crust and lower crust; Kronbichler et al., 2012). As the medium was considered incompressible, we assumed that the density (ρ) in Eq. (1) satisfied the following equation:
where ρ0 is the reference density at reference temperature T0 (293 K).
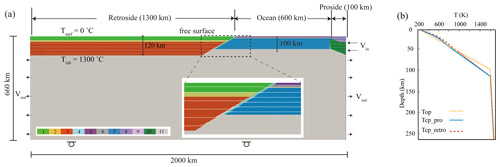
Figure 1(a) Reference model configuration and boundary conditions. Different colors reflect different lithologies, where 1 and 8 are the continental upper crust, 2 and 9 are the continental lower crust, 3 and 10 are the continental lithospheric mantle, 4 is the weak zone, 5 is the sediment, 6 is the oceanic crust, 7 is the oceanic lithospheric mantle, and 11 is the sub-lithospheric mantle (Table S1). The white lines are isotherms of 200 ∘C increments in the range of 200 to 1200 ∘C. Tsurf is the surface temperature, and Tlab is the bottom temperature of continental lithosphere. Vin and Vout denote where material flows in and out. (b) Initial distributions of procontinental (Tcp_pro), retrocontinental (Tcp_retro), and oceanic (Top) lithospheric temperatures.
2.2 Rheology
Our models are based on the common assumption that solid Earth materials are treated as highly viscous fluids. Thus, we apply a viscoplastic rheology (Glerum et al., 2018). The viscous regime uses a composite of diffusion and dislocation creep that can be conveniently formulated, as follows (Karato and Wu, 1993; Karato, 2008):
where is the square root of second invariant of the deviatoric strain rate. In the case of diffusion creep, n=1 and m>0, while for dislocation creep n>1 and m=0. Definitions and values of other symbols are shown in Table S1 in the Supplement. Surface erosion and sedimentation are neglected.
The plastic yielding is defined by the Drucker–Prager criterion as Eq. (8) (Davis and Selvadurai, 2002):
where C is the cohesion, and ϕ is the initial friction angle. We also include strain weakening in the plastic regime, through which C and ϕ are linearly weakened by a factor of 2 or 4 between plastic strains of 0.5 and 1.5.
The effective viscosity is eventually given by
where i is one of the subscripts among diff, disl, comp, and yield. ηmax and ηmin are user-defined viscosity cutoffs (Table S1).
2.3 Initial model configuration and boundary conditions
The numerical model domain is 2000 km × 660 km in the horizontal and vertical directions. It contains a retrocontinental lithosphere and a procontinental lithosphere, with an oceanic lithosphere in between (Fig. 1). A weak zone with a width of 10 km (gabbro; Wilks and Carter, 1990) abuts the oceanic plate to facilitate subduction. The continental lithosphere is 120 km thick, consisting of a 25 km thick upper crust (wet quartzite; Gleason and Tullis, 1995), a 10 km lower crust (wet anorthite; Rybacki et al., 2006), and an 85 km lithospheric mantle. The oceanic lithosphere (∼90 Ma) contains a 4 km thick sediment layer (gabbro; Wilks and Carter, 1990), an 8 km thick oceanic crust layer (gabbro; Wilks and Carter, 1990), and an 88 km thick lithospheric mantle. Dry olivine (Hirth and Kohlstedt, 2003) is used for the mantle. All material properties are listed in Table S1. The numerical resolution incrementally increases along the depth direction from 2 km × 2 km to 8 km × 8 km.
Temperature is fixed at the model surface (0 ∘C) and the base of the lithosphere (1300 ∘C), while various continental Tmoho is defined ranging from 450–600 ∘C. The initial continental lithospheric temperature profile follows Chapman (1986), taking into account the thickness of each lithologic layer (Eqs. 11–13). According to these equations, Tmoho and Hr are not independent parameters; we thus fixed Tmoho when investigating the influence of Hr. Specially, we first choose a surface (TT), Moho temperature (TB), and radioactive heat production (H) and then calculate the surface heat flow (qT), based on Eq. (12). After that, we substitute the above TT, qT, and H into Eq. (11) to obtain the continental crustal temperature structure. The oceanic lithospheric temperature distribution follows the half-space cooling model (Turcotte and Schubert, 2002), and in all models, we use the same initial oceanic lithospheric thermal structure. Besides, a temperature gradient of 0.5 ∘C km−1 is assumed for the sublithospheric mantle (Huangfu et al., 2019).
TZ is the temperature at depth Z. T is the temperature, q is the heat flux, and the subscripts “T” and “B” denote the top and bottom boundaries of each lithologic layer, respectively. ΔZ is the layer thickness, H is the volumetric heat production, and k is the thermal conductivity.
We apply a free-surface and free-slip lower boundary and impose a 5 cm yr−1 convergence rate to the trailing end of the procontinental lithosphere. Equivalent material flows out through both side walls of the mantle domain to keep mass balance within the whole computational domain (Fig. 1).
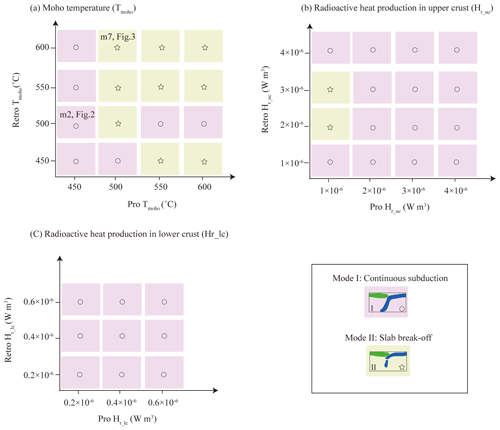
We conducted 48 numerical experiments by varying the Moho temperature, upper crustal Hr_uc, and lower crustal Hr_lc of the retrocontinent and procontinent, respectively, to capture different continental thermal structures. Two distinct continental collision evolutionary paths were recognized, namely (i) continuous subduction and (ii) continental subduction with a slab break-off. All the simulations are summarized in Table S2.
3.1 Continuous subduction without slab break-off (Mode I)
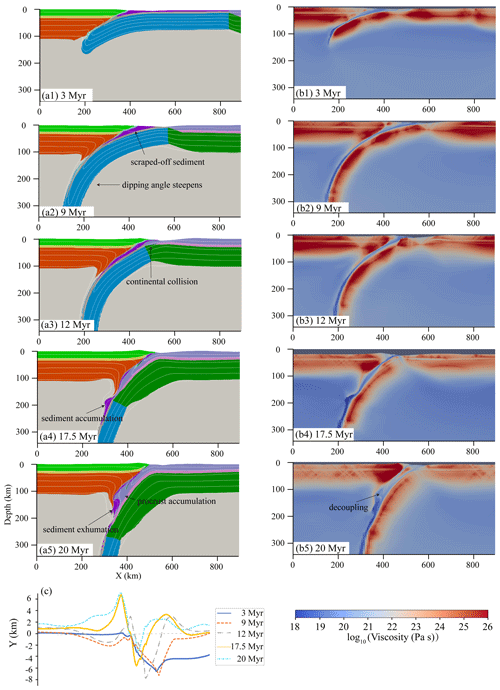
Figure 2 shows the development of the continuous subduction mode, and it takes the Model m2 (reference model; Table S2) as an example. The model started with a relatively shallow angle subduction characterized by the oceanic plate dips downward along the low-viscosity weak zone (Fig. 2a1; 3 Myr). During this stage, a portion of oceanic sediment was scraped off and stacked at the surface, accompanied by the slight uplift of the retrocontinental foreland (Fig. 2a2 and c). As the subduction goes on, the dipping angle of the slab in depth gradually steepens due to the increasing slab pull (Fig. 2a2; 9 Myr). At ∼11.5 Myr (Fig. 2a3), continents collide with each other after the full consumption of the oceanic plate. Under the continued oceanic slab pulling, the procontinental lithosphere inherited the subduction, which is characterized by further subducting the angle steepening that resulted in the superposition of retrocontinental upper crust and oceanic sediment on the procontinental forepart. With the proceeding of procontinental subduction, the collision wedge uplifted prominently (Fig. 2c). After that, a large part of the oceanic sediment previously scraped off was then entrained and subducted with the procontinental crust, followed by the rapid uplift at the retro side of the collision zone and the retro-ward advance of the suture (Fig. 2c). From ∼17.5 Myr on, the buoyant procontinental upper crust began to detach from the underlying lithosphere, mixed with the exhumed oceanic sediment, and accumulated together in the subduction channel (Figs. 2a4 and a5). During this time, uplift within the collision zone gradually expands to the retrocontinental interior (Fig. 2c).
3.2 Continental subduction with a slab break-off (Mode II)
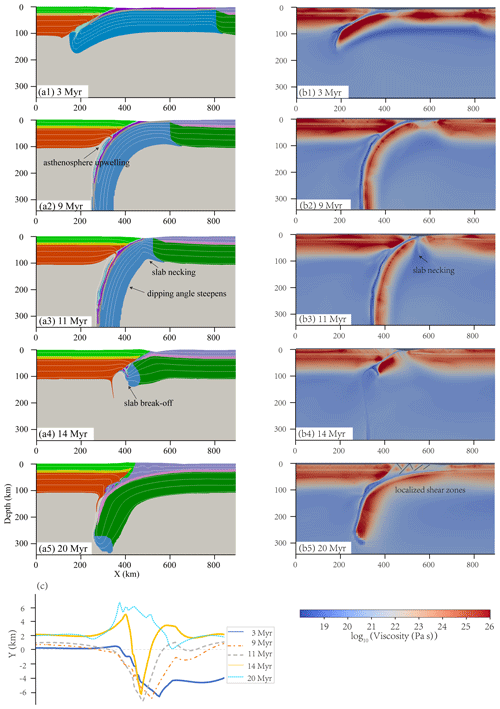
In Model m7, both the pro- and retrocontinent have higher Tmoho than Model m2 (Table S2). The lithospheric deformation behaviors and the evolution of the model during the oceanic subduction phase are quite similar to those observed in Model m2 (Fig. 3a1). The only difference is that the slab steepened more rapidly at a later stage, which gave rise to the decoupling between the retrocontinental lithosphere and the oceanic plate. Such a process created an ideal space for the asthenospheric upwelling and resulted in the significant weakening of the retrocontinental lithosphere (Fig. 3a2; 8.5 Myr). After ∼10.2 Myr, the combined effect of the increasing slab pull and asthenosphere upwelling promoted necking around the oceanic–procontinental lithospheric transition zone (Fig. 3a3; 11 Myr). The procontinental lithosphere then arrived at the trench and initiated subducting along the inclined weak zone, thus accommodating most of the ongoing convergence. During this stage, the continuous compression and rebound after slab break-off significantly uplifted the collision zone. Later on, the upper part of the retrocontinental lithosphere indented into the procrust, scraping off most of the procontinental upper crust and causing significant thickening and localized shear zones there, while leaving the small residual portion to subduct with the lithosphere. Subsequently, the accumulated orogenic wedge gradually grew into a relatively wide surface uplift.
3.3 Sensitivity tests of continental lithospheric thermal structure on the evolution of continental convergence
A regime diagram (Fig. 4) of all the models summarizes the template simulations investigating the effects of continental Tmoho and Hr, and two contrasting end members of continental collision modes are identified. Models with a cold procontinental Tmoho (≤450 ∘C) generally exhibit a continuous subduction mode without slab break-off. Meanwhile, the hotter the retrocontinental Tmoho, the steeper the subducting angle is (Figs. 4a and 5a). In comparison, Mode II dominates among the models with a relative hot procontinental Tmoho (≥500 ∘C), especially when the retrocontinental Tmoho is greater than 550 ∘C (Fig. 4a). In addition, Hr is a second-order controlling parameter compared to the Tmoho, as it has a greater propensity to alter the upper part of lithospheric deformation styles than the continental collision mode (Fig. 6c–i).
4.1 How does continental Moho temperature influence the trajectory of the collision system?
As mentioned above, models incorporating a cold prolithosphere generally evolve into continuous subduction without slab break-off. It may come from the fact that a cold prolithosphere is strong enough to maintain its strength and that it also keeps coupling with the retrolithosphere during plate convergence. Thus, the prolithosphere suffers moderate roll-back, under the condition that the stress is not sufficient to yield the lithosphere and generate break-off (Fig. 2 and S1 in the Supplement). Based on further analysis of this mode of models, we notice that the subducting angle increases as the retrocontinental Tmoho increases, accompanied by much more procrust accumulation at shallow and intense retrolithospheric mantle destruction (Fig. 5a–d). The mechanism behind this is that increasing the retrocontinental Tmoho can weaken the retrolithosphere and increase the thermal structural difference between the two continents, which may lead to plate decoupling. As a consequence, it is more likely for the prolithosphere to roll back as the magnitude of decoupling increases. Besides, weakening of the retrolithosphere may also offer a favorable condition for the intrusion of accumulated procrustal material into it.
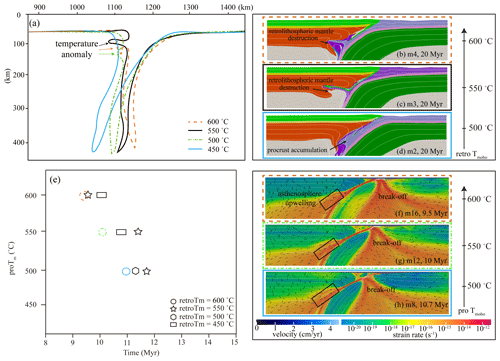
Figure 5(a) Geometries of subducting plate in models with different retrocontinental Tmoho outlined by 800 ∘C isotherms. Compositional fields of models with decreasing retrocontinental Tmoho, (b) m4, retro Tmoho=600 ∘C, (c) m12, retro Tmoho=550 ∘C, (d) m8, and retro Tmoho=500 ∘C. White lines denote the isotherms (200 ∘C increments). Panel (e) shows the relationship between the times of slab break-off and continental Tmoho. Panels (f)–(h) are strain rate of models with various procontinental Tmoho.
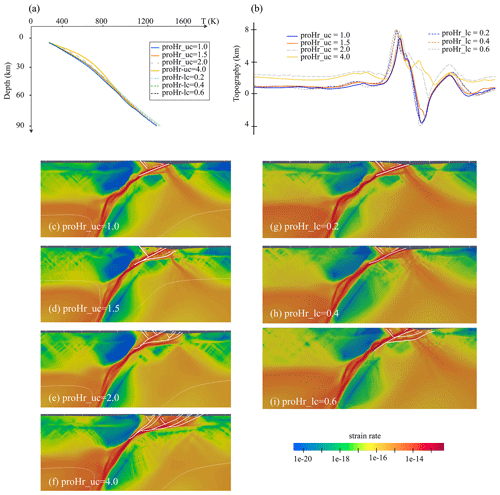
Figure 6Temperature profiles (a), topography (b), and strain rate (c–i; at 20 Myr) of models with different crustal Hr.
Regarding Mode II, models with hot procontinental Tmoho (≥500 ∘C) always evolve into continental subduction, following a slab break-off. In these models, when the retrocontinental Tmoho is determined (1) as the procontinental Tmoho decreases, the procontinental lithosphere becomes cold, which results in a rheologically strong lithosphere that can be subjected to greater deformation; the slab thus breaks off much later (Fig. 5e). This is consistent with many of the previous numerical studies (van de Zedde and Wortel, 2001; van Hunen and Allen, 2011; Duretz et al., 2011). However, it appears that Duretz and Gerya (2013) proposed an apparent opposite tendency. It may come from the fact that these models do not use a layered crust. As a consequence, a strong crust is more likely to result in strong crust–mantle coupling and a deeper slab break-off under slower convergence, while a weak crust leads to crust–mantle decoupling that may evolve into delamination. (2) The depth of the slab break-off in our models is between ∼30–60 km, which is in the range indicated by Davies and von Blanckenburg (1995), Li et al. (2002), and Duretz et al. (2011, 2012). (3) After slab break-off, the buoyant continental lithosphere experiences a rebound accompanied by strong surface uplift within a short duration (Fig. 3c), which coincides with Duretz and Gerya (2013) and Magni et al. (2017). Slab break-off is often considered to be an early process of continental collision, and numerous numerical simulations have been conducted to investigate it. Comparing their results with our models, we suggest that slab break-off is closely related to the rheological strength of the lithosphere. Therefore, the parameters that have prominent impacts on it, such as oceanic plate age, convergence velocity, continental crustal structure, layered crustal rheological strength, and the strength of the interface between the subducting and overriding plates, etc. (Gerya et al., 2004; Burov, 2011; Duretz et al., 2011; Magni et al., 2017; Koptev et al., 2022), may significantly influence the evolutionary path of slab break-off.
In conclusion, we propose that continental Tmoho is an important parameter in shaping the continental collision system and especially influences the fate of subduction. The hotter the procontinent, the weaker and easier it is to evolve into a slab break-off. The hotter either the procontinent or the retrocontinent, the less coupled it is with the adjacent plate. In addition, as a result of ongoing subduction, the slab rolls back rapidly, which may generate a gap between the adjacent plates. The asthenosphere then upwells into it, which in turn aggravates the roll-back. This contributes to the development of intense strain localization in the prolithosphere and finally leads to slab break-off (Figs. 3, S2 and 5f–h).
4.2 How crustal radioactive heat production influences the trajectory of the collision system
Radioactive elements are thought to mainly exist in the continental crust, and the radioactive heat production that originates from their decay is one of the important internal heat sources in the Earth, which influences the continental lithospheric thermal structure significantly (Turcotte and Schubert, 2002; Faccenda et al., 2008). According to our model results, increasing the upper crustal Hr can distinctly increase the thermal gradient of the lithospheric upper part, under the effect of which the steep surface topography built at the early stage of continental collision would tend to be relatively gentle. In comparison, varying lower crustal Hr has much less influence on the variation in the continental lithospheric thermal gradient and the evolution of surface topography. Moreover, as the Hr in the crust increases, the lithospheric rheological strength decreases, which facilitates the growth of crustal shear zones. That is, the higher the crustal Hr, the more shear zones it may generate in the crust (Fig. 6c–i). In conclusion, crustal Hr is a crucial parameter in enhancing strain localization in the lithospheric upper part that is closely related to the growth of shear zones, while it exerts a second-order influence on altering the continental collision mode.
4.3 Implications for the development of lateral heterogeneity of Indian–Asian collision
The ∼2000 km long east–west Himalayan–Tibetan orogenic system was created by continental collision from ∼60 to 50 Ma, with the Nanga Parbat syntaxis as its west margin and the Namcha Barwa syntaxis in the east (Chen et al., 2015). It has been proven by contrasting along-strike lithospheric structures (Li et al., 2008; Chen et al., 2015; Kufner et al., 2021). By comparison, our models are capable of providing several first-order fits of the crust–mantle deformation behaviors to this natural collision system, especially at the Hindu Kush profile and the eastern Tibet profile.
Hindu Kush is the westernmost end of the Himalayan–Tibetan orogen. Previous seismic tomography studies have confirmed that there is a north-dipping, downward-steepening, and thinning high-velocity anomaly (HVA), accompanied by increasingly intense seismicity, underneath the region (Kufner et al., 2016, 2021). The inclined HVA is believed to be a subducting plate of Indian provenance and is part of the Indian–Asian collision system. The thinning of the HVA is in the extent between 180–220 km and was suggested to be at the transition zone between Indian continental lithosphere and Neo-Tethys oceanic lithosphere. In agreement with the observations, Model m2 has a similar tectonic background and shows an analogous continuous subduction characterized by a nearly vertical dipping angle and a slab necking at a depth of ∼220 km. In addition, the relative narrow collision orogen in the model is also consistent with the natural topography in this region (Figs. 7a and 2c). It is worth noticing that the observed inclined distribution of earthquakes seems to coincide with the subducting continental crust. This may offer a possible explanation for the active intermediate earthquakes beneath this region.
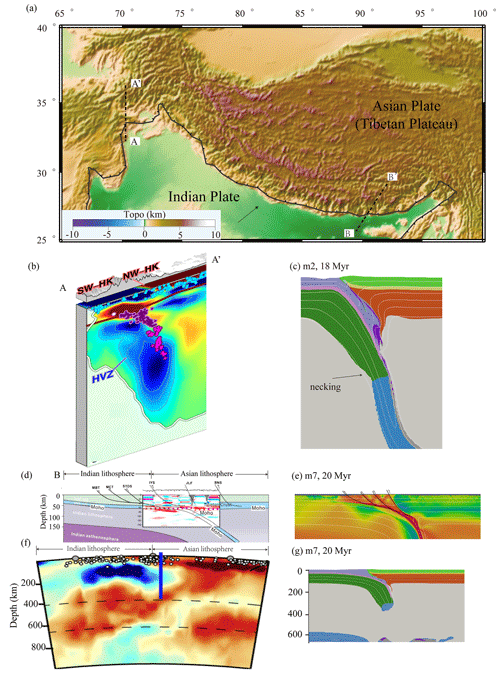
Figure 7(a) Geographic setting of Himalayan–Tibetan orogen. Schematic geologic cross sections across the (b) western (Hindu Kush; Kufner et al., 2021) and eastern Himalayan–Tibetan orogen (Li et al., 2008; Wang et al., 2019). Panel (c) shows the compositional field of Model m2 (mode I). Panels (e) and (g) are the strain rate and compositional field of Model m7 (Mode II), respectively.
The main part of the Himalayan–Tibetan orogen is the product of a collision between the cold Indian craton and the relative warm Asian continent after the closure of Neo-Tethys, the geological settings of which are quite analogous with our Model m7. During the continental collision phase, the Indus–Yarlung suture zone bordering the Indian and Asian lithospheres moved significantly, creating an ∼8 km mountain (the Himalayas) and a ∼4 km plateau (the Tibetan Plateau; Yin and Harrison, 2000). Unlike continuous subduction underlying the Hindu Kush, geological and seismological evidence shows that the eastern part of the profile is underlain by a shallower-angle subducting Indian lithosphere, following a slab break-off; these are also similar to the model results of Model m7 (Figs. 7b and 2c). Furthermore, previous field observations have shown that the northern part of the Indian continental crust is abundant with radioactive elements (Vidal et al., 1982; Scaillet et al., 1990; Macfarlane, 1992; Faccenda et al., 2008). Our sensitivity tests have recognized that continental crust with high radioactive heat production is more prone to result in brittle fractures and intense deformation of the lithospheric upper part, which may lead to the development of new shear zones (Fig. 6). This resembles the tectonic characteristics of large thrust fault zones in the Himalayas (Fig. 7b).
As a consequence, we speculate that the continental lithospheric thermal structural difference may be one of the key parameters that control the evolution of lateral heterogeneity along the Himalayan–Tibetan orogen and that the high content of crustal radioactive elements is one of the significant factors that dominates the growth of large thrust fault zones in the Himalayas.
In this work, we systematically discuss the influences of the continental lithospheric thermal structure on the evolution of the continental collision system based on high-resolution thermomechanical numerical experiments. The model results demonstrate that two end-members of continental collision are obtained because the continuous subduction mainly occurs with a relative cold overriding lithosphere (Tmoho≤450∘), and as the retrocontinental Tmoho increases, the subducting angle steepens. Slab break-off dominates when the model has a relatively hot procontinental Tmoho (≥500 ∘C), especially when the retrocontinental Tmoho is greater than 550 ∘C. Hr is a second-order controlling parameter compared with Tmoho in shaping the continental collision mode, while it is more prone to facilitating the growth of crustal shear zones.
The continental lithospheric thermal structure may have played a significant role in the development of lateral heterogeneity along the Himalayan–Tibetan orogenic belt. We suggest that the different evolutionary paths between the continuous subduction underlying the Hindu Kush and the continental subduction beneath eastern Tibet may come from the inherited lateral variation in the Indian lithospheric geothermal gradient. In addition, the high content of radioactive elements in the continental crust may be one of the important reasons for the development of deep and large thrust fault zones in this collision orogen.
The input files of ASPECT are available at the Open Science Framework repository at https://doi.org/10.5281/zenodo.8076545 (Liu, 2023).
The supplement related to this article is available online at: https://doi.org/10.5194/se-14-1155-2023-supplement.
MXL and DHY designed and oversaw the project. MXL performed all the numerical simulations. RQ participated in the discussions and revisions of the paper. All authors contributed to writing the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This work has been supported by the National Natural Science Foundation of China (grant nos. 42104097 and U1839206). The figures in this paper have been produced by Paraview V5.11.1, Generic Mapping Tools V5.4.2 (Wessel et al., 2013), Python V3.6.7, and Adobe Illustrator. We thank the Computational Infrastructure for Geodynamics for supporting the development of ASPECT (https://aspect.geodynamics.org, last access: 24 June 2023). The version of ASPECT (version 2.4.0-pre) that we used in this paper is built on the open-source finite element package deal II (version 10.0.0-pre) through the candi installation package (https://github.com/dealii/candi, last access: 24 June 2023). Additional dependencies include Trilinos (13.0.0) and p4est (2.2.0). All the numerical models were run on the TianHe-1A cluster at National Supercomputer Center in Tianjin. We thank Lin Chen and Alexander Koptev for their constructive and thoughtful comments that substantially improved the paper.
This work has been supported by the National Natural Science Foundation of China (grant nos. 42104097 and U1839206).
This paper was edited by Taras Gerya and reviewed by Lin Chen and Alexander Koptev.
Arndt, D., Bangerth, W., Blais, B., Fehling, M., Gassmöller, R., Heister, T., Heltai, L., Köcher, U., Kronbichler, M., Maier, M., Munch, P., Pelteret, J.-P., Proell, S., Simon, K., Turcksin, B., Wells, D., and Zhang, J.: The deal. II library, Version 9.3, J. Numer. Math., 29, 171–186, https://doi.org/10.1515/jnma-2021-0081, 2021.
Beaumont, C., Fullsack, P., and Hamilton, J.: Styles of crustal deformation in compressional orogens caused by subduction of the underlying lithosphere, Tectonophysics, 232, 119–132, https://doi.org/10.1016/0040-1951(94)90079-5, 1994.
Burov, E. B.: Rheology and strength of the lithosphere, Mar. Petrol. Geol., 28, 1402–1443, https://doi.org/10.1016/j.marpetgeo.2011.05.008, 2011.
Chapman, D. S.: Thermal gradients in the continental crust, Geol. Soc. Lond. Spec. Publ., 24, 63–70, https://doi.org/0.1144/GSL.SP.1986.024.01.07, 1986.
Chen, L. and Gerya, T. V.: The role of lateral lithospheric strength heterogeneities in orogenic plateau growth: Insights from 3-D thermo-mechanical modeling, J. Geophys. Res.-Solid, 121, 3118–3138, https://doi.org/10.1002/2016JB012872, 2016.
Chen, L., Song, X., D., Gerya, T., V., Xu, T., and Chen, Y.: Crustal melting beneath orogenic plateaus: Insights from 3-D thermo-mechanical modeling, Tectonophysics, 761, 1–15, https://doi.org/10.1016/j.tecto.2019.03.014, 2019.
Chen, Y., L, W., Yuan, X. H., Badal, J., and Teng, J. W.: Tearing of the Indian lithospheric slab beneath southern Tibet revealed by SKS-wave splitting measurements, Earth Planet. Sc. Lett., 413, 13–24, https://doi.org/10.1016/j.epsl.2014.12.041, 2015.
Davies, H. J. and von Blanckenburg, F.: Slab breakoff: A model of lithosphere detachment and its test in the magmatism and deformation of collisional orogens, Earth Planet. Sc. Lett., 129, 85–102, https://doi.org/10.1016/0012-821X(94)00237-S, 1995.
Davis, R. O. and Selvadurai, A. P. S.: Plasticity and Geomechanics, Cambridge University Press, Cambridge, ISBN 0521818303, 2002.
Duretz, T. and Gerya, T. V.: Slab detachment during continental collision: Influence of crustal rheology and interaction with lithospheric delamination, Tectonophysics, 602, 124–140, https://doi.org/10.1016/j.tecto.2012.12.024, 2013.
Duretz, T., Gerya, T. V., and May, D. A.: Numerical modelling of spontaneous slab breakoff and subsequent topographic response, Tectonophysics, 502, 244–256, https://doi.org/10.1016/j.tecto.2010.05.024, 2011.
Duretz, T., Schmalholz, S. M., and Gerya, T. V.: Dynamics of slab detachment, Geochem. Geophy. Geosy., 13, Q03020, https://doi.org/10.1029/2011GC004024, 2012.
Faccenda, M., Gerya, T. V., and Chakraborty, S.: Styles of post-subduction collisional orogeny: Influence of convergence velocity, crustal rheology and radiogenic heat production, Lithos, 103, 257–287, https://doi.org/10.1016/j.lithos.2007.09.009, 2008.
Gerya, T. V., Yuen, D. A., and Maresch, W. V.: Thermomechanical modelling of slab detachment, Earth Planet. Sc. Lett., 226, 101–116, https://doi.org/10.1016/j.epsl.2004.07.022, 2004.
Ghazian, R. K. and Buiter, S. J. H.: A numerical investigation of continental collision styles, Geophys. J. Int., 193, 113—1152, https://doi.org/10.1093/gji/ggt068, 2013.
Gleason, G. C. and Tullis, J.: A flow law for dislocation creep of quartz aggregates determined with the molten salt cell, Tectonophysics, 247, 1–23, https://doi.org/10.1016/0040-1951(95)00011-B, 1995.
Glerum, A., Thieulot, C., Fraters, M., Blom, C., and Spakman, W.: Nonlinear viscoplasticity in ASPECT: benchmarking and applications to subduction, Solid Earth, 9, 267–294, https://doi.org/10.5194/se-9-267-2018, 2018.
Heron, P. J. and Pysklywec, R. N.: Inherited structure and coupled crust-mantle lithosphere evolution: Numerical models of Central Australia, Geophys. Res. Lett., 43, 4962–4970, https://doi.org/10.1002/2016GL068562, 2016.
Hirth, G. and Kohlstedt, D.: Rheology of the upper mantle and the mantle wedge: A view from the experimentalists. Washington DC American Geophysical Union Geophysical Monograph Series, 138, 83–105, https://doi.org/10.1029/138GM06, 2003.
Huangfu, P., Wang, Y., Fan, W., Li, Z., and Zhou, Y.: Dynamics of unstable continental subduction: Insights from numerical modeling, Sci. China Earth Sci., 60, 218–234, https://doi.org/10.1007/s11430-016-5014-6, 2017.
Huangfu, P., Li, Z. H., Fan, W., and Shi, Y.: Dynamics of crustal overthrust versus underthrust in the continental collision zones: Numerical modelling, Terra Nova, 31, 332–342, https://doi.org/10.1111/ter.12384, 2019.
Karato, S.-I.: Deformation of Earth Materials: An Introduction to the Rheology of Solid Earth, Cambridge University Press, Cambridge, ISBN 9780511804892, https://doi.org/10.1017/CBO9780511804892, 2008.
Karato, S.-I. and Wu, P.: Rheology of the upper mantle: A synthesis, Science, 260, 771–778, https://doi.org/10.1126/science.260.5109.771, 1993.
Koptev, A., Ehlers, T. A., Nettesheim, M., and Whipp, D. M.: Response of a Rheologically stratified lithosphere to subduction of an indenter-shaped plate: Insights into localized exhumation at orogen syntaxes, Tectonics, 38, 1908–1930, https://doi.org/10.1029/2018TC005455, 2019.
Koptev, A., Nettesheim, M., and Ehlers, T. A.: Plate corner subduction and rapid localized exhumation: Insights from 3D coupled geodynamic and geomorphological modelling, Terra Nova, 34, 210–223, https://doi.org/10.1111/ter.12581, 2022.
Kronbichler, M., Heister, T., and Bangerth, W.: High accuracy mantle convection simulation through modern numerical methods, Geophys. J. Int., 191, 12–29, https://doi.org/10.1111/j.1365-246X.2012.05609.x, 2012.
Kufner S. K., Schurr, B., Sippl, C., Yuan, X. H., Ratschbacher, L., Akbar, A. M., Ischuk, A., Murodkulov, S., Schneider, F., Mechie, J., and Tilmann, F.: Deep india meets deep asia: lithospheric indentation, delamination and break-off under pamir and hindu kush (central asia), Earth Planet. Sc. Lett., 435, 171–184, https://doi.org/10.1016/j.epsl.2015.11.046, 2016.
Kufner, S. K., Kakar, N., Bezada, M., Bloch, W., and Schurr, B.: The Hindu Kush slab break-off as revealed by deep structure and crustal deformation, Nat. Commun., 12, 1685, https://doi.org/10.1038/s41467-021-21760-w, 2021.
Li, C., van der Hilst, R. D., Meltzer, A. S., and Engdahl, E. R.: Subduction of the Indian lithosphere beneath the Tibetan Plateau and Burma, Earth Planet. Sc. Lett., 274, 157–168, https://doi.org/10.1016/j.epsl.2008.07.016, 2008.
Li, L., Liao, X., and Fu, R.: Slab breakoff depth: A slowdown subduction model, Geophys. Res. Lett., 29, 11-11–11-13, https://doi.org/10.1029/2001GL013420, 2002.
Liao, J. and Gerya, T.: Partitioning of crustal shortening during continental collision: 2-D thermomechanical modeling, J. Geophys. Res., 122, 592–606, https://doi.org/10.1002/2016JB013398, 2017.
Liu, M. and Yang, D. H.: How do pre-existing weak zones and rheological layering of the continental lithosphere influence the development and evolution of intra-continental subduction?, J. Asian Earth. Sci., 238, 105385, https://doi.org/10.1016/j.jseaes.2022.105385, 2022.
Liu, M., Yang, D. H., and Huangfu, P. P.: Effects of plate velocity slowdown on altering continental collision patterns and crustal-lithospheric deformation during the collision process, Front. Earth Sci., 10, 814710, https://doi.org/10.3389/feart.2022.814710, 2022.
Liu, M. X.: The role of continental lithospheric thermal structure in the evolution of orogenic systems: Application to the Himalayan-Tibetan collision zone, Version v2, Zenodo [code], https://doi.org/10.5281/zenodo.8076545, 2023.
Liu, S., Sobolev, S. V., Babeyko, A. Y., and Pons, M.: Controls of the foreland formation pattern in the orogen-foreland shortening system: constraints from high-resolution geodynamic models, Tectonics, 41, e2021TC007121, https://doi.org/10.1029/2021TC007121, 2022.
Luth, S., Willingshofer, E., Sokoutis, D., and Cloetingh, S.: Analogue modelling of continental collision: Influence of plate coupling on mantle lithosphere subduction, crustal deformation and surface topography, Tectonophysics, 484, 87–102, https://doi.org/10.1016/j.tecto.2009.08.043, 2010.
Macfarlane, A. M.: The tectonic evolution of the core of the Himalaya, Langtang National Park, central Nepal, Massachusetts Institute of Technology, http://hdl.handle.net/1721.1/60426 (last access: 24 June 2023), 1992.
Magni, V., Allen, M. B., van Hunen, J., and Bouilhol, P.: Continental underplating after slab break-off, Earth Planet. Sc. Lett., 474, 59–67, https://doi.org/10.1016/j.epsl.2017.06.017, 2017.
Nettesheim, M., Ehlers, T. A., Whipp, D. M., and Koptev, A.: The influence of upper-plate advance and erosion on overriding plate deformation in orogen syntaxes, Solid Earth, 9, 1207–1224, https://doi.org/10.5194/se-9-1207-2018, 2018.
Pysklywec, R. N.: Evolution of subducting mantle lithosphere at a continental plate boundary, Geophys. Res. Lett., 28, 4399–4402, https://doi.org/10.1029/2001GL013567, 2001.
Rybacki, E., Gottschalk, M., Wirth, R., and Dresen, G.: Influence of water fugacity and activation volume on the flow properties of fine-grained anorthite aggregates, J. Geophys. Res., 111, B03203, https://doi.org/10.1029/2005JB003663, 2006.
Scaillet, B., France-Lanord, C., and Le Fort, P.: Badrinath-Gangotri plutons (Garhwal, India): petrological and geochemical evidence for fractionation processes in a high Himalayan leucogranite, J. Volcanol. Geoth. Res., 44, 163–188, https://doi.org/10.1016/0377-0273(90)90017-A, 1990.
Tang, J., Chen, L., Meng, Q., and Wu, G.: The effects of the thermal state of overriding continental plate on subduction dynamics: Two-dimensional thermal-mechanical modeling, Sci. China Earth Sci., 63, 1519–1539, https://doi.org/10.1007/s11430-019-9624-1, 2020.
Toussaint, G., Burov, E., and Jolivet, L.: Continental plate collision: Unstable vs. stable slab dynamics, Geology, 32, 33–36, https://doi.org/10.1130/G19883.1, 2004.
Turcotte, D. L. and Schubert, G.: Geodynamics, Cambridge University Press, ISBN 9780511807442, https://doi.org/10.1017/CBO9780511807442, 2002.
Ueda, K., Gerya, T. V., and Burg, J.-P.: Delamination in collisional orogens: Thermomechanical modeling, J. Geophys. Res., 117, B08202, https://doi.org/10.1029/2012JB009144, 2012.
van de Zedde, D. M. A. and Wortel, M. J. R.: Shallow slab detachment as a transient source of heat at midlithospheric depths, Tectonics, 20, 868–882, https://doi.org/10.1029/2001TC900018, 2001.
van Hunen, J. and Allen, M. B.: Continental collision and slab break-off: A comparison of 3-D numerical models with observations, Earth Planet. Sc. Lett., 302, 27–37, https://doi.org/10.1016/j.epsl.2010.11.035, 2011.
van Zelst, I., Crameri, F., Pusok, A. E., Glerum, A., Dannberg, J., and Thieulot, C.: 101 geodynamic modelling: how to design, interpret, and communicate numerical studies of the solid Earth, Solid Earth, 13, 583–637, https://doi.org/10.5194/se-13-583-2022, 2022.
Vidal, P., Cocherie, A., and Fort, P. L.: Geochemical investigations of the origin of the Manaslu leucogranite (Himalaya, Nepal), Geochim. Cosmochim. Ac., 46, 2279–2292, https://doi.org/10.1016/0016-7037(82)90201-0, 1982.
Vogt, K., Willingshofer, E., Matenco, L., Sokoutis, D., Gerya, T., and Cloetingh, S.: The role of lateral strength contrasts in orogenesis: A 2D numerical study, Tectonophysics, 746, 549–561, https://doi.org/10.1016/j.tecto.2017.08.010, 2018.
Wang, C. Y., Mooney, W. D., Zhu, L., Wang, X., Lou, H., and You, H., Cao, Z., Chang, L., and Yao, Z.: Deep structure of the eastern himalayan collision zone: evidence for underthrusting and delamination in the postcollisional stage, Tectonics, 38, 3614–3628, https://doi.org/10.1029/2019TC005483, 2019.
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J., and Wobbe, F.: Generic Mapping Tools: Improved Version Released, Eos Trans. Am. Geophys. Union, 94, 409–410, https://doi.org/10.1002/2013EO450001, 2013.
Wilks, K. R. and Carter, N. L.: Rheology of some continental lower crustal rocks, Tectonophysics, 182, 57–77, https://doi.org/10.1016/0040-1951(90)90342-6, 1990.
Willingshofer, E. and Sokoutis, D.: Decoupling along plate boundaries: Key variable controlling the mode of deformation and the geometry of collisional mountain belts, Geology, 37, 39–42, https://doi.org/10.1130/G25321A.1, 2009.
Yin, A. and Harrison, T. M.: Geologic Evolution of the Himalayan–Tibetan Orogen, Annu. Rev. Earth Planet. Sci., 28, 211–280, 2000.
Zhou, H. W. and Murphy, M. A.: Tomographic evidence for wholesale underthrusting of india beneath the entire tibetan plateau, J. Asian Earth Sci., 25, 445–457, https://doi.org/10.1016/j.jseaes.2004.04.007, 2005.