Stress drop sequences in the simplest pressure-sensitive ideal elasto-plastic media: implications for earthquake cycles

This study explores stress drops and earthquake sequences in the simplest pressure-sensitive elasto-plastic media using two-dimensional simulations, emphasizing the critical role of temporal and spatial resolution in accurately capturing stress evolution and strain localization during seismic cycles. Our analysis reveals that stress drops – triggered by plastic deformation once local stresses reach the yield criterion – resemble fault rupture mechanics, where accumulated strain energy is suddenly released, simulating earthquake-like behavior. Finer temporal and spatial discretization leads to sharper stress drops and lower minimum stress values, for simulations that have not converged yet. Displacement accumulates gradually during interseismic periods and intensifies during major stress drops, capturing key features of natural earthquake cycles. The histogram of stress drop amplitudes exhibits a non-Gaussian distribution. This “solid turbulence” behavior suggests that stress is redistributed across spatial and temporal scales, with implications for understanding the variability of stress drop magnitudes. Our results demonstrate that high-resolution elasto-plastic models can reproduce essential features of earthquake nucleation and stress drop behavior without relying on complex friction laws or velocity-dependent weakening mechanisms. These findings emphasize the necessity of incorporating plasticity into fault slip models to better understand the mechanisms of fault weakening and rupture. Furthermore, our work suggests that extending these models to three-dimensional fault systems and incorporating material heterogeneity and fluid interactions could offer deeper insights into seismic hazard assessment and earthquake mechanics.

1 Introduction

Understanding earthquake nucleation remains a significant challenge in geophysics, as it directly influences our ability to predict and mitigate seismic hazards. Earthquake nucleation is often conceptualized through the study of sliding behavior along fault surfaces, with models traditionally describing the interseismic period as one of near-elastic deformation in the surrounding crust, interrupted by phases of anelastic slip that eventually result in seismic rupture (Pranger et al., 2022). Such models typically rely on phenomenological rate- and state-dependent friction laws (Dieterich, 1978, 1979; Ruina, 1983), which have been highly successful in describing various aspects of the seismic cycle. However, these friction-based models may overlook critical physical processes that govern the transition from aseismic slip to seismic rupture, particularly when plastic deformation and off-fault processes are involved.

Numerical modeling of elasto-plastic strain localization in pressure-sensetive geomaterials has a long history, with early contributions from Cundall (1989, 1990), Poliakov et al. (1993, 1994), Poliakov and Herrmann (1994). Regularization of strain localization thickness was addressed by Duretz et al. (2019) and de Borst and Duretz (2020). A single-phase (visco)-hypoelastic-perfectly plastic medium was modeled in both 2D and 3D domains by Alkhimenkov et al. (2024b), while compaction-driven fluid flow and shear bands in porous media were numerically modeled in 3D by Alkhimenkov et al. (2024a).

One of the first computational earthquake dynamics models with slip-weakening rupture simulations was introduced by Andrews (1976). Numerical studies have suggested that plasticity plays a crucial role in earthquake rupture, particularly through off-fault plasticity mechanisms (e.g., Andrews, 1976, 2005). Off-fault plasticity refers to the deformation that occurs away from the main fault plane and can significantly influence the dynamics of rupture propagation. Previous works have explored the effects of off-fault plasticity in two-dimensional (2D) in-plane dynamic rupture simulations (Templeton and Rice, 2008; Kaneko and Fialko, 2011; Gabriel et al., 2013; Tong and Lavier, 2018; Allison and Dunham, 2018). For instance, Dal Zilio et al. (2022) presented a 2D thermomechanical computational framework for simulating earthquake sequences in a nonlinear visco-elasto-plastic compressible medium, highlighting the importance of including viscoelastic and plastic behavior in realistic models. Other studies highlighting the importance of plasticity in earthquake physics modeling include Erickson et al. (2017), Preuss et al. (2020), and Simpson (2023).

In addition to 2D studies, three-dimensional (3D) dynamic rupture simulations incorporating off-fault plasticity have provided deeper insights into the complexity of earthquake mechanics (Wollherr et al., 2018). Ma (2008); Ma and Andrews (2010) conducted some of the earliest 3D studies on dynamic rupture with plasticity. Another significant advancement was made by Uphoff et al. (2023), who utilized a discontinuous Galerkin method to model earthquake sequences and aseismic slip on multiple faults, demonstrating the versatility of numerical approaches in capturing the nuances of seismic phenomena.

The role of plasticity in earthquake nucleation has also been emphasized in laboratory experiments. Studies have shown that plastic deformation can precede seismic slip, indicating that the onset of plastic yielding may be a precursor to earthquake initiation (Johnson et al., 2008; Scuderi et al., 2016). These experimental findings support the incorporation of plasticity in numerical models to enhance the understanding of the nucleation process.

Despite these advancements, there remains a need for simplified models that can effectively capture the essential features of earthquake nucleation and stress drops while being computationally efficient. The simplest elasto-plastic models offer a promising avenue for such investigations. By focusing on basic physical principles, these models can provide insights into the fundamental mechanisms of earthquake nucleation, such as the role of stress accumulation and release, the interaction between elastic and plastic deformation, and the influence of material heterogeneity on seismic behavior.

In this study, we employ a two-dimensional elasto-plastic model to investigate stress drops and earthquake nucleation. The friction coefficient is assumed to be constant in all simulations, with no hardening or softening, which corresponds to an ideal plasticity model. We conduct a series of numerical simulations to explore the effects of temporal and spatial resolutions on the accuracy of stress and strain predictions. Our goal is to understand how these resolutions impact the modeled behavior of stress evolution, strain accumulation, and the nucleation of seismic events. Our approach involves detailed convergence tests for temporal and spatial discretizations, analysis of stress drop sequences, and examination of interseismic periods. An important goal is to ensure convergence of the numerical results, after which we focus on high-resolution, converged simulations. We also investigate the initial wave field patterns during earthquake nucleation to gain insights into the complex interplay between quasi-static and elasto-dynamic mechanics. Through this comprehensive study, we aim to highlight the critical role of high-resolution modeling in capturing the intricate dynamics of earthquake nucleation and stress drops, providing a foundation for future research and practical applications in seismic hazard assessment.

The distinct features of this study among other recent HPC simulations are:

• 1.

  We employ the simplest pressure-sensitive ideal plasticity model, characterized by a spatially and temporally constant friction coefficient.

• 2.

  We systematically investigate a previously proposed physics-based explanation for spontaneous stress drops using convergence-controlled, high-resolution GPU simulations, thereby extending the accessible resolution and fidelity of the theory.

• 3.

  We allow faults to emerge spontaneously from the evolving stress field, as it was done in a few previous studies. Our higher spatial/temporal resolution and GPU throughput produce a much larger population of emergent faults, enabling analyses that were previously intractable.

• 4.

  We demonstrate a scalable GPU implementation that enables high-resolution, convergence-verified simulations at practical runtimes, supporting systematic temporal and spatial resolution studies.

2 Mathematical formulation

2.1 Quasi-statics

The conservation of linear momentum is expressed as:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathrm{\nabla }}_j{\mathit{\sigma }}_{ij}+f_i=\mathrm{0},\end{array}$$

where σ_ij is the stress tensor, f_i is the body force, ∇ is the dell operator, $j=\mathrm{1},\mathrm{2},\mathrm{3}$ and Einstein summation convention is applied (summation over repeated indices). The stress tensor is decomposed into bulk (volumetric) and deviatoric components

$$\begin{array}{}\text{(2)}& {\mathit{\sigma }}_{ij}=-p{\mathit{\delta }}_{ij}+{\mathit{\tau }}_{ij},\end{array}$$

where p is pressure, τ_ij is the deviatoric stress tensor, δ_ij is the Kronecker delta. The strain rate is defined as

$$\begin{array}{}\text{(3)}& {\dot{\mathit{\epsilon }}}_{ij}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\mathrm{\nabla }}_i{v}_j+{\mathrm{\nabla }}_j{v}_i)\end{array}$$

The rheology is elasto-plastic, which is characterized by an additive decomposition of the strain rate into an elastic (volumetric and deviatoric) and plastic components

$$\begin{array}{}\text{(4)}& {\dot{\mathit{\epsilon }}}_{ij}={\dot{\mathit{\epsilon }}}^{\text{eb}}{\mathit{\delta }}_{ij}+{\dot{\mathit{\epsilon }}}_{ij}^{\text{ed}}+{\dot{\mathit{\epsilon }}}_{ij}^{\text{pl}},\end{array}$$

where the superscripts ⋅^eb, ⋅^ed, ⋅^pl denote elastic volumetric (bulk), elastic deviatoric and plastic parts, respectively. The plastic strain rate tensor is

$$\begin{array}{}\text{(5)}& {\dot{\mathit{\epsilon }}}_{ij}^{\text{pl}}=\dot{\mathit{\lambda }}{\displaystyle \frac{\partial Q}{\partial {\mathit{\sigma }}_{ij}}},\end{array}$$

where $\dot{\mathit{\lambda }}$ is the plastic multiplier rate and Q is the plastic flow potential. The volumetric (bulk) elastic strain rate is

$$\begin{array}{}\text{(6)}& {\dot{\mathit{\epsilon }}}^{\text{eb}}={\mathrm{\nabla }}_k{v}_k-{\dot{\mathit{\epsilon }}}_{kk}^{\text{pl}}=-{\displaystyle \frac{\mathrm{1}}{K}}{\displaystyle \frac{\mathrm{D}p}{\mathrm{D}t}},\end{array}$$

where $\mathrm{D}p/\mathrm{D}t$ is the material derivative (provided in the following section), the deviatoric elastic strain rate tensor is

$$\begin{array}{}\text{(7)}& {\dot{\mathit{\epsilon }}}_{ij}^{\text{ed}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}G}}{\displaystyle \frac{\mathcal{D}{\mathit{\tau }}_{ij}}{\mathcal{D}t}},\end{array}$$

where the Jaumann rate of deviator of Cauchy stress tensor, represented as $\mathcal{D}{\mathit{\tau }}_{ij}/\mathcal{D}t$, is provided in the following section. Combining Eqs. (4)–(5), the total strain rate can be reformulated as

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\dot{\mathit{\epsilon }}}_{ij}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\mathrm{\nabla }}_i{v}_j+{\mathrm{\nabla }}_j{v}_i)\\ =& -{\displaystyle \frac{\mathrm{1}}{\mathrm{3}K}}{\displaystyle \frac{\mathrm{D}p}{\mathrm{D}t}}{\mathit{\delta }}_{ij}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}G}}{\displaystyle \frac{\mathcal{D}{\mathit{\tau }}_{ij}}{\mathcal{D}t}}+\dot{\mathit{\lambda }}{\displaystyle \frac{\partial Q}{\partial {\mathit{\sigma }}_{ij}}}.\end{array}\end{array}$$

This system of equation is the static elasto-plastic model routinely used in solid mechanics (Zienkiewicz and Taylor, 2005).

Large strain formulation

The inelastic response is described using hypoelastic constitutive theory. Hypoelasticity involves formulating the constitutive equations for stress in terms of objective (frame-invariant) stress rates (de Souza Neto et al., 2011).

The scalar pressure material derivative is represented by the following equation:

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{D}p}{\mathrm{D}t}}={\displaystyle \frac{\partial p}{\partial t}}+v_k{\displaystyle \frac{\partial p}{\partial x_k}}.\end{array}$$

The Jaumann rate of deviator of Cauchy stress tensor, represented as $\mathcal{D}{\mathit{\tau }}_{ij}/\mathcal{D}t$, is defined by (de Souza Neto et al., 2011):

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathcal{D}{\mathit{\tau }}_{ij}}{\mathcal{D}t}}={\displaystyle \frac{\partial {\mathit{\tau }}_{ij}}{\partial t}}+v_k{\displaystyle \frac{\partial {\mathit{\tau }}_{ij}}{\partial x_k}}-{\dot{w}}_{ik}{\mathit{\tau }}_{jk}-{\dot{w}}_{jk}{\mathit{\tau }}_{ik},\end{array}$$

where ${\dot{w}}_{ij}$ is the vorticity tensor defined as: ${\dot{w}}_{ij}=({\mathrm{\nabla }}_i{v}_j-{\mathrm{\nabla }}_j{v}_i)/\mathrm{2}$.

2.2 Elasto-dynamics

The conservation of linear momentum is extended by addition of inertia (under small strain assumption):

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathrm{\nabla }}_j{\mathit{\sigma }}_{ij}+f_i=\mathit{\rho }{\displaystyle \frac{\partial v_i}{\partial t}},\end{array}$$

where v is the velocity and ρ is the density.

2.3 Plasticity

Plasticity is implemented using a non-associated, pressure-dependent Drucker–Prager criterion (Drucker and Prager, 1952; de Souza Neto et al., 2011; De Borst et al., 2012). According to this criterion, plastic yielding begins when the second invariant of the deviatoric stress, J₂, and the pressure (minus the mean stress), p, meet the following condition:

$$\begin{array}{}\text{(12)}& \sqrt{J_{\mathrm{2}}}-\sin \left(\mathit{\phi }\right)p=\cos \left(\mathit{\phi }\right)c,\end{array}$$

where c is the cohesion and φ is the angle of internal friction. In terms of the stress tensor, plastic deformations occur when the stresses reach the yield surface. The yield function F and the plastic potential Q for the Drucker–Prager criterion are defined as:

$$\begin{array}{}\text{(13)}& F(\mathit{\tau },p)=\sqrt{J_{\mathrm{2}}}-\sin \left(\mathit{\phi }\right)p-\cos \left(\mathit{\phi }\right)c,\end{array}$$

where φ is the internal friction angle.

$$\begin{array}{}\text{(14)}& Q(\mathit{\tau },p)=\sqrt{J_{\mathrm{2}}}-\sin \left(\mathit{\psi }\right)p,\end{array}$$

where ψ≤φ is the dilation angle. In two dimensions under plane strain conditions, with ${\dot{\mathit{ϵ}}}_{zz}=\mathrm{0}$, the Drucker–Prager criterion is equivalent to the Mohr–Coulomb criterion (Templeton and Rice, 2008). In 2D, the second invariant of the deviatoric stress, J₂, is expressed as:

$$\begin{array}{}\text{(15)}& J_{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\tau }}_{ij}{\mathit{\tau }}_{ji}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}({\mathit{\tau }}_{xx}^{\mathrm{2}}+{\mathit{\tau }}_{yy}^{\mathrm{2}}+{\mathit{\tau }}_{zz}^{\mathrm{2}})+{\mathit{\tau }}_{xy}^{\mathrm{2}}.\end{array}$$

As long as F≤0, the material remains in the elastic regime. Once F reaches zero (F=0), plasticity is activated. If the material remains in a plastic state ($\partial F/\partial t=\mathrm{0}$), plastic yielding continues. The current implementation of perfect plasticity requires small time increments and is computationally expensive. To ensure spontaneous strain localization, strain softening is often introduced, which promotes the formation of shear bands (Lavier et al., 1999; Moresi et al., 2007; Popov and Sobolev, 2008; Lemiale et al., 2008). However, there are concerns about the thermodynamic admissibility of such solutions (Duretz et al., 2019). Additionally, the softening or hardening moduli are small compared to the shear modulus and can be neglected as a first-order approximation (Vermeer, 1990), leading to the ideal plasticity model used in the present study.

For the case of regularized plasticity, the yield function is defined as (Heeres et al., 2002):

$$\begin{array}{}\text{(16)}& F(\mathit{\tau },p)=\sqrt{J_{\mathrm{2}}}-\sin \left(\mathit{\phi }\right)p-\cos \left(\mathit{\phi }\right)c-{\mathit{\eta }}^{\text{vp}}\dot{\mathit{\lambda }}.\end{array}$$

3 Numerical implementation

3.1 Discretization

The numerical domain is discretized using a staggered grid in both space and time (Virieux, 1986). This method provides a variant of the conservative finite volume approach (Dormy and Tarantola, 1995). For the elasto-dynamic equations, an explicit time integration method is employed, offering second-order accuracy in both space and time. Detailed representations of the discrete equations are available in Alkhimenkov et al. (2021). For the quasi-static equations, the discrete scheme achieves second-order accuracy in space. Advection is carried out using an upwind scheme, which is first-order. Consequently, due to the application of the pseudo-transient method, the solution demonstrates first-order accuracy in time (Alkhimenkov and Podladchikov, 2025). The quasi-static equations are solved with the accelerated pseudo transient method (described below), while the dynamic wave-propagation is only visualized to illustrate the transient fields and does not affect the quasi-static evolution.

3.2 Accelerated pseudo transient method

The solution of the quasi-static equations is achieved using the matrix-free accelerated pseudo-transient (APT) method (Frankel, 1950; Räss et al., 2022; Alkhimenkov and Podladchikov, 2025). The core concept of this method involves solving dynamic equations with appropriate attenuation of the dynamic fields instead of directly solving inertialess equations. To achieve this, the equations are written in their non-dimensional residual form and iterated over “pseudo-time” until convergence is reached. Once the dynamic fields attenuate to a specific precision (e.g., to 10⁻¹²), the solution of the quasi-static equations is attained. In other words, the quasi-static problem serves as an attractor for the dynamic problem with damping. The APT method is capable of handling numerical domains with more than a billion grid cells. Additionally, since all operations are local, this method can be naturally parallelized using GPUs, which is the approach taken in this study.

3.3 Implementation of plasticity

In the return mapping algorithm, the following steps are performed:

• 1.

  Calculate the components of the trial deviatoric stresses, ${\mathit{\tau }}_{ij}^{\text{trial}}$.

• 2.

  Compute the trial second invariant of the deviatoric stresses, $J_{\mathrm{2}}^{\text{trial}}$, using ${\mathit{\tau }}_{ij}^{\text{trial}}$.

• 3.

  Determine F^trial using the equation:

  $$\begin{array}{}\text{(17)}& F^{\text{trial}}=\sqrt{J_{\mathrm{2}}^{\text{trial}}}-\left(\sin \right(\mathit{\phi })p+\cos (\mathit{\phi }\left)c\right).\end{array}$$

When the material is in the plastic state, the trial deviatoric stress components, ${\mathit{\tau }}_{ij}^{\text{trial}}$, are re-scaled according to:

$$\begin{array}{}\text{(18)}& {\mathit{\tau }}_{ij}^{\text{new}}={\mathit{\tau }}_{ij}^{\text{trial}}\left(\mathrm{1}-{\displaystyle \frac{F^{\text{trial}}}{\sqrt{J_{\mathrm{2}}^{\text{trial}}}}}\right)\equiv {\mathit{\tau }}_{ij}^{\text{trial}}\stackrel{\mathrm{̃}}{\mathit{\lambda }},\end{array}$$

where $\stackrel{\mathrm{̃}}{\mathit{\lambda }}=\mathrm{1}-\frac{F^{\text{trial}}}{\sqrt{J_{\mathrm{2}}^{\text{trial}}}}$ is the scaling parameter. This re-scaling process is iterated over “pseudo-time” until the updated trial deviatoric stresses, ${\mathit{\tau }}_{ij}^{\text{new}}$, satisfy the plasticity criterion, ensuring F^trial=0 (thus, $\stackrel{\mathrm{̃}}{\mathit{\lambda }}=\mathrm{1}$ and no re-scaling occurs). A regularized version of this procedure modifies formula (18) to (assuming non-zero dilatation angle ψ):

$$\begin{array}{}\text{(19)}& \stackrel{\mathrm{̃}}{\mathit{\lambda }}=\mathrm{1}-{\displaystyle \frac{F^{\text{trial}}\mathrm{\Delta }t{G}^{\mathrm{e}}}{\sqrt{J_{\mathrm{2}}}(G^{\mathrm{e}}\mathrm{\Delta }t+K\mathrm{\Delta }t\sin \mathit{\phi }\sin \mathit{\psi }+{\mathit{\eta }}^{\text{vp}})}}.\end{array}$$

where η^vp is the regularization parameter having units of viscosity, [Pa s]. The numerical viscosity η^vp is usually set to a small value. If this value is too high, the shear bands become very thick; conversely, if the value is too small, the thickness of the shear band is just one pixel. The correct value of the viscosity damper lies between these limits. In the following section, we examine how the choice of viscosity damper affects the solution. This implementation of plasticity through re-scaling deviatoric stress components is equivalent to the standard procedure using the plastic multiplier rate, $\dot{\mathit{\lambda }}$, which is defined as

$$\begin{array}{}\text{(20)}& \dot{\mathit{\lambda }}={\displaystyle \frac{F^{\text{trial}}}{\mathrm{\Delta }t{G}^{\mathrm{e}}+K\mathrm{\Delta }t\sin \mathit{\phi }\sin \mathit{\psi }+{\mathit{\eta }}^{\text{vp}}}}.\end{array}$$

For a more detailed explanation of how plasticity with regularization is implemented in single-phase media, refer to Duretz et al. (2018, 2019, 2021).

3.4 Model configuration, boundary conditions, and non-dimensionalization

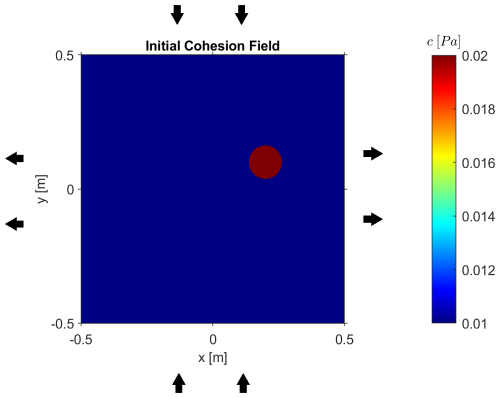
The computational domain is a square with dimensions $x,y\in [-L_x/\mathrm{2},L_x/\mathrm{2}]\times [-L_y/\mathrm{2},L_y/\mathrm{2}]$ (Fig. 1). All simulations in this study are performed using a simple initial model configuration and non-dimensional equations. To ensure a consistent dimensionless framework, we define the following characteristic scales: length $l^{*}=L_x$ and time $t^{*}=\mathrm{1}/a$. Here, L_x represents the domain size in the x-direction, $L_x=L_y=\mathrm{1}$ and a denotes the background strain rate. Deformation evolves over timescales inversely proportional to the initial background strain rate a₀ at t=0. The ratio of cohesion c to the pressure scale p^* is defined as $r=\frac{c_{\mathrm{0}}}{G_{\mathrm{0}}}$, G₀=1 and $c_{\mathrm{0}}={\mathrm{10}}^{-\mathrm{2}}$.

For all computations, we set the coefficient of internal friction to μ=0.5. Pure shear boundary conditions are applied by prescribing normal velocities at the left and right boundaries:

$$\begin{array}{}\text{(21)}& v_x=ax\end{array}$$

and at top and bottom boundaries

$$\begin{array}{}\text{(22)}& v_y=-ay,\end{array}$$

which corresponds to the extension in x-dimension and compression in y-dimension. At all boundaries, free-slip boundary conditions are implemented. The following initial condition is implemented: p=0,

$$\begin{array}{}\text{(23)}& {\displaystyle }{\mathit{\tau }}_{xx}=c_{\mathrm{0}},\text{(24)}& {\displaystyle }{\mathit{\tau }}_{yy}=-c_{\mathrm{0}}.\end{array}$$

We introduce a circular inclusion in the non-dimensional cohesion c, representing a localized stiff inclusion. The expression in the dimensionless framework is as follows:

$$\begin{array}{}\text{(25)}& {\displaystyle }c=\left\{\begin{array}{ll}\mathrm{2}{c}_{\mathrm{0}},& \text{if }\sqrt{(x+L_x/\mathrm{10}{)}^{\mathrm{2}}+(y+L_y/\mathrm{5}{)}^{\mathrm{2}}}<{\mathrm{0.0625}}^{\mathrm{2}},\\ c_{\mathrm{0}},& \text{otherwise}.\end{array}\right.\end{array}$$

We impose loading increments applied to the strain components.

Figure 1 Heterogeneous initial setup of cohesion c. The arrows indicate the pure shear boundary condition which is applied at the model boundaries.

4 Results

4.1 Integrated stress ${\mathit{\sigma }}_{xx}^{\mathsf{\text{INT}}}$

To analyze the evolution of the simulated system, we evaluate the integrated axial stress ${\mathit{\sigma }}_{xx}^{\mathsf{\text{INT}}}$ along a vertical line segment using the following expression:

$$\begin{array}{}\text{(26)}& {\mathit{\sigma }}_{xx}^{\text{INT}}={\displaystyle \frac{\mathrm{1}}{L_y}}\underset{\mathrm{0}}{\overset{L_y}{\int }}\left(-p(x_{\mathrm{0}},y)+{\mathit{\tau }}_{xx}(x_{\mathrm{0}},y)\right)\mathrm{d}y,\end{array}$$

where x₀ is a fixed coordinate in the x-direction ($x_{\mathrm{0}}=L_x/\mathrm{4}$).

4.1.1 Convergence study

To determine the necessary spatial and temporal resolutions (i.e., the resolution with respect to loading increments), we performed a convergence study. Simulations were conducted with different spatial resolutions, ranging from N=63² to N=2047² (N is the number of grid cells in x-dimension), while keeping the regularization viscosity constant across all cases. The results are shown in Fig. 2.

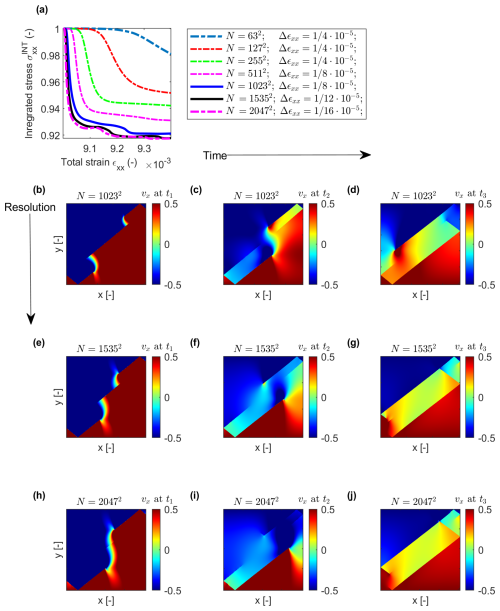
Figure 2 Convergence study. Panel (a) shows the integrated stress ${\mathit{\sigma }}_{xx}^{\mathsf{\text{INT}}}$ as a function of total strain for multiple resolutions. Panels (b)–(j) show the velocity field v_x at three different time steps (t₁–t₃) and three different resolutions: N=1023², N=1535², N=2047². t₁ corresponds to the total strain ε=0.022, t₂ corresponds to the total strain ε=0.026, and t₃ corresponds to the total strain ε=0.04. Regularization parameter is ${\mathit{\eta }}^{\text{vp}}=\mathrm{1}/\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$ in all simulations.

At low resolution (e.g., N=63²), the model does not capture sharp stress drops. However, as resolution increases, stress drops become increasingly pronounced. Notably, both the amplitude and clarity of the stress drops converge for resolutions of N=1023² and higher.

Figure 3 illustrates the strain localization pattern at time t₃ for four different resolutions. Starting at N=1023², the structure and distribution of shear bands remain qualitatively similar, indicating convergence of the deformation pattern.

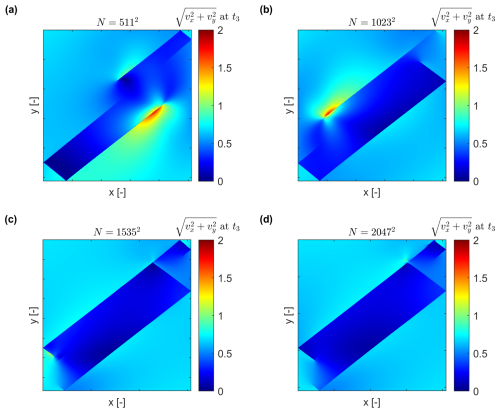
Figure 3 The total velocity field $\sqrt{v_x^{\mathrm{2}}+v_y^{\mathrm{2}}}$. Simulations at t₃ for four different resolutions: N=511², N=1023², N=1535², and N=2047². t₃ corresponds to the total strain ε=0.04.

The total (Eulerian) displacement in the x- and y-directions is updated from the velocities using

$$\begin{array}{}\text{(27)}& u_x^{\left(n\right)}=u_x^{(n-\mathrm{1})}+v_x^{\left(n\right)}\mathrm{\Delta }t,u_y^{\left(n\right)}=u_y^{(n-\mathrm{1})}+v_y^{\left(n\right)}\mathrm{\Delta }t.\end{array}$$

where n and n−1 denote the current and previous time steps, respectively. The incremental (Eulerian) displacement is then given by

$$\begin{array}{}\text{(28)}& \mathrm{\Delta }{u}_x=u_x^{\left(n\right)}-u_x^{(n-\mathrm{1})},\mathrm{\Delta }{u}_y=u_y^{\left(n\right)}-u_y^{(n-\mathrm{1})}.\end{array}$$

Strain components are computed from (Eulerian) displacement gradients as

$$\begin{array}{}\text{(29)}& {\displaystyle }\mathrm{\nabla }\cdot \mathbf{u}& {\displaystyle }={\displaystyle \frac{\partial u_x}{\partial x}}+{\displaystyle \frac{\partial u_y}{\partial y}},\text{(30)}& {\displaystyle }{\mathit{\epsilon }}_{xx}& {\displaystyle }={\displaystyle \frac{\partial u_x}{\partial x}}-\frac{\mathrm{1}}{\mathrm{3}}\mathrm{\nabla }\cdot \mathbf{u},\text{(31)}& {\displaystyle }{\mathit{\epsilon }}_{yy}& {\displaystyle }={\displaystyle \frac{\partial u_y}{\partial y}}-\frac{\mathrm{1}}{\mathrm{3}}\mathrm{\nabla }\cdot \mathbf{u},\text{(32)}& {\displaystyle }{\mathit{\epsilon }}_{xy}& {\displaystyle }=\frac{\mathrm{1}}{\mathrm{2}}\left({\displaystyle \frac{\partial u_x}{\partial y}}+{\displaystyle \frac{\partial u_y}{\partial x}}\right).\end{array}$$

Finally, the (Eulerian) deviatoric strain measure is defined as

$$\begin{array}{}\text{(33)}& J_{\mathrm{2}}^u=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}({\mathit{\epsilon }}_{xx}^{\mathrm{2}}+{\mathit{\epsilon }}_{yy}^{\mathrm{2}})+{\mathit{\epsilon }}_{xy}^{\mathrm{2}}}.\end{array}$$

Note that Eulerian-type fields are plotted only for visualisation in all figures, and these plotted quantities are not used in the actual calculations. A zoomed-in view of ${\log }_{\mathrm{10}}\left(J_{\mathrm{2}}^u\right)$ field is provided in Fig. 4, where we observe that the thickness of the shear bands spans several grid cells even at N=511² (panel a), and more than ten grid cells at N=1023² (panel b). This confirms that the regularization is effective – if it were not, the shear bands would collapse to 1–3 grid cells irrespective of resolution.

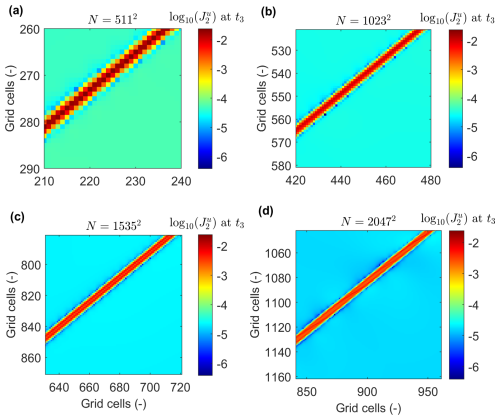
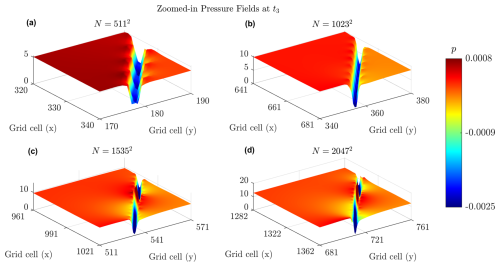
Figure 4 ${\log }_{\mathrm{10}}{J}_{\mathrm{2}}^u$ field. Zoomed-in view of simulations at t₃ for four different resolutions: N=511² (a), N=1023² (b), N=1535² (c), and N=2047² (d). t₃ corresponds to the total strain ε=0.04.

Figure 5 shows the pressure field p at time t₃ for four spatial resolutions. As resolution increases from N=511² to N=2047², finer pressure structures become apparent, highlighting the emergence of sharp gradients. All snapshots correspond to a total strain of ε=0.04. Based on these results, we conclude that a resolution of N=1023² is sufficient for capturing both stress drop dynamics and shear band structure while maintaining a balance between accuracy, computational cost, and memory requirements.

Figure 5 Pressure field p. Zoomed-in view of simulations at t₃ for four different resolutions: N=511² (a), N=1023² (b), N=1535² (c), and N=2047² (d). t₃ corresponds to the total strain ε=0.04.

5 Earthquake sequence

In this section, we analyze the stress response of the system over a complete loading cycle comprising 16 000 incremental steps. We focus on three aspects: (i) the sequence of stress drops that emerge as strain accumulates, (ii) the statistical distribution of these drops, and (iii) the wavefield dynamics resulting from a single stress drop event. All results presented in this section are obtained from a fully converged simulation with spatial resolution N=1023², constant regularization viscosity, and pseudo-transient iterations that ensure convergence at each step.

5.1 Numerical convergence and stability

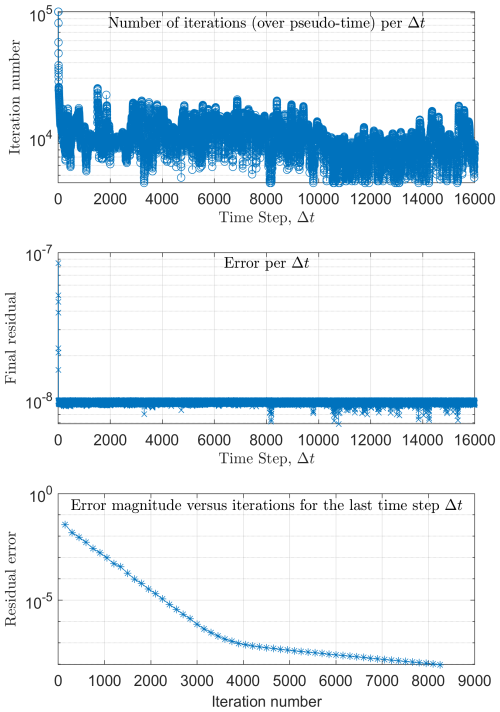
To ensure that the stress drops analyzed in this study arise from physically meaningful simulation, we monitor the convergence behavior of the pseudo-transient iterations used to solve the elasto-plastic equations at each time step. Figure 6 shows the number of iterations required per physical time step (top panel), the corresponding final residual at convergence (middle panel), and the residual curve versus pseudo-time iterations for the final step (bottom panel). The residual error is calculated using the L^∞ norm. The number of iterations per step remains moderate throughout the simulation, and the final residuals consistently remain below a prescribed threshold, confirming that the nonlinear solver converges consistently even during dynamic events such as stress drops. These diagnostics support the reliability of the stress evolution and wavefield results presented in the following sections.

Figure 6 Convergence diagnostics for pseudo-transient iterations. Top: Number of iterations per physical time step. Middle: Final residual error per time step. Bottom: Residual magnitude versus iteration number for the final time step.

5.2 Final velocity and pressure fields

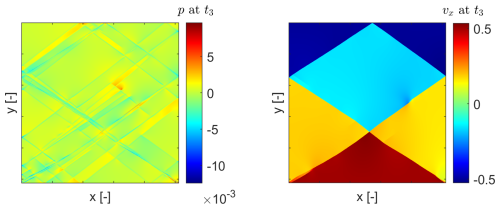
The final velocity and pressure distributions highlight the complex flow and stress responses at the end of the simulation, as shown in Fig. 7. The velocity field v_x exhibits sharp gradients in zones of intense shear, while the solid-phase pressure p shows localized shear bands.

Figure 7 Final spatial fields of velocity v_x and solid pressure p after 16 000 incremental steps.

5.3 Stress drops

Figure 8 presents the evolution of integrated axial stress ${\mathit{\sigma }}_{xx}^{\mathsf{\text{INT}}}$ as a function of total applied strain for 16 000 loading increments (Fig. 9 presents the same result in a logarithmic scale). The main panel (Fig. 8a) shows the full sequence, while the three lower panels provide zoomed-in views of the early (0–$\mathrm{1}/\mathrm{3}$), middle ($\mathrm{1}/\mathrm{3}$–$\mathrm{2}/\mathrm{3}$), and late ($\mathrm{2}/\mathrm{3}$–1) loading stages, where individual stress drops become clearly visible. Throughout the loading process, numerous stress drops are observed. These drops correspond to abrupt changes in the system's stress state, occurring when strain localization reaches a critical threshold and further deformation in the prescribed direction becomes unsustainable. At these points, the system undergoes a rapid stress redistribution, manifested as discrete decreases in the integrated stress ${\mathit{\sigma }}_{xx}^{\mathsf{\text{INT}}}$.

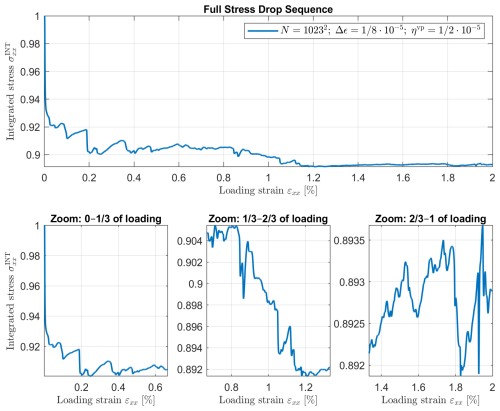
Figure 8 Evolution of the normalized integrated stress as a function of total applied strain in a converged simulation with N=1023² grid cells, strain increment $\mathrm{\Delta }\mathit{\epsilon }=\mathrm{1}/\mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$, and viscoplastic regularization ${\mathit{\eta }}^{\text{vp}}=\mathrm{1}/\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$. The main panel shows the full sequence of stress drops over the entire deformation interval. The three lower panels provide zoomed-in views of the early (0–$\mathrm{1}/\mathrm{3}$), middle ($\mathrm{1}/\mathrm{3}$–$\mathrm{2}/\mathrm{3}$), and late ($\mathrm{2}/\mathrm{3}$–1) loading stages, highlighting the multiscale and irregular nature of stress release events in the model.

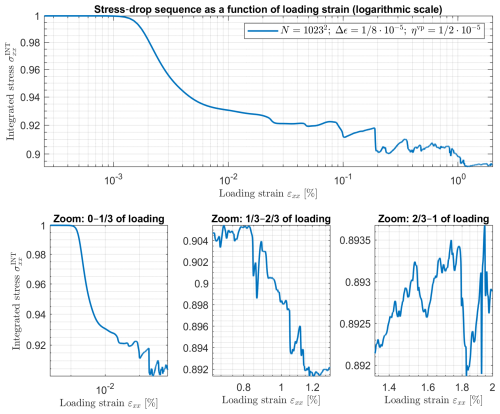
Figure 9 Evolution of the normalized integrated stress as a function of total applied strain in a converged simulation in a logarithmic scale with N=1023² grid cells, strain increment $\mathrm{\Delta }\mathit{\epsilon }=\mathrm{1}/\mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$, and viscoplastic regularization ${\mathit{\eta }}^{\text{vp}}=\mathrm{1}/\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$. The main panel shows the full sequence of stress drops over the entire deformation interval. The three lower panels provide zoomed-in views of the early (0–$\mathrm{1}/\mathrm{3}$), middle ($\mathrm{1}/\mathrm{3}$–$\mathrm{2}/\mathrm{3}$), and late ($\mathrm{2}/\mathrm{3}$–1) loading stages, highlighting the multiscale and irregular nature of stress release events in the model.

These events are indicative of dynamic rupture-like behavior, resembling the rapid stress release that occurs during seismic slip in natural earthquakes. However, we note that in this initial study, we focus only on the qualitative resemblance and do not provide a detailed analysis of slip rates or rupture propagation speeds. The observed sequence of stress drops mimics the typical behavior of fault systems, where interseismic periods of stress accumulation are interrupted by sudden stress release events. This behavior supports the interpretation of the model as capturing essential features of earthquake cycles within an elasto-plastic framework.

5.3.1 Histogram of stress drop amplitudes

The histogram of stress drop amplitudes shown in Fig. 10 provides a quantitative representation of the frequency and magnitude of stress drops observed over the course of the full simulation (16 000 loading increments). The distribution is clearly non-Gaussian, spanning more than five orders of magnitude in amplitude. It is unimodal and asymmetric, with a pronounced peak near ${\log }_{\mathrm{10}}\left(\mathrm{\Delta }\mathit{\sigma }\right)\approx -\mathrm{4.5}$ and long tails toward both smaller and larger events. Small stress drops are significantly more frequent, but large-magnitude stress releases are still present.

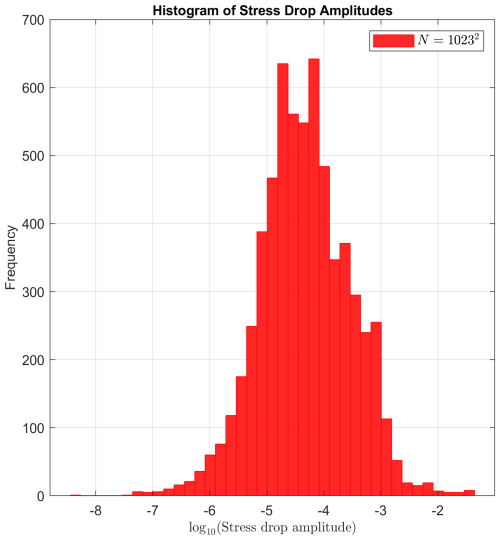
Figure 10 Histogram of stress drop amplitudes computed from a high-resolution simulation (N=1023²). The amplitude of each drop is defined as the difference in integrated axial stress between consecutive local maxima and minima, and plotted on a base-10 logarithmic scale. The resulting distribution is non-Gaussian and asymmetric, spanning over five orders of magnitude, with frequent small drops and rarer large-scale stress releases – consistent with turbulence-like plastic deformation dynamics.

This behavior is reminiscent of turbulence-like spectra in other complex systems, where intermittent bursts coexist with background fluctuations. In the context of solid deformation, this has been described as “solid turbulence” and was first explored by Poliakov et al. (1994), who analyzed the multifractal structure of shear localization in elasto-plastic media. In our model, the broad-tailed nature of the histogram reflects a complex interaction between localized plastic yield and global elastic stress redistribution. As in fluid turbulence – where energy cascades from large to small scales – stress in the solid is redistributed across multiple spatial and temporal scales, leading to intermittent bursts of plastic deformation.

Understanding this type of emergent behavior is crucial for modeling seismicity, where stress drops represent analogs of earthquake events. The prevalence of small events and the presence of occasional larger ones are qualitatively consistent with the Gutenberg–Richter-like relationship. However, we emphasize that our current study does not perform a statistical fit (e.g., power-law or log-normal) to extract quantitative scaling exponents. Such an analysis would be required to firmly establish the statistical nature of the tail and its connection to real seismicity. Overall, the histogram supports the idea that even minimal elasto-plastic models, with no prescribed faults or complex frictional laws, can give rise to rich and realistic emergent behavior.

5.3.2 Wave propagation due to a single stress drop

Figure 11 shows the snapshots of wave fields following a single stress drop. The wave response is visualized in terms of velocity (v_x) and pressure (p) at different physical time steps. Panels (a) and (b) present the initial wavefield immediately after the stress drop. The velocity and pressure distributions are spatially complex and dominated by shear-dominated nucleation patterns, qualitatively resembling a double-couple source mechanism. The volumetric pressure field also exhibits localized amplitudes, indicating simultaneous compressional response.

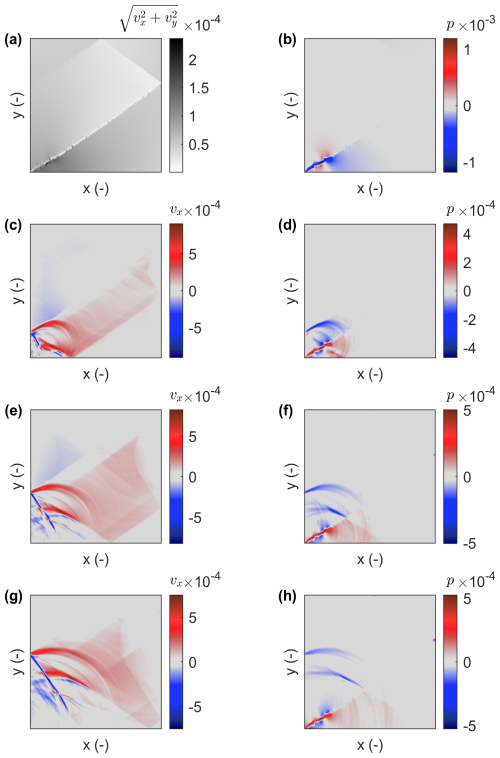
Figure 11 Wave propagation following a single stress drop. Panels (a) and (b) show the initial wavefields: (a) velocity magnitude $\sqrt{v_x^{\mathrm{2}}+v_y^{\mathrm{2}}}$, and (b) pressure p. Panels (c, d), (e, f), and (g, h) show the evolution of the velocity (v_x) and pressure (p) fields after 360, 720, and 1080 physical time steps, respectively. The pattern indicates nucleation dominated by shear (double-couple-like) and volumetric pressure release, consistent with the early stages of dynamic rupture.

Panels (c, d), (e, f) and (g, h) show the evolution of the wavefield after 360, 720, and 1080 time steps, respectively. The velocity field, initially concentrated near the nucleation region, spreads outward as the system relaxes dynamically. The pressure field also evolves, exhibiting outward-propagating features that reflect the elastic response of the medium. These results indicate that a localized stress drop in a plastic medium generates complex wave activity, with both velocity and pressure fluctuations contributing to the redistribution of energy. The simulation is performed with a time step size of $\mathrm{\Delta }t=\mathrm{4}\times {\mathrm{10}}^{-\mathrm{5}}$.

6 Discussion

6.1 The nature of stress drops

As shown in Fig. 8, numerous stress drops occur throughout the loading process. From a theoretical standpoint, the initial stress drop – following the onset of strain localization – has been analyzed by, for example, Vermeer (1990) and Le Pourhiet (2013). Subsequent stress drops are associated with transitions between quasi-static loading intervals. These events represent moments when the system shifts from one quasi-equilibrium state to another due to the breakdown of stable deformation paths. Specifically, when local stresses exceed the yield criterion, plastic deformation is activated, causing a redistribution of stress and a rapid release of stored energy in the form of a stress drop.

This process mimics the mechanics of fault rupture, where accumulated strain energy is suddenly released during seismic events. The sharp, discrete stress drops observed in our simulations – particularly at high spatial and temporal resolutions – are consistent with such rupture-like behavior.

Beyond the magnitude of individual stress drops, the spatial distribution of strain localization plays a key role in governing how stress is released. Localized shear bands serve as preferential paths for stress concentration and redistribution, determining the geometry and timing of stress release. The interplay between elastic loading during interseismic intervals and localized plastic deformation during stress drops offers a minimal yet effective model of the earthquake cycle.

6.2 Role of regularization in elasto-plastic simulations

Regularization plays a critical role in numerical simulations of elasto-plastic materials, especially when strain localization is involved. Without regularization, simulations may produce unphysical results such as infinitely narrow shear bands and grid-dependent failure modes. In this study, the viscoplastic regularization parameter η^vp was carefully selected to ensure numerical stability while preserving physically realistic stress and strain fields.

Excessive regularization, however, can overly smooth these fields, suppressing strain localization and significantly reducing the occurrence and sharpness of stress drops. This effect is clearly observqed in low-resolution simulations, where the regularization length scale becomes comparable to or larger than the grid resolution. Conversely, insufficient regularization can result in non-convergent or unstable solutions.

Our results demonstrate that appropriate regularization enables the model to capture both large-scale and fine-scale features of dynamic deformation – specifically, the spatial organization of shear bands and the timing and magnitude of stress drops. These findings align with prior work emphasizing the importance of regularization in elasto-plastic modeling, particularly for resolving localized deformation while maintaining convergence and computational stability (Popov and Sobolev, 2008; Duretz et al., 2018).

6.3 3D simulations with zero regularization

Alkhimenkov et al. (2023) conducted three-dimensional simulations of a single-phase elasto-plastic model without regularization. These results provide valuable insight into how strain localization and stress drops manifest in fully three-dimensional domains. Notably, the trends observed in 3D – both in terms of spatial and temporal resolution – are consistent with the 2D results presented in this study.

Extending the analysis to three dimensions is essential for a more realistic representation of fault systems, which are inherently three-dimensional. In 3D, the stress and strain fields exhibit additional complexity, including the influence of out-of-plane stresses on rupture propagation. The fact that unregularized 3D simulations produce physically meaningful and qualitatively similar results further validates the robustness of the elasto-plastic framework employed here. This also suggests that certain dynamic features – such as stress drop sequences and fault-like deformation – can emerge naturally in elasto-plastic systems even in the absence of artificial smoothing.

6.4 Implications for earthquake sequences and fault mechanics

The results of both 2D and 3D (Alkhimenkov et al., 2023) simulations offer important insights into earthquake nucleation and fault mechanics. The stress drops observed in our models are directly analogous to the rapid release of accumulated stress during natural seismic events, supporting the idea that pressure-sensitive elasto-plastic models can replicate key features of rupture initiation. The pattern of stress drops does not correspond to log-normal or normal distributions. The pattern, separated by intervals of gradual strain accumulation, mirrors the fundamental structure of the seismic cycle.

As deformation progresses, the emergence of multiple shear bands becomes evident. Importantly, stress drops do not always occur on newly formed bands – instead, they frequently reoccur along existing localized zones of weakness. This behavior is consistent with observations of natural fault systems, where pre-existing fault planes accommodate repeated episodes of stress accumulation and release over multiple cycles. Our results highlight the capacity of simple elasto-plastic models to reproduce not only the mechanical ingredients of rupture, but also the spatial memory and cyclic behavior observed in fault systems.

6.5 Comparison to rate-and-state friction models

While this study focuses on elasto-plasticity as the primary mechanism governing stress drops and strain localization, it is instructive to compare our approach to traditional rate-and-state friction (RSF) models. RSF models have been widely used to describe fault slip behavior, particularly due to their ability to capture velocity-weakening and velocity-strengthening effects that are critical for earthquake nucleation and stability analyses.

In contrast, the elasto-plastic model presented here does not rely on any velocity-dependent constitutive law. Instead, stress drops emerge naturally through local plastic yielding when the material reaches a yield criterion. This distinction is significant: it suggests that fault weakening and slip can be modeled purely through stress-based plasticity, without invoking empirical velocity dependence.

Furthermore, classical RSF models typically describe fault slip on a predefined, spatially fixed fault interface. In our model, by contrast, faults emerge spontaneously as localized zones of plastic strain, allowing for the generation, reactivation, and migration of shear bands. This feature provides an important advantage in capturing fault system evolution in heterogeneous or evolving tectonic environments, which cannot be represented by single-fault RSF frameworks.

6.6 Limitations and future work

While the present study offers valuable insights into the mechanics of stress drops and fault-like behavior in elasto-plastic materials, several limitations remain.

First, the model assumes homogeneous material properties. In reality, natural fault zones are highly heterogeneous, with variations in lithology, porosity, cohesion, and pre-existing damage that significantly affect strain localization and rupture dynamics. Incorporating spatially variable properties would allow for a more realistic simulation of fault behavior and could reveal additional mechanisms of rupture complexity.

Second, the model currently neglects fluid-rock interactions. Fluids are known to play a critical role in fault weakening, particularly through pore pressure buildup and fluid-induced instabilities. Future extensions of this model should incorporate poroelasticity or two-phase flow to study the coupling between deformation and fluid transport, especially in overpressured or fluid-saturated fault zones.

Finally, while the present study includes detailed two-dimensional simulations, the primary findings are limited to 2D geometries. Three-dimensional simulations provide a more realistic framework for fault mechanics, capturing effects such as off-plane deformation, complex rupture geometries, and interactions among multiple shear bands. Alkhimenkov et al. (2023) performed 3D simulations of elasto-plastic deformation and observed multiple stress drops consistent with the results presented here. However, that study did not focus on earthquake nucleation or the dynamics of earthquake sequences. Future high-resolution 3D studies will be essential for advancing elasto-plastic modeling of seismic processes, particularly in relation to rupture initiation, stress transfer, and fault interaction in realistic geological settings.

7 Conclusions

In this study, we investigated stress drops and earthquake-like behavior in idealized elasto-plastic media using two-dimensional numerical simulations. The first stress drop occurs following the onset of strain localization, a process driven by structural softening (Vermeer, 1990; Le Pourhiet, 2013; Sabet and de Borst, 2019). This structural softening mechanism, which received relatively little attention until recently (Sabet and de Borst, 2019), is explored here as a cause of spontaneous strain localization in an ideal plasticity model with a constant friction coefficient. Subsequent stress drops are associated with transitions between quasi-static loading intervals, during which the system moves from one equilibrium state to another due to the inability of strain localization to continue growing in the same direction. This behavior is consistent with fault offset theories developed by Forsyth (1992); Buck (1993) and validated by Lavier et al. (1999). Forsyth (1992) emphasized that Anderson's theory for faulting applies strictly to infinitesimal displacements. The initial orientation of a fault corresponds to the orientation that minimizes the regional stress required for slip initiation. However, Forsyth (1992) demonstrated that the additional horizontal stress necessary to maintain slip along the same fault increases linearly with accumulated displacement. Consequently, after only a few hundred meters of slip on a typical fault, it becomes mechanically more favorable to nucleate a new fault than to continue slip on the pre-existing one. Switching from sliding along an active fault to nucleation of a new fault is a fundamental cause of sudden stress drops and a potential mechanism for earthquake cycles.

Our results underscore the critical importance of both temporal and spatial resolution in capturing the evolution of stress and strain fields throughout the seismic cycle. Convergence tests demonstrate that finer discretization sharpens stress drops and leads to lower minimum stress values, emphasizing the need for high-resolution modeling to accurately resolve dynamic stress changes. Analysis of the interseismic periods and stress drops reveals a typical cycle: gradual displacement accumulation followed by abrupt, localized deformation. This mirrors the natural earthquake cycle, in which periods of aseismic slip are interrupted by rapid seismic events that release accumulated strain energy. Moreover, wavefield analysis following a single stress drop revealed complex nucleation patterns, offering insight into the mechanics of rupture initiation.

One of the key contributions of this work is the demonstration that simple pressure-sensitive elasto-plastic models – with constant friction coefficient in time and space – can reproduce key features of earthquake sequences and stress drop behavior, provided sufficient spatial and temporal resolution. Notably, this is achieved without the use of complex frictional laws or velocity-dependent weakening mechanisms. Our results show that plastic yielding alone can account for fundamental aspects of fault slip and rupture. A second important contribution is that faults are not prescribed a priori, as in conventional rate-and-state models; instead, new faults emerge spontaneously from the evolving stress field, offering a key advantage in modeling complex fault dynamics.

These findings have important implications for seismic hazard assessment and the development of predictive models. First, they highlight the need for high-resolution numerical models to capture the transient, localized phenomena that govern earthquake nucleation. Second, they reaffirm the critical role of plastic deformation in fault weakening and rupture, suggesting that plasticity should be incorporated alongside traditional frictional formulations in future modeling efforts. Finally, although this study focuses on two-dimensional idealized settings, the insights gained provide a foundation for extending the framework to more realistic three-dimensional, heterogeneous systems. Future research could explore the interaction between plasticity, material heterogeneity, and fluid migration, thereby contributing to a more comprehensive understanding of the physical mechanisms underlying seismic events. Advancing these models brings us closer to developing robust, physics-based tools for earthquake forecasting and seismic risk mitigation.