A systematic comparison of experimental set-ups for modelling extensional tectonics

Analogue modellers investigating extensional tectonics often use different machines, set-ups and model materials, implying that direct comparisons of results from different studies can be challenging. Here we present a systematic comparison of crustal-scale analogue experiments using simple set-ups simulating extensional tectonics, involving either a foam base, a rubber base, rigid basal plates or a conveyor base system to deform overlying brittle-only or brittle-viscous models. We use X-ray computed tomography (CT) techniques for a detailed 3-D analysis of internal and external model evolution.

We find that our brittle-only experiments are strongly affected by their specific set-up, as the materials are directly coupled to the model base. Experiments with a foam or rubber base undergo distributed faulting, whereas experiments with a rigid plate or conveyor base experience localized deformation and the development of discrete rift basins. Pervasive boundary effects may occur due to extension-perpendicular contraction of a rubber base. Brittle-viscous experiments are less affected by the experimental set-up than their brittle-only equivalents since the viscous layer acts as a buffer that decouples the brittle layer from the base. Under reference conditions, a structural weakness at the base of the brittle layer is required to localize deformation into a rift basin. Brittle-viscous plate and conveyor base experiments better localize deformation for high brittle-to-viscous thickness ratios since the thin viscous layers in these experiments allow deformation to transfer from the experimental base to the brittle cover. Brittle-viscous-base coupling is further influenced by changes in strain rate, which affects viscous strength. We find, however, that the brittle-to-viscous strength ratios alone do not suffice to predict the type of deformation in a rift system and that the localized or distributed character of the experimental set-up needs to be taken into account as well.

Our set-ups are most appropriate for investigating crustal-scale extension in continental and selected oceanic settings. Specific combinations of set-up and model materials may be used for studying various tectonic settings or lithospheric conditions. Here, natural factors such as temperature variations, extension rate, water content and lithology should be carefully considered. We hope that our experimental overview may serve as a guide for future experimental studies of extensional tectonics.

1 Introduction

1.1 Analogue experimental set-ups for investigating extensional tectonics

Tectonic analogue modellers have historically used different experimental apparatus and model materials to investigate continental extension. These experiments have provided the scientific community with highly valuable insights into the evolution of basins and initial rift structures. However, a robust comparison between various experiments is challenging because of the variety of experimental set-ups and model materials that have been applied. Experiments have, for example, used set-ups involving (a combination of) basal foam bars, basal rubber sheet, rigid basal plates or conveyor-belt-style basal sheets with moving sidewalls to deform model materials (e.g. Allemand et al., 1989; Acocella et al., 1999; Bahroudi et al., 2003; Amilibia et al., 2005; Alonso-Henar et al., 2015; Philippon et al., 2015). Alternatively, extension can be achieved through gravitational gliding or spreading, in which case no moving sidewalls or an extending base needs to be applied (e.g. Gartrell, 1997; Fort et al., 2004; Acocella et al., 2005). Analogue materials used to simulate brittle parts of the lithosphere include, among others, quartz or feldspar sand, silica flour, micro-beads, and (kaolinite) clay (Hubbert, 1951; Elmohandes, 1981; Serra and Nelson, 1988; Clifton and Schlische, 2001; Autin et al., 2010; Abdelmalak et al., 2016; Klinkmüller et al., 2016, Fig. 1). Pure silicone oils and silicone putties are frequently used as analogues for ductile parts of the lithosphere (Weijermars and Schmeling, 1986; Basile and Brun, 1999; Michon and Merle, 2000; Sun et al., 2009; Rudolf et al., 2015, Fig. 1).

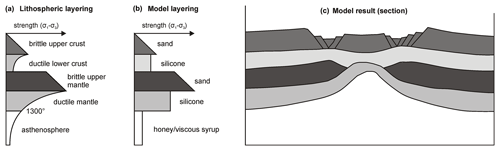
Figure 1 Example of model layering to simulate extension in a stable four-layer lithosphere. (a) Strength profile of the natural example with a brittle upper crust, a ductile lower crust, a strong brittle upper mantle and a ductile lower mantle that blends into the underlying asthenosphere at a temperature of 1300 ^∘C. (b) Model materials representing the various layers: sand for the brittle parts of the lithosphere and viscous silicone (mixtures) for the ductile crust and mantle. The asthenosphere is simulated with honey or viscous syrup. (c) Cross section at the end of an asymmetric extension experiment. Adapted from Allemand and Brun (1991) with permission from Elsevier.

Vendeville et al. (1987) present experiments that highlight several factors controlling the geometry of fault systems in extensional tectonics. The study used rubber sheet set-ups with a brittle sand layer for homogeneous thin-skinned deformation, brittle-viscous gravity-spreading models resting on a solid base and experiments with the whole brittle-viscous lithospheric analogue floating on a simulated asthenosphere. The results provide a first impression of the differences between these set-ups, revealing the correlation between fault spacing and layer thickness in brittle materials, rift localization in brittle-viscous settings and isostatic effects such as tilted margins due to the influence of the asthenosphere. Yet the many experimental parameters were widely different from experiment to experiment, making a quantitative comparison difficult.

Allemand and Brun (1991) test the influence of two-layer brittle-viscous material layering but using a conveyor belt set-up to achieve both symmetric and asymmetric extension with a velocity discontinuity (VD). The basal sheets diverge, here representing a fault in the underlying (not-simulated) brittle lithospheric mantle. Asymmetric extension is shown to generate strongly asymmetric rift geometries, in both brittle and brittle-viscous models. The rifts under symmetric extension conditions also develop a degree of structural asymmetry. The similarities of results from four-layer (lithospheric-scale) models (Fig. 1) to their two-layer model results support the validity of applying a VD to simulate faults in the brittle upper mantle. Model parameters such as layer thickness, material properties and extension velocities are, however, not clearly defined, again making a direct comparison of these experiments challenging.

Brun (1999) summarizes extension experiments with a focus on layer rheology and extension velocity. He shows that an increase in extension velocity in crustal-scale brittle-viscous conveyor belt models leads to an increase in viscous strength and brittle-viscous coupling, favouring widespread deformation or wide rifting. By contrast, low extension velocities lead to localized extension or narrow rifting. A similar effect is obtained by changing the brittle-to-viscous thickness ratio: a high ratio of 3:1 leads to low brittle-viscous coupling and narrow rifting, whereas a small ratio of 1:1 leads to high coupling and wide rifting. On a lithospheric scale, however, the behaviour of the upper mantle becomes important as well (Fig. 1); a single fault in a strong upper mantle layer may induce narrow deformation in the overlying crustal layers, whereas a weak upper mantle promotes distributed deformation. The models also suggest that within such wide rifts local weaknesses can account for the development of core complexes. In addition to providing a summarizing scheme similar to Brun (1999), Corti et al. (2003) show how magma presence can control rift initiation in narrow rifts and cause a wide rift to shift to core complex mode. The authors also describe the additional effects of oblique extension and multiple extension phases on rift evolution. However, the models presented in both review articles come from numerous studies and are often performed with very different techniques and parameters.

The additional significance of VDs in the brittle upper mantle was investigated by Michon and Merle (2000, 2003) by means of brittle-viscous base plate experiments, where the VD is situated at the edge of the plate. A single VD leads to asymmetric extension and the development of a single rift, whereas a double-VD experiment may form two or more rift basins, depending on the initial distance between the VDs. This is valid for high strain rates, as low strain rates focus deformation (narrow rifting), decreasing the number of rift basins. Apart from the varying strain rates and VDs, the other parameters such as model size, materials and layer thickness remained fixed.

Schreurs et al. (2006) compared results of a brittle-viscous plate base extension experiment that was run by five analogue laboratories. The overall experimental procedure was kept as similar as possible using, for example, the same foil to cover the base of the apparatus, the same extension velocity and the same viscous material (polydimethylsiloxane, PDMS). But differences occurred in brittle materials (different types of sand and a wet clay) and model dimension (width and length). This study illustrated the overall large-scale structural similarities, but also showed differences in fault dip angle and fault spacing that were related to differences in model materials and/or model set-up.

1.2 Analogue materials used in extension experiments

Brittle Mohr–Coulomb-type granular materials have very similar internal friction angles with respect to their natural analogues (ranging between ca. 25 and 40^∘; Schellart, 2000; Klinkmüller et al., 2016). Granular materials such as dry quartz sand have a very low cohesion and are considered a good analogue for large-scale models aiming at the brittle crust or the crust and lithospheric mantle (Fig. 1). By contrast, high-cohesion materials, such as silica flour and clay (C=40–750 Pa; Eisenstadt and Sims, 2005; Guerit et al., 2016), are better suitable for modelling the uppermost kilometres of the crust where cohesion is an important rheological factor. Intermediate cohesion values can be obtained by mixing granular materials (Abdelmalak et al., 2016; Montanari et al., 2017). Low-friction micro-beads with internal friction angles of ca. 20^∘ allow for the modelling of structural weaknesses or weak crustal lithologies (e.g. Colletta et al., 1991; Panien et al., 2005). The density of brittle analogue materials depends on various factors such as its specific density, grain size and shape, sorting, and handling techniques, as well as water content (for clays), but lies generally between ca. 1400 and 1800 kg m⁻³ (e.g. Krantz, 1991; Eisenstadt and Sims, 2005; Klinkmüller et al., 2016).

Pure silicone oils consist of polydimethylsiloxane (PDMS), are transparent, have a density of ca. 1000 kg m⁻³ (Weijermars and Schmeling, 1986) and a Newtonian viscosity between ca. 10³ and 10⁵ Pa s at room temperature and at typical experimental deformation rates (Rudolf et al., 2015; Schellart and Strak, 2016). Silicone putties are mixtures of polyborondimethylsiloxane (PBDMS) and inert fillers (Weijermars, 1986), and have higher densities than pure silicone oils. Examples of opaque silicone putties commonly used in analogue modelling include Rhodorsil Gomme GS1R (Cobbold and Quinquis, 1980), Rhodorsil Silbione 70009 (Nalpas and Brun, 1993) and Dow Corning DC3179 (Dixon and Summers, 1985). Their density range varies between ca. 1140 and 1420 kg m⁻³ and they display Newtonian viscosities between ca. 10⁴ and 4×10⁵ Pa s at room temperature (e.g. Casas et al., 2001; Cagnard et al., 2006; Konstantinovskaya et al., 2007). It should be noted that the viscosity of silicone-based materials can in some cases strongly depend on temperature (Cagnard et al., 2006) and also ageing processes have an effect on silicone behaviour (Rudolf et al., 2015, and references therein). Pure silicone oils and silicone putties can be mixed with, for instance, sand or metallic powders to modify the material's density and viscosity (e.g. Calignano et al., 2015; Zwaan et al., 2016). Other substances, such as paraffin and gelatin mixtures can be applied when power-law or temperature-dependent rheological behaviour is required (e.g. Zulauf and Zulauf, 2004; Boutelier and Oncken, 2011). In lithosphere-scale models, the weak ductile behaviour of the asthenospheric mantle is simulated with low-viscosity materials, such as honey, glucose syrup, mixtures of polytungstate with glycerol or even pure water (Mart and Dauteuil, 2000; Chemenda et al., 2002; Schellart et al., 2002, 2003; Willingshofer et al., 2005; Molnar et al., 2017). These normally exhibit Newtonian behaviour. Further details and references concerning the abovementioned and other analogue model materials can be found in a comprehensive review article by Schellart and Strak (2016).

1.3 Aims of this study

The analogue modelling work summarized above reveals a trend from a rather qualitative modelling approach to a more quantitative approach. Older studies tend to present a range of models with widely different parameters (for materials and set-up), which are often not fully described. By contrast, newer studies often specify such data in much detail, allowing repetition by analogue and also numerical means. Yet direct comparisons between the various methods remain challenging, especially since these methods aim to simulate different tectonic settings (see also Sect. 2.2 and 2.3). In theory, the scaling principles that have elevated analogue modelling from a qualitative to a quantitative method can be applied to compute how models should compare to each other (e.g. Hubbert, 1937; Ramberg, 1981; Weijermars and Schmeling, 1986). In practice, however, such calculations remain approximate. Different material handling techniques (laboratory traditions, the human factor) or climatic conditions (room temperature, humidity) may influence material behaviour and thus model results with the same set-up can vary from laboratory to laboratory (e.g. Krantz, 1991; Schreurs et al., 2006, 2016; Rudolf et al., 2015). Furthermore, our understanding of experimental material rheology may be incomplete or poorly constrained since some parameters are difficult to properly determine (e.g. Schellart, 2000; Eisenstadt and Sims, 2005; Schreurs et al., 2006; Dooley and Schreurs, 2012, and references therein; Ritter et al., 2016). Thus, the need for reference studies of lithospheric extension with standardized model parameters remains, and to our knowledge no such work is available to date.

The aim of this study is to systematically compare a series of simple crustal-scale normal-gravity laboratory experiments involving commonly used set-ups and to discuss the tectonic settings to which these would apply. We use either a foam base, a rubber base, rigid base plates or conveyor-belt-style plastic sheets as a mechanism to deform the overlying brittle or brittle-viscous experimental materials. This forms a total of 16 reference experiments. Various additional experiments serve to examine the effects of among others, varying extension velocity, layer thickness and brittle-to-viscous thickness ratio. We also apply X-ray computed tomography (XRCT or CT) for obtaining a highly detailed 3-D view of the internal as well as the external evolution of our experiments. We furthermore address the various boundary effects occurring in our experiments, a crucial factor that may strongly influence experimental results. We hope that the opportunities and challenges associated with our experimental set-ups and results, combined with the summary of materials above, may form an inspiration for future experimental work.

Table 1 Material properties.

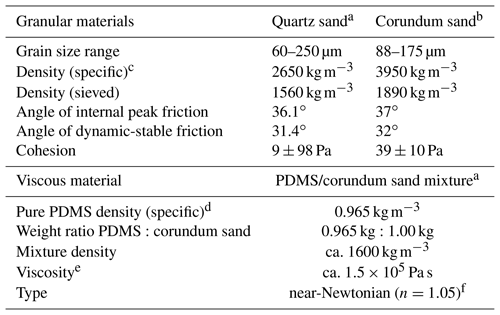
^a Quartz sand, and viscous mixture characteristics after Zwaan et al. (2016, 2018b, c). ^b Corundum sand characteristics after Panien et al. (2006). ^c Specific densities of quartz and corundum sands after Carlo AG (2019). ^d PDMS specific density after Weijermars (1986). ^e The viscosity value holds for model strain rates < 10⁻⁴ s⁻¹. ^f Stress exponent n (dimensionless) represents sensitivity to strain rate.

2 Materials and methods

2.1 Material properties

We ran brittle (single-layer) and brittle-viscous (two-layer) experiments to simulate a brittle upper crust and a complete brittle-ductile crust, respectively (Fig. 2). Reference brittle-only experiments contain a 4 cm thick layer of fine quartz sand (∅=60–250 µm angle of internal peak and stable friction: 36.1 and 31.4^∘, respectively; Zwaan et al., 2016, 2018b). The sand is sieved from ca. 30 cm height into the experimental apparatus to guarantee a sand density of ca. 1560 kg m⁻³. The sand is flattened using a scraper at every 1 cm thickness during preparation of the experiment, causing slight density variations, which subsequently appear on CT images as a “layering” (Fig. 4f, g). The reference experiments with a brittle-ductile layering are built of an additional 4 cm thick, near-Newtonian viscous layer (viscosity η; ca. 1.5×10⁵ Pa s; stress exponent n=1.05) consisting of a 1:1 weight mixture of SGM-36 polydimethylsiloxane (PDMS) silicone and corundum sand (ρ_specific=3950 kg m⁻³; Panien et al., 2006; Zwaan et al., 2016, 2018c; Carlo AG, 2019). The obtained density of the viscous material (ca. 1600 kg m⁻³) is close to that of the overlying quartz sand layer (1560 kg m⁻³). This results in a density profile that avoids the buoyant rise of the viscous material that would occur for a layering involving pure, low-density PDMS (ρ=965 kg m⁻³; Weijermars, 1986). Further material properties are listed in Table 1.

2.2 Experimental design

The experimental apparatus consists of a fixed base and two longitudinal sidewalls, which can move outward independently from each other above a fixed support table, their motion controlled by precise computer-guided stepper motors. The initial width of the experiment is 30 cm in all set-ups, which is considerably less than their length (as specified below). This high length-to-width ratio diminishes the influence of boundary effects at the short sidewalls. Through modification of the apparatus we can use four different methods to transfer deformation from the base of the set-up to the overlying experimental materials: by applying either a foam base or rubber sheet base for a distributed deformation setting or a base of rigid plates or conveyor belt system for focussed deformation (Fig. 2). The confinement along the short sidewalls varies according to the set-up, as explained below. Since the various set-ups differ significantly, we also specify which type of tectonic setting or crustal rheology is simulated (Fig. 3). An additional overview of the similarities and differences between our set-ups by means of (relative) velocities and shifts in reference frames is provided in Appendix A (Fig. A1).

2.2.1 Distributed extension set-ups

A foam base (F series experiments) induces distributed extension (e.g. Schreurs and Colletta, 1998; Schlagenhauf et al., 2008; Zwaan et al., 2016; Zwaan and Schreurs, 2017). An 8 cm thick RG 50 polyurethane foam base is first compressed between the sidewalls with the experiment subsequently constructed on top (Fig. 2a–c). As the sidewalls move apart during an experiment, the foam expands, causing the overlying materials to deform (Fig. 2b, c). Rubber sidewalls at the short ends of the set-up confine the materials, with the distributed extension of the rubber decreasing boundary effects there (Fig. 2a). All foam base experiments have a length of 79 cm for an initial length-to-width ratio of 2.6.

For the rubber base set-up (R series experiments) a 1.5 mm thick Neoprene rubber sheet is spanned between the two long sidewalls (e.g. Vendeville et al., 1987; Bahroudi et al., 2003; Bellahsen et al., 2003; Bellahsen and Daniel, 2005; Fig. 2d–f). Note that this is slightly different from set-ups applying a narrow rubber sheet between two rigid base plates. When these are subsequently moved apart, a limited band of distributed deformation occurs above the rubber while the plate edges essentially act as VDs (e.g. McClay and White, 1995; McClay et al., 2002; Corti et al., 2007; Henza et al., 2010). Instead, we use a full rubber base for our experiments in order to allow for a comparison with the foam base set-up and to achieve distributed extension throughout the experiment. When the long sidewalls move apart, the rubber sheet is stretched and extends uniformly along a velocity gradient with a constant slope, causing distributed deformation (Fig. 2e, f). The short sides of the experiment are free in experiments with only a brittle layer; that is, not confined by a sidewall that may influence the experimental results. The short sidewalls of the brittle-ductile rubber base experiments are enclosed by a sand talus so that the viscous material cannot escape sideways (Fig. 2d). Since the large forces involved in stretching a large rubber sheet may cause damage to the experimental apparatus, the length of the rubber base experiments is kept to 50 cm. Therefore, the initial length-to-width ratio is 1.7.

Previous authors have applied a rubber or foam base with an overlying brittle layer to simulate distributed thin-skinned extension (e.g. Bahroudi et al., 2003; Schlagenhauf et al., 2008). In nature, distributed extension in the brittle crust could develop in a setting with high brittle-ductile coupling between a brittle upper crust and a strong ductile lower crust (Fig. 3a), either due to high strain rates or high viscosity (Brun, 1999; Buiter et al., 2008; Allken et al., 2012; Zwaan et al., 2016). Note that the sub-crustal mantle has no direct influence in this case. By contrast, experiments with brittle-viscous layers on top of a rubber or foam base would simulate a normal brittle-ductile crust on top of a viscously deforming weak mantle (Fig. 3b). This setting, in which the strength of the lithosphere is determined by the brittle crust (Bürgman and Dresen, 2008), can be expected in a hot lithosphere, for instance above a mantle plume (Saunders et al., 1992; Burov et al., 2007) or in regions subject to enhanced radiogenic heating (Mareschal and Jaupart, 2013).

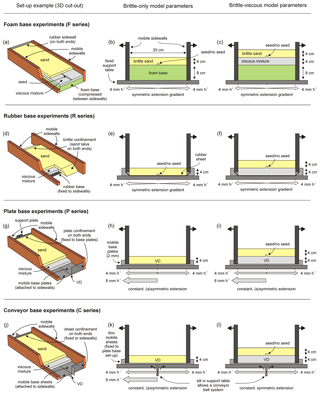
Figure 2 Experimental design adopted for our reference experiments. See Table 2 for a complete overview of the specific parameters applied in this study. Note that the 3-D cut-out views show examples of reference experiments with brittle-viscous layering. VD: velocity discontinuity. For details on the additional experimental parameters, see Table 2.

2.2.2 Localized extension set-ups

The plate base set-up (P series experiments) involves two 2 mm thick rigid plastic plates that are fixed to the long sidewalls (Fig. 2g–i) (e.g. Tron and Brun, 1991; Brun and Tron, 1993; Bonini et al., 1997; Keep and McClay, 1997; Michon and Merle, 2000; Gabrielsen et al., 2016). When these plates move apart with the long sidewalls, velocity discontinuities (VDs) develop at the basal edges of the plates. The support table below the plates prevents material from escaping (Fig. 2h, i). The short sidewalls are confined by a similar plate system that is fixed to the horizontal plates, thus moving in sync and creating the same boundary conditions as at the base of the apparatus (Fig. 2g). In contrast to the set-ups applying distributed extension described above, the rigid base plates allow both symmetric and asymmetric extension. In the former case, two moving VDs occur as the edges of both non-overlapping plates move apart, whereas the latter case results in only one VD (similar to Michon and Merle, 2000, see also Fig. A1). The initial length of the base plate experiments is 90 cm, so that the length-to-width ratio is 3. Although we did not measure the boundary friction between the plastic plates and quartz sand, it is likely to be close to the values reported by Panien et al. (2006) for similar quartz sand on top of either plastic or PVC: ca. 21^∘.

The final set-up is a modified version of the plate base set-up involving a “conveyor belt” type of deformation (C series experiments) (e.g. Allemand and Brun, 1991; Tron and Brun, 1991; Dauteuil and Brun, 1993; Keep and McClay, 1997; Román-Berdiel et al., 2000). Sub-millimetre-thick plastic sheets or foil (“Alkor” foil 120010 formerly produced by Alkor-Venilia and now available as “Gekkofix 11325” http://www.gekkofix.com last access: 19 May 2019; Klinkmüller et al., 2016) are fixed to the plate base set-up and are led down through a slit in the support table, along the central axis of the experiment (Fig. 2j–l). When the long sidewalls move apart, the sheets are pulled upward through the slit (Fig. 2k, l). In contrast to the plate base experiments, a single VD occurs, which remains located at the centre of the experiment. Since this is true for both symmetrical and asymmetrical experiments (Fig. 2k, l), the plate base and conveyor belt set-ups are different. Yet the asymmetric conveyor belt mechanism is, after a switch of reference frame, the same as the asymmetric plate base mechanism (Fig. A1) and should thus produce an identical result. The same sheet system is applied on the short sidewalls in order to have a continuous confinement (Fig. 2j). These conveyor belt experiments have the same length-to-width ratio as the plate base experiments, i.e. 3. The angle of boundary friction of the foil with quartz sand lies between 15 and 21^∘ (Schreurs et al., 2016).

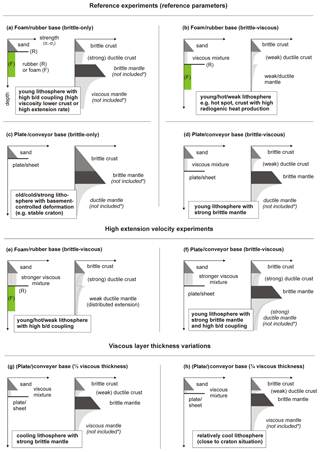
Figure 3 Schematic experimental and natural strength profiles (always left and right, respectively), indicating the lithospheric setting that experiments may represent. The strength profiles of our experiments are qualitative (no scale for stress) and we have exaggerated the viscous strength for visualization purposes. Natural strength profiles can be affected by numerous factors, as discussed in Sect. 4.7 and illustrated quantitatively in Fig. 12. Dotted lines in (e) and (f) indicate the schematic strength profile under reference conditions for comparison. Symbol ^* means the effects of these parts of the lithosphere are not simulated in the given case. b / d is brittle/ductile.

Both the plate base and conveyor base experimental designs involve localized deformation at VDs. These VDs simulate a discrete fault (or shear zone) in a strong layer underlying the experimental materials. In the case of our brittle-only experiments, this would translate to a fault at the base of the upper crust. In order to have a fault in the lower crust, the latter needs to behave in a brittle fashion, which in our case would be expected in an old, cool crust (Fig. 3c). On a smaller scale, one can also interpret the VD as a reactivated basement fault affecting overlying strata (e.g. Acocella et al., 1999; Ustaszewski et al., 2005). Concerning our brittle-viscous crustal experiments, the VD translates to a fault in a strong upper mantle (e.g. Allemand and Brun, 1991; Michon and Merle, 2000). Such a setting can be expected in a young stable lithosphere with a strong brittle mantle (Fig. 3d). Note that VDs could be produced by differential motion focussed along various types of (linear) irregularities or inherited structures within the lithosphere, but that these may be challenging to simulate. For instance, Morley (1999) points out that (1) VDs in analogue experiments cannot serve to reproduce irregularities within the overlying layers, but only structures at the base of these layers, and that (2) VDs by definition represent discrete features, rather than pervasive structures (e.g. foliations) that may be present throughout a volume of rock.

Table 2 List of experimental parameters.

b / v: Brittle-viscous. CT: CT-scanned models. ^a Valid for a lower crustal viscosity (η) of 10²¹ Pa s. ^b See Appendix B for calculations. ^c Two-phase experiment with 40 mm of extension at 8 mm h⁻¹ followed by 20 mm of extension at 40 mm h⁻¹. ^d Total extension: 60 mm. ^e Initial experiment width 25 cm instead of 30 cm. ^f 54 mm total extension; rubber sheet ripped partly after ca. 2 h (40 mm extension). ^g Experiments with a total 40 mm thickness (20 mm brittle, 20 mm viscous) and 20 mm total extension. ^h Attempt to reduce boundary effects (see text and Fig. C2 in Appendix C for details).

2.3 Additional experimental parameters and definition of coupling

For every experimental set-up, we test brittle-only materials and brittle-viscous layering, with a reference layer thickness of 4 cm, so that brittle-only and brittle-viscous experiments are 4 and 8 cm thick, respectively. However, for specific experiments, we either apply a 4 cm thick brittle-viscous layering, or we modify the brittle-to-viscous thickness ratio by decreasing the thickness of the viscous layer to 2 or 1 cm, in order to capture the effects that a different crustal layering may have on extensional structures (details in Table 2). This decrease in viscous layer thickness can be either due to a thinner, viscous lower crust, assuming that the brittle crustal thickness remains the same (Fig. 3g, h), or an increase in brittle crustal thickness with a constant Moho depth. In both cases, this would result in a relative strengthening of the crust with respect to the default layering. Brittle-to-viscous strength ratios are given in Table 2, based on the calculations in Appendix B.

We also apply “seeds” to localize deformation in several experiments (Fig. 2, Table 2). These seeds are 1 cm thick, semi-cylindrical viscous rods of the previously described PDMS/corundum sand mixture that are placed at the base of the brittle layer. The seeds are continuous and stretch along the full axis of the experiment. They form weak zones within the sand pack, where deformation may localize, since the strong sand cover is locally thinner and thus weaker (e.g. Zwaan et al., 2016). Although we acknowledge that surface processes can influence rift evolution (e.g. Burov and Cloetingh, 1997; Bialas and Buck, 2009; Zwaan et al., 2018a), we neither apply erosion nor sedimentation in our experiments, since we aim to directly evaluate differences in experimental results obtained by differences in simple experimental set-ups.

Our reference extension velocity is 8 mm h⁻¹, with both long sidewalls moving 4 mm h⁻¹ for symmetrical extension, or a single sidewall moving 8 mm h⁻¹ for asymmetrical extension (Fig. 2). Considering a reference duration of 5 h, the total extension equals 40 mm (or ca. 13 %, given an initial width of ca. 30 cm). In addition, we varied the extension velocity for selected experiments. In the case of the brittle-only experiments, however, this should not affect brittle deformation structures because of the time-independent mechanical behaviour of the sand that directly overlies the model base. For brittle-viscous experiments, variations in extension velocity are equivalent to variations in viscous strength (e.g. Brun, 1999; Buiter et al., 2008) and will thus affect the strength contrast and coupling between the brittle and viscous materials (Fig. 3e, f; Table 2; Appendix B). In the experiments with a foam or rubber base, a strengthening of the viscous material, due to an increase in extension rate, can be seen as simulating strengthening of a hot lithosphere with increased brittle-ductile coupling between the upper and lower crust, but still a relatively weak mantle (compare Fig. 3b with Fig. 3e). In the plate base or conveyor base set-up equivalent, a higher extension rate would then represent a similarly hot crust subject to increased brittle-ductile coupling overlying a brittle upper mantle (compare Fig. 3d with Fig. 3f). Higher extension rates may also affect the degree of coupling between the analogue materials and base of the set-up, which can have an important influence on the development of a rift system (e.g. Corti et al., 2003). We therefore distinguish the following types of coupling: brittle-basal (between the brittle layer and the base of the set-up in brittle-only models), brittle-viscous (between brittle and viscous layers in brittle-viscous experiments) and viscous-basal (between a viscous layer and the base of the set-up in brittle-viscous experiments). In addition, we can also describe to what degree the brittle cover is decoupled from the base of the set-up by the viscous layer in brittle-viscous experiments.

Furthermore, a thin (ca. 0.5 mm thick) grid made of dark (corundum) sand with a 4×4 spacing applied to the surface of each experiment allows a first-order assessment of surface deformation by means of top-view images, without influencing the experimental results. Furthermore, every component of the machine around the experiment consists of X-ray-transparent materials to allow for CT scanning and various experiments are analysed with CT techniques to reveal their 3-D internal evolution. Most experiments marked in Table 2 as “CT-scanned” were a rerun of previous tests performed without CT scanning. Various other experiments were also repeated and did indicate little structural variation, thus good reproducibility is ensured (Table 2; details presented in Appendix C; Figs. C1, C2). Moreover, surface view videos and 3-D CT imagery depicting the evolution of our experiments are available as a data publication (Zwaan et al., 2019).

Table 3 Scaling parameters.

UC: Upper Crust
^a Valid for reference set-ups

2.4 Scaling

We calculate stress ratios (convention: ${\mathit{\sigma }}^{*}={\mathit{\sigma }}_{\mathrm{experiment}}/{\mathit{\sigma }}_{\mathrm{nature}}$) based on Hubbert (1937) and Ramberg (1981):

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\sigma }}^{*}={\mathit{\rho }}^{*}{h}^{*}{g}^{*},\end{array}$$

where ρ^*, h^* and g^* represent the density, length and gravity ratios, respectively.

The strain rate ratio ${\dot{\mathit{\epsilon }}}^{*}$ is derived from the stress ratio σ^* and the viscosity ratio η^* (Weijermars and Schmeling, 1986):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\dot{\mathit{\epsilon }}}^{*}={\mathit{\sigma }}^{*}/{\mathit{\eta }}^{*}.\end{array}$$

Subsequently, the velocity ratio v^* and time ratio t^* can be obtained as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\dot{\mathit{\epsilon }}}^{*}=v^{*}/h^{*}=\mathrm{1}/t^{*}.\end{array}$$

Natural values for lower crustal viscosity may have a wide range depending on the specific tectonic setting (η=10¹⁹–10²³ Pa s; e.g. Buck, 1991; Brun, 1999; Bürgman and Dresen, 2008). We assume an intermediate lower crustal viscosity of 10²¹ Pa s, which is in line with recent findings (Shinevar et al., 2015, and references therein). An hour in our experiments thus translates to 0.84 Myr in nature and our reference velocity (8 mm h⁻¹) converts to a velocity of ca. 5 mm yr⁻¹ in nature, close to typical values for initial continental rifting (1–5 mm yr⁻¹, e.g. Saria et al., 2014). The scaling parameters are summarized in Table 3.

To ensure dynamic similarity between brittle natural and experimental materials, we calculate the ratio R_s, which is a function of gravitational stress and cohesive strength (C) (Ramberg, 1981; Mulugeta, 1998):

$$\begin{array}{}\text{(4)}& {\displaystyle }{R}_{\mathrm{s}}=\left(\mathit{\rho }gh\right)/C\end{array}$$

when adapting an intermediate cohesion of ca. 8 MPa for upper crustal rocks, we obtain an R_s value of 68 for both nature and our experiments. This cohesion is relatively low compared to the ca. 20–40 MPa measured for continental rocks (e.g. Handin, 1969; Jaeger and Cook, 1976; Twiss and Moores, 1992), but should be reasonable given that the strength of the earth's crust is generally reduced due to previous phases of tectonic activity.

For verifying the dynamic similarity of viscous materials, the Ramberg number R_m applies (Weijermars and Schmeling, 1986):

$$\begin{array}{ll}{\displaystyle }{R}_{\mathrm{m}}& {\displaystyle }=\text{gravitational stress/viscous strength}\\ \text{(5)}& {\displaystyle }& {\displaystyle }=\left(\mathit{\rho }g{h}^{\mathrm{2}}\right)/\left(\mathit{\eta }v\right).\end{array}$$

Our experimental and the equivalent natural R_m values are the same: ca. 75.

The reference experiments are thus properly scaled. Scaling the other experiments can be more challenging. When adopting a lower crust viscosity of 10²¹ Pa s, many experiments would seem to extend unrealistically fast (Table 2). However, when assuming a higher lower crustal viscosity of 10²² or even 10²³ Pa s (e.g. Buck, 1991), the equivalent natural extension rates to those listed in Table 2 are more reasonable.

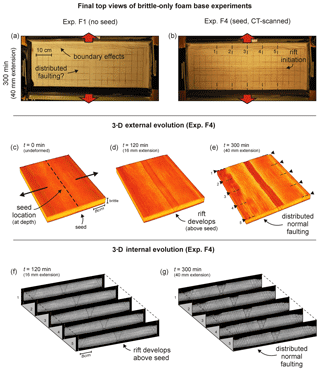
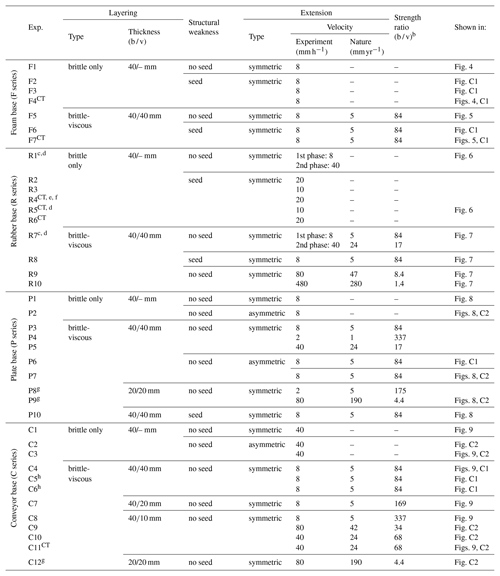
Figure 4 Foam base (brittle-only) results. (a, b) Top views depicting the final surface structures of models F1 (no seed) and F4 (with seed). The brittle layer is 4 cm thick and the extension velocity is 8 mm h⁻¹. Note that the boundary effects are present on both sides of the experiment, but these are partially invisible due to shadow. (c–d) 3-D evolution of CT-scanned experiment F4. (f, g) 3-D internal evolution of CT-scanned experiment F4.

3 Results

3.1 Foam base experiments (F series)

Figure 4 shows the results of two brittle-only foam base experiments (set-up in Fig. 2a, b). Experiment F1 (without seed) develops no distinct structures except for significant boundary effects along the longitudinal sidewalls towards the end of the experiment (Fig. 4a). In contrast, the seed in experiment F4 localizes deformation in the centre of the experiment, although faulting along the long sidewalls is also visible at the surface (Fig. 4b). The CT data from experiment F4 (with seed) reveals the evolution of these structures in more detail (Fig. 4c–g). After ca. 60 min (8 mm) of extension, a rift starts forming above the seed and becomes visible at the surface after 120 min (16 mm of extension, Fig. 4d, f). This main rift structure continues developing towards the end of the experiment (Fig. 4e, g). The CT images show how additional faulting occurs: first along the sidewalls (Fig. 4d, f), later on throughout the experiment so that at the end of the experiment, pervasive sidewall-parallel striking normal faulting is omnipresent (Fig. 4e, g). Note that this distributed faulting is not visible on the top-view images due to the low fault offsets at the surface that do not cast shadows on the experiment surface (Fig. 4b), and may very well be present in the experiment without seed as well (F1, Fig. 4a).

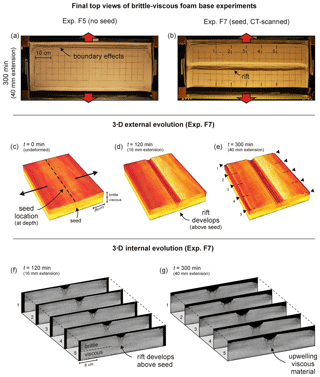
Figure 5 Foam base (brittle-viscous) results. (a, b) Top views depicting the final surface structures of experiments F5 (no seed) and F7 (with seed). Both the brittle and viscous layers are 4 cm thick and the extension velocity is 8 mm h⁻¹. Note that the boundary effects are present on both sides of the experiment, but these are partially invisible due to shadow. (c–d) 3-D evolution of CT-scanned experiment F7. (f, g) 3-D internal evolution of CT-scanned experiment F7.

The evolution of foam base experiments with a brittle-viscous layering is summarized in Fig. 5 (set-up in Fig. 2a, c). Experiment F5, without a seed, forms no central rift basin (Fig. 5a). Instead, all deformation is concentrated as boundary effects along the long sidewalls. By contrast, experiment F7, with a seed, produces a well-developed symmetric rift structure. Still this experiment also produces some minor faulting along the long sidewalls (Fig. 5b). CT images illustrate the 3-D evolution of experiment F7 (Fig. 5c–g). Soon after initiation (30 min, 4 mm extension), a central rift structure with two main boundary faults develops above the seed. As the experiment progresses, this structure continues evolving: the rift basin grows deeper and the brittle material situated between the initial boundary faults starts breaking up due to internal faulting (Fig. 5d, f). Some boundary effects develop, but are relatively minor with respect to the central rift structure (Fig. 5d–g). Towards the end of the experiment the brittle layer is almost breached by the upwelling viscous layer (Fig. 5e, g). In this experiment, deformation is strongly focussed on the rift structure and no distributed faulting can be distinguished.

Figure 6 Rubber base (brittle-only) results. (a, b) Top views depicting surface structures of experiments R1 (no seed) and R5 (with seed) after 40 mm of extension. Note that panel (a) represents the first phase of experiment R1 (8 mm h⁻¹, until 40 mm extension) and (a') the second phase where an additional 20 mm of extension with an enhanced extension velocity of 20 mm h⁻¹ was applied to the same experiment to amplify fault structures. Experiment R5 was run with an extension velocity of 10 mm h⁻¹. These deviations from the reference extension velocity (8 mm h⁻¹) are permissible, since the behaviour of sand is time-independent. The sand layer is 4 cm thick in both experiments. Note that the boundary effects are present on both sides of the experiment, but these are partially invisible due to shadow. (c–d) 3-D evolution of CT-scanned experiment R5. (f, g) 3-D internal evolution of CT-scanned experiment R5.

3.2 Rubber base experiments (R series)

The surface evolution of two selected rubber base experiments built of only sand is depicted in Fig. 6 (set-up in Fig. 2d, e). Experiment R1 (Fig. 6a, a') has no seed to localize deformation and, as a consequence, deformation focuses along the sidewalls. In addition, remarkable conjugate faults develop within the standard experiment duration (300 min, 40 mm of extension), but are not well visible on our top-view images since they do not create significant topography (Fig. 6a). However, an additional phase of extension in experiment R1 (30 min at 40 mm h⁻¹) helps to highlight these conjugate faults (Fig. 6a'). In contrast to experiment R1, experiment R5 contains a viscous seed that focuses faulting along the experiment's central axis (Fig. 6b). As a result, this experiment develops a central rift structure. Similar to experiment R1, well-defined conjugate faults occur as well.

The CT-derived 3-D images from experiment R5 (Fig. 6c–g) reveal how deformation localizes along the seed and the sidewall in the initial stages, forming a cylindrical central rift structure (Fig. 6d). However, after some 20–25 mm of extension, the conjugate sets of vertical strike–slip faults start developing (Fig. 6f), which become pervasive toward the end of the experiment (Fig. 6e, g). This curious feature is the result of along-strike compression, as the orthogonally extending rubber sheet contracts perpendicular to the extension direction (Fig. 6a'). Yet the rift structure continues to evolve toward the end of the experiment run (Fig. 6e, g).

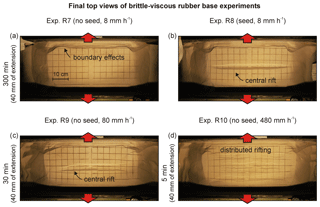
Figure 7 Rubber base (brittle-viscous) results. Top views depicting the final surface structures of (a, b) experiments R7 and R8 (reference extension velocity of 8 mm h⁻¹) and (c, d) R9 and R10 (high extension velocity experiments: 80 and 480 mm h⁻¹, respectively). Note that boundary effects, although partially invisible due to shadow, are present on all sides of the experiment and therefore especially in the corners.

Figure 7 shows results of four brittle-viscous rubber base experiments (set-ups in Fig. 2d, f). Experiment R7, without seed, produces no clear surface structures except for strong boundary effects along the sidewalls (Fig. 7a). In contrast, experiment R8 (with seed) experiences early fault localization (after 30 min a rift becomes visible at the surface), which continues evolving towards the end of the experiment (Fig. 7b). However, this experiment also develops strong boundary effects along the long sidewalls and at the corners, where some viscous material flows into the gap between the original sand buffer and the retreating sidewalls. The rift structure is best developed in the centre of the experiment and dies out towards the short sidewalls, involving slight block rotation of the sand layer in the four corners of the experiment (Fig. 7b).

Experiment R9 was run at an increased extension velocity of 80 mm h⁻¹ (Fig. 7c) and produces a central rift that is quite similar to the rift in experiment R8 (Fig. 7b), even though no seed is included. Significantly higher extension velocities (480 mm h⁻¹ in experiment R10) result in strongly distributed deformation with multiple rifts (Fig. 7d). These three experiments without a seed at different extension rates (Fig. 7a, c, d) reveal the effect of decreasing strength contrasts between the brittle and viscous layers (strength ratios of 84, 8.4 and 1.4, respectively, Table 2), of which the implications are discussed in Sect. 4.4.

3.3 Plate base experiments (P series)

Experiments P1 and P2 consist of a brittle sand layer on top of plastic rigid base plate(s) (Figs. 2h, 8a, b). In experiment P1 we apply symmetric extension, whereas in experiment P2 extension is asymmetric. Both experiments initially develop a rift above the velocity discontinuity along the central axis of the experiment. However, with continued extension experiment P1 develops a rift basin with a central horst block in the middle, which does not develop in experiment P2 (Fig. 8a, b). Otherwise, both rift structures have the same width. No boundary effects occur along the long sidewalls.

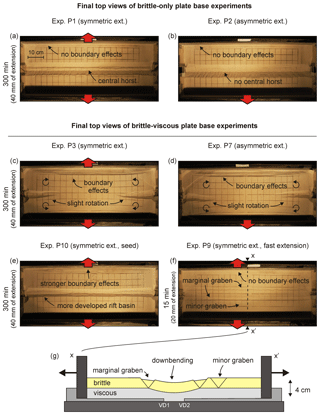
Figure 8 Overview depicting our plate base results. (a, b) Top views of brittle-only experiments P1 (symmetric extension) and P2 (asymmetric extension). (c–f) Brittle-viscous experiments in map view: (c–d) experiments P3 and P7 (reference extension velocity experiments, without seed), (e) Exp. P10 (reference extension velocity, with seed), (f) Exp. P9 (40 mm total thickness, high extension velocity of 80 mm h⁻¹, no seed). Note that boundary effects are present on both sides of the experiment, but these are partially invisible due to shadow. (g) Schematic section depicting the internal structures of experiment P9 interpreted from surface data and the topography of the stretched viscous material as observed after removal of the sand at the end of the simulation. Note the two VDs; the base plates are 2 mm thick each.

Figure 8c–g shows the results of the plate base experiments with brittle-viscous layering (set-up in Fig. 2g, i). Experiments P3 and P7 are following symmetrical and asymmetrical extension, respectively. No seed is included. The structural evolution is similar for both experiments. Rifting initiates at the short sidewalls, where both the base plates and confining plates are moving apart (Figs. 2g, i, 8c, d). These rifts propagate slightly towards the centre of the experiment, but strong boundary effects along the long sidewalls take up much of the extension there and no continuous rift structure develops in the centre of the experiment (Fig. 8c, d). As a result, block rotation (ca. 3^∘ around a vertical axis near the tips of the propagating rifts) occurs at the short ends of the experiments (Fig. 8c, d). The surface structures are largely the same in both experiments, suggesting that the application of symmetric or asymmetric extension does not have a significant influence on this type of experiment.

The application of a seed on top of the viscous layer (Exp. P10, in symmetric extension) results in early localization and rift development along the central axis of the experiment (Fig. 8e). This structure continues developing throughout the experiment, yet more extension is accommodated towards the short sidewalls than the middle section, where boundary effects along the long sidewalls take up a larger part of the deformation, similar to experiments P3 and P7 (Fig. 8c, d).

The thick viscous layer in experiments P3 and P7 likely dampens the influence of the basal boundary condition on the sand layer. We therefore ran further tests (experiments P8 and P9, both with half the reference layer thicknesses, keeping the same brittle-to-viscous ratio, i.e. 2 cm brittle and 2 cm viscous material, without seed). Both these experiments did not produce a continuous rift basin either. However, experiment P9, with a high 80 mm h⁻¹ extension velocity and a low brittle-to-viscous strength ratio of 4.4 (compared to the reference ratio of 84), produces interesting basin geometries (Fig. 8f, g). Instead of developing a simple rift structure, the viscous layer at the centre of the experiment is strongly stretched, creating a depression with continuous rift basins at its margin due to what seems to be passive down-bending as the underlying viscous layer is stretched (Fig. 8g). Secondary graben structures develop further away from the central depression, indicating a degree of distributed deformation. Notably, no boundary effects occur along the long sidewalls in contrast to the other brittle-viscous plate base experiments.

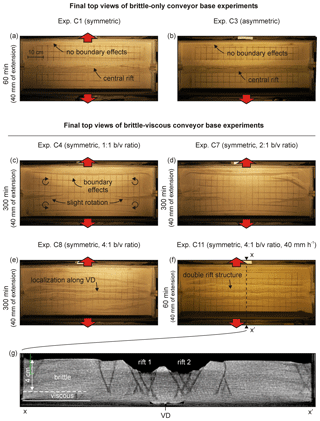
Figure 9 Overview of conveyor base results (all without seed). Top views depicting the final surface structures of (a, b) brittle-only experiments C1 and C3, (c, d) brittle-viscous Exp. C4 (reference layering and extension velocity), (d) experiment C7 (reference extension velocity, brittle-to-viscous ratio: 2), (e) Exp. C8 (reference extension velocity, brittle-to-viscous ratio: 4) and (f) Exp. C11 (elevated extension velocity: 40 mm h⁻¹, brittle-to-viscous ratio: 4). Note that the boundary effects (if present) occur on both sides of the experiment, but may be partially invisible due to shadow. (g) CT section depicting the internal structures of Exp. C11.

3.4 Conveyor base experiments (C series)

Figure 9 shows the results of the conveyor base set-up with only a brittle layer (experiments C1 and C3) (set-up in Fig. 2j, k). Both experiments develop a large rift structure along the central axis of the experiment (Fig. 9a, b), rather similar to the plate base experiments P1 and P2 (Fig. 8a, b). We do, however, not directly observe a difference between results obtained with symmetrical and asymmetrical extension.

The results of the brittle-viscous experiments show more diversity than their brittle-only counterparts (Figs. 2j, l, 9c–g). Experiment C4, with symmetrical extension, develops two rifts that originate from the short sidewalls and propagate towards the experiment centre (Fig. 9c). They do, however, not connect, as boundary effects along the long sidewalls take up most of the deformation in the centre, similar to the structures observed in the plate base equivalents (experiments P3 and P7, Fig. 8c, d). We did not run an asymmetrical extension experiment with brittle-viscous layering since we did not expect significant differences. Instead, we attempted to reduce boundary effects along the short sidewalls by applying lubricants or adding a sand buffer as proposed by Tron and Brun (1991) (experiments C5 and C6, respectively). Unfortunately, the boundary effects remained or got worse (See Appendix C, Fig. C1). Furthermore we ran the conveyor base equivalent of experiment P9 (2 cm sand, 2 cm viscous material and 80 mm h⁻¹ extension; Fig. 8f, g), labelled C12, with very similar results to the plate base experiment (Fig. C2).

We also tested the effect of decreasing viscous layer thickness in experiments C7 and C8, thus simultaneously decreasing and increasing the brittle-to-viscous thickness and strength ratios, respectively. In experiment C7 (Fig. 9d), the thickness and strength ratios are 2 and 168, which does not lead to a significantly different structural evolution compared to the reference set-up of experiment C4 (Fig. 9c). However, decreasing the viscous layer thickness further to 1 cm (thickness and strength ratios: 4 and 337) in experiment C8 (Fig. 9e) causes localization of faulting along the central axis of the experiment during early stages of deformation, and the development of a dual rift on both sides of the VD with a horst in the middle. This central structure subsequently remains in place but faulting becomes more widespread towards the end of the experiment (Fig. 9e).

Additional tests with higher extension velocities (80 and 40 mm h⁻¹ for experiments C9 and C10/C11, respectively; see Table 2, Fig. 9f, and Appendix C, Fig. C2) have shown to improve rift localization, as faulting is less widely developed than in experiment C8 (Fig. 9e). Experiment C10 was subsequently rerun in the CT scanner as experiment C11 for further analysis (Fig. 9g). We observe that these specific experiments develop the same features: a double-rift system on either side of the VD, of which the internal structures become more complex with time, and a central intact, but subsided, horst in the rift centre (Fig. 9g). We also observe the development of minor additional rift basins striking parallel. Slight boundary effects occur along the long sidewalls in experiments C10 and C11 as well (Fig. 9f, g).

Table 4 Overview of links between our experimental set-ups and initial conditions, the resulting structures observed in our experiments and their potential natural analogues.

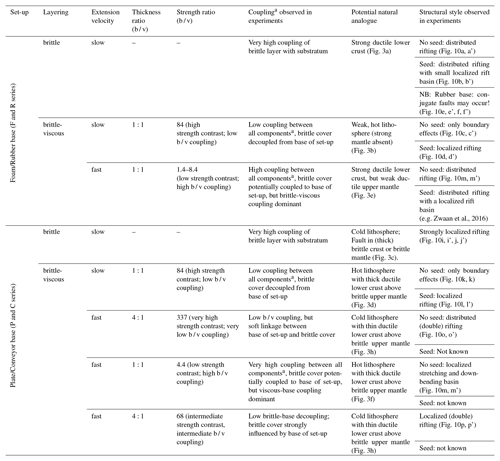
b / v: brittle-viscous. ^a We distinguish four types of coupling and decoupling: brittle-basal, brittle-viscous and viscous-basal coupling, as well as cover-basal decoupling due to the
presence of a viscous layer (see Sect. 2.3). ^b All components: all parts of the experiment, i.e. the sand layer, viscous layer and substratum (base of the set-up).

4 Discussion

4.1 General structures

We present a schematic overview of our experimental results in Fig. 10, summarizing the general structures in map view and section, and Table 4, linking these observations with potential natural settings. A clear distinction exists between the brittle-only experiments (left-hand half of upper three rows in Fig. 10) and the brittle-viscous experiments (right-hand half of upper three rows in Fig. 10) since the viscous layer acts as a buffer between the deformation-inducing base and the overlying sand. In the brittle-only experiments, no such buffer exists and deformation induced by the base of the set-up is directly transmitted to the overlying sand cover, leading to more distinct structural differences between the experimental series. In addition, the bottom row of Fig. 10 summarizes the structures observed in the high extension velocity experiments and the tests with high brittle-to-viscous ratios, leading to different degrees of coupling and more complex surface structures. Our experimental results are discussed in more detail below.

Figure 10 Schematic summary of our experimental results. (a–l) Experiments with reference brittle-to-viscous ratios (1:1) and reference extension velocities (8 mm h⁻¹). (^* means plate base experiment result only). All sections shown go through the central part of the experiment where boundary effects are minimal. (m–p) Additional brittle-viscous experiments with high extension velocities (80 mm h⁻¹) and/or high brittle-to-viscous ratios (4:1).

4.2 Brittle-only reference experiments

In the foam base experiments, the sand above the foam directly experiences the distributed deformation induced by the expanding foam, causing fault development throughout the experiment, but also along the long sidewalls (Figs. 4a, 10a). Schlagenhauf et al. (2008) report similar but more pronounced distributed rifting, possibly enhanced by a higher degree of extension of their foam base (20 % vs. our 13 %) and a thicker sand pack (8 cm vs. our 4 cm). Seeds do localize rift basins in our experiments (Figs. 4b–g, 10b), but these structures only account for a minor part of the extension as the rifts experience little subsidence with respect to most other experiments (e.g. P1 and P2 in Figs. 8a, b, 10). The brittle-only rubber base experiments produce similar structures as the brittle-only foam base experiments: distributed deformation and a minor axial rift when a seed is applied (Figs. 6, 10e, f). Significant faulting develops at the long sidewalls and migrates towards the centre of the experiment (Fig. 6c–g), which could be explained by stronger strain gradients in the rubber near the sidewalls (Ackermann, 1997). A similar effect could possibly occur in the foam base experiments as well, explaining the comparable boundary effects (Fig. 4). It is worth noting that the results from our experiments with a full rubber base (distributed faulting) differ from those obtained with narrow rubber sheets between base plates (localized and well-developed rift basins, e.g. McClay and White, 1995; McClay et al., 2002; Schlische and Withjack, 2009). This is because in the latter experiments, deformation is strongly concentrated above the rubber sheets, with the edges of the plates acting as VDs. These models produce well-developed rift structures but mix two basal boundary conditions (distributed extension and VDs) making it more difficult to identify equivalent natural conditions (Morley, 1999, see also Sect. 4.6).

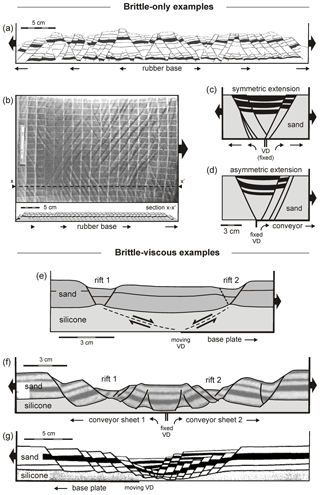
Figure 11 Examples of previously published analogue models of extensional tectonics. (a) Cross section of a brittle-only rubber base model, as used for homogeneous thin-skinned deformation. Note the conjugate fault sets. Adapted from Vendeville et al. (1987) with permission from the Geological Society, London. (b) Top view and cross section of a brittle-only rubber base model similar to panel (a), although developing the conjugate fault sets due to extension-perpendicular contraction of the rubber sheet (Poisson effect). Adapted from Bahroudi et al. (2003) with permission from Elsevier. (c–d) Cross sections of brittle-only conveyor base experiments with (c) symmetric or (d) asymmetric extension, both including syn-rift sedimentation. Here the VD may represent a basement structure controlling deformation in the overlying strata. Redrawn after Allemand and Brun (1991) with permission from Elsevier. (e–g) Cross sections of brittle-viscous models with a plate base or conveyor belt set-up, with the VD representing a fault in the strong brittle mantle affecting the overlying crustal analogues. (e) Brittle-viscous plate base model with asymmetric extension, illustrating the relation between the velocity discontinuity (VD) and the two rift basins. Compare with experiment C11 (Figs. 9f, g, C2). Redrawn (with permission from Elsevier) after Michon and Merle (2003), who investigated the European Cenozoic Rift System and the influence of VDs in a strong upper lithospheric mantle. (f) Symmetric extension model with conveyor set-up and brittle-viscous layering, designed to simulate the influence of a strong mantle on a two-layer crust. Adapted from Tron and Brun (1991) with permission from Elsevier. (g) Brittle-viscous plate base model with asymmetric extension. Note that this experiment includes syn-rift sedimentation and aims to reproduce the North Sea Viking Graben. Modified after Brun and Tron (1993) with permission from Elsevier. Black arrows indicate extensional motion. VD: velocity discontinuity.

Our rubber base experiments also develop conjugate strike–slip faults due to the contraction of the rubber perpendicular to the extension direction (Poisson effect) (Smith and Durney, 1992; Venkat-Ramani and Tikoff, 2002, Figs. 4a', 10e, f). Such structures are not always observed in other model studies applying a rubber base set-up (e.g. Vendeville et al., 1987; Fig. 11a). The Poisson effect-related structures we obtain are probably due to the relatively low length-to-width ratio rubber base we use (ca. 1.7). Narrow rubber base models by McClay and White (1995) and McClay et al. (2002) with much higher length-to-width ratios (6 and 4, respectively) do not undergo any visible contraction perpendicular to the extension direction, whereas an experiment by Bahroudi et al. (2003) with a length-to-width ratio of 0.8 develops strong conjugate faulting (Fig. 11b). The faults in Bahroudi et al. (2003) have a normal fault component as well, possibly because the rubber was stretched from one side only. It is furthermore interesting to note that the Poisson effect may occur in very different types of models or materials. Chemenda et al. (2002), for instance, applying an elasto-plastic mixture of various components floating on water to simulate the lithosphere and asthenosphere, also obtain pervasive conjugate faults due to extension-perpendicular contraction.

Contrary to their rubber and foam base equivalents, a strong localization of faulting above the velocity discontinuity (VD) occurs in the brittle-only plate base and conveyor base experiments (Figs. 8a, b, 9a, b, 10i, j). The plates and sheets translate overlying materials, except at the velocity discontinuity, where extension localizes and deep rift basins form. The centre of the rift basins in both the asymmetric and symmetric experiments lies practically at the same level as the experimental base at the end of the experiment (4 cm depth, scaling to a 20 km deep basin in nature) (Figs. 8a, b, 9a, b, 10i, j). In nature, isostatic compensation would have reduced basin depth, but this effect is absent here. Such experiments may, therefore, best be used for investigating initial (small) amounts of extension (e.g. maximum of half the thickness of the brittle crust). Larger amounts of extension could be simulated when significant sedimentation is applied, preserving a more realistic topography by filling in the generated “accommodation space” and providing additional material for the formation of new structures (e.g. Allemand and Brun, 1991; Brun and Tron, 1993; Keep and McClay, 1997; Gabrielsen et al., 2016, Fig. 11c, d). The small horst structure along the axis of the symmetric extension plate base experiment (Figs. 8a, 10i) is likely formed when both plates move away, leaving a small quantity of material behind in the middle. Previous authors have shown the impact extension asymmetry can have on rift geometry by creating strongly asymmetric rift basins (Allemand et al., 1989; Allemand and Brun, 1991; Panien et al., 2005, Fig. 11c, d). Yet these effects are not directly observed in our experiments, possibly due to the relatively minor total extension, the absence of syn-rift sedimentation or because we lack the necessary cross sections as these models were not CT scanned.

4.3 Brittle-viscous reference experiments

The presence of a viscous layer in our experiments leads to quite different structures with respect to those observed in their brittle-only counterparts (Fig. 10). The brittle-viscous foam and rubber base cases produce basically the same structures: when no seed is present, faulting only occurs along the sidewalls, whereas a seed strongly concentrates deformation as well, resulting in a central rift structure (Figs. 5, 7a, b, 10c, d, g, h). The decoupling of the sand from the foam or rubber base allows the brittle cover to behave as rigid blocks, more or less passively floating on the viscous layer (Zwaan et al., 2018a). By contrast, the sand in the brittle-only experiments is directly coupled to the base, forcing a pervasive type of faulting (Fig. 10a, b, e, f). Due to this decoupling effect of the viscous layer, no conjugate strike–slip fault sets occur in our brittle-viscous rubber base experiments nor in those experiments performed by Bellahsen et al. (2003) or Bellahsen and Daniel (2005). The fact that the rifts in our rubber base experiments are less developed towards the short ends of the set-up is most likely caused by the use of a sand talus to contain the viscous material there (Figs. 2d, 7b–d). This creates a deformation contrast between the immobile talus and the deforming material above the rubber sheet, an effect that could potentially be reduced by using a rubber sidewall, as in the foam set-up (Figs. 2a, 5).

In contrast to the results of the brittle-only experiments that show strong differences depending on the set-up, those of the brittle-viscous plate base and conveyor base experiments are quite similar to their foam and rubber base equivalents (Fig. 10), most likely due to the tendency of the viscous material to easily spread out when subject to relatively slow extension rates. All of these experiments, however, see minor rifting initiating at the short sides of the set-up, because there the materials are confined by sidewalls or sheets that move in sync with the long sidewalls, imposing the same boundary conditions there as at the base of the set-up. The resulting additional drag enhances the extensional deformation at these short edges, forcing the development of rifts, which propagate toward the centre of the experiment (Figs. 8c–e, 9c, d, 10k, l). In the centre, however, the viscous spreading mechanism is dominant, so that we observe the same structures as in the other brittle-viscous experiments (Fig. 10). This “short sidewall effect” is also present when applying a seed (Figs. 8e, 10l), causing the rifts to be more developed at the short ends of the experiment, and may also have occurred in a model by Mart and Dauteuil (2000). Their experiment involves a curious propagating rift system, initiating at the short edge of the set-up, which has a similar plate confinement as in our experiments. We see similar rift initiation from the sides of the model in the work by Autin et al. (2010, 2013) as well. In order to reduce this type of boundary effect, higher strain rates can be applied (Fig. 9e–f). However the use of a sand talus to confine the short ends of the experiment, as suggested by Tron and Brun (1991), does not reduce these boundary effects in our experiments, as the sand is even more strongly coupled to the experimental materials, the side plates or sheets, causing more friction (experiment C5, Appendix C2, Fig. C2). This is expressed by the internal friction angle of our quartz sand being higher than that of quartz sand with respect to the plastic plates or sheets used at the short sidewalls (36.1^∘ versus ca. 20^∘)

As with the reference brittle-only experiments, we do not observe a clear difference between symmetric and asymmetric extension. Yet previous authors have shown that asymmetric extension may affect brittle-viscous experiments as well. This is, however, mostly in combination with a relatively thin viscous layer that allows for a more direct transfer of deformation from the set-up base to the sand cover (e.g., Allemand et al., 1989). By contrast the relatively thick viscous layer in our reference experiments acts as a buffer, decoupling the sand from the extending plates or sheets at the base of the experiments (see also Sect. 4.5).

4.4 Velocity effects: distributed extension versus passive down-bending and marginal graben formation

As discussed in Sect. 4.3, the reference brittle-viscous foam and rubber base experiments without a seed see the brittle cover decoupled from the set-up base. Increasing the extension rate as in experiments R9 and R10 (Fig. 7c, d, Table 2) seems to increase the influence of the set-up: distributed extension is induced at the base and observed at the surface of the experiments. Yet the lower strength ratios (8.4 and 1.4 for experiments R9 and R10, compared to the reference ratio of 84, see Table 2) also indicate higher brittle-viscous coupling, which is known to cause distributed or wide rifting (e.g. Brun, 1999; Buiter et al., 2008; Zwaan et al., 2016; Figs. 7c, d, 10m). Since both the enhanced cover-basal and high brittle-viscous coupling should lead to similar results, it is challenging to determine which factor is dominant. Still the type of deformation in these experiments is not as evenly distributed as in their brittle-only equivalents (Figs. 4, 10a, b, e, f), suggesting that the influence of the base is secondary compared to the effects of brittle-viscous coupling. We can also infer that the central rift in experiment R9 (Fig. 7c) probably forms due to some wide rifting effect: the higher the extension rate (while keeping all other parameters constant), the higher the brittle-viscous coupling and the more rifts develop, as illustrated by experiment R10 (Fig. 7d).

Yet considering the results from the high-velocity rubber-base experiments R9 and R10 (Figs. 7c, d, 10m), those of the high-velocity brittle-viscous plate or conveyor base experiments P9 (Figs. 8f, g, 10n) and C12 (Fig. C2) may seem somewhat remarkable; instead of developing distributed rifting, these experiments generate a “down-bent” depression bordered by marginal grabens (Figs. 8f, g, 10n, C2), that may also be present in the models by Gabrielsen et al. (2016). The high extension velocity in P9 and C12 (80 mm h⁻¹) causes high coupling between the viscous layer and the brittle cover (strength ratio: 4.4), as well as between the viscous layer and the base. This basal coupling leads to intense stretching (necking) above the VD(s) and subsequent downward “bending” of the sand cover (Fig. 8g). High coupling between the viscous layer and the base also explains why no apparent boundary effects are visible along the longitudinal sidewalls. The bending of the brittle layer at the edge of the system causes local extension in the sand and the formation of marginal grabens, which seems to resemble the structures along the Western Escarpment of the Afar (northernmost sector of the East African Rift System) in Ethiopia (e.g. Abbate and Sagri, 1969; Chorowicz et al., 1999). However, interesting as these structures may be, the high extension velocities may approach unrealistic values (see Sect. 2.4), highlighting the importance of careful model scaling.

As previous studies have shown, increasing brittle-viscous coupling can be linked to more distributed faulting styles (e.g. Davy et al., 1995; Schueller et al., 2005, 2010; Dyksterhuis et al., 2007; Moresi et al., 2007; Buiter et al., 2008; Zwaan et al., 2016), which is seen in our rubber base experiments as well (experiments R9 and R10; Figs. 7c, d, 10m). However, the experiments in these previous studies generally use a very weak or free-slip base, allowing their models to be (fully) controlled by the rheology of the brittle-viscous layers. When such basal boundary conditions are not met, coupling between the viscous layer and the substratum is also an important factor as illustrated by our plate and conveyor base experiments (experiments P9 and C12) (Figs. 8f, g, 10n, C2). We thus identify a competition between brittle-viscous coupling and viscous-basal coupling in such systems, depending on which the resulting structures may vary widely. Within the context of extensional tectonics, this is in line with the concept that the strength of the uppermost mantle can have a significant influence on the deformation of the overlying crustal layers (e.g. Brun, 1999; Corti et al., 2003).

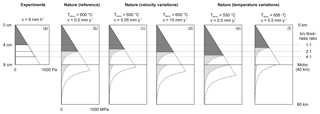
Figure 12 Strength profiles calculated for our reference experiments (a) and various natural cases (b–f). Reference values for the natural example are T_moho=600 ^∘C and v=0.5 mm yr⁻¹ (b). Extension velocity variations are shown in (c) and (d) and variations due to different Moho temperatures are depicted in (e) and (f). The crust and mantle flow laws used here are anorthosite dislocation creep (Rybacki et al., 2006) and olivine dislocation creep (Hirth and Kohlstedt, 2003). Note that the filled-in profile represents a wet lithosphere, whereas the dotted profiles delineate a dry lithosphere scenario. The horizontal lines indicate various brittle-to viscous ratios (see discussion in text).

4.5 Effects of different brittle-to-viscous thickness ratios

Our brittle-viscous plate and conveyor base experiments with the reference parameters but no seed (P3, P7, C4, Figs. 8c–d, 9c, 10k) fail to produce proper rift basins, in contrast to their brittle-only equivalents (experiments P1, P2, C1 and C3, Figs. 8a, b, 9a, b, 10i, j). Instead, we either need a seed as in the foam and rubber base experiments (experiment P10, Figs. 8e, 10l) or a high brittle-to-viscous thickness ratio (> 2) to localize deformation (experiments C8 and C11, Fig. 9e–g). The decrease in viscous layer thickness in experiments C7 and C8 causes increasing strength contrasts: from the reference value of 84 to 169 and 337, respectively (Table 2), corresponding to a trend towards localized (narrow) rifting (Fig. 9c–e). This is in line with the model results presented by Brun (1999), for example. However, increasing the extension rate in experiment C11 (resulting in a lower strength contrast) does not lead to distributed deformation, but to more localized faulting. Similar to the high extension rate examples discussed in Sect. 4.4, our results thus suggest that brittle-to-viscous strength ratios alone are not sufficient to properly infer a specific rifting mode, but that additional factors such as viscous-basal coupling need to be considered as well.

Furthermore, in the experiments with high brittle-to-viscous ratios (i.e. C8 and C11), we obtain double-rift structures rather than the single-rift basins seen in our brittle-only experiments and previous publications (Figs. 8a, b, 9a, b, 10i, j, 9e–g). For instance, Brun and Tron (1993) apply a relatively thin viscous layer (brittle-to-viscous ratio of ca. 2) and obtain well-developed rift structures in symmetric extension (Fig. 11g). The relatively thin viscous layer probably allows for a shift to a brittle-dominated system, leading to rift localization near the VD, similar to our brittle-only plate and conveyor base experiments (Fig. 8a, b, 9a, b). However, the extension model by Tron and Brun (1991, Fig. 11f) produces the same double rift structure including the additional faults away from the central rifts as our experiment C11 (Fig. 9f, g). Also Keep and McClay (1997) and Schreurs et al. (2006) obtained two rifts with symmetrical extension experiments involving a conveyor or plate base and a brittle-to-viscous ratio of 4 and 6, respectively. A lateral transfer of deformation through the viscous layer, away from the VD (i.e. “soft linkage”; e.g. Stewart et al., 1996) is the probable cause of this dual rift arrangement (Michon and Merle, 2000, 2003, Fig. 11e). This feature seems to occur in lithospheric-scale models involving the asthenosphere as well (Allemand and Brun, 1991; Brun and Beslier, 1996; Cappelletti et al., 2013; Nestola et al., 2015, Fig. 1). A single-rift structure may form due to factors as higher strain rates (Keep and McClay, 1997; Michon and Merle, 2000), asymmetric extension or possibly syn-rift sedimentation (e.g. Brun and Tron, 1993; Fig. 11g). The formation of a single- or dual-rift structure is most likely influenced by the viscosity of the viscous layer as well. Experiments with high brittle-to-viscous thickness ratios thus seem to be highly sensitive to various parameters. Whether the various thickness ratios mentioned above are realistic depends on the specific tectonic setting that is simulated, as lithospheric rheological profiles are known to vary considerably in extensional settings (e.g. Brun, 1999; Burov, 2011; Tetreault and Buiter, 2018; see also Sect. 4.7).

4.6 Boundary effects and experimental confinement

Most of our reference experiments, except for the brittle-only plate and conveyor base experiments, develop some degree of normal faulting along the long sidewalls (Fig. 10). In the brittle-only experiments, this may be due to enhanced local stretching of the rubber base (Ackermann, 1997), an effect quite possibly present in the foam base equivalents as well. The rigid sand layer in the brittle-viscous experiments on the other hand is subject to “inertia”, i.e. an inability to move and extend as easily as the viscous materials, leaving “gaps” along the sidewalls that take up significant amounts of deformation in the experiment (Zwaan et al., 2018a).

This “inertia” effect occurs in various model studies and may significantly affect the quality of the experimental result. Some authors seem to avoid these problems by simply ignoring them and focussing on the structures in the centre of the experiment. Others attempt to reduce faulting by applying a viscous layer that does not reach the model sidewalls (Tron and Brun, 1991; Schreurs et al., 2006; Gabrielsen et al., 2016). However, by narrowing the viscous layer, the boundaries of the viscous material become rheological contrasts that may trigger faulting themselves, thus causing a new type of boundary effect (e.g. Bonini et al., 1997). This also raises the question of what the viscous layer represents in nature if not a continuous viscous lower crust. Even narrower patches of viscous material, for instance simulating a weak zone in the crust due to magmatism, may lead to narrower rift structures (e.g. Brun and Nalpas, 1996; Dauteuil et al., 2002) and the seeds in our experiments can be seen as the most extreme exponent of this trend. The inferred width of the structural weakness is also relevant for set-ups involving a narrow rubber base fixed between two base plates (e.g. McClay and White, 1995; McClay et al., 2002; Corti et al., 2007; Henza et al., 2010). In such experiments, all deformation tends to focus above the rubber sheet, with its edges acting as VDs, imposing the boundaries of the rift system (see also Sect. 4.2).

Our results show that the type of confinement along the short edges of the brittle-viscous experiment forms another important factor generating boundary effects, which is similar to the findings by Schreurs et al. (2006). In the foam base experiments, the rubber sheet sidewalls cause little to no additional deformation, yet the sand talus confinement in the rubber base experiments generates significant boundary effects, and enhanced rifting is associated with the plate base and conveyor base confinements. However, the similarity of the structures in the centre of all our reference brittle-viscous experiments (due to the likely dominance of the viscous spreading mechanism under low brittle-viscous coupling conditions) may suggest that, if the short edge boundary effects can be reduced, the type of extension mechanism would be of little influence under our standardized conditions. Therefore, we could perhaps have obtained comparable results for brittle-viscous experiments, even without a method to induce deformation directly at the base of the experimental materials: only moving apart the two longitudinal sidewalls may suffice to cause uniform spreading of the viscous layer (e.g. Le Calvez and Vendeville, 2002; Marques, 2012). However, the results of such experiments may again vary with different strain rates, layering and layer thickness, materials, application of sedimentation, etc., highlighting the challenges of directly comparing the results from different modelling studies and the need to specify all relevant parameters and boundary conditions, as well as any resulting boundary effects.

4.7 Recommendations for further extension experiments

Our extension experiments represent different rheological stratifications and extension conditions, and may serve as a guide for future modelling studies aiming at investigating extension in specific tectonic settings (Fig. 3). Since the overview presented in Fig. 3 remains schematic, we calculated a series of rheological profiles for natural cases to allow for a direct rheological comparison to the experimental strength profiles (Fig. 12). We used the rheological values of Table 3 with laboratory flow laws often adopted for the lower crust and lithospheric mantle (Hirth and Kohlstedt, 2003; Rybacki et al., 2006) and we varied both extension velocity (0.5 to 10 mm yr⁻¹) and Moho temperature (550 and 650 ^∘C). The calculations show that extension velocity has a relatively minor influence on the rheological profile with respect to temperature and dry or wet versions of the flow laws. The plots also indicate that our reference brittle-to-viscous thickness ratio of 1:1, although often used in analogue models (Corti et al., 2003, and references therein), is quite low (compare Fig. 12a with Fig. 12b) and may only occur in a relatively wet and hot lithosphere (Figs. 3b, 12f). This may for instance be in accordance with the situation in the East African Rift System (Fadaie and Ranalli, 1990; Corti, 2009), but a 2:1 or 3:1 ratio would fit better with the calculations for a normal-temperature lithosphere (Fig. 12b–d). A strong upper mantle, as inferred for (brittle-viscous) plate and conveyor base set-ups, only occurs in a wet cold lithosphere (Fig. 12e) or in a completely dry lithosphere (dotted lines in Fig. 12), yet the complete absence of hydrous minerals may be unrealistic (Xia and Hao, 2010). Furthermore, our strength profile calculations are based on monomineralic flow laws (anorthosite and olivine; Hirth and Kohlstedt, 2003; Rybacki et al., 2006), whereas continental rocks are of course polymineralic. Different rheological profiles for natural settings can be obtained by not only varying the thermal gradient, but also by variations in water content, temperature or by simply using other flow laws. We choose lower crust and mantle flow laws (Rybacki et al., 2006; Hirth and Kohlstedt, 2003, respectively) that are fairly recent and neither overly weak nor strong in comparison with other flow laws.

The rheological calculations highlight that one should carefully consider the various factors that may influence the strength of the lithosphere in a given tectonic setting before selecting a specific experimental set-up. It is also important to stress that although the materials involved may only represent the upper parts of the crust, deeper parts of the lithosphere (basement or mantle) are simulated via the chosen experimental extension mechanism (Fig. 3). This is most evident for brittle-only experiments that are directly coupled to the set-up (Fig. 10). However, we have shown that for low extension velocity brittle-viscous experiments, which aim at representing a hot lithosphere, any extension mechanism should suffice due to the high degree of decoupling (Fig. 10). This decoupling effect could also allow for a simple way to model an oceanic lithosphere, which is generally considered to comprise a brittle oceanic crust and a viscous lithospheric mantle (e.g. Benes and Scott, 1996). Note, however, that in such experiments an imposed weakness seems to be necessary to create any rift structure at all (Fig. 10). Since efforts should be made to keep boundary effects to a minimum, we recommend using the foam base method for such brittle-viscous models (see also Sect. 4.6).

Our experiments could be extended to include more layers (three- or four-layer lithospheres) (e.g. Corti et al., 2003, and references therein) and an underlying asthenosphere that would allow for an assessment of the effect of isostatic compensation on a stretching lithosphere. In such cases a strong lithosphere would strongly affect rifting processes (Brun, 1999; Corti et al., 2003), whereas in the case of a weak lithosphere (Figs. 3b, e, 12f) the (rising) asthenosphere may have an important impact. The presence of an asthenosphere analogue would also allow the vertical motions associated with a major fault or shear zone in the strong upper mantle (e.g. Vendeville et al., 1987; Allemand and Brun, 1991, Fig. 1). In the commonly used plate and conveyor base set-ups, such a fault is represented by the VD, yet any associated vertical motions are not simulated. The symmetric conveyor belt extension mechanism may not be well suited to crustal-scale models, as the continuous “upwelling” of the plastic sheets resembles a convection cell system, which could be taken to simulate sub-lithospheric mantle behaviour and would therefore be more appropriate for lithospheric-scale models driven by mantle convection. For crustal-scale wide rift experiments we recommend using an asymmetric plate base or conveyor belt mechanism instead, which are the same after a shift of reference frame (Appendix A).

It could also be worthwhile to repeat our experiments with other brittle materials and viscous analogues, which may better capture the behaviour of the lithosphere (overview in Schellart and Strak, 2016). The use of temperature-dependent materials would allow for the inclusion of temperature effects (e.g. Boutelier and Oncken, 2011), which can strongly control rifting as shown by numerical simulations (Tetreault and Buiter, 2018). Also the feedbacks between magmatism and rifting need to be further explored (e.g. Corti et al., 2003, 2015). A next necessary step in modelling large-scale rift structures is to include surface processes as well (e.g. Burov and Cloetingh, 1997; Bialas and Buck, 2009; Zwaan et al., 2018a)

We would like to stress the importance of standardized modelling methods and strict laboratory procedures (e.g. Klinkmüller et al., 2016). Different handling techniques, laboratory conditions and personal preferences may cause variations in, for instance, sand density (e.g. Krantz, 1991) or rheology of viscous materials (Rudolf et al., 2016) and can have significant effects on model results (Schreurs et al., 2006, 2016). By means of standardized procedures within a modelling group, these variations can be reduced. Yet reproducing the same model results in different laboratories will probably always remain a challenge (see efforts by Schreurs et al., 2006, 2016).

5 Conclusions

We present a systematic comparison of four set-ups commonly used for analogue modelling of crustal-scale extension. We examine distributed extension obtained by a foam or rubber base and localized extension by rigid basal plates or conveyor-belt basal sheets. We find the following points:

• Brittle-only experiments are strongly affected by the experimental set-up, as the materials are directly coupled to the base of the set-up. Foam base or rubber base experiments therefore undergo distributed deformation and wide rifting, whereas plate base or conveyor base experiments experience localized deformation and narrow rifting.

• Strong boundary effects may occur due to extension-perpendicular contraction effects during stretching of a rubber base (Poisson effect; e.g. Smith and Durney, 1992). This may be mitigated by using a high length-to-width ratio for rubber base set-ups.

• Brittle-viscous experiments are less affected by the experimental set-up than brittle-only equivalents as the viscous layer acts as a buffer that decouples the brittle layer from the base of the set-up. In our reference experiments this decoupling implies that a seed must be inserted in order to produce a rift basin.

• Brittle-viscous experiments with low brittle-viscous strength contrasts and a rubber base set-up show distributed rifting as expected based on previous studies. Yet plate and conveyor base experiments (expected localized extension) with high strain rates (expected distributed extension) develop intense localized stretching of the viscous layer, leading to the formation of a down-bent basin with marginal grabens. This suggests that the brittle-viscous strength ratio on its own does not determine the style of deformation in a rift system, but that the nature of the underlying substratum is important as well.

• Brittle-viscous plate and conveyor base experiments with higher brittle-to-viscous thickness ratios (thus decreasing brittle-viscous coupling) achieve better fault localization, which is in line with previous work. However, higher strain rates in these experiments (which increase brittle-viscous coupling) improve localization, highlighting once again that brittle-viscous coupling is not the only parameter influencing the fault style of rift systems.

• Of the brittle-viscous experiments we tested, the least boundary effects occur for a set-up involving a foam base and a stretchable rubber sidewall. This sidewall method could also be applied to a rubber base set-up to minimize boundary effects. In contrast, the plate base and conveyor base set-ups can experience major boundary effects along their short sidewalls that may proof difficult to reduce.

The significant differences between experimental results obtained with the different set-ups – sometimes due to seemingly small differences in, for instance, extension velocity or layer thicknesses – indicate the need to accurately specify model parameters and boundary conditions in order to allow for meaningful comparisons between (analogue) modelling studies. The combination of rheological stratification and experimental set-up defines the tectonic setting that is investigated. Our set-ups can be applied to study extension of crustal materials in various tectonic settings or lithospheric conditions with different levels of basement control. Here factors as temperature, extension rate, water content and lithology should be taken into account (Fig. 12). We advise to avoid the symmetric conveyor belt method for crustal-scale models.

Finally, we recommend that every laboratory standardize its procedures and methods as much as possible in order to minimize variations due to different handling techniques and personal preferences.

Appendix A: Schematic overview of relations between experimental set-ups

Figure A1 provides an overview of the various set-ups and how these compare to each other by means of extension velocities and shifts of reference frames. All symmetric extension set-ups are different: foam/rubber base experiments (Fig. A1a, b) develop an extension gradient, whereas the plate and conveyor base experiments develop velocity discontinuities (Fig. A1d, e and i, j, respectively). Also the plate and conveyor set-ups are different from each other (e.g. moving and fixed VDs occur in plate base and conveyor base configurations, respectively, as is revealed after applying a shift of reference frame, Fig. A1e, j). Asymmetric extension set-ups differ from their symmetric equivalents as well, but are between themselves, after a shift of reference frame, basically the same (Fig. A1f, g, k, l).

Figure A1 Schematic overview of relations between experimental set-ups, illustrated with shifts of reference frame (v= velocity, VD = velocity discontinuity). Compare with Fig. 2. (a–b) Foam and rubber base set-ups in which the base induces an extension gradient. (c–g) Plate base set-ups. (h–l) Conveyor base set-ups. Shifts of reference frame are used to highlight the direct differences between set-ups. Note that most set-ups fundamentally differ as indicated by the “≠” sign, except for the asymmetric plate base and conveyor base set-ups (f–g, k–l), which are fundamentally the same. The latter are indicated by the “=” sign. Darker colours indicate mobile parts of the set-ups, whereas brighter colours indicate static parts.

Appendix B: Brittle and viscous strength calculations

B1 Brittle domain

For calculating brittle strength in our experiments, we use the Mohr–Coulomb yield criterion written in terms of principal stresses σ₁ and σ₃:

$$\begin{array}{}\text{(B1)}& {\displaystyle }\mathrm{1}/\mathrm{2}({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})=\mathrm{1}/\mathrm{2}({\mathit{\sigma }}_{\mathrm{1}}+{\mathit{\sigma }}_{\mathrm{3}})\sin \left(\mathit{\phi }\right)+C\cos \left(\mathit{\phi }\right),\end{array}$$

where σ₁ is the maximum compressive stress, φ the angle of internal friction and C the cohesion.

$\mathrm{1}/\mathrm{2}({\mathit{\sigma }}_{\mathrm{1}}+{\mathit{\sigma }}_{\mathrm{3}})$ represents the mean stress, which we equate to lithostatic pressure ρgz. Brittle layer strength is then obtained by integrating over the thickness of the brittle layer h_b:

$$\begin{array}{ll}{\displaystyle }\underset{o}{\overset{h_{\mathrm{b}}}{\int }}({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})\mathrm{d}z& {\displaystyle }=\underset{o}{\overset{h_{\mathrm{b}}}{\int }}\left(\mathrm{2}\mathit{\rho }gz\sin \right(\mathit{\phi })+\mathrm{2}C\cos (\mathit{\phi }\left)\right)\mathrm{d}z\\ \text{(B2)}& {\displaystyle }& {\displaystyle }=\mathit{\rho }g{h}_{\mathrm{b}}^{\mathrm{2}}\sin \left(\mathit{\phi }\right)+\mathrm{2}C{h}_{\mathrm{b}}\cos \left(\mathit{\phi }\right)\end{array}$$

B2 Viscous domain

Strength profiles for viscous layers depend on the viscosity of the material η and the principal strain rates ${\dot{\mathit{\epsilon }}}_{\mathrm{1}}$ and ${\dot{\mathit{\epsilon }}}_{\mathrm{3}}$:

$$\begin{array}{}\text{(B3)}& {\displaystyle }({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})=\mathrm{2}\mathit{\eta }{\dot{\mathit{\epsilon }}}_{\mathrm{1}}-\mathrm{2}\mathit{\eta }{\dot{\mathit{\epsilon }}}_{\mathrm{3}}.\end{array}$$

We simply assume pure shear for the initial stages of the experiment and thus ${\dot{\mathit{\epsilon }}}_{\mathrm{1}}=\mathrm{2}V/\mathrm{2}W=V/W$ and ${\dot{\mathit{\epsilon }}}_{\mathrm{3}}=-{\dot{\mathit{\epsilon }}}_{\mathrm{1}}$ (where V and Ware half the extension velocity and half the width of the experiment, respectively), so that

$$\begin{array}{}\text{(B4)}& {\displaystyle }({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})=\mathrm{4}\mathit{\eta }V/W.\end{array}$$

Viscous layer strength then becomes:

$$\begin{array}{}\text{(B5)}& {\displaystyle }\underset{o}{\overset{h_{\mathrm{v}}}{\int }}({\mathit{\sigma }}_{\mathrm{1}}-{\mathit{\sigma }}_{\mathrm{3}})\mathrm{d}z=\underset{o}{\overset{h_{\mathrm{v}}}{\int }}(\mathrm{4}\mathit{\eta }V/W)\mathrm{d}z=\mathrm{4}\mathit{\eta }V{h}_{\mathrm{v}}/W,\end{array}$$

where h_v represents viscous layer thickness.

Appendix C: Experimental reproducibility

Figures C1 and C2 show the surface results of repeated experiments in order to evaluate their reproducibility. In most cases, the structures are very similar. Although the boundary effects in P6 and P7 (Fig. C1) do show some variation, the structures in the centre are the same in both cases (no rift). Experiments C4–C6 seem quite different (Fig. C1), but C5 and C6 are tests to reduce boundary effects. As proposed by Tron and Brun (1991), we added sand to confine the short ends of the experiment, but instead of improving the situation this measure increases boundary effects, most likely due to the higher friction of sand. In C6 (Fig. C1) we added a lubricant (hand soap) between the sides and the model. Since there was no improvement, we aborted the experiment after 120 min. Note that asymmetric brittle-viscous plate base experiment P6 and symmetric brittle-viscous conveyor belt experiment C4 are quite similar, due to viscous decoupling effects. Also asymmetric brittle-only plate/conveyor base experiments P2, C2 and C3 produce the same structures (Fig. C2), since both the plate base and conveyor base set-ups are, after a shift of reference frame, identical in asymmetric extension conditions. The double rift structure in conveyor base experiment C10 is almost identical to the version generated in C11 (Fig. C2), although the curving nature of the normal faults does provide local variations in rift width. High-velocity models P9 and C12 develop very similar structures, although those in the conveyor belt set-up (C12) are better developed than in plate base experiment P9 (Fig. C2). Note that the additional rift basins in C12 are also present in P10, but not very visible due to their less evolved state and the unfavourable lighting conditions.

Figure C1 Reproducibility tests. Final top views of experiments F2–F4 (brittle-only, foam base, with seed), F6 and F7 (brittle-viscous foam base, with seed), P6 and P7 (brittle-viscous plate base experiments, no seed) and C4–C6 (brittle-viscous conveyor base, no seed). Note that C5* and C6** were attempts to decrease boundary effects by replacing part of the basal viscous layer with sand (transparent overlay) or adding a lubricant (hand soap) along the short ends of the set-up, respectively. The former, however, increased boundary effects, whereas the latter did not significantly change surface structures and was therefore halted after 2 h. Extension velocities are 8 mm h⁻¹ in all cases. Note that boundary effects are present on both sides of the experiment, but these are partially invisible due to shadow.

Figure C2 Reproducibility tests. Final top views of experiments P2, C2 and C3 (brittle-only asymmetric plate base P and conveyor base C), C9–C11 (brittle-viscous conveyor base experiments, 4:1 brittle-viscous thickness ratio, high velocity: 40 mm h⁻¹ for experiments C10 and C11 and 80 mm h⁻¹ for experiment C9) and experiments P9 and C12 (brittle-viscous plate base P and conveyor base C, half layer thickness, high extension velocity: 80 mm h⁻¹).