Precision of continuous GPS velocities from statistical analysis of synthetic time series

We use statistical analyses of synthetic position time series to estimate the potential precision of GPS (Global Positioning System) velocities. The synthetic series represent the standard range of noise, seasonal, and position offset characteristics, leaving aside extreme values. This analysis is combined with a new simple method for automatic offset detection that allows an automatic treatment of the massive dataset. Colored noise and the presence of offsets are the primary contributor to velocity variability. However, regression tree analyses show that the main factors controlling the velocity precision are first the duration of the series, second the presence of offsets, and third the noise level (dispersion and spectral index). Our analysis allows us to propose guidelines, which can be applied to actual GPS data, that constrain velocity precisions, characterized as a 95 % confidence limit of the velocity biases, based on simple parameters: (1) series durations over 8.0 years result in low-velocity biases in the horizontal (0.2 mm yr⁻¹) and vertical (0.5 mm yr⁻¹) components; (2) series durations of less than 4.5 years are not suitable for studies that require precisions lower than mm yr⁻¹; (3) series of intermediate durations (4.5–8.0 years) are associated with an intermediate horizontal bias (0.6 mm yr⁻¹) and a high vertical one (1.3 mm yr⁻¹), unless they comprise no offset. Our results suggest that very long series durations (over 15–20 years) do not ensure a significantly lower bias compared to series of 8–10 years, due to the noise amplitude following a power-law dependency on the frequency. Thus, better characterizations of long-period GPS noise and pluri-annual environmental loads are critical to further improve GPS velocity precisions.

1 Introduction

GPS (Global Positioning System) and more recently GNSS (Global Navigation Satellite System) have become classical datasets to study present-day tectonics, from active plate boundary regions (e.g., Serpelloni et al., 2013; McClusky et al., 2000) to intraplate domains (e.g., Frankel et al., 2011; Tarayoun et al., 2018). GPS data processing, and thus the associated precision of GPS velocities, has significantly improved in the last 20 years owing, for example, to the contribution of studies on noise characteristics (Williams et al., 2003a, b), ionospheric effects (Petrie et al., 2010), or multipath and geometry effects (King and Watson, 2010). However, several state-of-the-art applications of GPS velocities require that the velocities be defined with increasingly better precisions, potentially as low as 0.1 mm yr⁻¹ or better. Typical examples of such requirements are associated with debates regarding intraplate strain buildup (Calais et al., 2006; Frankel et al., 2011), regional tectonic models (Vernant et al., 2006), or fault interseismic coupling variations (Vigny et al., 2005; Métois et al., 2012).

To first order, three types of factors and processes limit the precision of GPS velocities. The first two categories are associated with raw data processing, such as antenna phase center, satellite orbit, or atmospheric delay corrections (e.g., Tregoning and Watson, 2009), and with the GPS station environment (e.g., monument stability or multipath; King and Watson, 2010). Most of these effects are difficult to assess and integrate individually in a detailed uncertainty analysis and are commonly treated as correlated noise in velocity uncertainty calculations (Williams et al., 2003a, b). The third category relates to post-processing analysis of the position time series, in particular reference frame definition (Argus et al., 1999), periodic signals (Blewitt and Lavallée, 2002), and position offsets due to equipment modifications, earthquakes, or undefined sources (Williams, 2003a; Gazeaux et al., 2013).

The detection and correction of offsets in time series is investigated in numerous scientific domains, for example in biostatistics (Olshen et al., 2004), quantitative marketing (DeSarbo et al., 2007), image processing (Pham et al., 2000), or climate and meteorology (Beaulieu et al., 2008). In geodynamic GPS applications, failure to take offsets into account can have major consequences. For example, Thomas et al. (2011) estimated velocities of about 2.1 mm yr⁻¹ lower than those of Argus et al. (2011), leading to very different interpretations of the data for estimating uplift rates in East Antarctica. Multiple automatic methods exist for offset detection in GPS position time series, but their reliability is limited. Gazeaux et al. (2013) created a detailed synthetic dataset, DOGEX, to test the capabilities of several commonly used detection methods. They argue that the manual detection method is more reliable and allows the detection of smaller offsets than automatic methods, albeit with a detection rate of ca. 50 %. Consequently, Gazeaux et al. (2013) consider that geophysical interpretations of velocities smaller than ca. 1.0 mm yr⁻¹ must be subject to particular caution, depending on the offset detection method employed.

In this study, we estimate the potential precision of GPS velocities through a statistical analysis of synthetic position time series that are representative of standard GPS data. We focus on continuous time series with a daily sampling frequency (i.e., permanent rather than campaign mode) to test the effect of colored noise, periodic signals, and position offsets (with a new method for automatic offset detection). The use of synthetic data allows a detailed analysis of the velocity estimations compared to the target (“true”) velocities and of the specific contribution of each parameter that can be treated independently. By contrast, such an analysis would not be possible with real GPS data in which the true value and role of each parameter cannot be fully de-convolved. The parameter range used in the synthetic data is representative of typical average data and excludes the potential effect of transient phenomena, such as slow slip or postseismic events, or that of pluri-annual hydrological processes. The impact of such phenomena is addressed in several recent studies (e.g., Altamimi et al., 2016; Chanard et al., 2018) and could be included in more detailed synthetic analyses beyond our present study. Our main objective is to quantify the importance of specific factors and to obtain an estimate of the possible bias according to the characteristics of the series. We chose to generate our own synthetic dataset rather than using DOGEX from Gazeaux et al. (2013). The DOGEX dataset is more detailed (presence of gaps, presence of offsets a few days apart, variation in the target velocity); its use would be more complex to treat statistically but could be done in future studies. We illustrate our results with an application to a typical regional geodetic network in the context of a low rate of deformation (the REseau NAtional GNSS Permanent, RENAG, France; RESIF, 2017).

Hereafter, the following terminology is used to discuss the results of our analysis:

• velocity bias – for each time series, the calculated velocity is compared with the true (imposed) velocity. The absolute value of the difference between the two is termed “velocity bias” and represents the deviation of the calculated velocity compared to the truth. We choose the term “bias” rather than “accuracy” in order to avoid confusion (e.g., a high accuracy associated with a small number) and different definitions of accuracy. For each analysis, the velocity bias distribution is characterized by statistical estimators given in the next two points.

• 95 % confidence limit (denoted v₉₅) – this estimator is the 95 % quantile of the bias distribution and represents 95 % confidence in the estimated velocities.

• probability of 0.1 mm yr⁻¹ (denoted p₀₁) – this estimator is the percentile associate with a velocity bias of 0.1 mm yr⁻¹; e.g., p₀₁=75 % indicates a 75 % probability that the velocity bias be smaller than or equal to 0.1 mm yr⁻¹.

• precision – we limit the usage of the term “precision” to the general concept of “quality” of a velocity estimation, regardless of its origin and whether it corresponds to a systematic error (bias) or a measurement repeatability (dispersion).

• standard error and uncertainty – for each time series, the calculated velocity and other parameters are associated with standard errors estimated as part of the linear inversion (cf. Sect. 3). These standard errors are used as estimators of the uncertainty in each calculated velocity.

2 Synthetic time series

In order to test the factors that control the precision of velocity estimations, we simulate sets of 3600 daily position time series defined by a constant velocity, annual and semiannual periodic motions, instantaneous offsets, and random colored noise:

$$\begin{array}{ll}{\displaystyle }x\left(t\right)& {\displaystyle }=vt+A_{\mathrm{1}}\sin \left({\mathit{\omega }}_{\mathrm{1}}t+{\mathit{\varphi }}_{\mathrm{1}}\right)+A_{\mathrm{2}}\sin \left({\mathit{\omega }}_{\mathrm{2}}t+{\mathit{\varphi }}_{\mathrm{2}}\right)\\ \text{(1)}& {\displaystyle }& {\displaystyle }+C_{i}H\left(t,t_i\right)+D\mathrm{rand}\left(k,t\right),\end{array}$$

where the time t is incremental date (with an arbitrary start at t=2000); v is the constant velocity throughout the whole series (set at 0.0 mm yr⁻¹); A_1∕2, ω_1∕2, and φ_1∕2 are the amplitude, period, and phase of the annual and semiannual motions; C_i and t_i are the amplitude and time of the ith offset (with H the Heaviside function); k is the spectral index of the colored noise; and D a measure of the noise amplitude, expressed as the rms (root mean square) dispersion of the position time series. Figure 1 shows an example of the decomposition of an average synthetic series.

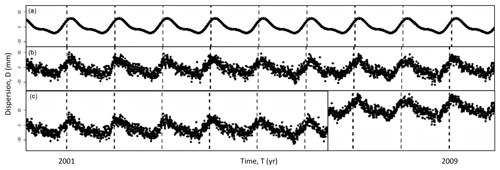
Figure 1 Decomposition of an example synthetic time series: (a) seasonal (annual and semiannual) signals; (b) seasonal signals combined with random colored noise; (c) seasonal signal, colored noise, and a simulated offset (vertical black line).

The ranges of values of the parameters are chosen to represent the standard characteristics of horizontal and vertical components in three recent state-of-the-art GPS analyses using Precise Point Positioning and Double-Difference processing (Santamaria-Gomez et al., 2011; Nguyen et al., 2016; Masson et al., 2018):

• v=0.0 mm yr⁻¹

• ${\mathit{\varphi }}_{\mathrm{1},\mathrm{2}}=\mathrm{0}$ day

• ω₁=365.25 day

• ω₂=182.63 day

• A₁=1.5 or 3.0 mm

• A₂=0.6 or 1.2 mm

• $C_i=(-\mathrm{6.0})$–(6.0) mm

• H=0 if t<t_i or 1 if t>t_i

• D=(0.6)–(4.4) mm

• $k=(-\mathrm{0.9})$–(−0.1).

This choice of time series description and parameter values ensures a good representation of the majority of real GPS time series but excludes both extreme parameter values (e.g., extremely noisy series) and pluri-annual or transient tectonic events such as slow slip events or postseismic deformation.

The annual and semiannual seasonal signals have a low impact on the determination of the long-term velocity (cf. Sect. 3 and Blewitt and Lavallée, 2002). Because of its minor role, we only integrate the effect of seasonal signal through three combinations of annual (A₁) and semiannual (A₂) amplitudes (1.5 and 0.6, 3.0 and 0.6, 3.0 and 1.2 mm) to illustrate first-order small, medium, and large seasonal effects on the position time series. The random noise added to the synthetic time series corresponds to the standard formula of the colored noise model (Agnew, 1992):

$$\begin{array}{}\text{(2)}& P\left(f\right)=P_{\mathrm{0}}{\left({\displaystyle \frac{f}{f_{\mathrm{0}}}}\right)}^k,\end{array}$$

where f is the frequency, P₀ and f₀ are normalizing constants, and k is the spectral index (Mandelbrot and Van Ness, 1968). We use the Kasdin (1995) formulation to generate colored noise sequences characterized by their spectral indices k, and the noise dispersion D of the series expressed as an rms:

$$\begin{array}{}\text{(3)}& D=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{x}_i^{\mathrm{2}}},\end{array}$$

where N is the number of daily positions x (prior to periodic and offset integration). The chosen range of noise dispersion (0.6–4.4 mm) corresponds to the 90th percentiles of position time series in our reference studies (Santamaria-Gomez et al., 2011; Nguyen et al., 2016). Figure 2 shows the distribution of position dispersion in Nguyen et al. (2016), illustrating the bimodal aspect of the horizontal (0.7–3.2 mm) and vertical (2.7–4.5 mm) positions.

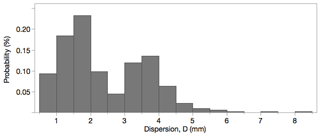
Figure 2 Distribution of position dispersion (measured as rms) in Masson et al. (2018) solution for western Europe with bimodal structure of the horizontal (0.7–3.2 mm) and vertical (2.7–4.5 mm) positions.

Recent studies based on large datasets propose a range of variation in the noise spectral index k between −0.8 and −0.4 (cf. Santamaria-Gomez et al., 2011; Nguyen et al., 2016). For our study, we use a slightly extended range of k from −0.9 to −0.1 in order to include the effects of older noisy data (lower k) and hypothetical nearly white series (k close to 0). For the former, $k=-\mathrm{0.9}$ corresponds to the average spectral index of studies on older and noisier data (Williams et al., 2004), keeping in mind that such data can present lower $k=-\mathrm{1.2}$ for very few series. For the latter, we consider the ongoing effort to identify, model, and correct for a pluri-annual climatic signal (e.g., Chanard et al., 2018), with the potential effect of “whitening” the time series by reducing the long-period amplitudes (i.e., $k=-\mathrm{0.1}$).

Offsets in time series are defined as an instantaneous change in the position. The position and the number of offsets are chosen randomly in each series, with respectively 2, 3, 4, 5, 6, or 7 maximum offsets for time series duration 3–6, 6–9, 9–12, 12–15, 15–18, or 18–21 years, and a minimum time of 200 days between two consecutive offsets. We use a minimum time lapse of 200 days between two consecutive offsets. Although not realistic, this lapse of time avoids distorting the overall statistics with consecutive offsets that are treated to a single offset in our detection method (cf. Sect. 4). The offset amplitude varies randomly between −6.0 and 6.0 mm with uniform distribution, excluding offsets of absolute amplitude smaller than 1.0 mm. This amplitude range corresponds to more than 80 % of the values from the SOPAC archives used by Gazeaux et al. (2013) and those from Nguyen et al. (2016). In the western Europe network (Nguyen et al., 2016), the average amplitude is about 3.0 mm with a standard deviation of 3.0 mm. Although extreme values can reach ca. 10.0 and 25.0 mm for the horizontal vertical components, we limit our synthetic range to ±6.0 mm in order to stay within the time series dispersion (i.e., extremely large offsets are as easily detected and corrected as large ones).

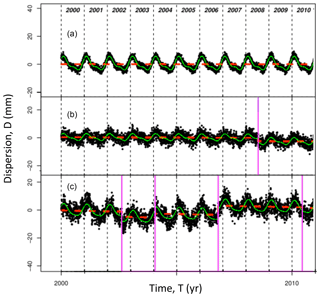
Figure 3 Examples of synthetic time series. Black dots represent daily positions. Green, red, and pink lines show modeled seasonal signal, velocity and offsets. The three examples illustrate the quality of the data used in our study: (a) a slightly noisy series ($k=-\mathrm{0.3}$, D=1.2 mm) without offset; (b) a moderately noisy series ($k=-\mathrm{0.4}$, D=2.3 mm) with 1 offset; (c) a noisy series ($k=-\mathrm{0.7}$, D=3.5 mm) with multiple offsets.

Figure 3 shows a variety of synthetic position time series illustrating the quality of the data used in our study. In these different examples we can already identify for which parameters or combinations of parameters it will be most difficult to determine the long-term velocity (fixed at 0.0 mm yr⁻¹). For series with the same duration, a high noise (k, D) and the presence of offsets seem to hinder the determination of the long-term velocity. In the rest of the study, we will quantify these different effects.

3 Effect of parameters on the velocity bias

In this section, we analyze the effect of each model parameter (independently and combined) on the velocity calculation. For each time series, all parameters are jointly estimated by a linear least-square inversion of the position model (Eq. 1), except for the noise parameters that are estimated independently using a spectral analysis of the residual positions. The results are analyzed using statistics of the velocity biases (absolute values of the differences between the estimated and true velocities; cf. Sect. 1). The various analyses are presented using whisker plots and two main indicators (cf. Sect. 1): the 95 % confidence limit of the bias distribution (v₉₅) and the probability of a bias equal to or smaller than 0.1 mm yr⁻¹ (p₀₁). We use regression tree analyses (Breiman et al., 1984) to hierarchize the role, defined as the importance (Ishwaran et al., 2007), of the parameters controlling the velocity biases.

The impact on velocity estimations of seasonal signals and offsets alone (without added noise) is extremely limited. A simple linear model including only a long-term velocity and either annual and semiannual sinusoids or Heaviside functions can be inverted to retrieve the exact parameter values, provided that the time series is long enough (at least ca. 3 years) and that it is not affected by several offsets at very near positions (a few days apart). Simple tests performed by inverting such series confirm this hypothesis by yielding velocity biases ca. 0.01 mm yr⁻¹ for the shortest series (<4 yr) and smaller than 0.01 mm yr⁻¹ in all other cases, including any of the three combinations of annual and semiannual seasonal terms. Thus, in the following, we focus on the effect of colored noise alone and colored noise with offsets, which are the main contributors to the velocity uncertainties.

3.1 Effect of colored noise

In order to estimate the impact of colored noise alone, we construct synthetic series using a subset of Eq. (1):

$$\begin{array}{}\text{(4)}& x\left(t\right)=vt+D\mathrm{rand}\left(k,t\right).\end{array}$$

We first analyze the effect of the three parameters – the duration of the series (T), the spectral index (k) and the noise dispersion (D) – independently of the others. Figure 4 shows the velocity biases as a function of these three parameters. The worst values of velocity bias due to noise alone can reach v₉₅=0.7 mm yr⁻¹ for the shortest series (T<5 yr). For series longer than 15 years, all v₉₅ are smaller than 0.1 mm yr⁻¹. A near-exponential decrease in v₉₅ is observed as a function of the duration of the series with a sharp slowdown from 15 years of data. The dependence of the velocity biases on noise parameters (k and D) shows an expected bias increase with smaller spectral indices (closer to −1) and higher noise amplitudes, with a near-exponential increase with D. Overall, the probability of velocity biases equal to or smaller than 0.1 mm yr⁻¹ is p₀₁=86 %. The 14 % of series with biases larger than 0.1 mm yr⁻¹ is associated with the shortest and noisiest series.

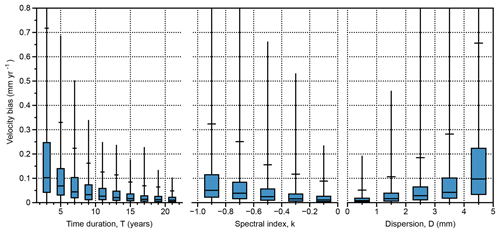
Figure 4 Whisker plots of velocity bias as a function of the duration (T), spectral index (k), and dispersion (D) for series including only colored noise. Whiskers diagrams show the data quartiles (25 %, 50 %, 75 %) in blue, the extremes (0 %, 100 %) with the vertical black line, and the 95 percentile (v₉₅) with the horizontal black line.

A joint analysis of the parameters using a regression tree indicates their relative importance, with the most important being the series duration T (56 %) followed by the spectral index k (35 %) and the noise dispersion D (9 %). Figure 5 shows the tree classification (Fig. 5a) and the whisker plots of the associated leaves (Fig. 5b). The branches and the associated leaves are ordered in order of importance and leaf size from left to right. The comparison signs (>  <) or (<  >) are relative to each tree separation, with the sign on the left corresponding to the left branch and the sign on the right corresponding to the right branch. Hereafter, we limit the tree classification to three node levels in order to only highlight the primary controlling elements.

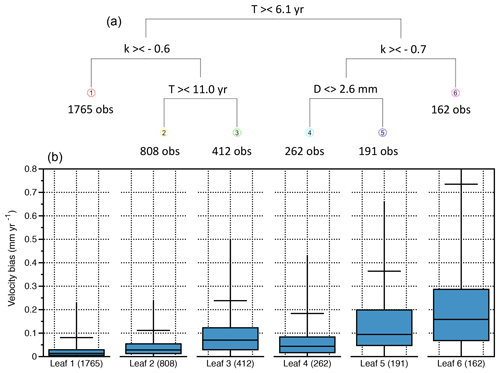
Figure 5 The regression tree classification (a) and the whisker plots of the associated leaves (b) for series including only colored noise. The horizontal top bar represents v₉₅.

The tree classification shows that v₉₅=0.1 mm yr⁻¹ is achieved for over two-thirds of the series (leaves 1 and 2), corresponding to all the long series (T > 11.0 yr, leaves 1 and 2) and those with average durations and large spectral indices (6.1 < T < 11.0 yr, k > −0.6, Leaf 1). The overall velocity bias increases for the other leaves. v₉₅=0.2 mm yr⁻¹ is still reached for combinations of average durations and small spectral indices (6.1 < T < 11.0 yr, k < −0.6, Leaf 3) or short durations, large spectral indices, and low-noise amplitude (T < 6.1 yr, k > −0.7, D < 2.6 mm, Leaf 4). The remaining cases (short duration, small spectral index, high noise) represent less than 10 % of the samples and result in large biases with v₉₅=0.4 mm yr⁻¹ (Leaf 5) and v₉₅=0.7 mm yr⁻¹ (Leaf 6).

Additionally, a significant piece of information emerging from the regression tree analysis is the relatively low coefficient of determination R²∼0.5, which indicates that the combinations of the three model parameters (T, k, D) only explain about 50 % of the dispersion in velocity biases. This points out the strong effect of the stochastic noise generation, which alone accounts for about half of the velocity variability. In other words, for a given set of parameters, the generated time series will show variable characteristics (noise structures) that randomly impact the velocity estimations. We illustrate this point by estimating the dispersion of velocity biases for a sample of 300 series with constant parameters T=10 yr, $k=-\mathrm{0.7}$, D=3.0 mm (belonging to Leaf 3 of the tree). The estimated velocities show an rms dispersion of 0.2 mm yr⁻¹, of the same order as dispersion observed in Leaf 3 (Fig. 5b). This effect is more important if the series is short.

As noted in the introduction to Sect. 3, seasonal signals have very little effect on the velocity estimations. This is also true for seasonal signals added to series with random noise, which yield similar results to those presented above for noise alone (e.g., p₀₁=86 %), with the seasonal parameters (A_1∕2 combinations) ranking with negligible importance in the tree classification (less than 1 %).

3.2 Effect of offsets

In order to test and estimate the effect of position offsets on velocity estimations, we analyze synthetic time series that include offsets added to seasonal signal and random noise (Eq. 1). This choice is justified by the very low effect of offsets alone (cf. introduction of Sect. 3) and the fact that this combination is representative of real data, thus providing useful estimations of the expected precision of actual velocities. In the case of real data, dealing with offsets requires either fixing their dates (from equipment logs or earthquake catalogs) or detecting their potential occurrences. In Sect. 4, we will come back to how to consider the latter. In this section, we quantify the two end-member cases in which we either do not know and therefore do not solve any offset or we know and solve all of them.

3.2.1 Effect of unresolved offsets

In this first simple case, we test time series with a single offset that is not solved and quantify the importance of the offset parameters (amplitude C₁ and position in the series t₁) in addition to the parameters T, k, and D considered previously. A regression tree analysis indicates that the velocity variability is primarily controlled by the time series duration T (importance 49 %), as in the case of noise alone, followed closely by the amplitude of the offset (40 %). The position of the offset (5 %), the noise amplitude (3 %), and spectral index (3 %) rank in third, fourth, and fifth positions far beyond the two main parameters. The coefficient of determination is larger than for the noise alone (R²=0.8), indicating that the inclusion of a single offset contributes significantly to the overall velocity variability.

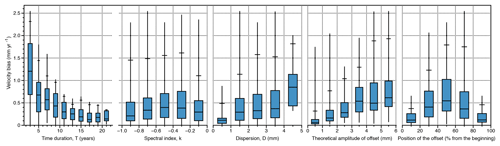
Figure 6 Whisker plots of velocity bias as a function of the duration (T), spectral index (k), dispersion (D), offset amplitude (amp_off), and offset position in percentage for series with only 1 offset unresolved. The horizontal top bar represents v₉₅.

This is illustrated in Fig. 6, which shows a distribution of velocity biases much larger than for the noise alone (cf. Fig. 4), with v₉₅ systematically above ca. 0.3 mm yr⁻¹. The presence of a single unresolved offset increases v₉₅ to 0.5 mm yr⁻¹ for long series (T > 13 yr) and up to 2.5 mm yr⁻¹ for short series. Only about one-fifth of the series are associated with velocity biases below 0.1 mm yr⁻¹ (p₀₁=18 %, compared to p₀₁=84 % for noise-alone series). As expected, the position of the offset in the series has a significant impact, with an offset placed at one end of the series causing a velocity bias much lower than an offset placed in the central part.

In a second series of tests, we include, but do not solve, several offsets (between 0 and 7 offsets depending on the series length; cf. Sect. 2). In this case, we cannot quantify the impact of the amplitudes and positions of the offsets as single parameters; instead we use the ratio of the number of offsets to the series duration T, which illustrates the proportion of offsets in the series. A regression tree analysis indicates the following parameter importance: T (53 %), ratio of number of offsets to T (44 %), D (2 %), and k (1 %), similar to the case of a single offset discussed above. About two-thirds of the series are associated with velocity biases below 0.1 mm yr⁻¹ (p₀₁=67 %). The largest velocity biases occur on the shortest series. Uncorrected offsets are therefore a dominant element in the determination of the velocity. These conclusions on the role of the position and magnitude of the offsets in the time series are consistent with the analytical analysis in Williams (2003b).

3.2.2 Effect of resolved offsets

As in the previous section, we first analyze the simple case of a series with one offset, but for which we fix the date and solve for the amplitude during the inversion. Thus, the velocity biases are affected by the possible imperfection of the estimated amplitude of the offsets, primarily due to the series colored noise. The regression tree analysis indicates that, when the offset amplitude is solved, the offset parameters become of very low importance (amplitude and position at 2 % each), while the series duration and noise parameters recover the same importance and order as in the case of noise alone: T 52 %, k 31 %, and D 13 % (cf. Sect. 3.1). The regression tree and associated velocity bias statistics are similar to that of the noise-alone analysis (cf. Fig. S1 in the Supplement). v₉₅ of all tree leaves is approximately 3 times lower than in the case of an unresolved offset but slightly larger than in the case of noise alone, in particular for short series.

Considering series with a variable number of offsets, for which we fix the date and solve for the amplitude, the importance of the parameters becomes intermediate between the noise-alone and single-offset cases: T 42 %, ratio of number of offsets to T 21 %, k 20 %, and D 17 %. Resolving the offset amplitudes reduces their importance (21  % vs. 44 %) but their presence remains a significant source of velocity variability, contrary to the case of a single solved offset by series. This is readily explained by the fact that the offset amplitudes are not perfectly resolved due to complex interaction between the offset positions, their amplitudes, and the noise structure that result in potentially very short linear segments in the series. This is illustrated by the probabilities of biases lower than 0.1 mm yr⁻¹ (p₀₁=71 %), slightly lower than in the case of noise-only series (p₀₁=86 %).

This latest result represents the lower bounds of velocity biases for series with several offsets, assuming that all offset dates are know. In reality, we do not know the exact nature and dates of all potential offsets (e.g., Gazeaux et al., 2013), so it is necessary to detect them before solving for their amplitude. In the next section, we propose a new detection method and test its impact on velocity biases.

4 A new approach for offset detection and impact on velocity bias

4.1 Methodology of offset detection

Real GPS time series are associated with an indeterminate number of offsets, which are classically included as instantaneous changes in position in the series inversion (cf. Eq. 1). Offset dates t_i can be based on equipment logs, catalogs of earthquakes, or routines that detect them in the position series (Gazeaux et al., 2013). Here we propose a slightly different approach that does not consist of seeking where there are offsets but rather of seeking where there are none.

This simple principle is implemented by defining artificial offset dates that are regularly spaced in the series every Δd days. The series is then inverted to estimate all offset amplitudes (C_i) and their associated standard errors (σ_ci) jointly with the other model parameters (velocity, seasonal signal, etc.). The offset with the smallest amplitude (C_S) is then identified and a simple significance test is performed:

$$\begin{array}{}\text{(5)}& \left|C_{\mathrm{S}}\right|\ge b\cdot {\mathit{\sigma }}_{\mathrm{cs}}.\end{array}$$

If the amplitude (C_S) is larger than its scaled standard error (b⋅σ_cs), the offset is considered significant. Because the test is performed on the smallest offset and the offset standard errors are similar in the majority of cases, we then consider that all offsets are significant and we keep them in the model. In the opposite case, the smallest offset is rejected and the inversion is redone with the remaining offsets in order to test the new smallest offset, until a significant offset is found or none remains.

This very simple approach can be implemented in most time series analysis and only requires an empirical calibration of the two parameters Δd and b. After several tests, we set the former to Δd=20 days, which corresponds to the lower limit before the method breaks down (i.e., too many undifferentiated offsets). The latter is set to b=20, which allows a good compromise between the detection of real offsets defined in the synthetic series and the detection of false positives (cf. Sect. 4.2).

This empirical calibration is not possible on real data, but considering that our synthetic data are representative of real data with the previous cautions, we can use this parameterization. In using Δd=20 days, all possible epochs are not tested. The assumption is that a real offset at any given epoch will be caught by the forced artificial offset located less than 10 days directly before or after. As such, we do not find the exact date of the real offset but its approximate date (within 10 days). This method cannot resolve real offsets situated within a few (10–20) days of each other. They will be lumped into a single artificial offset, but we assume that its effect on the estimated velocity will be a good proxy of the combined effect of the real offsets. This method is developed as a simple and efficient way to test the impact of offsets and their resolution on the velocity estimations. Several things could be done in future studies to improve it, including a finer calibration of the parameters, taking into account consecutive offsets, and an exhaustive scan of all epochs. Details on the parameter calibration and the detection levels are available in Supplement Sect. S2.

4.2 Detection ability

By applying our method to series with only one offset, it is possible to determine the conditions of offset detections. Overall, 67 % of the offsets are detected. The detection capacity depends primarily on the duration of the time series T, combined with the series noise amplitude D and the offset amplitude C. For the shortest time series (T < 6 yr), we detect 21 % of offsets. They correspond to the series with the largest offsets (C > 3.0 mm) and the smallest noise amplitudes (D < 2.1 mm). There is no offset detection in the series with large noise amplitude (D > 2.1 mm). For the time series of 6 to 18 years, we can detect offsets of small amplitudes (C=1.0–3.0 mm) in series with low noise levels (D < 2.1 mm) and large offsets (C > 4.0 mm) in all series. For the longest time series of more than 18 years, one widens the range of detection still further. Offsets larger than 3.0 mm are systematically detected and those between 2.0 and 3.0 mm are detected at 49 %. The very small offsets (C < 2.0 mm) are detected only in the low-noise series (D < 2.1 mm).

By applying our method to series with several offsets, the detection ability is decreased due to offset and noise interactions. Overall, the performance level is characterized by ca. 52 % of true detections (and so 48 % of missed detections) of the theoretical total number of offsets and about 20 % of false positives (cf. Supplement Sect. S2 for detection calibrations). These statistics are similar or slightly better than those of the most efficient automatic and manual detection methods analyzed in Gazeaux et al. (2013). Although not perfect, our method allows us to obtain robust and quantitative results and is suitable for processing of very large datasets such as our synthetic series or regional and global massive processing efforts that become increasingly common (e.g., Kreemer et al., 2014) and that could not be analyzed “by hand”.

4.3 Impact on the determination of the velocities

The application of the offset detection method to a full dataset with multiple offsets, variable noise, and seasonal signals provides a sample that can be considered as close as possible to actual GPS data. We use this analysis to provide constraints on the potential velocity precision in real data. Overall, nearly two-thirds of series are associated with velocity bias smaller than 0.1 mm yr⁻¹ (p₀₁=61 %). This is lower than in the cases of noise alone (p₀₁=86 %) or fully resolved offsets (p₀₁=71 %) but significantly better than in the case of unresolved offsets (p₀₁=33 %). The difference between the results of the offset detection method and those of the fully resolved offsets (ca. 10 %) is mainly associated with undetected offsets in the former.

For the regression tree analysis, the integration of a parameter associated with offsets is complex. Although these parameters (numbers total of offsets, of true and false detections, positions in the series, amplitudes) are known in our synthetic data, this is not the case in real datasets. Tests on several offset parameters indicate that the total number of offsets in the series (N_off) is both the simplest and the one with the highest prediction capacity. This new regression tree (Fig. 7) confirms the major role of the series duration (T 55 %) and noise dispersion (D 16 %) in explaining the variability in the velocities, but the total number of offsets now take the second position (N_off 25 %), above the noise dispersion. It is particularly worth noting that the number of offsets is in fact a binary predicator (splitting value N_off=0.5) corresponding to either the absence (N_off=0) or the presence (N_off≥1) of offsets in the series.

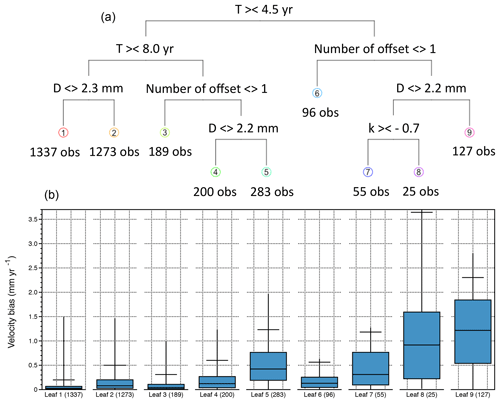
Figure 7 The regression tree classification (a) and the whisker plots of the associated leaves (b) for the full dataset with multiple offsets, variable noise, and seasonal signals with the application of the offset detection method. The horizontal top bar represents v₉₅.

To first order, the regression tree results can be divided into three categories:

• The lowest velocity biases (v₉₅∼0.2–0.3 mm yr⁻¹) are associated with either long (T > 8.0 yr) and low-noise dispersion (D < 2.3 mm) series or with series of intermediate duration (4.5 < T < 8.0 yr) with no offset (leaves 1 and 3). These represent over 42 % of the dataset.

• Intermediate biases (v₉₅∼0.5–0.6 mm yr⁻¹) are associated with series characterized by long duration and high-dispersion series (Leaf 2), intermediate duration and low dispersion (Leaf 4), or short duration (T < 4.5 yr) but no offset (Leaf 6). Altogether, these represent another 43 % of the dataset.

• The remaining ca. 15 % correspond to high biases (v₉₅ > 1.0 mm yr⁻¹) and is mostly associated with short durations (leaves 7, 8, 9) or intermediate duration and high dispersion (Leaf 5).

Tree nodes associated with the series dispersion D indicate that a systematic separation can be made at D=2.2–2.3 mm (Fig. 7a). As shown in Fig. 2, the separation between horizontal and vertical component dispersion occurs ca. D=2.5 mm, close to the node splitting value. Thus, we can consider that the node split based on the series dispersion represent a first-order distinction between (mostly) horizontal and vertical GPS components, although noisy horizontal and very clean vertical data can obviously be positioned in different categories.

On these bases, a fairly simple set of rules can be derived from the regression tree analysis that may be applicable to actual GPS data used for high-precision (sub mm yr⁻¹) studies, considering the fact that series duration is the key parameter:

• Duration of 8.0 years or more ensures a low-velocity bias in both horizontal (v₉₅=0.2 mm yr⁻¹) and vertical (v₉₅=0.5 mm yr⁻¹) components.

• Short series with less than 4.5 years duration cannot be used for high-precision studies (v₉₅ > 1.0 mm yr⁻¹), except in the rare cases when one can be certain that they contain no significant offset.

• For intermediate durations (4.5 < T < 8.0 yr), only series with no offset can provide a low-velocity bias (v₉₅=0.3 mm yr⁻¹). All others are associated with an intermediate horizontal biases (v₉₅=0.6 mm yr⁻¹) and a high vertical one (v₉₅=1.3 mm yr⁻¹).

The strong dependency on the absence or presence of one or more offsets in intermediate and short series corresponds to the effect described in Sect. 3.2 and confirms that the resolution of the offset amplitude is limited by the complex interactions between offsets and noise structures. This effect is very strongly reduced (or possibly suppressed) when offsets affect long (T > 8.0 yr) series. For those, the velocity variability is independent of offset presence (Fig. 7a) because such series maintain relatively long “offset-free” segments that ensure a good resolution of the velocity.

Finally, it is significant that no tree node exists that distinguishes very long series. In other words, the effect of the series duration is limited to ca. 4.5 and 8.0 yr. This is consistent with the observation made in the noise-alone analysis that the decay of the noise effect as a function of time stagnates ca. 15 to 21 years (cf. Fig. 4 and Sect. 3.1). Our results may indicate an overall lower limit on the velocity bias of ca. 0.1 mm yr⁻¹ due to the colored nature of the time series noise. In other words, longer series may not be able to significantly reduce the velocity bias without additional efforts to whiten the noise through better data processing or taking into account pluri-annual signals. However, this hypothesis is only valid under the simple noise model (linear spectra, Eq. 2) used in our synthetic data. Alternative noise models exist that suggest a flattening of the spectra at long periods (e.g., Gauss–Markov model, Langbein et al., 2004), which would strongly limit the pluri-annual effect and allow a much stronger impact of long series duration. The actual nature of GPS noise at periods longer than 5–10 years is poorly defined (Santamaria-Gomez et al., 2011; Hackl et al., 2011) and is thus a major unknown in analyses of velocity precision.

4.4 Validation of velocity standard errors

For each series, the velocity standard error is calculated using the Williams (2003) generic expression for colored noise with a non-integer spectral index. In order to estimate the spectral index and amplitude of the colored noise, we use a simplified least-square inversion in which we fit a linear model to the series power spectrum limited to periods between 1∕12 and T∕2 years (with T the length of the time series). In contrast with a more complex nonlinear method, such as maximum likelihood, this simple approach does not solve for the noise crossover frequency and thus only provides a first-order estimate of the noise parameters and velocity standard errors.

We can test the robustness of these standard errors in comparison with their associated velocity biases by computing the ratio of the velocity bias to its standard error for each individual time series. A ratio of 1 corresponds to a standard error equal to its velocity bias; a ratio smaller (greater) than 1 corresponds to a standard error greater (smaller) than its velocity bias. Owing to our stochastic approach and assuming Gaussian distributions of the velocities and standard errors, appropriate standard error calculations should result in ca. 68 % of the ratio population smaller than 1 (i.e., 68 % of the velocity biases are included in their standard errors) and ca. 95 % of the population smaller than 2 (i.e., 95 % of the velocity biases are included in twice their standard errors). In our dataset, only 54 % of the ratio are smaller than 1 and 75 % are smaller than 2 (Fig. 8). These percentages are low and suggest that, on average, our velocity standard errors are too small by a factor of ca. 1.6.

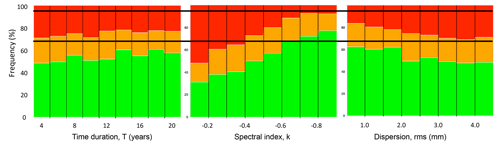
Figure 8 Distribution of the ratio of the velocity bias to its standard error for each individual time series. A ratio of 1 corresponds to a standard error equal to its velocity. A ratio smaller (greater) than 1 corresponds to a standard error greater (smaller) than its velocity. Ratio: less than 1 in green, less than 2 in orange, and greater than 2 in red. The black lines correspond to the 68 % and 95 % marks for normal distributions of the velocities and standard errors.

This result is primarily controlled by the series spectral index, while the series duration and dispersion have little effect (Fig. 8). Series with indices ca. −0.6 > k > −0.9 are associated with ratio percentages close to the 68 and 95 % marks. In contrast, series with high indices (k > −0.6) present ratios that are too low especially for very high indices (k > −0.4). These results suggest that the simplified (linear spectra) approach yields reasonable results for series with near-flicker (k < −0.6) noise characteristics but significantly underestimates the standard errors for series with near-white (k > −0.4) noise.

5 Application to the RENAG data

The statistical analyses of synthetic data presented in the previous sections provide guidelines to estimate the precision of velocities from actual GPS data. Using the regression tree classification of the full synthetic dataset with automatic offset detection (Sect. 4.3), actual time series can be classified according to the primary controlling parameters (duration, presence of offsets, noise amplitude and spectral index) and associated with a velocity bias distribution (Fig. 7). In the following application to the French RENAG network (RESIF, 2017), we use the 95 % confidence limit (v₉₅) estimator to provide a measure of the velocity precision of these real data. This estimator can be viewed as the classical velocity “uncertainty at 95 % confidence” (twice the standard error).

5.1 Offsets due to equipment changes

The RENAG network comprises 74 stations whose equipment modifications are fully documented (cf. http://webrenag.unice.fr, last access: 29 March 2018), thus providing a good test case for our offset detection method. On the 222 time series with durations between 2.0 and 18.4 years, the comparison of detected offsets with the station logs show that a change in receiver is very rarely associated with an offset (only 6 % of the 137 cases), whereas a change in antenna causes an offset almost systematically (75 % of the 8 cases) with average amplitudes of 2.0–3.0 mm in the horizontal and ca. 13.0 mm in the vertical components. However, these percentages are not robust due to the small sample sizes (especially the antenna changes). A more robust analysis would require a larger dataset, as well as the distinction between equipment changes within large data gaps or near the ends of the time series. Additionally, the offset detection method could be improved to integrate the probability that an offsets occurs on all three components of the same station rather than individually as it is currently done.

5.2 Potential velocity precision of the RENAG stations

The time series data of the 74 RENAG stations come from a Precise Point Positioning solution, combined with noise reduction using a regional common-mode technique (Masson et al., 2018; Nguyen et al., 2016). The time series of each station position component (north, east, up) are treated independently. We consider that the number of detected offsets is similar to the total number of offsets (N_off parameter in the regression tree), assuming that undetected offsets have small amplitudes and a small impact on the velocity estimations. This hypothesis is problematic for short series where the detection capacity is low (cf. Sect. 4.2) and for which it is likely that offsets were not detected, leading to a misclassification of series in Leaf 6.

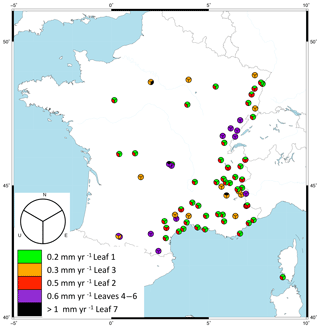
Figure 9 Map of the RENAG stations with the v₉₅ velocity bias of each component according to the tree classification.

Figure 9 shows a map of the RENAG stations with the v₉₅ value associated with each component according to the tree leaves. Roughly half (53 %) of the 74 stations are associated with the highest precisions in the horizontal (north and east, v₉₅=0.2 mm yr⁻¹) and vertical (v₉₅=0.5 mm yr⁻¹) components. In a few cases (12 %), the east component is degraded to a slightly larger precision v₉₅=0.5 mm yr⁻¹. About one-third (30 %) of the stations correspond to cases with no detected offsets and identical precision in all three components, either v₉₅=0.3 mm yr⁻¹ or v₉₅=0.6 mm yr⁻¹ depending on the duration of the time series.

Recent studies of GPS data in western Europe have shown tectonic signals at the limit of GPS resolution. The most significant signal corresponds to a systematic uplift of 1.0–2.0 mm yr⁻¹ in the central and northern regions of the Western Alps (Nguyen et al., 2016; Nocquet et al., 2016). The pattern of uplift and its lateral variations can provide important information on the associated dynamic (e.g., postglacial rebound versus slab tear; Chéry et al., 2016; Nocquet et al., 2016). Our analysis suggests that the 95 % confidence level of the RENAG velocities in the Alps is ca. 0.5 mm yr⁻¹, which may still be too large to provide strong constraints on the dynamic processes. In parallel with the vertical signal, horizontal deformation is starting to emerge in the GPS data analysis that show radial extension rates ca. 0.2–0.5 mm yr⁻¹ in the Western Alps and Pyrenees (Nguyen et al., 2016; Rigo et al., 2015; Walpersdorf et al., 2018). Such rates are at the limit of the 95 % confidence level estimated for individual RENAG stations (Fig. 9). This is especially true of stations in the French Jura, which show a relatively low precision v₉₅≈0.6 mm yr⁻¹ due to their recent installation and short time series (T < 3.5 yr). These examples highlight the importance of network redundancy and high station density in order to strengthen the deformation analysis by relying on several nearby stations to reduce aleatory noise in individual GPS time series.

6 Conclusions

We used statistical analyses of synthetic position time series to determine the potential precision on continuous GPS velocities. Our results are representative of standard GPS time series, leaving aside cases with extreme noise levels (e.g., random walk) or transient tectonic signals (e.g., slow slip events). The statistical analyses are discussed in terms of distributions of the velocity biases (absolute deviation from the true velocity for each series) and the associated 95 % confidence limit estimator (noted v₉₅). The latter can be viewed as a measure of the potential velocity precision of actual GPS data.

In the synthetic datasets, random noise combined with the presence of position offsets is the primary contributor to the variability in the estimated velocities, whereas seasonal signals have a negligible effect. Using regression tree analyses, we show that the duration of the time series is the main parameter controlling the data classification and the velocity biases. It is followed by the absence/presence of at least one offset and by the series dispersion due to random noise. Within the range of tested values, the nature of the random noise (near-white to near-flicker) does not contribute to the velocity variability at a significant level.

We derive a set of guidelines, which can be applied to actual GPS data, that provide constraints on the velocity bias using first-order time series parameters (duration, presence of offsets, and noise dispersion; cf. Fig. 7). The velocity biases are given by the v₉₅ estimator (95 % confidence limit of the class distribution):

• Series with a duration of 8.0 years or more are associated with a low-velocity bias in the horizontal (v₉₅=0.2 mm yr⁻¹) and vertical (v₉₅=0.5 mm yr⁻¹) components, regardless of their other characteristics (offset presence, nature the noise).

• Series with a duration of less than 4.5 years cannot be used for applications that require a precision better than 1.0 mm yr⁻¹, except when they are not affected by any offset (v₉₅=1.0 mm yr⁻¹ horizontal and vertical).

• Series of intermediate duration (4.5–8.0 years) and no offset are associated with a low bias (v₉₅=0.3 mm yr⁻¹). Those, more common, with at least one offset are associated with an intermediate horizontal bias (v₉₅=0.6 mm yr⁻¹) and a high vertical one (v₉₅=1.3 mm yr⁻¹).

A significant outcome of our analysis is that, beyond 8 years of data, it is the presence of offsets and the noise level that have the greatest impact on the velocity bias and not the lengthening of the series (within the limit of the 21 years tested here). This suggests that the lengthening of the series is not a sufficient condition to significantly reduce the bias in estimated velocities (below the 0.1 mm yr⁻¹ level). This effect derives directly from our noise model definition, in which the noise amplitude follows a linear power-law dependency on the frequency (Eq. 2). As a result, the noise amplitude constantly increases with long periods, explaining the very small effect of the time series duration past ca. 10 years (cf. Fig. 4). Alternative noise models, such as Gauss–Markov, which predicts a flattening of the power spectrum at long periods, would likely change our results and reinstate a strong duration dependency for very long series. This shows the importance of a better characterization of the GPS noise nature at very long periods and of current efforts to model and correct for long-period signals such as pluri-annual environmental loads.