the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysing stress field conditions of the Colima Volcanic Complex (Mexico) by integrating finite-element modelling (FEM) simulations and geological data
Roberto Sulpizio
Gianluca Norini
Gianluca Groppelli
Antonio Costa
Lucia Capra
Giacomo Lo Zupone
Michele Porfido
Andrea Gabrieli
In recent decades, finite-element modelling (FEM) has become a very popular tool in volcanological studies and has even been used to describe complex system geometries by accounting for multiple reservoirs, topography, and heterogeneous distribution of host rock mechanical properties. In spite of this, the influence of geological information on numerical simulations is still poorly considered. In this work, 2D FEM of the Colima Volcanic Complex (Mexico) is provided by using the Linear Static Analysis (LISA) software in order to investigate the stress field conditions with increasingly detailed geological data. By integrating the published geophysical, volcanological, and petrological data, we modelled the stress field considering either one or two magma chambers connected to the surface via dykes or isolated (not connected) in the elastic host rocks (considered homogeneous and non-homogeneous). We also introduced tectonic disturbance, considering the effects of direct faults bordering the Colima Rift and imposing an extensional far-field stress of 5 MPa. We ran the model using the gravity in calculations. Our results suggest that an appropriate set of geological data is of pivotal importance for obtaining reliable numerical outputs, which can be considered a proxy for natural systems. Beside and beyond the importance of geological data in FEM simulations, the model runs using the complex feeding system geometry and tectonics show how the present-day Colima volcanic system can be considered in equilibrium from a stress state point of view, in agreement with the long-lasting open conduit dynamics that have lasted since 1913.
- Article
(7982 KB) - Full-text XML
- BibTeX
- EndNote
Magmatism and tectonism are strongly related to regional and local stress fields, affecting both the orientation of faults and the location of volcanic vents (Geyer et al., 2016). The stress field around a magmatic source originates from three main contributions: (1) the background stress, composed of a vertical gravitational load, a lateral horizontal load (lithostatic confinement), and tectonic regime; (2) the stress field caused by the loading of the volcano edifice; and (3) the stress field generated by the magmatic pressure (e.g. Marti and Geyer, 2009; Currenti and Williams, 2014). In recent years, a large number of semi-analytical and numerical methods have been proposed for the solution of the stress field of natural systems (e.g. Cayol and Cornet, 1998; Simms and Graven, 2004; Manconi et al., 2007; Long and Grosfils, 2009; Currenti et al., 2010; Currenti and Williams, 2014; Zehner et al., 2015), taking into account the static–elastic deformation in a multilayered half-space (e.g. Dieterich and Decker, 1975; Bonafede et al., 2002; Wang et al., 2003; Gudmundsson and Brenner, 2004; Zhao et al., 2004; Pritchard and Simons, 2004; Gottsmann et al., 2006; Geyer and Gottsmann, 2010; Zhong et al., 2019). Following successful application in mechanical engineering, the use of finite-element modelling (FEM) has been extensively introduced in volcanology in order to investigate the effects of topography, lithologic heterogeneities, tectonic stresses, and the gravity field on the stress of volcanic systems (e.g. Cailleau et al., 2003, 2005; Buchmann and Conolly, 2007; Manconi et al., 2009; Masterlark et al., 2012) including volcanoes (e.g. Fujita et al., 2013; Charco and Galán del Sastre, 2014; Coco et al., 2016; Ronchin et al., 2015; Hickey et al., 2015; Cabaniss et al., 2018; Rivalta et al., 2019). There are several examples of the use of FEM for volcanic areas, which span from the influence of layered materials on the surface deformation process during volcanic inflation (e.g. Darwin volcano, Galapagos Islands; Manconi et al., 2007; Albino et al., 2010) to processes affecting chamber rupture (e.g. Grosfils, 2007; Long and Grosfils, 2009). The local stress around a volcanic feeding system depends on the geometry of the magma plumbing system, including the chamber(s) and dykes forming it, and on the mechanical properties of the host rock around it (e.g. Marti and Geyer, 2009), especially on changes in the Young modulus (e.g. Gudmundsson, 2011; Jeanne et al., 2017; Heap et al., 2020). For instance, limestone, lava flows, welded pyroclastic units, and intrusive rocks can be very stiff (high Young modulus from ca. 1.7 to 27 GPa for limestones, Touloukian et al., 1989; ca. 5.4 GPa for volcanic rocks, Heap et al., 2020), but young and non-welded pyroclastic units may be very soft (low Young modulus ca. 1.7–3.1 GPa, Margottini, 2013). Therefore, the local stress may abruptly change from one layer to another (e.g. Gudmundsson, 2006). Irrespective of the scope of the numerical investigation, the importance of applying accurate physical constraints to FEM has already been discussed in many studies (e.g. Folch et al., 2000; Newman et al., 2001; Fernández et al., 2001; Currenti et al., 2010; Geshi et al., 2012). However, in the last decade, few investigations have been carried out to assess the influence of the amount and quality of geological data on FEM computations (Kinvig et al., 2009; Norini et al., 2010, 2019; Cianetti et al., 2012; Ronchin et al., 2013; Chaput et al., 2014). To bridge this gap, in this work we use the Linear Static Analysis (LISA) software (version 8.0; https://www.lisafea.com/, last access: 10 December 2020) to study the subsurface field state in the Colima Volcanic Complex (CVC, Mexico) at increasing geological detail. The CVC area is a good candidate for testing the response of FEM software against different geological conditions, being constituted by a large volcanic complex (Lungarini et al., 2005) within a tectonic graben filled with volcano-clastic material (Fig. 1a; Norini et al., 2010, 2019). The FEM was run starting from simple homogeneous vs. stratified lithology of the subsurface in successively more detail through the addition of single and double magma chambers, feeder dykes, faults, and extensional far-field tectonic stress (Fig. 1b).
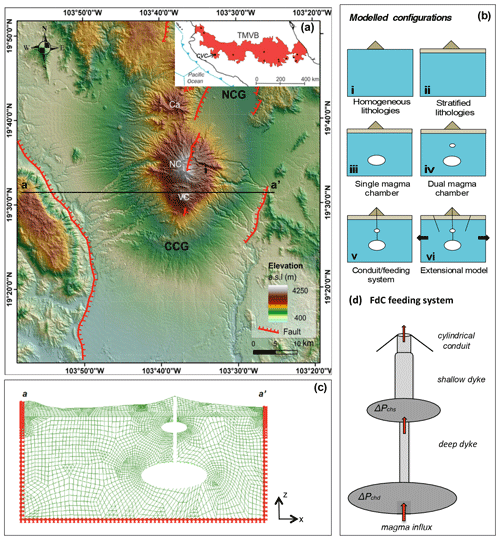
Figure 1(a) Morphotectonic map of the Colima Volcanic Complex (NC: Nevado de Colima volcano; FC: Fuego de Colima volcano) and Colima Rift with the main tectonic and volcano-tectonic structures (NCG: northern Colima graben; CCG: central Colima graben; from Norini et al., 2019). In the inset, the location of the Colima Volcanic Complex (CVC) within the Trans-Mexican Volcanic Belt (TMVB) is shown in the frame of the subduction-type geodynamic setting of Central America (from Davila et al., 2019); (b) general sketch of the geometrical configurations used in LISA; (c) example of mesh of the investigated area for the dual magma chamber model with conduits (case v in b), considering zero displacement along the bottom and left and right sides. Note that for case (vi) in (b) the zero displacement is removed from the lateral sides; (d) sketch of the Fuego de Colima feeding system composed of a 15 km deep magma chamber connected to the surface via a 6 km deep magma chamber and dykes. ΔPchs and ΔPchd are the magmatic overpressures in the shallow and deep chambers, respectively (modified from Massaro et al., 2019).
2.1 Geological framework
The Pleistocene–Holocene CVC is one of the most prominent volcanic edifices within the Trans-Mexican Volcanic Belt (TMVB) (Macías et al., 2006; Capra et al., 2016; Norini et al., 2019, Fig. 1a). In this area, the Rivera microplate and the Cocos plate subduct beneath the North America Plate along the Middle American Trench, forming a triple junction that delimits the tectonic units known as the Jalisco Block (JB) and the Michoacán Block (MB) (Luhr and Carmichael, 1985; Allan, 1986; Rosas-Elguera et al., 1996, 1997; Ferrari et al., 1999; Rosas-Elguera et al., 2003; Frey et al., 2007). The three rifts of this system are the Tepic–Zacoalco (TZR), the Chapala–Tula (CTR), and the Colima Rift (CR). The still active N–S-trending Colima Rift (CR) was formed during an extensional phase that occurred after the Late Cretaceous–Paleogene compressive and transpressive phase (Allan, 1986; Bandy et al., 1995; Cortés et al., 2010). While opening, the CR was gradually filled with Pliocene–Quaternary lacustrine sediments, alluvium, and colluvium (e.g. Allan, 1986, 1991; Norini et al., 2010). The geometry, kinematics, and dynamics of the CR have been studied on the basis of field, seismic, and geodetic data, mainly collected in its northern and central sectors (see Fig. 1 in Norini et al., 2010). The magnitude of vertical displacement of the northern and central sectors is ca. 2.5 km by adding the topographic relief of the bounding fault scarps (1.5–1.6 km) to the calculated sediment depth (Allan, 1985; Serpa et al., 1992). Field data and focal mechanism solutions are consistent with a direction of opening of the northern and central sectors oriented from E–W to NW–SE, with mainly normal and minor right-lateral displacements of the bounding faults (Barrier et al., 1990; Suárez et al., 1994; Rosas-Elguera et al., 1996; Norini et al., 2010, 2019; Garduño-Monroy et al., 1998). In contrast to field and seismic evidence of long-term slightly dextral oblique extension, recent GPS geodetic measurements suggest a possible sinistral oblique extension of the CR (Selvans et al., 2011). In both cases, the stress regime is mainly extensional, with an approximately E–W orientation of the minimum horizontal stress in the basement of the CVC (Barrier et al., 1990; Suárez et al., 1994; Rosas-Elguera et al., 1996; Selvans et al., 2011; Norini et al., 2010, 2019). The CVC stands within the central sector of the CR on top of the Cretaceous limestones, late Miocene–Pleistocene volcanic rocks, and Pliocene–Holocene lacustrine sediments, alluvium, and colluvium (Allan, 1985, 1986, 1991; Cortés et al., 2010; Norini et al., 2010; Escudero and Bandy, 2017). It is formed by three andesitic stratovolcanoes: Cantaro (2900 m a.s.l.), Nevado de Colima (4255 m a.s.l.), and, in the southern part, the youngest and active Volcán de Colima (3763 m a.s.l.) (Norini et al., 2019).
2.2 Eruptive activity
The eruptive history of the CVC started in the northeast area with the formation of the Cantaro volcano at ca. 1–1.5 Ma, followed by Nevado de Colima starting at ca. 0.53 Ma, which is composed of voluminous andesitic lava domes and deposits associated with caldera-forming eruptions and partial sector collapses (Robin et al., 1987; Roverato et al., 2011; Roverato and Capra, 2013; Cortés et al., 2019). The youngest – Volcán de Colima – comprises the Paleofuego edifice, which suffered several sector collapses that formed a horseshoe-shaped depression where the new active cone (also known as Volcán de Fuego) grew up. Its activity was characterized by dome growths and collapses, extrusion of lava flows, and Vulcanian and occasionally sub-Plinian explosive eruptions (Saucedo et al., 2010; Massaro et al., 2018, 2019).
2.3 The CVC plumbing system
Seismic tomography (Spica et al., 2017) highlights a 15 km deep low-velocity body (LVB) which was interpreted as a deep magmatic reservoir. It is confined within the CR, suggesting a structural control of the normal fault system on it (Spica et al., 2014). The LVB has an extent of ca. 55 km × 30 km in the N–S and E–W directions, respectively, showing an averaged thickness <8 km. Escudero and Bandy (2017) obtained a higher-resolution tomographic image of the CVC subsurface area, showing that the most active magma generation zone is now under the Fuego de Colima edifice. The ambient seismic noise tomographic study of Spica et al. (2014) indicates a shallow magma chamber above ca. 7 km of depth, in agreement with petrological studies (Medina-Martínez et al., 1996; Luhr, 2002; Zobin et al., 2002; López-Loera et al., 2011; Reubi et al., 2013, 2019; Macías et al., 2017). Cabrera-Gutiérrez and Espíndola (2010) suggested that the shallow active magma storage has a volume of ca. 30 km3. It is connected to the surface by conduits, whose path is facilitated by the presence of the CR fault zone, which provides a natural pathway for fluids (e.g. Allan, 1986; Norini et al., 2010, 2019). The arrangement of dykes and the alignment of volcanic centres of the CVC suggest that the dykes swarm draining the magma chambers developed along the NNE–SSW-trending, steep, eastward-dipping normal fault exposed on the northern CVC flank (Norini et al., 2010, 2019). Massaro et al. (2018) provided a first-order geometrical reconstruction of the Fuego de Colima feeding system during the 1913 sub-Plinian eruption by using volcanological data (Saucedo et al., 2010, 2011; Bonasia et al., 2011) as inputs and constraints for numerical simulations. Results showed good matches for a hybrid configuration of the shallow conduit feeding system composed of a ca. 5500 m long, 200–2000 m wide, and 40 m thick dyke passing into a shallower (500 m long, 40 m diameter) cylindrical conduit. The shallow magma chamber top was set at 6 km of depth with a dyke–cylinder transition at 500 m below the summit as inferred from geophysical data (Salzer et al., 2014; Arámbula-Mendoza et al., 2018).
In this study, we used the commercial 8.0 version of LISA (https://www.lisafea.com/, last access: 10 December 2020), a general-purpose finite-element analysis (FEA) software developed in the 1990s based on the formulations proposed by Rao (1989) and successively integrated from other sources (Michaeli, 1991; Schwarz, 1991; Babuška et al., 1995; Bathe et al., 1999). Despite LISA originally being used for structural analysis (Rao, 1989, 2013), it successfully predicts the stress–strain behaviour of rock masses in elastic models, in particular the deformation mechanisms, even in layered rock masses (Gabrieli et al., 2015).
Table 1Element types used in LISA considering the final conduit feeding system configuration and the E–W cross section (a–a′ – Fig. 1d, panel vi). The total number of elements is 4209.

3.1 Modelling approach
The stress field of the CVC plumbing system is simulated considering an E–W cross section, parallel to the extension associated with the active CR (Norini et al., 2010), as shown in Fig. 1a–b (a–a′). Since the extent of the CVC magma chambers in the NNE–SSW direction is typically much longer than the dimensions of the E–W cross section (Spica et al., 2017), 2D solutions of either numerical or analytical models describing E–W elongated magma chambers in the crust can be reasonably adopted (Jaeger et al., 2009; Costa et al., 2011). A topographic profile and 2D plane along the chosen E–W cross section of the CVC area were obtained in ESRI ArcGIS from a digital elevation model (DEM; resolution 50 m; Instituto Nacional de Estadística y Geografía – INEGI, https://en.www.inegi.org.mx/, last access: 10 December 2020) and imported into Autodesk Auto-Cad R13 using a third-degree spline approximation. The IGES file was then imported into LISA for the mesh discretization. The investigated domain extends 60 × 30 km in an x–z Cartesian coordinate system with the three- and four-node finite-element discretization (Table 1). Zero normal displacements are assigned at the bottom and the lateral boundaries, while the upper boundary represents the free-stress ground surface (Fig. 1c). The FEM is carried out by using a plane strain approximation, implying that the deformation in the third direction is assumed to be negligible. As reported by Zehner et al. (2015), FEM of geological structures requires accurate discretization of the computational domain. It follows that the unstructured tetrahedral meshes have to fulfil the following requirements: (i) sufficient mesh quality, with the tetrahedrons not too acute-angled, since numerical instabilities can occur; (ii) incorporation of geometry for defining boundary conditions and constraints; and (iii) local adaption, which is a refinement of the mesh in the vicinity of physical sources in order to avoid numerical errors during the simulation. In this work, we adopted a mesh composed of 4660 plane continuum elements, which have been refined in the regions of higher gradients (i.e. near the contours of the magmatic feeding system). In our simulations, the extent of the rock layers (Table 2) refers to that used by Norini et al. (2010, 2019). The configuration of the CVC feeding system (i.e. depth, shape, and dimensions of the magma chambers and feeder dykes) derives from the literature (Spica et al., 2014, 2017; Massaro et al., 2018, 2019), and it is simplified in Fig. 1d. In particular, magma chambers and dykes are considered to be pressurized finite-size bodies in an elastic crustal segment acting as fluid-filled holes. The boundary condition (pressurization) is provided by applying internal forces that act on the walls. This approach has been used extensively in several analytical and numerical models that treat magma reservoirs as internally pressurized ellipsoidal cavities within an elastic half-space in order to gain insight into the behaviour of magma plumbing systems (Pinel and Jaupart, 2004; Gudmundsson, 2006; Grosfils, 2007; Andrew and Gudmundsson, 2008; Hautmann et al., 2009; Currenti and Williams, 2014). Previously published studies indicate that differences between, and problems with, elastic models derive principally from the key role played by gravity (e.g. Lister and Kerr, 1991; Watanabe et al., 2002; Gerbault et al., 2012; Albino et al., 2018). Some authors have argued regarding whether it is appropriate or not to account for the gravity body force in models of volcanic systems (e.g. Currenti and Williams, 2014; Grosfils et al., 2015). When the gravitational loading is not included in the model, the volcanic deformation results from a change with respect to a stage previously at equilibrium (e.g. Gerbault et al., 2018). In this work, we carried out simulations considering the effect of the gravitational loading in the host rock, implemented via body forces. The model initial condition has a pre-assigned lithostatic stress, whose computation, in the presence of topography and material heterogeneities, is not trivial because it requires applying the gravity load preserving the original non-deformed geometry of the mesh (Cianetti et al., 2012). Due to the presence of a lithostatic stress field, the load applied at the reservoir boundaries represents a superposition of the magmatic overpressure and lithostatic component. We define the magmatic pressure as either excess pressure (ΔPe, magmatic minus lithostatic pressure but below the tensile strength of wall rocks) or overpressure (or driving pressure, ΔPo), which is the magmatic pressure exceeding the tensile strength of wall rocks (Gudmundsson, 2012). The first pertains to FEM using isolated magma chambers (single or double), while the second is used for models with connected magma chambers (with a conduit feeding system). We also took into account the effect of the existing faults of the CR system even though LISA cannot include a frictional law to represent the fault movement (Chaput et al., 2014). As reported in Jeanne et al. (2017), the damage induced by faults increases from the host rocks to the fault core, implying a reduction in the effective elastic moduli. In this light, we represented the faults bordering the CR as two damage zones (ca. 70∘ of inclination, ca. 1 km thick, and down to 10 km of depth) showing reduced elastic properties with respect to the surrounding rocks. To take into account the effect of the far-field extensional regime, we applied a uniform stress of 5 MPa to the lateral boundaries of the domain, as reported by Marti and Geyer (2009). Considering the E–W cross section (a–a′; Fig. 1a), we provide six domain configurations: (i) the homogeneous lithology model in which the volcanic domain is only composed of andesite rocks; (ii) the non-homogeneous lithology model wherein different geological units are considered; (iii) the single magma chamber model composed of a non-homogeneous lithology and a 15 km deep magma chamber; (iv) the dual magma chamber model composed of a non-homogeneous and 6 and 15 km deep magma chambers; (v) a conduit feeding system model composed of non-homogeneous lithology, 6 and 15 km deep magma chambers connected through a deep dyke, and a shallow conduit connecting to the surface; (vi) an extensional model with a 5 MPa horizontal extensional stress (far field); and (vii) a faulted model, in which two damaged zones mimicking the CR faults (local stress) are also added. The number of nodes is set at 4426 for the only substratum and single magma chamber models, at 4161 for the dual magma chamber model, and at 3737 for the conduit feeding system and faulted models. It is important to note that simulation outputs are shown using different colour scales. Although such a choice may make the visual comparison of the different runs difficult, it preserves the necessary details of stress distribution, which would have been lost using a common colour scale. Finally, in the following we refer to σ1 as the greatest compressive stress and σ3 as the least compressive stress.
Table 2Rock mass and mechanical properties of the geological units used in FEM from Norini et al. (2010, 2019).

4.1 Stratigraphy and rock mechanics
Four units forming the CVC system were defined from the available geological data (Table 2): (i) a basement (Unit B) of Cretaceous limestones and intrusive rocks forming the bedrock underlying the CVC; (ii) graben fill deposits (Unit GF): Quaternary alluvial, colluvial, and lacustrine deposits filling the graben; (iii) Fuego de Colima deposits (Unit FC) of andesitic lavas and pyroclastic deposits forming the Paleofuego–Fuego de Colima edifices; and (iv) volcaniclastic deposits (Unit VD) covering the southern flank of the CVC (e.g. Cortés et al., 2010; Norini et al., 2010, 2019). We assumed constant mechanical characteristics within each unit using the typical rock mass properties of density (ρ), the Young modulus (E), and the Poisson ratio (ν) (Table 2). The rock masses are considered dry for (eventual) pore pressure to be neglected. Only for Unit GF was a higher value for the Poisson ratio used close to the surface in order to mimic high water content in the graben sediments. The maximum thickness of the graben fill (about 1 km) is assumed from the literature (Allan, 1985; Serpa et al., 1992; Norini et al., 2010, 2019). For Units B and GF rock mass proprieties are derived from Hoek and Brown (1997) and Marinos and Hoek (2000), while for volcanic materials (units FC and VD; Table 2) they are estimated according to the approach proposed by Del Potro and Hurlimann (2008). In order to describe the effects of the CG faults on stress field distribution, the mechanical properties are locally degraded in proximity to the faults themselves.
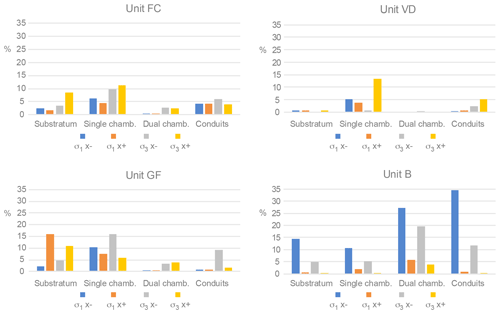
Figure 2Results of the sensitivity analysis carried out on the Young modulus variations within each rock layer of the domain considering different configurations (stratified substratum model – nodes: 4426; single magma chamber model – nodes: 4426; dual magma chamber model – nodes: 4161; dual magma chamber model with conduits – nodes: 3737). For each geological unit (B, FC, GF, VD), the relative global variation in L2 (%) is provided for σ1 and σ3. The x(−) and x(+) vectors indicate the Young modulus variation by an order of magnitude with respect to the xref vector, containing the stress values calculated by using the values of material properties indicated in Table 2.
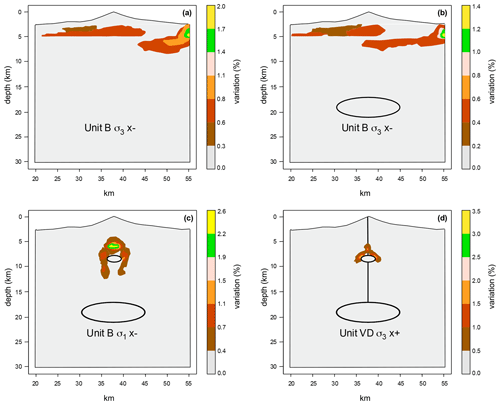
Figure 3Spatial variation (%) of the L2 norm's components at varying Young modulus values for the selected cases of Units B and VD: (a) Unit B in the stratified substratum model (nodes: 4426); (b) Unit B in the single magma chamber model (nodes: 4426); (c) Unit B in the dual magma chamber model (nodes: 4161); (d) Unit VD in the dual magma chamber model with conduits (nodes: 3737). Symbols x(−) and x(+) have the same meaning as in Fig. 2.
4.2 Geometry of the plumbing system
In our 2D model, we assumed the CVC is composed of two magma chambers connected by dykes and to the surface by a conduit (Fig. 1d). The shape of the magma chambers and dykes is represented by elliptical cross sections with the major (2a) and minor (2b) axes. Generally, magma chambers have a sill-like shape that is often imaged in seismic studies of volcanoes and rift zones (Macdonald, 1982; Sinton and Detrick, 1992; Mutter et al., 1995; MacLeod and Yaouancq, 2000; Canales et al., 2009). Most of them are not totally molten but rather a mixture of melt and crystal mush (i.e. Parfitt and Wilson, 2008). Various estimates have been made to infer the actual amount of melt in a magmatic body, showing that it is only ca. 10 % of the total chamber volume (Gudmundsson, 2012, and references therein). After Spica et al. (2017), the 15 km deep low-velocity body (LVB) is ca. 7000 km3. Therefore, if we assume the melt as 10 %, the deep magma chamber volume would be ca. 700 km3. Simplifying this volume in an elliptical sill-like geometry, the magma chamber dimensions (i.e. axes) have to be scaled according to those of the LVB (55 × 30 × 8 km; Spica et al., 2017) using 2a=14 km, 2b=3.6 km, and 2c=26 km, with 2c being elongated in the NW–SE direction. For the shallow part of the feeding system, we have no detailed geophysical constraints. However, Massaro et al. (2019) reproduced the nonlinear cyclic eruptive activity at Fuego de Colima in the last 20 years through numerical modelling using a shallow magma chamber volume in the range of 20–50 km3, also according to the estimation of Cabrera-Gutiérrez and Espíndola (2010). Here we assume a volume of 30 km3 using 2a=3.5 km, 2b=2 km, and 2c=8 km as the dimensions of the shallow magma chamber. Numerous theoretical and field studies have established that host rock stresses dictate the magma pathways (e.g. Maccaferri et al., 2011; Gudmundsson, 2011). During ascent to the surface, the dykes align themselves with the most energy-efficient orientation, which is roughly perpendicular to the least compressive stress (e.g. Gonnermann and Taisne, 2015; Rivalta et al., 2019), providing the magma-driving pressure remains small compared to the deviatoric stress (Pinel et al., 2017; Maccaferri et al., 2014a). This behaviour, however, can be modulated in the presence of significant variations in fracture toughness of the surrounding rock due to stratification (Maccaferri et al., 2010) or to old and inactive fracture systems (Norini et al., 2019). Although for oblate magma chambers the propagation of dykes is most probable from the tip areas, in our simulations the orientation of dykes is assumed to be vertical because of the preferential pathways represented by the CR fault planes (Spica et al., 2014). We set the dimensions of feeder dykes in agreement with Massaro et al. (2018): deep dyke 2ad=2 km; shallow dyke 2a varies from 1 km at the bottom to 500 m in the upper part of the volcano; width of both deep and shallow dyke m (Fig. 1d). It is worth noting that it is outside the scope of this work to provide the conditions for rupture of the magma chamber, since LISA accounts only for the elastic regime. For these reasons, we fixed ΔPe and ΔPo (for isolated and connected magma chambers, respectively) in the range of 10–20 MPa for the 15 km deep chamber and 5 MPa for the 6 km deep one. For the dykes and conduit, ΔPo is set to 10 MPa in the deeper dyke and 5 MPa in the shallower dyke, while in the upper 500 m of conduit it is 0.4 MPa.
In this section we report the sensitivity analysis carried out to quantify the approximation of the Young modulus variation in FEM outputs and a description of the model outputs when adding complexity to the input geological–geophysical data.
5.1 Sensitivity analysis of Young modulus
Using the single magma chamber model as a reference case, we quantified the influence of Young modulus variation in each geological unit. Taking into account the mechanical properties of rocks (Table 2) as reference values, we compared the stress state of the computational domain on changing the Young modulus by (±) 1 order of magnitude. This sensitivity analysis, although incomplete, may lead to increased awareness of the selection of input data when running an FEM. The sensitivity analysis was carried out on a reduced simulation domain (the x axis was set to 35 km) in order to diminish the influence of binding effects along the domain borders. We applied the Euclidean norm (L2) method to illustrate the results. The L2 norm applied on a vector space x (having components ) is strongly related to the Euclidean distance from its origin and is equal to
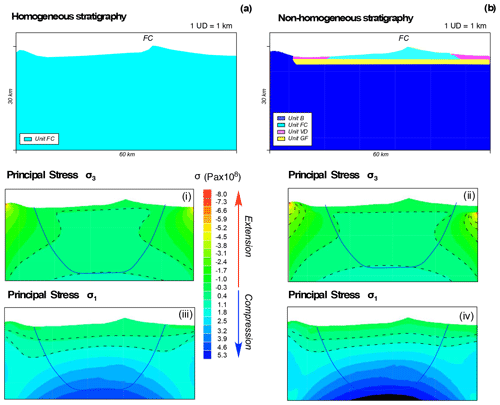
Figure 4E–W gravitational modelling of the CVC domain. The scale of the mesh is expressed in units of design (1 UD = 1 km). The domain extends 60 km along the x axis and 30 km along the z axis. The number of nodes used in the mesh is set to 4426. The magnitude and pattern of the principal stresses (dotted black lines) are reported for (a) the homogeneous stratigraphy (Unit FC: andesitic lavas and pyroclastic deposits) and for (b) the non-homogeneous stratigraphy (Unit FC; Unit B: Cretaceous limestones and intrusive rocks forming the bedrock underlying the CVC; Unit GF: Quaternary alluvial, colluvial, and lacustrine deposits filling the graben; Unit VD: volcaniclastic deposits covering the southern flank of the CVC). The blue line contours the unperturbed part of the domain, which extends ca. 30 km horizontally and ca. 25 km vertically. Note that the scale of stress values is the same for the all simulations.
In our case, the vector space x is composed of all nodes of the computational domain (Table 1). We defined xref as the vector containing the results for the maximum and minimum principal stress when using the selected values of material properties (Table 1), and x(−) and x(+) are the vectors upon varying the Young modulus by 1 order of magnitude in each unit. In Fig. 2 the global relative variations in L2 of σ1 and σ3 caused by the variation of the Young modulus in each unit are reported for each model configuration (i.e. non-homogeneous lithology, single magma chamber, dual magma chamber, and dual magma chamber model with conduits) as follows:
All the models show variability of less than 15 %, with a few exceptions within Unit B that have variability of over 30 % (Fig. 2). In this light, the spatial distribution of the major variations seems not to significantly affect the final stress distributions because (i) they are located near the mesh borders (Fig. 3a and b), and (ii) when not at the mesh borders, the variations are limited to a few percent (Fig. 3c and d). It means that a 1 order of magnitude variation in the Young modulus produces variation in FEM outputs distributed over a large domain, and the change affecting the single nodes is limited to a few percent.
5.2 Homogeneous and non-homogeneous lithology
In Fig. 4 we report gravity-loaded models with homogeneous lithology composed of andesitic lavas (Fig. 4a) and non-homogeneous lithology composed of carbonates (Unit B) and alluvial, volcaniclastic, and pyroclastic deposits (Units GF and VD; Fig. 4b). It is important to stress that the x–z zero displacement assigned at the bottom and at the lateral boundaries of the domain created substantial artefacts in the results (i.e. curved patterns of stress), especially considering σ3 (Fig. 4, panels i and ii) whereby the boundary effect on the x axis is amplified by the presence of the upper free surface. It follows that the only unperturbed area extends ca. 30 km horizontally and ca. 15 km vertically (within the blue contour in Fig. 4). It is worth noting that the homogeneous and non-homogeneous models show quite similar stress pattern results (Fig. 4).
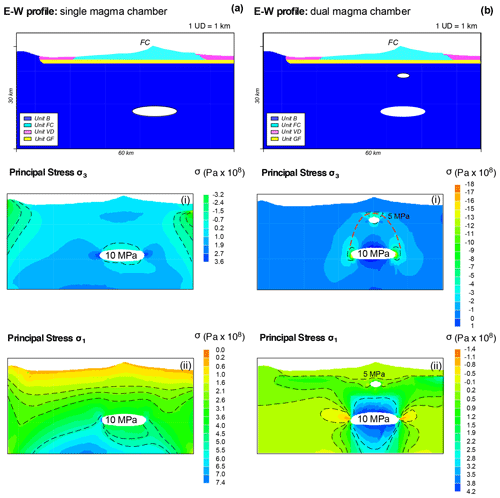
Figure 5E–W gravitational modelling of the CVC domain with a non-homogeneous stratigraphy. The magnitude and pattern of the principal stresses are reported for (a) the single magma chamber model represented by a magma chamber (2a=14 and 2b=3.6 km) at 15 km of depth and (b) the dual magma chamber model composed of a 15 km deep magma chamber (2a=14 and 2b=3.6 km) and a shallow 6 km deep one (2a=3.5 and 2b=2 km). The magma chambers are not connected. ΔPo is set to 10 and 5 MPa for the 15 km deep and 6 km deep magma chambers, respectively. The number of nodes is set to 4426 and 4161 for the single and dual magma chamber models, respectively. Black dotted lines highlight the passage from different stress values. The red dotted line in (b) (panel i) indicates the formation of the stress arch. Note that the scales of stress values are different for each panel in order to maximize the simulation details.
5.3 Gravitational modelling using inferred feeding system geometry
In Figs. 5 and 6 we show three cross-sectional profiles describing the feeding system starting from a single magma chamber to two chambers, then adding the conduits, and finally considering the full complexity by adding the effects of far-field stress and CR faults. Figure 5a describes the σ3 (panel i) and σ1 (panel ii) stress distribution for the single magma chamber model and ΔPe=10 MPa. No significant differences in the magnitude and pattern of stresses are visible using ΔPe = 20 MPa (Appendix Fig. A1). The addition of the shallow magma chamber significantly changes the values and pattern of both σ3 and σ1 (Fig. 5b). In particular, σ3 and σ1 stresses describe a typical inflation pattern produced by excess pressure in the magma chamber(s) (Anderson, 1936; Gudmundsson, 2006, 2012), producing well-defined stress arches of σ3 (red dotted lines in Fig. 5bi) and divergent strong gradients of σ1 around the deep magma chamber (Fig. 5bii). Very slight differences in the magnitude and pattern of stresses appear when using ΔPo = 10 MPa (Fig. 5b) or 20 MPa (Appendix Fig. B1). Looking at Fig. 6, it is evident how the insertion of the conduits in the CVC feeding system dramatically changes the stress distribution, with the disappearance of the stress arch and a nearly constant stress in the computational domain except around the deep magma chamber tips.
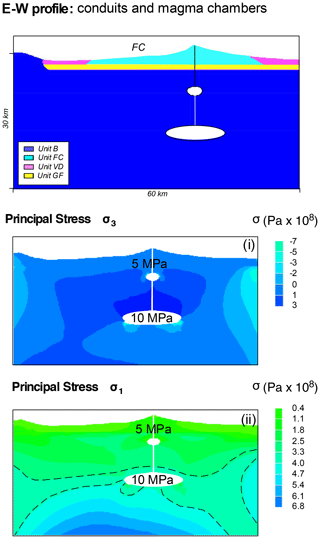
Figure 6E–W gravitational modelling of the CVC domain with a non-homogeneous stratigraphy accounting for a dual magma chamber system connected by dykes via the surface (deep magma chamber, 2a=14 and 2b=3.6 km at 15 km of depth; shallow magma chamber, 2a=3.5 and 2b=2 km at 6 km of depth). The magnitude and pattern of the principal stresses are shown. The number of nodes used is set to 3737. ΔPo is set to 10 and 5 MPa for the 15 km deep and 6 km deep magma chambers, respectively. The black dotted lines in (ii) the passage from different stress values. Note that the scales of stress values are different for each panel in order to maximize the simulation details.
5.4 Application of an extensional stress field
In order to explore the influence of the extensional far-field stress on stress patterns (Fig. 1a), we ran simulations applying 5 MPa (a typical low value for rift zones; Turcotte and Schubert, 2002; Moeck et al., 2009; Maccaferri et al., 2014b; Sulpizio and Massaro, 2017) along the lateral boundaries of the computational domain (Fig. 7). In the case of a single magma chamber (ΔPe = 10 MPa; Fig. 7, panels i–ii), the addition of the far-field stress reduces the confinement effect due to the no-displacement condition imposed along the x–z directions (plane strain approximation). When considering the double magma chamber configuration (ΔPo=10 MPa in the deep chamber and ΔPo=5 MPa in the shallower one), the presence of the far-field stress produces slight changes in the stress magnitude and pattern for both σ3 and σ1 (Fig. 7, panels iii and iv) with respect to Fig. 5b. Very similar effects appears in the complete feeding system configuration model (Fig. 7, panels v–vi). Also, in this case using ΔPo=20 MPa in the deep magma chamber does not significantly affect the model outputs (Appendix B).
5.5 Faults bordering the Colima Rift
The effect of faults bordering the CR on the final feeding system configuration is simulated through two damage zones by degrading their elastic properties. Adding these elements does not significantly alter the stress distribution observed in Fig. 7v and vi but only provides a slight reduction in both σ1 and σ3 intensities around their edges (Fig. 7vii and viii). The different distance of the two damage zones from the feeding system produces a small asymmetry in both σ1 and σ3 patterns with respect to simulations without damage zones, especially near the deep magma chamber (Fig. 7v–viii).
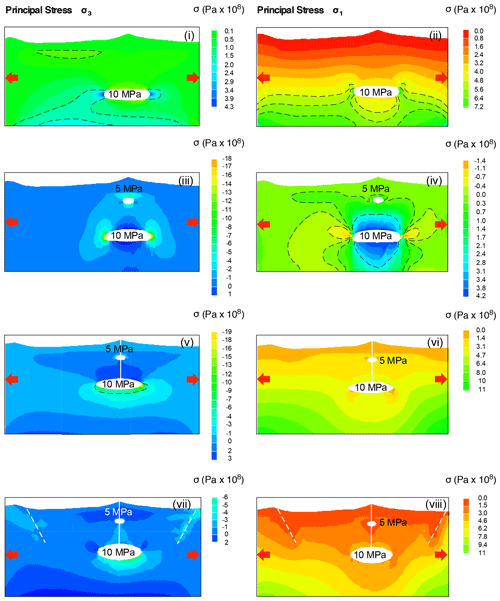
Figure 7E–W gravitational modelling of the CVC domain with a non-homogeneous stratigraphy considering the extensional field stress. The magnitude and pattern of the principal stresses are shown for the single magma chamber model (i–ii), the dual magma chamber model (iii–iv), and the dual magma chamber model with conduits (v–viii). Note that in (vii–viii) the faults bordering the Colima graben are shown. For all configurations an extensive far-field stress of 5 MPa is applied at the lateral boundaries of the domain. In panels (vii–viii) the additional effect of the local extensive field is simulated using a reduced value of material properties (Table 2). ΔPo is set to 10 and 5 MPa for the 15 km deep and 6 km deep magma chambers, respectively. Black dotted lines highlight the passage from different stress values. The red arrows indicate the direction of the applied far-field stress. Note that the scales of stress values are different for each panel in order to maximize the simulation details.
6.1 FEM analysis at increasing geological detail
The study highlights some important features of crustal stress distribution in terms of changing the geological and geophysical constraints used as input conditions (Spica et al., 2014, 2017; Massaro et al., 2018). Although the results have to be considered a first-order approximation, the changes in stress distribution are appreciable and useful for a better understanding of the advantages of FEM. Under the assumptions of plane strain and gravitational loading, the use of homogeneous or non-homogeneous lithology provides negligible effects on stress intensity and pattern (Fig. 4). This is likely due to the limited thickness of the shallow units (Units FC, VD, and GF; Table 2) in the simulated domain, the results of which are dominated by Unit B (Table 2). However, this does not mean that the influence of the upper units may still be negligible using smaller scales of the simulated domain. Analysing the single magma chamber model outputs, it emerges that ΔPe limits the effects of gravitational loading. In contrast, the dual magma chamber geometry better describes the inflation induced by ΔPe within magma chambers, with the formation of the stress arch in the σ3 plot. It is worth noting that for both the single and dual magma chamber models, changing ΔPe from 10 to 20 MPa slightly affects the magnitude of the stress but not its general pattern (Appendices A and B). The presence of dykes in the magma feeding system dramatically changes the σ3 and σ1 patterns (Fig. 6), which become quite homogeneous throughout the computational domain, with the only exception of sidewall effects induced by the zero displacement conditions. The addition of extensional field stress of 5 MPa reduces the sidewall effects and produces an almost homogeneous stress distribution in the upper part of the computational domain above the top of the deep magma chamber. This, along with the additional inclusion of the damage zones introduced to mimic the effects of CR faults, describes a volcanic system close to equilibrium, in which pressure within the volcano feeding system almost equilibrates the lithostatic stress (Sulpizio et al., 2017).
6.2 Some implications of the stress state of the CVC inferred from FEM
The results from the most complete FEM runs highlight an almost homogeneous stress distribution in the CVC area. This means the dual magma chamber model and the application of far-field stress provide a stable geometry, which limits the stress changes to a few megapascals (MPa). The majority of stress variations are located at the tips of the magma chambers, as expected for pressurized or under-pressurized cavities in the lithosphere (Marti and Geyer, 2009), implying that the whole feeding system is in a quasi-equilibrium state. Even if we consider the scenario of complete emptying of the upper conduit and part of the shallow magma chamber, as occurred occasionally during the past sub-Plinian and Plinian eruptions (Luhr, 2002; Saucedo et al., 2010; Massaro et al., 2018), this would result in the restoration of the stress arch, which is still a stable stress configuration. Even complete emptying of the shallow magma chamber would probably be ineffective for triggering a large collapse (caldera-forming) of the feeding system. Beside and beyond the limitations due to the first-order approximation of the FEM analysis, other sources of uncertainty in the discussion about the present and future stress state of the CVC come from not considering gravity-driven processes, such as volcano spreading due to plastic deformation of Unit GF (Norini et al., 2010, 2019) and detailed regional tectonics (Norini et al., 2010, 2019). The effect of the two fault systems bordering the CR is simulated here by degrading the mechanic properties of rocks in an area of about 1 km width up to a depth of 10 km. Although the effects are negligible at the scale of the computational domain, the possibility cannot be excluded that there are some local significant effects that cannot be resolved using the described approach.
The presented study highlights the importance of using complete and detailed geological and geophysical data when dealing with FEM of volcanic areas. The different geological detail used in the model runs showed how the stress pattern critically depends on the geometry of the volcano feeding system, with huge differences in having a single or double magma chamber system and, in particular, whether or not the magma chamber(s) are connected to the surface by feeder dykes and conduits. The geometry of the feeding system is prevalent in model outputs with respect to varying rock properties (i.e. Young modulus) of 1 order of magnitude. In the case of CVC, the use of subsurface homogeneous or stratified lithology does not influence the FEM outputs much, with the subsurface geology of the computational domain being dominated by carbonates (Unit B). Beside and beyond the results obtained by analysing the influence of detailed geological and geophysical data, the presented modelling confirms the close-to-equilibrium state of the volcano, which is the expected stress distribution induced by a feeding system directly connected to the surface. The complete emptying of the upper conduit and part of the shallow magma chamber has in the past led to sub-Plinian and Plinian eruptions. This process permits the restoration of the stress arch and maintains a stable subsurface stress configuration. It follows that large-magnitude, caldera-forming eruptions are possible only if the bigger deep magma chamber is also involved and significantly emptied during an eruption.
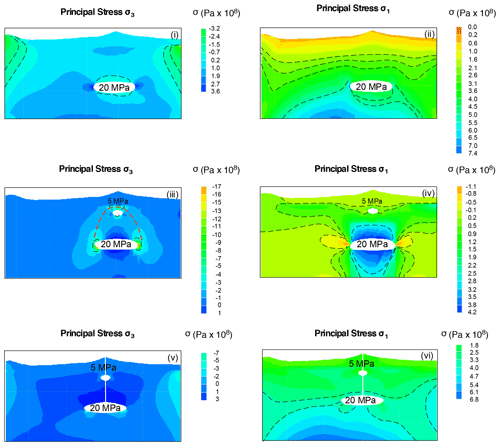
Figure A1E–W gravitational modelling of the CVC domain (stratified lithology) for all configurations investigated. The magnitude and pattern of the principal stress account for the (i–ii) single magma chamber model (number of nodes: 4426), (iii–iv) dual magma chamber model (number of nodes: 4161), and (v–vi) dual magma chamber model with conduits (number of nodes: 3737). The dimensions of the deep magma chamber are 2a=14 and 2b=3.6 km at 15 km of depth; shallow magma chamber: 2a=3.5 and 2b=2 km at 6 km. ΔPe and ΔPo are equal to 20 MPa for the deep chamber and 5 MPa for the shallower. Black dotted lines highlight the passage from different stress values. Note that the scales of stress values are different for each panel in order to maximize the simulation details.
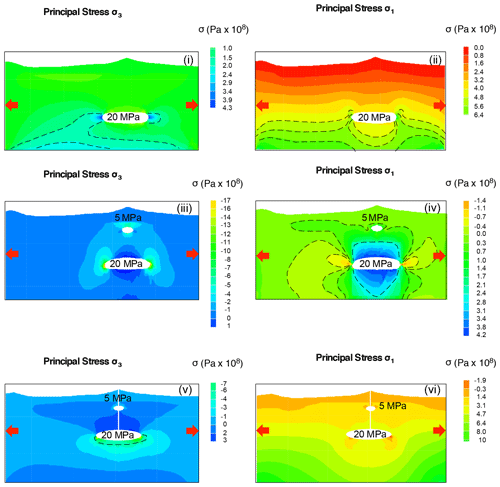
Figure B1E–W gravitational modelling of the CVC domain (stratified lithology) considering a far extensional stress field of 5 MPa for all configurations investigated. The magnitude and pattern of the principal stress account for the (i–ii) single magma chamber model (number of nodes: 4426), (iii–iv) dual magma chamber model (number of nodes: 4161), (v–vi) dual magma chamber model with conduits (number of elements: 3737). The dimensions of the deep magma chamber are 2a=14 km and 2b=3.6 km at 15 km of depth; shallow magma chamber: 2a=3.5 km and 2b=2 km at 6 km. ΔPe and ΔPo are equal to 20 MPa for the deep chamber and 5 MPa for the shallower. Black dotted lines highlight the passage from different stress values. The red arrows indicate the direction of the applied far-field stress. Note that the scales of stress values are different for each panel in order to maximize the simulation details.
The LISA code is available at https://lisafea.com/ (last access: 10 December 2020; Sonnenhof Holdings (Canada) (2013), 2013).
SM, RS, AC, GN, and GG conceived the study. SM and RS wrote the bulk of the paper with the input of all the co-authors. SM and GL compiled the numerical simulations and formulated the adopted methodology. MP and SM carried out the sensitivity analysis. RS, AC, SM, GN, GG, LC, GL, MP, and AG worked on the interpretation of the results.
The authors declare that they have no conflict of interest.
Silvia Massaro thanks LISA customer service for the support received.
The research leading to these results has received funding from the GEMex Project (to G. Norini), funded by the European Union's Horizon 2020 research and innovation programme under grant agreement no. 727550.
This paper was edited by Joachim Gottsmann and reviewed by Adelina Geyer and Virginie Pinel.
Rao, S. S.: The Finite Element Method in Engineering second edition, Elsevier, ISBN 0-08-033419-9, 1989. a, b
Michaeli, W.: Extrusionswerkzeuge für Kunststoffe und Kautschuk: Bauarten, Gestaltung und Berechnungsmöglichkeiten, Hanser Verlag, 1991. a
Schwarz, H. R.: Methode der finiten Elemente neubearbeitete, Teubner Stuttgart ISBN 3-519-22349-X, 1991. a
Margottini, C., Canuti, P., and Sassa, K.: Landslide science and practice, Springer, Berlin, 2013. a
Rao, S. S.: The Finite Element Method in Engineering, Elsevier, 2013. a
Albino, F., Pinel, V., and Sigmundsson, F.: Influence of surface load variations on eruption likelihood: application to two Icelandic subglacial volcanoes, Grímsvötn and Katla, Geophys. J. Int., 181, 1510–1524 2010. a
Albino, F., Amelung, F., and Gregg, P.: The role of pore fluid pressure on the failure of magma reservoirs: insights from Indonesian and Aleutian arc volcanoes, J. Geophys. Res.-Sol. Ea., 123, 1328–1349, 2018. a
Allan, J.: Sediment depth in the NCG from 3-D interpretation of gravity, Geofis. Int., 24, 21–29, 1985. a, b, c
Allan, J.: Geology of the Northern Colima and Zacoalco grabens, Southwest Mexico: Late Cenozoic rifting in the Mexican Volcanic Belt, Geol. Soc. Am. Bull., 97, 473–485, 1986. a, b, c, d, e
Allan, J.: Pliocene-Holocene rifting and associated volcanism in Southwest Mexico: an exotic terrane in the making, in: The Gulf and Peninsular Provinces of the Californias, edited by: Dauphin, J. P. and Simoneit, B. R. T., American Association of Petroleum Geologists, Chapter 21, Part III, Regional Geophysics and Geology, 1991. a, b
Anderson, E.: The dynamics of formation of cone sheets, ring dykes and cauldron subsidence, Vol. 56, Proc. R. Soc. Edinburgh, 1936. a
Andrew, R. and Gudmundsson, A.: Volcanoes as elastic inclusions: Their effects on the propagation of dykes, volcanic fissures, and volcanic zones in Iceland, J. Volcanol. Geoth. Res., 177, 1045–1054, 2008. a
Arámbula-Mendoza, R., Reyes-Dávila, G., Dulce, M., González-Amezcua, M., Navarro-Ochoa, C., Martínez-Fierros, A., and Ramírez-Vázquez, A.: Seismic monitoring of effusive-explosive activity and large lava dome collapses during 2013–2015 at Volcán de Colima, J. Volcanol. Geoth. Res., 351, 75–88, 2018. a
Babuška, I., Ihlenburg, F., Paik, E., and Sauter, S.: A generalized finite element method for solving the Helmholtz equation in two dimensions with minimal pollution, Comput. Method. Appl. M., 128, 325–359, 1995. a
Bandy, W., Mortera-Gutiérrez, C., Urrutia-Fucugauchi, J., and Hilde, T.: The subducted Rivera-Cocos plate boundary: where is it, what is it, and what is its relationship to the Colima Rift?, Geophys. Res. Lett., 22, 3075–3078, 1995. a
Barrier, B., Bourgois, J., and Michaud, F.: The active Jalisco triple junction rift system., C. R. Acad. Sci. Paris, 310, 1513–1520, 1990. a, b
Bathe, K., Zhang, H., and Ji, S.: Finite element analysis of fluid flows fully coupled with structural interactions, Comput. Struct., 72, 1–16, 1999. a
Bonafede, M., Parenti, B., and Rivalta, E.: On strike-slip faulting in layered media, Geophys. J. Int., 149, 698–723, 2002. a
Bonasia, R., Capra, L., Costa, A., Macedonio, G., and Saucedo, R.: Tephra fallout hazard assessment for a Plinian eruption scenario at Volcan de Colima, J. Volcanol. Geoth. Res., 203, 12–22, 2011. a
Buchmann, T. and Conolly, P.: Contemporary kinematics of the Upper Rhine Graben: A 3D finite element approach, Global Planet. Change, 58, 287–309, 2007. a
Cabaniss, H., Gregg, P., and Grosfils, E.: The role of tectonic stress in triggering large silicic caldera eruptions, Geophys. Res. Lett., 45, 3889–3895, 2018. a
Cabrera-Gutiérrez, R. and Espíndola, J.: The 1998–1999 eruption of Volcán de Colima, Mexico: an application of Maeda's viscoelastic model, Geofis. Int., 49, 83–96, 2010. a, b
Cailleau, B., Walter, T., Janle, P., and Hauber, E.: Modeling volcanic deformation in a regional stress field: Implications for the formation of graben structures on Alba Patera, Mars, J. Geophys. Res., 108, https://doi.org/10.1029/2003JE002135, 2003. a
Cailleau, B. and. Walter, T., Janle, P., and Hauber, E.: Unveiling the origin of radial grabens on Alba Patera volcano by finite element modelling, Icarus, 176, 44–56, 2005. a
Canales, J., Nedimović, M., Kent, G., Carbotte, S., and Detrick, R.: Seismic reflection images of a near-axis melt sill within the lower crust at the Juan de Fuca ridge, Nature, 460, 89–93, 2009. a
Capra, L., Macías, J., Cortés, A., Dávila, N., Saucedo, R., Osorio-Ocampo, S., Arce, J., Galvilanes-Ruiz, J., Corona-Càvez, P., Gàrcia-Sancez, L., Sosa-Ceballos, G., and Vasquez, R.: Preliminary report on the July 10–11, 2015 eruption at Volcán de Colima: Pyroclastic density currents with exceptional runouts and volume, J. Volcanol. Geoth. Res., 310, 39–49, 2016. a
Cayol, V. and Cornet, F.: Effects of topography on the interpretation of the deformation field of prominent volcanoes: Applicationto Etna., Geophys. Res. Lett., 25, 1979–1982, 1998. a
Chaput, M., Pinel, V., Famin, V., Michon, L., and Froger, J.: Cointrusive shear displacement by sill intrusion in a detachment: A numerical approach, Geophys. Res. Lett., 41, 1937–1943, 2014. a, b
Charco, M. and Galán del Sastre, P.: Efficient inversion of three-dimensional finite element models of volcano deformation, Geophys. J. Int., 196, 1441–1454, 2014. a
Cianetti, S., Giunchi, C., and Casarotti, E.: Volcanic deformation and flank instability due to magmatic sources and frictional rheology: the case of Mount Etna, Geophys. J. Int., 191, 939–953, 2012. a, b
Coco, A., Gottsmann, J., Whitaker, A., Rust, C., Currenti, G., Jasim, A., and Bunney, S.: Numerical models for ground deformation and gravity changes during volcanic unrest: simulating the hydrothermal system dynamics of an active caldera, PhD thesis, Oxford Brookes University, 2016. a
Cortés, A., Garduño, V., Macías, J., Navarro-Ochoa, C., Komorowski, J., Saucedo, R., and Gavilanes, J.: Geologic mapping of the Colima volcanic complex (Mexico) and implications for hazard assessment, Geol. S. Am S., 464, 249–264, 2010. a, b, c
Cortés, A., Komorowski, J., Macías, J., Capra, L., and Layer, P.: Late Pleistocene-Holocene debris avalanche deposits from Volcán de Colima, Mexico, in: Volcan de Colima, Springer, Berlin, Heidelberg, 2019. a
Costa, A., Gottsmann, J., Melnik, O., and Sparks, R.: A stress-controlled mechanism for the intensity of very large magnitude explosive eruptions, Earth Planet. Sc. Lett., 310, 161–166, 2011. a
Currenti, G. and Williams, C.: Numerical modeling of deformation and stress fields around a magma chamber: Constraints on failure conditions and rheology., Phys. Earth Planet. In., 226, 14–27, 2014. a, b, c, d
Currenti, G., Bonaccorso, A., Del Negro, C., Scandura, D., and Boschi, E.: Elasto-plastic modeling of volcano ground deformation, Earth Planet. Sc. Lett., 296, 311–318, 2010. a, b
Davila, N., Capra, L., Ferres, D., Gavilanes-Ruiz, J., and Flores, P.: A stress-controlled mechanism for the intensity of very large magnitude explosive eruptions, Chronology of the 2014–2016 Eruptive Phase of Volcán de Colima and Volume Estimation of Associated Lava Flows and Pyroclastic Flows Based on Optical Multi-Sensors, Remote Sens.-Basel, 310, 161–166, 2019. a
Del Potro, R. and Hurlimann, M.: Geotechnical classification and characterization of materials for stability analyses of large volcanic slopes, Eng. Geol., 98, 1–17, 2008. a
Dieterich, J. and Decker, R.: Finite element modeling of surface deformation associated with volcanism, J. Geophys. Res., 80, 4094–4102, 1975. a
Escudero, C. and Bandy, W.: Ambient seismic noise tomography of the Colima Volcano Complex, B. Volcanol., 79, 1, 2017. a, b
Fernández, J., Tiampo, K., Jentzsch, G., Charco, M., and Rundle, J.: Inflation or deflation? New results for Mayon Volcano applying elastic‐gravitational modeling, Geophys. Res. Lett., 28, 2349–2352, 2001. a
Ferrari, L., Rosas-Elguera, J., Márquez, A., Oyarzun, R., Doblas, M., and Verma, S.: Alkalic (ocean-island basalt type) and calc-alkalic volcanism in the Mexican volcanic belt: A case for plume-related magmatism and propagating rifting at an active margin?: Comment and Reply, Geology, 27, 1055–1056, 1999. a
Folch, A., Fernández, J., Rundle, J., and Martí, J.: Ground deformation in a viscoelastic medium composed of a layer overlying a half-space: a comparison between point and extended sources, Geophys. J. Int., 140, 37–50, 2000. a
Frey, H., Lange, R., Hall, C., Delgado-Granados, H., and Carmichael, I.: A Pliocene ignimbrite flare-up along the Tepic-Zacoalco rift: evidence for the initial stages of rifting between the Jalisco block (Mexico) and North America, Geol. Soc. Am. Bull., 119, 49–64, https://doi.org/10.1130/B25950.1, 2007. a
Fujita, E., Kozono, T., Ueda, H., Kohno, Y., Yoshioka, S., Toda, N., and Ida, Y.: Stress field change around the Mount Fuji volcano magma system caused by the Tohoku megathrust earthquake, Japan, B. Volcanol., 75, 679, 2013. a
Gabrieli, A., Wilson, L., and Lane, S.: Volcano–tectonic interactions as triggers of volcanic eruptions, P. Geologist. Assoc., 126, 675–682, 2015. a
Garduño-Monroy, V., Saucedo-Girón, R., Jiménez, Z., Gavilanes-Ruiz, J., and Uribe-Cifuentes, R. M.: La Falla Tamazula, límite suroriental del Bloque Jalisco, y sus relaciones con el Complejo Volcánico de Colima, México, Rev. Mexic. Ciencias Geológ., 15, 132–144, 1998. a
Gerbault, M., Cappa, F., and Hassani, R.: Elasto-plastic and hydromechanical models of failure around an infinitely long magma chamber, Geochem. Geophys. Geosys., Q03009; https://doi.org/10.1029/2011GC003917, 2012. a
Gerbault, M., Hassani, R., Novoa Lizama, C., and Souche, A.: Three‐dimensional failure patterns around an inflating magmatic chamber, Geochem. Geophys. Geosyst., 19, 749–771, 2018. a
Geshi, N., Kusumoto, S., and Gudmundsson, A.: Effects of mechanical layering of host rocks on dike growth and arrest, J. Volcanol. Geoth. Res., 223, 74–82, 2012. a
Geyer, A. and Gottsmann, J.: The influence of mechanical stiffness on caldera deformation and implications for the 1971–1984 Rabaul uplift (Papua New Guinea), Tectonophysics, 483, 399–412, 2010. a
Geyer, A., Marti, J., and Villaseñor, A.: First-order estimate of the Canary Islands plate-scale stress field: Implications for volcanic hazard assessment, Tectonophysics, 679, 125–139, 2016. a
Gonnermann, H. and Taisne, B.: Magma transport in dikes, in: The encyclopedia of volcanoes, Elsevier, Academic Press, 215–224, 2015. a
Gottsmann, J., Folch, A., and Rymer, H.: Unrest at Campi Flegrei: A contribution to the magmatic versus hydrothermal debate from inverse and finite element modeling, J. Volcanol. Geoth. Res., 111, B07203, https://doi.org/10.1029/2005JB003745, 2006. a
Grosfils, E.: Magma reservoir failure on the terrestrial planets: Assessing the importance of gravitational loading in simple elastic models, J. Volcanol. Geoth. Res., 166, 47-75, https://doi.org/10.1016/j.jvolgeores.2007.06.007, 2007. a, b
Grosfils, E., McGovern, P., Gregg, P., Galgana, G., Hurwitz, D., Long, S. M., and Chestler, S.: Elastic models of magma reservoir mechanics: a key tool for investigating planetary volcanism, Geol. Soc. Sp., 401, 239–267 2015. a
Gudmundsson, A.: How local stresses control magma-chamber ruptures, dyke injections, and eruptions in composite volcanoes, Earth Sci. Rev., 79, 1–31, https://doi.org/10.1016/j.earscirev.2006.06.006, 2006. a, b, c
Gudmundsson, A.: Deflection of dykes into sills at discontinuities and magma-chamber formation, Tectonophysics, 500, 50–64, https://doi.org/10.1016/j.tecto.2009.10.015, 2011. a, b
Gudmundsson, A.: Magma chambers: Formation, local stresses, excess pressures, and compartments, J. Volcanol. Geoth. Res., 237, 19–41, 2012. a, b, c
Gudmundsson, A. and Brenner, S.: How mechanical layering affects local stresses, unrests, and eruptions of volcanoes, J. Geophys. Res., 31, L16606, https://doi.org/10.1029/2004GL020083, 2004. a
Hautmann, S., Gottsmann, J., Sparks, R., Costa, A., Melnik, O., and Voight, B.: Modelling ground deformation caused by oscillating overpressure in a dyke conduit at Soufrière Hills Volcano, Montserrat, Tectonophysics, 471, 87–95, 2009. a
Heap, M., Villeneuve, M., Albino, F., Farquharson, J., Brothelande, E., Amelung, F., and Baud, P.: Towards more realistic values of elastic moduli for volcano modelling, J. Volcanol. Geoth. Res., 390, 106684, 2020. a, b
Hickey, J., Gottsmann, J., and Mothes, P.: Estimating volcanic deformation source parameters with a finite element inversion: The 2001–2002 unrest at Cotopaxi volcano, Ecuador, J. Geophys. Res.-Sol. Ea., 120, 1473–1486, https://doi.org/10.1002/2014JB011731, 2015. a
Hoek, E. and Brown, E.: Practical estimates or rock mass strength, Int. J. Rock Mech. Min., 34, 1165–1186, 1997. a
Jaeger, J., Cook, N., and Zimmerman, R.: Fundamentals of rock mechanics, John Wiley and Sons, Blackwell Publishing, USA, 2009. a
Jeanne, P., Guglielmi, Y., Rutqvist, J., Nussbaum, C., and Birkholzer, J.: Field characterization of elastic properties across a fault zone reactivated by fluid injection, J. Geophys. Res., 122, 6583–6598, 2017. a, b
Kinvig, H., Geyer, A., and Gottsmann, J.: On the effect of crustal layering on ring-fault initiation and the formation of collapse calderas, 186, 293–304, 2009. a
Lister, J. and Kerr, R.: Fluid-mechanical models of crack propagation and their application to magma transport in dykes, B. Volcanol., 96, 10049–10077, 1991. a
Long, S. and Grosfils, E.: Modeling the effect of layered volcanic material on magma reservoir failure and associated deformation, with application to Long Valley caldera, California, J. Volcanol. Geoth. Res., 186, 349–360, 2009. a, b
Luhr, J.: Petrology and geochemistry of the 1991 and 1998–1999 lava flows from Volcan Colima, Mexico, J. Volcanol. Geoth. Res., 117, 169–194, 2002. a, b
Luhr, J. and Carmichael, I.: Contemporaneous eruptions of calc-alkaline and alkaline magmas along the volcanic front of the Mexican Volcanic Belt, Geofis. Int., 24, 203–216, 1985. a
Lungarini, L., Troise, C., Meo, M., and De Natale, G.: Finite element modelling of topographic effects on elastic ground deformation at Mt. Etna, J. Volcanol. Geoth. Res., 144, 257–271, 2005. a
López-Loera, H., Urrutia-Fucugauchi, J., and Alva-Valdivia, L.: Estudio aeromagnético del complejo volcánico de Colima, occidente de México – implicaciones tectónicas y estructurales, Rev. Mex. Cienc. Geológ., 28, 349–370, 2011. a
Maccaferri, F., Bonafede, M., and Rivalta, E.: A numerical model of dyke propagation in layered elastic media, Geophys. J. Int., 180, 1107–1123, 2010. a
Maccaferri, F., Bonafede, M., and Rivalta, E.: A quantitative study of the mechanisms governing dike propagation, dike arrest and sill formation, J. Volcanol. Geoth. Res., 208, 39–50, 2011. a
Maccaferri, F., Rivalta, E., Keir, D., and Acocella, V.: Off-rift volcanism in rift zones determined by crustal unloading, Nat. Geosci., 7, 297–300, 2014a. a
Maccaferri, F., Rivalta, E., Keir, D., and Acocella, V.: Off-rift volcanism in rift zones determined by crustal unloading, Nat. Geosci., 7, 279–300, https://doi.org/10.1038/ngeo2110, 2014b. a
Macdonald, K.: Mid-ocean ridges: fine scale tectonic, volcanic and hydrothermal processes within the plate boundary zone., Ann. Rev. Earth Planet. Sci., 10, 155–190, 1982. a
Macías, J. L., Sosa-Ceballos, G., Arce, J. L., Gardner, J. E., Saucedo, R., and Valdez-Moreno, G.: Storage conditions and magma processes triggering the 1818 CE Plinian eruption of Volcán de Colima, J. Volcanol. Geoth. Res., 340, 117–129, 2017. a
Macías, J., Saucedo, R., Gavilanes, J., Varley, N., Velasco, G. S., Bursik, M., Vargas, G. V., and Cortés, A.: Flujos piroclásticos asociados a la actividad explosiva del Volcán de Colima y perspectivas futuras, GEOS, Vol. 25, 2006. a
MacLeod, C. and Yaouancq, G.: A fossil melt lens in the Oman ophiolite: implications for magma chamber processes at fast spreading ridges, Earth Planet. Sci. Lett., 176, 357–373, 2000. a
Manconi, A., Walter, T., and Amelung, F.: Effects of mechanical layering on volcano deformation, Geophys. J. Int., 170, 952–958, 2007. a, b
Manconi, A., Longpré, M., Walter, T., Troll, V., and Hansteen, T.: The effects of flank collapses on volcano plumbing systems, Geology, 37, 1099–1102, 2009. a
Marinos, P. and Hoek, E.: GSI: a geologically friendly tool for rock mass strength estimation, Proc. GeoEng. Conference, Melbourne, 19–24 November 2000, 1422–1446, 2000. a
Marti, J. and Geyer, A.: Central vs flank eruptions at Teide–Pico Viejo twin stratovolcanoes (Tenerife, Canary Islands)., J. Volcanol. Geoth. Res., 181, 47–60, 2009. a, b, c, d
Massaro, S., Sulpizio, R., Costa, A., Capra, L., and Lucchi, F.: Understanding eruptive style variations at calc-alkaline volcanoes: the 1913 eruption of Fuego de Colima volcano (Mexico), B. Volcanol., 80, 62, https://doi.org/10.1007/s00445-018-1235-z, 2018. a, b, c, d, e, f
Massaro, S., Costa, A., Sulpizio, R., Coppola, D., and Capra, L.: Cyclic activity of Fuego de Colima volcano (Mexico): insights from satellite thermal data and non-linear models, J. Geophys. Res.-Sol. Ea., 10, 1429–1450, 2019. a, b, c, d
Masterlark, T., Feigl, K., Haney, M., Stone, J., Thurber, C., and Ronchin, E.: Nonlinear estimation of geometric parameters in FEMs of volcano deformation: Integrating tomography models and geodetic data for Okmok volcano, Alaska, J. Geophys. Res.-Sol. Ea., B02407, https://doi.org/10.1029/2011JB008811, 2012. a
Medina-Martínez, F., Espíndola, J., De la Fuente, M., and Mena, M.: A gravity model of the Colima, México region, Geofis. Int., 35, 409–414, 1996. a
Moeck, I., Schandelmeier, H., and Holl, H.: The stress regime in a Rotliegend reservoir of the Northeast German Basin, Int. J. Earth. Sci., 98, 1643–1654, 2009. a
Mutter, J., Carbotte, S., Su, W., Xu, L., Buhl, P., Detrick, R., Kent, G.M., Orcutt, J., and Harding, A.: Seismic images of active magma systems beneath the East Pacific Rise between 17-degrees-05's and 17-degrees-35's, Science, 268, 391–395, 1995. a
Newman, A., Dixon, T., Ofoegbu, G., and Dixon, J.: Geodetic and seismic constraints on recent activity at Long Valley Caldera, California: evidence for viscoelastic rheology, J. Volcanol. Geoth. Res., 105, 183–206, 2001. a
Norini, G., Capra, L., Groppelli, G., Agliardi, F., Pola, A., and Cortes, A.: Structural architecture of the Colima Volcanic Complex, J. Geophys. Res., 115, 2010. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Norini, G., Agliardi, F., Crosta, G., Groppelli, G., and Zuluaga, M.: Structure of the Colima Volcanic Complex: Origin and Behaviour of Active Fault Systems in the Edifice, in: Volcán de Colima, Springer, Berlin, Heidelberg, 27–54, 2019. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Parfitt, E. and Wilson, L.: The role of volatiles, in: Fundamentals of Physical Volcanology, Blackwell Publishing, USA, 64–76, 2008. a
Pinel, V. and Jaupart, C.: Magma storage and horizontal dyke injection beneath a volcanic edifice, Earth Planet. Sci. Lett., 221, 245–262, 2004. a
Pinel, V., Carrara, A., Maccaferri, F., Rivalta, E., and Corbi, F.: A two-step model for dynamical dike propagation in two dimensions: Application to the July 2001 Etna eruption, J. Geophys. Res.-Sol. Ea., 122, 1107–1125, https://doi.org/10.1002/2016JB013630, 2017. a
Pritchard, M. and Simons, M.: An InSAR-based survey of volcanic deformation in the central Andes, Geochem. Geophys. Geosys., Q02002, https://doi.org/10.1029/2003GC000610, 2004. a
Reubi, O., Blundy, J., and Varley, N.: Volatiles contents, degassing and crystallisation of intermediate magmas at Volcan de Colima, Mexico, inferred from melt inclusions, Contrib. Mineral. Petr., 165, 1087–1106, 2013. a
Reubi, O., Blundy, J., and Pickles, J.: Petrological monitoring of Volcán de Colima magmatic system: the 1998 to 2011 activity, in :Volcán de Colima, Springer, Berlin, Heidelberg, 219–240, 2019. a
Rivalta, E., Corbi, F., Passarelli, L., Acocella, V., Davis, T., and Di Vito, M.: Stress inversions to forecast magma pathways and eruptive vent location, Sci. Adv., 5, eaau9784, https://doi.org/10.1126/sciadv.aau9784, 2019. a, b
Robin, C., Mossand, P., Camus, G., Cantagrel, J., Gourgaud, A., and Vincent, P.: Eruptive history of the Colima volcanic complex (Mexico), J. Volcanol. Geoth. Res., 31, 99–113, 1987. a
Ronchin, E., Masterlark, T., Molist, J., Saunders, S., and Tao, W.: Solid modeling techniques to build 3D finite element models of volcanic systems: an example from the Rabaul Caldera system, Papua New Guinea, Comput. Geosci., 52, 325–333, 2013. a
Ronchin, E., Geyer, A., and Martí, J.: Evaluating topographic effects on ground deformation: insights from finite element modeling, Surv. Geophys., 36, 513–548, 2015. a
Rosas-Elguera, J., Ferrari, L., Garduño-Monroy, V., and Urrutia-Fucugauchi, J.: Continental boundaries of the Jalisco block and their influence in the Pliocene-Quaternary kinematics of western Mexico, Geology, 24, 921–924, 1996. a, b, c
Rosas-Elguera, J., Ferrari, L., Martinez, M., and Urrutia-Fucugauchi, J.: Stratigraphy and tectonics of the Guadalajara region and triple-junction area, western Mexico, Int. Geol. Rev., 39, 125–140, https://doi.org/10.1080/00206819709465263, 1997. a
Rosas-Elguera, J., Alva-Valdivia, L., Goguitchaichvili, A., Urrutia-Fucugauchi, J., Ortega-Rivera, M., Prieto, J., and Lee, J.: Counterclockwise rotation of the Michoacan Block: implications for the tectonics of western Mexico, Int. Geol. Rev., 45, 814–826, 2003. a
Roverato, M. and Capra, L.: Características microtexturales como indicadores del transporte y emplazamiento de dos depósitos de avalancha de escombros del Volcán de Colima (México), Rev. Mexic. Ciencias Geológ., 30, 512–525, 2013. a
Roverato, M., Capra, L., Sulpizio, R., and Norini, G.: Stratigraphic reconstruction of two debris avalanche deposits at Colima Volcano (Mexico): insights into pre-failure conditions and climate influence, J. Volcanol. Geoth. Res., 207, 33–46, 2011. a
Salzer, J., Nikkhoo, M., Walter, T., Sudhaus, H., Reyes-Dàvila, G., Bretòn-Gonzalez, M., and Aràmbula, R.: Satellite radar data reveal short-term pre-explosive displacements and a complex conduit system at Volcan de Colima, Mexico, Front. Earth Sci., 27, https://doi.org/10.3389/feart.2014.00012, 2014. a
Saucedo, R., Macías, J., Gavilanes, J., Arce, J., Komorowski, J., Gardner, J., and Valdez-Moreno, G.: Eyewitness, stratigraphy, chemistry, and eruptive dynamics of the 1913 Plinian eruption of Volcán de Colima, Mexico, J. Volcanol. Geoth. Res., 191, 149–166, 2010. a, b, c
Saucedo, R., Macìas, J., Gavilanes, J., Arce, J., Komorowski, J., Gardner, J., and Valdez-Moreno, G.: Corrigendum to Eyewitness, stratigraphy, chemistry, and eruptive dynamics of the 1913 plinian eruption of Volcan de Colima, Mexico, J. Volcanol. Geoth. Res., 191, 149–166, 2011. a
Selvans, M., Stock, J., DeMets, C., Sanchez, O., and Marquez-Azua, B.: Constraints on Jalisco Block motion and tectonics of the Guadalajara triple junction from 1998–2001 Campaign GPS Data, Pure Appl. Geophys., 168, 1435–1447, 2011. a, b
Serpa, L., Smith, S., Katz, C., Skidmore, C., Sloan, R., and Pavlis, T.: A geophysical investigation of the southern Jalisco block in the state of Colima, Mexico, Geofis. Int., 31, 475–492, 1992. a, b
Simms, M. and Graven, G.: Thermal convection in faulted extensional sedimentary basins: theoretical results from finite-element modelling, Geofluids, 4, 109–130, 2004. a
Sinton, J. M. and Detrick, R. S.: Mid-ocean ridge magma chambers, J. Geophys. Res.-Sol. Ea., 97, 197–216, 1992. a
Spica, Z., Cruz-Atienza, V., Reyes-Alfaro, G., Legrand, D., and Iglesias, A.: Crustal imaging of western Michoacán and the Jalisco Block, Mexico, from ambient seismic noise, J. Volcanol. Geoth. Res., 289, 193–201, 2014. a, b, c, d, e
Spica, Z., Perton, M., and Legrand, D.: Anatomy of the Colima volcano magmatic system, Mexico, Earth Planet. Sci. Lett., 459, 1–13, 2017. a, b, c, d, e, f
Sulpizio, R. and Massaro, S.: Influence of stress field changes on eruption initiation and dynamics: a review, Front. Earth Sci., 5, https://doi.org/10.3389/feart.2017.00018, 2017. a
Sulpizio, R., Lucchi, F., Forni, F., Massaro, S., and Tranne, C.: Unravelling the effusive-explosive transitions and the construction of a volcanic cone from geological data: The example of Monte dei Porri, Salina Island (Italy), J. Volcanol. Geoth. Res., 327, 1–22, 2017. a
Suárez, G., Garcia-Acosta, V., and Gaulon, R.: Active crustal deformation in the Jalisco block, Mexico: evidence for a great historical earthquake in the 16th century, Tectonophysics, 234, 117–127, 1994. a, b
Sonnenhof Holdings (Canada): The use of the CAD kernel OCC is covered by the Open CASCADE Technology Public License version 6.3. The Netgen nglib, Pthreads-win32 and ZedGraph libraries used by the software are covered by the GNU Lesser General Public License Version 2.1., available at: https://lisafea.com/ (last access: 10 December 2020), 2013. a
Touloukian, Y., Judd, W., and Roy, R.: Physical Properties of Rocks and Minerals, Hemisphere Publications, New York, USA, 1989. a
Turcotte, D. and Schubert, G.: Geodynamics, 2nd edition, Cambridge University Press, United Kingdom, 2002. a
Wang, R., Martin, F., and Roth, F.: Computation of deformation induced by earthquakes in a multi-layered elastic crust-FORTRAN programs EDGRN/EDCMP, Comput. Geosci., 29, 195–207, 2003. a
Watanabe, T., Masuyama, T., Nagaoka, K., and Tahara, T.: Analog experiments on magmafilled cracks, Earth Planet Space, 54, 1247–1261, 2002, a
Zehner, B., Jana, H., Börner, J., and Görz, I. S. K.: Workflows for generating tetrahedral meshes for finite element simulations on complex geological structures, Comput. Geosci., 79, 105–117, 2015. a, b
Zhao, S., Muller, R., Takahashi, Y., and Kaneda, Y.: 3D finite-element modelling of deformation and stress associated with faulting: effect of inhomogeneous crustal structures, Geophys. J. Int., 157, 629–644, 2004. a
Zhong, X., Dabrowski, M., and Jamtveit, B.: Analytical solution for the stress field in elastic half-space with a spherical pressurized cavity or inclusion containing eigenstrain, Geophys. J. Int., 216, 110–111, 2019. a
Zobin, V., Luhr, J., Taran, Y., Bretón, M., Cortés, A., De la Cruz-Reyna, S.and Domínguez, T., Galindo, I., Gavilanes, J., Muñiz, J., Navarro, C., Ramírez, J., Reyes, G., Ursúa, M., Velasco, J., Alatorre, E., and Santiago, H.: Overview of the 1997–2000 activity of Volcán de Colima, Mexico, J. Volcanol. Geoth. Res., 117, 1–19, 2002. a





