the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Can anaerobic oxidation of methane prevent seafloor gas escape in a warming climate?
Christian Stranne
Matt O'Regan
Martin Jakobsson
Volker Brüchert
Marcelo Ketzer
Assessments of future climate-warming-induced seafloor methane (CH4) release rarely include anaerobic oxidation of methane (AOM) within the sediments. Considering that more than 90 % of the CH4 produced in ocean sediments today is consumed by AOM, this may result in substantial overestimations of future seafloor CH4 release. Here, we integrate a fully coupled AOM module with a numerical hydrate model to investigate under what conditions rapid release of CH4 can bypass AOM and result in significant fluxes to the ocean and atmosphere. We run a number of different model simulations for different permeabilities and maximum AOM rates. In all simulations, a future climate warming scenario is simulated by imposing a linear seafloor temperature increase of 3 ∘C over the first 100 years. The results presented in this study should be seen as a first step towards understanding AOM dynamics in relation to climate change and hydrate dissociation. Although the model is somewhat poorly constrained, our results indicate that vertical CH4 migration through hydraulic fractures can result in low AOM efficiencies. Fracture flow is the predicted mode of methane transport under warming-induced dissociation of hydrates on upper continental slopes. Therefore, in a future climate warming scenario, AOM might not significantly reduce methane release from marine sediments.
- Article
(4330 KB) - Full-text XML
-
Supplement
(255 KB) - BibTeX
- EndNote
The atmospheric concentration of CH4 increased by a factor of 2.5 since the pre-industrial era, and anthropogenic emissions now account for 50 %–65 % of annual global CH4 emissions (Stocker et al., 2013). CH4 is an important greenhouse gas accounting for 20 % of the observed postindustrial climate warming (Kirschke et al., 2013). Marine sediments along continental margins contain large reservoirs of CH4 stored as solid gas hydrate (Milkov, 2004; Wallmann et al., 2012). The stability of submarine CH4 hydrate is primarily a function of temperature and pressure at and beneath the seafloor. Natural hydrate deposits are therefore susceptible to destabilization via ocean warming (Archer et al., 2009; Kretschmer et al., 2015; Dickens et al., 1995). The observed increase in atmospheric CH4 content is presently attributed mostly to anthropogenic land use. However, a warming climate can lead to destabilization of the part of the marine hydrate reservoir sensitive to temperature perturbations, potentially leading to CH4 transport from sediments to the oceans and atmosphere, where the CH4 becomes a positive feedback on climate warming. As a result, anthropogenic-induced destabilization of natural marine CH4 hydrate has been proposed as a climate warming mechanism that could exhibit threshold behaviour, implying that if climate warming continues, this feedback could cause an abrupt and irreversible transition into a warmer climate state (Stocker et al., 2013).
Although estimates of future CH4 gas release to the atmosphere from hydrate destabilization on regional and global scales vary by orders of magnitude (Biastoch et al., 2011; Hunter et al., 2013; Kretschmer et al., 2015) and are likely overestimated (Stranne et al., 2016b), the Fifth Assessment Report of the Intergovernmental Panel on Climate Change evaluated the risk of a catastrophic CH4 release during the 21st century as very unlikely (Stocker et al., 2013). In part, this is because much of the CH4 escaping from the seafloor will be consumed in the water column before reaching the atmosphere (Mau et al., 2007; McGinnis et al., 2006). On longer timescales, however, the effect of widespread hydrate dissociation on our climate may be irreversible. This is due to the difference between timescales for release (discharge) and accumulation (recharge) – the recovery timescale from the perturbed state is significantly longer than the time it takes for the system to reach this perturbed state (Dickens, 2001; Kennett et al., 2003).
A mechanism that has been largely overlooked in this context, however, is anaerobic oxidation of methane (AOM) in marine sediments (Ruppel and Kessler, 2017). About 85 % of the annual global CH4 production and 60 % of its consumption are based on microbial processes, and in marine sediments AOM is the dominant biogeochemical CH4 sink (Egger et al., 2018; Knittel and Boetius, 2009; Martens and Berner, 1977; Reeburgh, 2007). AOM is carried out by microbes within the sulfate reduction zone (SRZ), a feature found in all anoxic marine sediments where the transport of methane from below and sulfate from above provides a source of energy through AOM (Barnes and Goldberg, 1976; Knittel and Boetius, 2009; Malinverno and Pohlman, 2011). It is estimated that, on a global scale, more than 90 % of the CH4 produced in ocean sediments is consumed by AOM (Hinrichs and Boetius, 2002; Reeburgh, 2007). AOM is therefore a critical process that needs to be considered when modelling future climate-warming-induced CH4 release from marine sediments.
Numerical methods for predicting future ocean warming-induced methane release from the marine hydrate reservoir span a wide range of complexities, from the simplest approaches where gas escape from the seafloor is estimated as a function of temperature change (Biastoch et al., 2011; Hunter et al., 2013; Kretschmer et al., 2015) to more sophisticated models that include coupled hydraulic–thermodynamic behaviour of multiphase fluid flow in hydrate-bearing porous media (Darnell and Flemings, 2015; Reagan et al., 2011; Reagan and Moridis, 2008; Stranne et al., 2016a; Thatcher et al., 2013). One example of the latter is the TOUGH+HYDRATE (T+H) model which predicts the evolution of pressure, temperature, salinity and the phase saturation distributions in hydrate-bearing systems (Moridis, 2014). Stranne et al. (2017) integrated a geomechanical coupling into the T+H model (referred to as T+H-GeoMech in the text) and showed that such coupling is critical since dissociation of methane increases pore pressure and leads to hydraulic fracturing. Hydraulic fractures increase the permeability of sediments and dramatically affect rates of dissociation and seafloor gas release. As the majority of the global marine methane hydrate reservoir is dominated by low-permeability, fine-grained (silt and clay) sediments (Boswell and Collett, 2011), hydraulic fracturing is an important mechanism controlling potential rates of methane release induced by climate warming. However, as pointed out by Ruppel and Kessler (2017), AOM in marine sediments is yet another important process that is missing in current numerical hydrate models.
In a warming world, AOM is the main mechanism that can potentially prevent the transfer of huge quantities of methane from sediments to the oceans. The efficiency of AOM under climate warming is still, however, a poorly constrained issue (Knittel and Boetius, 2009; Ruppel and Kessler, 2017). Although AOM efficiently controls the methane flux from the world's seafloors in general (Egger et al., 2018; Knittel and Boetius, 2009; Martens and Berner, 1977; Reeburgh, 2007), there are observational and model-based studies (Luff and Wallmann, 2003; Martens and Val Klump, 1980) suggesting that the rate of vertical CH4 migration controls the efficiency of AOM (also referred to as the microbial filter). Buffett and Archer (2004) speculate that slow diffusive transport of CH4 likely results in AOM within the sediments with negligible effect on climate, while a more rapid liberation of CH4 (in response to climate warming) can lead to fractured pathways within the sediment that bypass the microbial filter and allow for a larger proportion of the CH4 to reach the ocean and atmosphere. This idea is supported by Stranne et al. (2017), who showed that warming-induced hydrate dissociation in moderate- to low-permeability sediments (clays and silty clays) leads to formation of hydraulic fractures and rapid release of CH4 from the seafloor.
In a review paper by Knittel and Boetius (2009), they list the following as one of the key future issues: “How will global climate change, with regard to the expected increase in temperature and sea level, affect the stability of gas hydrate reservoirs and the efficiency of microbial methane consumption?”. In a more recent review paper on the interaction between climate change and CH4 hydrates (Ruppel and Kessler, 2017), the authors identify the quantification of the AOM sink in marine sediment as one of the key directions for future research. While Ruppel and Kessler (2017) recommend the use of numerical hydrate models for improved predictions of future warming-induced seafloor CH4 release, they explicitly stress the need for better handling of AOM in such modelling efforts.
The present study aims at taking a step in this direction, through the addition of a simplistic but novel and fully coupled AOM module to the T+H-GeoMech code. As in Stranne et al. (2017), we focus on the featheredge of hydrate stability – the part of the marine hydrate reservoir most sensitive to ocean warming (Ruppel, 2011). We address the hypothesis of Buffett and Archer (2004) by investigating how the efficiency of the microbial filter varies as a function of the intrinsic permeability of the sediment (which in turn controls the vertical migration of CH4) during seafloor warming-induced hydrate dissociation. In other words, to what extent can vigorous CH4 flow through dynamic hydraulic fractures bypass the microbial filter? In all model simulations, a future climate warming scenario is simulated by imposing a linear seafloor temperature increase of 3 ∘C over the first 100 years (Table 1).
2.1 Model setup
T+H-GeoMech (Moridis, 2014; Stranne et al., 2017) is set up for midlatitude conditions with an initial bottom water temperature of 5 ∘C and a gas hydrate stability zone (GHSZ) extending down to 20 m below the seafloor (m b.s.f.). This represents the most sensitive featheredge of hydrate stability on the upper continental slope. The initial hydrate deposit is homogeneously distributed within the GHSZ and is in thermodynamic equilibrium with the initial seafloor temperature, geothermal heat flow and the sediment bulk thermal conductivity profile. The model domain extends to 200 m b.s.f. and consists of 160 grid cells with a size of 0.17 m between 0 and 25 m b.s.f. and 19 m between 25 and 200 m b.s.f. We assume that the upper 5 m of the sediment column is within the SRZ and is initially depleted of CH4 (Bhatnagar et al., 2011). See Table 1 for a list of parameter values used in the model simulations.
2.2 AOM module
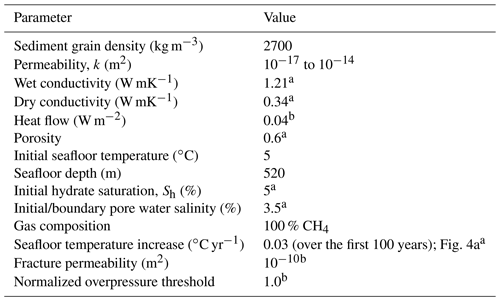
The total vertically integrated CH4 mass within the model domain is distributed between three pools (Fig. 1a): the hydrate pool (MHyd(t)), the gas pool (MGas(t)) and the dissolved pool (MDis(t)). CH4 can move between these pools over time (t) and leave the system either through AOM within the SRZ (FAOM(t,z)), where z is depth below seafloor, or through gas/dissolved CH4 flux at the seafloor–ocean interface (FGas(t)∕FDis(t)). The FAOM(t,z) is described as a sink on MDis(t), which means that gaseous CH4 is not directly available for AOM. However, because pore water tends to be fully saturated in the presence of gas, AOM does act as a sink on MGas(t), as the constant reduction in CH4 pore water saturation draws CH4 from MGas(t) to MDis(t).
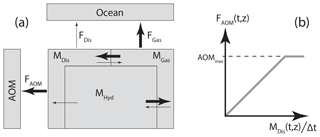
Figure 1(a) A schematic overview of the three CH4 mass pools within the sediments and the general direction of the CH4 mass transport during hydrate dissociation, within and out of the system (illustrated by the thick arrows). (b) Modelled FAOM(t,z) as a function of the dissolved CH4 saturation (where Δt is the time step) and predefined AOMmax.
Observed AOM rates span from µmol cm−3 d−1 in subsurface SRZs of deep margins to a few µmol cm−3 d−1 in surface sediments above gas hydrates (Knittel and Boetius, 2009). In this study, we cover the range of maximum bulk oxidation rates within the SRZ (AOMmax) from zero to 1 µmol cm−3 d−1 in Cases A1–A7 (Table 2, Fig. 2), within a predefined and constant depth of the SRZ extending, in the base case, to 5 m b.s.f. In each time step, the maximum amount of AOM is calculated (AOMmax multiplied by the time step and grid cell volume) in all grid cells within the SRZ. If the dissolved CH4 content within a grid cell is smaller than or equal to the maximum amount of AOM, the dissolved CH4 content is set to zero. The AOM within that particular grid cell is then limited by the dissolved CH4 saturation. If the dissolved CH4 content within a grid cell is larger than the maximum AOM, then the dissolved CH4 content is reduced by this amount. The AOM within that grid cell is then limited by the predefined maximum AOM capacity of the system. This means that the modelled AOM rate is a linear function of dissolved CH4 content (which is ultimately controlled by the CH4 supply from below) up to a point where the predefined AOMmax takes over (Fig. 1b). In each grid cell where AOM occurs, an equal mass of water is added in order to keep mass balance within the system (i.e. CH4 and NaCl are the only two dissolved species in the model, and therefore the end products from AOM are added to the water fraction of the pore space).
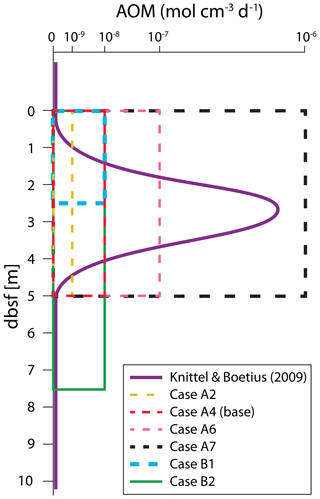
Figure 2Conceptual AOM rate as a function of depth below seafloor (b.s.f., solid purple) based on Knittel and Boetius (2009) and a visual representation of some of the model simulation cases performed in the present study. In Cases A1–A7, the base of the SRZ is prescribed at 5 m b.s.f. We simulate two cases (B1–B2) with the SRZ extending down to 2.5 and 7.5 m b.s.f., respectively, both with an AOMmax of 10−8 mol cm−3 d−1. Note that the x axis is non-linear and that all boxes (each representing a simulation case) have their upper left corner situated at the origin.
Table 2Summary of the simulation cases performed in the present study. Each case involves 13 200-year simulations for permeabilities ranging between 10−17 and 10−14 m2 (in total 143 simulations).

The base of the SRZ may be found at decimetres to tens of metres below the seafloor, depending on the burial rate of reactive organic matter, the depth of the methane production zone, the flux of methane and sulfate and their consumption rates (Egger et al., 2018; Knittel and Boetius, 2009). Our constant SRZ depth of 5 m b.s.f. represents a value commonly used in numerical modelling applied to marine gas hydrates (Kretschmer et al., 2015; Reagan and Moridis, 2008; Stranne et al., 2016a; Wallmann et al., 2012) and measured in high CH4 flux areas at the featheredge (Miller et al., 2015; Rodrigues et al., 2017). Rodrigues et al. (2017) measured SRZ depths between 3 and 4 m b.s.f. in areas with high gas flow and approximately 7 m b.s.f. in background areas. We perform a sensitivity test on SRZ depth by running two additional suites of simulations with SRZ depth equal to 2.5 and 7.5 m in Cases B1–B2, respectively (Fig. S1 in the Supplement). The initial hydrate saturation (expressed as the percentage of pore space, Sh) in the baseline simulations is 5 %, homogeneously distributed within the GHSZ (except for the SRZ, which is initially depleted of hydrate). We perform a sensitivity test on the hydrate saturation by running two suites of simulations with Sh equal to 2.5 % and 7.5 % in Cases C1–C2, respectively (Fig. S2).
The efficiency of the microbial filter is defined as
where Case Ax is one of the cases listed in Table 2. In other words, AOM efficiency is the percentage of CH4 escape in the “zero AOM” case (Case A1) that is instead oxidized within the SRZ.
As shown in Stranne et al. (2017), the upward transport of CH4 within destabilized hydrate-bearing sediments can be divided into three flow regimes. These flow regimes depend on the sediment permeability and encompass the expected range of permeabilities for hemipelagic sediments composed predominantly of terrigenous silts and clays (Fig. 3).
Figure 3Typical range of permeability for unconsolidated sediments and marine sediments. Data sources are as follows: black – Freeze and Cherry (1979); green – Spinelli et al. (2004), porosity–permeability marine data compilation for porosities between 40 % and 85 %; blue – Neuzil (1994). Data from Neuzil (1994) are a compilation of laboratory permeability data for natural clay, silt sand mixtures from marine and terrestrial sources with porosities of 40 %–90 %.
The low-permeability fracture flow regime ( m2) is dominated by highly non-linear flow with irregular bursts of gas occurring at the seafloor through the opening and closing of hydraulic fractures (see Stranne et al., 2017, for details). When considering a centennial timescale, fracture flow results in the largest vertical transport of CH4 gas towards the seafloor. In the matrix flow regime, which is predicted in higher-permeability substrate ( m2), CH4 percolates through the porous media in a continuous, regular fashion through intergranular pore spaces. This slower flow regime will continue long after the hydrate deposit has been depleted because overpressure persists within the sediments and continues to drive vertical flow. This is distinct from fracture flow that ends the moment hydrate dissociation stops, because excess pore pressure no longer builds up within the sediments to create hydraulic fractures. These two regimes are separated by a mid-permeability low-flow regime (10 m2) where the permeability is high enough to allow gas transport away from the dissociation front (limiting the build-up of excess pore pressure and the formation of hydraulic fractures), while at the same time being low enough so that only small amounts of CH4 reach the near-seafloor sediments on a centennial timescale. The development of the sediment column in terms of hydrate saturation, GHSZ, aqueous saturation and gas saturation for two model simulations with different permeabilities (Case A4) is shown in Fig. 4b–g. Seafloor CH4 release as a function of time for the three fluid flow regimes is shown in Fig. 5a, d and g. Note that we use the terms “CH4 escape” and “CH4 gas escape” interchangeably throughout the text, as the dissolved fraction of the seafloor CH4 escape is negligible (Figs. 5, 6c).
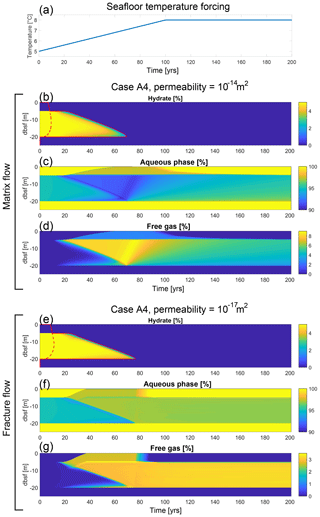
Figure 4(a) Model simulations are all forced by a linear seafloor temperature increase of 3 ∘C over the first 100 years. Modelled hydrate saturation (b, e), aqueous saturation (c, f) and gas saturation (d, g) as a function of time and depth b.s.f. for two simulations (Case A4) with permeability of 10−14 m2 (b–d) and 10−17 m2 (e–g), respectively. Also shown in panels (b) and (e) is the GHSZ, where the solid red line indicates the boundary for unstable conditions and the dashed red line indicates the boundary for stable conditions (area in between is at the melting point). The pressure development and the phase transition boundary at different times are shown in Fig. S3.
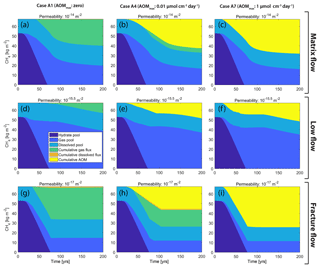
Figure 5CH4 mass budget over time showing the five components of Fig. 1 with the dissolved and gaseous fluxes separated. Displayed are three examples (high, mid- and low permeability; rows) for three different cases (Cases A1, A4 and A7; columns). Note that difference in cumulative CH4 gas escape (green area) between high and low permeability is significantly larger in Case A4 (b, h) compared to Case A1 (a, g).
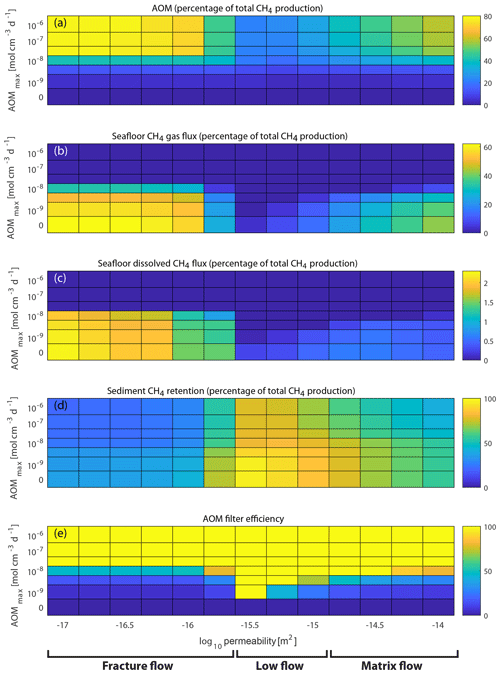
Figure 6Case A1–A7 simulation results after 100 years (each tile represents one model simulation). Panels (a)–(d) show percentages of the total CH4 production from hydrate dissociation after 100 years, which is identical in all cases and equal to 53 kg m−2 (the sum of panels a–d equals 100 %). (a) The total cumulative AOM increases with increased AOMmax rates but is also a function of the vertical CH4 flow rate within the sediments (highest values for the fractured flow regime, lowest values for the low-flow regime and intermediate values for the matrix flow regime). (b, c) The cumulative CH4 release (b, gaseous; c, dissolved) decreases with increased AOMmax and also reflects vertical CH4 flow rates within the sediments (as discussed above). (d) Sediment CH4 retention is weakly dependent on AOMmax (some of the CH4 that would reside within the SRZ in the zero AOM case would instead be consumed by AOM) but generally reflects the vertical CH4 flow rates. (e) The AOM filter efficiency is defined as the fraction of CH4 escape reduction compared to the corresponding zero AOM case (Case A1). For cases with AOMmax larger than 10−8 cm−3 d−1, the model predicts that the microbial filter is 100 % effective, regardless of permeability, meaning that no CH4 can escape from the seafloor. For lower AOMmax rates, the picture is more complex.
While permeability and fracture dynamics control the supply of CH4 to the SRZ, the fate of CH4 that reaches the SRZ is determined by the AOMmax rate. A high AOMmax rate leads to complete oxidation of the CH4 before it can escape from the seafloor, while a low AOMmax leads to a large fraction of the CH4 bypassing the microbial filter and escaping into the ocean. However, for intermediate AOMmax rates (around 10−8 cm−3 d−1; Case A4), the efficiency of the microbial filter becomes a function of permeability (or flow regime). For the low-permeability fracture flow regime, with large vertical transport of CH4, AOM is limited by the prescribed AOMmax rate; thus, an increase in CH4 supply to the SRZ does not result in increased AOM but larger CH4 escaping from the seafloor. For the low-flow regime, the opposite is true – all the supplied CH4 to the SRZ is oxidized and none escapes, meaning that AOM becomes a sole function of the CH4 supply. The matrix flow regime is somewhere in between these two extremes, and thus AOM and gas release are both strong functions of the CH4 supply into the SRZ from below.
3.1 Case A4 (base case)
The fate of CH4 produced from hydrate dissociation in Case A4 is visualized in Fig. 5b, e and h (where CH4 production equals the hydrate reduction, shown as the dark blue area) and in Fig. 7a, c and e. It should be noted that the total CH4 production is identical in all cases and equal to the amount of CH4 initially stored in the hydrate deposit.
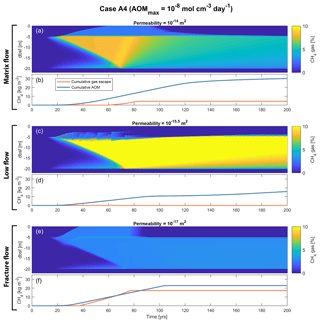
Figure 7Example of simulation outputs from Case A4, highlighting the different dynamics of the three gas flow regimes within the sediments. Shown are sediment CH4 gas saturation (percentage of pore space) with time and depth below the seafloor, and cumulative CH4 gas escape and cumulative AOM with time, for three different permeabilities, representing higher-permeability matrix flow (a, b), mid-permeability low flow (c, d) and lower-permeability fracture flow (e, f). Note that the hydrate deposit is initially situated between 5 and 20 m b.s.f. and that gas is forming at the upper and lower edges of the deposit, which is gradually thinning and is completely dissociated after around 75 years into the simulations.
Figure 7 illustrates the radically different transport capacities of sediments with different permeability. In low-permeability sediments (Fig. 7e), fractures start to appear soon after the onset of hydrate dissociation (around 20 years into the simulation), effectively transporting most of the CH4 gas away from the dissociation front and up towards the SRZ. The AOM capacity (as controlled by AOMmax) is smaller than the CH4 supply, resulting in gas being released from the seafloor between 40 and 75 years into the simulation. Once the hydrate deposit is completely dissociated, fractures can no longer be created and the seafloor gas escape is immediately shut down. The remaining CH4 within the SRZ is then consumed by AOM over the next 30 years (75 to 105 years into the simulation; Fig. 7f). The amount of CH4 still residing within the sediment after 100 (200) years is about 24 % (22 %) of the produced CH4 from hydrate dissociation (Fig. 6d). The transport of CH4 in low-permeability sediments is mainly through fractures, which gives rise to variability of seafloor gas release on different timescales (Fig. 8a–c). This highly non-linear response to a constant seafloor warming is related to the opening and closing of fractures within the sediments, which occurs on timescales down to the order of hours (Fig. 8d).
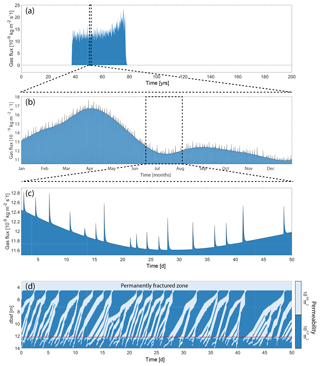
Figure 8Fracture flow in low-permeability sediments for the base case simulation (Case A4 with permeability of 10−17 m2). Seafloor gas flux for the whole simulation (a), over 1 year (b) and over 50 d (c). (d) Fracture propagation within the sediments over the same period as panel (c). The horizontal red line marks the upper boundary of the hydrate deposit at this particular time, and the permanently fractured zone is the upper part of the sediments where the presence of gas alone is enough to create fractures (see Stranne et al., 2017, for details).
The CH4 transport through high-permeability sediments is on average slower than in the low-permeability case, which is reflected by the higher CH4 gas concentrations developing below the SRZ and by the gentler slope of the gas front rising up towards the seafloor with time (compare Fig. 7a with Fig. 7e). After about 60 years into the simulation, the vertical CH4 transport finally overcomes the microbial filter and CH4 gas starts to escape from the seafloor (Fig. 7b). The seafloor gas release continues for about 25 years (which is significantly shorter than the low-permeability gas release that continues for a period of about 40 years; Fig. 7f). After about 85 years into the simulation, the CH4 supply to the SRZ is smaller than the AOM capacity (imposed by AOMmax), leading to a shutdown of seafloor CH4 gas release and complete oxidation of any CH4 that is transported into the SRZ. Due to the high permeability, gas continues to flow into the SRZ (although tapering off over time), where it is consumed by AOM. The amount of CH4 retained within the sediments after 100 years is around 55 % (Fig. 6d). Sediments continue to oxidize CH4, and after 200 years CH4 retention is only about 35 %.
The CH4 transport rate through mid-permeability sediments is significantly smaller than that through higher- and lower-permeability sediments, which is illustrated by the high CH4 gas concentrations building up below the SRZ (Fig. 7c). Much of the CH4 that ends up in the SRZ is mainly transported there through occasional fracturing. The CH4 transport through fractures is not fast and large enough for any gaseous or dissolved CH4 to escape the microbial filter, and the fraction of the produced CH4 residing within the sediments is about 81 % (70 %) after 100 (200) years, which is significantly higher than the other cases (Fig. 6d).
The simulations in our base case (Case A4) show that, under some circumstances, sediment permeability and the associated flow dynamics control not only the transport of CH4 from the dissociation front towards the seafloor (Stranne et al., 2017) but also the amount of CH4 that escapes AOM within the SRZ. In Case A4, the efficiency of the microbial filter increases from about 45 % in low-permeability fracture flow-dominated sediments to 100 % in mid-permeability sediments and then decreases towards 80 % in high-permeability sediments (Fig. 6e). In absolute terms, this corresponds to a total CH4 escape after 100 years of about 18 kg m−2 in sediments with a permeability of 10−17 m2 compared to a total CH4 escape of around 4 kg m−2 in sediments with a permeability of 10−14 m2 – more than a factor of 4 difference, although part of the difference is associated with fluid flow dynamics within the sediments (Stranne et al., 2017).
While AOM is important for understanding the potential impact of hydrate dissociation on climate across different timescales (Buffett and Archer, 2004), the strong AOM sink for CH4 in marine sediments has not been previously assessed with numerical multiphase hydrate models (Ruppel and Kessler, 2017). In this study, we have integrated a simplistic but novel and fully coupled AOM module to the T+H-GeoMech code (Stranne et al., 2017) in order to investigate how AOM in marine sediments modify seafloor CH4 release during dissociation of a marine hydrate deposit.
The results presented in Stranne et al. (2017) show that when naturally occurring marine hydrate deposits in low-permeability sediments (clay-dominated hemipelagic sediments; Fig. 3) are destabilized, transport of CH4 towards the seafloor is facilitated by the formation of hydraulic fractures. This results in faster flow and ultimately larger fluxes of CH4 compared to transport through higher-permeability sediments (silts and sands). Here, we show that, in addition, this type of fracture flow can circumvent the microbial filter more efficiently. The net effect can be substantial. In our base case (AOM mol cm−3 d−1), the cumulative gas release after 100 years of seafloor warming is around 18 kg m−2 in sediments with a permeability of 10−17 m2, zero in sediments with a permeability of 10−15 m2 and about 4 kg m−2 in sediments with a permeability of 10−14 m2 (Fig. 5b, e and h). This is in line with previous speculations (Archer et al., 2009; Buffett and Archer, 2004).
With an imposed upper limit of the AOM rate within the SRZ of around 10−8 cm−3 d−1, the model can reproduce the observed relation between AOM efficiency and vertical CH4 transport (Boetius and Wenzhöfer, 2013; Martens and Val Klump, 1980). For higher AOM capacities (AOM cm−3 d−1), AOM is sole function of the supply of CH4 from beneath, and no gas escapes from the sediments. For lower capacities (AOM cm−3 d−1), on the other hand, the microbial filter efficiency is only marginal.
The efficiency of the microbial filter at some deep-sea cold seeps has been found to be rather limited (down to ∼20 %, Boetius and Wenzhöfer, 2013). In order to get such low efficiency in our simulations, the maximum bulk AOM rate (AOMmax) has to be lower than 10−8 mol cm−3 d−1 (Fig. 6e). This is lower than what is often observed in these geological settings using experimental radiotracer-based methods (Niemann et al., 2006; Treude et al., 2003). There are at least two plausible explanations for this apparent discrepancy (in addition to differences in the definition of AOM efficiency): (1) high rates of AOM up to mol cm−3 d−1 are observed to be highly localized spanning often no more than a few decimetres in studied sediment cores (e.g. Dale et al., 2010), which means that the average bulk AOM rate integrated over the full SRZ depth might be significantly lower; (2) deep-sea cold seeps might be very different from those forming at the featheredge of hydrate stability under rapid seafloor warming. Present-day cold seep systems have often been active for longer periods of time, sometimes tens of thousands of years (Berndt et al., 2014; Wallmann et al., 2018), and CH4 is likely transported through high-permeability channels known as subsurface gas chimneys (Giambalvo et al., 2000; Saffer, 2015; Suess, 2010) or faults (Nakajima et al., 2014) through the GHSZ. Such channelled flow from the deep geosphere allows for significantly larger CH4 transport than that through dynamic hydraulic fracturing (as considered in this study) because high-permeability channels stay open regardless of the in situ pore pressure. From the relation between vertical transport of CH4 and AOM efficiency as found in observations and also presented in this study, a larger CH4 transport would then also lead to lower AOM efficiencies. During rapid anthropogenic warming-induced hydrate dissociation, however, such high-permeability channels might not exist at the featheredge of the gas hydrate stability zone. We speculate, therefore, that the resulting flow would not resemble present-day cold seeps where gas is transported through subsurface gas chimneys or faults but that it would be more similar to that simulated in the present study, with the gas being transported either through elastic and highly dynamic (opening and closing) fractures in low-permeability sediments or percolating through the porous media in higher-permeability sediments.
There are limitations to the modelling approach applied in this study, and the results should be seen as a first step towards understanding AOM dynamics in relation to climate change and hydrate dissociation. One important limitation is that the model code does not consider kinetics, i.e. the rate of biogeochemical reactions. This means that the true efficiency of the microbial filter might be lower than reported here. We model AOM as a linear function of the CH4 supply, with an upper AOM limit imposed by the AOMmax parameter. In reality, microbial communities are dynamic and adapt not only to the supply of CH4 from beneath but also to changes in salinity, temperature and sulfate fluxes (Michaelis et al., 2002; Nauhaus et al., 2007; Treude et al., 2003). Experimental studies show that, for instance, a temperature increase of only 2 ∘C can increase anaerobic organic matter degradation by 40 % (Roussel et al., 2015). In diffusive systems, the AOM process has been shown to operate at the thermodynamic limit for cell metabolism (Hoehler and Alperin, 1996), whereas advective systems apparently deliver CH4 in amounts that allow for abundant cell growth and the development of thick biofilms capable of very high AOM rates (up to 10−4 mol cm−3 d−1 (Boetius et al., 2000; Nauhaus et al., 2007; Treude et al., 2003). This implies that, while AOM is a highly complex process, the AOM rate within marine sediments is, to a first order, controlled by the CH4 supply which is consistent with our model assumptions (Fig. 1b). We do not know what a realistic value of the maximum bulk AOM capacity could be or what is controlling it, but we note that an AOMmax rate of 10−8 mol cm−3 d−1 reproduces the observed relation between AOM efficiency and CH4 transport, at least qualitatively. It is possible that with the inclusion of proper kinetics and additional controls on the AOM process, there would be no need to impose such limitation on the AOM capacity.
Because the largest proportion of the sediment column is anoxic, the most important CH4 sink in marine sediments globally is AOM (Knittel and Boetius, 2009). As a general rule, AOM dominates the CH4 consumption within the sediments, while aerobic oxidation of CH4 (AeOM) dominates the CH4 consumption within the water column (Reeburgh, 2007; Valentine, 2011). AeOM in the benthic layer can, however, also be an important CH4 sink. It has been shown that at some contemporary cold seeps, AeOM dominates over AOM (Boetius and Wenzhöfer, 2013). In this study, we focus on AOM, but as the AOM module does not discriminate between different types of oxidation, the modelled bulk CH4 oxidation within the SRZ can in a sense be regarded as including all methane oxidation in the presence of sulfate, which thereby extends methane oxidation up to the seafloor where in reality other electron acceptors such as oxygen may oxidize methane.
Another limitation of the present model is the assumption of a static SRZ depth. In reality, the SRZ depth is dynamic, with a tendency to increase with decreasing methane flux from below (Borowski et al., 1996; Sivan et al., 2007). As the capacity of the microbial filter to oxidize CH4 that passes through the SRZ depends on the SRZ depth (Fig. S1b), this tendency could decrease the filter efficiency during rapid dissociation of marine hydrates. Overall, the limitations of our modelling approach (including the lack of kinetics and of a dynamic SRZ depth) suggests that the AOM efficiency reported here can be regarded as an upper limit.
In general, the modelling results show that the total mass of CH4 consumed by AOM over time becomes a function of either (1) the supply of CH4 to the SRZ – when the AOM capacity (imposed by AOMmax) is so high that all the CH4 transported to the SRZ is consumed by AOM or (2) the imposed AOM capacity itself – when the capacity is so low that there is an oversupply of CH4 to the SRZ, which then also leads to CH4 escaping the seafloor. In our simulations, the first case is true when AOM mol cm−3 d−1 (efficiency of the microbial filter is 100 %), while the second case is true when AOM mol cm−3 d−1 (AOM is negligible and the CH4 escape is controlled by the sediment permeability). For values of AOMmax in between, on the order of 10−8 mol cm−3 d−1, the AOM efficiency is to a large extent controlled by fluid flow rates (or sediment permeability), which is in line with observations. For example, during low-permeability CH4 flow through fractures, the AOM efficiency (45 %) is about half that of high-permeability matrix flow (>80 %). The combination of larger CH4 transport and lower AOM efficiency in low-permeability sediments ( m2) results in a seafloor CH4 release that is more than a factor of 4 larger than in high-permeability sediments ( m2).
Although AOM in marine sediments is rarely considered when assessing future climate-warming-induced seafloor CH4 release, there is a wealth of articles suggesting that it represents an important component of the marine CH4 cycle. In this study, we can mimic the observed tendency of decreased AOM efficiencies with increased vertical CH4 transport by imposing a maximum AOM bulk rate within the SRZ of about 10−8 mol cm−3 d−1. We find that the AOM efficiency during fracture-dominated flow is less than 50 %, and this is likely an overestimation due to limitations in the AOM parameterization. Fracture flow is the predicted mode of methane transport under warming-induced dissociation of hydrates on upper continental slopes, and thus, in a scenario with rapidly warming seafloors, more (and possibly significantly more) than half of the CH4 can escape AOM within the sediments and reach the ocean/atmosphere. These initial results are admittedly poorly constrained and will hopefully be augmented in future studies where kinetics and additional controls on AOM can be implemented. However, because evidence of ongoing anthropogenic warming-induced hydrate dissociation is inconclusive (Ruppel and Kessler, 2017) and observational data are still scarce, we have to at least partly rely on numerical hydrate models for the time being.
All data supporting the figures and text of this paper are available upon request from the corresponding author. The model code can be purchased from Berkeley Lab Marketplace (http://marketplace.lbl.gov, last access: 12 September 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/se-10-1541-2019-supplement.
CS conceived the study, developed the model, performed the experiments, made the figures and wrote most of the paper. MO, MJ, VB and MK contributed to the text and to the interpretations of the results.
The authors declare that they have no conflict of interest.
This research has been supported by the Swedish Research
Council (VR) (grant nos. 2014-478 and 2018-04350).
The
article processing charges for this open-access
publication were covered by Stockholm University.
This paper was edited by Kei Ogata and reviewed by two anonymous referees.
Archer, D., Buffett, B., and Brovkin, V.: Ocean methane hydrates as a slow tipping point in the global carbon cycle, P. Natl. Acad. Sci. USA, 106, 20596–20601, https://doi.org/10.1073/pnas.0800885105, 2009.
Barnes, R. O. and Goldberg, E. D.: Methane production and consumption in anoxic marine sediments, Geology, 4, 297–300, https://doi.org/10.1130/0091-7613(1976)4<297:MPACIA>2.0.CO;2, 1976.
Berndt, C., Feseker, T., Treude, T., Krastel, S., Liebetrau, V., Niemann, H., Bertics, V. J., Dumke, I., Dünnbier, K., Ferré, B., Graves, C., Gross, F., Hissmann, K., Hühnerbach, V., Krause, S., Lieser, K., Schauer, J., and Steinle, L.: Temporal Constraints on Hydrate-Controlled Methane Seepage off Svalbard, Science, 343, 284–287, https://doi.org/10.1126/science.1246298, 2014.
Bhatnagar, G., Chatterjee, S., Chapman, W. G., Dugan, B., Dickens, G. R., and Hirasaki, G. J.: Analytical theory relating the depth of the sulfate-methane transition to gas hydrate distribution and saturation, Geochem. Geophy. Geosy., 12, Q03003, https://doi.org/10.1029/2010GC003397, 2011.
Biastoch, A., Treude, T., Rüpke, L. H., Riebesell, U., Roth, C., Burwicz, E. B., Park, W., Latif, M., Böning, C. W., Madec, G., and Wallmann, K.: Rising Arctic Ocean temperatures cause gas hydrate destabilization and ocean acidification, Geophys. Res. Lett., 38, L08602, https://doi.org/10.1029/2011GL047222, 2011.
Boetius, A. and Wenzhöfer, F.: Seafloor oxygen consumption fuelled by methane from cold seeps, Nat. Geosci., 6, 725, https://doi.org/10.1038/ngeo1926, 2013.
Boetius, A., Ravenschlag, K., Schubert, C. J., Rickert, D., Widdel, F., Gieseke, A., Amann, R., Jørgensen, B. B., Witte, U., and Pfannkuche, O.: A marine microbial consortium apparently mediating anaerobic oxidation of methane, Nature, 407, 623–626, https://doi.org/10.1038/35036572, 2000.
Borowski, W. S., Paull, C. K., and Ussler, W.: Marine pore-water sulfate profiles indicate in situ methane flux from underlying gas hydrate, Geology, 24, 655–658, https://doi.org/10.1130/0091-7613(1996)024<0655:MPWSPI>2.3.CO;2, 1996.
Boswell, R. and Collett, S. T.: Current perspectives on gas hydrate resources, Energ. Environ. Sci., 4, 1206–1215, https://doi.org/10.1039/C0EE00203H, 2011.
Buffett, B. and Archer, D.: Global inventory of methane clathrate: sensitivity to changes in the deep ocean, Earth Planet. Sc. Lett., 227, 185–199, https://doi.org/10.1016/j.epsl.2004.09.005, 2004.
Dale, A. W., Sommer, S., Haeckel, M., Wallmann, K., Linke, P., Wegener, G., and Pfannkuche, O.: Pathways and regulation of carbon, sulfur and energy transfer in marine sediments overlying methane gas hydrates on the Opouawe Bank (New Zealand), Geochim. Cosmochim. Ac., 74, 5763–5784, https://doi.org/10.1016/j.gca.2010.06.038, 2010.
Darnell, K. N. and Flemings, P. B.: Transient seafloor venting on continental slopes from warming-induced methane hydrate dissociation: TRANSIENT SEAFLOOR VENTING FROM HYDRATES, Geophys. Res. Lett., 42, 10765–10772, https://doi.org/10.1002/2015GL067012, 2015.
Dickens, G. R.: Modeling the Global Carbon Cycle with a Gas Hydrate Capacitor: Significance for the Latest Paleocene Thermal Maximum, in: Natural Gas Hydrates: Occurrence, Distribution, and Detection, edited by: Paull, C. K. and Dillon, W. P., 19–38, American Geophysical Union, https://doi.org/10.1029/GM124p0019, 2001.
Dickens, G. R., O'Neil, J. R., Rea, D. K., and Owen, R. M.: Dissociation of oceanic methane hydrate as a cause of the carbon isotope excursion at the end of the Paleocene, Palaeogeogr. Palaeocl., 10, 965–971, https://doi.org/10.1029/95PA02087, 1995.
Egger, M., Riedinger, N., Mogollón, J. M., and Jørgensen, B. B.: Global diffusive fluxes of methane in marine sediments, Nat. Geosci., 11, 421–425, https://doi.org/10.1038/s41561-018-0122-8, 2018.
Freeze, R. A. and Cherry, J. A.: Groundwater, 604 pp., Prentice-Hall, Englewood Cliffs, NJ, 1979.
Giambalvo, E. R., Fisher, A. T., Martin, J. T., Darty, L., and Lowell, R. P.: Origin of elevated sediment permeability in a hydrothermal seepage zone, eastern flank of the Juan de Fuca Ridge, and implications for transport of fluid and heat, J. Geophys. Res.-Solid, 105, 913–928, https://doi.org/10.1029/1999JB900360, 2000.
Hinrichs, K.-U. and Boetius, A.: The Anaerobic Oxidation of Methane: New Insights in Microbial Ecology and Biogeochemistry, in: Ocean Margin Systems, edited by: Wefer, P. D. G., Billett, D. D., Hebbeln, D. D., Jørgensen, P. D. B. B., Schlüter, P. D. M., and van Weering, D. T. C. E., 457–477, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-662-05127-6_28 2002.
Hoehler, T. M. and Alperin, M. J.: Anaerobic methane oxidation by a methanogen-sulfate reducer consortium: geochemical evidence and biochemical considerations, in: Microbial Growth on C1 Compounds: Proceedings of the 8th International Symposium on Microbial Growth on C1 Compounds, held in San Diego, USA, 27 August–1 September 1995, edited by: Lidstrom, M. E. and Tabita, F. R., 326–333, Springer Netherlands, Dordrecht, 1996.
Hunter, S. J., Goldobin, D. S., Haywood, A. M., Ridgwell, A., and Rees, J. G.: Sensitivity of the global submarine hydrate inventory to scenarios of future climate change, Earth Planet. Sc. Lett., 367, 105–115, https://doi.org/10.1016/j.epsl.2013.02.017, 2013.
Kennett, J. P., Cannariato, K. G., Hendy, I. L., and Behl, R. J.: Methane hydrates in quaternary climate change: the clathrate gun hypothesis, 54, 1–9, 2003.
Kirschke, S., Bousquet, P., Ciais, P., Saunois, M., Canadell, J. G., Dlugokencky, E. J., Bergamaschi, P., Bergmann, D., Blake, D. R., Bruhwiler, L., Cameron-Smith, P., Castaldi, S., Chevallier, F., Feng, L., Fraser, A., Heimann, M., Hodson, E. L., Houweling, S., Josse, B., Fraser, P. J., Krummel, P. B., Lamarque, J.-F., Langenfelds, R. L., Quéré, C. L., Naik, V., O'Doherty, S., Palmer, P. I., Pison, I., Plummer, D., Poulter, B., Prinn, R. G., Rigby, M., Ringeval, B., Santini, M., Schmidt, M., Shindell, D. T., Simpson, I. J., Spahni, R., Steele, L. P., Strode, S. A., Sudo, K., Szopa, S., Werf, G. R. van der, Voulgarakis, A., van Weele, M., Weiss, R. F., Williams, J. E., and Zeng, G.: Three decades of global methane sources and sinks, Nat. Geosci., 6, 813, https://doi.org/10.1038/ngeo1955, 2013.
Knittel, K. and Boetius, A.: Anaerobic Oxidation of Methane: Progress with an Unknown Process, Annu. Rev. Microbiol., 63, 311–334, https://doi.org/10.1146/annurev.micro.61.080706.093130, 2009.
Kretschmer, K., Biastoch, A., Rüpke, L., and Burwicz, E.: Modeling the fate of methane hydrates under global warming, Global Biogeochem. Cy., 29, 610–625, https://doi.org/10.1002/2014GB005011, 2015.
Luff, R. and Wallmann, K.: Fluid flow, methane fluxes, carbonate precipitation and biogeochemical turnover in gas hydrate-bearing sediments at Hydrate Ridge, Cascadia Margin: numerical modeling and mass balances, Geochim. Cosmochim. Ac., 67, 3403–3421, 2003.
Malinverno, A. and Pohlman, J. W.: Modeling sulfate reduction in methane hydrate-bearing continental margin sediments: Does a sulfate-methane transition require anaerobic oxidation of methane?, Geochem. Geophy. Geosy., 12, Q07006, https://doi.org/10.1029/2011GC003501, 2011.
Martens, C. S. and Berner, R. A.: Interstitial water chemistry of anoxic Long Island Sound sediments. 1. Dissolved gases1, Limnol. Oceanogr., 22, 10–25, https://doi.org/10.4319/lo.1977.22.1.0010, 1977.
Martens, C. S. and Val Klump, J.: Biogeochemical cycling in an organic-rich coastal marine basin – I. Methane sediment-water exchange processes, Geochim. Cosmochim. Ac., 44, 471–490, https://doi.org/10.1016/0016-7037(80)90045-9, 1980.
Mau, S., Valentine, D. L., Clark, J. F., Reed, J., Camilli, R., and Washburn, L.: Dissolved methane distributions and air-sea flux in the plume of a massive seep field, Coal Oil Point, California, Geophys. Res. Lett., 34, L22603, https://doi.org/10.1029/2007GL031344, 2007.
McGinnis, D. F., Greinert, J., Artemov, Y., Beaubien, S. E., and Wüest, A.: Fate of rising methane bubbles in stratified waters: How much methane reaches the atmosphere?, J. Geophys. Res., 111, C09007, https://doi.org/10.1029/2005JC003183, 2006.
Michaelis, W., Seifert, R., Nauhaus, K., Treude, T., Thiel, V., Blumenberg, M., Knittel, K., Gieseke, A., Peterknecht, K., Pape, T., Boetius, A., Amann, R., Jørgensen, B. B., Widdel, F., Peckmann, J., Pimenov, N. V., and Gulin, M. B.: Microbial Reefs in the Black Sea Fueled by Anaerobic Oxidation of Methane, Science, 297, 1013–1015, https://doi.org/10.1126/science.1072502, 2002.
Milkov, A. V.: Global estimates of hydrate-bound gas in marine sediments: how much is really out there?, Earth-Sci. Rev., 66, 183–197, https://doi.org/10.1016/j.earscirev.2003.11.002, 2004.
Miller, D. J., Ketzer, J. M., Viana, A. R., Kowsmann, R. O., Freire, A. F. M., Oreiro, S. G., Augustin, A. H., Lourega, R. V., Rodrigues, L. F., Heemann, R., Preissler, A. G., Machado, C. X., and Sbrissa, G. F.: Natural gas hydrates in the Rio Grande Cone (Brazil): A new province in the western South Atlantic, Mar. Petrol. Geol., 67, 187–196, https://doi.org/10.1016/j.marpetgeo.2015.05.012, 2015.
Moridis, G. J.: TOUGH+HYDRATE v1.2 User's Manual: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media, eScholarship, available at: http://escholarship.org/uc/item/3mk82656 (last access: 25 March 2015), 2014.
Nakajima, T., Kakuwa, Y., Yasudomi, Y., Itaki, T., Motoyama, I., Tomiyama, T., Machiyama, H., Katayama, H., Okitsu, O., Morita, S., Tanahashi, M., and Matsumoto, R.: Formation of pockmarks and submarine canyons associated with dissociation of gas hydrates on the Joetsu Knoll, eastern margin of the Sea of Japan, J. Asian Earth Sci., 90, 228–242, https://doi.org/10.1016/j.jseaes.2013.10.011, 2014.
Nauhaus, K., Albrecht, M., Elvert, M., Boetius, A., and Widdel, F.: In vitro cell growth of marine archaeal-bacterial consortia during anaerobic oxidation of methane with sulfate, Environ. Microbiol., 9, 187–196, https://doi.org/10.1111/j.1462-2920.2006.01127.x, 2007.
Neuzil, C. E.: How permeable are clays and shales?, Water Resour. Res., 30, 145–150, https://doi.org/10.1029/93WR02930, 1994.
Niemann, H., Lösekann, T., de Beer, D., Elvert, M., Nadalig, T., Knittel, K., Amann, R., Sauter, E. J., Schlüter, M., Klages, M., Foucher, J. P., and Boetius, A.: Novel microbial communities of the Haakon Mosby mud volcano and their role as a methane sink, Nature, 443, 854–858, https://doi.org/10.1038/nature05227, 2006.
Reagan, M. T. and Moridis, G. J.: Dynamic response of oceanic hydrate deposits to ocean temperature change, J. Geophys. Res., 113, C12023, https://doi.org/10.1029/2008JC004938, 2008.
Reagan, M. T., Moridis, G. J., Elliott, S. M., and Maltrud, M.: Contribution of oceanic gas hydrate dissociation to the formation of Arctic Ocean methane plumes, J. Geophys. Res., 116, C09014, https://doi.org/10.1029/2011JC007189, 2011.
Reeburgh, W. S.: Oceanic Methane Biogeochemistry, Chem. Rev., 107, 486–513, https://doi.org/10.1021/cr050362v, 2007.
Rodrigues, L. F., Ketzer, J. M., Lourega, R. V., Augustin, A. H., Sbrissa, G., Miller, D., Heemann, R., Viana, A., Freire, A. F. M., Morad, S., Rodrigues, L. F., Ketzer, J. M., Lourega, R. V., Augustin, A. H., Sbrissa, G., Miller, D., Heemann, R., Viana, A., Freire, A. F. M., and Morad, S.: The influence of methane fluxes on the sulfate/methane interface in sediments from the Rio Grande Cone Gas Hydrate Province, southern Brazil, Brazilian J. Geology, 47, 369–381, https://doi.org/10.1590/2317-4889201720170027, 2017.
Roussel, E. G., Cragg, B. A., Webster, G., Sass, H., Tang, X., Williams, A. S., Gorra, R., Weightman, A. J., and Parkes, R. J.: Complex coupled metabolic and prokaryotic community responses to increasing temperatures in anaerobic marine sediments: critical temperatures and substrate changes, FEMS Microbiol. Ecol., 91, fiv084, https://doi.org/10.1093/femsec/fiv084, 2015.
Ruppel, C. D.: Methane Hydrates and Contemporary Climate Change, Nature Education Knowledge, 3, 29, 2011.
Ruppel, C. D. and Kessler, J. D.: The interaction of climate change and methane hydrates, Rev. Geophys., 55, 2016RG000534, https://doi.org/10.1002/2016RG000534, 2017.
Saffer, D. M.: The permeability of active subduction plate boundary faults, Geofluids, 15, 193–215, https://doi.org/10.1111/gfl.12103, 2015.
Sivan, O., Schrag, D. P., and Murray, R. W.: Rates of methanogenesis and methanotrophy in deep-sea sediments, Geobiology, 5, 141–151, https://doi.org/10.1111/j.1472-4669.2007.00098.x, 2007.
Spinelli, G. A., Giambalvo, E. R., and Fisher, A. T.: Sediment permeability, distribution, and influence on fluxes in oceanic basement, Hydrogeology of the Oceanic Lithosphere, 1, 151–188, 2004.
Stocker, T. F., Qin, D., Plattner, G. K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, B., and Midgley, B. M.: IPCC, 2013: climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change, Cambridge Univ. Press, Cambridge, UK, 2013.
Stranne, C., O'Regan, M., Dickens, G. R., Crill, P., Miller, C., Preto, P., and Jakobsson, M.: Dynamic simulations of potential methane release from East Siberian continental slope sediments, Geochem. Geophy. Geosy., 17, 872–886, https://doi.org/10.1002/2015GC006119, 2016a.
Stranne, C., O'Regan, M., and Jakobsson, M.: Overestimating climate warming-induced methane gas escape from the seafloor by neglecting multiphase flow dynamics, Geophys. Res. Lett., 43, 2016GL070049, https://doi.org/10.1002/2016GL070049, 2016b.
Stranne, C., O'Regan, M., and Jakobsson, M.: Modeling fracture propagation and seafloor gas release during seafloor warming-induced hydrate dissociation, Geophys. Res. Lett., 44, 2017GL074349, https://doi.org/10.1002/2017GL074349, 2017.
Suess, E.: Marine cold seeps, in: Handbook of Hydrocarbon and Lipid Microbiology, edited by: Timmis, K. N., McGenity, T. J., Meer, J. R., and Lorenzo, V., Springer, Berlin Heidelberg, 187–203, 2010.
Thatcher, K. E., Westbrook, G. K., Sarkar, S., and Minshull, T. A.: Methane release from warming-induced hydrate dissociation in the West Svalbard continental margin: Timing, rates, and geological controls, J. Geophys. Res.-Solid, 118, 22–38, https://doi.org/10.1029/2012JB009605, 2013.
Treude, T., Boetius, A., Knittel, K., Wallmann, K., and Jørgensen, B. B.: Anaerobic oxidation of methane above gas hydrates at Hydrate Ridge, NE Pacific Ocean, Mar. Ecol.-Prog. Ser., 264, 1–14, 2003.
Valentine, D. L.: Emerging topics in marine methane biogeochemistry, Annu. Rev. Mar. Sci., 3, 147–171, 2011.
Wallmann, K., Pinero, E., Burwicz, E., Haeckel, M., Hensen, C., Dale, A., and Ruepke, L.: The Global Inventory of Methane Hydrate in Marine Sediments: A Theoretical Approach, Energies, 5, 2449–2498, https://doi.org/10.3390/en5072449, 2012.
Wallmann, K., Riedel, M., Hong, W. L., Patton, H., Hubbard, A., Pape, T., Hsu, C. W., Schmidt, C., Johnson, J. E., Torres, M. E., Andreassen, K., Berndt, C., and Bohrmann, G.: Gas hydrate dissociation off Svalbard induced by isostatic rebound rather than global warming, Nat. Commun., 9, 83, https://doi.org/10.1038/s41467-017-02550-9, 2018.